Introduction

Proper determination of unconfined compressive strength (UCS) and Young’s modulus (E) of rocks is of crucial importance in the design of geotechnical engineering structures such as dams and tunnels. The latter is a key parameter in deformation analysis and the former gives good estimation of the rock bearing capacity. In other words, inappropriate estimation of the aforementioned rock parameters, i.e. UCS and E, could be catastrophic as it can lead to underestimation of the ultimate bearing capacity as well as the load corresponding to an allowable settlement for a problem of interest. The unconfined compression test is a laboratory test normally used to determine elastic modulus and strength of the rock. The test is conducted using standard procedures such as those of the International Society for Rock Mechanics (ISRM). However, there are some impeding factors in direct determination of UCS and E in the laboratory. For instance, preparing the required rock core samples is often difficult, especially for rocks that are highly fractured and those that exhibit significant lamination and foliation (Singh et al. 2012; Monjezi et al. 2012). At preliminary design stage, direct determination of UCS and E can be too expensive and time consuming (Yilmaz and Sendir 2002; Gokceoglu and Zorlu 2004; Kahraman 2014). Nevertheless, alternative and indirect approaches of predicting the rock strength and modulus are available, such as traditional and multiple regression models and soft computing techniques.

Many attempts have been made in developing conventional (also called indirect) methods of UCS or E estimation. These alternative methods for predicting UCS and E, are often in forms of simple regression between UCS or E and simple index tests of rocks such as the Schmidt hammer (Singh et al. 1983; Yasar and Erdogan 2004; Nazir et al. 2013b; Karaman and Kesimal 2014), ultrasonic velocity, or V p (Kahraman 2001; Cobanglu and Celik 2008), Brazilian tensile strength (Gokceoglu and Zorlu 2004; Kahraman et al. 2012; Nazir et al. 2013a), point-load index (Sulukcu and Ulusay 2001; Basu and Aydin 2006; Tandon and Gupta 2014) and slake durability index (Moradian et al. 2010; Yagiz 2011) tests.

In addition, some researchers addressed the successful application of multiple regression analysis (MRA) in predicting rock strength and module of elasticity (Gokceoglu and Zorlu 2004; Yilmaz and Yuksek 2009). However, there are some reported cases where these correlations are found to be insufficient to provide highly reliable values of the UCS and E (Dehghan et al. 2010; Beiki et al. 2013). In general, the use of these equations is recommended only for specific rock types (Beiki et al. 2013). Furthermore, statistical prediction methods suffer from a disadvantage in respect to new available data: If different from the original data, the form of the obtained equations needs to be updated (O’Rourke 1989; Rezaei et al. 2012).

Recent studies have highlighted the application of soft computation techniques such as the artificial neural network (ANN) and the adaptive neuro-fuzzy inference system (ANFIS) in geotechnical engineering problems. This is attributed to the well-established fact that soft computation techniques are feasible, quick and promising tools for the solving of engineering problems, particularly when the contact natures between independent variables and dependent variables are unknown (Garret 1994; Yilmaz and Yuksek 2009; Atici 2011; Rezaei et al. 2012; Asadi et al. 2013; Yesiloglu-Gultekin et al. 2013; Marto et al. 2014; Momeni et al. 2014a). Also from an economic point of view, implementation of these techniques is advantageous as direct or indirect determination of UCS or E in the laboratory is relatively costly.

This article presents an ANFIS model for prediction of UCS and E for Main Range granite in Malaysia. For comparative purposes, the prediction performance of the ANFIS model is compared with the ANN model and MRA.

Previous investigations

Numerous researchers have been working on the prediction of UCS using soft computing methods. Meulenkamp and Grima (1999) predicted UCS using a back propagation (BP) neural network. They used 194 different types of rock samples including sandstone, limestone, dolomite and others. In their study, Equotip hardness reading, density, porosity, rock type and grain size were considered as inputs for UCS prediction. According to their conclusion, the ANN is able to generalise much better than statistical models. Sonmez et al. (2004) used a fuzzy inference system (FIS) and regression techniques for prediction of UCS and the elasticity modulus based on petrographic data from 164 samples of Ankara agglomerate. Based on their findings, fuzzy logic can provide high performance prediction capacity to determine UCS; however, their findings suggest that, for predicting E, the regression equations are more suitable. In another study, Gokceoglu and Zorlu (2004) implemented fuzzy model and regression techniques to predict the UCS and E of problematic rocks. The point load index, block punch index, ultrasonic velocity and tensile strength of 82 samples were considered as inputs in their predictive models. They concluded that the fuzzy model provides the most reliable predictions when compared with the simple and multiple regression models. Dehghan et al. (2010) used feed forward neural network and regression analyses to predict UCS and E. In their study, some rock index parameters such as point load index, p-wave (ultrasonic) velocity, porosity and Schmidt hammer rebound number were considered as inputs to predict UCS and E for 30 travertine rock data sets. They concluded that the ANN method outperforms regression analyses. Mishra and Basu (2013) applied MRA and FIS models for the estimation of UCS in three different rocks and compared the results of these methods with simple regression. They found that both the MRA and FIS models exhibited better predictive performances compared to the MRA model. Cevik et al. (2011) reported the feasibility of ANN in predicting the UCS of sedimentary rock samples. In their model, the origin of rocks, two/four-cycle slake durability indices and clay contents of 56 rock sample sets were set as inputs for prediction of UCS. In another study, Yesiloglu-Gultekin et al. (2013) suggested the superiority of the ANFIS model compared to the ANN model and MRA in predicting the UCS of granite samples in Turkey. They used 75 rock sample sets in the development of their predictive models. Overall, the inputs of their proposed predictive models of UCS included the rock tensile strength, block punch index, point load index and p-wave velocity. Finally, they recommended that the best ANFIS prediction performance is expected when tensile strength and p-wave velocity values are used as model inputs.

Singh et al. (2001) proposed a number of correlations between strength parameters (UCS, axial point load strength and tensile strength) and some index parameters (mineral composition, grain size, aspect ratio, form factor, area weighting and orientation of foliation planes of weakness) of schistose rock. They used the petrographic properties to predict strength parameters using a BP neural network. Their findings show that the ANN prediction model is more accurate than the proposed correlations. A fuzzy triangular chart was utilised by Gokceoglu (2002) to predict UCS using the petrographic composition. To this end, he produced 15 membership functions for 15 data sets and showed that the FIS model is able to predict UCS values. The relationships between petrographic properties and strength of sandstone were investigated by Zorlu et al. (2008). They predicted the UCS of sandstone using MRA and ANN techniques. Comparison of the MRA and ANN models showed that the ANN model can predict UCS with a higher prediction capacity. Yagiz et al. (2012) developed ANN and non-linear regression techniques to predict UCS and E of 54 carbonate rocks. They concluded that the ANN model indicates better results in predicting UCS and E compared to the nonlinear regression technique. Some recent studies on the prediction of UCS and E using soft computation techniques are tabulated in Table 1.

Table 1 Recent works on UCS and E prediction using soft computation techniques
Full size table

Case study and test procedure

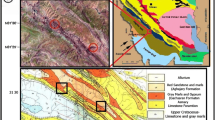
The rock samples for the current study were collected from a water transfer tunnel project. The tunnel was designed to transfer raw water from the Semantan River in Pahang State to Selangor State. This is to meet the additional water demands for Selangor state and Kuala Lumpur. The tunnel was excavated to cross the Main Range, which lies between Pahang and Selangor States. This mountain range forms the backbone of Peninsular Malaysia with elevation ranging from 100 to 1,400 m. The main rock type is granite, locally termed as Main Range granite, with typical intact strength between 150 and 200 MPa.

The tunnel is 44.6 km in length with a diameter of 5.2 m and a longitudinal gradient of 1/1,900. It is designed to operate under free flow conditions with a maximum discharge of 27.6 m3/s of raw water. For tunnel excavation, a tunnel boring machine (TBM) was primarily used for about 35 km of the length throughout the main tunnel route, while the remaining tunnel portions, which include access work adits, were excavated using the conventional drill and blast method. Three TBM sections and four conventional drill and blast sections were planned for excavation of this tunnel. Figure 1 shows the geological map around the tunnel site and also displays the location of boreholes.

Fig. 1
figure 1

Geological map around the tunnel site

Full size image

Selected borehole core samples were transported to a laboratory to verify the relevant engineering and physical properties of the granite. The end surfaces of the trimmed cores were carefully lapped to obtain the required finishing and shape. A total of 45 granite rock samples were prepared for the laboratory tests. Samples were checked for any existing cracks and other small-scale discontinuities that may lead to an undesirable variation in properties and premature failures. The rock physical properties tested include dry density (ρ dry) and V p. Additionally, uniaxial compression tests were performed to determine the UCS and E of the granite. Knowing the axial strain as well as the stress measured through relevant transducers, the Young’s moduli of rock samples were measured. All test and sample preparation procedures were conducted in accordance with ISRM (2007) standards.

Petrographic analyses of the granite samples were also carried out using a polarizing petrological microscope. For this purpose, thin sections of the samples were prepared to identify the percentage of different minerals; some photomicrograph results are shown in Fig. 2. The samples exhibit holocrystalline and non-porphyritic mineral texture, and in general mainly consist of interlocking coarse-grained crystals of quartz (Qtz), alkali feldspar (Kpr), plagioclase (Plg) and biotite (Bi). Such texture is typical of plutonic igneous rock. The test results of all 45 data sets are tabulated in Table 2. Note that micas are represented by three minerals: muscovite, biotite and sericite.

Fig. 2
figure 2

Thin-section photomicrograph of sample BH23_67.45–67.60

Full size image
Table 2 Mineralogical and other properties of the granite samples
Full size table

Data analyses

In order to analyze the laboratory test results, different statistical and simulation techniques were employed in this study. The following sections describe implementation of the aforementioned methods to predict the UCS and E of granite samples. Subsequently, the values of UCS and E obtained from laboratory tests were compared with the corresponding predicted values of UCS and E.

Simple regression

In this study, simple regression analysis was initially undertaken in order to establish the predictive equations between independent or input variables (ρ dry, V p, Qtz, Kpr, Mica, Chl and Plg) and dependent or output variables (UCS and E). The relationships between UCS and E with input parameters were analyzed and some linear, exponential, logarithmic and power equations were proposed, as tabulated in Tables 3 and 4, respectively. The standard error and coefficient of determination (R 2) were used to evaluate the reliability of the obtained equations.

Table 3 Results of simple regression analyses for UCS prediction
Full size table
Table 4 Results of simple regression analyses for E prediction
Full size table

Multiple regression

Multiple regression analysis can be used to obtain the best-fit equation when there is more than one input parameter. The form of the MRA formula is y = b 1 x 1 + b 2 x 2 + b n x n  + c, where {b 1 , b 2,…, b n } are the coefficients of regression, and c is a constant value of y when all input parameters are zero. The main theoretical weakness of all regression techniques is that they can only ascertain relationships, but never determine the exact underlying causal mechanism (Yilmaz and Yuksek 2009).

Many MRAs were carried out to predict UCS and E using different input parameters, as tabulated in Table 5. According to this table, the values of standard error as well as R 2 for both UCS and E are very close when different input parameters were used. It is worth mentioning that when these analyses were performed, the models with R 2 of more than 0.50 were taken into consideration. Nevertheless, the model number 8 in Table 5 was selected due to the fact that a predictive model with a lower number of inputs is of advantage as this can reduce the model complexity.

Table 5 Results of multiple regression analyses for UCS and E
Full size table

In total, it was found that, among all parameters presented in Table 2, ρ dry, V p, Qtz and Plg were better correlated with UCS and E. Therefore, these parameters were selected for the subsequent analyses. It should be mentioned that the statistical software package SPSS 18.0 was used for analysis of the MRA models. The obtained correlations using MRA analyses are presented in Eqs. 1 and 2:

$$ {\text{UCS }} = { 69}. 50 5\rho_{\text{dry}} + \, 0.0 2 5 { }V_{\text{p}} \, {-} \, 0. 4 7 9 {\text{ Qtz }}{-}{ 1}. 4 3 9 {\text{ Plg }}{-} 1 5 8. 7 9 6, $$
(1)
$$ E = {-} 3 4. 5 1 9\rho_{\text{dry}} + \, 0.0 1 9 { }V_{\text{p}} \, + { 1}. 2 1 7 {\text{ Qtz }}{-} \, 0. 6 1 2 {\text{ Plg }} + { 22}. 6 8 1. $$
(2)

Model summaries of MRA for prediction of UCS and E are illustrated in Table 6.

Table 6 Model summaries of the MRA model for prediction of UCS and E
Full size table

Artificial neural network

The ANN is an artificial intelligence technique that has been demonstrated to solve many composite engineering problems successfully. It is an information-processing system in which system information is processed by several interconnected simple elements that are known as nodes or neurons, positioned in the network layers. The best ANN has been identified as the multilayer perceptron (MLP) model, which is composed of three different layers: input, output and hidden layers (Dreyfus 2005; Jahed Armaghani et al. 2013). The nodes are linked from one layer to the next, but this connection is not within the same layer. After processing the information, the connection links transmit the information between the neurons. A weight is assigned to each link, which is multiplied into the transmitted signal. The total weighted input signal of each node is usually transmitted via a nonlinear activation function.

Performance of an ANN is directly dependent on the architecture of layers and the number of neurons, which is the pattern of the connections between the neurons (Hajihassani et al. 2014). The BP algorithm is considered the most popular and effective learning algorithm for multilayered networks (Tawadrous and Katsabanis 2007). In BP, the connection weights are adjusted to reduce the errors of output (Jahed Armaghani et al. 2014). Initially, the network runs with connection weights that are selected randomly. In a feed-forward (FF) BP algorithm, the signals flow from the input layer to the output layer. Finally, a desired output is computed by the network, and then the difference between the actual outputs and the desired one is calculated. Network error is defined as the difference between the real values and those predicted by the system. The network error in each step is propagated back, and the individual weights are updated accordingly. This process is iterated until the error converges to a level that is known by some cost functions, such as root mean squared error (RMSE) (Simpson 1990; Kosko 1994). The scenario for the pth pattern in an FF neural network is presented in the following steps:

  1. 1.

    The ith node in the input layer holds a value of x pi for the pth pattern.

  2. 2.

    Net input to the jth neuron in the hidden layer for pattern p is:

    $$ {\text{net}}_{pj} = \mathop \sum \limits_{i}^{N} W_{ij} O_{pi} , $$
    (3)

    where W ij is the weight from node i to j. The output from each unit j is the threshold function, f j , which acts on the weighted sum. In this MLP model, f j is the sigmoid function as follows:

    $$ f({\text{net}}) = 1/( 1 { } + {\text{e}}^{{{-}K_{\text{net}} }} );(0\,<\,f({\text{net}}) < 1), $$
    (4)

    where k is a positive constant that controls the function spread.

  3. 3.

    Output of the jth node is defined as:

    $$ O_{pj} = f_{j} ({\text{net}}_{pj} ). $$
    (5)
  4. 4.

    Net input to the kth neuron of the output layer is:

    $$ {\text{net}}_{k} = \mathop \sum \limits_{j}^{N} W_{kj} X_{pj} , $$
    (6)

    where W kj is the weight value between the kth output layer node and the ith hidden layer.

  5. 5.

    Output of the kth node of the output layer is:

    $$ O_{pk} = f_{k} ({\text{net}}_{k} ). $$
    (7)
  6. 6.

    E p is the function error for a pattern, p:

    $$ E_{p} = \frac{1}{2}\mathop \sum \limits_{k}^{N} (t_{pk} - O_{pk} )^{2} , $$
    (8)

    where O pk and t pk are the real and target outputs for pattern p on neuron k, respectively.

As mentioned previously, ρ dry, V p, Qtz and Plg were selected as model inputs to predict UCS and E. In this study, all 45 data sets were randomly distributed into two different data set categories, namely training and testing. In this manner, 80 % of the data sets were assigned for training purposes while the further 20 % was used for testing of the network performance. In order to obtain superior performance of the ANN model, it is necessary to determine the optimal network architecture. According to Hornik et al. (1989), a network with one hidden layer can approximate any continuous function. Therefore, one hidden layer was utilized in this study. Establishing the number of neurons in the hidden layer is the most critical task in the ANN architecture (Sonmez et al. 2006; Sonmez and Gokceoglu 2008). Different equations have been proposed to determine the number of neurons in hidden layers by several researchers, as tabulated in Table 7. According to this table, for the problem at hand, the number of neurons that might be used in the hidden layer varies between 2 and 9. In order to determine the optimum number of neurons in the hidden layer, using the trial-error method, several networks with one hidden layer were trained and tested as tabulated in Tables 8 and 9 for the prediction of UCS and E, respectively. As shown in these tables, each model was iterated five times. These tables show the results in terms of R 2 and RMSE for the training and testing data sets. According to the presented results, model number 3 with four hidden nodes (second iteration) and model number 2 with three hidden nodes (4th iteration) indicate higher prediction performances for UCS and E, respectively, compared to other models. Therefore, these models, i.e., models 2 and 3, were chosen as the best ANN models for prediction of UCS and E, respectively. It should be mentioned that model performance was evaluated based on both training and testing data sets. It is also worth mentioning that in construction of ANN models, the learning rate and momentum coefficient were set to 0.05 and 0.9, respectively.

Table 7 The proposed number of neurons for the hidden layer
Full size table
Table 8 Performances of trained ANN models in predicting UCS
Full size table
Table 9 Performances of trained ANN models in predicting E
Full size table

Adaptive neuro-fuzzy inference system

The ANFIS was developed by Jang (1993). This system is capable of approximating any actual continuous function at any accuracy level (Jang et al. 1997). Therefore, a functional mapping can be modeled by ANFIS that approximates the prediction process of the internal system parameter. ANFIS is an artificial intelligence method that integrates the FIS concept into the ANN and has been extensively utilized in the field of geotechnical engineering (Grima et al. 2000; Gokceoglu et al. 2004; Iphar et al. 2008; Yilmaz and Yuksek 2009; Sezer et al. 2014). Mapping relations between the input and output parameters through hybrid learning for the determination of the membership function distribution can be simulated by ANFIS. A typical ANFIS network architecture with two input variables (x, y) and one output (f) is shown in Fig. 3. It is comprised of five layers in the inference system, and each layer includes several nodes, which are defined by the node function.

Fig. 3
figure 3

a First order Sugeno fuzzy reasoning; b equivalent ANFIS architecture (following Jang et al. 1997)

Full size image

For previous layers, the output neuron is identified as the input signal in the present layer. After manipulation by the node function in the present layer, the output will serve as input signal for the next layer. To describe the procedure of ANFIS in brief, x and y as inputs and f as output are considered in the FIS models. Therefore, two fuzzy "if-then" rules can be constructed as follows (Takagi and Sugeno 1985):

$$ {\text{If}}\,x\,{\text{is}}\,A1\,{\text{and}}\,y\,{\text{is}}\,B1\,{\text{then}}\;f1 = p1x + q1y + r1,\;({\text{rule }}1) $$
$$ {\text{If}}\,x\,{\text{is}}\,A2\,{\text{and}}\,y\,{\text{is}}\,B2\,{\text{then}}\;f2 = p2x + q2y + r2, \, ({\text{rule }}2) $$

where A 1, A 2, B 1 and B 2 are the membership functions for inputs x and y; p 1, q 1, r 1, p 2, q 2 and r 2 are the parameters of the output function. In the following, the five-layer ANFIS including two fuzzy rules, x and y (inputs), and one output (f) is presented (Jang 1993; Jang et al. 1997):

Layer 1 All nodes i in this layer are adaptive nodes:

$$ O_{ 1,i} = \mu A_{i} (x), $$
(9)
$$ O_{ 1,i} = \mu B_{i} (y), $$
(10)

for i = 1, 2 where x and y are considered as input neurons, and A and B are the linguistic labels. Also, µA i (x) and µB i (y) are the membership functions.

Layer 2 The nodes are labeled Π and identified by a circle. The output neuron is created by all the incoming signals:

$$ O_{ 2,i} = \omega_{i} = \mu A_{i} (x)\,\mu B_{i} (y){\text{ with }}i = { 1},{ 2}. $$
(11)

The output neuron ω i presents the firing strength of a rule.

Layer 3 Every node in this layer is a fixed node to be marked by a circle and labeled as N. The output is computed by the ratio of the ith rule’s firing strength over the sum of all rules’ firing strength:

$$ O_{3,i} = \varpi_{i} = \omega_{i} /(\omega_{1} + \omega_{2} ){\text{ with }}i = \, 1, \, 2. $$
(12)

Layer 4 In this layer, every node is an adaptive node with the node function as follows:

$$ O_{4,i} = \varpi_{i} f_{i} = \varpi_{i} (p_{i} x + q_{i} y + r_{i} ), $$
(13)

where parameters p i , q i and r i are named the consequent parameters. A normalized firing strength is named ϖ i .

Layer 5 In this layer (final step), the output amount is created by the sum of all incoming signals:

$$ O_{5,i} = \sum_{i} \varpi_{i} f_{i} = \sum_{i} \varpi_{i} f_{i} /\sum_{i} \varpi_{i} ;i = \, 1, \, 2. $$
(14)

BP gradient descent is the basic learning rule of the ANFIS, which computes error signals recursively from the output layer backward to the input nodes. Based on the architecture in Fig. 3b, the output (f) can be stated as a linear combination of the consequent parameters. To learn the fuzzy model employing differentiable functions, the ANFIS utilizes a hybrid-learning rule as it is easy to use. The classical BP technique is used by the ANFIS to learn the parameters of membership functions. Also, the conventional least-squares predictor is applied by the ANFIS to learn the parameter of the first-order polynomial of the Takagi-Sugeno-Kang fuzzy model (Jang et al. 1997).

In the procedure of the ANFIS, there are two different passes of hybrid learning (forward and backward). In the forward pass, functional signals go forward until the fourth layer, and the consequent parameters are investigated by the least-squares estimate. Similar to the ANN procedure, the system errors are propagated back and the premise parameters are updated using the gradient descent in the backward pass. The final output can be defined as follows:

$$ f = \frac{{\omega_{1} }}{{\omega_{1} + \omega_{2} }}f_{1} + \frac{{\omega_{1} }}{{\omega_{1} + \omega_{2} }}f_{2} = \varpi_{1} (p_{1} x + q_{1} y + r_{1} ) + \varpi_{2} (p_{2} x + q_{2} y + r_{2} ) = (\varpi_{1} x)p_{1} + (\varpi_{1} y)q_{1} + (\varpi_{1} )r_{1} + (\varpi_{2} x)p_{2} + (\varpi_{2} y)q_{2} + (\varpi_{2} )r_{2} , $$
(15)

in which p 1, q 1, r 1, p 2, q 2 and r 2 are consequent parameters. The advantage of using the ANFIS model is that the consequent parameters and optimal premise parameters can be efficiently obtained in the learning process.

In this study, a hybrid intelligent system (ANFIS) for predicting UCS and E of granite was also applied. Similar to the ANN analyses part, all data sets were distributed randomly to training (80 %) and testing (20 %) data sets. In fact the idea behind using the testing data set is to verify the generalization capability of the proposed neural network model. The use of the random sampling procedure has been reported in several studies (Alvarez and Babuska 1999; Singh et al. 2001; Rabbani et al. 2012; Tonnizam Mohamad et al. 2014). In order to determine the number of fuzzy rules, using a trial-error method, many models of the fuzzy rule combinations (e.g., 2 and 3) were employed for the UCS and E data sets separately. Eventually, it was found that input parameters with three fuzzy rules outperform the other ANFIS models for both UCS and E prediction. For the ANFIS modeling part, to select the optimum number of fuzzy rules, a parametric study was conducted. It was found that a number of 81 fuzzy rules (3 × 3 × 3 × 3) shows the best performance in predicting UCS and E. However, Table 10 shows parameter types and their values used in the ANFIS model. In the next step of the modeling, ANFIS models were constructed to predict UCS and E. Prediction performance of these two outputs are presented in Table 11. As shown in these tables, each model was repeated five times using different training and testing data sets. Based on the tabulated results in this table, considering the results of both the training and testing data sets, model number 3 for UCS prediction and model number 4 for E prediction indicate higher prediction performances among all five models. Therefore, model number 3 and model number 4 were selected for prediction of UCS and E respectively. In this study, all ANFIS models were trained by utilizing 100 epochs. The assigned membership functions with categories of low, medium and high for the best models of UCS and E are shown in Figs. 4, 5, 6 and 7. It is worth mentioning that these membership functions were assigned after the ANFIS training stage. Moreover, a linear type of membership function was used for the output (UCS and E). In order to estimate the membership functions parameters, a hybrid optimization method was utilized. It should be noted that all ANN and ANFIS models used to predict UCS and E were trained with the help of MATLAB version 7.14.0.739. Additionally, SPSS 18.0 was utilized for RMSE and statistical calculations.

Table 10 Different parameters used in ANFIS model
Full size table
Table 11 Performances of the five ANFIS models in predicting UCS and E
Full size table
Fig. 4
figure 4

Assigned membership functions for the ρ dry input parameter

Full size image
Fig. 5
figure 5

Assigned membership functions for the V p input parameter

Full size image
Fig. 6
figure 6

Assigned membership functions for the Qtz input parameter

Full size image
Fig. 7
figure 7

Assigned membership functions for the Plg input parameter

Full size image

Results and discussion

In this study an attempt has been made to show the capability of the MRA, ANN and ANFIS models to predict the UCS and E of granite. The models of ANFIS, ANN and MRA, for the prediction of UCS and E, were constructed using four inputs (ρ dry, V p, Qtz and Plg) and two outputs. The graph of predicted UCS and E using the MRA technique against the measured UCS and E for all 45 samples is displayed in Fig. 8. As indicated in this figure, the relatively low R 2 values, equal to 0.545 and 0.667, reveal the low reliability of the MRA technique for prediction of UCS and E ,respectively. Figures 9 and 10 show the predicted UCS and E by employing an ANN model plotted against the measured UCS and E values for the training and testing data sets, respectively. The R 2 values of 0.912 and 0.906 for the training and testing of UCS prediction and also 0.927 and 0.918 for training and testing of the E prediction show that the ANN approach is able to predict UCS and E with relatively suitable accuracy. Furthermore, in the prediction of UCS and E using the ANFIS model, R 2 values of 0.985 and 0.994 for the training and testing of UCS and 0.987 and 0.995 for the training and testing of E suggest the superiority of this model in predicting the UCS and E of granite (see Figs. 11, 12).

Fig. 8
figure 8

R 2 of measured and predicted values of UCS and E using the MRA model

Full size image
Fig. 9
figure 9

R 2 values of the measured and predicted UCS for training and testing data sets using the ANN model

Full size image
Fig. 10
figure 10

R 2 values of the measured and predicted E for the training and testing data sets using the ANN model

Full size image
Fig. 11
figure 11

R 2 values of the measured and predicted UCS for the training and testing data sets using the ANFIS model

Full size image
Fig. 12
figure 12

R 2 values of the measured and predicted E for the training and testing data sets using the ANFIS model

Full size image

In this study, the RMSE and amount of value account for (VAF) were computed to control the capacity performance of the predictive models developed, as applied by Alvarez and Babuska (1999) and Gokceoglu (2002):

$$ {\text{RMSE }} = \sqrt {\frac{1}{N}\mathop \sum \limits_{i = 1}^{N} (y - y^{'} )^{2} } , $$
(16)
$$ {\text{VAF}} = \, \left[ { 1{-}\frac{{{\text{var}} (y - y^{'} )}}{{{\text{var}} (y)}}} \right] \times 100, $$
(17)

where y and y′ are the obtained and estimated values, respectively, and N is the total number of data. The model is excellent if the RMSE is zero and VAF is 100. Performance indices obtained by predictive models for all 45 data sets are shown in Table 12. As tabulated in this table, the ANFIS predictive model can provide higher performance in the prediction of UCS and E in comparison to other predictive models. In order to demonstrate a better comparison, the RMSE and VAF values for predictive models are displayed in Fig. 13. According to this figure, the RMSE and VAF values reveal that the performance capacity of the ANFIS predictive model is higher than that of both the MRA and ANN predictive models.

Table 12 Performance indices of the predictive models for all 45 data sets
Full size table
Fig. 13
figure 13

Comparison of the RMSE and VAF values for MRA, ANN and ANFIS predictive models

Full size image

The results demonstrate that all aforementioned models are applicable when predicting the UCS and E of granite. However, these approaches should be used according to the situation. The ANFIS predictive model may be used when a high degree of accuracy is required. Moreover, the MRA predictive model can be used in conditions where a simple estimation of UCS and E is desired.

Conclusion

A total of 45 granite rock samples were collected during site investigation of the Pahang-Selangor raw water transfer tunnel to predict their UCS and E values. Subsequently, MRA, ANN and ANFIS predictive models were applied to predict UCS and E using four inputs: ρ dry, ultrasonic velocity, Qtz content and Plg. Prediction results showed that the ANFIS predictive model can predict UCS and E much better than the ANN and MRA predictive models. The R 2 values (for all data sets) equal to 0.985 and 0.990 for UCS and E, respectively, express the high reliability of the ANFIS predictive model, while these values were 0.911 and 0.919 for the ANN model and 0.545 and 0.667 for the MRA model. Nevertheless, these predictive models can be applied to predict UCS and E depending on the situation. In terms of performance, it was also shown that using ANFIS constitutes a feasible approach to minimizing uncertainties when designing rock engineering projects. The ANFIS displays several benefits as it combines the advantages of ANN and FIS techniques to demonstrate a high prediction capacity in complex, nonlinear and multivariable engineering problems.