1 Introduction

With an aim to build more rational and safer structures, it is very important to study the mechanical behavior and failure mechanism of rocks. As deformational characteristics of anisotropic rock changes with orientation of stress state, it will be more difficult to predict behavior of such rock mass and structures on such rock materials. Study of deformational behavior of rock mass has been in several stages with various researchers trying to delineate engineering properties of rocks with the help of empirical models. Deformational behavior of isotropic rocks at elevated pressure has been studied by various researchers [1–3]. Deformational behavior of anisotropic rocks has been described by five elastic constants by Chenevert and Gatli [4]. In situ test to study the deformational behavior of rock is in most cases expensive and time-consuming. On the other hand, laboratory tests require good quality core samples which are not possible to get in many cases when the rock is fractured, fissured, thinly bedded or weak. Various empirical models have been suggested by Bieniawski, Barton et al., Serafim and Pereira, Nicholson and Bieniawski, Hoek and Brown, Palmstrom and Singh, Barton and Singh et al. [5–12] for estimation purpose of deformational modulus of rock. Several equivalent material models [13–15] have also been proposed for the study of deformation of rock mass. Similarly, different index parameters, petrographic and physical parameters have also been studied for the purpose of correlating the same with mechanical properties of rocks. The determination of such index and petrographical properties in the laboratory requires smaller samples.

Barton’s [6, 11] mainly uses Q-values for the estimation of deformational modulus, whereas, Bieniawski [5], Serafim and Pereira [7], and Nicholson and Bieniawski [8] uses RMR for the same. Hoek and Brown [9] have used GSI for the estimation of deformational characteristics of rockmass. RMi values have been considered for the prediction of deformational modulus by Palmstorm and Singh [10]. Kayabasi et al. [12] have proposed a model based on modulus ratio of intact rock, rock quality designation, and weathering degree against another model proposed by the same based on the elasticity modulus instead of modulus ratio. Empirical models lack due to the fact that these models are unable to account for the effect of a large number of variables in varying conditions and mostly get biased due to the data availability and rock mass heterogeneity. The generalization principle of inconspicuous phenomena by way of statistics had not been very accurate in all cases [16]. Restrictive and incorrect assumptions in relation to unavailable data tend to make empirical models more questionable [17].

In view of such considerations, a fundamentally different approach has been used in this study for the prediction of deformational modulus and texture coefficient. Intelligent systems have been lately in use in various geotechnical studies. Fuzzy set theory has been used earlier for prediction of strength and deformational modulus from rock mass properties and test data [18]. The simple use of fuzzy set theory introduces a degree of biasness in relation to the setting up of deterministic rules based on the user’s interpretation of available data. However, the use of artificial neural networks (ANN) scores over such methods due to its computational superiority and generalization principles. In the present investigation, connectionist models have been built using two different algorithms and the generalization efficiency checked by varying different parameters of the network.

Connectionist modeling, commonly known as ANN, is a broad scale non-linear dynamic system which has the ability of acquiring, representing and computing a ‘non 1:1 mapping’ from one multivariate space to another, given a set of data representing the mapping [19]. A function for which every element of the range of the function does not correspond to exactly one element of the domain is called non 1:1(non one to one mapping) function. The mapping is learnt through the network by a training procedure in a supervised or an unsupervised manner during which the network is exposed to a set of chosen input data along with their target data. The primary ability of the model lies in its ability to process information by its dynamic state response to external inputs. Most statistical models constrain the data to be modeled along a particular geometry. This, may, actually be highly unfavorable to model non-linear relations. However, ANN has been found to efficiently model nonlinearity by a parallel processing approach. Added to this is the advantage of memorization of experiential knowledge, self-organization, self-adaptation, and self-learning. The model functions by the optimization of connection weights existing between parallelly processed units known as neurons, which are the fundamental processing unit of the network. A paradigm used in this study was ‘backpropagation’ learning algorithm optimized by resilient backpropagation and one step secant (OSS) algorithm. The training process consisted of adjusting the synaptic weights in order to reach a desired design objective. The synaptic weights are hold by the interconnections between the neurons, which actually determines the nature and strength of the interconnection. The neurons can be suitably arranged in layers. The system can effectively give prediction values after training which closely resembles output values by the use of stored knowledge.

2 Site specifications and rock mass properties

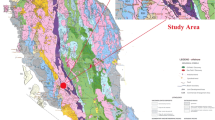
For the present study, four types of rocks have been studied. The rocks were taken from a tectonically active and complex sequence of rocks from a large underground excavation in the Himalayan region. The rocks exposed in the area are metamorphosed rocks like gneisses, augen gneiss, quartzite schist, biotite schist, quartz mica schist, sericite schist, chlorite schist, amphibolite, and pegmatite. These rocks belong to Wangatu Jeori Gneissic Complex of Precambrian age. They are surrounded by Jutogh series of carbonaceous slates, limestone, quartzites and schist, separated from the main central thrust (MCT) which is one of the shear zones in this region. Granite bodies are also exposed at some places. These granites and augen gneiss are predominate most of the Eastern region towards Nathpa and schist in Western region towards Jhakri village of Rampur, HP, India. The rocks are openly folded and suffered more than two generations of foldings and are intersected by a number of steeply dipping faults and shear zones. Major fold axes trend in a NW–SE to E–W direction. Superimposed on these broad folds are numerous minor folds with varying trends. The metamorphism of these rocks is essentially of regional type over an extensive area where intensive folding under pressure has converted the texture into the schistose or gneissose. The foliation trend of these metamorphosed rocks generally varies from N 70° W–S 70° E to N 70° E–S 70° having an average dip of the order of 35° in the Northerly direction. These rocks are surrounded by the Jutogh group, Salkhala group, and Rampur group of formations and separated from them by thrusted or faulted contacts. The rock formations are exposed to essentially regional metamorphism as the rocks indicate low-grade metamorphism over an extensive area. The schistose are intruded with quartz veins of varying thickness. Small scale crenulation folds affect the quartz mica schist, which are mainly the expression of changes in mineralogy and fabric that required accommodating the distortion of the rock body. This makes the rock mass stronger than it would have been with planar foliation, because sliding is not likely to occur along the folded foliation plane, unless the fold axis is parallel to the potential sliding direction.

As shown in Fig. 1, (1) Lesser Himalayan (LH) Rampur Group—(A), (B) Rampur Volcanics, (C) Carbonaceous phyllite. (2) Kulu—Bajura Nappe—augen mylonite. (3) Higher Himalayan Crystallines (HHC)—(A) Jeori Group, staurolite/garnetiferous schist, banded biotite gneiss, augen gneiss (a), amphibolite (b), quartz mica schist (c), and Wangtu granite gneiss/granite (d), (B) Karcham Group—garnet/staurolite/kyanite/sillimanite schist/gneiss, calc-silicate, augen gneiss and migmatite (a) and Akpa leucogranite (b). (4) Tethyan sedimentary zone (TSZ). Abbreviations: KT, Kulu Thrust; MCT, Main Central Thrust; VT, Vaikrita Thrust; R, Rampur; K, Karchham [34].

Fig. 1
figure 1

Geological map of the area

Full size image

Regional mapping of the area has brought to light new concrete set up and formations. Jeori Gneissic complex is a part of one authochthonous–parautochthonous complex below Rampur group. The former is thrust over the latter. Structurally, the rocks of Wangatu Jeori Gneissic complex form the northern limb of a syncline and their strike direction varies from N 60° W – S 60° E to N 80° W – S 80° E with Southerly dip of 25° to 35°.

3 Artificial neural networks

Artificial Neural Networks have been variously defined by various researchers. According to Haykin [20], it is a massively parallel distributed processor made up of simple processing units, which has a natural propensity for storing experiential knowledge and making it available for use. In its functioning, it resembles brain in two ways: the knowledge is acquired by the model by a learning process and the connections between the neurons carry the stored knowledge as optimized weights. Thus, ANN, variously known as connectionist models or cognitive systems, can be defined as a network of many simple processing units, each possibly having a small amount of localized dynamic memory. The units are related by connection channels, which usually carry numeric data, encoded by any of various means. Much of its computational efficiency is due to its parallel processing units, due to which it remains in a dynamic state response. Any neural network is characterized by its neuron pattern, net topology and the training or learning algorithms that define their purposes [21]. The development process of a neural network can broadly be classified into three steps: defining the network architecture, training the network, and testing the network [22]. The first step is with defining the number of layers, the number of neurons.

Individual processing units are arranged in layers in a multi layered neural system. A typical three layered feed forward backpropagation network has been shown in Fig. 2. The theory relating to ANN can more elaborately be found in Rumelhart and McClelland [23], as well as in Hertz [24], Yegnanarayana [25], and Haykin [20]. There is a single input layer and output layer which gets the feed and gives the output, respectively. In between them lies the hidden layer(s) containing neurons (parallel processing units). With enough and adequate number of hidden units, the network aptly recognizes and stores the pattern inherent in the dataset and hence, with recollection of the locally stored memory, the network produces suitable output features for arbitrary input features.

Fig. 2
figure 2

Model of a Three Layered Feed Forward Backpropagation Network

Full size image

For jth neuron in a layer, let there be ‘n’ number of inputs (x 1 , x 2 , x 3,…, x n ). W ij is the weight between the ith input and the jth neuron. Let the input at activation node be Net j which is mathematically equivalent to:

$$ {\text{Net}}_{j} = \sum\limits_{i = 1}^{n} {W_{ij} X_{i} } $$
(1)

The output of the activation node can be typically represented by\( O_{j} = f\left( {{\text{Net}}_{j} } \right) \), where the output depends typically on the range of the non-linear functions used at the activation node. A transfer function processes the input data that comes to the corresponding neuron. Biases are included at the transfer functions so as to differentiate between different processing units. The biases are referred to as pseudo-temperatures of neurons. A typical training procedure consists of forward pass of the input values to calculate the output, the subsequent calculation of error and the backward pass of the error derivative so as to optimize the weight and bias or threshold vector. In the forward pass, the network is presented with a set of input data along with its desired output values. During the initial forward pass, the network functions with a randomly initialized weight and bias vector. At the output layer, the error is obtained as:

$$ e_{k} = t_{k} - O_{k} $$
(2)

where, t k and O k are the desired output and actual output, respectively.

The error performance function (ERF) used in this case is like:

$$ \begin{gathered} E = 0.5\left[ {\frac{1}{n}\sum\limits_{k = 1}^{n} {e_{k}^{2} } + {\frac{1}{\omega + b}}\left( {\sum {W^{2} + \sum {B^{2} } } } \right)} \right] \hfill \\ \hfill \\ \end{gathered} $$
(3)

where, 0.5 is the performance ratio, ω is the dimension of the weight matrix and b is the dimension of the bias matrix. The summation for W and B are for all the values in the weight and bias matrices. E is the weighted sum of mean squared errors and mean squared weights and biases, the weightage being equal. The main aim of the learning process is to minimize the error function following a gradient descent manner and optimizing the weight and bias matrices in the process, which is actually the memory of the network.

According to the Resilient Backpropagation algorithm (Rprop) [26], the update of the weight and bias matrix is varied according to the sign of the derivative of the ERF. For the first iteration, the weight change value is equal to a given value. For further iterations, the derivative of ERF is calculated and is matched with that of the older value. If the sign changes, then the update value is decreased by a specific value. For no change in sign of derivative of ERF, the update value is increased by a specific value, which is initialized to the network. If there is no change in the value of the ERF derivative the update value is kept same [27]. The update value is then checked with the maximum update value and the network moves to the next iteration.

For the OSS algorithm [28], a secant approximation is done to reduce the storage problem relating to the Quasi-Newton method. The Hessian matrix is taken as identity matrix instead of storing the Hessian matrix, which would have actually scored storage problems. For the sake of simplicity, the weight and bias matrix is set as a single vector. The computation of parameter η, which determines the learning rate, is done by a line search algorithm, which is actually an iterative process to search the best estimation of η. The line search is nothing but an iterative process in which estimates of η are given. With variation in value of η for constant value of update, i.e., for a particular update, the argument of ERF traces a line in the ω + β dimensional plane. The line search is continued till a better approximation is available. The update to weights for a particular iteration at step (n + 1) is given as:

$$ \Updelta W\left( {n + 1} \right) = \eta \left( {sW} \right) $$
(4)

where, η is the parameter which minimizes the ERF along the search direction.

The first search direction is along the negative of the gradient of the ERF. The subsequent search directions are computed by sW(n + 1).

sW(n + 1) is given as :

$$ sW\left( {n + 1} \right) = - gW\left( {n + 1} \right) + A\left( {n + 1} \right) \times \Updelta W\left( n \right) + B\left( {n + 1} \right) \times \Updelta gW\left( n \right) $$
(5)

where,

$$ \begin{gathered} A\left( {n + 1} \right) = - \left[ {\left( {1 + {\frac{{\Updelta gW\left( n \right)^{\text{T}} \times \Updelta gW\left( n \right)}}{{\Updelta W\left( n \right)^{\text{T}} \times \Updelta gW\left( n \right)}}}} \right) \times B\left( {n + 1} \right)} \right] + {\frac{{\Updelta gW\left( n \right)^{\text{T}} \times gW\left( {n + 1} \right)}}{{\Updelta W\left( n \right)^{\text{T}} \times \Updelta gW\left( n \right)}}} \hfill \\ B\left( {n + 1} \right) = {\frac{{\Updelta W\left( n \right)^{\text{T}} \times gW\left( {n + 1} \right)}}{{\Updelta W\left( n \right)^{\text{T}} \times \Updelta gW\left( n \right)}}}, \hfill \\ \end{gathered} $$
(6)

where, gW(n + 1) is the gradient for step n + 1, ΔW(n) is the weight update for step n, ΔgW(n)T is the transpose matrix of change in gradient at step n + 1. With all these updated values, the network runs for the next iteration. The training stops when the performance goal is reached or epochs are completed.

4 Parametric study

For the study of deformational modulus, simple rock properties like uniaxial compressive strength, tensile strength, and axial point load index strength, and physical properties of rocks like void ratio and porosity were taken. A simple correlation test of void ratio and porosity with texture coefficient, however, shows no notable correlation. However, the combined effect of all these variables on deformational modulus and texture coefficient is notable. Though not in a typical linear geometry, the variables may really be separable at some non-linear degree. The scatter between the various parameters has been given in the scatter diagrams in Figs. 3 and 4. Basic rock properties are always more effective while drawing more realistic conclusion about another rock properties. Hence, for the training of the network to get deformational modulus, these basic properties had been selected instead of any other calculated variable. The geotechnical analysis of the samples of cylindrical shape (Nx size) was done in the laboratory as per ISRM standards [29]. The samples were prepared from the representative block specimens brought from the field by core drilling in them at desired orientation of the foliation planes (Fig. 5). For each data, five tests were carried out and the mean taken. For the petrographic study, a high-resolution semi-automatic image analysis system was used having VIDS III interface card. An optional macro-stand is also available in addition to microscope for imaging from positives/negatives, instead of images of actual samples. A detailed description of the variables and their tests follows this section.

Fig. 3
figure 3

Scatter diagram of Deformation Modulus versus Uniaxial Compressive and Tensile Strength

Full size image
Fig. 4
figure 4

Scatter diagram of Deformational Modulus versus Axial Point Load Index

Full size image
Fig. 5
figure 5

Core sample photos

Full size image

4.1 Uniaxial compressive strength

Uniaxial Compressive Strength (UCS) was determined by direct compression test for the present study. Nx sized rock specimen were compressed by placing them between the plates of MTS Servo Controlled Stiff Testing Machine (Fig. 6). Uniform loading of 1 × 103 T/s was applied till failure appeared on the rock surface. By an automatic arrangement, the post failure behavior is also recorded.

Fig. 6
figure 6

MTS Servo Controlled Stiff Testing machine

Full size image

4.2 Tensile strength

Tensile strength was also determined in the laboratory by Brazilian test. Rock specimen of size ratio (length:diameter) equal to 1:2 were kept in Brazilian case and compressional forces applied along diameter. The strain at which the rock fails under tensional forces is termed as tensile strength. Like UCS, this can also found out indirectly from point load index tests.

The test was carried out as per ISRM (1978) standards. The tensile strength can be calculated by the following formula:

$$ \sigma_{\text{t}} = {\text{ 2F}}/\pi .{\text{d}}.{\text{t}} $$

where, σt is uniaxial tensile strength (MPa), F load (Pa), d diameter of the disc (mm), and t thickness of the disc (mm).

4.3 Axial point load strength

Easiest among all these strength tests, this is determined by keeping the sample between two standard conical platens and is uniformly loaded. In this technique, the L/D ratio can be taken 1–1.5. Samples of irregular shapes can also be taken with H/W ratio approximately equal to 1–1.5. For a rock sample failing at a load of P and with distance between platens as D, the point load index strength equals to P/D 2.

4.4 Void ratio and porosity

These two physical properties were included as a benchmarking variable mainly. Due to their representative values, they brought in a rock classifier effect when fed into the network. However, they appeared to have no significant correlation with the texture coefficient.

4.5 Texture coefficient and deformational modulus

Texture coefficient (TC) was determined using petrographic studies. It is generally calculated from area weighting, aspect ratio and factor analysis. Factor analysis is a statistical method used to describe variability among observed variables in terms of a potentially lower number of unobserved variables called factors. In other words, it is possible, e.g., that variations in three or four observed variables mainly reflect the variations in a single unobserved variable, or in a reduced number of unobserved variables. Factor analysis searches for such joint variations in response to unobserved latent variables. The area weighting is based upon grain packing density within the reference boundary. Determination of TC has already been related to strength properties as proposed by Howarth and Rowlands [30]. The area weighting is distinctively determined in schistose rocks. Aspect ratio was determined by analysis of thin film section taken from the rock core samples. It is generally defined as the ratio of the grain’s length to breadth. Length and breadth are defined as maximum and minimum Feret’s diameter. Form factor was also determined to ultimately analyze the values and get the TC. TC is given as:

$$ {\text{TC }} = {\text{ AW }}\left[ {\left( {N_{0} / \, N_{0} + \, N_{ 1} \times \, 1/{\text{FF}}_{0} } \right) \, + \, \left( {N_{0} / \, N_{0} + \, N_{ 1} \times {\text{ AR}}_{ 1} \times {\text{ AF}}_{ 1} } \right)} \right] $$
(7)

All texture coefficient values were obtained for the core samples at different orientation angles.

Deformational modulus tests consists of in situ tests like, dilatometer test, plate jacking, etc. which are time consuming as well as expensive. Indirectly, they can be determined by estimating them at 50% of peak strength for all orientations of rocks from the stress–strain curves. Load deformation curves can be obtained from MTS loading under uniaxial compression mode. The deformational modulus values can thus be obtained from such curves.

5 Network specifications

Pattern mapping has been one of the major problem when the data shows non linear behavior and hence can be best matched by parallel processing units having the highest levels of non-linear calculation accuracy. The performance of the network lies wholly on the efficiency of the mapping criteria, which again depends on the information provided as input–output pairs. Once the input values are fed to the network and the feed forward passes goes underway, efficiency lies greatly on the design of the network. There are no simple ways to determine in advance the minimal number of hidden nodes needed to obtain a desired performance index [31]. The effect of underfitting and overfitting of the network remains an important consideration other than just specifying number of layers, neurons and functions to be used. With too many epochs, a network can easily get overfitted, in which case it remembers more insignificant information. Too many neurons can also lead to overfitting. Studies [32] have given that continuing to run the network to a high epoch or aiming at global minima is only helpful when there is many more cases in the training set than there are degrees of freedom in the network.

For the present study, two different networks trained by two algorithms have been tested. Both these methods have suitable advantages over conventional networks working simply on a gradient descent rule. The OSS is a partial compromise between standard Conjugate Gradient algorithm and Quasi-Newton algorithm. The OSS has the advantage of converging faster than the conjugate gradient algorithms and does away with the storage problem faced in Quasi-Newton algorithm. The motivation of use of such methods is to circumvent the difficulty caused by nonpositive definite Hessian matrices [33]. In case of multi layer perceptrons (MLPs), the used sigmoid function literally “squashes” the input values by compressing the whole lot of data into a small range. Hence, for very high input values in relation to majority of values, the sigmoidal functions have a tendency to give very little slope values. Thus, the effect comes on to the network in a negative way by not updating the weight and bias matrix even when they are far from their optimal values. Rprop does away with this negative effect by directing the weight upload not by the value of the derivative of the performance function but by its change in sign. Thus, a prerequisite for the use of Rprop remains that all the net input function, weight function and the transfer function must remain derivable in the range of work. The weight change occurs according to a predefined upload value and its subsequent increment or decrement.

A total of 176 rock data sets were taken for the analysis and the statistical analysis was done to calculate the variations (Table 1). The dataset was randomly divided into two sets: ‘training dataset’ and ‘testing dataset’. The testing dataset consisted of 15 datasets. The network was run for different number of iterations and different number of neurons for both the algorithm and the results of the performance noted.

Table 1 Descriptive statistics of variables involved
Full size table

For both the networks, a transfer function configuration consisting of tangential sigmoid function for the input and hidden layer and a purely linear function for the output layer was used. The tangential sigmoidal function has this unique property of mapping any neuron output from the range of (−α, +α) to the range of (−1, +1). The last layer of the network has been characterized by the linear function, which does not limit the network output to a small range unlike other sigmoidal functions.

6 Network performance

The network was designed with five neurons in the input layer representing the five input variables. The output layer consisted of two nodes representing the two outputs. The network was typically trained to give the best results. With the basic structure of the network designed and executed, the effect of change of neuron number and epochs on the performance was noted. The results of the Rprop and OSS network are discussed in the following section.

6.1 Resilient backpropagation network

The network was found to give best results at 700 epochs with 16 neurons in the hidden layer. For a general check of the performance of the network, the performance function was changed to mean absolute error (MAE). The variation of the epoch number to 800 showed increase in the performance function, MAE, to 0.022. The reason can be traced to the fact that the network gets overfitted for 800 epochs. For 700 epochs, the value was 0.020. The accuracy of prediction of deformational modulus and texture coefficient for 700 epochs was noted to be 97.32 and 98.34%, respectively. The performance of the network was checked by decreasing the hidden neuron number to 15. For 800 epochs, the mean absolute percentage error was found to be 2.93 and 1.73% for deformational modulus and texture coefficient, respectively. With 700 epochs, the MAE increased to 0.026 and the mean absolute percentage error was 3.33 and 1.75%, respectively for deformation modulus and texture coefficient. Increasing or decreasing the epoch number produced underfitting and overfitting, the result being seen as increase in the performance function value. For 17 hidden neurons, the performance function remained same for 700 and 800 epochs. However, the individual mean absolute percentage errors showed a variance. With 700 epochs, the mean absolute percentage error was 2.75 and 1.72% for deformation modulus and texture coefficient, respectively (Table 2; Fig. 7). For 800 epochs, the values were 2.76 and 1.50%, respectively.

Table 2 Comparison of experimental versus predicted values for Rprop network. (at 700 epochs and with 16 hidden neurons)
Full size table
Fig. 7
figure 7

Line diagram of predicted versus experimental. a Deformational Modulus. b Texture coefficient for Rprop network

Full size image

6.2 One step secant network

The network with secant algorithm was found to give better results at lower epoch values. This can be traced to the fact that the algorithm makes a better approximation of the Hessian matrix and functions a little faster. With 16 hidden neurons, the network gives the best results. For 150 epochs, the MAE gives a value of 0.021, which increases either way when the epoch number is increased or decreased. The values of mean absolute percentage error are 2.78 and 1.62% for 150 epochs. The MAE increased to 0.022 when the epoch number was varied to 100 or 200. Signs of overfitting and underfitting of the network are clear from the performance function value. With 15 hidden neurons, the performance function shows a slide in value with increase in epoch number. The greatest slide was observed when the epoch was varied from 150 to 200. However, after 250 epochs the network gets shows signs of overfitting. The prediction accuracy was found to be 97.1 and 98.33% for deformational modulus and texture coefficient at 200 epochs. The network was, however, under-trained with 13 hidden neurons. The mean absolute percentage error was 3.74 and 2.06% for deformational modulus and texture coefficient (Table 3).

Table 3 Comparison of experimental versus predicted values for OSS network. (at 150 epochs and with 15 hidden neurons)
Full size table

A comparative analysis of the use of the two algorithms for prediction of deformational modulus and texture coefficient shows that Rprop network is more efficient in pattern mapping of the computed variables (Fig. 8). However, it takes longer time in terms of epoch number to get optimum result as compared to secant algorithm. In any case, Rprop is faster than traditional neural network algorithms using simple gradient descent algorithms. It is also more efficient in terms of prediction as it descends along the gradient plane even for small values of slopes when the network has not really reached its optimum value.

Fig. 8
figure 8

Line diagram of predicted versus experimental. a Deformational Modulus. b Texture coefficient for OSS network

Full size image

7 Statistical modeling

A comparison of the efficiency of non-linear non 1:1 mapping of neural networks with statistical models have been done in the following section. Conventional statistical analysis in the form of multivariate regression analysis is done for the efficacy check of the connectionist model. The results are incorporated in this section.

7.1 Multivariate analysis

Multivariate analysis has been performed on the experimental data sets. The input variables taken were same as that of the neural model. UCS, tensile strength, axial point load strength, void ratio, and porosity were taken as independent variables. The dependent variables considered were deformation modulus and texture coefficient. The comparative analysis of the actual and predicted values has been given in Table 4 and Fig. 9. The ultimate prediction equations obtained are as follows (Eqs. 8, 9):

$$ {\text{Deformational}}\;{\text{Modulus}}\;(E_{t} ) = 0.0 6 4 5 + \left( {0.00 6\times {\text{UCS}}} \right) - \left( {0.0 5 9\times \sigma_{t} } \right) + \left( {0. 1 5 3\times t_{\text{lp}} } \right) + \left( { 1 7 8. 7 3 5\times {\text{V}}.{\text{R}}.} \right) - \left( { 2. 2 4 7\times P} \right) $$
(8)
Table 4 Comparison of experimental versus predicted values for multivariate analysis
Full size table
Fig. 9
figure 9

Line diagram of predicted versus experimental. a Deformational Modulus. b Texture Coefficient for multivariate analysis

Full size image
$$ {\text{Texture}}\;{\text{coefficient}}\;({\text{TC}}) = 0.0 5 9 + \left( {0.00 1\times {\text{UCS}}} \right) - \left( {0.0 1 3\times \sigma_{t} } \right) + \left( {0.0 6 6\times t_{\text{lp}} } \right) - \left( { 2 3 5. 4 2 2\times {\text{V}}.{\text{R}}.} \right) + \left( { 2. 6 3 1\times P} \right) $$
(9)

The mean absolute percentage error for deformational modulus and texture coefficient is 8.14 and 14.48%, respectively (Table 4).

8 Efficiency check of intelligent prediction

As a part of checking the efficiency of the neural models over the statistical analysis, a simple t test has been performed. A hypothesis test is a clear and conclusive efficiency check apart from the simple values of MAE and mean absolute percentage error. A null hypothesis is made to check the mean of the error samples which have been believed to have different variance as they belong to two different populations. A statistical analysis assumes that errors are normally distributed with different variance and mean.

For two samples with μ1 and μ2 as sample mean, and variances as σ 21 and σ 22 , the value of t-statistic is obtained as:

$$ t{\text{-statistic}} = {\frac{{\mu_{1} - \mu_{2} - \Updelta_{0} }}{{\sqrt {\left( {{\frac{{\sigma_{1}^{2} }}{n}} - {\frac{{\sigma_{2}^{2} }}{n}}} \right)} }}} $$
(10)

A hypothesis check of equality of two error means is done against both one sided test and two sided test. From the values obtained, the null hypothesis can be rejected at 5% level of significance. The degree of freedom for the test was found to be 19. The check was performed for the 15 error values obtained in both the test.

9 Discussions

The MAPE values for the network prediction and the statistical modeling have been outlined in table. For the network, the MAPE values for the optimized network have been presented. A study of the root mean square error (RMSE) for the Rprop network, OSS network and statistical modeling has also been performed. The RMSE values for the Rprop network with 16 hidden neurons and optimized at 700 epochs are 3.72 and 2.12 for deformational modulus and texture coefficient, respectively. For OSS network optimized at 150 epochs with 15 hidden layer neurons, the RMSE values for deformational modulus and texture coefficient are 4.21 and 1.89, respectively. A comparison with studies made before to predict deformational modulus gives that the neural network approach gives significantly lower values of RMSE. The OSS network, in particular, gives highly satisfying results in this regard. However, care must be taken of this fact that this approach uses fundamentally different inputs rather than those used in various previous works [5–15]. The RMSE values as has been found out by Kayabasi et al. [12] in their work for different formulae for deformational modulus are 15.07 for Bieniawski formula [5], 5.83 for Serafim and Pereira [7] formula, 6.31 for Hoek and Brown [9] formula, 4.96 for Kayabasi et al. [18] and 4.74 and 4.49 for Kayabasi et al. [12]. The RMSE values found in this case are significantly less than these findings. Moreover, most of the prediction formulae had their applicability limitation due to the variables in use in those cases. The Bieniawski formulae [5] was limited in use for only rocks having RMR > 50, whereas Serefim and Pereira formula [7] was for rocks with RMR ≤ 50. Again, for the Hoek and Brown formulae [9] to be applicable the UCS of the rock in investigation had to be ≤100 MPa. However, for the present approach, no such limitation holds and values of simply determinable variables for rocks have been used as inputs or independent variables.

10 Conclusions

Connectionist modeling or use of artificial neural network to predict the deformational modulus and texture coefficient have given results much more impressive than traditional statistical analysis can do. The efficiency check by performance functions like MAE and mean absolute percentage error and that with the t-statistic at a level of significance of 5% shows clearly that connectionist modeling can by far be a better way of predicting deformational modulus and texture coefficient from simple intrinsic properties of rock which are obtainable easily and also less time-taking tests. Among the intelligent algorithms existing, the use of resilient backpropagation and OSS can obviously give better results. The use of resilient backpropagation with a higher number of epochs gives the best results. Determining texture coefficient from petrographic studies also requires time. The prediction of the same from other seemingly uncorrelated variables is notable. As far as pattern matching is concerned, connectionist modeling scores over all other methods. The network has also been able to do a far better generalization than other models. The system does not take any of the predefined variables used generally to get deformational modulus.

The method can easily be used with effectiveness in all situations to get deformational modulus and texture coefficient from far simpler tests which has vital importance for any design and planning to have a better safety and stability. Expensive and tedious tests can easily be avoided by use of such modeling. Other algorithms can also be used to get results of the same order. Faster and better predicting values can be given by more generalized algorithms which would obviously help in reducing the number of inputs and decreasing the work needed.