Dynamic opposite learning enhanced artificial ecosystem optimizer for IIR system identification

Abstract

The contrive principle of the adaptive infinite impulse response (IIR) filter is to find the filter parameters based on the error function, thus obtaining the best model of the unbeknown plant. Since the error function has a multimodal error surface, it is challenging to get the ideal identification result by traditional methods. In this work, a modified artificial ecosystem optimizer based on the novel dynamic opposite learning (DOL) strategy and a well-designed nonlinear adaptive weight coefficient, called the DAEO, is proposed to minimize the error function. The DOL adopted a random model to dynamically generate the asymmetric opposite solutions of the current population for generation jumping and population formation. To obtain more chances to find the optimal parametric solution, the DAEO is formed from two phases: The first phase produces the initial population by adopting DOL strategy, and the second phase is that DOL is employed as an extra phase to renew the AEO population in each iteration. The asymmetric search area of DOL holistically enhances the exploitation ability of DAEO, and the dynamically changing feature increases the diversity of the swarm, improving the exploration capability of the algorithm. Meanwhile, introducing the well-designed nonlinear adaptive weight coefficient makes search agents explore search space adaptively and poises exploration and exploitation phases. The classical set of benchmark problems is employed to test the performance of DAEO. The experimental results indicate that DAEO ranked first in terms of mean and variance values compared with other algorithms, except f₁₃. Furthermore, the DAEO algorithm is also applied to the IIR system identification problem. Simulation results on five benchmarked IIR systems show DAEO outperforms the comparison approach in improving the accuracy of recognition results and can obtain the minimum values of 0 and 1.69E-05 for mean square error (MSE) in the same-order and reduced-order system, respectively, which proves that DAEO is effective and valuable.

1 Introduction

Adaptive infinite impulse response (IIR) filter has the advantages of high accuracy, low order, and fewer parameters. Therefore, it has drawn the increasing concern of many researchers and scholars and has been successfully applied to all kinds of complex engineering fields, such as target tracking [1], communication systems [2, 3], signal processing [4, 5], navigation and positioning [6], signal denoising [7,8,9], and data transmission [10]. The implementation of IIR system identification primarily relies on two aspects: choosing the suitable identification structure and evaluating the filter parameters acquired by the adaptive algorithm. Fortunately, the structure of the majority of systems has been determined through system rationale and working experience and can represent the actual system well. Therefore, the IIR filter identification problem is generally reduced to the parameter optimization problem, which is based on minimization of error from the output of the adaptive filter and the output of the plant to model the unknown system to obtain the optimal model of the actual system [11]. In other words, when this error is minimum, the best IIR filter can be achieved.

However, the error surface (objective function) of the adaptive IIR filter is usually multimodal, non-convex, and non-quadratic [12]. Therefore, traditional gradient-based optimization approaches, such as Newton's method, least squares method, and its variants, can easily fall into local extremes of the error surface and fail to obtain the global optimal solution [13].

To overcome the above disadvantages, the researchers utilized an efficient and robust metaheuristic algorithm for IIR system identification. For example, Yao et al. first adopted genetic algorithm (GA) to estimate parameters for linear and nonlinear systems, which can obtain good results [14]. Krusienski et al. applied particle swarm optimization algorithm (PSO) to construct IIR filter [15]. This algorithm can obtain the minimum value of the MSE. However, GA and PSO are easy to have premature convergence problems, and GA cannot perform local search in high-dimensional space. Later, Panda et al. used the cat swarm optimization (CSO) algorithm to estimate the parameters of IIR modeling [16]. This method can give the desired results. However, this algorithm cannot balance the balance between exploration and exploitation and still suffers from the tendency to fall into local optima. Mandal et al. used an improved differential evolution algorithm (DEWM) to structure IIR filters [17]. This algorithm increases the diversity of the population by wavelet mutation and, to some extent, improves the performance of the algorithm. However, the algorithm requires more control parameters to be adjusted, which reduces the convergence speed. Saha et al. adopted an improved bat algorithm (OBA) to work out IIR identification [18]. Upadhyay et al. applied a modified harmony search algorithm (OHS) to IIR identification [19]. These two methods are based on the opposite learning method to expand the search space and improve the exploration capability of the algorithm, but for complex optimization problems, the above algorithm still suffers from premature convergence. Jiang et al. adopted a novel hybrid algorithm (HPSO–GSA) to deal with filter design problems [20]. Lagos-Eulogio et al. presented a hybrid algorithm (CPSO-DE) to obtain optimal filter parameters [21]. These two methods can obtain desirable recognition results, but the performance of the algorithms also depends on the parameter values and may be affected by premature convergence and stagnation. M Kumar et al. applied a modified interior search algorithm with Lévy flight to IIR system identification [22]. Luo et al. adopted an improved whale optimization algorithm (RWOA) to deal with the identification problem [13]. This algorithm can get a fast convergence rate at the beginning of the iteration, but the population tends to lose diversity and fall into local extremes at the end of the iteration. Despite the advantages of the above studies, most of them have the problem of local convergence in the face of complex optimization problems. Moreover, according to the theory of no-free-lunch (NFL), there is no optimization algorithm that can solve all optimization problems [23]. Therefore, it inspires researchers and scholars to propose new methods to cope with the IIR identification problem.

Artificial ecosystem-based optimizer (AEO) is an effective swarm optimization algorithm motivated by energy flow in the ecosystem [24]. It mimics the natural patterns of living organisms through production, consumption, and decomposition phases. The AEO algorithm has the advantages of an uncomplicated structure and fewer control parameters. Moreover, the poise between exploration and exploitation of the AEO mainly relied on the degression value in the search process, saving time, and burden. To further improve the search capabilities of AEO, dynamic opposite learning (DOL) is first embedded in AEO, which guides individuals to learn in an asymmetrical dynamic search area. This method will significantly boost the possibility of obtaining the global solution. Secondly, a self-adaptive nonlinear weight coefficient was adopted to better poise the relationship between exploration and exploration. The classical test function set entirely verifies the effectiveness of the DAEO algorithm. The DAEO algorithm is also utilized for the IIR system identification and compared with the other algorithms. Experimental results show that DAEO can obtain better parameters for adaptive IIR filters, verifying the effectiveness and excellence of the proposed algorithm. Motivated by the above discussion, our aim is to propose a dynamic opposite learning enhanced artificial ecosystem algorithm (DAEO) that determines the parameters of the filter to obtain an optimal set of parameters so as to the output of the adaptive IIR filter can accurately trace that of the unknown system when both systems are supplied with the same input signal. The main contributions of this paper are as follows: (1) A novel DOL strategy is embedded in AEO for the first time, increasing the diversity of the population and helping individuals to find the best solution quickly. (2) A new adaptive nonlinear weight coefficient is designed to balance the global and local search capability of DAEO. (3) The DAEO is proposed as a new optimization tool for IIR system identification. Experiment on benchmark functions and IIR system cases validates the feasibility and effectiveness of the approach.

The research content of the paper is formed as follows: Adaptive IIR filter system identification is described in Sect. 2. The basic definition of AEO is shown in Sect. 3. Section 4 introduces the DAEO algorithm. To attest to the advantageous performance of the DAEO, two kinds of experimental results are presented in Sect. 5. Discussion and analyses of simulation results are conducted in Sect. 6. Finally, Sect. 7 gives conclusions and future directions.

2 Adaptive IIR system identification

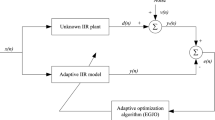
Adaptive IIR filter is one of the effective methods to deal with model identification problems. The primary work of system recognition is to adjust the adaptive IIR filter coefficients through the optimization algorithm to make the output of the filter closer to that of the unbeknown actual system when the same input signal is transmitted to both the unbeknown actual system and the adaptive filter [13]. The flow of filter identification is presented in Fig. 1.

Fig. 1

System identification of adaptive IIR filter

In Fig. 1, $X\left(t\right)$ expresses the input signal values of the filter and unknown actual system at time instant $t$, ${y}_{0}\left(t\right)$ represents the noiseless output value of unbeknown actual system at time instant $t$, $V\left(t\right)$ expresses the noise value of the recognition system at time instant $t$, and $y\left(t\right)$ represents the actual export of the unbeknown actual model with noise added. $\widehat{y}\left(t\right)$ expresses the export of the IIR filter at time instant $t$, and $e\left(t\right)$ denotes the error between the export of the actual system and the export of the adaptive IIR filter.

The relationship between input and output of the IIR system can be denoted by the following difference equation [25]:

$$\hat{y}\left( t \right) = \mathop \sum \limits_{i = 0}^{M} \hat{b}_{i} X\left( {t - i} \right) - \mathop \sum \limits_{i = 1}^{N} \hat{a}_{i} \hat{y}\left( {t - i} \right)$$

(1)

where $N\left(\ge M\right)$ represents the order of the adaptive IIR filter. Based on Eq. (1), the transport function of the IIR filter is described as follows [26]:

$$G_{M} \left( z \right) = \frac{{\mathop \sum \nolimits_{i = 0}^{M} \hat{b}_{i} z^{ - i} }}{{1 + \mathop \sum \nolimits_{i = 1}^{N} \hat{a}_{i} z^{ - i} }}$$

(2)

where ${\widehat{b}}_{i}$ and ${\widehat{a}}_{i}$ express the input and output optimization parameters of the filter, severally.

It is assumed that the transport function construction of the unbeknown real system is the same as that of the IIR filter, and the transport function of the unbeknown system is given as [11]:

$$G_{p} \left( z \right) = \frac{{\mathop \sum \nolimits_{i = 0}^{M} b_{i} z^{ - i} }}{{1 + \mathop \sum \nolimits_{i = 1}^{N} a_{i} z^{ - i} }}$$

(3)

where ${a}_{i}$ and ${b}_{i}$ represent the real parameters of actual system.

IIR system identification aims to utilize an adaptive IIR filter with the transfer function ${G}_{M}\left(z\right)$ to identify an unknown system with the transfer function ${G}_{p}\left(z\right)$. In this case, the problem transforms into an optimization problem when the adaptive IIR filter parameters ${\left[{\widehat{a}}_{i},{\widehat{b}}_{i}\right]}^{T}$ approximate the unknown system parameters ${\left[{a}_{i},{b}_{i}\right]}^{T}$. As shown in Fig. 1, the error $e\left(t\right)$ is minimized using an optimization algorithm to obtain the optimal parameter vector $\widehat{w}={\left[{a}_{1},{a}_{2},\cdots ,{a}_{N},{b}_{0},{b}_{1},\cdots ,{b}_{M}\right]}^{T}$. The error is usually expressed by mean square error (MSE), which is computed as follows.

$$MSE = \frac{1}{L}\mathop \sum \limits_{t = 1}^{L} \left( {y\left( t \right) - \hat{y}\left( t \right)} \right)^{2}$$

(4)

where $L$ represents the number of input samples.

The IIR system identification problem has been extensively studied in the literature [13,14,15,16,17,18,19,20,21,22]. In this paper, we try to apply an improved AEO algorithm (DAEO) to the optimal design of the IIR filter ${G}_{M}\left(z\right)$ and thus to fit the system model ${G}_{p}\left(z\right)$ to be identified. In fact, the problem can ultimately be reduced to nonlinear optimization problems with multiple local extrema. Equation (4) is the fitness function (error surface function) for IIR model identification. The DAEO algorithm uses the fitness function to determine the merit of the currently obtained parameters. If the order of the IIR filter ${G}_{M}\left(z\right)$ and the order of the unknown system model ${G}_{p}\left(z\right)$ to be identified are equal, then only one global optimum exists for the error surface function MSE. Conversely, then there exist multiple local minima for the error surface MSE. In practical applications, the system model to be identified is considered as a black box structure. Therefore, the order of the IIR filter and the order of the unknown system model are usually not equal, which means that the fitness function usually has many local minima. In summary, due to the complexity of the error surface of the IIR model for identifying, which is actually an optimization problem with multiple local extrema, it has essential applications in practical optimization problems. Therefore, the use of a suitable optimization algorithm is crucial to the identification results.

3 Artificial ecosystem optimizer (AEO)

The artificial ecosystem optimizer is an efficient metaheuristic algorithm presented by Zhao et al. in 2019 [24]. There are three main operators in the AEO, which are production, consumption, and decomposition. The optimization process goes through the following stages:

3.1 Production

In AEO, the best agent (${X}_{n}$) is regarded as decomposer. The producer is considered the worst agent (${X}_{1}$) in the current population, which can direct other searching agents, such as herbivores and omnivores, to search in promising areas. A new agent (producer) is created through the production phase between the best agent ${X}_{n}$ and a randomly selected agent ${X}_{rand}$ within the search area to replace the previous position. The updated model for the production phase is shown as follows:

$$a = \left( {1 - t/T_{max} } \right)r_{1}$$

(5)

$$X_{rand} = r\left( {ub - lb} \right) + lb$$

(6)

$$X_{1} \left( {t + 1} \right) = \left( {1 - a} \right)X_{n} \left( t \right) + aX_{rand} \left( t \right)$$

(7)

where ${r}_{1}$ denotes a random number inside the extent from 0 to1, $r\in \left[\mathrm{0,1}\right]$ is a random vector, parameter $a$ is weight coefficient, ${T}_{max}$ is the total iteration times, and $t$ expresses present iteration value. $\mathrm{lb}$ and $\mathrm{ub}$ are lower and upper boundaries of the search area.

3.2 Consumption

The search agents in this phase are called consumers, which can eat either the producer or other consumers with low energy levels, or both. There are three types of consumers, each using a different strategy to get the best candidate solution.

The first type, named herbivore, can only eat producer and renews itself by Eq. (8).

$$X_{i} \left( {t + 1} \right) = X_{i} \left( t \right) + CF\left( {X_{i} \left( t \right) - X_{1} \left( t \right)} \right),\;\;i \in \left[ {2, \cdots ,n} \right]$$

(8)

where $CF$ is consumption factor, and it is considered as random walk with levy flight behavior to avoid the parameter setting, which is calculated as follows:

$$CF = \frac{1}{2}\frac{{v_{1} }}{{\left| {v_{2} } \right|}},\;\;v_{1} \sim N\left( {0,1} \right),\;\;v_{2} \sim N\left( {0,1} \right)$$

(9)

where $N\left(\mathrm{0,1}\right)$ denotes a normal distribution.

The second mold is carnivore that can only randomly choose other consumers with advanced energy levels for food. The model of the carnivore is expressed by Eq. (10).

$$X_{i} \left( {t + 1} \right) = X_{i} \left( t \right) + CF\left( {X_{i} \left( t \right) - X_{j} \left( t \right)} \right),\;\;i \in \left[ {3, \cdots ,n} \right],\;\;j = randi\;\left( {\left[ {2,i - 1} \right]} \right)$$

(10)

The third type is omnivore, which signifies that not only producers but also consumers with high energy levels can eat randomly. It updates its location by Eq. (11).

$$X_{i} \left( {t + 1} \right) = X_{i} \left( t \right) + CF\left( {r_{2} \left( {X_{i} \left( t \right) - X_{1} \left( t \right)} \right) + \left( {1 - r_{2} } \right)\;\left( {X_{i} \left( t \right) - X_{j} \left( t \right)} \right)} \right),\;\;i = 3, \cdots ,n,\;\;j = randi\left( {\left[ {2,i - 1} \right]} \right)$$

(11)

where ${r}_{2}\in \left[\mathrm{0,1}\right]$ is a random number, and $j=randi\left(\left[2,i-1\right]\right)$.

3.3 Decomposition

On the basis of ecosystem function, decomposition is a critical phase that provides energy for producers. The decomposition stage is shown as follows:

$$X_{i} \left( {t + 1} \right) = X_{n} \left( t \right) + DF\left( {gX_{n} \left( t \right) - kX_{i} \left( t \right)} \right),\;\;\forall i \in n,\;DF = 3u,\;\;\;\;\;\;u\sim N\left( {0,1} \right),\;g = r_{3} randi\left( {\left[ {1\;\;2} \right]} \right) - 1,\;k = 2r_{3} - 1$$

(12)

where $DF$ is the decomposition factor. $g$ and $k$ represent the weight coefficient.

Since the AEO algorithm has been proposed, it has been proved to provide very competitive results compared with other well-known swarm intelligence algorithms. This algorithm has attracted the attention of many scholars and has also been increasingly used in many application areas [27,28,29]. Although the basic AEO shows good performance, it still has the disadvantage of slow convergence and low accuracy. The reasons for this phenomenon are as follows: The first one is that updating methods that rely only on linear weight parameters may degrade the performance of the algorithm, causing imbalance between exploration and exploitation of the algorithm, resulting in producing suboptimal solutions. The second is that no effective means is added to keep the diversity of the swarm from fending off declining into local optima. To address the above deficiencies, a novel enhanced AEO algorithm (DAEO) is proposed in this paper, which will be described in detail in the following sections.

The pseudo-code of AEO is displayed in Algorithm 1.

4 Proposed DAEO algorithm

In this paper, the variant of the AEO algorithms is proposed to enhance the performance of the algorithm, where two strategies are implemented. In the following subsection, we first introduce the nonlinear weight coefficient and dynamic opposite learning strategy and then present our DAEO in detail.

4.1 Proposed nonlinear weight coefficient

For metaheuristic algorithms, exploration and exploitation of the algorithm are executed together. Excessive exploitation will prevent the search agent from moving toward the global solution. Excessive exploration will decrease the quality of the solution. Therefore, the performance of the evolutionary algorithm can be enhanced by balancing the two stages. According to the working principle of AEO, parameter $a$ controls the exploration and exploitation capability of the algorithm. The higher value of $a$ is propitious to the exploration of the algorithm, while the lower value of $a$ is propitious to local exploitation of the algorithm. The parameter $a$ that plays an essential role in the transition from exploration to exploitation obtains a smaller value as the iteration times grow. According to Eq. (7), the update of the new position depends mainly on two components: the product of the position of the randomly selected search agent ${X}_{rand}$ and $a$ and the product of the current best position and $\left(1-a\right)$. The variation of original parameter $a$ with the number of iterations is shown in Fig. 2. The parameter $a$ takes values ranging from 1 to 0 during the iterative process. According to Algorithm 1, the proportion of parameters $a$ greater than 0.5 is small, which leads to a further reduction of the exploration capability. The algorithm mainly focuses on the exploitation stage. All of these will lead to premature convergence and local extremum. Moreover, many optimization issues need good nonlinear changes to avoid the local optimal solution. The value of parameter $a$ cannot imitate the actual situation. Therefore, a nonlinear adaptive weight coefficient is proposed. Since the search process of the AEO is nonlinear, our goal is to spend more time in the exploration than in the exploitation. Therefore, the nonlinear adaptive weight coefficient in DAEO is described as follows:

$$a = r_{1} cos\left( {t/T_{max} } \right)$$

(13)

Fig. 2

Comparison of parameters

Compared with the original weight coefficient, the nonlinear weight is more focused on exploration during iterations. The nonlinear parameter is compared with the original parameter, as shown in Fig. 2. Equation (13) and Fig. 2 indicate that the higher value of the proposed nonlinear parameter during the iteration indicates that it tends to be an exploration for a longer time.

4.2 Dynamic opposite learning (DOL) strategy

The opposition-based learning (OBL) is adopted to enhance the quality of the solution space of the algorithm, which gives more chances to approach the global solution by introducing the opposite point[30]. Much literature shows that effective expansion of search space can increase the optimization performance of different algorithms [31, 32]. However, if the local extremum exists in the searching area from the present position to the reverse position, the OBL strategy will tend to converge to the local optimal position. A dynamic opposite learning (DOL) strategy is applied to solve these problems, and the idea is exemplified in Fig. 3 [33]. First, a random reverse number ${X}^{AO}$ which is expressed as ${X}^{AO}=rand*{X}^{O}$ is set to avoid the candidate solution declining into local extremum. ${X}^{O}$ is opposite number calculated by OBL. By replacing ${X}^{O}$ with ${X}^{AO}$, the asymmetric search area which is dynamically adjusted with the ${X}^{AO}$ will be formed to change symmetric search space. Then, the DOL strategy can get a random number $\widehat{X}$ from $X$ to ${X}^{AO}$ as the asymmetric opposite solution of $X$ $\left(\widehat{X}=X+rand\left({X}^{AO}-X\right)\right)$. Although ${X}^{AO}$ makes the search space diverse, as the iteration goes on, the scope of the search space may become smaller, which will decrease the exploration capacity of the algorithm. To palliate this effect, the weighting factor $W$ is applied to get the optimal performance of DOL. DOL is redeclared as $\widehat{X}=X+W*rand\left({X}^{AO}-X\right)$, where $W$ is an invariant number. The asymmetry of search space can prevent the algorithm from declining into the local extremum and enhance the exploitation capability. The dynamics of the search area enhance the diversity of the swarm and makes it has a good exploration capacity.

Fig. 3

DOL asymmetric dynamic search area

The model of the DOL is displayed as follows:

4.2.1 Dynamic opposite number

${\varvec{X}}\in \left[{\varvec{l}}b,{\varvec{u}}b\right]$ is defined as an actual value. The dynamic reverse value $\widehat{X}$ can be computed by Eq. (14), where $lb$ and $ub$ are the boundaries of the search space. $rand$ is a random number with a scope of (0,1). $\left(W>0\right)$ is the weighting coefficient and is usually set to 1.

$$\hat{X} = X + w*rand*\left( {rand*\left( {ub + lb - X} \right) - X} \right)$$

(14)

4.2.2 Dynamic opposite point

$X=\left({X}_{1},{X}_{2},\ldots ,{X}_{D}\right)$ represents search agent in the population, which is a point in D-dimensional space. Its opposite position in the search area will be expressed by $\widehat{X}=\left({\widehat{X}}_{1},{\widehat{X}}_{2},\ldots ,{\widehat{X}}_{D}\right)$. Therefore, the values of all multi-dimensional dynamic reverse points in $\widehat{X}$ will be calculated by Eq. (15).

$$\hat{X}_{j} = X_{j} + w*rand*\left( {rand*\left( {ub_{j} + lb_{j} - X_{j} } \right) - X_{j} } \right)\;\;j = 1:D$$

(15)

4.2.3 DOL-based optimization process

• 1. Generate the ecosystem population $X$ as ${X}_{i}$ where $\left(i=\mathrm{1,2},\cdots ,n\right)$.

• 2. Dynamically update interval boundaries $\left[lb,ub\right]$ by $lb=\mathit{min}\left(X\right)$,$ub=\mathit{max}\left(X\right)$, and determine the dynamic opposite positions of ecosystem $X$ as ${\widehat{X}}_{i}$ where $\left(i=\mathrm{1,2},\cdots ,n\right)$, according to Eq. (15). If ${\widehat{X}}_{i}\notin \left[l,u\right]$, ${\widehat{X}}_{i}$ should be reset as a random number in $\left[lb,ub\right]$.

• 3. Select the $n$ search agents with good fitness values from $\left\{X\cup \widehat{X}\right\}$ as new population.

4.3 DAEO framework

The segment describes the primary details of the DAEO algorithm. To overcome the shortcoming of the AEO, the nonlinear weight coefficient and DOL strategy are put forward to enhance the performance of the algorithm. The steps of the DAEO are listed as follows:

Step 1. DAEO initialization: DAEO randomly produces the initial population according to the population size and the boundary value of the search space.

Step 2. Apply DOL: According to Eq. (15), the DOL was adopted to obtain the reverse solution of each solution. Then, DOL selects $n$ search agents with good fitness values as the new population from the generated population and its reverse solutions which are obtained in Step 2.

Step 3. Update position: The weight factor $a$ is calculated by replacing Eq. (5) with Eq. (13). Then, the position of search agents will be renewed based on Eq. (6)–(12). If the search agent is out of the search area, it will be amended.

Step 4. Fitness evaluation: The fitness values of all search agents in the population are calculated, which gets the best value as the best solution.

Step 5. Execution termination: The optimum solution will be output if the terminus situation is satisfied. Otherwise, Steps 2–4 are executed.

The pseudo-code of DAEO is displayed in Algorithm 2. The flow diagram of the proposed algorithm is shown in Fig. 4.

Fig. 4

The proposed DAEO algorithm

4.4 Time complexity analysis

In this segment, the worst time complexity of the original AEO algorithm and the proposed DAEO algorithm is calculated by using $big-O$. The complexity of AEO and DAEO is described as follows:

4.4.1 Original AEO

The original AEO generates population of ecosystem in $O\left(n\times d\right)$, where $n$ is the population size and $d$ is dimension.

It takes $O\left(n\right)$ to calculate the fitness value.

The position renewal in the original AEO needs $O\left(n\times d\right)$.

Therefore, for ${T}_{max}$ iterations, the total time complexity of the AEO needs $O\left(n\times d\times {T}_{max}\right)$.

4.4.2 The proposed DAEO

The initial population of DAEO needs $O\left(n\times d\right)$, where $n$ is the population size and $d$ is dimension.

It takes $O\left(n\right)$ to calculate the fitness value.

DOL-based strategy needs $O\left(n\times d\right)$.

The position renewal in the DAEO needs $O\left(n\times d\right)$.

In summary, for ${T}_{max}$ iterations, the total time complexity of the DAEO needs $O\left(n\times d\times {T}_{max}\right)$. Therefore, from what has been described above, we may safely draw the conclusion that the two algorithms are the same in terms of complexity.

5 Experiment and results

To ensure the efficiency of the proposed DAEO algorithm for the system identification optimization problem, the DAEO algorithm should first be evaluated and tested on several benchmark test problems. A common way is to use benchmark functions with different characteristics to evaluate optimization algorithms with stochasticity. Various scholars have adopted these benchmark functions to verify the performance of their algorithms [34, 35]. Using these functions makes it possible to ensure that the results obtained by the algorithm are not accidental. Experiment 1: We first present the test functions used in this work, and then, in order to evaluate the DAEO algorithm, the results of the algorithm are compared with those of other algorithms. Experiment 2: DAEO is applied to five benchmark IIR systems using the same-order and reduced-order systems to obtain the filter parameters, aiming to verify the capability of the DAEO to work out actual problems.

5.1 Experiment 1: test functions

In this segment, a group of challenging functions is employed to validate the performance of DAEO. Table 1 includes 21 functions with various characteristics and complexity levels, which are symbolized by the letter $f$ and numbered ${f}_{1}$, ${f}_{2}$,…, ${f}_{21}$ [36, 37]. In Table 1, $\left({f}_{1}\sim {f}_{21}\right)$ is the objective function that the algorithm needs to optimize, "Dim" represents the number of the function variables, "Range" represents the search range of the variables, and "${f}_{min}$" represents the theoretical optimal value of the function. The functions $\left({f}_{1}\sim {f}_{7}\right)$ are high-dimensional unimodal functions, which are employed to examine the local search capability of the algorithm. The functions $\left({f}_{8}\sim {f}_{15}\right)$ are high-dimensional multimodal functions, which are used to test the global search capability of the algorithm. The functions $\left({f}_{16}\sim {f}_{21}\right)$ are fixed-dimensional multimodal functions that can reveal the ability to verify the balance between exploration and exploitation of algorithms in realizing more complex and challenging landscapes.

Table 1 Benchmark functions

5.1.1 Comparative study

To better validate the performance of the proposed algorithm, DAEO is compared with other six algorithms, including moth–flame optimization algorithm (MFO) [38], salp swarm algorithm (SSA) [39], a hybrid algorithm of particle swarm optimization and gravitational search algorithm (PSOGSA) [40], grey wolf optimizer (GWO) [41], whale optimization algorithm (WOA) [42], and artificial ecosystem-based optimizer (AEO) [24]. For an impartial comparison, each algorithm executes 30 times independently, and the total iteration times are 800. The population size of all algorithms is 30, and the main parameter settings are set in Table 2. All algorithms were implemented on a PC with an Intel Core i5-10,400 and 8 GB of RAM using MATLAB R2017 (a). In this study, the Wilcoxon nonparametric rank-sum test [43] was also employed to test significant differences between the DAEO and the other algorithms on benchmark function. The $P$-values of comparisons are listed in Table 4.

Table 2 The parameter settings of algorithms

5.1.2 Simulation result

In order to fully evaluate the solution quality of the DAEO algorithm, the mean and standard deviation values obtained for each benchmark function executed 30 times independently are presented in Table 3. These two indexes are utilized to evaluate the overall performance of the algorithm. Moreover, the convergence behavior of the average fitness values of all algorithms applied to 21 classic benchmark functions is presented in Fig. 5.

Table 3 DAEO optimization results on benchmark functions

Table 4 p-value results of Wilcoxon.

Fig. 5

Convergence diagrams of benchmark functions $f_{{1}} \sim f_{21}$

The data marked in bold in Table 3 are the best values obtained by comparing the results calculated by the seven algorithms under each test function. From Table 3, it is clear that DAEO obtained the best results in terms of the mean and standard deviation of all unimodal functions f₁ ~ f₇ . In particular, for ${f}_{1}\sim {f}_{5}$, DAEO can obtain the theoretical optimal values of the test function. For unimodal functions, the global optimal solution is within a narrow parabolic-shaped valley, thus making it difficult for many algorithms to search for the global optimum. But DAEO shows superior performance. From the convergence curves of the unimodal functions in Fig. 5, it can be seen that DAEO outperforms all other algorithms in terms of convergence speed, converging rapidly toward the optimal solution. It is clear that DAEO displays the best mining ability in the comparison algorithm.

Unlike unimodal functions, the number of local optima for multimodal functions grows exponentially. Therefore, these functions are more appropriate for verifying the exploration ability of the algorithm. In multimodal functions, compared to other algorithms, DAEO obtained the best values on ${f}_{8}\sim {f}_{15}$, except for function ${f}_{13}$. In particular, DAEO can obtain the theoretical values of the test functions on ${f}_{8}$, ${f}_{9}$, ${f}_{11}$, ${f}_{14}$, and ${f}_{15}$ as well. In terms of mean value, although it failed to achieve the best results on ${f}_{13}$, DAEO ranked only behind AEO and WOA, indicating that DAEO has a strong competitive capability compared to the other algorithms. Furthermore, the convergence curves in Fig. 5 show that DAEO converges faster than other algorithms in most multimodal benchmark functions and is more promising in other cases. The above results indicate that DAEO gives an excellent exploration capability.

The ability to maintain a suitable balance between exploration and exploitation can be well verified on the fixed-dimensional test problem. In Table 3, the mean value obtained by the DAEO algorithm ranks first compared with other algorithms. Good results are obtained for DAEO on all fixed-dimensional functions. The excellent performance of DAEO is well verified on the convergence curve. At the beginning of the iteration, DAEO has converged to the global optimal solution. Among the 21 benchmark functions, in addition to ${f}_{13}$, the standard variance obtained by DAEO also ranks first, indicating that the DAEO algorithm has strong robustness. To evaluate the statistically meaningful differences between the algorithms, Wilcoxon's nonparametric statistical test with a significance level of 5% was used. In particular, if the $P$-values are less than 5%, the algorithm has a statistically significant advantage. The $P$-values in Table 4 further demonstrate the advantage of DAEO because lots of the $P$-values are much smaller than 0.05.

5.2 Experiment 2: DAEO for IIR filter identification

In the segment, the DAEO is applied to the IIR filter identification application to verify the effectiveness of the algorithm. Definitions of the IIR system identification problem set are shown in Table 5 [13, 22]. Usually, they are split into two categories: One is the real-order filter model, and the other is the reduced-order filter model. The six state-of-the-art algorithms, including PSO[15], BA[12], M-ISA[22], RWOA[13], RGWO[44], and LWOA [45], are adopted to compare with the DAEO algorithm.

Table 5 Five IIR system identification problems

5.2.1 Parameter setup

In all cases, the input signal is a white sequence, and the number of input samples is 100. The parameters for all algorithms are listed as follows: The population size of each algorithm is 30, and the total iteration times are 500. The main control parameter settings for adopted algorithms are set in Table 6. In addition, to remove the impact of the randomness of the algorithm, each algorithm is executed 30 times independently.

Table 6 The parameter settings of algorithms

5.2.2 Experimental results of system identification

Five various model cases are applied to the simulation experiment. Tables 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25 and 26 exhibit the simulation results, which include the parameter estimates and MSE values for identification. In these tables, “Parameter value” indicates the parameter value of system identification obtained by different algorithms. “Actual values” represent the true value of the variable to be evaluated. “Parameters” represent the variables that need to be evaluated in the test example. The objective function for system identification is the MSE described in Sect. 2 and is used as a metric. The performance analysis for all algorithms is ensured by determining the best, worst, mean, and standard variance of the MSE for the unknown system. These values are calculated by running the values obtained from 30 simulations for each example using the algorithm. For ease of viewing, in all tested examples, the best results obtained by the identification algorithm in terms of each adopted performance metric are marked in bold in the respective tables.

Table 7 Parameter values of all algorithms for model 1 (case 1)

Table 8 MSE values of all algorithms for model 1 (case 1)

Table 9 Parameter values of all algorithms for model 1 (case 2)

Table 10 MSE values of all algorithms for model 1 (case 2)

Table 11 Parameter values of all algorithms for model 2 (case 1)

Table 12 MSE values of all algorithms for model 2 (case 1)

Table 13 Parameter values of all algorithms for Test model 2 (case 2)

Table 14 MSE values of all algorithms for model 2 (case 2)

Table 15 Parameter values of all algorithms for model 3 (case 1)

Table 16 MSE values of algorithms for model 3 (case 1)

Table 17 Parameter values of all algorithms for model 3(case 2)

Table 18 MSE values of all algorithms for model 3 (case 2)

Table 19 Parameter values of all algorithms for model 4 (case 1)

Table 20 MSE values of all algorithms for model 4 (case 1)

Table 21 Parameter values of all algorithms for model 4 (case 2)

Table 22 MSE values of all algorithms for model 4 (case 2)

Table 23 Parameter values of all algorithms for model 5 (case 1)

Table 24 MSE values of all algorithms for model 5 (case 1)

Table 25 Parameter values of all algorithms for model 5 (case 2)

Table 26 MSE values of all algorithms for model 5 (case 2)

Model 1 For the first test example, a second-order system is considered, whose transport function is expressed by Eq. (16).

$$G_{p} \left( z \right) = \frac{{0.05 - 0.4Z^{ - 1} }}{{1 - 1.1314Z^{ - 1} + 0.25Z^{ - 2} }}$$

(16)

In this instance, ${G}_{p}\left(z\right)$ is modeled to demonstrate the superior performance of the DAEO using the same-order system described in case 1 and the reduced-order system in case 2.

Case 1.

The second-order filter can simulate the real second-order system well. Hence, the transport function of the adaptive filter is expressed by Eq. (17).

$$G_{M} \left( z \right) = \frac{{b_{0} - b_{1} Z^{ - 1} }}{{1 - a_{1} Z^{ - 1} - a_{2} Z^{ - 2} }}$$

(17)

The problem of system identification is simplified to optimize the molecule and denominator parameters ${b}_{0}$, ${b}_{1}$ and ${a}_{1}$, ${a}_{2}$, separately. The obtained parameters are shown in Table 7, which led to the optimal approximation to the unknown system using the swarm intelligence algorithm. As can be seen from Table 7, the values of the parameters obtained by the DAEO and M-ISA algorithms are in perfect agreement with the actual values of the system parameters compared to the other algorithms. In Table 8, the MSE values obtained by the DAEO algorithm are all 0, which is better than those acquired by other algorithms. The best MSE values obtained are 2.69E-03, 9.72E-03, 6.07E-33, 1.05E-05, 4.88E-05, 7.47E-08, and 0 for PSO, BA, M-ISA, LWOA, RWOA, RGWO, and DAEO, respectively. From the above discussion, it can be seen that the DAEO-based system identification approach produces the best results in terms of MSE compared to PSO, BA, M-ISA, LWOA, RWOA, and RGWO.

Figure 6 shows the convergence of the mean values of MSE using different algorithms. It can be seen from Fig. 6 that DAEO requires 400 iterations to obtain the minimum value of MSE, while other algorithms fall into local optimum prematurely. Furthermore, the convergence speed of DAEO is much faster than that of the other six algorithms. From Fig. 7 and the variance values in Table 8, it can be concluded that DAEO has better robustness compared to other algorithms. In terms of the mean of MSE, the performance ranking of all algorithms is DAEO > RGWO > M-ISA > LWOA > RWOA > PSO > BA.

Fig. 6

Converge diagram for model 1, case 1

Fig. 7

ANOVA graph for model 1, case 1

Case 2.

The second-order system can also be simulated by the first-order filter with the following transport function:

$$G_{M}^{^{\prime}} \left( z \right) = \frac{{b_{0}^{^{\prime}} }}{{1 - a_{1}^{^{\prime}} Z^{ - 1} }}$$

(18)

A reduced-order filter is adopted to recognize the unbeknown system. In this case, there is no accurate value but the approximate value. Here, MSE and convergence curves are used to evaluate performance metrics for the identification problem of the reduced-order system. Statistical results are used to analyze the performance of PSO, BA, M-ISA, LWOA, RWOA, RGWO, and DAEO. The MSE values obtained for all algorithms are listed in Table 10. The mean values of MSE for PSO, BA, M-ISA, LWOA, RWOA, RGWO, and DAEO are 1.61E−02, 2.06E−02, 1.13E−02, 1.46E−02, 1.31E−02, 1.20E−02, and 1.02E−02, respectively. From Table 10, it can be concluded that DAEO outperforms PSO, BA, M-ISA, LWOA, RWOA, and RGWO when modeled using the reduced-order system. From the MSE values listed in Table 10, it can be concluded that DAEO obtains a better approximation for the second-order IIR system compared to other algorithms. Figure 8 describes the convergence behavior of the MSE values using various algorithms. As can be seen from Fig. 8, DAEO has reached convergence in 300 iterations with the mean value of about 1.02E-02. From the variance values in Table 10 and Fig. 9, it can be obtained that DAEO has a small variance value indicating that DAEO has better robustness. Therefore, in terms of the mean of MSE, the performance of these algorithms is ranked as DAEO > M-ISA > RGWO > RWOA > LWOA > PSO > BA.

Fig. 8

Converge diagram for model 1, case 2

Fig. 9

ANOVA graph for model 1, case 2

Model 2 For the second test example, the transport function of the third-order system is defined as follow:

$$G_{p} \left( z \right) = \frac{{ - 0.3 + 0.4Z^{ - 1} - 0.5Z^{ - 2} }}{{1 - 1.2Z^{ - 1} + 0.5Z^{ - 2} - 0.1Z^{ - 3} }}$$

(19)

Case 1.

The third-order filter can simulate the real third-order system well. Hence, the transport function of the filter is expressed by Eq. (20).

$$G_{M} \left( z \right) = \frac{{b_{0} + b_{1} Z^{ - 1} + b_{2} Z^{ - 2} }}{{1 - a_{1} Z^{ - 1} - a_{2} Z^{ - 2} - a_{3} Z^{ - 3} }}$$

(20)

In this example, optimization of the system parameters, ${b}_{0}$,${b}_{1}$,${b}_{2}$,${a}_{1}$,${a}_{2}$,${a}_{3}$, is performed using PSO, BA, M-ISA, LWOA, RWOA, RGWO, and DAEO. The estimated parameters are listed in Table 11. It can be observed from Table 11 that the parameter values obtained with DAEO are in perfect agreement with the actual parameter values compared to other algorithms. Figure 10 depicts the convergence graph of the mean value of MSE for all algorithms. It can be seen that the convergence curve of DAEO keeps decreasing after the 100th iteration, while other algorithms fall into local optima at the beginning of the iteration. In addition, the MSE values obtained by all algorithms are listed in Table 12. The mean values of MSE obtained for PSO, BA, M-ISA, LWOA, RWOA, RGWO, and DAEO are 2.38E-02, 2.71E-01, 2.08E-03, 6.68E-03, 5.65E-03, 5.93E-04, and 2.13E-10, respectively. From these measurements, it can be concluded that the system identified using the DAEO method has the smallest MSE and can effectively handle the system identification problem. Based on the MSE values in Table 12, it can be finally inferred that the use of DAEO to identify the third-order IIR system model outperforms other existing comparative algorithms. The variance diagram also displays that the DAEO algorithm has better stability (Fig. 11). The performance of the algorithms adopted can be ranked as follows: DAEO > RGWO > M-ISA > RWOA > LWOA > PSO > BA.

Fig. 10

Converge diagram for model 2, case 1

Fig. 11

ANOVA graph for model 2, case 1

Case 2.

The third-order system can also be simulated by the second-order filter with the following transport function:

$$G_{M}^{^{\prime}} \left( z \right) = \frac{{b_{0}^{^{\prime}} + b_{1}^{^{\prime}} Z^{ - 1} }}{{1 - a_{1}^{^{\prime}} Z^{ - 1} - a_{2}^{^{\prime}} Z^{ - 2} }}$$

(21)

Table 13 shows the approximate solutions of the parameters obtained by all the algorithms. The MSE values of the system generated by the optimized parameters are shown in Table 14. The MSE values obtained using DAEO are better than any other algorithm. From the MSE values obtained in Table 14, it can be concluded that the DAEO-based system identification is superior to the other compared algorithms. The excellent performance of DAEO is also well demonstrated in Figs. 12 and 13, where DAEO has good convergence speed and accuracy compared to other algorithms, and the BA traps in the local optimal solution prematurely. It is well suited for achieving optimal MSE values in other algorithms. According to the performance of the system identification, the order of the algorithms is DAEO > RGWO > M-ISA > RWOA > LWOA > PSO > BA.

Fig. 12

Converge diagram for model 2, case 2

Fig. 13

ANOVA graph for model 2, case 2

Model 3 For the third test example, the transport function of the fourth-order system is expressed by Eq. (22).

$$G_{p} \left( z \right) = \frac{{1 - {0}{\text{.9}}Z^{ - 1} + {0}{\text{.81}}Z^{ - 2} { - 0}{\text{.729}}Z^{ - 3} }}{{1 + {0}{\text{.04}}Z^{ - 1} + 0.{2775}Z^{ - 2} - 0.{2101}Z^{ - 3} + {0}{\text{.14}}Z^{ - 4} }}$$

(22)

Case 1.

The fourth-order filter can simulate the real fourth-order system well. Hence, the transport function of the filter is expressed by Eq. (23).

$$G_{M} \left( z \right) = \frac{{b_{0} + b_{1} Z^{ - 1} + b_{2} Z^{ - 2} + b_{3} Z^{ - 3} }}{{1 - a_{1} Z^{ - 1} - a_{2} Z^{ - 2} - a_{3} Z^{ - 3} - a_{4} Z^{ - 4} }}$$

(23)

The problem of system identification is simplified to optimize the molecule and denominator parameters ${b}_{0}$,${b}_{1}$,${b}_{2}$, ${b}_{3}$ and ${a}_{1}$, ${a}_{2}$, ${a}_{3}$, ${a}_{4}$, separately. Table 15 shows the best parameters obtained for the optimization of the error surface of the unknown system using different evolutionary algorithms. As can be seen from Table 15, the parameters obtained by DAEO are in full agreement with the actual parameter values of the system compared to other algorithms. Table 16 shows the MSE values of the fourth-order system identification problem. The mean values of MSE obtained are 5.73E-02, 4.97E + 01, 1.28E-03, 1.28E-02, 7.37E-03, 6.10E-04, and 5.65E-05 for PSO, BA, M-ISA, LWOA, RWOA, RGWO, and DAEO, respectively. From the above numerical results, it can be seen that the proposed DAEO-based system identification approach obtains the optimal results in terms of MSE. Figure 14 shows the convergence curves of the mean values for MSE, which DAEO has a better convergence accuracy. In Fig. 15, most of the algorithms show strong robustness. Therefore, for the optimization of the parameters of the fourth-order IIR system, the performance ranking of the adopted algorithm is DAEO > RGWO > M-ISA > RWOA > LWOA > PSO > BA.

Fig. 14

Converge diagram for model 3, case 1

Fig. 15

ANOVA graph for model 3, case 1

Case 2.

The fourth-order system can also be simulated by the third-order filter with the following transport function:

$$G_{M}^{^{\prime}} \left( z \right) = \frac{{b_{0}^{^{\prime}} + b_{1}^{^{\prime}} Z^{ - 1} + b_{2}^{^{\prime}} Z^{ - 2} }}{{1 - a_{1}^{^{\prime}} Z^{ - 1} - a_{2}^{^{\prime}} Z^{ - 2} - a_{3}^{^{\prime}} Z^{ - 3} }}$$

(24)

Table 17 shows the approximate solutions of the parameters obtained by all the algorithms. The exact parameters are not available since the reduced-order filter model is used. The MSE values are presented in Table 18. The observed mean values of MSE are 4.46E-02, 3.86E-01, 7.02E-03, 1.59E-02, 1.05E-02, 8.15E-03, and 4.12E-03 for PSO, BA, M-ISA, LWOA, RWOA, RGWO, and DAEO. From the above results, it can be inferred that the DAEO algorithm produces better effects for the IIR system identification compared to other algorithms. The convergence process of the MSE values is displayed in Fig. 16. It is obvious that all algorithms fall into local optimal solutions in early iterations. However, DAEO reaches the minimum fitness value in about 30 iterations compared to other algorithms. Figure 17 shows the variance graphs for all algorithms, where DAEO possesses smaller values, indicating that DAEO possesses good robustness. Based on the above discussion, it can be concluded that DAEO provides a good approximation for fourth-order IIR systems compared to other algorithms, which are ranked in terms of performance as DAEO > M-ISA > RGWO > RWOA > LWOA > PSO > BA.

Fig. 16

Converge diagram for model 3, case 2

Fig. 17

ANOVA graph for model 3, case 2

Model 4 For the fourth test example, the transport function of the fifth-order system is expressed by Eq. (25).

$$G_{p} \left( z \right) = \frac{{{0}{\text{.1084}} + {0}{\text{.5419}}Z^{ - 1} + {1}{\text{.0837}}Z^{ - 2} + {1}{\text{.0837}}Z^{ - 3} + {0}{\text{.5419}}Z^{ - 4} + {0}{\text{.1084}}Z^{ - 5} }}{{1 + {0}{\text{.9853}}Z^{ - 1} + {0}{\text{.9738}}Z^{ - 2} + {0}{\text{.3864}}Z^{ - 3} + {0}{\text{.1112}}Z^{ - 4} + {0}{\text{.0113}}Z^{ - 5} }}$$

(25)

Case 1

The fifth-order filter can simulate the real fifth-order system well. Hence, the transport function of the adaptive filter is expressed by Eq. (26).

$$G_{M} \left( z \right) = \frac{{b_{0} + b_{1} Z^{ - 1} + b_{2} Z^{ - 2} + b_{3} Z^{ - 3} + b_{4} Z^{ - 4} + b_{5} Z^{ - 5} }}{{1 - a_{1} Z^{ - 1} - a_{2} Z^{ - 2} - a_{3} Z^{ - 3} - a_{4} Z^{ - 4} - a_{5} Z^{ - 5} }}$$

(26)

The assessed parameter values for the same-order system are presented in Table 19, and there is no algorithm to obtain the exact parameter values. The MSE values (best, worst, mean, and variance) obtained by the various algorithms are listed in Table 20. The mean values of MSE are 2.43E-01, 2.68E + 10, 4.83E-04, 4.09E-02, 2.20E-03, 2.02E-04, and 3.58E-05 for PSO, BA, M-ISA, LWOA, RWOA, RGWO, and DAEO. It can be seen that DAEO has the best approximation of the actual values for the system parameters compared to other algorithms. Figure 18 shows the convergence curve of the mean value of the MSE. As can be seen from Fig. 18, DAEO requires about 100 iterations to converge to the minimum fitness value, while BA falls prematurely into the local optimal solution. Furthermore, based on the convergence curve of DAEO, it can be inferred that the convergence rate of DAEO is higher than other algorithms. The MSE variance values in Table 20 and Fig. 19 also show that DAEO has good robustness. Based on the above values, the performance of these algorithms is ranked as DAEO > RGWO > M-ISA > RWOA > LWOA > PSO > BA.

Fig. 18

Converge diagram for model 4, case 1

Fig. 19

ANOVA graph for model 4, case 1

Case 2.

The fifth-order system can also be simulated by the fourth-order filter with the following transport function:

$$G_{M}^{^{\prime}} \left( z \right) = \frac{{b_{0}^{^{\prime}} + b_{1}^{^{\prime}} Z^{ - 1} + b_{2}^{^{\prime}} Z^{ - 2} + b_{3}^{^{\prime}} Z^{ - 3} + b_{4}^{^{\prime}} Z^{ - 4} }}{{1 - a_{1}^{^{\prime}} Z^{ - 1} - a_{2}^{^{\prime}} Z^{ - 2} - a_{3}^{^{\prime}} Z^{ - 3} - a_{4}^{^{\prime}} Z^{ - 4} }}$$

(27)

Table 21 shows the approximate solutions of the parameters obtained by seven algorithms. Since there is no exact value for case 2, the performance of the algorithm is measured by the MSE value and the convergence rate. The MSE values are listed in Table 22. The mean values of MSE are 9.73E-02, 5.21E + 00, 3.18E-04, 1.10E-02, 2.08E-03, 2.85E-04, and 5.12E-05 for PSO, BA, M-ISA, LWOA, RWOA, RGWO, and DAEO, respectively. From the above observations, it can be seen that the proposed DAEO algorithm gives the best results in terms of system identification compared to other algorithms. Figure 20 shows the convergence graphs of the different algorithms. The DAEO algorithm converges rapidly and reaches the minimum fitness value in about 80 iterations. From Fig. 21, the DAEO algorithm is very stable in solving the IIR model problem. In summary, in terms of its MSE value and convergence rate, the performance ranking of the adopted algorithm is DAEO > RGWO > M-ISA > RWOA > LWOA > PSO > BA.

Fig. 20

Converge diagram for model 4, case 2

Fig. 21

ANOVA graph for model 4, case 2

Model 5 For the fifth test example, the transport function of a sixth-order system is expressed by Eq. (28).

$$G_{p} \left( z \right) = \frac{{{1 - 0}{\text{.4}}Z^{ - 2} { - 0}{\text{.65}}Z^{ - 4} + {0}{\text{.26}}Z^{ - 6} }}{{1{ - 0}{\text{.77}}Z^{ - 2} { - 0}{\text{.8498}}Z^{ - 4} + {0}{\text{.6486}}Z^{ - 6} }}$$

(28)

Case 1.

The sixth-order filter can simulate the real sixth-order system well. Hence, the transport function of the filter is expressed by Eq. (29).

$$G_{M} \left( z \right) = \frac{{b_{0} + b_{2} Z^{ - 2} + b_{4} Z^{ - 4} + b_{6} Z^{ - 6} }}{{1 - a_{2} Z^{ - 2} - a_{4} Z^{ - 4} - a_{6} Z^{ - 6} }}$$

(29)

Table 23 presents the results of the optimal parameters of the unknown system obtained by applying the metaheuristic algorithm, none of which can obtain the exact parameter values. Table 24 shows the MSE values for the sixth-order system identification problem. As can be seen from Table 24, the results obtained by DAEO are the best compared to other algorithms in terms of the best, worst, and mean values of MSE. Based on the MSE values in Table 24, it can be concluded that DAEO gives the best approximation of the parameters of the sixth-order IIR system. Figure 22 shows the convergence curves of various algorithms for the mean of the MSE. In Fig. 22, DAEO requires about 80 iterations to converge to the minimum fitness value, while BA and PSO are prone to fall into local optima at the beginning of the iterations. Based on the above discussion, the performance ranking of all algorithms in the system identification problem is DAEO > M-ISA > RGWO > RWOA > LWOA > PSO > BA (Fig. 23).

Fig. 22

Converge diagram for model 5, case 1

Fig. 23

ANOVA graph for model 5, case 1

Case 2.

The sixth-order system can also be simulated by the fifth-order filter with the flowing transport function.

$$G_{M}^{^{\prime}} \left( z \right) = \frac{{b_{0}^{^{\prime}} + b_{1}^{^{\prime}} Z^{ - 1} + b_{2}^{^{\prime}} Z^{ - 2} + b_{3}^{^{\prime}} Z^{ - 3} + b_{4}^{^{\prime}} Z^{ - 4} + b_{5}^{^{\prime}} Z^{ - 5} }}{{1 - a_{1}^{^{\prime}} Z^{ - 1} - a_{2}^{^{\prime}} Z^{ - 2} - a_{3}^{^{\prime}} Z^{ - 3} - a_{4}^{^{\prime}} Z^{ - 4} - a_{5}^{^{\prime}} Z^{ - 5} }}$$

(30)

Table 25 shows the approximate solutions of the parameters obtained by seven algorithms. Due to the use of the reduced-order system, there is no exact value. The recognition performance of the algorithm is mainly measured by the MSE value and the convergence rate. For the system identification problem, the fitness values (MSE) of all algorithms are listed in Table 26. From the MSE values in Table 26, it can be summarized that the DAEO-based system identification surpasses all other algorithms. Figure 24 shows the convergence graph of the reduced-order system, where the DAEO obtains the minimum error at the 100th iteration and has a fast convergence rate. In Fig. 25, most of the algorithms have good stability. Based on the above numerical results, the algorithms used can be ranked as DAEO > RGWO > M-ISA > RWOA > LWOA > PSO > BA.

Fig. 24

Converge diagram for model 5, case 2

Fig. 25

ANOVA graph for model 5, case 2

6 Discussion analysis

DAEO is applied to function optimization and IIR system identification problems. Experimental results in Sects. 5.1 and 5.2 indicate the effectiveness and practicability of the proposed DAEO algorithm. As can be seen from Fig. 5 in experiment 1, in terms of convergence behavior, DAEO lies at the bottom on most functions and accelerates the detection of the global optimal solution. Taking the function ${f}_{1}$ as an example, DAEO can sustain good acceleration during the iterative process, while AEO has good convergence speed but is not as good as DAEO. GWO and WOA have poor convergence speed at the beginning of the iteration; although it decreases later in the iterations, their convergence accuracy is also not good, while MFO, SSA, and PSOGSA fall into stagnation too early. In experiment 2, compared with other algorithms for IIR model recognition, the DAEO provides the best evaluation parameters and the best optimization accuracy in all cases. In the same-order system for models 1, 2, and 3, it is obtained from Tables 7, 11, and 15 that DAEO obtains parameter values in agreement with the actual parameter values. Although in Table 7, M-ISA also obtains parameter values in agreement with the actual values, the MSE values of M-ISA and other algorithms are not as good as the values of DAEO algorithm. In the same-order system for models 4 and 5, it can be seen from Tables 19 and 23 that none of the algorithms obtains parameter values consistent with the actual parameter values, but DAEO obtains MSE values (except for the variance values of DAEO in Table 23) better than the reported algorithms. The MSE values obtained for all algorithms in the reduced-order system also indicate that DAEO outperforms the other algorithms in terms of recognition performance, convergence, and robustness, while BA ranks the worst among the reported algorithms.

Our proposed DAEO performs better than other comparing algorithms in the two experiments due to the nonlinear weight coefficient and the dynamic opposite learning strategy. By studying the artificial ecosystem optimizer (AEO), we understand that the consumption stage represents the global search process of AEO. The producer in population is presented as the worst individual with the largest object function value, and the updated producer will guide consumers to search different regions directly or indirectly. Although the producer is updated with the participation of decomposers (the best individual), to some extent, the exploration capability of the algorithm is significantly weakened, and its search space keeps away from promising areas. Therefore, before the individuals update their position, we added the DOL strategy to form the new population. Its dynamic asymmetric search space helps the algorithm enhance the probability of obtaining good solutions and makes the global search of AEO more precise. Additionally, the DAEO always got the best population during the iteration; therefore, the searching individual could renew its position according to the optimal solution space. DAEO will have a higher probability of seeing the promising areas. Moreover, for any optimization algorithm, the poise between exploration and exploitation is essential. In the AEO, $\alpha$ controls the balance between exploration and exploitation of the algorithm. In the process of iteration, parameter $\alpha$ gets a small value in most cases, which is not conducive to the global search of the algorithm. Hence, a nonlinear weight parameter is used to make the algorithm more flexible. It enhances the algorithm's exploration capability at the iteration process, which is to achieve a good balance. Finally, DAEO maintains the simple structure of AEO, and its control parameters are less than other algorithms. Therefore, the above advantages make DAEO more suitable for practical applications and effectively deal with the function optimization and the IIR model system identification problem.

7 Conclusions and future directions

The paper has posted a modified version of the AEO algorithm adopting the DOL strategy and an adaptive nonlinear weight coefficient, and the novel scheme is called the DAEO. The DOL strategy forms a dynamic asymmetric search space by computing the reverse solution to the present solution to improve the overall performance of the algorithm. Since the search process in the AEO  displayed an inappropriate balance relationship between exploration and exploitation. Hence, in the DAEO, an adaptive nonlinear weight coefficient was presented to build a better balance between the two stages during the search. To verify the effectiveness of the DAEO algorithm, the experiment is split into two parts. The first part is that DAEO outperforms the original AEO and other algorithms in terms of optimal global ability and convergence performances in the challenging test set. Also, DAEO is examined with the statistical analysis, i.e., the Wilcoxon nonparametric rank-sum test, and compared with the other six comparison algorithms to prove the effectiveness of the algorithm. The second part is to choose five typical IIR filter models from the related literature, which have the same order and reduced order. Simulation results manifest that the proposed algorithm has good optimization precision, convergence rate, and stability than other algorithms dealing with filter identification problems.

Although the recognition accuracy obtained by DAEO is better than that of other algorithms in the system recognition problem, there is still room for continued improvement, and the decomposition mechanism of DAEO tends to fall into local optimum in the late iteration, which reduces the mining ability of the algorithm. Therefore, effective methods and strategies will be proposed in the future to improve the performance of DAEO and further extend the application field of the algorithm.