Adaptive infinite impulse response system identification using an enhanced golden jackal optimization

Abstract

Golden jackal optimization (GJO) is inspired by the cooperative attacking behavior of golden jackals and mainly simulates searching for prey, stalking and enclosing prey, and pouncing on prey to solve complicated optimization problems. However, the basic GJO has the disadvantages of premature convergence, a slow convergence rate and low computation precision. To enhance the overall search and optimization abilities, an enhanced golden jackal optimization (EGJO) method with the elite opposition-based learning technique and the simplex technique is proposed to address adaptive infinite impulse response system identification. The intention is to minimize the error fitness value and obtain the appropriate control parameters. The elite opposition-based learning technique boosts population diversity, enhances the exploration ability, extends the search range and avoids search stagnation. The simplex technique accelerates the search process, enhances the exploitation ability, improves the computational precision and increases the optimization depth. EGJO can not only achieve complementary advantages to avoid search stagnation but also balance exploration and exploitation to arrive at the best value. Three sets of experiments are used to verify the effectiveness and feasibility of EGJO. The experimental results clearly demonstrate that the optimization efficiency and recognition accuracy of EGJO are superior to those of AOA, GTO, HHO, MDWA, RSO, WOA, TSA and GJO. EGJO has a faster convergence rate, higher computation precision, better control parameters and better fitness value, and it is stable and resilient in solving the IIR system identification problem.

1 Introduction

The adaptive IIR filter has higher computational accuracy and lower design order to achieve good frequency selection characteristics, and it has been extensively used in control systems, network communication, signal processing, geological exploration, biomedicine and so on. In IIR model identification, the design is essentially a global optimization problem of multidimensional variables, and the error surface contains some local extrema. Modeling is accomplished by comparing the input value of the unknown system with the output value of the adaptive IIR filter [1,2,3,4,5]. Some optimization techniques have been introduced to adjust the control parameters and enhance the overall performance of model identification, such as the arithmetic optimization algorithm (AOA) [6], gorilla troop optimization (GTO) [7], Harris hawks optimization (HHO) [8], movable damped wave algorithm (MDWA) [9], rat swarm optimization (RSO) [10], whale optimization algorithm (WOA) [11], and tunicate swarm algorithm (TSA) [12].

Niu et al. [13] suggested an enhanced artificial ecosystem optimization algorithm to address IIR system identification, and the algorithm’s recognition accuracy was higher than those of other approaches. Ababneh et al. [14] found a unique cuckoo search algorithm to optimize the IIR filter, and the proposed algorithm had great robustness and stability in identifying the best result. Mohammadi et al. [15] applied a revised inclined plane system optimization method to design the IIR filter’s parameters, and this algorithm attained rapid convergence efficiency and excellent optimization accuracy. Chang [16] created a new Hammerstein model based on the IIR system and Volterra neural network to identify nonlinear discrete systems, and the algorithm verified the validity and reliability of the model. Durmuş [17] used a modified average differential evolution algorithm to accomplish IIR system identification, and this method had extensive optimization ability to generate better control parameters. Kowalczyk et al. [18] published a new approach based on an IIR filter matrix to design hardware architecture, and the approach found a quicker optimization frequency and superior calculation precision. Mittal [19] tried to combine moth flame optimization with the variable neighborhood search technique to optimize the IIR filter’s parameters, and this hybrid method produced better results than comparison algorithms. Ababneh et al. [20] created a differential evolution optimization method to construct IIR filters, and the results indicated that this method had strong utilization and exploration to determine the best resolution. Mohammadi et al. [21] devised an enhanced particle swarm optimization method for IIR filters, and this approach identified the best solution and good optimization parameters. Liang et al. [22] adopted a modified slime mold algorithm to perform IIR filter design, and this algorithm had powerful stability in discovering the most suitable value. Agrawal et al. [23] studied how to create digital IIR filters according to various techniques, and the results confirmed the robustness and effectiveness of the methods. Bui et al. [24] utilized the design of an electrocardiogram signal for the IIR filter, and the proposed method had certain stability and superiority. Singh et al. [25] established a teacher-learner-based optimization method to perform adaptive IIR system identification, and the optimization outcomes of this method were better. Kumar et al. [26] integrated the interior search algorithm with the Lèvy technique to design adaptive IIR filters and proposed an extraction and utilization method to discover the best parameters and solution. Luo et al. [27] devised an updated whale optimization algorithm to investigate IIR system identification, and this approach produced superior overall results. Chang et al. [28] constructed a revised particle swarm optimization method based on multiple subpopulations to handle IIR filters, and this algorithm had a relatively strong detection performance in identifying the best solution. Zhao et al. [29] established a modified selfish herd optimization method for IIR filters, and this approach had better calculation accuracy and strong durability. Ali et al. [30] devised a salp swarm algorithm for IIR filters, and this method obtained better parameters and the best solution. Dhabal et al. [31] offered an enhanced global-best-guided cuckoo search algorithm to construct IIR filters, and the improved algorithm exhibited a better convergence efficiency and calculation precision. Cuevas et al. [32] summarized some optimization methods for IIR system identification. Mohammadi et al. [33] utilized evolutionary algorithms to design IIR filters, and these algorithms had strong robustness and stability in obtaining the best value. Mohammadi et al. [34] proposed an inclined plane system optimization algorithm to design an IIR filter, and this method had a strong search ability to obtain the global optimal solution. Mohammadi et al. [35] later applied another modified inclined plane system optimization algorithm for the IIR filter, and this proposed method had strong optimization efficiency and high calculation accuracy. Mohammadi et al. [36] analyzed swarm intelligence and evolutionary computation techniques to design IIR filters, and the reliability and accuracy of this swarm intelligence method were superior to those of evolutionary computation. Mohammadi et al. [37] described an inclined plane system optimization algorithm that had strong robustness and reliability and was widely used in various fields. Agrawal et al. [38] used the fractional derivative to design a new IIR filter, and this method was effective. Agrawal et al. [39] presented a novel approach based on the fractional derivative and swarm intelligence to design IIR filters, and the proposed approach had good optimization performance. Kumar et al. [40] combined fractional derivatives and swarm optimization to perform the Hilbert transform, and this method balanced exploration and exploitation to achieve higher computation precision. Agrawal et al. [41] employed fractional derivative constraints and hybrid particle swarm optimization to design an IIR filter, and this method had strong stability and reliability. Janjanam et al. [42] proposed a global gravitational search algorithm-assisted Kalman filter to evaluate nonlinear system identification, and this method had better optimization results. Saha et al. [43] utilized the harmony search algorithm to design IIR filters, and this algorithm had strong global and local abilities to determine the best value. Ahirwal et al. [44] integrated the cuckoo optimization algorithm and other optimization methods to design the EEG/ERP adaptive noise canceller, and the proposed method had a high computational efficiency and convergence accuracy. Ahirwal et al. [45] combined the evolutionary method with the adaptive noise canceller to enhance the SNR of contaminated EEG, and this method had strong stability and robustness. Ahirwal et al. [46] proposed the bounded-range artificial bee colony algorithm to resolve adaptive filtering of EEG/ERP, and the method achieved certain superiority and reliability.

GJO is motivated by the cooperative attacking behavior of golden jackals; it mainly imitates searching for prey, stalking and enclosing prey, and pouncing on prey to identify the best solution [47]. The basic GJO has the disadvantages of premature convergence, a slow convergence rate and low computation precision. The elite opposition-based learning technique and simplex technique are introduced into the basic GJO to enhance the convergence rate and computation precision. The elite opposition-based learning technique increases population variety and broadens the search region to avoid search stagnation and boost global search [48, 49]. The simplex technique accelerates the optimization process and increases the search depth to optimize the computational precision and boost local search [50, 51]. EGJO is applied to perform IIR system identification, and the intention is to minimize the error fitness value and obtain the appropriate control parameters. The experimental results demonstrate that EGJO not only stabilizes exploration and exploitation to avoid falling into a locally optimal value but also has excellent durability and robustness to arrive at the best solution. Additionally, EGJO has a faster convergence rate, greater computation precision, and stronger stability and robustness; the effectiveness and feasibility of EGJO have been verified.

This paper is arranged as follows. Section 2 defines the adaptive IIR system identification problem. Section 3 outlines GJO. Section 4 explores EGJO. In Sect. 5, the EGJO-based adaptive IIR system identification method is presented. The experimental results and analysis are presented in Sect. 6. Finally, conclusions and future research are addressed in Sect. 7.

2 Adaptive IIR system identification problem

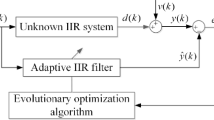
The adaptive IIR filter utilizes a lower order and coefficients to ensure the overall control level of the system; it has found broad potential applications in model identification, noise elimination, prediction spectrum optimization and automatic equalization. System identification is a significant and constructive approach for performing mathematical modeling of an unidentified plant by anatomizing the input and output data. Some problems of signal processing are usually regarded as system identification problems. Some swarm intelligence optimization algorithms are introduced to tune the parameters of the IIR filter and minimize the error value of the actual system and model system, which enhances the optimization ability and search ability to satisfy various performance indicators and discover an accurate solution. A schematic of adaptive IIR system identification employing EGJO is shown in Fig. 1.

Fig. 1

Schematic of adaptive IIR system identification employing EGJO

In adaptive IIR system identification, the following mathematical function is computed:

$$ \sum\limits_{l = 0}^{L} {a_{l} y} (n - l) = \sum\limits_{k = 0}^{K} {b_{k} x(n - k} ) $$

(1)

where $x(n)$ and $y(n)$ represent the input and output, $L$ and $K$ are the orders of the feedforward and feedback IIR filters, $L$ is greater than $K$, $a_{l}$ is the pole coefficient, and $b_{k}$ is the zero coefficient. The transfer function is computed as:

$$ H(z) = \frac{{\sum\nolimits_{k = 0}^{K} {b_{k} z^{ - k} } }}{{1 + \sum\nolimits_{l = 0}^{L} {a_{l} z^{ - l} } }} $$

(2)

In the IIR filter, $y_{0} (n) = d(n) + v(n)$ is the response of the unidentified IIR plant, $y_{0} (n)$ represents the output data of an unidentified IIR plant, $v(n)$ is the additional white Gaussian noise, and $e(n) = y_{0} (n) - y(n)$ is the error between the authentic plant and the IIR model. Adaptive system identification is transformed into mathematical optimization. The mean square error (MSE) is computed as:

$$ {\text{MSE}} = J(w) = \frac{1}{N}\sum\limits_{n = 1}^{N} {e^{2} (n)} $$

(3)

where $N$ expresses the entire quantity of specimens, $w$ expresses the coefficient vector, and $w = (a_{1} ,a_{2} , \ldots ,a_{L} ,b_{0} ,b_{1} , \ldots ,b_{K} )^{T}$.

3 GJO

The basic GJO method inspired by the cooperative attacking behavior of golden jackals is a novel optimization technique. In GJO, each golden jackal represents a candidate solution or search agent. The cooperative attacking behavior of a golden jackal pair is illustrated in Fig. 2. The correspondence between the problem region and GJO region is described in Table 1.

Fig. 2

A Pair of golden jackals, B golden jackal searching for prey, C stalking and enclosing of prey, D and E pouncing on prey

Table 1 Correspondence between the problem region and GJO region

3.1 Search space formulation

In GJO, we initialize the random prey population to obtain the uniformly distributed candidate solutions in the search region. The initial solution is computed as:

$$ Y_{0} = Y_{\min } + {\text{rand}}(Y_{\max } - Y_{\min } ) $$

(4)

where $Y_{0}$ expresses the positions of the initial golden jackal population, ${\text{rand}}$ expresses a uniform arbitrary vector in [0,1], and $Y_{\min }$ and $Y_{\max }$ express the lower and upper limits of the solution, respectively.

The first and second fittest individuals are a jackal pair, and the initial matrix individual is computed as:

$$ {\text{Prey}} = \left[ {\begin{array}{*{20}c} {Y_{1,1} } & {Y_{1,2} } & \cdots & {Y_{1,d} } \\ {Y_{2,1} } & {Y_{2,2} } & \cdots & {Y_{2,d} } \\ \vdots & \vdots & \vdots & \vdots \\ {Y_{n,1} } & {Y_{n,2} } & \cdots & {Y_{n,d} } \\ \end{array} } \right] $$

(5)

where $Y_{i,j}$ expresses the jth dimension of the ith prey, $n$ is the entire quantity of prey, and $d$ represents the variables of the situation. The matrix is computed as:

$$ F_{\text{OA}} = \left[ {\begin{array}{*{20}c} {f(Y_{1,1} ;Y_{1,2} ;Y_{1,d} )} \\ {f(Y_{2,1} ;Y_{2,2} ;Y_{2,d} )} \\ \vdots \\ {f(Y_{n,1} ;Y_{n,2} ;Y_{n,d} )} \\ \end{array} } \right] $$

(6)

where $F_{OA}$ is a matrix that includes the fitness values of the prey and $f$ expresses the fitness function. The fittest individual is interpreted as a male jackal, and the second fittest is interpreted as a female jackal. The jackal pair represents a single individual position.

3.2 Exploration phase or searching for prey

Golden jackals can predict and capture prey according to their own attacking characteristics, but the prey occasionally quickly evades and escapes the foraging jackals. Hence, the female jackals follow the male jackals to wait and search for other prey in the search region. The positions are computed as:

$$ Y_{1} (t) = Y_{{\text{M}}} (t) - E \cdot \left| {Y_{{\text{M}}} (t) - rl \cdot {\text{Prey}}(t)} \right| $$

(7)

$$ Y_{2} (t) = Y_{{{\text{FM}}}} (t) - E \cdot \left| {Y_{{{\text{FM}}}} (t) - rl \cdot {\text{Prey}}(t)} \right| $$

(8)

where $t$ is the current iteration, ${\text{Prey}}(t)$ is the position vector, and $Y_{{\text{M}}} (t)$ and $Y_{{{\text{FM}}}} (t)$ are the current positions of the male and female jackals, respectively. $Y_{1} (t)$ and $Y_{2} (t)$ are the updated positions of the male and female jackals.

The evading energy of prey $E$ is computed as:

$$ E = E_{1} \cdot E_{0} $$

(9)

where $E_{1}$ expresses the diminishing energy of the prey and $E_{0}$ is the original state of the energy.

$$ E_{0} = 2 \cdot r - 1 $$

(10)

where $r$ is an arbitrary value in [0,1].

$$ E_{1} = c_{1} \cdot (1 - {{(t} \mathord{\left/ {\vphantom {{(t} T}} \right. \kern-0pt} T})) $$

(11)

where $T$ is the maximum number of iterations, $c_{1}$ is a constant with a value of 1.5, and $E_{1}$ linearly decreases from 1.5 to 0 as iteration proceeds.

$rl$ is an arbitrary vector based on the Lévy distribution, which is computed as:

$$ rl = 0.05 \cdot {\text{LF}}(y) $$

(12)

$LF$ is the fitness function of the Levy flight, which is computed as:

$$ {\text{LF}}(y) = {{0.01 \times (\mu \times \sigma )} \mathord{\left/ {\vphantom {{0.01 \times (\mu \times \sigma )} {\left( {\left| {v^{{{{(1} \mathord{\left/ {\vphantom {{(1} \beta }} \right. \kern-0pt} \beta })}} } \right|} \right)}}} \right. \kern-0pt} {\left( {\left| {v^{{{{(1} \mathord{\left/ {\vphantom {{(1} \beta }} \right. \kern-0pt} \beta })}} } \right|} \right)}};\;\;\;\sigma = \left( {\frac{{\Gamma (1 + \beta ) \times \sin {{(\pi \beta } \mathord{\left/ {\vphantom {{(\pi \beta } 2}} \right. \kern-0pt} 2})}}{{\Gamma \left( {\frac{1 + \beta }{2}} \right) \times \beta \times \left( {2^{{\frac{\beta - 1}{2}}} } \right)}}} \right)^{{{1 \mathord{\left/ {\vphantom {1 \beta }} \right. \kern-0pt} \beta }}} $$

(13)

where $\mu$ and $v$ are arbitrary values in (0,1) and $\beta$ is a constant with a value of 1.5.

The updated positions of the golden jackals are computed as:

$$ Y(t + 1) = \frac{{Y_{1} (t) + Y_{2} (t)}}{2} $$

(14)

3.3 Exploitation phase or enclosing and pouncing on prey

The evading energy of the prey will swiftly decrease when it is attacked by a jackal pair, and the golden jackals instantly enclose and capture the prey. The positions are computed as:

$$ Y_{1} (t) = Y_{{\text{M}}} (t) - E \cdot \left| {rl \cdot Y_{{\text{M}}} (t) - {\text{Prey}}(t)} \right| $$

(15)

$$ Y_{2} (t) = Y_{{{\text{FM}}}} (t) - E \cdot \left| {rl \cdot Y_{{{\text{FM}}}} (t) - {\text{Prey}}(t)} \right| $$

(16)

where $t$ is the current iteration, ${\text{Prey}}(t)$ is the position vector, and $Y_{{\text{M}}} (t)$ and $Y_{{{\text{FM}}}} (t)$ are the current positions of the male and female jackals, respectively. $Y_{1} (t)$ and $Y_{2} (t)$ are the refreshed positions of the male and female jackals. Some parameters have been provided in the previous section, such as $E$ and $rl$. Finally, the position update of the golden jackal is computed by Formula (17).

To better represent the optimization process, the pseudocode of GJO is depicted in Algorithm 1.

4 EGJO

To address the limitations of weak optimization efficiency and slow search speed, the elite opposition-based learning technique and the simplex technique are incorporated into the basic GJO to achieve supplementary superiority and avoid search stagnation, which increases the convergence rate and enhances the computation precision.

4.1 Elite opposition-based learning technique

The elite opposition-based learning technique is an efficacious and stable approach that increases the population variety, broadens the search region, avoids premature convergence and strengthens the global search. The search technique utilizes the feasible or reverse solution to assess the fitness value of prey and then sorts out the best individual to complete the iteration. Assuming that the search agent with the optimal fitness value is regarded as an elite individual, the elite individual is computed as $x_{{\text{e}}} = (x_{{{\text{e}},1}} ,x_{{{\text{e}},2}} , \ldots ,x_{{{\text{e}},D}} )$, the feasible solution is computed as $x_{i} = (x_{i,1} ,x_{i,2} , \ldots ,x_{i,D} )$, and the reverse solution is computed as $x_{i}^{\prime } = (x_{i,1}^{\prime } ,x_{i,2}^{\prime } , \ldots ,x_{i,D}^{\prime } )$. The formula is:

$$ x_{i,j}^{\prime } = k \cdot (da_{j} + db_{j} ) - x_{e,j} , \, i = 1,2, \ldots ,n; \, j = 1,2, \ldots ,D $$

(17)

where $n$ expresses the population size, $D$ expresses the problem dimension, $k$ expresses an arbitrary value such that $k \in (0,1)$, and $da_{j}$ and $db_{j}$ express the dynamic limits of the $j{\text{th}}$ decision variable and are computed as:

$$ da_{j} = \min (x_{i,j} ), \, db_{j} = \max (x_{i,j} ) $$

(18)

The dynamic limit can save the best solution and adjust the search region of the inverse solution. The search agent $x_{i,j}^{^{\prime}}$ is computed as:

$$ x_{i,j}^{\prime } = {\text{rand}}(da_{j} ,db_{j} ),\;{\text{if }}x_{i,j}^{\prime } < da_{j} {\text{ or }}x_{i,j}^{\prime } > db_{j} $$

(19)

4.2 Simplex technique

The simplex technique is a significant and practical method that accelerates the search process, improves the computational precision, increases the optimization depth and strengthens the local search. The simplex technique retains the best solution by evaluating the feasible solution with respect to the initial solution. The simplex technique schematic is illustrated in Fig. 3, and the optimization stages are computed as follows:

Fig. 3

Simplex technique schematic

Step 1 Estimate the fitness value of each prey, where $X_{g}$ expresses the optimal value, $X_{b}$ expresses the suboptimal value and $X_{s}$ expresses the refreshed value; then, evaluate the fitness values $f(X_{g} )$, $f(X_{b} )$ and $f(X_{s} )$.

Step 2 Estimate the central point $X_{{\text{c}}}$ between $X_{g}$ and $X_{b}$.

$$ X_{{\text{c}}} = \frac{{X_{g} + X_{b} }}{2} $$

(20)

Step 3 Estimate and obtain the reflection point $X_{{\text{r}}}$ based on $X_{{\text{c}}}$ and $X_{s}$, and evaluate the fitness value $f(X_{{\text{r}}} )$.

$$ X_{{\text{r}}} = X_{{\text{c}}} + \alpha (X_{{\text{c}}} - X_{s} ) $$

(21)

where $\alpha$ expresses reflectivity with a value of 1.

Step 4 If $f(X_{g} ) > f(X_{{\text{r}}} )$, extend the current solution.

$$ X_{{\text{e}}} = X_{{\text{c}}} + \gamma (X_{{\text{r}}} - X_{{\text{c}}} ) $$

(22)

where $X_{{\text{e}}}$ expresses the extension point and $\gamma$ expresses the extension coefficient with a value of 1.5. Then, evaluate the fitness value $f(X_{{\text{e}}} )$. If $f(X_{g} ) > f(X_{{\text{e}}} )$, modify $X_{s}$ with $X_{{\text{e}}}$; otherwise, modify $X_{s}$ with $X_{{\text{r}}}$.

Step 5 If $f(X_{s} ) < f(X_{{\text{r}}} )$, perform a compression operation to obtain the best solution.

$$ X_{t} = X_{{\text{c}}} + \beta (X_{s} - X_{{\text{c}}} ) $$

(23)

where $X_{t}$ expresses the compression point and $\beta$ expresses the compression coefficient with a value of 0.5. If $f(X_{s} ) > f(X_{t} )$, modify $X_{s}$ with $X_{t}$; otherwise, modify $X_{s}$ with $X_{r}$.

Step 6 If $f(X_{s} ) > f(X_{{\text{r}}} ) > f(X_{g} )$, a further compression operation is required to obtain a contraction point $X_{w}$.

$$ X_{w} = X_{c} - \beta (X_{s} - X_{{\text{c}}} ) $$

(24)

where $\beta$ expresses the contraction coefficient with a value of 0.5. If $f(X_{s} ) > f(X_{w} )$, modify $X_{s}$ with $X_{w}$; otherwise, modify $X_{s}$ with $X_{{\text{r}}}$.

EGJO not only achieves supplementary superiority to enhance the breadth and depth of the search but also arbitrarily switches between exploration and exploitation to yield a greater computation accuracy. The pseudocode of EGJO is shown in Algorithm 2.

5 EGJO-based adaptive IIR system identification

EGJO effectively utilizes the three search mechanisms to handle IIR system identification, and the purpose is to minimize the error fitness value and obtain the best control parameters. The correspondence between the IIR system identification region and EGJO region is described in Table 2. EGJO based on adaptive IIR system identification is depicted in Algorithm 3. The flowchart of EGJO for adaptive IIR system identification is illustrated in Fig. 4.

Table 2 Correspondence between the IIR system identification region and EGJO region

Fig. 4

Flowchart of EGJO for adaptive IIR system identification

The computational complexity of each algorithm is considered to be the evaluation function that best links the input value with the method’s run-time. Big-O notation is an effectual metric to analyze the optimization performance and evaluate computational complexity. The elite opposition-based learning technique and the simplex technique are added to the basic GJO to improve stability. EGJO is based on the cooperative attacking behavior of golden jackals, which simulates searching for prey, stalking and enclosing prey, and pouncing on prey to effectively solve a complicated optimization problem. This section provides a concise explanation of EGJO’s computational complexity. EGJO has three important steps: initialization, calculating the fitness value and updating the positions of the golden jackal-based exploration phase and exploitation phase. In EGJO, $N$ is the population size, $T$ is the maximum iteration number, and $D$ is the optimization dimension. The computational complexity of initialization is $O(N)$. The computational complexity of refreshing the golden jackals’ positions is $O(T \times N) + O(T \times N \times D)$, which includes searching for prey and updating the positions of all jackals. Therefore, the computational complexity of EGJO requires $O(N \times (T + T \times D + 1))$, and EGJO strikes a balance between exploration and exploitation to discover the best solution.

6 Experimental results and analysis

6.1 Experimental setup

The numerical experiment is performed on a machine with an Intel Core i7-8750H 2.2 GHz CPU, a GTX1060, and 8 GB memory running Windows 10. MATLAB R2018b is employed to design each algorithm.

6.2 Parameter settings

To demonstrate its practicality and availability, EGJO is employed to perform IIR system identification. Additionally, EGJO is compared with other algorithms, such as the AOA, GTO, HHO, MDWA, RSO, WOA, TSA and GJO. The parameters are representative experimental values determined from the source articles. The initial parameters of each algorithm are described in Table 3.

Table 3 Initial parameters of each algorithm

6.3 Results and analysis

Three experimental datasets utilizing various orders of IIR models are employed to examine the overall optimization efficiency of EGJO. Case 1 contains a second-order system and a first-order IIR filter model. Case 2 contains a second-order system and a second-order IIR filter model. Case 3 contains a higher-order system and a higher-order IIR filter model. The fitness function is computed according to the mean squared error (MSE), and the purpose of optimization is to determine better control parameters and the best solution.

For case 1, each algorithm utilizes a first-order IIR filter model to identify a second-order system, and the transfer functions of the second-order system $H_{P} (z)$ and first-order IIR filter model $H_{{\text{M}}} (z)$ are computed as:

$$ H_{P} (z) = \frac{{0.05 - 0.4z^{ - 1} }}{{1 - 1.1314z^{ - 1} + 0.25z^{ - 2} }} $$

(25)

$$ H_{{\text{M}}} (z) = \frac{b}{{1 - az^{ - 1} }} $$

(26)

For case 2, each algorithm utilizes a second-order IIR filter model to identify a second-order system, and the transfer functions of the second-order system $H_{P} (z)$ and second-order IIR filter model $H_{M} (z)$ are computed as:

$$ H_{P} (z) = \frac{1}{{1 - 1.4z^{ - 1} + 0.49z^{ - 2} }} $$

(27)

$$ H_{{\text{M}}} (z) = \frac{b}{{1 + a_{1} z^{ - 1} + a_{2} z^{ - 2} }} $$

(28)

For case 3, each algorithm utilizes a higher-order IIR filter model to identify a higher-order system, and the transfer functions of the higher-order system $H_{P} (z)$ and higher-order IIR filter model $H_{{\text{M}}} (z)$ are computed as:

$$ H_{P} (z) = \frac{{1 - 0.4z^{ - 2} - 0.65z^{ - 4} + 0.26z^{ - 6} }}{{1 - 0.77z^{ - 2} - 0.8498z^{ - 4} + 0.6486z^{ - 6} }} $$

(29)

$$ H_{{\text{M}}} (z) = \frac{{b_{0} + b_{1} z^{ - 1} + b_{2} z^{ - 2} + b_{3} z^{ - 3} + b_{4} z^{ - 4} }}{{1 + a_{1} z^{ - 1} + a_{2} z^{ - 2} + a_{3} z^{ - 3} + a_{4} z^{ - 4} }} $$

(30)

EGJO is applied to perform IIR system identification. The purpose is to obtain the best control parameters and the minimum fitness value. The experimental results (MSE) of each algorithm are described in Tables 4, 5 and 6. The parameter estimation of each algorithm is described in Tables 7, 8 and 9. For each algorithm, the population size is 30, the maximum iteration number is 500, and the number of independent runs is 30. Best, worst, mean and Std represent the optimal value, worst value, mean value and standard deviation, respectively, which are taken as fundamental indicators to analyze robustness and sustainability. The optimal value is shown in bold, and the ranking is determined by the standard deviation. The elite opposition-based learning technique increases the population variety, broadens the search region, delays search stagnation and enhances the global search. The simplex technique accelerates the search process, improves the computational precision, increases the optimization depth and enhances the local search. EGJO combines the characteristics of these two search mechanisms to achieve supplementary superiority and enhance the total search ability. For cases 1 and 2, the optimal value is viewed as the minimum mean squared error (MSE) of the IIR filter model, which directly reflects the computational accuracy and optimization performance. The optimal values of EGJO are superior to those of the AOA, GTO, HHO, MDWA, RSO, WOA, TSA and GJO. The worst values and mean values of EGJO are superior to those of the other algorithms, which demonstrates that EGJO has strong robustness and superiority. The algorithm’s robustness and reliability are directly reflected in the standard deviation. The algorithm’s dependability increases with decreasing standard deviation. The standard deviations of EGJO are the smallest among all the algorithms, and its ranking is first, which demonstrates that EGJO has cost advantages and reliability. EGJO can switch exploration and exploitation to obtain the best control parameters. For case 3, the optimal values, worst values and mean values of EGJO are superior to those of the other algorithms. The standard deviations of EGJO are larger than those of GTO and HHO and better than those of the AOA, MDWA, RSO, WOA, TSA and GJO. The parameters of EGJO are better than those of the other algorithms. The experimental results imply that EGJO has sufficient robustness and reliability to achieve higher computation precision and better control parameters.

Table 4 Experimental results (MSE) of each algorithm for case 1

Table 5 Experimental results (MSE) of each algorithm for case 2

Table 6 Experimental results (MSE) of each algorithm for case 3

Table 7 The parameter estimation of each algorithm for case 1

Table 8 The parameter estimation of each algorithm for case 2

Table 9 The parameter estimation of each algorithm for case 3

The elite opposition-based learning technique and the simplex technique are added to the basic GJO to obtain complementary advantages to solve various optimization problems. The elite opposition-based learning technique avoids search stagnation and enhances the global search by increasing the population variety and expanding the search region. The simplex technique improves the computational precision and enhances the local search by accelerating the optimization process and increasing the search depth. EGJO has the characteristics of simple principles, easy implementation, few optimization parameters, avoidance of search stagnation, fast convergence rate, high computation precision, strong stability and robustness. EGJO utilizes effectual search mechanisms to switch between exploration and exploitation and then determine the optimal control parameters and the global optimal solution. The convergence curves of the algorithms are illustrated in Fig. 5a, c, e. The convergence rate and computational precision of EGJO are superior to those of the other algorithms, which indicates that EGJO has strong robustness and dependability. The ANOVA tests of the algorithms are illustrated in Fig. 5b, d, f. For cases 1 and 2, the standard deviations of EGJO are lower than those of the other algorithms. For case 3, the standard deviations of EGJO are higher than those of GTO and HHO and lower than those of the AOA, MDWA, RSO, WOA, TSA and GJO. The experimental results reveal that EGJO has excellent reliability and robustness to achieve a better convergence precision and lower standard deviation; it is an efficacious and constructive method for solving the IIR system identification problem.

Fig. 5

Experimental results for cases 1–3

The results of the p-value Wilcoxon rank-sum test are described in Table 10. The histograms of the p value test are illustrated in Fig. 6. Wilcoxon’s rank-sum test is adapted to check whether there is a significant distinction between EGJO and the other algorithms [52]. $p < 0.05$ shows that the distinction is significant. $p \ge 0.05$ shows that the distinction is not significant. The experimental results reflect that there is a remarkable distinction between EGJO and the other algorithms, and the data have a particular level of reliability and authenticity that is not generated by chance.

Table 10 Results of the p-value Wilcoxon rank-sum test

Fig. 6

Experimental results of the p-value test for cases 1–3

Statistically, EGJO is derived from the cooperative attacking behavior of golden jackals to simulate searching for prey, stalking and enclosing prey, and pouncing on prey to determine the best solution. EGJO is employed to perform IIR system identification for the following reasons. First, the elite opposition-based learning technique and the simplex technique are integrated into the basic GJO. The elite opposition-based learning technique boosts the population variety, broadens the search region, decreases premature convergence and strengthens the global search. The simplex technique accelerates the search process, improves the computational precision, increases the optimization depth and strengthens the local search. EGJO achieves supplementary superiority to avoid falling into a local optimum. Second, EGJO has efficient and unique optimization mechanisms to update the positions of the golden jackals and reach the optimal solution. The control parameter $\left| E \right|$ is used to adjust exploration and exploitation. If $\left| E \right| \ge 1$, EGJO utilizes the search for prey to predict and find the prey, which enhances the exploration ability. If $\left| E \right| < 1$, EGJO utilizes enclosing and pouncing on the prey to adjust its position and capture the prey. Third, EGJO has simple principles, easy implementation, few optimization parameters, avoidance of search stagnation, a fast convergence rate, high computation precision and excellent stability and robustness. To summarize, EGJO balances exploration and exploitation to arrive at the best fitness value, which is a constructive and efficacious approach for performing IIR system identification.

7 Conclusions and future research

To address the shortcomings of premature convergence, a slow convergence rate and low computation precision faced by basic GJO, EGJO based on the elite opposition-based learning technique and the simplex technique are proposed to perform IIR system identification. The intention is to discover the optimal parameters and global optimal solution. The elite opposition-based learning technique increases the population variety and broadens the search region to avoid search stagnation and enhance the exploration ability. The simplex technique accelerates the optimization process and increases the search depth to improve the computational precision and enhance the exploitation ability. Therefore, EGJO can not only utilize the mechanisms of searching for prey, stalking and enclosing prey, and pouncing on prey to achieve supplementary superiority and avoid premature convergence but also has strong robustness and adaptability to balance exploration and exploitation and determine the best value. To verify the practicality and availability of EGJO, EGJO is compared with AOA, GTO, HHO, MDWA, RSO, WOA, TSA and GJO through three sets of experiments. EGJO has strong global and local abilities to avoid premature convergence and obtain the best fitness value. The experimental results demonstrate that EGJO has a faster convergence rate, higher computation precision, stronger robustness and better optimization efficiency in discovering the global optimal solution. Additionally, EGJO is an efficacious and constructive approach for performing IIR system identification.

In future research, we will apply and evaluate EGJO on at least one to three real-world problems. We will further verify the effectiveness and feasibility of EGJO by comparing it to the latest works. We will evaluate EGJO on all 23 benchmark functions. We will introduce efficacious search mechanisms, unique coding methods and hybrid algorithms to achieve supplementary superiority and enhance the optimization ability, which will improve the convergence rate and the computation precision. Additionally, the modified GJO will be used to study the quality detection of the typical understory crops of Dendrobium huoshanense and Camellia oleifera with local characteristics. We will achieve the rapid collection of multidimensional data of the internal composition and external representation of understory crops and use hyperspectral technology and image processing methods to perform the intelligent detection and classification of understory crops. This will enable fast and accurate grading of the quality of understory crops, which is of key significance for improving the added value of crops.