1 Introduction

In the last few years, the adaptive infinite impulse response (IIR) filter has become very popular and has increasingly attracted the attention of many researchers and scholars [1, 2]. It is very popular in diverse fields of application, such as control systems [3], communication [4], signal processing [5], and image processing [6]. In the case of several system identification problems, adaptive IIR filters tend to model the unknown system in accordance with some error function between the output of the candidate model and the output of the plant [7]. To acquire an ideal identification, it is necessary to search the appropriate filter parameters to enable the error surface between the output of the adaptive filter and the output of the plant to achieve the minimum value.

There is a major concern that the error surfaces produced by the IIR filter are typically multimodal, which makes them difficult to minimize, and they are quite easily trapped in local minima. To overcome this problem, researchers have attempted to use efficient and robust evolutionary computing algorithms inspired by nature for IIR system identification. In this case, IIR system identification is modeled as a minimization problem and then solved using an evolutionary computing algorithm [8]. For example, Krusienski and Jenkins [2] used the particle swarm optimization algorithm (PSO), which is a popular and classical evolutionary computing algorithm inspired by the social behavior of flocking birds, to create the adaptive IIR filter structure. Later, Zou et al. [7] proposed an improved version of PSO called IPSO to process IIR system identification. The simulation results indicated the efficiency of IPSO compared with different versions of the PSO algorithm. Patwardhan et al. [9] used the cuckoo search algorithm (CS), which is inspired by the lifestyle of birds, to handle IIR feedback system identification. Panda et al. [10] exploited the cat swarm optimization algorithm, which is derived from the behavior of cats, to handle different cases of IIR modeling. Furthermore, Saha et al. [11] used the gravitational search algorithm (GSA), which is based on the law of gravity, to solve the IIR model, whereas Karaboga [12] used IIR models to test the efficiency of the artificial bee colony algorithm, which is inspired by the behavior of bees searching for food. The results reported in these studies show that these evolutionary computing algorithms can efficiently solve the IIR system identification problem. Despite the merits of the aforementioned studies, according to the well-known no-free-lunch theorem (NFL), no single optimization algorithm exists that can outperform all other algorithms for all optimization problems [13]. Because the IIR model has different cases, it is possible that an algorithm performs well on a test case, but poorly on another case. Therefore, this has stimulated researchers and scholars to investigate the efficiency of new algorithms to solve the IIR model identification problem and problems in other fields.

The whale optimization algorithm (WOA) is a newly proposed metaheuristic introduced by Mirjalili et al. [14] based on the bubble-net feeding technique of baleen whales. Compared with other algorithms, the WOA can provide competitive results and has superior performance. The merits of this algorithm are that it is easy to implement, the structure is very simple, and it requires few control parameters. Thus, the original version of the WOA has attracted the attention of many scholars and has been applied in a wide variety of application studies [15,16,17,18,19,20]. Although the basic WOA has been shown to perform well in the aforementioned studies, when compared with other traditional algorithms, it still has some drawbacks, such as slow convergence and becoming stuck easily in local optima. Consequently, different WOA variants have been proposed to improve its performance. An improved WOA was developed by Oliva et al. [21], who combined the features of the standard WOA with chaotic maps to improve performance and applied it to the parameter estimation of photovoltaic cells. Hu et al. [22] also proposed a modified version of WOA. They introduced the inertia weight into the WOA to improve performance, tested the modified algorithm on benchmark functions, and predicted the daily air quality index. Moreover, Trivedi et al. [23] developed a new variant of the WOA using a hybridization of the PSO algorithm called PSO-WOA for global numerical function optimization. Another novel adaptive WOA algorithm for global optimization was proposed by Bhesdadiya et al. [24] and used as an adaptive mechanism to update the whale’s position. A Kaveh [25] proposed an enhanced WOA by modifying the updating mechanism of the basic WOA and applied it to the size optimization of a skeletal structure. Mafarja and Mirjalili [26] proposed a hybrid WOA with simulated annealing and used it for feature selection. Considering all these improvements to the basic WOA, we found that they are appropriate for different types of practical applications; however, these WOA variants are not suitable for solving all classes of practical problems according to the NFL [13].

In this paper, we propose a modified WOA called RWOA that integrates a ranking-based mutation operator with the basic WOA to make the basic WOA converge faster, and more robust and suitable for practical applications. The RWOA was applied to solve the IIR model identification problem and was compared with existing evolutionary computing algorithms. The simulation results demonstrated clearly that our proposed RWOA exhibited superior identification performance.

The remainder of this paper is organized as follows: In Sect. 2, we present the problem of adaptive IIR filter model identification. In Sect. 3, we present the steps involved in whale optimization. In Sect. 4, we present our proposed RWOA. We describe the simulation results and analyze them in Sect. 5. Finally, we discuss our conclusions and future work in Sect. 6.

2 Adaptive IIR Filter Model

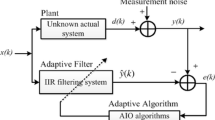
The adaptive IIR filter has been widely used in system identification because a number of problems encountered in signal processing can be modeled as a system identification problem. For the system identification configuration, to make the filter’s output close to the output of an unknown system, the main task of the adaptive algorithm is to search for appropriate filter coefficients. The block diagram for an adaptive IIR system identification is shown in Fig. 1.

Fig. 1
figure 1

Adaptive IIR filter for system identification

Full size image

The input–output relationship of the IIR system can be described as follows [27, 28]:

$$ \sum\limits_{l = 0}^{L} {a_{1} y(n - l) = \sum\limits_{k = 0}^{K} {b_{k} x(n - k)} } $$
(1)

where \( x(n) \) and \( y(n) \) denote the input and output of the filter, respectively, and \( L( \ge K) \) represents the filter’s order. Let \( a_{0} = 1 \). Then the transfer function of this IIR filter is defined as

$$ H\left( z \right) = \frac{{\sum {_{k = 0}^{K} b_{k} z^{ - k} } }}{{1 + \sum {_{l = 1}^{L} a_{l} z^{ - l} } }} . $$
(2)

In the design method, \( H_{\text{p}} (z) \) is the transfer function of the unknown plant and \( H_{\text{m}} (z) \) is the transfer function of the IIR model. From Fig. 1, it is clear that the output of the IIR filter is \( y(n) \); \( d({\text{n}}) = y_{0} (n) + v(n) \) is the overall response of the unknown IIR plant; \( y_{0} (n) \) is the output of the unknown plant; and \( v(n) \) is additive white Gaussian noise. The equation \( e(n) = d(n) - y(n) \) represents the error signal. Hence, the main goal of identification is to formulate a minimization problem that can be defined as the cost function \( J(w) \) as follows:

$$ {\text{MSE}} = J(w) = \frac{1}{N}\sum\limits_{n = 1}^{N} {e^{2} (n)} , $$
(3)

where \( N \) denotes the number of input samples used for the calculation of the objective function. The mean square error (MSE) is equal to \( J(w) \), which produces the coefficient vectors of the IIR model, where \( w = (a_{1} , \ldots a_{L} ,b_{0} ,b_{1} , \ldots b_{K} )^{T} \). The objective of the algorithm is to minimize the MSE through adjusting coefficient vector \( w \) of transfer function \( H_{\text{p}} (z) \).

3 Whale Optimization Algorithm (WOA)

The WOA is a novel metaheuristic algorithm, which was proposed by Mirjalili and Lewis [14]. The WOA simulates the special foraging behavior of humpback whales, whereby they search for and attack prey (herds and small fish), which is called the bubble-net hunting strategy. Figure 2 shows the bubble-net hunting model.

Fig. 2
figure 2

Bubble-net hunting behavior of humpback whales

Full size image

Figure 2 clearly shows that the humpback whale hunts prey by creating distinctive bubbles and swimming in a “9”-shaped path. The motivation of the WOA is this special hunting method. In addition to simulating the bubble-net strategy in the WOA, the whale also has another strategy, which is simulating encircling the prey. This can be summarized as follows: first, the humpback whale observes the location of the prey (fish herds) and then encircles them to hunt them using the bubble-net strategy. The formulas of the two hunting strategies that is, the encircling prey strategy and bubble-net feeding strategy, proposed in the WOA are defined as

$$ \overrightarrow {X} (t + 1) = \left\{ {\begin{array}{*{20}l} {\overrightarrow {X*} (t) - \overrightarrow {A} \cdot \overrightarrow {D} } \hfill & {{\text{if}}\,p < 0.5} \hfill \\ {\overrightarrow {D'} \cdot e^{bl} \cdot \cos (2\pi l) + \overrightarrow {X*} (t)} \hfill & {{\text{if}}\,p \ge 0.5} \hfill \\ \end{array} } \right. $$
(4)

where p is an arbitrary number in \( [0,1] \), \( \overrightarrow {D'} = \left| {\overrightarrow {X*} (t) - \overrightarrow {X} (t)} \right| \) represents the length from the ith whale to the best position of the leader whale (the best location acquired thus far), l denotes a random value in \( \left[ { - 1,1} \right] \), \( b \) denotes a constant that defines the shape of a logarithmic spiral, \( \cdot \) denotes constituent-by-constituent multiplication, \( t \) denotes the current iteration, \( \overrightarrow {D} = \left| {\overrightarrow {C} \cdot \overrightarrow {X*} (t) - \overrightarrow {X} (t)} \right| \), \( X^{*} \) denotes the position vector of the optimum measure acquired thus far, and \( X(t) \) denotes the position vector. Note that \( X^{*} \) must be updated at every step of the optimization if there exists a better solution. Here, \( \overrightarrow {A} = 2\overrightarrow {a} \cdot \overrightarrow {r} - \overrightarrow {a} \; \), \( \overrightarrow {C} = 2 \cdot \overrightarrow {r} \; \), and the values of \( \overrightarrow {A} \) are in the range \( \left[ { - a,a} \right] \), where the value of \( \overrightarrow {a} \) linearly decreases from 2 to 0 because it is calculated as \( a = 2 - 2*t/t_{\text{max} } \). Note that in the exploration and exploitation stages, the value of \( \overrightarrow {a} \) remains the same and the value of r is in the range [0, 1].

Equation (4) contain two formulas, where the first is the mathematical model of the encircling prey strategy of the humpback whale and the second is the mathematical model of the bubble-net hunting strategy. Note that humpback whales swim around prey inside a contracting circle or move with a conical logarithmic spiral motion to prey on fish herds simultaneously. We assume that the humpback whale adopts these two hunting mechanisms with a probability of 50%, and then variable p switches between these two components with a 50% probability. We know that both the exploitation stage and exploration stage are the main stages of the optimizing problem in population-based algorithms. Therefore, in the WOA, vector \( \overrightarrow {A} \) is used for exploration to scan for prey, and its value is greater than 1 or less than − 1. When \( \left| {\overrightarrow {A} } \right| \ge 1 \), the whales are forced into exploration to determine the global optimum and eliminate many local minima. The mathematical model is formulated as

$$ \overrightarrow {D} = \left| {\overrightarrow {C} \cdot \overrightarrow {{X_{\text{rand}} }} - \overrightarrow {X} } \right| $$
(5)
$$ \overrightarrow {X} (t + 1) = \overrightarrow {{X_{\text{rand}} }} - \overrightarrow {A} \cdot \overrightarrow {D} $$
(6)

where \( \overrightarrow {{X_{\text{rand}} }} \) is chosen from the current generation and indicates a random position vector (a random whale). When \( \left| {\overrightarrow {A} } \right| \ge 1 \), the WOA focuses on exploration using Eq. (6), so the whale updates its position according to \( \overrightarrow {{X_{\text{rand}} }} \), which is a stochastically chosen whale, whereas when \( \left| {\overrightarrow {A} } \right| < 1 \), the WOA focuses on exploitation, and the whale updates its position based on the best searching agent acquired thus far. The flowchart of the WOA is illustrated in Fig. 3.

Fig. 3
figure 3

Flowchart of the WOA

Full size image

4 Modified Whale Optimization Algorithm with Ranking-Based (RWOA)

As mentioned, in this paper, we present a modified version of the WOA called the RWOA for solving IIR system identification problems. The RWOA combines a ranking-based mutation operator with the pure WOA to speed up the rate of convergence and results in smoothly balanced intensification and diversification. Therefore, this approach improves the quality of the basic WOA. In the following subsection, we first briefly review the ranking-based mutation operator and then present our RWOA in detail.

4.1 Ranking-Based Mutation Operator

  1. 1.

    Ranking Assignment For the purpose of choosing information about a good search agent from the WOA population, it is necessary to assign a rank for each whale according to the related fitness. First, the population (each whale) is sorted in ascending order (i.e., from best to worst) according to the fitness of each individual (each whale). The rank of an individual is assigned as

    $$ R_{i} = N_{\text{p}} - i,\quad i = 1,2, \ldots ,N_{\text{p}} , $$
    (7)

    where \( N_{\text{p}} \) indicates the number of the population. From Eq. (7), the highest rank is assigned to the best individual (best whale) in the current population and then other individuals acquire their corresponding ranking order.

  2. 2.

    Selection Probability When each individual is ranked, selection probability \( P_{i} \) of the ith individual (whale) is modeled as

    $$ P_{i} = \frac{{R_{i} }}{{N_{\text{p}} }},\quad i = 1,2, \ldots ,N_{\text{p}} . $$
    (8)

    Algorithm 1 presents the ranking-based mutation operator of “DE/rand/1.” In nature, useful information is always contained in good species; hence, good species always have a greater probability of being selected to propagate a new generation. Similar to nature, in accordance with the approach described in Algorithm 1, it is clear that the higher the ranking of the individual, the greater the probability that the individual is chosen as the base vector or terminal vector in the mutation operator to propagate useful information about the population to the offspring. Note that the starting vector is not selected based on its selection probability because, assuming that both the vectors in the difference vector are selected from better vectors, the searching step-size of the difference vector may have a probability that decreases quickly, which results in premature convergence [29, 30].

    figure a

4.2 Main Procedure of the RWOA

The RWOA combines the aforementioned ranking-based mutation operator with the basic WOA. The main procedure of the proposed enhanced RWOA is summarized in Fig. 4.

Fig. 4
figure 4

Flowchart of the enhanced RWOA

Full size image

4.2.1 Complexity Analysis

In this section, both the time and space complexity of the RWOA are analyzed.

Time Complexity The time complexity of the RWOA is briefly analyzed in this subsection. The RWOA contains five major steps: initialization, ranking-based mutation, encircling prey (exploration phase), attacking prey (exploitation phase), and halting judgment. In the RWOA, N is the number of search agents, T is the maximum number of iterations, and D is the dimension of the problem. The initialization step contains a double loop (N and D times), so its time complexity is O(N * D). The ranking-based mutation stage, exploration phase, and exploitation phase all contain a triple loop (N, D, and T times), so the time complexity for each step is O(N * D * T). The time complexity of the last step, that is, the halting judgment step, is O(1). Thus, the total time complexity of the proposed RWOA is O(N * D * T). Table 1 shows a comparison of the time complexity for the RWOA and WOA.

Table 1 Comparison of the time complexity
Full size table

Space Complexity The proposed RWOA uses the number of search agents (whales), which is N, to calculate the space complexity, and the dimension of the problem to be solved is D. Therefore, the total space complexity of the RWOA is O(N * D). The WOA also uses N search agents to calculate the space complexity, so its related total space complexity is O(N * D), which is the same as that of the RWOA.

4.2.2 Advantages of the RWOA

Our proposed enhanced RWOA has some major advantages, which are summarized as follows:

  1. (A)

    Because good parents are more likely to be chosen, the ranking-based mutation operator is quite useful for improving the exploitation ability of the enhanced RWOA; hence, it enhances the entire performance compared with the basic WOA algorithm.

  2. (B)

    Our RWOA has an uncomplicated structure, which means that it does not destroy the simple structure of the basic WOA. The enhanced RWOA only requires a small amount of extra execution time when ranking the population and choosing individuals, but the extra computational cost is negligible. According to the complexity analysis of the RWOA and WOA, the enhanced RWOA does not significantly change the entire complexity of the pure WOA.

5 Modified RWOA for IIR System Identification

In this section, our proposed enhanced RWOA algorithm is used to solve the IIR system identification problem, which is mentioned in Sect. 2. In this case, \( N \) whales, which search in the search zone, represent the estimated parameter vectors of the filters. The locations of all the whales are updated using the enhanced RWOA to obtain the minimum error between the output of the filter and an unknown plant. The fitness for the \( i{\text{th}} \) whale at position \( \vec{X}_{i} \) is represented by the objective function given by Eq. (3). The flowchart of the enhanced RWOA for IIR model identification is presented in Fig. 5.

Fig. 5
figure 5

Flowchart of the enhanced RWOA algorithm for IIR system identification

Full size image

5.1 Experimental Results

To verify the performance of our enhanced RWOA for identifying different IIR systems, an extensive experiment was conducted on three types of benchmark IIR plants, with orders two, three, and four, which were chosen from Refs. [7, 10, 12, 27]. The RWOA was compared with five state-of-the-art algorithms: PSO [31], BA [32], GSA [33], GOA [34], and pure WOA [14]. The objective function, which is the MSE described in Sect. 2, was used as the metric. In the simulations, the problem parameters were set as follows: The input used a white sequence, which contained 100 samples; additive noise was not considered in our study. The proposed RWOA was implemented in the MATLAB programming language for the four algorithms. All the experiments were run on a computer with an AMD Athlon (tm) II*4640 processor and 4 GB of RAM using MATLAB R2012a.

The experimental results obtained for all the IIR plants test cases that contained full and reduced orders are presented in Tables 3, 4, 6, 7, 9, and 10, and illustrated in Figs. 6, 7, 8, 9, 10, and 11 for the MSE and convergence characteristics. The best average (Mean) and standard deviation (Std) are highlighted in bold. Additionally, the estimated values obtained by all the algorithms are presented in Tables 2, 5, and 8.

Fig. 6
figure 6

Average MSE curve for model-1, case 1

Full size image
Fig. 7
figure 7

Average MSE curve for model-1, case 2

Full size image
Fig. 8
figure 8

Average MSE curve for model-2, case 1

Full size image
Fig. 9
figure 9

Average MSE curve for model-2, case 2

Full size image
Fig. 10
figure 10

Average MSE curve for model-3, case 1

Full size image
Fig. 11
figure 11

Average MSE curve for model-3, case 2

Full size image
Table 2 Comparison of parameter estimation for model-1, case 1
Full size table

The Wilcoxon nonparametric statistical test [35] was also implemented for our simulations to test the difference in significance between the RWOA and the other algorithms on three types of benchmark IIR plants. It was necessary to conduct the statistical test because of the stochastic nature of metaheuristics [36, 37]. p values < 0.05 prove the statistically significant superiority of the results. The statistical results of the p values are summarized in Table 10. Note that p values > 0.05 are underlined in the table.

5.1.1 Parameter Setup

The simulation parameters used for all the algorithms were as follows: For a fair comparison, the population size for each algorithm was set to \( N = 30 \) and the maximum number of termination iterations for each algorithm was set to \( T = 500 \). In addition to the basic control parameters, each of the algorithms also had special control parameters. For our proposed RWOA, the scaling factor was set to \( F = 0.7 \) and the component \( \vec{a} \) was linearly diminished from 2 to 0 through the course of the iteration. For the pure WOA, the value of \( \vec{a} \) was the same as that for the RWOA and decreased linearly from 2 to 0 through the course of the iteration. For the PSO, cognitive constant \( c_{1} \) was 1.5 and social constant \( c_{2} \) was 2. Inertia constant \( \omega \) was 1. For the BA, loudness \( A_{0} \) was set to 0.9 and pulse rate \( r_{0} \) was 0.5. For the GSA, gravitational constant \( G_{0} \) was 1 and coefficient of decrease \( \alpha \) was 20. For the last algorithm, GOA, the constant of intensity of attraction \( f \) was set to 0.5 and the constant of attractive of large scale \( l \) was set to 1.5. All the algorithms in our experiment were run 30 times for all the IIR plant test cases to obtain quantitative results.

Model 1 For the first experiment, the transfer function of a second-order plant is modeled as

$$ H_{\text{p}} (z) = \frac{{0.05 - 0.4z^{ - 1} }}{{1 - 1.1214z^{ - 1} + 0.25z^{ - 2} }} . $$
(9)

Case 1

The transfer function of this second-order plant can be defined as a second-order model:

$$ H_{\text{m}} (z) = \frac{{a_{0} + a_{1} z^{ - 1} }}{{1 - b_{1} z^{1} - b_{2} z^{ - 2} }} . $$
(10)

Table 2 lists the estimated parameters acquired by the six algorithms, and it shows that GOA estimated the coefficients slightly better than the RWOA, and these two algorithms performed better than the other four algorithms. This indicates that the RWOA had a strong ability to acquire accurate estimated parameters. Table 3 presents the statistical results in terms of MSE. Clearly, the standard deviation of the MSE using the RWOA was slightly better than that of the PSO, but outperformed those of the other algorithms. The average MSE obtained using the RWOA was superior to that of the basic WOA and the other four algorithms. Figure 6 shows the convergence for the average MSE values acquired by the six algorithms in solving the second-order plant problem. Figure 6 shows that the RWOA outperformed the other algorithms because it had the fastest convergence to the global optimum among the other algorithms, followed by the GOA and PSO. However, Fig. 6 also shows that the WOA, BA, and GSA were easily trapped in local optima, which resulted in stagnation. The p values reported in Table 11 also indicate that the results of the RWOA for the model-1, case 1 IIR model were significantly better than those of the other algorithms. This is evidence that the RWOA had high performance in terms of solving the second-order IIR model.

Table 3 Results of the MSE obtained by the BA, GSA, PSO, GOA, WOA, and RWOA for model-1, case 1
Full size table

Case 2

A reduced-order IIR filter can model the second-order plant. Hence, a first-order IIR model is used to model the second-order plant defined in Eq. (9). The transfer function is

$$ H_{\text{m}} (z) = \frac{{a_{0}^{{}} }}{{1 - b_{1} z^{ - 1} }}. $$
(11)

Table 4 shows that the RWOA provided the best average results and standard deviation in terms of the MSE, which were slightly superior to those of the basic PSO and outperformed those of the other algorithms in solving this IIR model. As shown in Fig. 7, the RWOA algorithm converged much faster and had the lowest MSE values compared with the other five algorithms. Furthermore, the p values in Table 11 also prove that the superiority of the RWOA was significant in three out of five cases.

Table 4 Results of the MSE obtained by the BA, GSA, PSO, GOA, WOA, and RWOA for model-1, case 2
Full size table

Model 2 For the second experiment (Table 5), the transfer function of a third-order-plant is

Table 5 Comparison of parameter estimation for model-2, case 1
Full size table
$$ H_{\text{p}} (z) = \left[ {\frac{{ - 0.2 - 0.4z^{ - 1} + 0.5z^{ - 2} }}{{1 - 0.6z^{ - 1} + 0.25z^{ - 2} - 0.2z^{ - 3} }}} \right]. $$
(12)

Case 1

This third-order plant can be defined as a third IIR filter given by the transfer function

$$ H_{\text{m}} (z) = \left[ {\frac{{a_{0} + a_{1} z^{ - 1} + a_{2} z^{ - 2} }}{{1 - b_{1} z^{ - 1} - b_{2} z^{ - 2} - b_{3} z^{ - 3} }}} \right]. $$
(13)

The results of the MSE obtained by the algorithms presented in Table 6 show that the GSA and RWOA had almost the same quality of solution, and these two algorithms performed much better than the other algorithms. Figure 8 shows that the RWOA converged much faster than the BA, PSO, GOA, and WOA, but was slightly worse than the GSA. Table 5 shows a list of values of the best estimated model parameters after 500 iterations for each algorithm. It shows that both the RWOA and GOA obtained estimated values that matched very well with the actual values, and proves that the RWOA and GOA performed better than the BA, GSA, PSO, and WOA in terms of estimating the values of the system. According to the p values presented in Table 11, the results of the RWOA were not significantly better than those of the GSA and GOA, but were better than those of the remaining three algorithms.

Table 6 Results of MSE obtained by the BA, GSA, PSO, GOA, WOA, and RWOA for model-2, case 1
Full size table

Case 2

In this section, a second-order IIR is used to model the third-order plant shown in Eq. (12) as follows:

$$ H_{\text{m}} (z) = \left[ {\frac{{a_{0} + a_{1} z^{ - 1} }}{{1 - b_{1} z^{ - 1} - b_{2} z^{ - 2} }}} \right]. $$
(14)

The convergence for all six algorithms is compared in Fig. 9, which shows clearly that the minimum MSE acquired for the RWOA was approximately the same as that achieved by the GSA, and these two algorithms outperformed the other algorithms, followed by GOA. During the optimization process, the PSO and WOA acquired the same minimum MSE value, and the performance of BA was the worst of all the algorithms and stagnated in an early period. The comparison in terms of MSE is listed in Table 7, which shows clearly that the average MSE obtained by all the algorithms after 500 iterations was 70E − 03, 3.94E − 04, 1.40E − 03, 9.31E − 04, 1.50E − 03, and 4.59E − 04 for the BA, GSA, PSO, GOA, WOA, and RWOA, respectively. These results show that the proposed RWOA provided very competitive results for this IIR case. The p values in Table 11 also provide evidence that the superiority of the RWOA was significant compared with all the other algorithms, except the GOA.

Table 7 Results of the MSE obtained by the BA, GSA, PSO, GOA, WOA, and RWOA for model-2, case 2
Full size table

Model 3 For the third experiment, a fourth-order plant with a transfer function as shown in Eq. (16) is modeled to test the efficiency of the RWOA:

$$ H_{\text{p}} (z) = \left[ {\frac{{1 - 0.9z^{ - 1} + 0.81z^{ - 2} - 0.729z^{ - 3} }}{{1 + 0.04z^{ - 1} + 0.2775z^{ - 2} - 0.2101z^{ - 3} + 0.14z^{ - 4} }}} \right]. $$
(15)

Case 1

In this section, this fourth-order plant can be defined as a fourth-order IIR filter given by the transfer function

$$ H_{\text{m}} (z) = \left[ {\frac{{a_{0} + a_{1} z^{ - 1} + a_{2} z^{ - 2} + a_{3} z^{ - 3} }}{{1 - b_{1} z^{ - 1} - b_{2} z^{ - 2} - b_{3} z^{ - 3} - b_{4} z^{ - 4} }}} \right]. $$
(16)

The results in Table 8 show that the RWOA estimated the coefficients more accurately than the WOA algorithm and the other four algorithms. Table 9 shows that the RWOA provided the best average results according to the four criteria “Best,” “Worst,” “Mean,” and “Std,” which were much smaller than those of the other algorithms. Figure 10 shows a qualitative measurement of the performance of all six algorithms in terms of the MSE values. It shows clearly that the BA, GSA, GOA, and PSO became trapped in local optima quite soon, and then their convergence rates remained flat over approximately 50 iterations. Although the basic WOA took approximately 200 iterations to achieve the corresponding lowest MSE, which was faster than the RWOA, which converged to the corresponding lowest MSE after 450 iterations, the minimum MSE for the RWOA was much smaller than that of the basic WOA. The p values shown in Table 10 for the IIR model-3, case 1 suggest that the RWOA was statistically significantly superior to the other five algorithms because all the p values in this case were less than 0.05. All of the results confirmed the superior ability of the RWOA in solving the fourth-order IIR filter problem.

Table 8 Comparison of parameter estimation for model-3, case 1
Full size table
Table 9 Results of the MSE obtained by the BA, GSA, PSO, GOA, WOA, and RWOA for model-3, case 1
Full size table
Table 10 Results of MSE obtained by the BA, GSA, PSO, GOA, WOA and RWOA for model-3, case 2
Full size table

Case 2

In this case, the fourth-order plant shown in Eq. (15) is modeled using a reduced order, which is a third-order IIR. The transfer function of this model is defined as

$$ H_{\text{m}} (z) = \left[ {\frac{{a_{0} + a_{1} z^{ - 1} + a_{2} z^{ - 2} }}{{1 - b_{1} z^{ - 1} - b_{2} z^{ - 2} - b_{3} z^{ - 3} }}} \right]. $$
(17)

The comparison of the statistical results for all the algorithms is presented in Table 10. Similar to the previous experiment, the RWOA had the best average results and the smallest standard deviation in terms of MSE. The convergence characteristics for reduced-order modeling are shown in Fig. 11. The figure shows that the WOA, BA, GSA, GOA, and PSO were trapped in a local minimum very early and result in premature. However, the RWOA did not stagnate and continued to search for its corresponding minimum MSE during the optimization process. In this case, all the results show that the RWOA outperformed the other algorithms with the fastest convergence speed and smallest MSE value. Moreover, the p values in Table 11 provide strong evidence that the results of the RWOA for the IIR model-3, case 2 were significantly better than those of all the other algorithms.

Table 11 p values calculated for the Wilcoxon rank-sum test for three IIR models
Full size table

5.2 Discussion

In this section, we discuss our incorporation of a ranking-based mutation operator into the basic WOA method before whales update their position, which we called RWOA. The RWOA was applied to three sets of IIR system identification. From the experimental results, we found that our proposed RWOA approach was effective and efficient. It provided the best results compared with other algorithms for solving the IIR model identification problem in four cases, whereas in the other two cases, it was slightly worse than the GSA algorithm, but still much better than the remaining algorithms. The well-known NFL proves that no single heuristic algorithm exists that is best for dealing with all optimization problems and outperforms all other algorithms [13]; therefore, it is reasonable that the RWOA performed well in the majority of cases, but not all.

The reasons that the performance of our proposed RWOA was superior to all the other compared algorithms, including the basic WOA, for solving different IIR models is attributed to the ranking-based mutation operator because this mechanism helped to improve the probability of choosing good solutions, and then they had more of a chance to propagate to the offspring. Thus, the exploitation ability of the basic WOA was enhanced and the entire performance also improved. Additionally, the RWOA always saved the best obtained solution during the optimization process; hence, the search agent could update its position according to the best obtained solution (the best hunting agent). Therefore, guiding search agents always existed for the exploitation of the most promising regions in the search space. Moreover, because of the value of parameter \( A \), which helped the RWOA to conduct exploration and exploitation simultaneously, when \( \left| A \right| > 1 \), half the iterations were forced to perform exploration to search for a more promising space. By contrast, when \( \left| A \right| < 1 \), the remaining iterations were devoted to exploitation. This mechanism helped the RWOA to be more flexible, and it had a superior ability to avoid local optima, which was helpful for obtaining a tradeoff between the exploration and exploitation ability of the RWOA. Finally, the RWOA maintained the simple framework of the basic WOA, and it had fewer parameters to control than other algorithms, such as the BA, GSA, PSO, and GOA, during the optimization process. A good combination of the above four components thus lead to the RWOA being suitable to real applications and efficiently solving the different IIR models.

It is also worth discussing the poor performance of the BA, GSA, PSO, and GOA in this subsection. These four algorithms belong to the class of swarm-based algorithms. In contrast to evolutionary algorithms, they have no mechanism for significant abrupt movements in the search space, and this is likely to be the reason for the poor performance of the BA, GSA, PSO, and GOA. Although the RWOA is also a swarm-based algorithm, its mechanisms, summarized in the previous paragraph, are the main reasons why it is advantageous in terms of IIR system identification.

The comprehensive study conducted in this paper clearly demonstrates that the RWOA has the ability to avoid local optima and obtain the global optimal solution, which makes it suitable for IIR system identification. All the statistical results proved the superiority of the RWOA.

6 Conclusions and Future Work

In this paper, we proposed a modified version of the WOA called the RWOA, in which a ranking-based mutation operator was embedded into the standard WOA to speed up the rate of convergence and then enhance the algorithm’s exploitation capability. This new approach was applied to the identification of three sets of benchmark IIR plants. The performance assessment of the RWOA for different unknown identification systems with different corresponding reduced models was also presented in this paper. Additionally, the Wilcoxon rank-sum nonparametric statistical test was conducted at a 5% significance level to assess whether the results of the RWOA differed from the best results of the other algorithms in a statistically significant manner. The comparison efficiency for parameter identification achieved using the RWOA and the other five state-of-the-art evolutionary algorithms, including the basic WOA, and the simulation results clearly demonstrated that the RWOA exhibited superior identification performance in terms of convergence speed, accuracy (average MSE), and robustness (Std values of MSE) within a statistically significant framework (the Wilcoxon test). Incorporating a ranking-based mutation operator into the pure WOA helped to improve identification accuracy because it was useful to allow good solutions to have high selection probabilities so that they had more opportunities to propagate to the next generation.

Our future work will consider the following two issues: First, we will apply our RWOA to solve more practical engineering optimization problems. Additionally, we will develop other swarm-based algorithms to deal with IIR system identification.