Infinite impulse response system identification using average differential evolution algorithm with local search

Abstract

In this article, a new metaheuristic algorithm named average differential evolution with local search (ADE-LS) has been developed and implemented to find the optimal coefficients of unknown infinite impulse response (IIR) system as a system identifier. The developed method minimizes the error between unknown system output and the adaptive IIR filter output. Rapid convergence is aimed for the global solution in system identification problem using the ADE-LS based adaptive IIR filter modelling with local search. In this way, more precise prediction of filter coefficients is ensured in the filter design with multimodal error surface. ADE-LS algorithm is applied to four benchmarked IIR systems commonly studies in literature to show its performance. Results found by using ADE-LS are compared to other methods reported in terms of convergence rate and the mean square error value. The attained results approve the efficiency of the suggested method.

1 Introduction

IIR filters are one of the digital filter types commonly used in the areas such as communication, signal processing and parameter estimation [1,2,3,4]. Another application area they are approved due to having a recursive and feedback structure is system identification area. IIR system identification problem is defined as characterizing an unknown system using an adaptive IIR filter [1, 5,6,7]. In other words, it is aimed to approach the adaptive filter coefficients to the unknown system coefficients. For this, same input signal is applied to the unknown system and adaptive filter and the responses of both of them are monitored. In this way, the problem turns into an optimization problem of minimizing the error between the unknown system output and adaptive filter output.

Traditional methods such as least mean square (LMS) are given in the literature for the solution of this problem [8, 9]. However, error surface is not quadratic in IIR filtering and it is multimodal depending on the filter coefficients. Therefore, gradient-based learning algorithms cannot rapidly converge on the global optimum in the optimization process and they easily stick around the local minima. Another essential issue is the requirement of stability-monitoring for the learning of adaptive IIR filters from higher orders. Because, IIR filter will be instable if the poles stay out of the unit circle during the learning process. Researchers have leaned towards using metaheuristic algorithms to overcome these hardships.

Many metaheuristic algorithms are used in IIR system identification and filtering as well as various fields [10, 11]. Cat swarm optimization (CTO) has been applied to IIR system identification problems [12]. The suggested method has been shown to have more rapid calculation time and produced less error than other methods. Harmony search algorithm (HSA) has been applied to adaptive IIR filter design problem [13]. The MSE value between the unknown system and adaptive filter outlets has been minimized and many system identification problems have been solved. In another study, craziness particle swarm optimization (CPSO) technique has been applied to IIR plant benchmark set for the adaptive filter design [14]. The suggested method provides a more rapid convergence and lower MSE values than other methods. In [15], bat algorithm (BA) has been used in the solution of IIR system identification problems in different orders. The results of the suggested method have been compared to other metaheuristics. It has been expressed that BA has provided more rapid convergence and has found the adaptive filter coefficients more precisely.

Other studies related to IIR system identification are also reported in the literature [16,17,18,19,20]. Various intelligent search techniques in which metaheuristics such as opposite HSA (OHSA), particle swarm optimization (PSO), hybrid gravitational search algorithm (HGSA) and teacher learner based optimization (TLBO) take the lead are successfully applied to adaptive IIR filter design. Generally used metaheuristic algorithms provide good results in the area of system identification and ensure more precise prediction of system parameters. Thereof, the adaptive IIR system design using heuristic algorithms is a current issue. In the studies in which various aforementioned smart search techniques are used; it is emphasized that generally rapid convergence of the used algorithm to global solution and local optimum escape ability are important in the solution of IIR system identification problem. For this reason, these two issues have been focused in this study.

The ADE algorithm was successfully applied to optimal parameter prediction problem in our previous study [21]. It is a population based algorithm and provides the cooperative development of all individuals in the population. The main contribution of this work is to develop ADE (ADE-LS) algorithm with local search for the solution of IIR system identification problem. ADE algorithm has been combined with multiple trajectory search (MTS), which is a strong local search technique, to increase the rapid convergence and local search ability of ADE. To show the efficiency of the improved method, it has been applied to compute the optimal coefficients of adaptive IIR filter for the system identification problem. Additionally, DE, PSO and backtracking search optimization algorithm (BSA) [22] methods have also been applied to the same IIR system benchmark set for comparison. The attained results are compared in terms of MSE and convergence speed.

2 IIR system identification

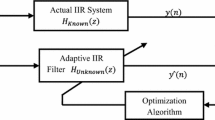
The IIR system identification problem is defined as estimating the coefficients of the unknown IIR system through an adaptive IIR filter model using a metaheuristic algorithm. In other words, metaheuristic algorithm iteratively searches for the adaptive IIR filter coefficients so that the input–output relationship of the filter closely matches the unknown system. Figure 1 shows the scheme of an IIR system identification problem using metaheuristic optimization algorithm.

Fig. 1

The schematic diagram of adaptive IIR system identification

In general, the relationship between the input–output of an IIR filter is defined by the difference equation below.

$$\sum\limits_{k = 0}^{N} {a_{k} y\;(n - k) = } \sum\limits_{k = 0}^{D} {b_{k} x\;(n - k)}$$

(1)

where a_k and b_k are filter coefficients, y(n) is the output of the filter, x(n) is the input of the filter, N is the order of numerator and D is the order of denominator. If the coefficient a₀ = 1 is assumed, the transfer function of IIR filter in z-domain is expressed as follow:

$$H(z) = \frac{Y(z)}{{X(z)}} = \frac{{\sum\nolimits_{k = 0}^{D} {b_{k}^{\prime } z^{ - k} } }}{{1 + \sum\nolimits_{k = 1}^{N} {a_{k}^{\prime } z^{ - k} } }}$$

(2)

The purpose in IIR system identification problem is to identify an unknown system with transfer function H_s(z) using an adaptive IIR filter with transfer function H_f(z). In this situation, the problem turns into an optimization problem as approaching adaptive IIR filter coefficients [a_k′, b_k′]^T to the unknown system coefficients [a_k, b_k]^T. As shown in Fig. 1; the error between the unknown system output and adaptive IIR filter output is minimized using metaheuristic algorithm for the solution of the problem.

The mean square error (MSE) objective function is defined as following:

$${\text{MSE}} = \frac{1}{L}\sum\limits_{n = 1}^{n = L} {\left( {y(n) - \hat{y}(n)} \right)}^{2}$$

(3)

The dB form of MSE is given by

$${\text{MSE}}\;({\text{dB}}) = 10\log_{10} ({\text{MSE}})$$

(4)

where $y(n)$ is the response of the actual system, $\hat{y}(n)$ is the response of the adaptive IIR filter and L is the number of input samples.

IIR system identification problem has been widely studied in the literature [12,13,14,15,16,17,18,19]. Definitions of the reported IIR system identification problem set are presented in Table 1. The unknown system is identified with filter models both from the same order and from the reduced order. ADE-LS algorithm suggested in this study is applied to this IIR system benchmark set. In addition, ADE, DE, PSO and BSA methods are applied to the same problems for comparison. Here, the task of the algorithms, as seen in the schematic representation in Fig. 1, it is to identify the unknown system by minimizing the error function. In other words, selected actual filter coefficients are estimated through an adaptive IIR filter model. The input signal is applied to both the actual IIR filter system and the IIR filter model. The difference of the outputs obtained from the actual system and the adaptive filter model is evaluated as the objective function (Eq. 3). Metaheuristics minimize this objective function throughout iterations by adjusting different coefficient combinations. The coefficient vector that provides the lowest MSE value is returned as the best solution.

Table 1 Four IIR system identification problems

3 Basic ADE algorithm

ADE algorithm is a newly metaheuristic algorithm and a version of DE algorithm [21]. It evolves possible solution vectors by taking the average of individuals in the current population. Thus, a cooperative search methodology is used to find a global solution.

Similar to other metaheuristics, the ADE algorithm has some evolutionary phases that follow initialization, evaluation, improvement, handling, selection and termination. The evolutionary process begins with the random production of possible solutions within the allowed limits. The creation of the initial population is expressed by the equation below.

$$\begin{aligned} & x_{i,G}^{j} = x_{i,\max } + {\text{rand}} \cdot (x_{i,\max } - x_{i,\min } ), \\ & \quad i = 1,2, \ldots {\text{PS}}\quad {\text{and}}\quad \, j = 1,2, \ldots D \\ \end{aligned}$$

(5)

Here x is the solution vector set, PS is the population size, D is the dimension of each solution vector, G is the number of generation, rand is the uniform random number in [0, 1], x_i,max and x_i,min are the maximum and minimum bound values of dimension j, respectively.

Each individual in the initial population is evaluated in terms of the objective function of the problem is defined as following.

$$f_{{{\text{obj}}}} (x),\;\vec{x}_{i,G} = \left[ {x_{1,G}^{j} , \ldots x_{{{\text{PS}},G}}^{j} } \right]^{{\text{T}}}$$

(6)

The next phase is the improvement of candidate solutions. In this phase, the average vector $\vec{A}_{G}$ of the G_th generation is calculated first. This vector is the mean value of solution vectors in the current population and is defined as follows:

$$\vec{A}_{G} = \frac{1}{{{\text{PS}}}}\sum\limits_{i = 1}^{{{\text{PS}}}} {\vec{x}_{i,G} } = (1{\text{/PS}})*\left( {\vec{x}_{1,G} + \vec{x}_{2,G} + \cdots + x_{{{\text{PS}},G}} } \right)$$

(7)

Afterwards, a mutant vector associated with the target solution vector is created. This process in which the target vector, best vector and average vector is taken into consideration is defined as follows:

$$\vec{u}_{i,G + 1} = \vec{x}_{{{\text{best}},G}} + \gamma \cdot {\text{rand}}\;[ - 1,1] \cdot \left[ {\vec{A}_{G} - \vec{x}_{i,G} } \right]$$

(8)

where $\vec{u}_{i,G + 1}$ is the mutant vector, $\vec{x}_{{{\text{best}},G}}$ is the best vector in the generation G, $\gamma$ is the scaling factor and ${\text{rand}}\;[ - 1,1]$ is a random number in [0, 1].

The final process of the improvement phase is crossover. Its purpose is to maintain genetic diversity throughout iterations. The target vector $\vec{x}_{i,\,G}$ and the mutant vector $\vec{u}_{i,G + 1}$ are subjected to a crossover with the C_r probability as defined below.

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x}_{i,G + 1}^{j} = \left\{ {\begin{array}{*{20}l} {{\text{if}}\;{\text{rand}}_{j} \;[0,1] \le C_{r} } \hfill & {u_{i,G + 1}^{j} } \hfill \\ {{\text{else}}} \hfill & {x_{i,G}^{j} } \hfill \\ \end{array} } \right\}$$

(9)

The dimensional boundaries of the candidate solution $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x}_{i,G + 1}^{j}$ obtained as a result of crossover are checked. If there is a violation, the value of the parameter is moved to the nearest variable limit [21].

In the selection phase, a selection is made between the target and the candidate solution in terms of fitness value to determine the solution to be passed on to the next generation. This selection can be shown with the following equation.

$$\vec{x}_{i,G + 1} = \left\{ {\begin{array}{*{20}l} {{\text{if}}\;f_{{{\text{obj}}}} \left( {\hat{x}_{i,G + 1} } \right) > f_{{{\text{obj}}}} \left( {\vec{x}_{i,G} } \right),} \hfill & {\hat{x}_{i,G + 1} } \hfill \\ {{\text{else}}} \hfill & {\vec{x}_{i,G} } \hfill \\ \end{array} } \right\}$$

(10)

where $f_{{{\text{obj}}}} \left( {\hat{x}_{i,G + 1} } \right)$ and $f_{{{\text{obj}}}} \left( {\vec{x}_{i,G} } \right)$ represent the fitness function of $\hat{x}_{i,G + 1}$ and $\vec{x}_{i,G}$, respectively.

The evolutionary stages described above are maintained until stopping criteria are met. When the final iteration number is reached, the calculation is terminated and the best solution is returned [21].

4 ADE with local search (ADE-LS)

The most essential problem in IIR system identification problem is that the error surface (namely objective function) of the unknown filter system is multimodal. Therefore, the search algorithm could stick around the local optimum during the optimization. In this situation, the error between the unknown system model and the adaptive IIR filter model increases and system identification fails. It is necessary for the search algorithms to make a rapid convergence to global solution and have increased escape ability from local optimums for more precise prediction of the unknown system parameters. For this reason, the main idea of this work is to increase the performance of ADE algorithm with local search for the solution of IIR system identification problem. The developed ADE algorithm with local search, which is called as ADE-LS, uses MTS local search technique [23]. The framework of ADE and ADE-LS can be described as in Algorithm 1.

MTS uses multiple agents to simultaneously search the search space. Main objective is to fitting the best in the close neighbourhood of a solution and in this way, an agent could find the local or global optimum. MTS applies the local search to the best solution to develop it. It conducts a search along one dimension for all the dimensions (decision variables) of that solution vector [23]. The framework of MTS is given in Algorithm 2.

Firstly, the search range (SR) is defined as in Eq. (11). At the beginning, SR is defined as the half value of the difference between the upper and lower limits of the decision variable. If the previous local search cannot improve, SR is narrowed down by half until it is less than 1E−15.

$${\text{SR}} = \left( {x(j)_{\max } - x(j)_{\min } } \right){/}2$$

(11)

where x(j)_max and x(j)_min are the upper and lower bound values of dimension j, respectively.

In the related dimension in which the search has been conducted; firstly, SR value is deducted from the value of this dimension as in Eq. (12). It is observed whether the objective function value defined Eq. (6) has improved or not. If there is an improvement, the search is sustained for the next dimension. If there has not been any improvement, the solution is restored and afterwards, 0.5*SR value is added to the dimension value as in Eq. (13). Again, it is observed whether the objective function value has improved or not. If there is an improvement, the search is sustained for the next dimension. If there has not been any improvement, the solution is restored and the original solution is returned. MTS sustains local search iterations until the maximum iteration number is reached [23].

$$x(j) = x(j) - {\text{SR}}\quad j = 1,2, \ldots D$$

(12)

$$x(j) = x(j) + 0.5*{\text{SR}}\quad j = 1,2, \ldots D$$

(13)

In this study, MTS being a local search technique has been integrated with ADE algorithm to increase its local search ability. This developed ADE-LS algorithm calculates the filter coefficients by being applied to the adaptive IIR filter design. ADE-LS tries to develop solution by conducting local search on the current best solution vector to reach global solution in every iteration during the optimization period. The flow chart of ADE-LS algorithm for IIR system identification problem is shown in Fig. 2.

Fig. 2

Flow chart of the ADE-LS algorithm for system identification

5 Simulation results and discussions

In this part, the performance of ADE-LS suggested for the solution of IIR system identification problem set is assessed. Same-order (case 1) and reduced-order (case 2) IIR filter models are considered for the prediction of the coefficients of four sample IIR systems coming from the literature. Results of the suggested ADE-LS are compared to the results of BSA, PSO, DE and ADE. Besides, the best results of the suggested method are compared to the results belonging to other methods reported in the literature for all samples.

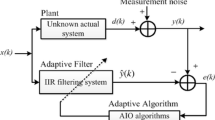
A simulation platform has been established for IIR system identification shown in block diagram Fig. 3. ADE-LS, ADE, DE, PSO and BSA algorithms have been coded in Matlab R2015. Simulation studies have been conducted on a PC having core i7 processor and 2.4 GHz with 8 GB RAM. All optimization algorithms have been run for 50 times independently for each problem.

Fig. 3

The simulation schematic of IIR system identification

As seen in Fig. 3, the input signal is applied to the transfer functions of both the actual IIR system (H_s(z)) and the adaptive filter model (H_f(z)) whose general form is defined as in Eq. (2). The difference of the outputs obtained from the real system and the adaptive filter model is minimized by metaheuristics. Thus, optimum filter coefficients [a_k′, b_k′]^T are estimated in order to closely follow the actual system output. For metaheuristics, solution vectors are defined as combinations of coefficients such as x_i = [a₁′, a₂′,… a_N′, b₀′, b₁′,…, b_D′]^T (i = 1…PS). The fitness value (quality) of each solution vector is evaluated according to the objective function defined in Eq. (3). The minimization of this error function is maintained throughout iterations. When the maximum iteration (Max_ite) is reached, the computational process of metaheuristics is terminated. The filter coefficients with the lowest MSE value are returned as the optimum solution.

For all cases, the input signal is a white noise with uniform distribution and the number of input samples is L = 200. The setting parameters of the used algorithms are given in Table 2. The values of these parameters are the same as the values reported in the original articles in the literature [21, 22, 24, 25] The MSE defined in Eq. (3) has been used as the performance metric in the comparisons. The results attained in terms of the statistical values and convergence characteristics of MSE are given in tables and figures in the following sub-parts.

Table 2 Setting parameters of BSA, PSO, DE, ADE and ADE-LS

5.1 Design examples and modelled systems

5.1.1 Example 1

In the first example problem, the second-order IIR system is modelled using a second-order IIR filter (for case 1) and a first-order IIR filter (for case 2). The statistical results obtained from 50 independent runs of ADE-LS and other methods are given in Tables 3 and 4. According to these tables, best solution in terms of the MSE values (normalized and dB) is obtained by ADE and ADE-LS for case 1. They find the global solution exactly. For case 2, the best MSE obtained is 4.4E−03 (− 23.5184 dB) for ADE-LS. The other algorithms take near to − 17 dB. The convergence graphs of the MSE (dB) for different methods are demonstrated in Fig. 4. From Fig. 4a, the convergence rate of ADE-LS is highest for case 1. It reaches the global optimum at the 200 iterations, while ADE and DE need 250 and 300 iterations, respectively. In case 2, there is no exact solution since reduced order filter model is used. Therefore, the final solution value is more important than the convergence rate. It is verified from Fig. 4b that, all algorithms get stuck early on the local optimum solution. The proposed ADE-LS algorithm converges near to − 23 dB thanks to its local search capability. It is perfect in achieving the best MSE value among the other algorithms.

Table 3 The MSE values of 50 runs for Example 1 (case 1)

Table 4 The MSE values of 50 runs for Example 1 (case 2)

Fig. 4

The convergence graphs of Example 1

For the same-order and reduced-order filter models, the coefficient values obtained for the best result are given in Tables 5 and 6, respectively. In case 1, four filter coefficients are optimized as the solution vector [a₁′, a₂′, b₀′, b₁′]^T. In case 2, two filter coefficients are optimized as the solution vector [a₁′, b₀′]^T. It is observed from Table 5 that all algorithms used generally obtain the exact values of the system coefficients. Since there is no exact result for case 2, the performance of the algorithms is compared in terms of MSE values and convergence speed. From Table 4 and Fig. 4b, it can be observed that ADE-LS performs best in identifying a system using reduced order model. The higher convergence speed of ADE-LS and a smaller MSE makes ADE-LS one of the best choices for reduced order system modelling.

Table 5 Optimized coefficients of Example 1 using same-order IIR filter model

Table 6 Optimized coefficients of Example 1 using reduced-order IIR filter model

The percentage improvement in the performance of ADE-LS over ADE, DE, PSO and BSA is graphically presented in Fig. 5 for both same-order and reduced-order system identification. The best MSE value is considered as a performance measure. The percentage of improvement in MSE obtained for ADE-LS compared to other algorithms except ADE is 99.99% for same-order system modelling. For this case, both ADE and ADE-LS exhibit the same performance.

Fig. 5

Percentage improvement in the performance of ADE-LS over other algorithms for Example 1

The percentage improvement noticed in MSE for reduced order system are 72.83%, 75.28%, 75.28% and 78.53% for ADE-LS compared to ADE, DE, PSO and BSA, respectively. Due to the reduced filter order, algorithms get stuck on local optimum solutions during the search process. The ADE-LS finds more feasible solutions thanks to its local search capability.

5.1.2 Example 2

In this example, the third-order IIR system is modelled using a third-order IIR filter (for case 1) and a second-order IIR filter (for case 2). The statistical results obtained from 50 independent runs of ADE-LS and other methods are given in Tables 7 and 8. According to these tables, the best MSE value (normalized and dB) is obtained by ADE-LS for two cases. In case 1, the ADE-LS finds the global solution exactly. In case 2, it reaches the MSE value of − 39.149 dB. The convergence graphs of the MSE (dB) values of Example 2 using different methods are demonstrated in Fig. 6. From Fig. 6a, the convergence rate of ADE-LS is faster than that of others. It reaches the global optimum at the 180 iterations. In case 2, there is no exact solution since reduced order filter model is used. It is verified from Fig. 6b that, all algorithms get stuck early on the local optimum solution. The proposed ADE-LS algorithm converges near to − 39 dB thanks to its local search capability. It is perfect in achieving the best MSE value among the other methods.

Table 7 The MSE values of 50 runs for Example 2 (case 1)

Table 8 The MSE values of 50 runs for Example 2 (case 2)

Fig. 6

The convergence graphs of Example 2

For the same-order and reduced-order filter models, the coefficient values obtained for the best result are given in Tables 9 and 10, respectively. In case 1, six filter coefficients are optimized as the solution vector [a₁′, a₂′, a₃′, b₀′, b₁′, b₂′]^T. In case 2, four filter coefficients are optimized as the solution vector [a₁′, a₂′, b₀′, b₁′]^T. It is observed from Table 9 that ADE-LS, ADE and DE obtain the exact values of the system coefficients. From Table 8 and Fig. 6b, it can be observed that ADE-LS performs best in identifying a system using reduced order model. The higher convergence speed of ADE-LS and a smaller MSE makes ADE-LS one of the best choices for reduced order system modelling.

Table 9 Optimized coefficients of Example 2 using same-order IIR filter model

Table 10 Optimized coefficients of Example 2 using reduced-order IIR filter model

Figure 7 exhibits the percentage improvement in MSE of ADE-LS in comparison with ADE, DE, PSO and BSA for both same-order and reduced-order system modelling. It indicates that the results obtained in terms of MSE value for the same-order system modelling using ADE-LS is tremendously improved compared to other algorithms. The percentage improvement observed in MSE for the reduced order system is 86.12%, 92.54%, 92.54% and 93.91% for ADE-LS compared to ADE, DE, PSO and BSA, respectively.

Fig. 7

Percentage improvement in the performance of ADE-LS over other algorithms for Example 2

5.1.3 Example 3

In this example, the fourth-order IIR system is modelled using a fourth-order IIR filter (for case 1) and a third-order IIR filter (for case 2). The statistical results obtained from 50 independent runs of ADE-LS and other methods are given in Tables 11 and 12. According to these tables, the best MSE value (normalized and dB) is obtained by ADE-LS for two cases. The ADE-LS reaches the MSE value of − 321.184 dB and − 36.811 dB for cases 1 and 2, respectively. The convergence graphs of the MSE (dB) values of Example 3 using different methods are demonstrated in Fig. 8. From Fig. 8a, the convergence rate of ADE-LS is highest for case 1. It reaches the global optimum at the 300 iterations. In case 2, there is no exact solution since reduced order filter model is used. It is verified from Fig. 8b that, all algorithms get stuck early on the local optimum solution. The proposed ADE-LS algorithm converges near to − 36 dB thanks to its local search capability. It is perfect in achieving the best MSE value among the other methods.

Table 11 The MSE values of 50 runs for Example 3 (case 1)

Table 12 The MSE values of 50 runs for Example 3 (case 2)

Fig. 8

The convergence graphs of Example 3

For the same-order and reduced-order filter models, the coefficient values obtained for the best result are given in Tables 13 and 14, respectively. In case 1, eight filter coefficients are optimized as the solution vector [a₁′, a₂′, a₃′, a₄′, b₀′, b₁′, b₂′, b₃′]^T. In case 2, six filter coefficients are optimized as the solution vector [a₁′, a₂′, a₃′, b₀′, b₁′ b₂′]^T. It is observed from Table 13 that ADE-LS and ADE obtain the exact values of the system coefficients. From Table 12 and Fig. 8b, it can be observed that ADE-LS performs best in identifying a system using reduced order model. The higher convergence speed of ADE-LS and a smaller MSE makes ADE-LS the best choices for reduced order system modelling.

Table 13 Optimized coefficients of Example 3 using same-order IIR filter model

Table 14 Optimized coefficients of Example 3 using reduced-order IIR filter model

The percentage improvement in the performance of ADE-LS over ADE, DE, PSO and BSA is graphically presented in Fig. 9. It shows that the results obtained in terms of MSE value for the same-order system modelling using ADE-LS are tremendously improved over the other methods. The percentage improvement noticed in MSE for the reduced order system is 88.42%, 96.46%, 96.58% and 96.40% for ADE-LS compared to ADE, DE, PSO and BSA, respectively.

Fig. 9

Percentage improvement in the performance of ADE-LS over other algorithms for Example 3

5.1.4 Example 4

In this example, the fifth-order IIR system is modelled using a fifth-order IIR filter (for case 1) and a fourth-order IIR filter (for case 2). The statistical results obtained from 50 independent runs of ADE-LS and other methods are given in Tables 15 and 16. According to these tables, the best MSE value (normalized and dB) is obtained by ADE-LS for two cases. The ADE-LS reaches the MSE value of − 142.87 dB and − 65.078 dB for cases 1 and 2, respectively. The convergence graphs of the MSE (dB) values of Example 4 using different methods are demonstrated in Fig. 10. From Fig. 10a, the convergence rate of ADE-LS is highest for case 1. It reaches the global optimum at the 300 iterations. In case 2, there is no exact solution since reduced order filter model is used. It is verified from Fig. 10b that, all algorithms get stuck early on the local optimum solution. The proposed ADE-LS algorithm converges near to − 65 dB thanks to its local search capability. It is successful in achieving the best MSE value among the other methods.

Table 15 The MSE values of 50 runs for Example 4 (case 1)

Table 16 The MSE values of 50 runs for Example 4 (case 2)

Fig. 10

The convergence graphs of Example 4

For the same-order and reduced-order filter models, the coefficient values obtained for the best result are given in Tables 17 and 18, respectively. In case 1, eleven filter coefficients are optimized as the solution vector [a₁′, a₂′, a₃′, a₄′, a₅′, b₀′, b₁′, b₂′, b₃′, b₄′, b₅′]^T. In case 2, nine filter coefficients are optimized as the solution vector [a₁′, a₂′, a₃′, a₄′, b₀′, b₁′, b₂′, b₃′, b₄′]^T. From Table 17, it is observed that only ADE-LS obtains the exact values of the system coefficients. This result is supported by the lower MSE value of ADE-LS given in Table 15. Thus, ADE-LS contributes to the best approximation of the actual value of system coefficients compared to other algorithms. From Table 16 and Fig. 10b, it can be observed that ADE-LS performs best in identifying a system using reduced order model. The higher convergence speed of ADE-LS and a smaller MSE makes ADE-LS one of the best choices for reduced order system modelling.

Table 17 Optimized coefficients of Example 4 using same-order IIR filter model

Table 18 Optimized coefficients of Example 4 using reduced-order IIR filter model

The improvement in the performance of the ADE-LS in the system identification problem over ADE, DE, PSO and BSA is shown in Fig. 11. A considerable improvement in the performance of ADE-LS in terms of MSE value for the same-order and reduced-order system modelling is over ADE, DE, PSO and BSA. It can be concluded that the ADE-LS gives superior performance when compared to the other algorithms.

Fig. 11

Percentage improvement in the performance of ADE-LS over other algorithms for Example 4

5.2 Comparison and analysis of obtained results

In the IIR system identification problem, the system coefficients are updated because it is aimed to close the filter model output to the unknown system output. This update process is to explore the optimal set of filter coefficients that minimize the error function. Therefore, the MSE value is considered as a performance metric to compare the methods used. Furthermore, since the error surface of the filter is multimodal, the obtained solutions are sub-optimal in many cases when searching for a global solution. Therefore, its convergence behaviour is observed to demonstrate the global search capability of the algorithm used.

The filter design examples presented in the previous section are different order IIR system identification problems, respectively, 2nd, 3rd, 4th and 5th order systems. As the filter order increases, the number of filter coefficients. Thus, the computational complexity of the problem also increases. On the other hand, a lower-order filter model than that of the transfer function of the unknown system is used to improve the phase response linearity of the filter. However, this case creates a multimodal environment where local minima problem may be encountered. In order to overcome this problem, the local search capability of the search algorithm must be strong.

When the results attained with different algorithms are generally assessed for IIR system identification problem, the suggested method finds the best solutions in all example problem solutions. The ADE-LS completely reaches the global solution in examples 1 and 2. It provides the lowest MSE value in the other cases. The ADE-LS is the best method in terms of the convergence behaviours. The curves of ADE-LS descend much faster than those of the other approaches for all cases, suggesting its better performance in search speed. It converges to the neighbourhood of the global optimum with a few iterations, especially in cases (case 1) where the unknown system and filter model are in the same order. The ADE-LS reaches the global solution in approximately 200, 180, 300 and 300 iterations for examples 1, 2, 3 and 4, respectively. The convergence graphs clearly show that the convergence speed of ADE-LS is faster than the others. The reason lies in its capability of attaining the smallest values of “Best” and ‘‘Mean’’ in statistical results, which signifies its high reliability.

Furthermore, the percentage improvement graphs shown in Figs. 5, 7, 9 and 11 demonstrate the effectiveness of the proposed method. In cases where system identification is of the same order, ADE-LS provides tremendous improvement over other methods for almost all design examples. The results obtained show the strength of its global search capability.

In the cases in which filter model from reduced order is used (case 2), all algorithms generally stick around the local optimum. Due to the multimodal environment, they suffer from premature convergence and get easily trapped to sub-optimal solution. In this status, the accuracy of the solution depends on the strength of the method’s ability to jump out of the local optima. The MTS local search technique explores more feasible solutions in different landscapes of the current best solution. Thus, a search agent may find its way to a local optimum or a global optimum. Convergence graphs show that the proposed method provides faster convergence speed and lower MSE values than other approaches. Local search provides the ADE an advantage in finding high quality solutions and making it easier to jump from the local optimum. The percentage improvement graphs shown in Figs. 5, 7, 9 and 11 also support these interpretations. The local search enhanced ADE-LS algorithm offers a significant improvement over other methods in reduced order system identification. It performs strongly in solving the multimodal design problem of an IIR filter.

As a result of these analyses, the proposed method guarantees high quality solutions, strong global and local search capability and fast convergence rate. These properties of ADE-LS make it much better suited for IIR system identification problems.

5.3 Comparison with reported methods

The best results of ADE-LS and the results reported in literature are listed in Table 19 for all cases. It is observed that ADE-LS outperforms all reported methods for all cases, except TLBO in Example 4. In this case, it finds the second best solution by MSE value of − 65 dB. Consequently, the proposed method is successful in terms of minimum MSE values.

Table 19 Comparison of the performance of MSE (dB) of the reported algorithms

6 Conclusion

Local search methods use a search agent to iteratively search for a more feasible solution in the close neighbourhood of a candidate solution. In this way, the agent may find more convenient local or global optimum. Local search contributes to the performance of search algorithms in the solution of multimodal problems such as the adaptive filter design problem handled in this study. Thereof, the local search ability of ADE algorithm has been developed to find the optimal IIR filter coefficients in this study. The developed ADE-LS algorithm has been applied to IIR system identification problem set. The attained results show that ADE-LS is better than other methods in all cases in terms of convergence speed and MSE. It succeeds to reach complete results for examples 1 and 2. It provides the best MSE values according to the reported results in other cases. It provides more convenient solutions without sticking around the local optimum thanks to its ability of local search in adaptive IIR filter modelling especially from the reduced order. Consequently, the newly developed algorithm shows a strong performance in the solution of the system identification problems. Development of ADE algorithm using different local search techniques and solution of more complex world problems are aimed for future studies.