Lax integrability and exact solutions of the generalized (3+1) dimensional Ito equation

Abstract

This article introduces a generalized (3+1) dimensional integrable Ito equation based on relevant literatures. Firstly, the bilinear form of the equation is obtained by Bell polynomial method, and various forms of Bäcklund transformations, Lax pair and infinite conservation laws of the equation are obtained, proving that the equation is integrable in the Lax sense. Secondly, using the trial function method and the mathematical calculation software Mathematica, various solutions of the equation are constructed, including N-soliton solutions, one-order breather wave solution and Lump-Type solution. Finally, the interactions between various functional solutions are analyzed through the three-dimensional and contour plots of the solutions.

1 Introduction

Mathematics is a subject with a wide range of applications. In many fields, people often study and analyze the phenomena and essence of things by establishing mathematical models [1, 2]. The models established when studying nonlinear phenomena and related problems are called nonlinear evolution equations (NLEEs). In recent years, the study of NLEEs has received widespread attention from scholars from all walks of life. It can be used to describe complex nonlinear phenomena in many scientific fields, such as fluid mechanics, mathematics, chemistry, optics, quantum mechanics, etc, and the exact solutions of NLEEs can provide important information for describing nonlinear phenomena [3,4,5,6]. Therefore, finding analytical solutions for NLEEs has become a key topic of concern for people. At present, scholars have done a lot of work on the research of NLEEs’ soliton solutions, Lump solutions, breather wave solutions and other analytical expression [7,8,9,10,11], and have proposed various solutions, such as the Hirota bilinear method [12,13,14], the Bäcklund transformation method [15], the Riccati projective equation method [16], the Lie symmetry method [17,18,19,20], the sine-cosine method [21, 22], the trial function method [23], the three wave method [24, 25] and the Darboux transformation method [26,27,28].

In the 1980s, Ito extended the bilinear KdV equation and established the famous (1+1) dimensional Ito equation

$$\begin{aligned} u_{2t}+u_{3xt}+3(2u_{x}u_{t}+uu_{xt})+3u_{2x}\partial _{x}^{-1}u_{t}=0 \end{aligned}$$

(1)

and (2+1) dimensional Ito equation [29]

$$\begin{aligned}&u_{2t}+u_{3xt}+3(2u_{x}u_{t}+uu_{xt})+3u_{2x}\partial _{x}^{-1}u_{t}+\alpha u_{yt}\nonumber \\&\quad +\beta u_{xt}=0. \end{aligned}$$

(2)

References [30,31,32,33] simultaneously studied equations Eqs. (1) and (2), and obtained multiple new results. For example, multiple-soliton solutions, Bäcklund transformation, Lax integrability and multiple wave solutions. References [34,35,36,37,38] applied different methods to obtain various forms of exact solutions for Eq. (2), including the Lump solution, breather wave solution, interaction solution, solitary wave solution and soliton solutions. The extended (3+1) dimensional Ito equation was first proposed in reference [39]

$$\begin{aligned} u_{2t}+6(u_{x}u_{t})_{x}+u_{3xt}+(\alpha u_{x}+\beta u_{y}+\gamma u_{z})_{t}=0, \end{aligned}$$

(3)

moreover, the Hirota bilinear method was applied to obtain multiple-soliton solutions and Lump solution for Eq. (3).

This article proposes a new generalized (3+1) dimensional Ito equation based on references [29,30,31,32,33,34,35,36,37,38,39]

$$\begin{aligned} u_{2t}+\lambda (u_{x}u_{t})_{x}+\xi u_{3xt}+(\alpha u_{x}+\beta u_{y}+\gamma u_{z})_{t}=0, \end{aligned}$$

(4)

where $\alpha ,\beta ,\gamma ,\lambda$ and $\xi$ are all arbitrary real numbers, $\alpha \ne \beta$ in Eqs. (3) and (4). When $\lambda =6,\xi =1$, Eq. (4) is transformed into Eq. (3).

The goal of this article is to apply Bell polynomial method and trial function method to study different forms of Bäcklund transformations, Lax pair, infinite conservation laws and exact solutions of Eq. (4). All the content obtained in the paper and the images drawn were obtained using mathematical calculation software Mathematica. The transformation (5) introduced when the equation is converted into bilinear form is the highlight of the paper. The three arbitrary function terms added in the transformation can be reduced when the equation is bilinear, so that more abundant solutions of the equation can be obtained, which has not been found in the previous literature. Compared to reference [39], this study investigates the integrability of the equation in the Lax sense, obtaining infinite conservation laws, various forms of Bäcklund transformations, and exact solutions, which are more valuable for research.

The main contents of this paper are as follows: In Sect. 2, the bilinear form of Eq. (4) is obtained by applying Bell polynomial method. In Sect. 3 and 4, obtained the double Bell polynomial Bäcklund transformation and bilinear Bäcklund transformation of Eq. (4), and obtained the Lax pair and infinite conservation laws of the equation through the double Bell polynomial Bäcklund transformation. In Sect. 5, three types of bilinear auto-Bäcklund transformations were obtained through the Hirota bilinear method and different equivalent exchange formulas. In Sect. 6 and 7, the N-soliton solutions and Lump-Type solution of Eq. (4) were obtained using the obtained bilinear equations. Based on the N-soliton solutions, obtain the one-order breather wave solution and the interaction solution between the one-order breather wave solution and the one-soliton solution of the equation through the complex conjugate method. The interaction solution between the obtained solution and different functional solutions was obtained through transformation. At last, Sect. 8 is the conclusion and outlook of this article.

2 The bilinear form of Eq. (4)

Introducing the potential function $q=q(x,y,z,t)$, we set

$$\begin{aligned} u=cq_{x}(x,y,z,t)+\kappa (y,z)+\zeta (y)+\varpi (z), \end{aligned}$$

(5)

where $\kappa (y,z),\zeta (y)$ and $\varpi (z)$ are arbitrary functions of their variables, respectively.

Substituting expression (5) into Eq. (4), divide the x product once, and take the constant of integration as zero to get

$$\begin{aligned}&cq_{tt}+c^{2}\lambda q_{xx}q_{xt}+c\xi q_{3xt}+c\alpha q_{xt}+c\beta q_{yt}+c\gamma q_{zt}\nonumber \\&\quad =0, \end{aligned}$$

(6)

when $c=1,\lambda =3\xi$, expression (6) can be transformed into

$$\begin{aligned} E(q)&=q_{tt}+3\xi q_{xx}q_{xt}+\xi q_{3xt}+\alpha q_{xt}+\beta q_{yt}\nonumber \\&\quad +\gamma q_{zt}=0, \end{aligned}$$

(7)

the above expression can be represented by a P-polynomial

$$\begin{aligned}&P_{tt}(q)+\xi P_{3xt}(q)+\alpha P_{xt}(q)\nonumber \\&\quad +\beta P_{yt}(q)+\gamma P_{zt}(q)=0. \end{aligned}$$

(8)

Under transformation $q(x,y,z,t)=2\ln f(x,y,z,t)$, we can get the bilinear form of Eq. (4)

$$\begin{aligned}&(D_{t}^{2}+\xi D_{x}^{3}D_{t}+\alpha D_{x}D_{t}+\beta D_{y}D_{t}\nonumber \\&\quad +\gamma D_{z}D_{t})f \cdot f=0, \end{aligned}$$

(9)

with f(x, y, z, t), g(x, y, z, t) are real functions with respect to variables x, y, z and t, where $D_{x},D_{y},D_{z},D_{t}$ are the bilinear operators defined by Hirota [40]

$$\begin{aligned} \begin{aligned}&D_{x}^{m}D_{y}^{n} D_{z}^{p} D_{t}^{q} f(x,y,z,t) \cdot g(x,y,z,t)\\&\quad =\big (\frac{\partial }{\partial x}-\frac{\partial }{\partial x^{'}}\big )^{m}\big (\frac{\partial }{\partial y}-\frac{\partial }{\partial y^{'}}\big )^{n}\big (\frac{\partial }{\partial z}-\frac{\partial }{\partial z^{'}}\big )^{p}\\&\qquad \big (\frac{\partial }{\partial t}-\frac{\partial }{\partial t^{'}}\big )^{q}\\&\qquad f(x,y,z,t)g(x^\prime ,y^\prime ,z^\prime ,t^\prime )|_{x=x^\prime ,y=y^\prime ,z=z^\prime ,t=t^\prime }. \end{aligned} \end{aligned}$$

(10)

with m, n, p and q being the non-negative integers.

3 Bilinear Bäcklund transformation and Lax pair

Below we use Bell polynomials to construct Bäcklund transformation and Lax pairs of generalized (3+1)-dimensional Ito equations.

Assuming $q^\prime$ is another solution to Eq. (8), introduce the following transformation

$$\begin{aligned} q= & {} 2\ln {F}=w-v,q^\prime =2\ln {G}=w+v,\nonumber \\ v= & {} \ln \frac{G}{F},w=\ln FG, \end{aligned}$$

(11)

we have

$$\begin{aligned} \begin{aligned}&E(q^\prime )-E(q)=E(w+v)-E(w-v)\\&\quad =2(v_{2t}+\gamma v_{zt}+\beta v_{yt}+\alpha v_{xt}+3\xi w_{xt}v_{2x}\\&\qquad +3\xi v_{xt}w_{2x}+\xi v_{3xt})\\&\quad =2\partial _{t}[\mathcal {Y}_{t}(v,w)+\gamma \mathcal {Y}_{z}(v,w) +\beta \mathcal {Y}_{y}(v,w)\\&\qquad +\alpha \mathcal {Y}_{x}(v,w)+\xi \mathcal {Y}_{3x}(v,w)]+h(v,w)\\&\quad =0, \end{aligned} \end{aligned}$$

(12)

where

$$\begin{aligned} h(v,w)=6\xi (w_{xt}v_{2x}-v_{x}w_{2xt}-v_{x}^{2}v_{xt}). \end{aligned}$$

(13)

To obtain the bilinear Bäcklund transformation of Eq. (4), we introduce the following restrictions

$$\begin{aligned} w_{xt}+v_{x}v_{t}+\mu v_{x}=0, \end{aligned}$$

(14)

where $\mu$ is an arbitrary parameter, on account of which, we have

$$\begin{aligned} h(v,w)=0, \end{aligned}$$

(15)

based on expressions (12),(14) and (15), the double Bell polynomial Bäcklund transformation of Eq. (4) can be obtained

$$\begin{aligned} \begin{aligned}&\partial _{t}[\mathcal {Y}_{t}(v,w)+\gamma \mathcal {Y}_{z}(v,w)+\beta \mathcal {Y}_{y}(v,w)\\&\quad +\alpha \mathcal {Y}_{x}(v,w)+\xi \mathcal {Y}_{3x}(v,w)]=0,\\&\qquad \mathcal {Y}_{xt}(v,w)+\mu \mathcal {Y}_{x}(v,w)=0. \end{aligned} \end{aligned}$$

(16)

From the relationship between double Bell polynomials and Hirota bilinear operators

$$\begin{aligned}&\mathcal {Y}_{n_{1}x_{1},\cdots ,n_{l}x_{l}}(v=\ln \frac{F}{G},w=\ln FG)=(FG)^{-1} D_{x_{1}}^{n_{1}}\nonumber \\&\quad \cdots D_{x_{l}}^{n_{l}}F\cdot G \end{aligned}$$

(17)

and expression (16), the following bilinear Bäcklund transformation for Eq. (4) is obtained

$$\begin{aligned} \begin{aligned}&(D_{t}+\beta D_{y}+\gamma D_{z}+\alpha D_{x}+\xi D_{x}^{3})F \cdot G=0,\\&\quad (D_{x}D_{t}+\mu D_{x})F \cdot G=0. \end{aligned} \end{aligned}$$

(18)

To obtain the Lax pair of Eq. (4), we introduce the Hopf-Cole transform

$$\begin{aligned} v=\ln \phi ,w=q+\ln \phi , \end{aligned}$$

(19)

substituting expression (19) into expression (16), we have

$$\begin{aligned}&\phi _{t}+\beta \phi _{y}+\gamma \phi _{z}+(\alpha +3\xi q_{2x}) \phi _{x}+\xi \phi _{3x}=0,\nonumber \\&\quad \phi _{xt}+q_{xt}\phi +\mu \phi _{x}=0, \end{aligned}$$

(20)

from expression $u=q_{x}(x,y,z,t)+\kappa (y,z)+\zeta (y)+\varpi (z)$, the Lax pair of Eq. (4) is obtained

$$\begin{aligned} \begin{aligned}&\phi _{t}+\beta \phi _{y}+\gamma \phi _{z}+(\alpha +3\xi u_{x})\phi _{x}+\xi \phi _{3x}=0,\\&\quad \phi _{xt}+u_{t}\phi +\mu \phi _{x}=0. \end{aligned} \end{aligned}$$

(21)

The expression (21) obtained above can also be rewritten as

$$\begin{aligned} L\phi =0\phi ,\phi _{t}=A\phi , \end{aligned}$$

(22)

where

$$\begin{aligned} A&=-\gamma \partial _{z}-\beta \partial _{y}-(\alpha +3\xi u_{x})\partial _{x}-\xi \partial _{x}^{3},\nonumber \\ L&=\partial _{x}\partial _{t}+u_{t}+\mu \partial _{x}, \end{aligned}$$

(23)

under condition $L_{t}=[A,L]$, Eq. (4) can be obtained, and then Eq. (4) is integrable in the Lax sense.

4 Infinite conservation laws

Next, we construct the infinite conservation laws of Eq. (4). Firstly, introducing the function $\eta =\eta (x,y,z,t)$, we set

$$\begin{aligned} \eta =\frac{q_{x}^\prime -q_{x}}{2}, \end{aligned}$$

(24)

from expression (11), we can obtain

$$\begin{aligned} v_{x}=\eta ,w_{x}=\eta +q_{x}, \end{aligned}$$

(25)

substituting expression (25) into expression (16), we have

$$\begin{aligned} \begin{aligned}&\partial _{t}\{\partial _{x}^{-1}\eta _{t}+\gamma \partial _{x}^{-1}\eta _{z} +\beta \partial _{x}^{-1}\eta _{y}\\&\quad +\alpha \eta +\xi [\eta ^{3}+3\eta (\eta _{x}+q_{xx})+\eta _{xx}]\}=0,\\&\quad \eta _{t}+q_{xt}+\eta \partial _{x}^{-1}\eta _{t}+\mu \eta =0. \end{aligned} \end{aligned}$$

(26)

Setting

$$\begin{aligned} \mu =\varepsilon ^{-2},\eta =\varepsilon +\sum \limits _{i=1}^{\infty } \mathcal {I}_{n}(q,q_{x},\cdots )\varepsilon ^{-n}, \end{aligned}$$

(27)

and substituting expression (27) into the second expression of expression (26), so that the power coefficients of $\varepsilon$ are zero, we have

$$\begin{aligned} \begin{aligned} \mathcal {I}_{1}&=-u_{x},\mathcal {I}_{2}=-\mathcal {I}_{1,x},\\ \mathcal {I}_{n}&=-\partial _{t}^{-1}\mathcal {I}_{n-2}-\partial _{t}^{-1} (\partial _{x}^{-1}\mathcal {I}_{n+1,t})\\&\quad -\partial _{t}^{-1} \left( \sum \limits _{k=1}^{n-1}\mathcal {I}_{k}\partial _{x}^{-1}\mathcal {I}_{n-k,t}\right) ,n=3,4,\cdots , \end{aligned} \end{aligned}$$

(28)

similarly, substituting expression (27) into the first expression of expression (26), so that the power coefficients of $\varepsilon$ are zero, the following infinite conservation laws are obtained

$$\begin{aligned} \mathcal {F}_{n,t}+\mathcal {H}_{n,x}+\mathcal {K}_{n,y}+\mathcal {V}_{n,z}=0,n=1,2,\cdots , \end{aligned}$$

(29)

where

$$\begin{aligned} \mathcal {K}_{n}&=\beta \partial _{x}^{-1}\mathcal {I}_{n,t}, \mathcal {V}_{n}=\gamma \partial _{x}^{-1}\mathcal {I}_{n,t},\nonumber \\ \mathcal {H}_{n}&=3\xi \mathcal {I}_{n+1,t}+\xi \mathcal {I}_{n,x,t},n=1,2,\cdots , \end{aligned}$$

(30)

$$\begin{aligned} \mathcal {F}_{1}&=\partial _{x}^{-1}\mathcal {I}_{1,t}+\alpha \mathcal {I}_{1} +3\xi \mathcal {I}_{1}^{2}+3\xi \mathcal {I}_{3}+3\xi \mathcal {I}_{1}u_{x}, \end{aligned}$$

(31)

$$\begin{aligned} \mathcal {F}_{2}&=\partial _{x}^{-1}\mathcal {I}_{2,t}+\alpha \mathcal {I}_{2} +6\xi \mathcal {I}_{1}\mathcal {I}_{2}+3\xi \mathcal {I}_{4}\nonumber \\&\quad +3\xi \mathcal {I}_{1}\mathcal {I}_{1,x} +3\xi \mathcal {I}_{2}u_{x}, \end{aligned}$$

(32)

$$\begin{aligned} \mathcal {F}_{3}&=\partial _{x}^{-1}\mathcal {I}_{3,t}+\xi \mathcal {I}_{1}^{3}+3\xi \mathcal {I}_{2}^{2} +\alpha \mathcal {I}_{3}+6\xi \mathcal {I}_{1}\mathcal {I}_{3}\nonumber \\&\quad +3\xi \mathcal {I}_{5}+3\xi \mathcal {I}_{2}\mathcal {I}_{1,x}+3\xi \mathcal {I}_{1}\mathcal {I}_{2,x}+3\xi \mathcal {I}_{3}u_{x}, \end{aligned}$$

(33)

$$\begin{aligned} \ldots \mathcal {F}_{n}&=\partial _{x}^{-1}\mathcal {I}_{n,t}+\alpha \mathcal {I}_{n} +3\xi \mathcal {I}_{n+2}+3\xi \mathcal {I}_{n}u_{x}\nonumber \\&\quad +3\xi \sum \limits _{k=1}^{n-1} \mathcal {I}_{k}\mathcal {I}_{n-k,x} +3\xi \sum \limits _{k=1}^{n}\mathcal {I}_{k}\mathcal {I}_{n+1-k}\nonumber \\&\quad +3\xi \sum \limits _{l+h+p=n,l= h\ne p}\mathcal {I}_{l}\mathcal {I}_{h}\mathcal {I}_{p} +\xi \sum \limits _{3k=n}\mathcal {I}_{k}^{3}\nonumber \\&\quad +6\xi \sum \limits _{m+o+r=n,m< o< r} \mathcal {I}_{m}\mathcal {I}_{o}\mathcal {I}_{r},n=4,5,\cdots , \end{aligned}$$

(34)

among them l, h, p, k, m, o and r are all positive integers.

5 Bilinear auto-Bäcklund transformations

In this section, we will use the Hirota bilinear method to construct the bilinear auto-Bäcklund transformations for Eq. (4). Assuming g(x, y, z, t) is another solution for bilinear equation (9), then we have

$$\begin{aligned}&(D_{t}^{2}+\xi D_{x}^{3}D_{t}+\alpha D_{x}D_{t}+\beta D_{y}D_{t}\nonumber \\&\quad +\gamma D_{z}D_{t})g \cdot g=0, \end{aligned}$$

(35)

setting

$$\begin{aligned} \begin{aligned} U&=[(D_{t}^{2}+\xi D_{x}^{3}D_{t}+\alpha D_{x}D_{t}+\beta D_{y}D_{t}\\&\quad +\gamma D_{z}D_{t})f \cdot f]g^2-f^2 {[}(D_{t}^{2}+\xi D_{x}^{3}D_{t}\\&\quad +\alpha D_{x}D_{t}+\beta D_{y}D_{t}+\gamma D_{z}D_{t})g \cdot g], \end{aligned} \end{aligned}$$

(36)

and using the commutative identity of the Hirota bilinear operator [40], we will obtain the bilinear auto-Bäcklund transformations of Eq. (4).

$$\begin{aligned}&(D_{y}D_{t}f \cdot f)g^2-f^2(D_{y}D_{t}g \cdot g)\nonumber \\&\quad =2D_{y}(D_{t}f \cdot g)\cdot (fg)=2D_{t}(D_{y}f \cdot g)\cdot (fg),\nonumber \\&(D_{z}D_{t}f \cdot f)g^2-f^2(D_{z}D_{t}g \cdot g)\nonumber \\&\quad =2D_{z}(D_{t}f \cdot g)\cdot (fg)=2D_{t}(D_{z}f \cdot g)\cdot (fg),\nonumber \\&(D_{x}D_{t}f \cdot f)g^2-f^2(D_{x}D_{t}g \cdot g)\nonumber \\&\quad =2D_{x}(D_{t}f \cdot g)\cdot (fg)=2D_{t}(D_{x}f \cdot g)\cdot (fg),\nonumber \\&(D_{t}^{2}f \cdot f)g^2-f^2(D_{t}^{2}g \cdot g)=2D_{t}(D_{t}f \cdot g)\cdot (fg), \end{aligned}$$

(37)

$$\begin{aligned}&(D_{x}^{3}D_{t}f \cdot f)g^2-f^2(D_{x}^{3}D_{t}g \cdot g)\nonumber \\&\quad =2D_{t}[(D_{x}^{3}f \cdot g)\cdot (fg)]\nonumber \\&\qquad -6D_{x}[(D_{x}D_{t}f \cdot g)\cdot (D_{x}f \cdot g)], \end{aligned}$$

(38)

$$\begin{aligned}&(D_{x}^{3}D_{t}f \cdot f)g^2-f^2(D_{x}^{3}D_{t}g \cdot g)\nonumber \\&\quad =3D_{x}[(D_{x}^{2}D_{t}f \cdot g)\cdot (fg)]\nonumber \\&\qquad -D_{t}[(D_{x}^{3}f \cdot g)\cdot (fg)]-3D_{x}\nonumber \\&\qquad \quad {[}(D_{x}^{2}f \cdot g) \cdot (D_{t}f \cdot g)]\nonumber \\&\qquad -3D_{t}[(D_{x}^{2}f \cdot g)\cdot (D_{x}f \cdot g)], \end{aligned}$$

(39)

$$\begin{aligned}&(D_{x}^{3}D_{t}f \cdot f)g^2-f^2(D_{x}^{3}D_{t}g \cdot g)\nonumber \\&\quad =2D_{x}[(D_{x}^{2}D_{t}f \cdot g)\cdot (fg)]\nonumber \\&\qquad \quad -2D_{t}[(D_{x}^{2}f \cdot g)\cdot (D_{x}f \cdot g)]-2D_{x} \nonumber \\&\qquad [(D_{x}D_{t}f \cdot g)\cdot (D_{x}f \cdot g)]\nonumber \\&\qquad -2D_{x}[(D_{x}^{2}f \cdot g) \cdot (D_{t}f \cdot g)]. \end{aligned}$$

(40)

Case I:

Setting

$$\begin{aligned} D_{x}D_{t}f \cdot g=\vartheta _{1}fg, \end{aligned}$$

(41)

where $\vartheta _{1}$ is a real constant.

Substituting expressions (37), (38) and (41) together into expression (36) yields

$$\begin{aligned} U_{1}&=2D_{t}\{[(D_{t}+\beta D_{y}+\gamma D_{z}+\xi D_{x}^{3}) f \cdot g]\cdot (fg)\}\nonumber \\&\quad +2D_{x}\{[(\alpha D_{t}+3\xi \vartheta _{1}D_{x})f \cdot g]\cdot (fg)\}, \end{aligned}$$

(42)

taking $U_{1}=0$, a bilinear auto-Bäcklund transformation for Eq. (4) is obtained

$$\begin{aligned} \begin{aligned}&(D_{x}D_{t}-\vartheta _{1})f \cdot g=0,\\&\quad (D_{t}+\beta D_{y}+\gamma D_{z}+\xi D_{x}^{3})f \cdot g=0,\\&\quad (\alpha D_{t}+3\xi \vartheta _{1}D_{x})f \cdot g=0. \end{aligned} \end{aligned}$$

(43)

Case II:

Setting

$$\begin{aligned} D_{x}^{2}f \cdot g=\vartheta _{2}fg, \end{aligned}$$

(44)

where $\vartheta _{2}$ is a real constant.

Substituting expressions (37), (39) and (44) together into expression (36) yields

$$\begin{aligned} \begin{aligned} U_{2}&=D_{t}\{[(2D_{t}+2\beta D_{y}+2\gamma D_{z}+3\vartheta _{2}\xi D_{x}\\&\quad -\xi D_{x}^{3})f \cdot g]\cdot (fg)\}+D_{x}\{[(3\xi D_{x}^{2}D_{t}\\&\quad +3\xi \vartheta _{2} D_{t}+2\alpha D_{t})f \cdot g]\cdot (fg)\}, \end{aligned} \end{aligned}$$

(45)

taking $U_{2}=0$, a bilinear auto-Bäcklund transformation for Eq. (4) is obtained

$$\begin{aligned} \begin{aligned}&(D_{x}^{2}-\vartheta _{2})f \cdot g=0,\\&\quad (2D_{t}+2\beta D_{y}+2\gamma D_{z}+3\vartheta _{2}\xi D_{x}\\&\quad -\xi D_{x}^{3})f \cdot g=0,\\&\quad (3\xi D_{x}^{2}D_{t}+3\xi \vartheta _{2} D_{t}+2\alpha D_{t})f \cdot g=0. \end{aligned} \end{aligned}$$

(46)

Case III:

Setting

$$\begin{aligned} D_{x}f \cdot g=\vartheta _{3}fg,D_{t}f \cdot g=\vartheta _{4}fg, \end{aligned}$$

(47)

where $\vartheta _{3}$ and $\vartheta _{4}$ being all the real constants.

Substituting expressions (37), (40) and (47) together into expression (36) yields

$$\begin{aligned} U_{3}&=D_{t}\{[(2D_{t}+2\beta D_{y}+2\gamma D_{z}-2\vartheta _{3}\xi D_{x}^{2})f \cdot g]\cdot \nonumber \\&\quad (fg)\}+D_{x}\{[(2\xi D_{x}^{2}D_{t}-2\xi \vartheta _{3}D_{x}D_{t}\nonumber \\&\quad -2\xi \vartheta _{4}D_{x}^{2}+2\alpha D_{t})f \cdot g]\cdot (fg)\}, \end{aligned}$$

(48)

taking $U_{3}=0$, a bilinear auto-Bäcklund transformation for Eq. (4) is obtained

$$\begin{aligned} \begin{aligned}&(D_{x}-\vartheta _{3})f \cdot g=0,\\&(D_{t}-\vartheta _{4})f \cdot g=0,\\&(D_{t}+\beta D_{y}+\gamma D_{z}-\vartheta _{3}\xi D_{x}^{2})f \cdot g=0,\\&(\xi D_{x}^{2}D_{t}-\xi \vartheta _{3}D_{x}D_{t} -\xi \vartheta _{4}D_{x}^{2}+\alpha D_{t})f \cdot g=0. \end{aligned} \end{aligned}$$

(49)

The bilinear auto-Bäcklund transformations obtained above are of great significance for solving the equation. When a known solution of Eq. (4) is known, the above bilinear auto-Bäcklund transformations can be iteratively applied to obtain an infinite sequence solution of Eq. (4).

6 N-Soliton and Interaction Solutions of Eq. (4)

6.1 One-soliton solution

Based on the perturbation method [40], it is assumed that Eq. (4) has a one-soliton solution of the following form

$$\begin{aligned} \begin{aligned} f=1+e^{\eta _{1}}, \end{aligned} \end{aligned}$$

(50)

where $\eta _{1}=a_{1}x+b_{1}y+c_{1}z+d_{1}t+\eta _{1}^{0}$, $a_{1},b_{1},c_{1},d_{1}$ and $\eta _{1}^{0}$ are all the real constants.

Substituting expression (50) into bilinear equation (9), we have

$$\begin{aligned} \begin{aligned} d_{1}=-(a_{1}\alpha +b_{1}\beta +c_{1}\gamma +a_{1}^{3}\xi ), \end{aligned} \end{aligned}$$

(51)

therefore, we obtain the following solution for Eq. (4)

$$\begin{aligned} u=2[ln(1+e^{\eta _{1}})]_{x}+\kappa (y,z)+\zeta (y)+\varpi (z), \end{aligned}$$

(52)

when $\kappa (y,z)=0,\zeta (y)=0,\varpi (z)=0$, solution (52) is transformed into a one-soliton solution

$$\begin{aligned} u=2[ln(1+e^{\eta _{1}})]_{x}. \end{aligned}$$

(53)

6.1.1 One-soliton solution and interaction solutions

Due to the arbitrariness of $\kappa (y,z)$,$\zeta (y)$ and $\varpi (z)$ in expression (52), various forms of analytical solutions to Eq. (4) can be obtained by selecting different arbitrary y functions, z functions and y, z functions. We obtain the interaction solutions between the one-soliton solution of Eq. (4) and the solutions of different functions by selecting different types of functions.

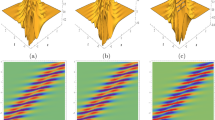
Case 1.1: Take parameters $a_{1}=\eta _{1}^{0}=1,b_{1}=3,c_{1}=2$ in solution (53) to obtain images of one-soliton solution in different spaces, their features are shown in Fig. 1. As can be seen from the figure, during the transmission process, the amplitude of the one-soliton solution remains unchanged, and the transmission process in different spaces is almost unchanged.

Case 1.2: Under the premise of the parameters taken in Case 1.1, when expression (52) takes $\kappa (y,z)=\cos (-y+z),\zeta (y)=\cos (2y),\varpi (z)=\cos (-z)$, the interaction solution between the one-soliton solution and the trigonometric function solution of Eq. (4) are obtained, the interaction phenomenon between solutions is shown in Fig. 2a.

Case 1.3: Under the premise of the parameters taken in Case 1.1, when expression (52) takes $\kappa (y,z)=\tanh (yz),\zeta (y)=\cosh (-2y)^{-1},\varpi (z)=\sinh (z+1)^{-1}$, the interaction solution between the one-soliton solution and the hyperbolic function solution of Eq. (4) are obtained, the interaction phenomenon between solutions is shown in Fig. 2b.

Case 1.4: Under the premise of the parameters taken in Case 1.1, when expression (52) takes $\kappa (y,z)=cn(y+z,0.7),\zeta (y)=cn(y^{2}-3,0.4),\varpi (z)=sn(2z+1,0.5)$, the interaction solution between the one-soliton solution of Eq. (4) and the Jacobian elliptic function solution are obtained, the interaction phenomenon between solutions is shown in Fig. 2c.

Case 1.5: Under the premise of the parameters taken in Case 1.1, when expression (52) takes $\kappa (y,z)=cn(z^{2}+y,0.2),\zeta (y)=\cos (2y+1),\varpi (z)=z\sin (4z)+\cosh (-z)^{-1}$, the interaction solution between the one-soliton solution of Eq. (4) and multiple functional solutions are obtained, the interaction phenomenon between solutions is shown in Fig. 2d.

Fig. 1

(Color online) The 3D plots of one-soliton solutions in different spaces. a $x=t=0$, b $z=t=0$, and c $y=t=0$

Fig. 2

(Color online) The 3D plots of interaction solutions between different functional solutions and one-soliton solution with $x=t=0$. a Interaction solution between one-soliton solution and trigonometric function solution, b interaction solution between one-soliton solution and hyperbolic function solution, c interaction solution between one-soliton solution and Jacobi elliptic function solution, and d interaction solution between one-soliton solution and multiple functional solutions

6.2 Two-soliton solutions

In order to obtain the two-soliton solutions of Eq. (4), we set

$$\begin{aligned} \begin{aligned} f=1+e^{\eta _{1}}+e^{\eta _{2}}+A_{12}e^{\eta _{1}+\eta _{2}}, \end{aligned} \end{aligned}$$

(54)

where $\eta _{i}=a_{i}x+b_{i}y+c_{i}z+d_{i}t+\eta _{i}^{0}(i=1,2)$, $a_{i},b_{i},c_{i},d_{i},\eta _{i}^{0}$ and $A_{12}$ are all the real constants.

Substituting expression (54) into bilinear equation (9), we obtain the following solution for Eq. (4)

$$\begin{aligned} u&=2[ln(1+e^{\eta _{1}}+e^{\eta _{2}}+A_{12}e^{\eta _{1}+\eta _{2}})]_{x}+\kappa (y,z)\nonumber \\&\quad +\zeta (y)+\varpi (z), \end{aligned}$$

(55)

where

$$\begin{aligned} d_{i}&=-(a_{i}\alpha +b_{i}\beta +c_{i}\gamma +a_{i}^{3}\xi ),(i=1,2),\nonumber \\ A_{12}&=\frac{(a_{1}-a_{2})[\alpha (a_{1}-a_{2})+\beta (b_{1}-b_{2}) +\gamma (c_{1}-c_{2})+\xi (a_{1}^{3}-a_{2}^{3})]}{(a_{1}+a_{2})[\alpha (a_{1}+a_{2}) +\beta (b_{1}+b_{2})+\gamma (c_{1}+c_{2})+\xi (a_{1}^{3}+a_{2}^{3})]}, \end{aligned}$$

(56)

Fig. 3

(Color online) The 3D plots and contour plots of two-soliton solutions. a, d $x=0,t=-2$, b, e $x=t=0$, and c, f $x=0,t=2$

when $\kappa (y,z)=0,\zeta (y)=0,\varpi (z)=0$, solution (55) is transformed into a two-soliton solutions

$$\begin{aligned} u=2[ln(1+e^{\eta _{1}}+e^{\eta _{2}}+A_{12}e^{\eta _{1}+\eta _{2}})]_{x}. \end{aligned}$$

(57)

Fig. 4

(Color online) The 3D plots of interaction solutions between different functional solutions and two-soliton solutions with $x=t=0$. a Interaction solution between two-soliton solutions and trigonometric function solution, b interaction solution between two-soliton solutions and hyperbolic function solution, c interaction solution between two-soliton solutions and Jacobi elliptic function solution, and d interaction solution between two-soliton solutions and multiple functional solutions

6.2.1 Two-soliton solutions and interaction solutions

We obtain the interaction solutions between the two-soliton solutions of Eq. (4) and the different functional solutions by selecting different arbitrary y functions, z functions and y, z functions.

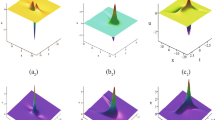
Case 2.1: Take parameters $a_{1}=b_{1}=\xi =\eta _{1}^{0}=\eta _{2}^{0}=1,a_{2}=1.2,b_{2}=c_{1}=3,c_{2}=0.5,\alpha =\beta =2,\gamma =0.8$ in solution (57) to obtain the two-soliton solutions of Eq. (4), it is shown in Fig. 3. It shows the collision process of two-soliton solutions in the (y, z) plane. As time t increases, the two-soliton solutions moves along the positive half axis of the y-axis and the positive half axis of the z-axis, and the velocity, amplitude and interaction mode of the solitons do not change.

Case 2.2: Under the premise of taking the parameters in Case 2.1, when $\kappa (y,z)=\sin (y-z),\zeta (y)=\sin (y),\varpi (z)=\sin (z)$ are taken in the expression (55), the interaction solution between the two-soliton solutions and the trigonometric function solution of Eq. (4) are obtained, the interaction phenomenon between solutions is shown in Fig. 4a.

Case 2.3: Under the premise of taking the parameters in Case 2.1, when $\kappa (y,z)=\tanh (2y+z),\zeta (y)=\sinh (3y)^{-1},\varpi (z)=\cosh (4z-1)^{-2}$ are taken in the expression (55), the interaction solution between the two-soliton solutions and the hyperbolic function solution of Eq. (4) are obtained, the interaction phenomenon between solutions is shown in Fig. 4b.

Case 2.4: Under the premise of taking the parameters in Case 2.1, when $\kappa (y,z)=cn(-2yz,0.1),\zeta (y)=sn(y-1,0.8),\varpi (z)=sn(z+3,0.25)$ are taken in the expression (55), the interaction solution between the two-soliton solutions of Eq. (4) and the Jacobian elliptic function solution are obtained, the interaction phenomenon between solutions is shown in Fig. 4c.

Case 2.5: Under the premise of taking the parameters in Case 2.1, when $\kappa (y,z)=\cosh (yz-1)^{-1},\zeta (y)=\sin (2y+2),\varpi (z)=zcn(z+1,0.2)+z^{-1}$ are taken in the expression (55), the interaction solution between the two-soliton solutions and multiple functional solutions of Eq. (4) are obtained, the interaction phenomenon between solutions is shown in Fig. 4d.

6.2.2 One-order breather wave solution and interaction solutions

Next, we obtain the breather wave solution of Eq. (4) through the complex conjugate method, and study the interaction between the breather wave solution and other functional solutions.

Case 3.1: Take parameters $a_{1}=a_{2}^{*}=0.1+0.5i,b_{1}=b_{2}^{*}=0.2+2i,c_{1}=c_{2}=\eta _{1}^{0}=\eta _{2}^{0}=1,\alpha =0.8,\beta =-0.2,\gamma =-0.6,\xi =-1$ in solution (57) and convert the two-soliton solutions of Eq. (4) into one-order breather wave solution, it is shown in Fig. 5. As can be clearly seen from the figure, with the increase of x and the decrease of t, the one-order breather wave solution moves along the positive half axis direction of the z-axis.

Case 3.2: Under the premise of the parameters taken in Case 3.1, when $\kappa (y,z)=\cos (y+z),\zeta (y)=\cos (-y+1)^{2},\varpi (z)=\sin (z-2)$ are taken in the expression (55), the interaction solution between the one-order breather wave solution and the trigonometric function solution of Eq. (4) are obtained, the interaction phenomenon between solutions is shown in Fig. 6a.

Case 3.3: Under the premise of the parameters taken in Case 3.1, when $\kappa (y,z)=\tanh (yz),\zeta (y)=\cosh (4y-1)^{-3},\varpi (z)=\sinh (2z+1)^{-1}$ are taken in the expression (55), the interaction solution between the one-order breather wave solution and the hyperbolic function solution of Eq. (4) are obtained, the interaction phenomenon between solutions is shown in Fig. 6b.

Case 3.4: Under the premise of the parameters taken in Case 3.1, when $\kappa (y,z)=sn(yz+3y,0.5),\zeta (y)=cn(y^{2},0.2),\varpi (z)=cn(z-2,0.6)$ are taken in the expression (55), the interaction solution between the one-order breather wave solution and the Jacobi elliptic function solution of Eq. (4) are obtained, the interaction phenomenon between solutions is shown in Fig. 6c.

Case 3.5: Under the premise of the parameters taken in Case 3.1, when $\kappa (y,z)=sn(e^{2yz},0.4),\zeta (y)=\sin (-y),\varpi (z)=\cosh (z+2)^{-1}$ are taken in the expression (55), the interaction solution between the one-order breather wave solution of Eq. (4) and various functional solutions are obtained, the interaction phenomenon between solutions is shown in Fig. 6d.

Fig. 5

(Color online) The 3D plots and contour plots of one-order breather wave solutions. a, d $x=-6,t=6$, b, e $x=t=0$, and c, f $x=6,t=-6$

Fig. 6

(Color online) The 3D plots of interaction solutions between different functional solutions and one-order breather wave solution with $x=t=0$. a interaction solution between one-order breather wave solution and trigonometric function solution, b interaction solution between one-order breather wave solution and hyperbolic function solution, c interaction solution between one-order breather wave solution and Jacobi elliptic function solution, and d interaction solution between one-order breather wave solution and multiple functional solutions

Fig. 7

(Color online) The 3D plots and contour plots of three-soliton solutions. a, d $x=0,t=-2$, b, e $x=t=0$, and c, f $x=0,t=2$

Fig. 8

(Color online) The 3D plots of interaction solutions between different functional solutions and three-soliton solutions with $x=t=0$. a Interaction solution between three-soliton solutions and trigonometric function solution, b interaction solution between three-soliton solutions and hyperbolic function solution, c interaction solution between three-soliton solutions and Jacobi elliptic function solution, and d interaction solution between three-soliton solutions and multiple functional solutions

Fig. 9

(Color online) The 3D plots of interaction solutions between different functions with $x=t=0$. a interaction solution between one-soliton solution and one-order breather wave solution, b interaction solution between one-soliton solution, one-order breather wave solution and trigonometric function solution, c interaction solution between one-soliton solution, one-order breather wave solution and hyperbolic function solution, d interaction solution between one-soliton solution, one-order breather wave solution and Jacobi elliptic function solution, and e interaction solution between one-soliton solution, one-order breather wave solution and multiple functional solutions

Fig. 10

(Color online) The 3D plots and contour plots of Lump-Type solutions with parameters $x=0,a_{0}=b_{5}=b_{3}=c_{2}=2,a_{1}=a_{3}=c_{4}=0.5,b_{4}=\alpha =1,a_{4}=0.3,a_{5}=1.2,c_{1}=1.7,c_{3}=0.4,c_{5}=1.5,\gamma =0.2$. a, d $t=-10$, b, e $t=0$, and c, f $t=10$

Fig. 11

(Color online) The 3D plots of interaction solutions between different functional solutions and Lump-Type. a interaction solution between Lump-Type and trigonometric function solution, b interaction solution between Lump-Type and hyperbolic function solution, c interaction solution between Lump-Type and Jacobi elliptic function solution, and d interaction solution between Lump-Type and multiple functional solutions

6.3 Three-soliton solutions

In order to obtain the three-soliton solutions of Eq. (4), we set

$$\begin{aligned} \begin{aligned} f&=1+e^{\eta _{1}}+e^{\eta _{2}}+e^{\eta _{3}}+B_{12}e^{\eta _{1}+\eta _{2}} +B_{13}e^{\eta _{1}+\eta _{3}}\\&\quad +B_{23}e^{\eta _{2}+\eta _{3}}+C_{123}e^{\eta _{1}+\eta _{2}+\eta _{3}}, \end{aligned} \end{aligned}$$

(58)

where $\eta _{i}=a_{i}x+b_{i}y+c_{i}z+d_{i}t+\eta _{i}^{0}(i=1,2,3)$, $a_{i},b_{i},c_{i},d_{i},\eta _{i}^{0},B_{12},B_{13},B_{23}$ and $C_{123}$ are all the real constants.

Substituting expression (58) into bilinear equation (9), we obtain the following solution for Eq. (4)

$$\begin{aligned} \begin{aligned} u=&2[ln(1+e^{\eta _{1}}+e^{\eta _{2}}+e^{\eta _{3}}+B_{12}e^{\eta _{1}+\eta _{2}}\\&+B_{13}e^{\eta _{1}+\eta _{3}}+B_{23}e^{\eta _{2}+\eta _{3}}\\&+C_{123}e^{\eta _{1}+\eta _{2}+\eta _{3}})]_{x}+\kappa (y,z)+\zeta (y)+\varpi (z), \end{aligned} \end{aligned}$$

(59)

where

$$\begin{aligned} \begin{aligned}&d_{i}=-(a_{i}\alpha +b_{i}\beta +c_{i}\gamma +a_{i}^{3}\xi ),(i=1,2,3),\\&C_{123}=B_{12}B_{13}B_{23},\\&B_{ij}=\frac{(a_{i}-a_{j})[\alpha (a_{i}-a_{j})+\beta (b_{i}-b_{j})+\gamma (c_{i}-c_{j})+\xi (a_{i}^{3}-a_{j}^{3})]}{(a_{i}+a_{j})[\alpha (a_{i}+a_{j})+\beta (b_{i}+b_{j})+\gamma (c_{i}+c_{j})+\xi (a_{i}^{3}+a_{j}^{3})]}. \end{aligned} \end{aligned}$$

(60)

here $i,j=1,2,3$, and $i<j$, when $\kappa (y,z)=0,\zeta (y)=0,\varpi (z)=0$, solution (59) is transformed into a three-soliton solutions

$$\begin{aligned} u&=2[ln(1+e^{\eta _{1}}+e^{\eta _{2}}+e^{\eta _{3}}+B_{12}e^{\eta _{1}+\eta _{2}}\nonumber \\&\quad +B_{13}e^{\eta _{1}+\eta _{3}}+B_{23}e^{\eta _{2}+\eta _{3}}+C_{123}e^{\eta _{1}+\eta _{2}+\eta _{3}})]_{x}. \end{aligned}$$

(61)

6.3.1 Three-soliton solutions and interaction solutions

Next, we will construct the interaction solutions between the three-soliton solutions of Eq. (4) and different functional solutions, selecting different $\kappa (y,z),\zeta (y)$ and $\varpi (z)$ in expression (59), we obtain various forms of analytical solutions of Eq. (4).

Case 4.1: Take parameters $a_{1}=2.6,a_{2}=2.5,a_{3}=b_{3}=3,b_{1}=c_{3}=0.5,b_{2}=2,c_{1}=4,c_{2}=3.2,\alpha =\beta =\gamma =\xi =\eta _{1}^{0}=\eta _{2}^{0}=\eta _{3}^{0}=1$ in solution (61) to obtain the three-soliton solutions of Eq. (4), it is shown in Fig. 7. It shows the collision process of three-soliton solutions in the y-plane. As time t increases, the three-soliton solutions moves along the y-axis positive half axis and z-axis positive half axis directions.

Case 4.2: Under the premise of taking the parameters in case 4.1, when $\kappa (y,z)=-4\sin (y-z),\zeta (y)=\sin (y),\varpi (z)=\cos (z+1)$ are taken in the expression (59), the interaction solution between the three-soliton solutions and the trigonometric function solution of Eq. (4) are obtained, the interaction phenomenon between solutions is shown in Fig. 8a.

Case 4.3: Under the premise of taking the parameters in case 4.1, when $\kappa (y,z)=-4\tanh (-y+z),\zeta (y)=\sinh (3y+4)^{-1},\varpi (z)=3\cosh (-2z)^{-1}$ are taken in the expression (59), the interaction solution between the three-soliton solutions and the hyperbolic function solution of Eq. (4) are obtained, the interaction phenomenon between solutions is shown in Fig. 8b.

Case 4.4: Under the premise of taking the parameters in case 4.1, when $\kappa (y,z)=sn(y+3z+y^{-2}z,0.5),\zeta (y)=cn(y,0.2),\varpi (z)=sn(-z+5,0.25)$ are taken in the expression (59), the interaction solution between the three-soliton solutions of Eq. (4) and the Jacobi elliptic function solution are obtained, the interaction phenomenon between solutions is shown in Fig. 8c.

Case 4.5: Under the premise of taking the parameters in case 4.1, when $\kappa (y,z)=\cosh (3yz-1)^{-1},\zeta (y)=cn(e^{y},0.55),\varpi (z)=\cos (z+2)$ are taken in the expression (59), the interaction solution between the three-soliton solutions of Eq. (4) and multiple functional solutions are obtained, the interaction phenomenon between solutions is shown in Fig. 8d.

6.3.2 One-order breather wave solution, one-soliton solution and interaction solutions

Next, we obtain the interaction solution between the one-order breather wave solution and the one-soliton solution of Eq. (4) through the complex conjugate method, and study the interaction between this solution and other functional solutions.

Case 5.1: Taking parameters $a_{1}=a_{2}^{*}=0.1+0.5i,a_{3}=-2.5,c_{1}=c_{2}=c_{3}=\eta _{1}^{0}=\eta _{2}^{0}=\eta _{3}^{0}=1,b_{1}=b_{2}^{*}=-1+3i,b_{3}=0.5,\alpha =-3.2,\beta =0.7,\gamma =-2,\xi =-1$ in solution (61), the three-soliton solutions of Eq. (4) are transformed into an interaction solution between the one-order breather wave solution and the one-soliton solution, it is shown in Fig. 9a.

Case 5.2: Under the premise of the parameters taken in Case 5.1, when $\kappa (y,z)=\sin (y+z),\zeta (y)=\sin (y)+\cos (2y),\varpi (z)=\cos (-z)+\sin (z+2)$ are taken in the expression (59), the interaction solution between the one-order breather wave solution, the one-soliton solution and the trigonometric function solution of Eq. (4) are obtained, the interaction phenomenon between solutions is shown in Fig. 9b.

Case 5.3: Under the premise of the parameters taken in Case 5.1, when $\kappa (y,z)=\cosh (2z+y)^{-1},\zeta (y)=\tanh (2y^{2}),\varpi (z)=\sinh (-2z+1)^{-1}$ are taken in the expression (59), the interaction solution between the one-order breather wave solution, the one-soliton solution and the hyperbolic function solution of Eq. (4) are obtained, the interaction phenomenon between solutions is shown in Fig. 9c.

Case 5.4: Under the premise of the parameters taken in Case 5.1, when $\kappa (y,z)=cn(yz,0.6),\zeta (y)=sn(y,0.3),\varpi (z)=sn(2z,0.2)$ are taken in the expression (59), the interaction solution between the one-order breather wave solution, one-soliton solution and Jacobi elliptic function solution of Eq. (4) are obtained, the interaction phenomenon between solutions is shown in Fig. 9d.

Case 5.5: Under the premise of the parameters taken in Case 5.1, when $\kappa (y,z)=z\tanh (yz+1),\zeta (y)=cn[\sin (-y),0.4],\varpi (z)=e^{\cos (z-2)}$ are taken in the expression (59), the interaction solution between the one-order breather wave solution, one-soliton solution and multiple functional solutions of Eq. (4) are obtained, the interaction phenomenon between solutions is shown in Fig. 9e.

6.4 N-soliton solutions

The N-soliton solutions of Eq. (4) can be obtained from the soliton solutions obtained above

$$\begin{aligned} u=2(ln f)_{x}, \end{aligned}$$

(62)

where

$$\begin{aligned} f= & {} \sum \limits _{\mu =0,1}exp\left( \sum \limits _{i=1}^{N}\mu _{i}\eta _{i}+\sum \limits _{1\le i \le j}A_{ij}\mu _{i}\mu _{j}\right) ,\nonumber \\ e^{A_{ij}}= & {} \frac{(a_{i}-a_{j})[\alpha (a_{i}-a_{j})+\beta (b_{i}-b_{j}) +\gamma (c_{i}-c_{j})+\xi (a_{i}^{3}-a_{j}^{3})]}{(a_{i}+a_{j})[\alpha (a_{i}+a_{j}) +\beta (b_{i}+b_{j})+\gamma (c_{i}+c_{j})+\xi (a_{i}^{3}+a_{j}^{3})]},\nonumber \\ \eta _{i}= & {} a_{i}x+b_{i}y+c_{i}z+d_{i}t+\eta _{i}^{0},\nonumber \\ d_{i}= & {} -(a_{i}\alpha +b_{i}\beta +c_{i}\gamma +a_{i}^{3}\xi ),(i,j=1,2,\cdots ,N), \end{aligned}$$

(63)

here, $\mu _{i}$ and $\mu _{j}$ are taken through 0, 1.

7 Lump-Type solution of Eq. (4)

In this section, we will construct the exact solution of the generalized (3+1) dimensional Ito equation through its bilinear form. Assuming Eq. (4) has the following form of Lump-Type solution

$$\begin{aligned} \begin{aligned} f=&a_{0}+(a_{1}x+a_{2}y+a_{3}z+a_{4}t+a_{5})^{2}\\&+(b_{1}x+b_{2}y+b_{3}z+b_{4}t+b_{5})^{2}\\&+(c_{1}x+c_{2}y+c_{3}z+c_{4}t+c_{5})^{2}, \end{aligned} \end{aligned}$$

(64)

where $a_{i}(i=0,1,\cdots ,5),b_{i},c_{i}(i=1,\cdots ,5)$ are all the undetermined constant.

Substituting expression (64) into bilinear form (9) to obtain a set of nonlinear algebraic equation (not listed). With mathematical calculation software Mathematica, the following solutions can be obtained

Case 6.1:

$$\begin{aligned} \begin{aligned} b_{1}=&-\frac{a_{1}a_{4}+c_{1}c_{4}}{b_{4}},a_{2}=\frac{c_{2}(a_{4} +a_{1}\alpha +a_{3}\gamma )}{c_{4}+c_{1}\alpha +c_{3}\gamma },\\ \beta =&-\frac{c_{4}+c_{1}\alpha +c_{3}\gamma }{c_{2}},\\ b_{2}=&\frac{c_{2}[b_{4}^{2}-(a_{1}a_{4}+c_{1}c_{4}) \alpha +b_{3}b_{4}\gamma ]}{b_{4}(c_{4}+c_{1}\alpha +c_{3}\gamma )}. \end{aligned} \end{aligned}$$

(65)

Case 6.2:

$$\begin{aligned} \alpha =&\frac{b_{4}c_{2}-b_{2}c_{4}+\gamma (b_{3}c_{2}-b_{2}c_{3})}{b_{2}c_{1}-b_{1}c_{2}},\nonumber \\ \beta =&-\frac{c_{1}(b_{4}+b_{3}\gamma )-b_{1}(c_{4}+c_{3}\gamma )}{b_{2}c_{1}-b_{1}c_{2}},\nonumber \\ a_{4}=&-\frac{b_{1}b_{4}+c_{1}c_{4}}{a_{1}},\nonumber \\ a_{3}=&\frac{1}{a_{1}\gamma (b_{2}c_{1}-b_{1}c_{2})}\{(b_{2}c_{1}-b_{1}c_{2})(b_{1}b_{4}+c_{1}c_{4})\nonumber \\&+a_{1}a_{2}[c_{1}(b_{4}+b_{3}\gamma )-b_{1}(c_{4}+c_{3}\gamma )]\nonumber \\&+a_{1}^{2}[-c_{2}(b_{4}+b_{3}\gamma ) +b_{2}(c_{4}+c_{3}\gamma )]\}. \end{aligned}$$

(66)

Case 6.3:

$$\begin{aligned} \begin{aligned}&b_{1}=-\frac{a_{1}a_{4}+c_{1}c_{4}}{b_{4}},\\&a_{2}=\frac{-c_{1}(a_{4}+a_{3}\gamma ) +a_{1}(c_{4}+c_{2}\beta +c_{3}\gamma )}{c_{1}\beta },\\&\alpha =-\frac{c_{4}+c_{2}\beta +c_{3}\gamma }{c_{1}},\\&b_{2}\\&\quad =-\frac{c_{1}b_{4}(b_{4}+b_{3}\gamma )+(a_{1}a_{4}+c_{1}c_{4})(c_{4} +c_{2}\beta +c_{3}\gamma )}{b_{4}c_{1}\beta }. \end{aligned} \end{aligned}$$

(67)

Case 6.4:

$$\begin{aligned} \begin{aligned} a_{3}&=\frac{b_{3}[a_{4}^{2}-\alpha (b_{1}b_{4}+c_{1}c_{4})+a_{2}a_{4}\beta ]}{a_{4}(b_{4} +b_{1}\alpha +b_{2}\beta )},\\ \gamma&=-\frac{b_{4}+b_{1}\alpha +b_{2}\beta }{b_{3}},\\ c_{2}&=\frac{b_{4}c_{3}-b_{3}(c_{4}+c_{1}\alpha )+c_{3} (b_{1}\alpha +b_{2}\beta )}{b_{3}\beta },\\ a_{1}&=-\frac{b_{1}b_{4}+c_{1}c_{4}}{a_{4}}. \end{aligned} \end{aligned}$$

(68)

Substituting expression (65) into expression (64), we have

$$\begin{aligned} f=&a_{0}+\Bigg (a_{1}x+\frac{c_{2}(a_{4}+a_{1}\alpha +a_{3}\gamma )}{c_{4}+c_{1} \alpha +c_{3}\gamma }y+a_{3}z\nonumber \\&+a_{4}t+a_{5}\Bigg )^{2}+\Bigg (-\frac{a_{1}a_{4}+c_{1}c_{4}}{b_{4}}x\nonumber \\&+\frac{c_{2}[b_{4}^{2}-(a_{1}a_{4}+c_{1}c_{4})\alpha +b_{3}b_{4}\gamma ]}{b_{4}(c_{4}+c_{1}\alpha +c_{3}\gamma )}y+b_{3}z\nonumber \\&+b_{4}t+b_{5}\Bigg )^{2}+(c_{1}x+c_{2}y+c_{3}z+c_{4}t+c_{5})^{2},\nonumber \\ \end{aligned}$$

(69)

where $b_{4}(c_{4}+c_{1}\alpha +c_{3}\gamma )\ne 0$.

Therefore, we obtain the following solution for Eq. (4)

$$\begin{aligned} \begin{aligned} u=&2(ln f)_{x}+\kappa (y,z)+\zeta (y)+\varpi (z), \end{aligned} \end{aligned}$$

(70)

when $\kappa (y,z)=0,\zeta (y)=0,\varpi (z)=0$, solution (70) is transformed into a Lump-Type solution

$$\begin{aligned} \begin{aligned} u=2(ln f)_{x}. \end{aligned} \end{aligned}$$

(71)

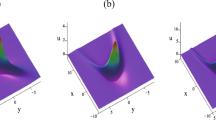
The three-dimensional and contour plots of solution (71) are shown in Fig. 10. By selecting different values of t, the image of the variation of the Lump-Type solution with time is obtained. The Lump-Type solution consists of an upward peak and a downward valley. As time t increases, the Lump-Type solution moves along the negative half axis of the y-axis and the negative half axis of the z-axis, and the amplitude does not change during the movement.

7.1 The interaction solutions between Lump-Type solution and different function solutions

We obtain the interaction solutions between the Lump-Type solution of Eq. (4) and different function solutions by selecting different functions $\kappa (y,z),\zeta (y)$ and $\varpi (z)$.

Case 7.1: Take parameters $a_{0}=a_{4}=\gamma =1,a_{1}=b_{3}=1.5,a_{3}=-1,a_{5}=-0.5,b_{4}=0.4,b_{5}=c_{1}=0.5,c_{2}=c_{3}=\alpha =2,c_{4}=0.6,c_{5}=3,\kappa (y,z)=\sin (-y+z)^{2},\zeta (y)=\cos (2y),\varpi (z)=\cos (z+1)\sin (2z)$ in solution (70) to obtain the interaction solution between the Lump-Type solution of Eq. (4) and the trigonometric function solution. the interaction phenomenon between solutions is shown in Fig. 11a.

Case 7.2: Take parameters $a_{1}=b_{5}=b_{3}=a_{5}=c_{5}=c_{4}=2,a_{0}=a_{4}=a_{3}=b_{4}=c_{2}=c_{3}=\gamma =1,c_{1}=5,\alpha =1.5,\kappa (y,z)=\tanh (y)+\tanh (z),\zeta (y)=\cosh (y+2)^{-1}-\cosh (-y)^{-1},\varpi (z)=\sinh (z)^{-1}+\sinh (3z)^{-1}$ in solution (70) to obtain the interaction solution between the Lump-Type solution of Eq. (4) and the hyperbolic function solution, the interaction phenomenon between solutions is shown in Fig. 11b.

Case 7.3: Take parameters $b_{3}=c_{5}=c_{1}=b_{4}=c_{2}=\alpha =2,a_{0}=0.3,a_{1}=a_{4}=b_{5}=a_{3}=c_{3}=\gamma =1,c_{4}=a_{5}=1.5,\kappa (y,z)=sn(y+2z,0.45),\zeta (y)=sn(y^{2},0.5),\varpi (z)=cn(z^{3},0.2)$ in solution (70) to obtain the interaction solution between the Lump-Type solution of Eq. (4) and the Jacobi elliptic function solution, the interaction phenomenon between solutions is shown in Fig. 11c.

Case 7.4: Take parameters $a_{1}=a_{0}=b_{5}=\gamma =1,a_{4}=b_{3}=a_{5}=c_{5}=c_{2}=2,c_{1}=5,\alpha =a_{3}=1.5,b_{4}=3,c_{3}=0.5,c_{4}=2.5,\kappa (y,z)=cn(yz,0.2),\zeta (y)=\sin (y),\varpi (z)=\cosh (z+2)^{-1}$ in solution (70) to obtain the interaction solution between the Lump-Type solution of Eq. (4) and various functional solutions, the interaction phenomenon between solutions is shown in Fig. 11d.

8 Conclusion

This article investigates a new generalized (3+1) dimensional Ito equation. This equation is extended from the equation in reference [39]. The soliton solutions (one-soliton solution, two-soliton solutions and three-soliton solutions) and Lump solution of Eq. (3) are obtained in reference [39], and the integrability of Eq. (3) in the Painlevé sense is studied. When $\kappa (y,z)=0,\zeta (y)=0,\varpi (z)=0,\xi =1,\lambda =6$, obtain the solution in reference [39]. When $\kappa (y,z)=0,\zeta (y)=0,\varpi (z)=0,\xi =1,\lambda =3,\gamma =a_{3}=b_{3}=c_{i}=0(i=1,\cdots ,5)$, the Lump-Type solution obtained in this paper can be transformed into the Lump solution in reference [35].

In this paper, the bilinear form of the equation is obtained by means of Bell polynomial method, and its double Bell polynomial Bäcklund transformation, bilinear Bäcklund transformation and bilinear auto-Bäcklund transformation are obtained. These Bäcklund transformations help to construct more abundant accurate solutions of the equation. In addition, the Lax integrability of the equation is studied and an infinite conservation laws is constructed. With the help of mathematical calculation software Mathematica, the dynamic characteristics of the obtained solution can be seen intuitively through the 3D map and Contour line map. We find that when the solution of the equation interacts with the Trigonometric functions solution, the shape of the solution presents periodic changes, as shown in Fig. 2a, 4a, 6a, 8a, 9b, 11a; When the solution of the equation interacts with the solution of the Hyperbolic functions, the solution of fracture shape will appear, as shown in Fig. 2b, 4b, 6b, 8b, 9c, 11b; When the solution of the equation interacts with the solution of the Elliptic function, it presents solutions of different forms, as shown in Fig. 2c, 4c, 6c, 8c, 9d, 11c; When the solution of the equation interacts with multiple functional solutions, the shape of the solution will show different forms due to the influence of Elliptic function, and the characteristics of the solution will not show morphological regularity, as shown in Fig. 2d, 4d, 6d, 8d, 9e, 11d; When the breather wave solution (Lump-Type solution) interacts with Trigonometric functions solution, Hyperbolic functions solution, Elliptic function solution and multiple function solutions, the morphology of the breather wave solution (Lump-Type solution) will not be affected by these functions, that is, the original breather wave solution (Lump-Type solution) interacts with different waves.

Using the arbitrariness of $\kappa (y,z),\zeta (y)$ and $\varpi (z)$ in hypothesis (5), we can obtain a large number of analytical expression of the equation, which is also the innovation of this paper and has strong flexibility. The infinite conservation laws studied in this article, the transformations made (5), and the interaction solutions between Lump-Type solution, breather wave solution, soliton solutions, and various functional solutions obtained have not been obtained in previous literature. The research methods for the Bäcklund transformation, Lax integrability and infinite conservation laws of equation in this article can be systematically used to discuss other equations. When discussing the exact solution of the equation, the introduced transformation is flexible. Because not all equations can be reduced when they are converted into bilinear form, the added arbitrary function term is not applicable to all equations. We hope that the results obtained in this article can be experimentally observed in nature and applied to nonlinear science. This new (3+1) dimensional model and its research may help open up a new perspective for future nonlinear evolutionary systems.