1 Introduction

A fascinating area of research in both mathematics and physics is nonlinear partial differential equations (NLPDEs), which are distinguished by their complex behavior resulting from the interaction of several variables. Their significance comes from the fact that they offer more realistic depictions of natural processes than linear PDEs, especially in domains like fluid dynamics where they clarify phenomena like wave propagation and turbulence. These equations have many practical uses in a variety of real-world contexts in addition to being crucial for explaining a wide range of natural phenomena (Swapna 2024; Ming 2017). In mathematics and the applied sciences, finding exact solutions to NLPDEs is crucial for a number of strong reasons. First, exact solutions are used as standards to ensure the accuracy and consistency of numerical techniques and simulations in modeling the behavior of complex system. Researchers may evaluate the efficacy of approximation approaches and pinpoint possible sources of error by contrasting numerical findings with exact solutions, which enhances the resilience of computational models. Furthermore, exact solutions can provide novel insights into the dynamics and behavior of nonlinear systems by exposing hidden patterns and symmetries that exist within systems. These results have real-world implications for engineering design, optimization, and control in addition to furthering theoretical understanding. Consequently, the multidisciplinary team of mathematicians and physicists has created a number of novel techniques with success such as Hirota’s bilinear transformation approach (Nakamura 1979; Hietarinta 1996), the Adomian decomposition technique (Lu and Zheng 2021; Kumar and Umesh 2022), the Jacobi elliptic function technique (Kovacic et al. 2016; Fan and Zhang 2002), the tanh-function approach (Malfliet 2004; Zayed et al. 2015), the extended tanh-method (Fan 2000; Zayed and Alurrfi 2015), the exponential function scheme (Aminikhah et al. 2010; Noor et al. 2010), the modified F-expansion method (Cai and Wang 2007; Cai et al. 2006), the auxiliary equation scheme (Jiong 2003; Akbulut and Kaplan 2018) the homotopsy perturbation method (Mohyud-Din and Noor 2009; Biazar and Aminikhah 2009), the \((G'/G)\) expansion technique (Ebadi et al. 2012) the homogenous balance method (Wang et al. 1996; Fan 2000), the modified simple equation scheme (Jawad et al. 2010; Biswas et al. 2018), the Riccati- Bernoulli sub-ODE scheme (Yang et al. 2015; Alharbi and Almatrafi 2020), the generalized exponential rational function method (GERF) (Ghanbari et al. 2019), first integration approach (Zhang et al. 2020; Taghizadeh et al. 2012; Zayed and Amer 2014), and the sine-cosine function method (Mirzazadeh et al. 2015; Raslan et al. 2017; Alquran and Qawasmeh 2013), etc. In 2022, Asjad et al. studied the space-time fractional modified third-order Korteweg-de Vries equation and the coupled Konno-Oono (CKO) equation using the Sardar-sub equation method (Rehman et al. 2022; Asjad et al. 2022). Recently Sagher et al. investigated Fokas system equation by using two efficient techniques (Sagher et al. 2024). Ashraf et al. studied a variety of novel optical solitons solutions for nonlinear time-fractional Clannish Random Walker’s parabolic (CRWP) equation in the manner of \(\beta \) derivative using a well-known analytical technique namely, extended direct algebraic method (Ullah et al. 2024). Recently Asghar et al. studied propagation of solitary wave in micro-crystalline materials by using new extended direct algebraic technique (Asghar et al. 2024). Faridi et al. investigated solitary waves solutions and dynamic visualization of the nonlinear schrödinger equation with efficient techniques (Majid et al. 2024). In this research, lump soliton (LS), multi-waves (MWs), periodic waves (PWs), lump one kink, and lump two kink, solutions of Landau–Ginzburg–Higgs model will be find by using distinct types of ansatz transformations. When analyzing the LGH model, ansatz transformations play a crucial role in the study of exact solutions to different nonlinear waves. This study can help the researchers to get better insights of pattern generation, wave propagation and energy transfer in nonlinear systems by studying diverse type of nonlinear waves. For complex system simulation, the results of ansatz transformations are highly effective for validating numerical techniques. They can be used to investigate the correctness and reliability of computational models developed by researchers. A lump soliton is a solitary wave solution that travels across a medium while maintaining its form and energy. Lump solitons are of great interest in several fields, such as condensed matter physics, plasma physics, and nonlinear optics. Multi-waves, which are often referred to as multi-solitons, are complex wave patterns that arise when several solitary waves occur simultaneously in a nonlinear medium. These waves can interact with one another while retaining their unique characteristics, resulting in complex patterns of energy transmission and exchange. Periodic waves are characterized by their regular, repeating oscillation patterns over space and time. These waves show a steady oscillation cycle in which the wave form appears periodically. In this manuscript, some ansatz transformations will be applied to obtained the multiple soliton solutions for a well-known model, the Landau–Ginzburg–Higgs model of the form

$$\begin{aligned} {w_{tt}} - {w_{xx}} - {a^2}w + {b^2}{w^3} = 0, \end{aligned}$$
(1.1)

where w stands for the potential of the ion-electrostatic cyclotron. The variables t and x, respectively, denote the nonlinearized temporal and spatial coordinates. Various practical applications of the LGH model exist in numerous fields. The analysis and solutions for nonlinear waves provided by the LGH model are very helpful in the optimization, design, and control of engineering systems. The LGH model can be used to explain the behavior of nonlinear systems, which could lead to the development of more dependable and efficient engineering solutions in domains such as signal processing, communication networks, and materials science. In theoretical physics, the LGH model is a theoretical framework that is crucial to comprehending the dynamics of phase transitions and symmetry breaking processes in particle physics and condensed matter. The LGH model is widely applied in condensed matter physics to investigate superconductivity and superfluidity, where it sheds light on how order emerges from chaos. In particle physics, the Higgs mechanism clarifies electroweak symmetry breaking, which is mainly explained by the LGH model. In general, the Landau-Ginzburg-Higgs model is a useful theoretical instrument with many applications in particle physics and condensed matter physics. It has increased our understanding of the fundamental forces and particles that govern the world and set the path for many technological developments through its discoveries into phase transitions, symmetry breaking, and the origin of mass. The rest of the paper is organized as follows: In Sect. 2, the the lump soliton solution will be obtained. In Sect. 3, the solution of lump one kink will be provided. In Sect. 4, the solution of lump two kink will be studied. In Sect. 5, the solution of periodic waves will be discussed. In Sect. 6, the solution of multi-waves will be discussed. In Sect. 7, we will discuss our results. The conclusion will be provided in Sect. 8.

2 Lump soliton solution

The lump soliton solution can be found by applying the following transformation (Yang et al. 2018):

$$\begin{aligned} w = 2{(\ln f)_{xx}}. \end{aligned}$$
(2.1)

The lump soliton solution of Eq. (1.1) can be found using Eq. (2.1), which will yield the bilinear form of the equation.

$$\begin{aligned} - {a^2}{f^4}f_x^2 + 6{f^2}f_t^2f_x^2 - 2{f^3}{f_{tt}}f_x^2 - 6{f^2}f_x^4 + 4{b^2}f_x^6 - 8{f^3}{f_t}{f_x}{f_{xt}} + 2{f^4}f_{xt}^2 + 2{f^4}{f_x}{f_{xtt}} + {a^2}{f^5}{f_{xx}} - 2{f^3}f_t^2{f_{xx}} + {f^4}{f_{tt}}{f_{xx}}\nonumber \\ + 12{f^3}f_x^2{f_{xx}} - 12{b^2}ff_x^4{f_{xx}} - 3{f^4}f_{xx}^2 + 12{b^2}{f^2}f_x^2f_{xx}^2 - 4{b^2}{f^3}f_{xx}^3 + 2{f^4}{f_t}{f_{xxt}} - {f^5}{f_{xxtt}} - 4{f^4}{f_x}{f_{xxx}} + {f^5}{f_{xxxx}}. \end{aligned}$$
(2.2)

Now, using the function \({\zeta _1}\), \({\zeta _2}\) and f given as (Ren et al. 2019):

$$\begin{aligned} {\left\{ \begin{array}{ll} f = \zeta _1^2 + \zeta _2^2 + {a_7},\\ {\zeta _1} = {a_1}x + {a_2}t + {a_3},\\ {\zeta _2} = {a_4}x + {a_5}t + {a_6}. \end{array}\right. } \end{aligned}$$
(2.3)

where \(1 \le {a_i} \le 7\), are the real parameters to be found. After replacing f into Eq. (2.2), we are able to derive the subsequent sets of parameters by eliminating the coefficients of x and t.

When \({a_1}={a_6}=0,\) we obtain the following solutions:

$$\begin{aligned}{} & {} {a_2} = \sqrt{ - \left( {\frac{4}{3}a_4^2 + \frac{{17}}{3}a_5^2} \right) }, {a_3} = \sqrt{\frac{{\frac{{ - 6{a^2}a_4^4{b^2} + 29a_4^4 - 16a_4^2a_5^2 - 13a_5^2}}{{ - 28a_4^2 - 119a_5^2}}}}{a}}, {a_4} = {a_4}, {a_5} = {a_5},\\{} & {} {a_7} = - \frac{3}{7}\frac{{2{a^2}a_4^4{b^2} + 9a_4^4 + 66a_4^2a_5^2 - 75a_5^4}}{{(4a_4^2 + 17a_5^2){a^2}}}. \end{aligned}$$

By using the above values in Eq. (2.1), we get

$$\begin{aligned} w = 2\frac{{(\zeta _1^2 + \zeta _2^2 + {a_7})(2a_4^2) - {{(2a_4^2x)}^2}}}{{{{(\zeta _1^2 + \zeta _2^2 + {a_7})}^2}}}, \end{aligned}$$
(2.4)

where

$$\begin{aligned} {\zeta _1}= 2a_4^2, {\zeta _2}= 4a_4^2{\left( {{a_5}t + {a_4}x} \right) ^2}, {\frac{4}{3}a_4^2 + \frac{{17}}{3}a_5^2}<0, {\frac{{ - 6{a^2}a_4^4{b^2} + 29a_4^4 - 16a_4^2a_5^2 - 13a_5^2}}{{ - 28a_4^2 - 119a_5^2}}}>0. \end{aligned}$$

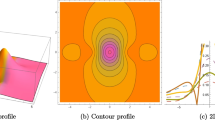
The graphical representation of solution (2.4) is given in the Figs 1, 2 and 3.

Fig. 1
figure 1

The visual depiction of w(x, t) for Eq. (2.4) is given. (a) 3D profile (b) contour profile (c) 2D profile, when \(a = 15,b = 10,{a_4} = 7,{a_5} = 5.\)

Full size image
Fig. 2
figure 2

The visual depiction of w(x, t) for Eq. (2.4) is given. (a) 3D profile (b) contour profile (c) 2D profile, when \(a = 0.5,b = 10,{a_4} = 7,{a_5} = - 0.5.\)

Full size image
Fig. 3
figure 3

The visual depiction of w(x, t) for Eq. (2.4) is given. (a) 3D profile (b) contour profile (c) 2D profile, when \(a = 5.5,b = - 10,{a_4} = 10,{a_5} = 5.5.\)

Full size image

3 Lump one kink solution

This section will provide the lump one kink solution for Eq. (1.1). For this, we study the following function (Ren et al. 2019):

$$\begin{aligned} {\left\{ \begin{array}{ll} f = \zeta _1^2 + \zeta _2^2 + {m_1}{e^{{H_1}(x,t)}} + {a_7},\\ {\zeta _1} = {a_1}x + {a_2}t + {a_3},\\ {\zeta _2} = {a_4}x + {a_5}t + {a_6},\\ {\mathrm{{H}}_1}(x,\mathrm{{t}})\mathrm{{ = }}{\mathrm{{b}}_1}x + {b_2}t, \end{array}\right. } \end{aligned}$$
(3.1)

where \(a_i\) and \(b_1, b_2, m_1, \) are the real parameters that need to be found. By replacing Eq. (3.1) into Eq. (2.2), we are able to derive the subsequent sets of parameters.

When \(a_1=0, a_6=0, a_7=0, b_1=0\), we obtain the following solutions:

$$\begin{aligned} {a_2} = \sqrt{ - \frac{{{a^2} + 6b_2^2}}{{3{a^2} + 3b_2^2}}} {a_5}, {a_3} = \frac{5}{3}\frac{{{a_5}\left( {2{a^2} + 3b_2^2} \right) {b_2}}}{{{{\left( {{a^2} + b_2^2} \right) }^2}\sqrt{ - \frac{{{a^2} + 6b_2^2}}{{3{a^2} + 3b_2^2}}} }}, {a_4} = \frac{{\sqrt{ - \frac{{ - 4{a^6} - 162{a^4}b_2^2 - 582{a^2}b_2^4 - 549b_2^6}}{{6{a^2} + 36b_2^2}}} }}{{{a^2} + b_2^2}}{a_5}, {a_5} = {a_5}, {b_2} = {b_2}. \end{aligned}$$

By using the above values in Eq. (2.1), we get

$$\begin{aligned} w = 2\frac{{\Omega {\kappa _1} - {\kappa _2}}}{{{\Omega ^2}}}, \end{aligned}$$
(3.2)

where

$$\begin{aligned}{} & {} f(x,t)= \Omega = {\zeta _1}{(x,t)^2} + {\zeta _2}{(x,t)^2} + {m_1}{e^{{H_1}(x,t)}} + {a_7}, \\{} & {} {\kappa _1}= - \frac{{2a_5^2\left( { - 4{a^6} - 162{a^4}b_2^2 - 582{a^2}b_2^4 - 549b_2^6} \right) }}{{{{\left( {{a^2} + b_2^2} \right) }^2}\left( {6{a^2} + 36b_2^2} \right) }}, \\{} & {} {\kappa _2} = - \frac{{4a_5^2\left( { - 4{a^6} - 162{a^4}b_2^2 - 582{a^2}b_2^4 - 549b_2^6} \right) {{\left( {{a_5}t + \frac{{{a_5}\sqrt{ - \frac{{ - 4{a^6} - 162{a^4}b_2^2 - 582{a^2}b_2^4 - 549b_2^6}}{{6{a^2} + 36b_2^2}}} x}}{{{a^2} + b_2^2}}} \right) }^2}}}{{{{\left( {{a^2} + b_2^2} \right) }^2}\left( {6{a^2} + 36b_2^2} \right) }}, \\{} & {} {\zeta _1}(x,t) = \frac{{5{a_5}{b_2}\left( {2{a^2} + 3b_2^2} \right) }}{{3{{\left( {{a^2} + b_2^2} \right) }^2}\sqrt{ - \frac{{{a^2} + 6b_2^2}}{{3{a^2} + 3b_2^2}}} }} + {a_5}\sqrt{ - \frac{{{a^2} + 6b_2^2}}{{3{a^2} + 3b_2^2}}} t, \\{} & {} {\zeta _2}(x,t) = {a_5}t + \frac{{{a_5}\sqrt{ - \frac{{ - 4{a^6} - 162{a^4}b_2^2 - 582{a^2}b_2^4 - 549b_2^6}}{{6{a^2} + 36b_2^2}}} x}}{{{a^2} + b_2^2}}, {H_1}(x,t) = {b_2}t, \\{} & {} { \frac{{ - 4{a^6} - 162{a^4}b_2^2 - 582{a^2}b_2^4 - 549b_2^6}}{{6{a^2} + 36b_2^2}}}<0, { \frac{{{a^2} + 6b_2^2}}{{3{a^2} + 3b_2^2}}}<0. \end{aligned}$$

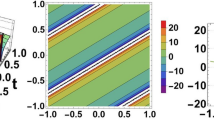
The graphical representation of solution (3.2) is given in the Figs 4 and 5.

Fig. 4
figure 4

The visual depiction of w(x, t) for Eq. (3.2) is given. (a) 3D profile (b) contour profile (c) 2D profile, when \(a = 05,b = 0.5,{a_5} = 0.09,{b_2} = 0.09,{m_1} = 5.\)

Full size image
Fig. 5
figure 5

The visual depiction of w(x, t) for Eq. (3.2) is given. (a) 3D profile (b) contour profile (c) 2D profile, when \(a = -0.5,b = -5,{a_5} = -0.05,{b_2} = -0.09,{m_1} = 3\)

Full size image

4 Lump two kink solution

This section will provide the lump two kink solution for Eq. (1.1). For this, we study the following function.

$$\begin{aligned} {\left\{ \begin{array}{ll} f = \zeta _1^2 + \zeta _2^2 + {m_1}{e^{{H_1}(x,t)}} + {m_2}{e^{{H_2}(x,t)}} + {a_7},\\ {\zeta _1} = {a_1}x + {a_2}t + {a_3},\\ {\zeta _2} = {a_4}x + {a_5}t + {a_6},\\ {\mathrm{{H}}_1}(x,\mathrm{{t}})\mathrm{{ = }}{\mathrm{{b}}_1}x + {b_2}t,\\ {\mathrm{{H}}_2}(x,\mathrm{{t}})\mathrm{{ = }}{\mathrm{{b}}_3}x + {b_4}t, \end{array}\right. } \end{aligned}$$
(4.1)

where \(a_i\), \(b_i\), \(m_1\), and \(m_2\) are the real constants that need to be found. By substituting Eq. (4.1) into Eq. (2.2), we obtain following value of parameters:

When \(a_2=a_6=a_7=b_1=0\), we obtain the following solutions:

$$\begin{aligned} {a_1} = \sqrt{ - 5} {a_4}, {a_3} = {a_3},{a_4} = {a_4}, {a_5} = {a_5}, {b_2} = \sqrt{ - 8{a^2} + 4b_3^2}, {b_3} ={b_3}, {b_4} =0, {m_1}={m_1}, {m_2}={m_2}. \end{aligned}$$

By using the above values in Eq. (2.1), we get

$$\begin{aligned} w = 2\frac{{\Omega {\kappa _1} - {\kappa _2}}}{{{\Omega ^2}}}, \end{aligned}$$
(4.2)

where

$$\begin{aligned}{} & {} f(x,t)= \Omega ={\zeta _1}{(x,t)^2} + {\zeta _2}{(x,t)^2} + {m_1}{e^{{H_1}(x,t)}} + {m_2}{e^{{H_2}(x,t)}} + {a_7},\\{} & {} {\kappa _1}= - 8a_4^2 + b_3^2{\mathrm{{e}}^{{b_3}x}}{m_2},{\kappa _2}= {\left( {{b_3}{\mathrm{{e}}^{{b_3}x}}{m_2} + 2{a_4}\left( {{a_5}t + {a_4}x} \right) + 2\mathrm{{i}}\sqrt{5} {a_4}\left( {{a_3} + \mathrm{{i}}\sqrt{5} {a_4}x} \right) } \right) ^2},\\{} & {} {\zeta _1}(x,t) = {a_3} + \mathrm{{i}}\sqrt{5} {a_4}x, {\zeta _2}(x,t) = {a_5}t + {a_4}x, {H_1}(x,t) = \sqrt{ - 8{a^2} + 4b_3^2} t, {H_2}(x,t) = {b_3}x, { - 8{a^2} + 4b_3^2}>0. \end{aligned}$$

The graphical representation of solution (4.2) is given in the Figs 6, 7 and 8.

Fig. 6
figure 6

The visual depiction of w(x, t) for Eq. (4.2) is given. (a) 3D profile (b) contour profile (c) 2D profile, when \(a = - 5,b = 9,{m_1} = 0.5,{m_2} = 7,{a_3} = - 5,{a_4} = 0.5,{a_5} = 0.5,{b_3} = - 0.05.\)

Full size image
Fig. 7
figure 7

The visual depiction of w(x, t) for Eq. (4.2) is given. (a) 3D profile (b) contour profile (c) 2D profile, when \(a = - 0.5,b = - 0.9,{m_1} = - 5,{m_2} = - 1.7,{a_3} = - 15,{a_4} = - 0.5,{a_5} = - 0.5,{b_3} = 0.05.\)

Full size image
Fig. 8
figure 8

The visual depiction of w(x, t) for Eq. (4.2) is given. (a) 3D profile (b) contour profile (c) 2D profile, when \(a = 0.05,b = - 9,{m_1} = 5,{m_2} = 0.5,{a_3} = - 16,{a_4} = - 0.6,{a_5} = 0.6,{b_3} = - 0.05.\)

Full size image

5 Periodic waves

This section will provide the periodic waves solution for Eq. (1.1). For this, we study the following function.

$$\begin{aligned} {\left\{ \begin{array}{ll} f = \zeta _1^2 + \zeta _2^2 + {m_1}\cos (\alpha (x,t)) + {a_7},\\ {\zeta _1} = {a_1}x + {a_2}t + {a_3},\\ {\zeta _2} = {a_4}x + {a_5}t + {a_6},\\ \alpha = {b_1}x + {b_2}t, \end{array}\right. } \end{aligned}$$
(5.1)

where \(a_i\), \(b_i\) and \(m_1\) are the real constants that need to be found. By substituting Eq. (5.1) into Eq. (2.2), we obtain following value of parameters:

When \({a_3} = {a_4} = {a_7} = {b_2} = 0\), we obtain the following solutions:

$$\begin{aligned} {a_1} = \frac{{\sqrt{85} }}{{\sqrt{3} b}}{a_6}, {a_2} = \frac{{\sqrt{ - 85} }}{b}{a_6}, {a_5} = \frac{{5\sqrt{119} }}{{\sqrt{3} b}}{a_6}, {a_6}={a_6}, {b_1} = \frac{a}{{\sqrt{2} }}. \end{aligned}$$

By using the above values in Eq. (2.1), we get

$$\begin{aligned} w = 2\frac{{\Omega {\kappa _1} - {\kappa _2}}}{{{\Omega ^2}}}, \end{aligned}$$
(5.2)

where

$$\begin{aligned}{} & {} f(x,t)= \Omega ={\zeta _1}{(x,t)^2} + {\zeta _2}{(x,t)^2} + {m_1}\cos (\alpha (x,t)) + {a_7}, \\{} & {} {\kappa _1} = \frac{{170a_6^2}}{{3{b^2}}} - \frac{1}{2}{a^2}{m_1}\cos \left( {\frac{{ax}}{{\sqrt{2} }}} \right) , {\kappa _2} = {\left( {\frac{{2\sqrt{\frac{{85}}{3}} {a_6}\left( {\frac{{\mathrm{{i}}\sqrt{85} {a_6}t}}{b} + \frac{{\sqrt{\frac{{85}}{3}} {a_6}x}}{b}} \right) }}{b} - \frac{{a{m_1}\sin \left( {\frac{{ax}}{{\sqrt{2} }}} \right) }}{{\sqrt{2} }}} \right) ^2}, \\{} & {} {\zeta _1} = \frac{{\mathrm{{i}}\sqrt{85} {a_6}t}}{b} + \frac{{\sqrt{\frac{{85}}{3}} {a_6}x}}{b}, {\zeta _2} = {a_6} + \frac{{5\sqrt{\frac{{119}}{3}} {a_6}t}}{b}, \alpha = \frac{{ax}}{{\sqrt{2} }}. \end{aligned}$$

The graphical representation of solution (5.2) is given in the Figs. 9 and 10.

Fig. 9
figure 9

The visual depiction of w(x, t) for Eq. (5.2) is given. (a) 3D profile (b) contour profile (c) 2D profile, when \(a = - 5,b = - 1.5,{a_6} = - 25,{m_1} = - 5.\)

Full size image
Fig. 10
figure 10

The visual depiction of w(x, t) for Eq. (5.2) is given. (a) 3D profile (b) contour profile (c) 2D profile, when \(a = - 5,b = - 5,{a_6} = - 5,{m_1} = - 1.5.\)

Full size image

6 Multi-waves

The multi-waves solution for Eq. (1.1) will be given in this section. The following transformation will be used for multi-waves solution:

$$\begin{aligned} {\left\{ \begin{array}{ll} f = {f_0}\cosh {\zeta _1} + {f_1}\cos {\zeta _2} + {f_2}\cosh {\zeta _3} + {a_{10}},\\ {\zeta _1} = {a_1}x + {a_2}t + {a_3},\\ {\zeta _2} = {a_4}x + {a_5}t + {a_6},\\ {\zeta _3} = {a_7}x + {a_8}t + {a_9}, \end{array}\right. } \end{aligned}$$
(6.1)

where \(1 \le {a_i} \le 10\), are the real parameters to be found. Substitute Eq. (6.1) into Eq. (2.2) to acquire the particular equations that yield values for the coefficients.

When \({a_1}= {a_6}={a_8}=0\), the following solutions are obtained:

$$\begin{aligned}{} & {} {a_2} = \frac{{\sqrt{2} {{\left( { - 2{a^2}{b^2} - 1} \right) }^{\frac{1}{4}}}}}{b}, {a_2}={a_2}, {a_4} = \frac{{\sqrt{\frac{1}{2} + \frac{1}{2}\sqrt{ - 2{a^2}{b^2} - 1} } }}{b}, {a_7} = \frac{1}{2}\frac{{\sqrt{ - 2 + 2\sqrt{ - 2{a^2}{b^2} - 1} } }}{b}, \\{} & {} {a_9}={a_9}, {a_{10}} = {a_{10}}, {f_0} = {f_0}, {f_1} = {f_1}, {f_2} = {f_2}. \end{aligned}$$

By substituting the above values in Eq. (2.1), yields

$$\begin{aligned} w = 2\frac{{\Omega {\kappa _1} - {\kappa _2}}}{{{\Omega ^2}}}, \end{aligned}$$
(6.2)

where

$$\begin{aligned}{} & {} f(x,t)= \Omega ={f_0}\cosh {\zeta _1}(x,t) + {f_1}\cos {\zeta _2}(x,t) + {f_2}\cosh {\zeta _3}(x,t) + {a_{10}}, \\{} & {} {\kappa _1} = - \frac{{\lambda {f_1}\cos \left( {\frac{{\sqrt{\lambda }x}}{b}} \right) }}{{{b^2}}} + \frac{{\left( { - 2 + 2\sqrt{ - 1 - 2{a^2}{b^2}} } \right) {f_2}\cosh \left( {{a_9} + \frac{{\sqrt{\lambda }x}}{{2b}}} \right) }}{{4{b^2}}}, \\{} & {} {\kappa _2} = {\left( { - \frac{{\sqrt{\lambda }{f_1}\sin \left( {\frac{{\sqrt{\lambda }x}}{b}} \right) }}{b} + \frac{{\sqrt{ - 2 + 2\sqrt{ - 1 - 2{a^2}{b^2}} } {f_2}\sinh \left( {{a_9} + \frac{{\sqrt{ - 2 + 2\sqrt{ - 1 - 2{a^2}{b^2}} } x}}{{2b}}} \right) }}{{2b}}} \right) ^2}, \\{} & {} \lambda = {\frac{1}{2} + \frac{1}{2}\sqrt{ - 1 - 2{a^2}{b^2}} }, { - 2{a^2}{b^2} - 1}>0. \end{aligned}$$

The graphical representation of solution (6.2) is given in the Figs 11, 12 and 13.

Fig. 11
figure 11

The visual depiction of w(x, t) for Eq. (6.2) is given. (a) 3D profile (b) contour profile (c) 2D profile, when \(a = - 3,b = 5,{a_3} = - 5,{a_9} = 4,{a_{10}} = - 2,{f_0} = 5,{f_1} = 8,{f_2} = 7.\)

Full size image
Fig. 12
figure 12

The visual depiction of w(x, t) for Eq. (6.2) is given. (a) 3D profile (b) contour profile (c) 2D profile, when \(a = - 3,b = 5,{a_3} = - 5,{a_9} = 4,{a_{10}} = - 2,{f_0} = - 2.5,{f_1} = 0.8,{f_2} = - 5.\)

Full size image
Fig. 13
figure 13

The visual depiction of w(x, t) for Eq. (6.2) is given. (a) 3D profile (b) contour profile (c) 2D profile, when \(a = 3,b = - 1,{a_3} = 5,{a_9} = 4,{a_{10}} = 0.5,{f_0} = - 2.5,{f_1} = - 0.8,{f_2} = - 5.\)

Full size image

7 Results and discussion

A lot of investigations have been carried out using the Landau–Ginzburg–Higgs model. Berman et al. studied LGH model and obtained analytical solutions (Barman et al. 2021). They obtained the analytical solutions for some families of solitons by using the generalized Kudryashov approach. Asjad et al. studied the same model to investigate analytical solutions using generalized projective Riccati method (Asjad et al. 2023). Recently Faridi and Al-Qahtani (2024) studied the LGH model and obtained optical soliton solutions using Khater method. Khalique and Lephoko studied conserved vectors and symmetry solutions for the LGH model (Khalique and Lephoko 2024). In this research, we studied a well known Landau–Ginzburg–Higgs model for lump soliton, lump one kink, lump two kink, periodic waves, and multi-waves by using some distinct ansatz transformation. In the Landau–Ginzburg–Higgs model, the derived results provide significant insights into the behavior of nonlinear waves. Developing an understanding of the interaction and propagation of these waves can enhance our comprehension of complex wave dynamics. The found solutions, including multi-waves, lump one kink, lump two kink, and lump solitons, have real-world applications in a variety of disciplines, including material science, quantum mechanics, solid-state physics, and electromagnetic studies. These solutions can be used to represent nonlinear wave dynamics and describe localized energy concentrations in waves. Lump soliton solution is shown by Eq. (2.4). The Eq. (3.2) illustrates the solution of lump one kink. The Eq. (4.2) shows the solution of lump two kink. Periodic waves solution is shown by Eq. (5.2). The Eq. (6.2) illustrates the solution of multi-waves. Figure 1 depicts the 3D, contour and 2D profiles of w which illustrates bright face of lump solution. Figure 2 depicts the 3D, contour and 2D profiles of w which describes two bright faces of lump solution. Figure 3 depicts the 3D contour and 2D profiles of w that show the periodic wave lump solution. Figures 4 and 5 show the 3D contour and 2D profiles of w which illustrates bright soliton solution of lump one kink. Figure 6 shows the 3D, contour and 2D profiles of w that describes a large bright soliton solution of lump two kink. Figure 7 describes the same properties of w. Figure 8 shows the 3D, contour and 2D profiles of w that depicts kink shaped soliton solution of lump two kink. Figure 9 depicts the 3D, contour and 2D profiles of w that shows bright face of periodic waves solution. Figure 10 depicts the 3D, contour and 2D profiles of w which show one bright and two dark faces of periodic waves solution. Figure 11 depicts the 3D, contour and 2D profiles of w which shows bright face of multi-waves solution. Figure 12 depicts the 3D, contour and 2D profiles of w which depicts periodic wave solution of multi-waves. At the end, Fig. 13 describes the 3D, contour and 2D profiles of w that show the periodic wave solution of multi-waves.

8 Conclusions

The main aim of our study is to find the analytical solutions of Landau–Ginzburg–Higgs model. We may investigate our current understanding of the dependence of nonlinear systems, specifically for analytical solutions to lump soliton, periodic wave, and multi-wave nonlinear waves, by studying the Landau–Ginzburg–Higgs model. Scholars can gain a deeper comprehension of the intricate dynamics and interactions of nonlinear waves in many physical regimes by utilizing the solutions of LGH model and novel ansatz transformations. Our findings reveal complicated symmetry and pattern formations of nonlinear systems, which deepens our understanding on the dynamics of wave phenomena confined in other physical systems like lump solitons and multi-waves. In order to show the physical behavior of solutions, specific findings can be observed in 2D, 3D, and contour profiles by choosing suitable parameter values. In comparison to previous methods in the analysis of nonlinear waves, the current methodology of using ansatz transformations in the study of the LGH model offers significant advantages. Our proposed methodology is significantly more efficient in comparison to other traditional methods, due to the strategically simplifying of difficult equations through transformations which generating explicit solutions efficiently. The obtained solutions are claimed to be new, interesting and remarkable with much wider class of free constants. They may be helpful in characterizing and elucidating the underlying structures of complex behaviors that are seen in the natural world. We will apply these transformations in our future study to investigate more interaction solutions of other nonlinear physical models. We expect that new results of this article and research methodology may aid in the solution of additional nonlinear evolution equations and provide an explanation for some physical events that are represented in nonlinear models.