1 Introduction

The study of nonlinear partial differential equations (NLPDEs) is pivotal to explore complex nonlinear phenomena across several physical disciplines such as condensed matter physics, plasma physics and solid state physics etc. Over the years, significant advancements have been achieved in the study of these equations. In the domain of literature, various computational methods have been developed to explore the characteristics of solutions. Some of the well-known methods include the extended direct algebraic method [1], \(\left( \frac{G'}{G},\frac{1}{G}\right) \)-expansion technique [2], Bilinear method [3], the reductive perturbation technique [4], sub-ordinary differential equations method [5], the exp-function method [6], Painlevé test [7, 8], Discrete singular convolution differential quadrature algorithm [9], Bilinear neural network method [10,11,12,13,14,15] the generalized exponential rational function method [16, 17], the Hirota bilinear method [18,19,20], the generalized Riccati equation mapping method [21]. Remarkably, the Darboux transformations methods [22], Lie symmetry method [23, 24] and the Weierstrass elliptic function method [25] have been widely utilized. These techniques are utilized to explore a wide range of solutions, including bright solitons, dark solitons, peaks, and more, which appear in nonlinear optics, are special waves that keeps their shape as they move because they carefully balance dispersion and nonlinearity [26, 27]. Bright solitons, known for their intense peaks, are created when the material self-focuses due to its nonlinearity. While dark solitons, which have areas of reduced intensity, form because the material self-spreads, countering the tendency to spread out [28].

The (\(2+1\))-dimensional generalized Benjamin–Ono equation [29] plays a crucial role in the study of internal waves within deep stratified fluids. It is represented as:

$$\begin{aligned} u_{xxxx}{+}c_1u_{tt}{+}c_2u_{xt}+c_3u_{xy}+c_4(u^2)_{xx}=0, \end{aligned}$$
(1)

where \(c_1, c_2, c_3\) and \(c_4\) signifying arbitrary constants. The gBO equation finds wide-ranging applications in various scientific disciplines. In optical fiber communications, it helps in modeling and analyzing wave propagation phenomena, aiding the design and optimization of communication systems. In plasma physics, the gBO equation contributes to understanding wave dynamics in plasma environments, crucial for fusion research and space physics. Moreover, in condensed matter physics, this equation has utility in describing certain types of wave behavior in materials, aiding the comprehension of complex physical processes. The versatility of the gBO equation makes it an indispensable tool for tackling challenges in diverse fields of study.

Furthermore, by taking particular value of the involved coefficients of the gBO equation, we have some other important NLPDEs.

  1. 1.

    When \(c_1=\frac{1}{\beta }\), \(c_2=0, c_3=\gamma c_1\) and \(c_4=\alpha c_1,\) along with the equation of line \(y=x\), then Eq. (1) transformed into the Boussinesq equation [30]:

    $$\begin{aligned} u_{xxxx}+\frac{1}{\beta }u_{tt}+\frac{\gamma }{\beta }u_{xx}+\frac{\alpha }{\beta }(u^2)_{xx}=0. \end{aligned}$$
    (2)
  2. 2.

    When \(c_1=\frac{1}{\beta }\), \(c_2=0, c_3=0\) and \(c_4=\frac{\alpha }{\beta },\) then Eq. (1) converted into the (\(1+1\))-dimensional Benjamin–Ono equation [31]:

    $$\begin{aligned} u_{xxxx}+\frac{1}{\beta }u_{tt}+\frac{\alpha }{\beta }(u^2)_{xx}=0. \end{aligned}$$
    (3)

In recent time, many researchers have tackled the gBO equation, employing a variety of techniques, as follows: Roudenko et al. [32] conducted a comprehensive analysis of the generalized Benjamin–Ono equation within the domain of real number line. They applied Petviashvili’s iteration method to numerically illustrate the solutions. Moreover, their work involved an exploration of how these solutions behaved under different decay rates, with a specific emphasis on the \(L^{2}-\)supercritical gBO equation. Simtrakankul et al. [33] applied the improved generalized Tanh–Coth method to study the (\(2+1\))-dimensional extension of the Benjamin–Ono equation with time-varying coefficients. Through this approach, they successfully derived solitary wave solutions, encompassing both single and combined solitons. Within their research, Ma et al. [29] tackled the (\(2+1\))-dimensional Benjamin–Ono equation, utilizing a combination of methods such as the bilinear method, test function, improved Tanh–Coth method and improved Tan–Cot method. Their investigation extended to the exploration of lump solutions, breather solitons, and various soliton solutions. Inspired by the above literature review, we have explore the gBO equation via the “Inverse \(\left( \frac{G'}{G}\right) \)-expansion method.”

This article is structured into multiple sections, each dedicated to providing a comprehensive exploration of the application of the Inverse \((G'/G)\)-expansion method to the gBO equation and its consequences.

  • In Sect. 1, we investigated the historical foundation of the gBO equation, offering valuable context to underscore its importance within the domain of nonlinear partial differential equations.

  • Within Sect. 2, we provide a fundamental steps of the “Inverse \((G'/G)\)-expansion method,” illustrating its step by step procedure for attaining exact solutions to the NLPDE.

  • Moving to Sect. 3, we explain how we used the Inverse \((G'/G)\)-expansion method to address the solutions of the gBO equation. This method helps us to find new and interesting solutions to the main problem. We then analyzed these solutions in detail by presenting them graphically, which allowed us to clearly see their behavior in waves.

  • In Sect. 4, we make a connection between our mathematical findings and real-world situations. This makes our research more useful in real life because it helps us understand how it connects to things we already know, it become more valuable and meaningful.

  • Furthermore, in Sect. 5, we illustrate the graphical behavior of the attained solutions under various parameter choices in the acceptable range space. This visual analysis provide deeper into the complexities of nonlinear wave phenomena.

  • In Sect. 6, we summarize our research study by giving a clear conclusion. We highlight the important things made using the Inverse \((G'/G)\)-expansion method on the gBO equation.

2 Inverse \(\left( \frac{G'}{G}\right) \)-expansion method

In this section, we present an overview of the Inverse \(\left( \frac{G'}{G}\right) \)-expansion method, a powerful method to extract the exact solutions to nonlinear partial differential equations (NLPDEs) spanning multiple disciplines such as engineering, physics, and mathematics.

  • The NLPDE can be expressed as:

    $$\begin{aligned} P(u,u_x,u_y,u_t,u_{xx},u_{yy},u_{tt},u_{xt},\dots ) = 0, \end{aligned}$$
    (4)

    where \(u=u(x,y,t)\) represents the wave amplitude and P denote a polynomial function that involves a range of partial derivatives of u concerning its independent variables x, y and t.

  • Consider a solution that takes a form of traveling wave:

    $$\begin{aligned} u(x,y,t) = Q(\eta ), \end{aligned}$$
    (5)

    where \(\eta =\alpha x+\beta y+\gamma t\). The constants \(\alpha \), \(\beta \) and \(\gamma \) are arbitrary.

  • Upon inserting the assumed solution into the NLPDE, it simplify into an ordinary differential equation (ODE). The ODE can be expressed as:

    $$\begin{aligned} N(Q(\eta ),Q'(\eta ),Q''(\eta ),\dots ) = 0, \end{aligned}$$
    (6)

    where \(Q'=\frac{dQ}{d\eta },\) represents the first derivative, \(Q''=\frac{d^2Q}{d\eta ^2}\), represents the second derivative and so on.

  • In order to tackle the ODE (6), we introduce a trial solution \(Q(\eta )\) that takes the form of a series expansion that depend on the ratio \(\left( \frac{G'(\eta )}{G(\eta )}\right) \) in the following manner:

    $$\begin{aligned} Q(\eta )= & {} {\mathcal {R}}_0 + \sum _{i=1}^{N}{\mathcal {R}}_i~\left( \frac{G'(\eta )}{G(\eta )}\right) ^i\nonumber \\{} & {} \quad + \sum _{i=1}^{N}{\mathcal {S}}_i~\left( \frac{G'(\eta )}{G(\eta )}\right) ^{-i}. \end{aligned}$$
    (7)

    Here, \({\mathcal {R}}_i\) and \({\mathcal {S}}_i~(0 \le i \le N)\) denotes undetermined constants that will be established later. Moreover, the function \(G(\eta )\) is a solution to the Riccati equation:

    $$\begin{aligned} G'(\eta ) = a G(\eta )^2+b G(\eta ) + c, \end{aligned}$$
    (8)

    where the constants a, b, and c are arbitrary.

  • On putting the trial solution \(Q(\eta )\) into the ODE (6) and equating the highest-order derivative term with the nonlinear term, we establish a system of algebraic equations governing the values of the arbitrary constants \({\mathcal {R}}_i\), \({\mathcal {S}}_i\), a, b, and c. Solving this system of algebraic equations allow us to determine the specific values for these arbitrary constants, and as a result, we obtain the exact solution to the original NLPDE.

  • Following these outlined steps, the Inverse \(\left( \frac{G'}{G}\right) \)-expansion method represents a systematic and highly efficient approach for deducing exact solutions for a diverse array of NLPDEs. This method proves to be a valuable tool for researchers working in various scientific and engineering domain (Fig. 1).

Fig. 1
figure 1

Diagram summarizing the key findings and concepts in this article

Full size image

3 Application of the inverse \(\left( \frac{G'}{G}\right) \)-expansion method

In this section, our motive is to apply the Inverse \((\frac{G'}{G})\)-expansion method to address the exact solutions of the gBO equation (1). Initially, we start with the transformation expressed as:

$$\begin{aligned} u(x,y,t)=Q(\eta ),\quad \text{ with }\quad \eta =\alpha x+\beta y+\gamma t. \end{aligned}$$
(9)

Making use of this transformation, the gBO Eq. (1) converted into the following equation

$$\begin{aligned}{} & {} \alpha ^4 Q^{(4)}(\eta )+Q''(\eta ) \left( \alpha \beta c_3+\alpha c_2 \gamma +c_1 \gamma ^2\right) \nonumber \\{} & {} \quad +2 \alpha ^2 c_4 \left( Q(\eta ) Q''(\eta )+Q'(\eta )^2\right) =0. \end{aligned}$$
(10)

Next, to determine the termination point of the series form solution (7), we are balancing the terms \(Q^{(4)}(\eta )\) and \(Q(\eta ) Q''(\eta )\) in Eq. (10) by the homogeneous balancing principle. By this procedure, we get that \(N = 2\), which means that our trial solution can be written as

$$\begin{aligned} Q(\eta )= & {} {\mathcal {R}}_0 + {\mathcal {R}}_1\left( \frac{G'(\eta )}{G(\eta )}\right) +{\mathcal {R}}_2\left( \frac{G'(\eta )}{G(\eta )}\right) ^2\nonumber \\{} & {} \quad + {\mathcal {S}}_1\left( \frac{G'(\eta )}{G(\eta )}\right) ^{-1} + {\mathcal {S}}_2\left( \frac{G'(\eta )}{G(\eta )}\right) ^{-2}. \end{aligned}$$
(11)

Utilizing the expression (11) into Eq. (10), and subsequently set the factor associated with \(G(\eta )\) to zero, we obtain a set of algebraic equations. Solving this system provides us some set of constraints, which play a crucial role in determining the specific form of the exact solutions to the gBO equation. These constraints ensure the compatibility of the trial solution (11) and the transformation (9) with the gBO equation, resulting in valid solutions for the given problem.

3.1 Analytical solutions for the gBO equation

3.2 First set of solutions

$$\begin{aligned} {\mathcal {R}}_1= & {} -b {\mathcal {R}}_2;{\mathcal {S}}_1=0;{\mathcal {S}}_2=0;\\ c_3= & {} \frac{-\alpha ^4 b^2 {\mathcal {R}}_2-\alpha \gamma c_2 {\mathcal {R}}_2-\gamma ^2 c_1 {\mathcal {R}}_2+12 \alpha ^4 {\mathcal {R}}_0}{\alpha \beta {\mathcal {R}}_2};\\ c_4= & {} -\frac{6 \alpha ^2}{{\mathcal {R}}_2};c=0. \end{aligned}$$

3.3 Case (i): investigating solutions when \(\Omega =b^2-4ac> 0\) provided \(ab\ne 0\)

The solutions for the ODE described in Eq. (10) are acquired as follows:

$$\begin{aligned} Q(\eta )= & {} \frac{e^{b \eta }}{\left( e^{b \eta }+1\right) ^2}\left( 2 {\mathcal {R}}_0 (\cosh (b \eta )+1)-b^2 {\mathcal {R}}_2\right) , \end{aligned}$$
(12)
$$\begin{aligned} Q(\eta )= & {} \frac{e^{b \eta } \left( 2 {\mathcal {R}}_0 \left( \sqrt{-b^2}-b \sinh (b \eta )\right) +\left( -b^2\right) ^{3/2} {\mathcal {R}}_2\right) }{2 \sqrt{-b^2} e^{b \eta }+b \left( -e^{2 b \eta }\right) +b}, \nonumber \\ \end{aligned}$$
(13)
$$\begin{aligned} Q(\eta )= & {} M+\frac{1}{4} b^2 {\mathcal {R}}_2 \text {csch}^2\left( \frac{b \eta }{2}\right) . \end{aligned}$$
(14)

Under the transformation (9), we determine the solutions of the gBO equation in the following manner:

$$\begin{aligned} u(x,y,t){=}{\mathcal {R}}_0{-}\frac{1}{4} b^2 {\mathcal {R}}_2 \text {sech}^2\left( \frac{1}{2} b (\alpha x{+}\beta y{+}\gamma t)\right) ,\nonumber \\ \end{aligned}$$
(15)
$$\begin{aligned} u(x,y,t)={\mathcal {R}}_0+\frac{\left( -b^2\right) ^{3/2} {\mathcal {R}}_2}{2 \left( \sqrt{-b^2}-b \sinh (b (\alpha x+\beta y+\gamma t))\right) },\nonumber \\ \end{aligned}$$
(16)
$$\begin{aligned} u(x,y,t){=}{\mathcal {R}}_0{+}\frac{1}{4} b^2 {\mathcal {R}}_2 \text {csch}^2\left( \frac{1}{2} b (\alpha x{+}\beta y{+}\gamma t)\right) .\nonumber \\ \end{aligned}$$
(17)

3.4 Case (ii): investigating solutions when \(\Omega =b^2-4ac<0\) provided \(ab\ne 0\)

The solutions for the ODE described in Eq. (10) are acquired as follows:

$$\begin{aligned} Q(\eta )= & {} \frac{\exp ({b \eta })}{\left( \exp ({b \eta })-1\right) ^2}\left( b^2 {\mathcal {R}}_2+2 {\mathcal {R}}_0 (\cosh (b \eta )-1)\right) ,\nonumber \\ \end{aligned}$$
(18)
$$\begin{aligned} Q(\eta )= & {} \frac{\exp ({b \eta })}{\left( \exp ({b \eta })+1\right) ^2}\left( 2 {\mathcal {R}}_0 (\cosh (b \eta )+1)-b^2 {\mathcal {R}}_2\right) .\nonumber \\ \end{aligned}$$
(19)

Consequently, the solutions for the gBO equation subject to the transformation (9) are as follows:

$$\begin{aligned} u(x,y,t)= & {} \frac{\exp ({b (\alpha x+\beta y+\gamma t)})}{\left( \exp ({b (\alpha x+\beta y+\gamma t)})-1\right) ^2}\nonumber \\{} & {} \quad \times \left( b^2 {\mathcal {R}}_2{+}2 {\mathcal {R}}_0 (\cosh (b (\alpha x{+}\beta y{+}\gamma t)){-}1)\right) ,\nonumber \\ \end{aligned}$$
(20)
$$\begin{aligned} u(x,y,t)= & {} \frac{\exp ({b (\alpha x+\beta y+\gamma t)})}{\left( \exp ({b (\alpha x+\beta y+\gamma t)})+1\right) ^2}\nonumber \\{} & {} \quad \times \left( 2 {\mathcal {R}}_0 (\cosh (b (\alpha x+\beta y{+}\gamma t)){+}1){-}b^2 {\mathcal {R}}_2\right) .\nonumber \\ \end{aligned}$$
(21)

3.5 Second set of solutions

$$\begin{aligned} {\mathcal {R}}_1= & {} 0;{\mathcal {R}}_2=0;{\mathcal {S}}_2=-\frac{{\mathcal {S}}_1 \left( b^2-4 a c\right) }{2 b};\nonumber \\ c_3= & {} \frac{16 a \alpha ^4 c-4 \alpha ^4 b^2-\alpha \gamma c_2-\gamma ^2 c_1}{\alpha \beta };c_4=0.\nonumber \\ \end{aligned}$$
(22)

3.6 Case (i): investigating solutions when \(\Omega =b^2-4ac>0\) provided \(ab\ne 0\)

The solutions for the ODE described in Eq. (10) are acquired as follows:

$$\begin{aligned} Q(\eta )= & {} {\mathcal {R}}_0-\frac{2 {\mathcal {S}}_1 \cosh ^4\left( \frac{1}{2} \eta \sqrt{\Omega }\right) \left( \sqrt{\Omega } \tanh \left( \frac{1}{2} \eta \sqrt{\Omega }\right) +b\right) ^2}{b \left( \Omega \right) }+\frac{2 {\mathcal {S}}_1 \cosh ^2\left( \frac{1}{2} \eta \sqrt{\Omega }\right) \left( \sqrt{\Omega } \tanh \left( \frac{1}{2} \eta \sqrt{\Omega }\right) +b\right) }{\Omega },\end{aligned}$$
(23)
$$\begin{aligned} Q(\eta )= & {} {\mathcal {R}}_0-\frac{2 {\mathcal {S}}_1 \sinh ^4\left( \frac{1}{2} \eta \sqrt{\Omega }\right) \left( \sqrt{\Omega } \coth \left( \frac{1}{2} \eta \sqrt{\Omega }\right) +b\right) ^2}{b \left( \Omega \right) }-\frac{2 {\mathcal {S}}_1 \sinh ^2\left( \frac{1}{2} \eta \sqrt{\Omega }\right) \left( \sqrt{\Omega } \coth \left( \frac{1}{2} \eta \sqrt{\Omega }\right) +b\right) }{\Omega },\end{aligned}$$
(24)
$$\begin{aligned} Q(\eta )= & {} {\mathcal {R}}_0-\frac{{\mathcal {S}}_1 \left( \Omega \right) \left( \sqrt{-\Omega } \left( \tan \left( \eta \sqrt{-\Omega }\right) -\sec \left( \eta \sqrt{-\Omega }\right) \right) -b\right) ^2}{2 b \left( -\Omega \right) \left( \sqrt{-\Omega } \sec ^2\left( \eta \sqrt{-\Omega }\right) -\sqrt{-\Omega } \tan \left( \eta \sqrt{-\Omega }\right) \sec \left( \eta \sqrt{-\Omega }\right) \right) ^2}\nonumber \\{} & {} \quad +\frac{{\mathcal {S}}_1 \left( \sqrt{-\Omega } \left( \tan \left( \eta \sqrt{-\Omega }\right) -\sec \left( \eta \sqrt{-\Omega }\right) \right) -b\right) }{\sqrt{-\Omega } \left( \sqrt{-\Omega } \sec ^2\left( \eta \sqrt{-\Omega }\right) -\sqrt{-\Omega } \tan \left( \eta \sqrt{-\Omega }\right) \sec \left( \eta \sqrt{-\Omega }\right) \right) }. \end{aligned}$$
(25)

Under the transformation (9), we determine the solutions of the gBO equation in the following manner:

$$\begin{aligned} u(x,y,t)= & {} {\mathcal {R}}_0-\frac{a c {\mathcal {S}}_1}{b^3-4 a b c}\nonumber \\{} & {} \quad -\frac{b {\mathcal {S}}_1 \sqrt{\Omega } \sinh \left( 2 \sqrt{\Omega } (\alpha x+\beta y+\gamma t)\right) }{2 \left( b^3-4 a b c\right) }\nonumber \\{} & {} \quad -\frac{b^2 {\mathcal {S}}_1 \cosh \left( 2 \sqrt{\Omega } (\alpha x+\beta y+\gamma t)\right) }{2 \left( b^3-4 a b c\right) }\nonumber \\{} & {} \quad +\frac{a c {\mathcal {S}}_1 \cosh \left( 2 \sqrt{\Omega } (\alpha x+\beta y+\gamma t)\right) }{b^3-4 a b c}\nonumber \\{} & {} \quad +\frac{b^2 {\mathcal {S}}_1}{2 \left( b^3-4 a b c\right) }, \end{aligned}$$
(26)
$$\begin{aligned}{} & {} u(x,y,t)={\mathcal {R}}_0-\frac{2 {\mathcal {S}}_1 \sinh ^4\left( \frac{1}{2} \sqrt{\Omega } (\alpha x+\beta y+\gamma t)\right) \left( \sqrt{\Omega } \coth \left( \frac{1}{2} \sqrt{\Omega } (\alpha x+\beta y+\gamma t)\right) +b\right) ^2}{b \left( \Omega \right) }\nonumber \\{} & {} \qquad \qquad -\frac{2 {\mathcal {S}}_1 \sinh ^2\left( \frac{1}{2} \sqrt{\Omega } (\alpha x+\beta y+\gamma t)\right) \left( \sqrt{\Omega } \coth \left( \frac{1}{2} \sqrt{\Omega } (\alpha x+\beta y+\gamma t)\right) +b\right) }{\Omega }, \end{aligned}$$
(27)
$$\begin{aligned}{} & {} u(x,y,t)={\mathcal {R}}_0+\frac{{\mathcal {S}}_1 \left( \sqrt{-\Omega } \left( \tan \left( \sqrt{-\Omega } (\alpha x+\beta y+\gamma t)\right) -\sec \left( \sqrt{-\Omega } (\alpha x+\beta y+\gamma t)\right) \right) -b\right) }{\sqrt{-\Omega } \left( \sqrt{-\Omega } \sec ^2\left( \sqrt{-\Omega } (\alpha x+\beta y+\gamma t)\right) -\sqrt{-\Omega } \tan \left( \sqrt{-\Omega } (\alpha x+\beta y+\gamma t)\right) \sec \left( \sqrt{-\Omega } (\alpha x+\beta y+\gamma t)\right) \right) }\nonumber \\ \end{aligned}$$
(28)
$$\begin{aligned}{} & {} \qquad -\frac{{\mathcal {S}}_1 \left( \Omega \right) \left( \sqrt{-\Omega } \left( \tan \left( \sqrt{-\Omega } (\alpha x+\beta y+\gamma t)\right) -\sec \left( \sqrt{-\Omega } (\alpha x+\beta y+\gamma t)\right) \right) -b\right) ^2}{2 b \left( -\Omega \right) \left( \sqrt{-\Omega } \sec ^2\left( \sqrt{-\Omega } (\alpha x+\beta y+\gamma t)\right) -\sqrt{-\Omega } \tan \left( \sqrt{-\Omega } (\alpha x+\beta y+\gamma t)\right) \sec \left( \sqrt{-\Omega } (\alpha x+\beta y+\gamma t)\right) \right) ^2}. \end{aligned}$$
(29)

3.7 Case (ii): investigating solutions when \(\Omega =b^2-4ac<0\) provided \(ab\ne 0\)

The solutions for the ODE described in Eq. (10) are acquired as follows:

$$\begin{aligned} Q(\eta )= & {} {\mathcal {R}}_0-\frac{{\mathcal {S}}_1 \left( \Omega \right) \left( \sqrt{-\Omega } \left( \tan \left( \frac{1}{4} \eta \sqrt{-\Omega }\right) -\cot \left( \frac{1}{4} \eta \sqrt{-\Omega }\right) \right) -2 b\right) ^2}{2 b \left( -\Omega \right) \left( \frac{1}{4} \sqrt{-\Omega } \csc ^2\left( \frac{1}{4} \eta \sqrt{-\Omega }\right) +\frac{1}{4} \sqrt{-\Omega } \sec ^2\left( \frac{1}{4} \eta \sqrt{-\Omega }\right) \right) ^2}\nonumber \\{} & {} +\frac{{\mathcal {S}}_1 \left( \sqrt{-\Omega } \left( \tan \left( \frac{1}{4} \eta \sqrt{-\Omega }\right) -\cot \left( \frac{1}{4} \eta \sqrt{-\Omega }\right) \right) -2 b\right) }{\sqrt{-\Omega } \left( \frac{1}{4} \sqrt{-\Omega } \csc ^2\left( \frac{1}{4} \eta \sqrt{-\Omega }\right) +\frac{1}{4} \sqrt{-\Omega } \sec ^2\left( \frac{1}{4} \eta \sqrt{-\Omega }\right) \right) }, \end{aligned}$$
(30)
$$\begin{aligned} Q(\eta )&={\mathcal {R}}_0{-}\frac{2 {\mathcal {S}}_1 \left( \Omega \right) \cos ^4\left( \frac{1}{2} \eta \sqrt{{-}\Omega }\right) \left( \sqrt{-\Omega } \tan \left( \frac{1}{2} \eta \sqrt{-\Omega }\right) {-}b\right) ^2}{b \left( -\Omega \right) ^2}\nonumber \\&\quad +\frac{2 {\mathcal {S}}_1 \cos ^2\left( \frac{1}{2} \eta \sqrt{-\Omega }\right) \left( \sqrt{-\Omega } \tan \left( \frac{1}{2} \eta \sqrt{-\Omega }\right) -b\right) }{-\Omega }.\nonumber \\ \end{aligned}$$
(31)

Consequently, the solutions for the gBO equation subject to the transformation (9) are as follows:

$$\begin{aligned} u(x,y,t)= & {} {\mathcal {R}}_0-\frac{{\mathcal {S}}_1 \left( \Omega \right) \left( \sqrt{-\Omega } \left( \tan \left( \frac{1}{4} \sqrt{-\Omega } (\alpha x+\beta y+\gamma t)\right) -\cot \left( \frac{1}{4} \sqrt{-\Omega } (\alpha x+\beta y+\gamma t)\right) \right) -2 b\right) ^2}{2 b \left( -\Omega \right) \left( \frac{1}{4} \sqrt{-\Omega } \csc ^2\left( \frac{1}{4} \sqrt{-\Omega } (\alpha x+\beta y+\gamma t)\right) +\frac{1}{4} \sqrt{-\Omega } \sec ^2\left( \frac{1}{4} \sqrt{-\Omega } (\alpha x+\beta y+\gamma t)\right) \right) ^2}\nonumber \\{} & {} \quad +\frac{{\mathcal {S}}_1 \left( \sqrt{-\Omega } \left( \tan \left( \frac{1}{4} \sqrt{-\Omega } (\alpha x+\beta y+\gamma t)\right) -\cot \left( \frac{1}{4} \sqrt{-\Omega } (\alpha x+\beta y+\gamma t)\right) \right) -2 b\right) }{\sqrt{-\Omega } \left( \frac{1}{4} \sqrt{-\Omega } \csc ^2\left( \frac{1}{4} \sqrt{-\Omega } (\alpha x+\beta y+\gamma t)\right) +\frac{1}{4} \sqrt{-\Omega } \sec ^2\left( \frac{1}{4} \sqrt{-\Omega } (\alpha x+\beta y+\gamma t)\right) \right) },\end{aligned}$$
(32)
$$\begin{aligned} u(x,y,t)= & {} {\mathcal {R}}_0-\frac{2 {\mathcal {S}}_1 \left( \Omega \right) \cos ^4\left( \frac{1}{2} \sqrt{-\Omega } (\alpha x+\beta y+\gamma t)\right) \left( \sqrt{-\Omega } \tan \left( \frac{1}{2} \sqrt{-\Omega } (\alpha x+\beta y+\gamma t)\right) -b\right) ^2}{b \left( -\Omega \right) ^2}\nonumber \\{} & {} \quad +\frac{2 {\mathcal {S}}_1 \cos ^2\left( \frac{1}{2} \sqrt{-\Omega } (\alpha x+\beta y+\gamma t)\right) \left( \sqrt{-\Omega } \tan \left( \frac{1}{2} \sqrt{-\Omega } (\alpha x+\beta y+\gamma t)\right) -b\right) }{-\Omega }. \end{aligned}$$
(33)

3.8 Third set of solutions

$$\begin{aligned} {\mathcal {R}}_0&\ne 0; {\mathcal {R}}_1\ne 0;{\mathcal {R}}_2\ne 0; {\mathcal {S}}_1\ne 0;{\mathcal {S}}_2\ne 0;\alpha =0;\nonumber \\ \beta&\ne 0; \gamma \ne 0;c_1=0;c_2\ne 0;c_3\ne 0;c_4\ne 0. \end{aligned}$$
(34)

3.9 Case (i): investigating solutions when \(\Omega =b^2-4ac> 0\) and \(ab\ne 0\)

The solutions for the ODE described in Eq. (10) are acquired as follows:

$$\begin{aligned} Q(\eta )= & {} \frac{{\mathcal {R}}_2 \left( \Omega \right) ^2 \text {sech}^4\left( \frac{1}{2} \eta \sqrt{\Omega }\right) }{4 \left( \sqrt{\Omega } \tanh \left( \frac{1}{2} \eta \sqrt{\Omega }\right) +b\right) ^2}\nonumber \\{} & {} \quad +\frac{4 {\mathcal {S}}_2 \cosh ^4\left( \frac{1}{2} \eta \sqrt{\Omega }\right) \left( \sqrt{\Omega } \tanh \left( \frac{1}{2} \eta \sqrt{\Omega }\right) +b\right) ^2}{\left( \Omega \right) ^2}\nonumber \\{} & {} \quad +\frac{2 {\mathcal {S}}_1 \cosh ^2\left( \frac{1}{2} \eta \sqrt{\Omega }\right) \left( \sqrt{\Omega } \tanh \left( \frac{1}{2} \eta \sqrt{\Omega }\right) +b\right) }{\Omega }\nonumber \\{} & {} \quad +\frac{{\mathcal {R}}_1 \left( \Omega \right) \text {sech}^2\left( \frac{1}{2} \eta \sqrt{\Omega }\right) }{2 \left( \sqrt{\Omega } \tanh \left( \frac{1}{2} \eta \sqrt{\Omega }\right) +b\right) }+{\mathcal {R}}_0,\end{aligned}$$
(35)
$$\begin{aligned} Q(\eta )= & {} \frac{{\mathcal {R}}_2 \left( \Omega \right) ^2 \text {csch}^4\left( \frac{1}{2} \eta \sqrt{\Omega }\right) }{4 \left( \sqrt{\Omega } \coth \left( \frac{1}{2} \eta \sqrt{\Omega }\right) +b\right) ^2}\nonumber \\{} & {} \quad +\frac{4 {\mathcal {S}}_2 \sinh ^4\left( \frac{1}{2} \eta \sqrt{\Omega }\right) \left( \sqrt{\Omega } \coth \left( \frac{1}{2} \eta \sqrt{\Omega }\right) +b\right) ^2}{\left( \Omega \right) ^2}\nonumber \\{} & {} \quad -\frac{2 {\mathcal {S}}_1 \sinh ^2\left( \frac{1}{2} \eta \sqrt{\Omega }\right) \left( \sqrt{\Omega } \coth \left( \frac{1}{2} \eta \sqrt{\Omega }\right) +b\right) }{\Omega }\nonumber \\{} & {} \quad -\frac{{\mathcal {R}}_1 \left( \Omega \right) \text {csch}^2\left( \frac{1}{2} \eta \sqrt{\Omega }\right) }{2 \left( \sqrt{\Omega } \coth \left( \frac{1}{2} \eta \sqrt{\Omega }\right) +b\right) }+{\mathcal {R}}_0, \end{aligned}$$
(36)
$$\begin{aligned} Q(\eta )= & {} \frac{{\mathcal {R}}_2 \left( -\Omega \right) \left( \sqrt{-\Omega } \sec ^2\left( \eta \sqrt{-\Omega }\right) -\sqrt{-\Omega } \tan \left( \eta \sqrt{-\Omega }\right) \sec \left( \eta \sqrt{-\Omega }\right) \right) ^2}{\left( \sqrt{-\Omega } \left( \tan \left( \eta \sqrt{-\Omega }\right) -\sec \left( \eta \sqrt{-\Omega }\right) \right) -b\right) ^2}\nonumber \\{} & {} \quad +\frac{{\mathcal {R}}_1 \sqrt{-\Omega } \left( \sqrt{-\Omega } \sec ^2\left( \eta \sqrt{-\Omega }\right) -\sqrt{-\Omega } \tan \left( \eta \sqrt{-\Omega }\right) \sec \left( \eta \sqrt{-\Omega }\right) \right) }{\sqrt{-\Omega } \left( \tan \left( \eta \sqrt{-\Omega }\right) -\sec \left( \eta \sqrt{-\Omega }\right) \right) -b}\nonumber \\{} & {} \quad +\frac{{\mathcal {S}}_2 \left( \sqrt{-\Omega } \left( \tan \left( \eta \sqrt{-\Omega }\right) -\sec \left( \eta \sqrt{-\Omega }\right) \right) -b\right) ^2}{\left( -\Omega \right) \left( \sqrt{-\Omega } \sec ^2\left( \eta \sqrt{-\Omega }\right) -\sqrt{-\Omega } \tan \left( \eta \sqrt{-\Omega }\right) \sec \left( \eta \sqrt{-\Omega }\right) \right) ^2}\nonumber \\{} & {} \quad +\frac{{\mathcal {S}}_1 \left( \sqrt{-\Omega } \left( \tan \left( \eta \sqrt{-\Omega }\right) -\sec \left( \eta \sqrt{-\Omega }\right) \right) -b\right) }{\sqrt{-\Omega } \left( \sqrt{-\Omega } \sec ^2\left( \eta \sqrt{-\Omega }\right) -\sqrt{-\Omega } \tan \left( \eta \sqrt{-\Omega }\right) \sec \left( \eta \sqrt{-\Omega }\right) \right) }+{\mathcal {R}}_0. \end{aligned}$$
(37)

Therefore, the solutions of the gBO equation under the transformation (9) are given by

$$\begin{aligned} u(x,y,t)&=\frac{{\mathcal {R}}_2 \left( \Omega \right) ^2 \text {sech}^4\left( \frac{1}{2} \sqrt{\Omega } (\beta y+\gamma t)\right) }{4 \left( \sqrt{\Omega } \tanh \left( \frac{1}{2} \sqrt{\Omega } (\beta y+\gamma t)\right) +b\right) ^2}+\frac{{\mathcal {R}}_1 \left( \Omega \right) \text {sech}^2\left( \frac{1}{2} \sqrt{\Omega } (\beta y+\gamma t)\right) }{2 \left( \sqrt{\Omega } \tanh \left( \frac{1}{2} \sqrt{\Omega } (\beta y+\gamma t)\right) +b\right) }\nonumber \\&\quad +\frac{4 {\mathcal {S}}_2 \cosh ^4\left( \frac{1}{2} \sqrt{\Omega } (\beta y+\gamma t)\right) \left( \sqrt{\Omega } \tanh \left( \frac{1}{2} \sqrt{\Omega } (\beta y+\gamma t)\right) +b\right) ^2}{\left( \Omega \right) ^2}\nonumber \\&\quad +\frac{2 {\mathcal {S}}_1 \cosh ^2\left( \frac{1}{2} \sqrt{\Omega } (\beta y+\gamma t)\right) \left( \sqrt{\Omega } \tanh \left( \frac{1}{2} \sqrt{\Omega } (\beta y+\gamma t)\right) +b\right) }{\Omega }+{\mathcal {R}}_0, \end{aligned}$$
(38)
$$\begin{aligned} u(x,y,t)&=\frac{{\mathcal {R}}_2 \left( \Omega \right) ^2 \text {csch}^4\left( \frac{1}{2} \sqrt{\Omega } (\beta y+\gamma t)\right) }{4 \left( \sqrt{\Omega } \coth \left( \frac{1}{2} \sqrt{\Omega } (\beta y+\gamma t)\right) +b\right) ^2}-\frac{{\mathcal {R}}_1 \left( \Omega \right) \text {csch}^2\left( \frac{1}{2} \sqrt{\Omega } (\beta y+\gamma t)\right) }{2 \left( \sqrt{\Omega } \coth \left( \frac{1}{2} \sqrt{\Omega } (\beta y+\gamma t)\right) +b\right) }\nonumber \\&\quad +\frac{4 {\mathcal {S}}_2 \sinh ^4\left( \frac{1}{2} \sqrt{\Omega } (\beta y+\gamma t)\right) \left( \sqrt{\Omega } \coth \left( \frac{1}{2} \sqrt{\Omega } (\beta y+\gamma t)\right) +b\right) ^2}{\left( \Omega \right) ^2}\nonumber \\&\quad -\frac{2 {\mathcal {S}}_1 \sinh ^2\left( \frac{1}{2} \sqrt{\Omega } (\beta y+\gamma t)\right) \left( \sqrt{\Omega } \coth \left( \frac{1}{2} \sqrt{\Omega } (\beta y+\gamma t)\right) +b\right) }{\Omega }+{\mathcal {R}}_0, \end{aligned}$$
(39)
$$\begin{aligned} u(x,y,t)&=\frac{{\mathcal {R}}_1 \sqrt{-\Omega } \left( \sqrt{-\Omega } \sec ^2\left( \sqrt{-\Omega } (\beta y+\gamma t)\right) -\sqrt{-\Omega } \tan \left( \sqrt{-\Omega } (\beta y+\gamma t)\right) \sec \left( \sqrt{-\Omega } (\beta y+\gamma t)\right) \right) }{\sqrt{-\Omega } \left( \tan \left( \sqrt{-\Omega } (\beta y+\gamma t)\right) -\sec \left( \sqrt{-\Omega } (\beta y+\gamma t)\right) \right) -b}\nonumber \\&\quad +\frac{{\mathcal {R}}_2 \left( -\Omega \right) \left( \sqrt{-\Omega } \sec ^2\left( \sqrt{-\Omega } (\beta y+\gamma t)\right) -\sqrt{-\Omega } \tan \left( \sqrt{-\Omega } (\beta y+\gamma t)\right) \sec \left( \sqrt{-\Omega } (\beta y+\gamma t)\right) \right) ^2}{\left( \sqrt{-\Omega } \left( \tan \left( \sqrt{-\Omega } (\beta y+\gamma t)\right) -\sec \left( \sqrt{-\Omega } (\beta y+\gamma t)\right) \right) -b\right) ^2}\nonumber \\&\quad +\frac{{\mathcal {S}}_1 \left( \sqrt{-\Omega } \left( \tan \left( \sqrt{-\Omega } (\beta y+\gamma t)\right) -\sec \left( \sqrt{-\Omega } (\beta y+\gamma t)\right) \right) -b\right) }{\sqrt{-\Omega } \left( \sqrt{-\Omega } \sec ^2\left( \sqrt{-\Omega } (\beta y+\gamma t)\right) -\sqrt{-\Omega } \tan \left( \sqrt{-\Omega } (\beta y+\gamma t)\right) \sec \left( \sqrt{-\Omega } (\beta y+\gamma t)\right) \right) }\nonumber \\&\quad +\frac{{\mathcal {S}}_2 \left( \sqrt{-\Omega } \left( \tan \left( \sqrt{-\Omega } (\beta y+\gamma t)\right) -\sec \left( \sqrt{-\Omega } (\beta y+\gamma t)\right) \right) -b\right) ^2}{\left( -\Omega \right) \left( \sqrt{-\Omega } \sec ^2\left( \sqrt{-\Omega } (\beta y+\gamma t)\right) -\sqrt{-\Omega } \tan \left( \sqrt{-\Omega } (\beta y+\gamma t)\right) \sec \left( \sqrt{-\Omega } (\beta y+\gamma t)\right) \right) ^2}+{\mathcal {R}}_0. \end{aligned}$$
(40)

3.10 Case (ii): investigating solutions when \(\Omega =b^2-4ac<0\), provided \(ab\ne 0\)

The solutions for the ODE described in Eq. (10) are acquired as follows:

$$\begin{aligned} Q(\eta )&=\frac{{\mathcal {R}}_2 \left( -\Omega \right) \left( \frac{1}{4} \sqrt{-\Omega } \csc ^2\left( \frac{1}{4} \eta \sqrt{-\Omega }\right) +\frac{1}{4} \sqrt{-\Omega } \sec ^2\left( \frac{1}{4} \eta \sqrt{-\Omega }\right) \right) ^2}{\left( \sqrt{-\Omega } \left( \tan \left( \frac{1}{4} \eta \sqrt{-\Omega }\right) -\cot \left( \frac{1}{4} \eta \sqrt{-\Omega }\right) \right) -2 b\right) ^2}+\frac{{\mathcal {R}}_1 \sqrt{-\Omega } \left( \frac{1}{4} \sqrt{-\Omega } \csc ^2\left( \frac{1}{4} \eta \sqrt{-\Omega }\right) +\frac{1}{4} \sqrt{-\Omega } \sec ^2\left( \frac{1}{4} \eta \sqrt{-\Omega }\right) \right) }{\sqrt{-\Omega } \left( \tan \left( \frac{1}{4} \eta \sqrt{-\Omega }\right) -\cot \left( \frac{1}{4} \eta \sqrt{-\Omega }\right) \right) -2 b}\nonumber \\&\quad +\frac{{\mathcal {S}}_2 \left( \sqrt{-\Omega } \left( \tan \left( \frac{1}{4} \eta \sqrt{-\Omega }\right) -\cot \left( \frac{1}{4} \eta \sqrt{-\Omega }\right) \right) -2 b\right) ^2}{\left( -\Omega \right) \left( \frac{1}{4} \sqrt{-\Omega } \csc ^2\left( \frac{1}{4} \eta \sqrt{-\Omega }\right) +\frac{1}{4} \sqrt{-\Omega } \sec ^2\left( \frac{1}{4} \eta \sqrt{-\Omega }\right) \right) ^2}+\frac{{\mathcal {S}}_1 \left( \sqrt{-\Omega } \left( \tan \left( \frac{1}{4} \eta \sqrt{-\Omega }\right) -\cot \left( \frac{1}{4} \eta \sqrt{-\Omega }\right) \right) -2 b\right) }{\sqrt{-\Omega } \left( \frac{1}{4} \sqrt{-\Omega } \csc ^2\left( \frac{1}{4} \eta \sqrt{-\Omega }\right) +\frac{1}{4} \sqrt{-\Omega } \sec ^2\left( \frac{1}{4} \eta \sqrt{-\Omega }\right) \right) }+{\mathcal {R}}_0, \end{aligned}$$
(41)
$$\begin{aligned} Q(\eta )&=\frac{{\mathcal {R}}_2 \left( -\Omega \right) ^2 \sec ^4\left( \frac{1}{2} \eta \sqrt{-\Omega }\right) }{4 \left( \sqrt{-\Omega } \tan \left( \frac{1}{2} \eta \sqrt{-\Omega }\right) -b\right) ^2}\nonumber \\&\quad +\frac{{\mathcal {R}}_1 \left( -\Omega \right) \sec ^2\left( \frac{1}{2} \eta \sqrt{-\Omega }\right) }{2 \left( \sqrt{-\Omega } \tan \left( \frac{1}{2} \eta \sqrt{-\Omega }\right) -b\right) }\nonumber \\&\quad +\frac{4 {\mathcal {S}}_2 \cos ^4\left( \frac{1}{2} \eta \sqrt{-\Omega }\right) \left( \sqrt{-\Omega } \tan \left( \frac{1}{2} \eta \sqrt{-\Omega }\right) -b\right) ^2}{\left( -\Omega \right) ^2}\nonumber \\&\quad +\frac{2 {\mathcal {S}}_1 \cos ^2\left( \frac{1}{2} \eta \sqrt{-\Omega }\right) \left( \sqrt{-\Omega } \tan \left( \frac{1}{2} \eta \sqrt{-\Omega }\right) -b\right) }{-\Omega }\nonumber \\&\quad +{\mathcal {R}}_0. \end{aligned}$$
(42)

Consequently, the solutions for the gBO equation subject to the transformation (9) are as follows:

$$\begin{aligned} u(x,y,t)&=\frac{{\mathcal {R}}_2 \left( -\Omega \right) \left( \frac{1}{4} \sqrt{-\Omega } \csc ^2\left( \frac{1}{4} \sqrt{-\Omega } (\beta y+\gamma t)\right) +\frac{1}{4} \sqrt{-\Omega } \sec ^2\left( \frac{1}{4} \sqrt{-\Omega } (\beta y+\gamma t)\right) \right) ^2}{\left( \sqrt{-\Omega } \left( \tan \left( \frac{1}{4} \sqrt{-\Omega } (\beta y+\gamma t)\right) -\cot \left( \frac{1}{4} \sqrt{-\Omega } (\beta y+\gamma t)\right) \right) -2 b\right) ^2}\nonumber \\&\quad +\frac{{\mathcal {R}}_1 \sqrt{-\Omega } \left( \frac{1}{4} \sqrt{-\Omega } \csc ^2\left( \frac{1}{4} \sqrt{-\Omega } (\beta y+\gamma t)\right) +\frac{1}{4} \sqrt{-\Omega } \sec ^2\left( \frac{1}{4} \sqrt{-\Omega } (\beta y+\gamma t)\right) \right) }{\sqrt{-\Omega } \left( \tan \left( \frac{1}{4} \sqrt{-\Omega } (\beta y+\gamma t)\right) -\cot \left( \frac{1}{4} \sqrt{-\Omega } (\beta y+\gamma t)\right) \right) -2 b}\nonumber \\&\quad +\frac{{\mathcal {S}}_2 \left( \sqrt{-\Omega } \left( \tan \left( \frac{1}{4} \sqrt{-\Omega } (\beta y+\gamma t)\right) -\cot \left( \frac{1}{4} \sqrt{-\Omega } (\beta y+\gamma t)\right) \right) -2 b\right) ^2}{\left( -\Omega \right) \left( \frac{1}{4} \sqrt{-\Omega } \csc ^2\left( \frac{1}{4} \sqrt{-\Omega } (\beta y+\gamma t)\right) +\frac{1}{4} \sqrt{-\Omega } \sec ^2\left( \frac{1}{4} \sqrt{-\Omega } (\beta y+\gamma t)\right) \right) ^2}\nonumber \\&\quad +\frac{{\mathcal {S}}_1 \left( \sqrt{-\Omega } \left( \tan \left( \frac{1}{4} \sqrt{-\Omega } (\beta y+\gamma t)\right) -\cot \left( \frac{1}{4} \sqrt{-\Omega } (\beta y+\gamma t)\right) \right) -2 b\right) }{\sqrt{-\Omega } \left( \frac{1}{4} \sqrt{-\Omega } \csc ^2\left( \frac{1}{4} \sqrt{-\Omega } (\beta y+\gamma t)\right) +\frac{1}{4} \sqrt{-\Omega } \sec ^2\left( \frac{1}{4} \sqrt{-\Omega } (\beta y+\gamma t)\right) \right) }+{\mathcal {R}}_0, \end{aligned}$$
(43)
$$\begin{aligned} u(x,y,t)&=\frac{{\mathcal {R}}_2 \left( -\Omega \right) ^2 \sec ^4\left( \frac{1}{2} \sqrt{-\Omega } (\beta y+\gamma t)\right) }{4 \left( \sqrt{-\Omega } \tan \left( \frac{1}{2} \sqrt{-\Omega } (\beta y+\gamma t)\right) -b\right) ^2}+\frac{{\mathcal {R}}_1 \left( -\Omega \right) \sec ^2\left( \frac{1}{2} \sqrt{-\Omega } (\beta y+\gamma t)\right) }{2 \left( \sqrt{-\Omega } \tan \left( \frac{1}{2} \sqrt{-\Omega } (\beta y+\gamma t)\right) -b\right) }\nonumber \\&\quad +\frac{4 {\mathcal {S}}_2 \cos ^4\left( \frac{1}{2} \sqrt{-\Omega } (\beta y+\gamma t)\right) \left( \sqrt{-\Omega } \tan \left( \frac{1}{2} \sqrt{-\Omega } (\beta y+\gamma t)\right) -b\right) ^2}{\left( -\Omega \right) ^2}\nonumber \\&\quad +\frac{2 {\mathcal {S}}_1 \cos ^2\left( \frac{1}{2} \sqrt{-\Omega } (\beta y+\gamma t)\right) \left( \sqrt{-\Omega } \tan \left( \frac{1}{2} \sqrt{-\Omega } (\beta y+\gamma t)\right) -b\right) }{-\Omega }+{\mathcal {R}}_0. \end{aligned}$$
(44)
Fig. 2
figure 2

Dynamic evolution of 1-peakon, 1-lump and 1-soliton for the solution (15) through 3D and contour plots

Full size image

4 Bridging the gap: exploring the practical applications of mathematical discoveries

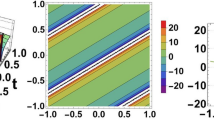
In this section, our focus is to bridge the gap between mathematical findings and their relevance to real-world phenomena. Using both 3D and contour plots, we provide a visual insight into the absolute nature of the solution (33). The visualizations vividly illustrate the presence of solitary waves, a phenomenon with significant implications. We have included an image illustrating solitary waves in an oceanic context, directly relating to a contour plot. This emphasizes the practical applicability of our findings to real-world phenomena, highlighting the clear connection between our mathematical discoveries and observed occurrences.

5 Graphical overview and interpretations

In this section, we analyze the derived solutions of the gBO equation graphically. For the deeper understanding of these solutions, we discuss the graphics by careful selection of the involved parameters within a suitable range space. We examine the real part of the solution to gain insights into how the solutions change and behave along the real axis, imaginary part to understand the patterns and characteristics exhibited along the imaginary axis, and the absolute value (magnitude) to identify regions of high or low magnitude, shedding light on the overall behaviour and stability of the solutions.

Fig. 3
figure 3

Dynamic evolution of 2-peakons, 2-lumps and 2-solitons for the solution (16) through 3D and contour plots

Full size image
Fig. 4
figure 4

Dynamic evolution of 3-peakons, 3-lumps and 3-solitons for the solution (17) through 3D and contour plots

Full size image
Fig. 5
figure 5

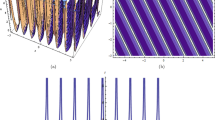
Dynamic evolution of multi-peakons, multi-lumps and multi-solitons for the solution (20) through 3D and contour plots

Full size image
Fig. 6
figure 6

Dynamic evolution of multi-peakons, multi-lumps and multi-solitons patterns for the solution (21) through 3D and contour plots

Full size image

In Fig. 2, we examine the 3D and contour patterns of the solution (15). Here, subgraph (a) represent 1-peakon for real component at \(b=5;\alpha =2;\beta =5 i;\gamma =i;{\mathcal {R}}_0=1;{\mathcal {R}}_2=2;\) where \(x\in [-0.07,0.07], y\in [-0.2,0.1]\), subgraph (b) shows the 1-lump soliton for the imaginary component at \(b=1;\alpha =3;\beta =7 i;\gamma =9 i;{\mathcal {R}}_0=0.2;{\mathcal {R}}_2=0.3;\) where \(x\in [-2,2], y\in [-3,-2.3]\), subgraph (c) illustrate the single-soliton for the absolute value at \(b=1.2;\alpha =4 i;\beta =2;\gamma =22 i;{\mathcal {R}}_0=1.2;{\mathcal {R}}_2=0.6;\) where \(x\in [-1,1], y\in [-1,1]\), subgraph (d) shows the corresponding contour plot of the real component in the interval \( \{x,-0.2,0.2\}, \{y,-0.15,0.01\}\), subgraph (e) represents the corresponding contour plot of the imaginary component in the interval \( \{x,-2,2\},\)\(\{y,-3,-2.3\} \), subgraph (f) represents the corresponding contour plot of the absolute value in the interval \( \{x,-0.8,1\},\{y,-1.5,1.5\}\).

Fig. 7
figure 7

Dynamic evolution of solitary waves for the solution (33) through 3D and contour plots, connecting with solitary waves in Ocean

Full size image

In Fig. 3, we explore 3D and contour patterns of the solution (16). Here, subgraph (a) represent 2-peakons for real component at \(b=1;\alpha =2.7;\beta =3 i;\gamma =19 i;{\mathcal {R}}_0=0.2;{\mathcal {R}}_2=0.3;\) where \(x\in [-1,1], y\in [-2.8,1.9]\), subgraph (b) shows the 2-lumps soliton for the imaginary component at \(b=1;\alpha =2.7;\beta =3 i;\gamma =19 i;{\mathcal {R}}_0=0.2;{\mathcal {R}}_2=0.3;\) where \(x\in [-1,1], y\in [-2.8,1.9]\), subgraph (c) illustrate the doubly-soliton for the absolute value at \(b=1;\alpha =2.7;\beta =3 i;\gamma =19 i;{\mathcal {R}}_0=0.2;{\mathcal {R}}_2=0.3;\) where \(x\in [-1,1], y\in [-2,1.9]\), subgraph (d) shows the corresponding contour plot of the real component in the interval \( \{x,-1.2,1.2\},\{y,-2.8,1.9\}\), subgraph (e) represents the corresponding contour plot of the imaginary component in the interval \( \{x,-1,1\},\)\(\{y,-2,1.9\} \), subgraph (f) represents the corresponding contour plot of the absolute value in the interval \( \{x,-1,1\},\{y,-2,1.9\}\).

In Fig. 4, we focus on 3D and contour patterns of the solution (17). Here, subgraph (a) represent 3-peakons for real component at \(b=1;\alpha =2;\beta =3 i;\gamma =19 i;{\mathcal {R}}_0=0.3;{\mathcal {R}}_2=0.4;\) where \(x\in [-1.5,1.5], y\in [-2.8,2.3]\), subgraph (b) shows the 3-lumps soliton for the imaginary component at \(b=1;\alpha =2;\beta =3 i;\gamma =19 i;{\mathcal {R}}_0=0.3;{\mathcal {R}}_2=0.4;\) where \(x\in [-1.5,1.5], y\in [-2.8,2.3]\), subgraph (c) illustrate the triple-soliton for the absolute value at \(b=1;\alpha =2;\beta =4 i;\gamma =19 i;{\mathcal {R}}_0=0.3;{\mathcal {R}}_2=0.4;\) where \(x\in [-1.7,1.7], y\in [-1,3.4]\), subgraph (d) shows the corresponding contour plot of the real component in the interval \( \{x,-2,2\},\)\(\{y,-2.8,2.8\}\), subgraph (e) represents the corresponding contour plot of the imaginary component in the interval \( \{x,-1.5,1.5\},\{y,-3,2.8\} \), subgraph (f) represents the corresponding contour plot of the absolute value in the interval \( \{x,-2,2\},\{y,-2.3,2\}\).

In Fig. 5, we analyze the 3D and contour patterns of the solution (20). Here, subgraph (a) represent multi-peakons for real component at \(b=5;\alpha =2.7;\beta =5 i;\gamma =5 i;{\mathcal {R}}_0=2;{\mathcal {R}}_2=3;\) where \(x\in [-1,1], y\in [-1,1]\), subgraph (b) shows the multi-lumps soliton for the imaginary component at \(b=5;\alpha =2.7;\beta =5 i;\gamma =5 i;{\mathcal {R}}_0=2;{\mathcal {R}}_2=3;\) where \(x\in [-1,1], y\in [-1,1]\), subgraph (c) illustrate the multi-soliton for the absolute value at \(b=5;\alpha =2.7;\beta =5 i;\gamma =5 i;{\mathcal {R}}_0=2;{\mathcal {R}}_2=3;\) where \(x\in [-1,1], y\in [-1,1]\), subgraph (d) shows the corresponding contour plot of the real component in the interval \( \{x,-1,1\},\{y,-0.5,0.5\}\), subgraph (e) represents the corresponding contour plot of the imaginary component in the interval \( \{x,-0.5,0.5\},\{y,-0.7,0.7\} \), subgraph (f) represents the corresponding contour plot of the absolute value in the interval \( \{x,-1,1\},\{y,-1,1\}\).

In Fig. 6, we presents the graphical view of the 3D and contour patterns of the solution (21). Here, subgraph (a) represent multi-peakons for real component at \( b=8;\alpha =0.44;\beta =5 i;\gamma =0.5 i;{\mathcal {R}}_0=0.3;{\mathcal {R}}_2=0.5;\) where \(x\in [-1,1], y\in [-2,2]\), subgraph (b) shows the multi-lumps soliton for the imaginary component at \( b=8;\alpha =0.44;\beta =5 i;\gamma =0.5 i;{\mathcal {R}}_0=0.3;{\mathcal {R}}_2=0.5;\) where \(x\in [-6,6], y\in [-2,2]\), subgraph (c) illustrate the multi-solitons for the absolute value at \( b=8;\alpha =0.44;\beta =5 i;\gamma =0.5 i;{\mathcal {R}}_0=0.3;{\mathcal {R}}_2=0.5;\) where \(x\in [-1,1], y\in [-2,2]\), subgraph (d) shows the corresponding contour plot of the real component in the interval \( \{x,-1,1\},\{y,-0.37,0.44\}\), subgraph (e) represents the corresponding contour plot of the imaginary component in the interval \( \{x,-1,1\},\{y,-0.37,0.44\} \), subgraph (f) represents the corresponding contour plot of the absolute value in the interval \( \{x,-1,1\}, \{y,-0.4,0.4\}\).

In Fig. 7, our focus turns to the observation of solitary waves within the context of the absolute value of the solution (33). Here, 3-dimensional plot is discussed with the choice of parameters \( a=0;b=5;c=0;\alpha =0.44;\beta =5 i;\gamma =0.5 i;{\mathcal {R}}_0=0;{\mathcal {S}}_1=0.5;\) where \(x\in [-0.2,0.3], y\in [-0.37,0.44]\) and the contour plot is depicted under the same choice of involved parameters within the range \(x\in [-0.2,0.3], y\in [-0.3,0.3]\). To illustrate the connection between our findings and their relevance to real-world phenomena, we have included an image that captures the solitary waves in the ocean, as represented by subgraph (c). This visual representation effectively bridges the gap between our mathematical findings and practical applications.

Peakons, lumps, solitons, and solitary waves are fascinating phenomena in the field of nonlinear wave theory. Peakons are unique solitary waves characterized by sharp peaks that maintain their shape while propagating. Lumps are compact, localized waves structures that do not spread out over time and space, often encountered in certain mathematical models. Solitons are solitary waves that can travel long distances without changing their shape or amplitude due to balance between dispersion and nonlinearity. They arise in various physical systems, such as water waves and certain nonlinear equations. On the other hand, solitary waves encompass all these phenomena, including peakons, lumps, and solitons, and they play a crucial role in understanding wave behavior in complex systems. These concepts illuminate the profound nature of waves dynamics, and offering valuable insights in diverse physical systems.

6 Conclusion

In conclusion, we have introduced a new method, the Inverse \(\left( \frac{G'}{G}\right) \)-expansion method, that helps us to find solutions for the NLPDEs in a simple polynomial form. Using this method, we have obtained exact soliton solutions for the gBO equation. These solutions are in various forms like trigonometric function, hyperbolic function, and exponential function. To better understand these solutions, we have created 3D and contour plots for the real component, imaginary component and absolute value of solutions given by Eqs. (15), (16), (17), (20), (21) and (33), which show patterns like 1-peakon, 1-lump, 1-soliton, 2-peakons, 2-lumps, 2-solitons, 3-peakons, 3-lumps, 3-solitons, multi-peakons, multi-lumps, multi-solitons, and solitary waves. Peakons, lumps, and solitons each exhibit unique characteristics. Peakons retain sharp peaks as they move, lumps remain compact without spreading, and solutions travels long distances while keeping their shape. These solitary waves reveal complex wave dynamics across various systems, offering profound insights into nonlinear phenomena. These dynamical representation helps us to see how these solutions behave with different choice of parameters under the suitable range space. Additionally, we have connected our mathematical findings to real-world applications, making our work relevant and applicable beyond the area of mathematics.