The $\varvec{(2+1)}$-dimensional Konopelchenko–Dubrovsky equation: nonlocal symmetries and interaction solutions

Abstract

The nonlocal symmetries for the $(2+1)$-dimensional Konopelchenko–Dubrovsky equation are obtained with the truncated Painlevé method and the Möbious (conformal) invariant form. The nonlocal symmetries are localized to the Lie point symmetries by introducing auxiliary dependent variables. The finite symmetry transformations are obtained by solving the initial value problem of the prolonged systems. The multi-solitary wave solution is presented with the finite symmetry transformations of a trivial solution. In the meanwhile, symmetry reductions in the enlarged systems are studied by the Lie point symmetry approach. Many explicit interaction solutions between solitons and cnoidal periodic waves are discussed both in analytical and in graphical ways.

1 Introduction

The local symmetries include Lie point symmetries, contact symmetries and more generally Lie–Bäcklund symmetries [1]. The local symmetries study is considered to be one of most effective methods for finding invariant solutions [2, 3]. To obtain new solutions of partial differential equations (PDEs) that are not obtainable through the local symmetry approach, several extensions to local symmetry methods have been proposed [4–7]. The nonlocal symmetries study is thus attracted lots of attention. The nonlocal symmetries can be obtained by algorithmic approach, inverse recursion operators, Möbious (conformal) invariant form, Darboux transformation, Bäcklund transformation (BT), nonlinearizations, self-consistent sources, etc. [4–18].

In this paper, we shall study the nonlocal symmetries of $(2+1)$-dimensional Konopelchenko–Dubrovsky (KD) equation and their applications. The nonlocal symmetries for the KD equation are obtained by the truncated Painlevé expansion and the Möbious (conformal) invariant form. By introducing two dependent variables, one can transform nonlocal symmetries into Lie point symmetries by extending original system. The finite symmetry transformation and similarity reductions are studied in the enlarged system. Many explicit soliton–cnoidal wave solutions are found for the KD equation. Those solutions cannot be obtained within the framework of the direct Lie’s symmetry approach.

The paper is organized as follows: In Sect. 2, the nonlocal symmetries for the KD equation are obtained with the truncated Painlevé method and the Möbious (conformal) invariant form. To solve the initial value problem related by the nonlocal symmetries, the nonlocal symmetries are localized by prolongation the KD equation. The finite symmetry transformations are obtained by solving the initial value problem of the Lie’s first principle. The multi-solitary wave solution of the KD equation is obtained using the finite symmetry transformations. In Sect. 3, the symmetry reductions for the extended systems are considered according to the Lie point symmetry theory. The corresponding explicit interaction solutions among one soliton and cnoidal waves are given. The last section is a simple summary and discussion.

2 Nonlocal symmetries and multi-solitary wave for KD equation

The $(2+1)$-dimensional Konopelchenko–Dubrovsky (KD) equation reads [19]

$$\begin{aligned}&u_{t} - u_{xxx} - 3 w_{y} + \frac{3}{2}\alpha ^2 u^2 u_{x} + 3\alpha u_{x} w - 6\beta u u_x = 0,\nonumber \\ \end{aligned}$$

(1a)

$$\begin{aligned}&u_y = w_x, \end{aligned}$$

(1b)

where $\alpha$ and $\beta$ are arbitrary constants. (1) is solvable by inverse scattering transformation [20]. Various methods for obtaining exact solution to the KD equation have been proposed [21–24]. The full symmetry group is studied by the general direct method and the formal function series method [25, 26]. Recently, the interactions between solitons and cnoidal periodic waves are found by the consistent Riccati/tanh expansion (CRE/CTE) methods [27, 28]. Here, we give the nonlocal symmetries by the truncated Painlevé method and the Möbious (conformal) invariant form. The symmetry reductions related to nonlocal symmetries will be discussed in the next section.

Based on the truncated Painlevé analysis of the KD equation, the Laurent series form is [29]

$$\begin{aligned} u=\frac{u_0}{\phi }+ {u_1}, \qquad w=\frac{w_0}{\phi }+{w_1}, \end{aligned}$$

(2)

where the function $\phi (x, y, t)=0$ is the equation of singularity manifold; the functions $u_0$, $u_1$, $w_0$ and $w_1$ are determined by substituting of expansion (2) into (1) and vanishing all coefficients of each power of $\phi$ independently. Comparing the coefficients of $(\phi ^{-4}, \phi ^{-2})$, we get

$$\begin{aligned} u_0 = -\frac{2}{\alpha }\phi _x, \quad w_0= -\frac{2}{\alpha }\phi _{y}. \end{aligned}$$

(3)

We proceed further and collect the coefficients of $(\phi ^{-3}, \phi ^{-1})$ to get

$$\begin{aligned} u_1= & {} \frac{1}{\alpha }\Bigl ( -\frac{\phi _{xx}}{\phi _x} - \frac{\phi _y}{\phi _x} + \frac{2\beta }{\alpha }\Bigr ), \nonumber \\ w_1= & {} \frac{1}{\alpha }\Bigl ( - \frac{\phi _t}{3\phi _x} - \frac{\phi _{xy}}{\phi _x} + \frac{\phi _{xxx}}{3\phi _x} + \frac{\phi _{y}^2}{2\phi _x^2}- \frac{\phi _{xx}^2}{2\phi _x^2} + \frac{2\beta ^2}{\alpha ^2}\Bigr ).\nonumber \\ \end{aligned}$$

(4)

Substituting the expressions (2), (3) and (4) into (1), the field $\phi$ satisfies the following Schwarzian KD form

$$\begin{aligned} \Bigl (\frac{\phi _t}{\phi _x}\Bigr )_x - \frac{\partial }{\partial x} \{\phi ; x\} - 3 \Bigl (\frac{\phi _y}{\phi _x}\Bigr )_y -\frac{3}{2}\Bigl (\frac{\phi _y^2}{\phi _x^2}\Bigr )_x =0, \end{aligned}$$

(5)

where $\{\phi ;x\}=\frac{\partial }{\partial x}\left( \frac{\phi _{xx}}{\phi _x}\right) -\frac{1}{2}\left( \frac{\phi _{xx}}{\phi _x}\right) ^2$ is the Schwarzian derivative.

According to the definition of residual symmetries (RS) [16], the nonlocal symmetries of the KD equation (1) can read out from the truncated Painlevé analysis (2)

$$\begin{aligned} \sigma ^u=-\frac{2}{\alpha }\phi _{x}, \quad \sigma ^w=-\frac{2}{\alpha }\phi _{y}. \end{aligned}$$

(6)

This nonlocal symmetries can also be obtained from the Schwarzian form (5) [30]. The Schwarzian form (5) is invariant under the Möbious transformation

$$\begin{aligned} \phi \rightarrow \frac{a\phi +b}{c\phi +d},\quad ac\ne bd, \end{aligned}$$

(7)

which means (5) possesses the symmetry $\sigma ^\phi = \phi ^2$ in special case $a=d=1,\, b=0,\, c=-\epsilon .$ The nonlocal symmetries (6) will be obtained with substituting the Möbious transformation symmetry $\sigma ^\phi$ into the linearized equation of (4).

For the nonlocal symmetries (6), the corresponding initial value problem is

$$\begin{aligned}&\frac{\mathrm{d}\overline{u}}{\mathrm{d}\epsilon }=-\frac{2}{\alpha }\phi _{x}, \quad \overline{u}|_{\epsilon =0}=u,\nonumber \\&\frac{\mathrm{d}\overline{w}}{\mathrm{d}\epsilon }=-\frac{2}{\alpha }\phi _{y}, \quad \overline{w}|_{\epsilon =0}=w. \end{aligned}$$

(8)

It is difficult to solve the initial value problem of the Lie’s first principle (8) due to the intrusion of the function $\phi$ and its differentiations [16]. To solve the initial value problem (8), one can localize the nonlocal symmetries to the local Lie point symmetries for the prolonged system. We introduce the potential fields to eliminate the space derivatives of field $\phi$

$$\begin{aligned} \phi _x= & {} g, \end{aligned}$$

(9)

$$\begin{aligned} \phi _y= & {} h. \end{aligned}$$

(10)

It is easily verified that the Lie point symmetries for the prolonged systems (1), (4), (9) and (10) have the form

$$\begin{aligned}&\sigma ^u = -\frac{2}{\alpha }g, \quad \sigma ^w = -\frac{2}{\alpha }h, \quad \sigma ^\phi = \phi ^2, \nonumber \\&\sigma ^g= 2\phi g,\quad \sigma ^h= 2\phi h. \end{aligned}$$

(11)

The initial value problem is correspondingly transformed

$$\begin{aligned}&\frac{\hbox {d}\overline{u}}{\hbox {d}\epsilon } = -\frac{2}{\alpha }g, \quad \overline{u}|_{\epsilon =0}=u,\nonumber \\&\frac{\hbox {d}\overline{w}}{\hbox {d}\epsilon } = -\frac{2}{\alpha }h, \quad \overline{w}|_{\epsilon =0}=w,\nonumber \\&\frac{\hbox {d}\overline{\phi }}{\hbox {d}\epsilon } = \phi ^2, \quad \overline{\phi }|_{\epsilon =0}=\phi ,\\&\frac{\hbox {d}\overline{g}}{\hbox {d}\epsilon } = 2\phi g, \quad \overline{g}|_{\epsilon =0}=g,\nonumber \\&\frac{\hbox {d}\overline{h}}{\hbox {d}\epsilon } = 2\phi h, \quad \overline{h}|_{\epsilon =0}=h.\nonumber \end{aligned}$$

(12)

By solving the above the initial value problem (12) for the enlarged KD systems (1), (4), (9) and (10), we get the BT theorem. BT can construct new solutions from known ones [31, 32].

Theorem

If $u, w, \phi , g, h$ are solution of the enlarged KD systems (1), (4), (9) and (10), then $\overline{u}, \overline{w}, \overline{\phi }, \overline{g}, \overline{h}$ are also solution of the enlarged KD systems

$$\begin{aligned} \overline{u}&= u + \frac{2\epsilon g}{\alpha (\epsilon \phi -1)}, \quad \overline{w} = w + \frac{2\epsilon h}{\alpha (\epsilon \phi -1)},\nonumber \\ \overline{\phi }&= \frac{\phi }{1 - \epsilon \phi }, \quad \overline{g}=\frac{g}{(1-\epsilon \phi )^2},\quad \overline{h}=\frac{h}{(1-\epsilon \phi )^2}. \end{aligned}$$

(13)

where $\epsilon$ is an arbitrary group parameter.

Using the finite symmetry transformations (13), one can obtain a new solution from any initial solution. For example, the multi-solitary wave solution for (5) is supposed as [33]

$$\begin{aligned} \phi = 1 + \sum ^{N}_{n=1} \exp (k_n x + l_n y + \omega _n t), \end{aligned}$$

(14)

where $k_n, l_n$ and $\omega _n$ are arbitrary constants. The multi-solitary wave solution (14) is the solution of (5) only with the relations

$$\begin{aligned} l_n= & {} \frac{k_n(k_1^2-k_1k_n+l_1)}{k_1}, \nonumber \\ \omega _n= & {} \frac{k_n(2k_1^3 - 6k_1^2k_n+4k_1k_n^2 + 6k_1 l_1 - 6k_nl_1 \omega _1)}{k_1}.\nonumber \\ \end{aligned}$$

(15)

Substituting (14) into (4), we get the trivial solution of (1)

$$\begin{aligned} u= & {} \frac{2\beta }{\alpha ^2} - \frac{k_1}{\alpha } - \frac{l_1}{\alpha k_1}, \,\, \end{aligned}$$

(16a)

$$\begin{aligned} w= & {} \frac{2\beta ^2}{\alpha ^3} + \frac{l_1^2}{2\alpha k_1^2} - \frac{k_1^2}{6\alpha } - \frac{l_1}{\alpha } - \frac{\omega _1}{3\alpha k_1}. \end{aligned}$$

(16b)

By using the finite symmetry transformations (13), a solution of Eq. (1) presents in the following form

$$\begin{aligned} u= & {} \frac{2\beta }{\alpha ^2} - \frac{k_1}{\alpha } - \frac{l_1}{\alpha k_1} \nonumber \\&+\, \frac{ \sum ^{N}_{n=1} 2\epsilon k_n\exp (k_n x + l_n y + \omega _n t)}{-1 +\epsilon + \alpha \sum ^{N}_{n=1}\epsilon \exp (k_n x + l_n y + \omega _n t)}, \nonumber \\ \end{aligned}$$

(17a)

$$\begin{aligned} w= & {} \frac{2\beta ^2}{\alpha ^3} \nonumber \\&+\, \frac{l_1^2}{2\alpha k_1^2} - \frac{k_1^2}{6\alpha } - \frac{l_1}{\alpha } - \frac{\omega _1}{3\alpha k_1} \nonumber \\&+\,\frac{ \sum ^{N}_{n=1} 2\epsilon l_n\exp (k_n x + l_n y + \omega _n t)}{-1 + \epsilon + \alpha \sum ^{N}_{n=1} \epsilon \exp (k_n x + l_n y + \omega _n t)}.\nonumber \\ \end{aligned}$$

(17b)

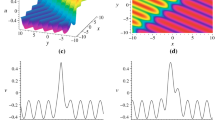
It means that a nontrivial solution (17) is obtained from a trivial solution (16) by using the finite symmetry transformations (13). Figure 1 shows the wave solution of the potential function $M=u_y=w_x$ with the parameters $n=3,\, \epsilon =-\frac{1}{2},\, k_1=1,\, k_2=-1,\, k_3=\frac{1}{2},\, l_1=-1,\, \omega _1=-2,\,\alpha =1,\, \beta =1$.

Fig. 1

Wave solution for the potential function $M=u_y=w_x$ with the parameters $n=3,\, \epsilon =-\frac{1}{2},\, k_1=1,\, k_2=-1,\,k_3=\frac{1}{2},\, l_1=-1,\, \omega _1=-2,\,\alpha =1,\, \beta =1$ and $x=0$

3 Similarity reductions related to nonlocal symmetries

By introducing the potential fields (9) and (10), the nonlocal symmetries become the usual local symmetries in the prolonged systems. We can thus use the symmetry reduction related to the nonlocal symmetries to study the prolonged systems. These symmetry reduction solutions cannot be obtained within the framework of the direct Lie’s symmetry method. The Lie point symmetries $\sigma ^k \,(k=u, w, \phi , g, h)$ for the prolonged systems are the solutions of the linearized prolonged systems (1) (4), (9) and (10)

$$\begin{aligned}&\sigma ^u_{\,t} - \sigma ^u_{\,xxx} - 3\sigma ^w_{\,y} + \frac{3}{2}\alpha ^2 (u^2 \sigma ^u)_x + 3\alpha \sigma ^u_{\,x}w\nonumber \\&\quad +\,3\alpha \sigma ^w u_x - 6\beta (u\sigma ^u)_x = 0, \end{aligned}$$

(18a)

$$\begin{aligned}&\sigma ^u_{\,y} - \sigma ^w_{\,x} = 0, \end{aligned}$$

(18b)

$$\begin{aligned}&\sigma ^{u} + \frac{1}{\alpha } \Bigl (\frac{\sigma ^\phi _{\,y}}{\phi _x} + \frac{\sigma ^\phi _{\,xx}}{\phi _x} - \frac{\sigma ^\phi _{\,x}\phi _{y}}{\phi _x^2} - \frac{\sigma ^\phi _{\,x}\phi _{xx}}{\phi _x^2}\Bigr )=0, \end{aligned}$$

(18c)

$$\begin{aligned}&\sigma ^{w} + \frac{\sigma ^\phi _{\,t} + 3\sigma ^{\phi }_{\,xy} - \sigma ^{\phi }_{\,xxx}}{3\alpha \phi _x} - \frac{\sigma ^\phi _{\,x}\phi _{t}}{3\alpha \phi _x^2} - \frac{\sigma ^\phi _{\,y}\phi _{y}}{\alpha \phi _x^2} - \frac{\sigma ^\phi _{\,x}\phi _{xy}}{\alpha \phi _x^2}\nonumber \\&\quad + \,\frac{\sigma ^\phi _{\,x}\phi _{xxx}}{3\alpha \phi _x^2} + \frac{\sigma ^\phi _{\,xx}\phi _{xx}}{\alpha \phi _x^2} + \frac{\sigma ^\phi _{\,x}\phi _y^2 - \sigma ^\phi _{\,x}\phi _{xx}^2}{\alpha \phi _x^3} =0, \end{aligned}$$

(18d)

$$\begin{aligned}&\sigma ^\phi _{\,x} - \sigma ^g = 0, \end{aligned}$$

(18e)

$$\begin{aligned}&\sigma ^\phi _{\,y} - \sigma ^h = 0. \end{aligned}$$

(18f)

The symmetry components $\sigma ^k \,(k=u, w, \phi , g, h)$ are supposed to have the forms

$$\begin{aligned}&\sigma ^u = X u_x + Y u_y + T u_t - U, \nonumber \\&\sigma ^w = X w_x + Y w_y + T w_t - W, \nonumber \\&\sigma ^\phi = X \phi _x + Y \phi _y + T \phi _t - \varPhi , \\&\sigma ^g = X g_x + Y g_y + T g_t - G, \nonumber \\&\sigma ^h = X h_x + Y h_y + T h_t - H, \nonumber \end{aligned}$$

(19)

where $X, Y, T, U, W, \varPhi , G, H$ are functions of $x, t, u, w, \phi , g, h$. From the implication of (19), the prolong systems are invariant under transformations

$$\begin{aligned}&u\rightarrow u + \epsilon \sigma ^u, \qquad w\rightarrow w + \epsilon \sigma ^w, \nonumber \\&\phi \rightarrow \phi + \epsilon \sigma ^\phi , \qquad g \rightarrow g + \epsilon \sigma ^g, \qquad h\rightarrow h + \epsilon \sigma ^h, \end{aligned}$$

(20)

with the infinitesimal parameter $\epsilon$.

Substituting (19) into the symmetry equations (18) and requiring $u, w, \phi , g, h$ to satisfy the prolonged systems, the overdetermined equations are obtained with collecting the coefficients of $u, w, \phi , g, h$ and its derivatives. The infinitesimals X, Y, T, U, W, $\varPhi$, G and H are given by solving the overdetermined equations

$$\begin{aligned}&X= \frac{1}{3}f_{1t} x + \frac{1}{6} f_{2t}y +\frac{1}{18}f_{1tt}y^2+f_3, \nonumber \\&Y =\frac{2}{3}f_{1t}y+f_2, \quad T = f_1 + C_4, \quad \varPhi = \frac{C_3\alpha }{2} \phi ^2 + C_2 \phi - C_1, \nonumber \\&G = C_3 \alpha \phi g + C_2g -\frac{1}{3}f_{1t} g, \nonumber \\&H=C_3\alpha \phi h + C_2 h - \frac{1}{6}f_{2t}g -\frac{1}{9}f_{1tt}gy, \nonumber \\ W&= -\frac{2}{3}f_{1t}w - \frac{1}{6}f_{2t}u - \frac{1}{9}f_{1tt}yu -C_3h\nonumber \\&\qquad +\frac{1}{9\alpha }f_{1tt}x +\frac{1}{54\alpha }f_{1ttt}y^2 + \frac{1}{18\alpha }f_{2tt}y+\frac{2\beta }{9\alpha ^2}f_{1tt}y \nonumber \\&\qquad +\frac{1}{3\alpha }f_{3t} +\frac{\beta }{3\alpha ^2}f_{2t}+\frac{4\beta ^2}{3\alpha ^3}f_{1t}, \nonumber \\&U = - \frac{1}{3}f_{1t} u - C_3 g + \frac{1}{9\alpha }f_{1tt} y + \frac{1}{6\alpha } f_{2t} + \frac{2\beta }{3\alpha ^2}f_{1t}, \end{aligned}$$

(21)

where $f_1, f_2$ and $f_3$ are arbitrary functions of t, $C_1, C_2, C_3$ and $C_4$ are arbitrary constants. The corresponding group invariant solutions can be obtained with the symmetry constraint condition $\sigma ^k=0$ defined by (19). It is equivalent to solve the following characteristic equations

$$\begin{aligned} \frac{\hbox {d}x}{X} = \frac{\hbox {d}y}{Y} = \frac{\hbox {d}t}{T}=\frac{\hbox {d}u}{U}=\frac{\hbox {d}w}{W}=\frac{\hbox {d}\phi }{\varPhi }=\frac{\hbox {d}g}{G}=\frac{\hbox {d}h}{H}.\nonumber \\ \end{aligned}$$

(22)

To solve the characteristic equations, two special cases are listed in the following.

Case I In this case $f_1=0$, without loss of generality, we rewrite the arbitrary functions $f_2$ and $f_3$ as

$$\begin{aligned} f_2= C_4 m_{1t}, \qquad f_3= m_{2t}, \end{aligned}$$

(23)

where $m_1$ and $m_2$ being arbitrary functions of t. The similarity solutions are after solving out the characteristic equations (22)

$$\begin{aligned}&\phi = -\frac{\varDelta }{C_3\alpha } \tanh \left( \frac{\varDelta }{2C_4}(t +\varPhi )\right) - \frac{C_2}{C_3\alpha },\nonumber \\&\varDelta =\sqrt{2C_1C_3\alpha +C_2^2}, \end{aligned}$$

(24a)

$$\begin{aligned}&g = - \frac{G}{ \cosh ^2 \left( \frac{\varDelta }{2C_4}(t + \varPhi )\right) }, \end{aligned}$$

(24b)

$$\begin{aligned}&h = - \frac{ \exp {(-\frac{2f_1}{3C_4})}}{\cosh ^2\left( \frac{\varDelta }{2C_4}(t +\varPhi )\right) } H \nonumber \\&\quad + \frac{\exp {(-\frac{2f_1}{3C_4})}G}{18C_4\cosh ^2\left( \frac{\varDelta }{2C_4}(t +\varPhi )\right) } \nonumber \\&\quad \times \int \exp ({\frac{2f_1}{3C_4}}) (2f_{1tt}y + 3C_4m_{1tt}) \hbox {d}t, \end{aligned}$$

(24c)

$$\begin{aligned}&u = U + \frac{2C_3}{\varDelta } G \tanh \left( \frac{\varDelta }{2C_4}(t +\varPhi )\right) + \frac{m_{1t}}{6\alpha }, \end{aligned}$$

(24d)

$$\begin{aligned}&w = W - \frac{1}{6}m_{1t} U - \frac{C_3}{3\varDelta } m_{1t} G \tanh \left( \frac{\varDelta }{2C_4}(t +\varPhi )\right) \nonumber \\&\quad - \frac{C_3}{6C_4} G \int \frac{m_{1t}}{\cosh ^2\left( \frac{\varDelta }{2C_4}(t +\varPhi )\right) } \hbox {d}t \nonumber \\&\quad + \frac{C_3}{9C_4^2}G \int \frac{ \exp {(-\frac{2f_1}{3C_4}})\int \exp ({\frac{2f_1}{3C_4}}) (2f_{1tt}y {+} 3C_4m_{1tt}) \hbox {d}t}{\cosh ^2\left( \frac{\varDelta }{2C_4}(t {+}\varPhi )\right) } \hbox {d}t\nonumber \\&\quad - \frac{2C_3}{C_4}H \int \frac{\exp (-{\frac{2f_1}{3C_4}})}{{\cosh ^2\left( \frac{\varDelta }{2C_4}(t +\varPhi )\right) }}\hbox {d}t \nonumber \\&\quad - \frac{1}{72\alpha }m_{1t}^2 + \frac{1}{18\alpha }m_{1tt}y + \frac{\beta }{3\alpha ^2}m_{1t} + \frac{m_{2t}}{3C_4\alpha }, \end{aligned}$$

(24e)

where the similarity variables $\xi =x-\frac{1}{6}m_{1t}y - \frac{m_2}{C_4}$, $\eta =y-m_1$ and the group invariant functions $\varPhi =\varPhi (\xi , \eta )$, $G=G(\xi , \eta )$, $H=H(\xi , \eta )$, $U=U(\xi , \eta )$ and $W=W(\xi , \eta )$. Substituting (24) into (9), (10), (4) and (5), the invariant functions G, H, U, W and $\varPhi$ satisfy the reduction systems

$$\begin{aligned}&G = \frac{\varDelta ^2}{2C_3C_4\alpha } \varPhi _\xi , \end{aligned}$$

(25a)

$$\begin{aligned}&H = \frac{\varDelta ^2}{2C_3C_4\alpha }\exp \left( \frac{2f_1}{3C_4}\right) \varPhi _\eta \nonumber \\&\qquad +\, \frac{\varDelta ^2}{36C_3C_4^2\alpha } \biggl (\int \exp \left( {\frac{2f_1}{3C_4}}\right) \left( 2y f_{1tt}\right. \nonumber \\&\qquad \left. +\, 3C_4m_{1tt}\right) \hbox {d}t - 3C_4 m_{1t}\exp \left( {\frac{2f_1}{3C_4}}\right) \biggr ) \varPhi _{\xi }, \end{aligned}$$

(25b)

$$\begin{aligned}&U = -\frac{\varPhi _\eta + \varPhi _{\xi \xi }}{\alpha \varPhi _\xi } + \frac{2\beta }{\alpha ^2}, \end{aligned}$$

(25c)

$$\begin{aligned}&W = -\frac{\varDelta }{C_4\alpha }\varPhi _\eta \tanh \left( \frac{\varDelta }{2C_4}(t +\varPhi )\right) - \frac{\varDelta ^2}{6C_4^2\alpha }\varPhi _\xi ^2 - \frac{1}{3\alpha \varPhi _\xi }\nonumber \\&\qquad - \frac{\varPhi _{\xi \eta }}{\alpha \varPhi _\xi } + \frac{\varPhi _{\xi \xi \xi }}{3\alpha \varPhi _\xi } + \frac{\varPhi _\eta ^2}{2\alpha \varPhi _\xi ^2} - \frac{\varPhi _{\xi \xi }^2}{2\alpha \varPhi _\xi ^2} \nonumber \\&\qquad + \frac{\varDelta ^2}{12C_4^2\alpha } \varPhi _\xi \int \frac{m_{1t}}{\cosh ^2\left( \frac{\varDelta }{2C_4}(t +\varPhi )\right) } \hbox {d}t + \frac{1}{36\alpha }m_{1t}^2 \!+\! \frac{2\beta ^2}{\alpha ^3}, \end{aligned}$$

(25d)

$$\begin{aligned}&\frac{\varDelta ^2}{C_4^2} \varPhi _{\xi \xi } \varPhi _{\xi }^4 - \varPhi _\xi ^2\varPhi _{\xi \xi \xi \xi } - 3 \varPhi _{\eta \eta }\varPhi _{\xi }^2\nonumber \\&\qquad + 4\varPhi _{\xi } \varPhi _{\xi \xi }\varPhi _{\xi \xi \xi } - 3 \varPhi _{\xi \xi }^3 + 3\varPhi _{\xi \xi }\varPhi _{\eta }^2 - \varPhi _{\xi }\varPhi _{\xi \xi } =0.\nonumber \\ \end{aligned}$$

(25e)

It is obvious that once the solutions $\varPhi$ are solved out with (25e), the fields for G, H, U and W can be solved out directly from (25a)–(25d). The explicit solutions for KD equation (1) are immediately obtained by substituting $\varPhi$, G, H, U and W into (24).

Fig. 2

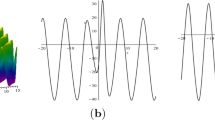
Plot of one kink soliton in the periodic wave background expressed by (28). The parameters are $m=0.9, \, n=0.5,\, k_1=-2,\, k=1,\, C_4=1,\, \alpha =1,\, \beta =1,\, m_1=t,\, m_2=t$. a The wave propagation pattern of the wave along t axis at $x = 0$ and $y = 0$. b One-dimensional image at $t = 0$ and $x = 0$. c The three-dimensional view at time $x = 0$

Fig. 3

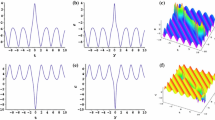
Plot of second type of one kink soliton in the quasiperiodic wave background expressed by (28). The parameters are $m=0.9, \, n=0.5,\, k_1=-2,\, k=1,\, C_4=1,\, \alpha =1,\, \beta =1,\, m_1=\cos (t),\, m_2=t$. a The wave propagation pattern of the wave along t axis at $x = 0$ and $y = 0$. b The three-dimensional view at time $x = 0$. c The density plot of the corresponding solution at time $x = 0$

Fig. 4

Plot of third type of special soliton–cnoidal wave interaction solution by (28). The parameters are $m=0.9,\, n=0.5,\, k_1=-2,\, k=1,\, C_4=1,\, \alpha =1,\, \beta =1,\, m_1=t,\, m_2=t^2$. a The wave propagation pattern of the wave along t axis at $x = 0$ and $y = 0$. b The three-dimensional view at time $x = 0$. c The density plot of the corresponding solution at time $x = 0$

The special soliton–cnoidal wave interaction solution for the reduction equation (25e) is

$$\begin{aligned} \varPhi = k_1\xi + l_1 \eta + a_1 E_\pi (\mathrm {sn}(k\xi + l\eta , m), n, m), \end{aligned}$$

(26)

where $k_1, l_1, a_1, k, l, n$ and m are constants and $E_{\pi }$ is the third incomplete elliptic integrals. Substituting (26) into (25e), vanishing all the coefficients of different powers of $\mathrm {sn}$ leads to the nontrivial solution for constants

$$\begin{aligned}&\varDelta ^2 = \frac{4k^2 (1-n)(m^2-n)}{nk_1^2} C_4^2, \quad a_1=\frac{k_1}{k},\nonumber \\&l=\frac{4k^2k_1(12m^2n-20m^2-7n^2+12n)+n}{12k_1 \sqrt{2n(2-n)(2m^2-n)}}, \nonumber \\&l_1 = \frac{k_1l}{4k} + \frac{1}{4k_1n}\nonumber \\&\quad \sqrt{4k_1^3n^2 {+} k_1^4 (192k^2m^2n{+} 16n^3k^2 {-} 64k^2n^2 {-} 64k^2n^2m^2 {+} \frac{9n^2l^2}{k^2})}. \end{aligned}$$

(27)

The solution u for (1) can be explicitly expressed by Jacobi elliptic functions

$$\begin{aligned} u&= \frac{\varDelta k_1 (nS^2-2)}{C_4\alpha (nS^2-1)} T + \Bigl ( C_4kn^2 (\alpha k_1 m_{1t} - 6\alpha l_1 +12\beta k_1)S^4\nonumber \\&\quad -\, 3nC_4(\alpha k k_1 m_{1t} - 4 \alpha k l_1 + 12\beta kk_1 ) S^2 \nonumber \\&\quad -\,12 \alpha C_4k_1k^2n S CD + 2C_4\alpha m_{1t} kk_1 - 3\alpha kl_1 -3\alpha lk_1\nonumber \\&\quad +\,12\beta k_1k \Bigr )\Bigg /\Bigl (kk_1 C_4\alpha ^2 (n^2S^4 - 3n S^2+2) \Bigr ) \end{aligned}$$

(28)

where $S=\mathrm {sn}(kx + ly - \frac{1}{6} km_{1t}y - lm_{1t} - \frac{km_2}{C_4}, m), \, C=\mathrm {cn}(kx + ly - \frac{1}{6} km_{1t}y - lm_{1t} - \frac{km_2}{C_4}, m), \, D=\mathrm {dn}(kx + ly - \frac{1}{6} km_{1t}y - lm_{1t} - \frac{km_2}{C_4}, m)$, $T= \tanh \left( \frac{\varDelta }{2C_4} t + \frac{k_1\varDelta }{2C_4}x + \frac{6\varDelta l_1 - k_1 \Delta m_{1t}}{12C_4} y - \frac{\varDelta l_1 m_1}{2C_4} - \frac{\Delta k_1 m_2}{2C_4^2}\right. \left. + \frac{k_1 \varDelta }{2C_4 k} E_\pi (S, n, m)\right)$, and the constants $\varDelta ,\, l$ and $l_1$ satisfy (27). The explicit solution (28) for the KD equation denotes the interaction between a soliton and cnoidal periodic waves. We can get many new types of interaction solutions because of the existence of the arbitrary functions $m_1$ and $m_2$ in (28). Figure 2 exhibits one kink soliton in the periodic wave background expressed by (28). Figure 3 exhibits the second type of special interaction solution between one kink soliton and the quasiperiodic wave by (28). Figure 4 exhibits the third type of special soliton–cnoidal wave structure by (28). For Figs. 2, 3 and 4, the arbitrary constants are $m=0.9, \, n=0.5,\, k_1=-2,\, k=1,\, C_4=1,\, \alpha =1,\, \beta =1$. The arbitrary functions $m_1$ and $m_2$ are selected $m_1=t,\, m_2=t$; $m_1=\cos (t),\, m_2=t$; $m_1=t,\, m_2=t^2$, respectively. For the density of Figs. 3c and 4c, the bright part is crest and the dark part is trough. By selecting different arbitrary functions, one kink soliton–cnoidal periodic wave becomes one soliton–cnoidal periodic wave solution from Figs. 2a and 4a. The interaction behaviors are thus different with selecting different arbitrary functions. These types of interaction solutions in Figs. 3 and 4 cannot be obtained by CRE/ CTE methods.

Case II $f_1=f_2=C_4=0$. Following the similar procedure as case I, the similarity solutions are given after solving out the characteristic equations (22)

$$\begin{aligned}&\phi = -\frac{\varDelta }{\alpha C_3} \tanh \left( \frac{\varDelta }{2f_3} (\phi {'}+x) \right) - \frac{C_2}{\alpha C_3}, \nonumber \\&\varDelta =\sqrt{2C_1C_3\alpha + C_2^2}, \end{aligned}$$

(29a)

$$\begin{aligned}&g = -\frac{g'}{\cosh ^2\left( \frac{\varDelta }{2f_3} (\phi {'}+x) \right) }, \end{aligned}$$

(29b)

$$\begin{aligned}&h =- \frac{h'}{\cosh ^2\left( \frac{\varDelta }{2f_3} (\phi {'}+x) \right) }, \end{aligned}$$

(29c)

$$\begin{aligned}&u = u{'} + \frac{2C_3}{\Delta } g' \tanh \left( \frac{\varDelta }{2f_3} (\phi {'}+x) \right) , \end{aligned}$$

(29d)

$$\begin{aligned}&w = w' \!+\! \frac{2C_3}{\Delta } h' \tanh \left( \frac{\varDelta }{2f_3} (\phi {'}+x) \right) \!+\! \frac{f_{3t}}{3\alpha f_3} (\phi {'}\!+\!x). \end{aligned}$$

(29e)

Substituting (29) into (9), (10), (4) and (5), the invariant functions $\phi {'}, g{'}, h{'}, u{'}$ and $w{'}$ satisfy the reduction systems

$$\begin{aligned}&g' = \frac{\varDelta ^2}{2\alpha C_3f_3} \end{aligned}$$

(30a)

$$\begin{aligned}&h' = \frac{\varDelta ^2}{2\alpha C_3f_3} \phi '_y, \end{aligned}$$

(30b)

$$\begin{aligned}&u' = - \frac{1}{\alpha } \phi '_y + \frac{2\beta }{\alpha ^2}, \end{aligned}$$

(30c)

$$\begin{aligned}&w' = \frac{1}{2\alpha } \phi '{_y^2} - \frac{1}{3\alpha } \phi '_t + \frac{\varDelta ^2}{6\alpha f_3^2} + \frac{2\beta ^2}{\alpha ^3}, \end{aligned}$$

(30d)

$$\begin{aligned}&3f_3 \phi '_{yy} + f_{3t} =0, \end{aligned}$$

(30e)

where $f_4$ and $f_5$ are arbitrary functions of t. From above the detail calculations, we have the following reduction theorem.

Theorem

If $\phi '$ is a solution of the reduction equation (30e), then the explicit solution for the KD equation reads

$$\begin{aligned} u= & {} \frac{\varDelta }{\alpha f_3} \tanh \left( \frac{\varDelta }{2f_3}(\phi '+x)\right) - \frac{1}{\alpha }\phi '_y + \frac{2\beta }{\alpha },\nonumber \\ w= & {} \frac{\varDelta }{\alpha f_3} \phi '_y \tanh \left( \frac{\varDelta }{2f_3}(\phi '+x)\right) + \frac{f_{3t}}{3\alpha f_3}\phi - \frac{\phi '_t}{3\alpha } + \frac{\phi '{_y^2}}{2\alpha }\nonumber \\&+ \frac{f_{3t}x}{3\alpha f_3} - \frac{\varDelta ^2}{6\alpha f_3^2} + \frac{2\beta ^2}{\alpha ^3}. \end{aligned}$$

(31)

4 Conclusion

The nonlocal symmetries of the KD equation are studied by the truncated Painlevé expansion and the Möbious invariant form. To solve the initial value problem related by the nonlocal symmetries, the nonlocal symmetries are localized by introducing multiple new dependent variables. The nonlocal symmetries become the local Lie point symmetries for the prolonged systems. The finite symmetry transformations of the prolonged KD systems are derived by solving the initial value problem related by the nonlocal symmetries. Based on the finite symmetry transformations, the multi-solitary wave solution for the KD equation is given from a trivial solution of the KD equation. With the help of the localization procedure, the nonlocal symmetries are used to find possible symmetry reductions. The interaction solution between soliton and cnoidal periodic waves is given as shown in (28). The interaction solution (28) includes the arbitrary functions $m_1$ and $m_2$. Some interesting interaction behaviors are shown by selecting different arbitrary functions in graphical way. These types of the interaction solutions may be useful for studying the ocean waves.

In this paper, with the aid of the nonlocal symmetries, new solutions of the KD equation are constructed by symmetry reductions of the enlarged systems. There exist other methods to construct the nonlocal symmetries [4–15]. Moreover, localization is viewed as an important step to extend applicability of nonlocal symmetries. Hence, one of the important problems is how to localize those types of nonlocal symmetries to the Lie point symmetries and how to obtain new interaction solutions with those various nonlocal symmetries. These fields merit our further study.