1 Introduction

The (\(2+1\))-dimensional negative-order modified Calogero–Bogoyavlenskii–Schiff (nmCBS) equation [1] reads:

$$\begin{aligned} u_y + u_{xxt} - 4u^2u_t - 4u_x\int uu_t \mathrm{d}x = 0, \end{aligned}$$
(1.1)

or equivalently

$$\begin{aligned} \begin{aligned}&u_y + u_{xxt} - 4u^2u_t - 4u_xv = 0, \\&uu_t - v_x = 0. \end{aligned} \end{aligned}$$
(1.2)

In [1], the (\(2+1\))-dimensional nmCBS equation (1.1) was derived by means of the inverse recursion operator [2, 3] of the modified CBS equation, and has multiple soliton solutions.

It is known that symmetry analysis [4, 5] and Painlevé analysis [6, 7] are effective methods to find exact solutions of nonlinear evolution equations (NLEEs) which model various nonlinear phenomena in physics and other related fields [8,9,10,11,12]. Recently, the study of nonlocal symmetry whose infinitesimal generator depends on integral of the dependent variable in a NLEE has attracted a lot of attention, since it can be used to generate exact interaction solutions between a soliton and other types of nonlinear waves. A few years ago, Lou [13] pointed out the connection of nonlocal symmetry with the Painlevé analysis, that is, the residue with respect to the singularity manifold in the truncated Painlevé expansion corresponds to a nonlocal symmetry. Such type of nonlocal symmetry is referred to as the residual symmetry. One can use it to find finite symmetry transformation and novel symmetry reduction through the localization of the residual symmetry [14,15,16,17,18,19]. The nth BT can be found after extending the residual symmetry to multiple residual symmetries [13, 20,21,22,23,24,25]. Hinting at the novel results of nonlocal symmetry reduction, Lou [26] further established the consistent Riccati expansion (CRE)/consistent tanh expansion (CTE) method for obtaining abundant interaction solutions, especially the interaction solution between a soliton and the cnoidal periodic wave [26,27,28,29,30,31,32,33,34]. In addition, by applying this method, we can identify integrability of NLEEs in the sense of having the CRE/CTE.

In this article, we study the residual symmetry and soliton-cnoidal wave interaction solution for the (\(2+1\))-dimensional nmCBS equation (1.1). The outline of the present paper is organized as follows. In Sect. 2, the residual symmetry of the (\(2+1\))-dimensional nmCBS equation is derived through the truncated Painlevé expansion method. Based on the residual symmetry, we obtain the nth BT in the form of determinant. In Sect. 3, we construct the soliton and soliton-cnoidal wave interaction solutions for the (\(2+1\))-dimensional nmCBS equation by solving a consistent differential equation, which is obtained by performing a straightening transformation to the Schwarzian nmCBS equation. Finally, we give some conclusions in Sect. 4.

2 Residual symmetry and nth BT

For the (\(2+1\))-dimensional nmCBS system (1.2), its truncated Painlevé expansion is of the form:

$$\begin{aligned} u = \frac{u_0}{\phi } + u_1, \quad v = \frac{v_0}{\phi ^2} + \frac{v_1}{\phi } + v_2, \end{aligned}$$
(2.1)

where \(\phi = \phi (x,y,t)\) is the singular manifold, and \(u_0\), \(u_1\), \(v_0\), \(v_1\) and \(v_2\) are functions of x, y and t, which are determined by vanishing all the coefficients of each power of \(\frac{1}{\phi }\) after substituting (2.1) into system (1.2). Some computations give us that:

$$\begin{aligned} \begin{aligned} u_0&= \phi _x, \quad v_0 = \frac{1}{2}\phi _x\phi _t, \\ u_1&= -\frac{1}{2}\frac{\phi _{xx}}{\phi _x}, \quad v_1 = -\frac{1}{2}\phi _{xt}, \\ v_2&= \frac{1}{4}\frac{\phi _y + \phi _{xxt}}{\phi _x} - \frac{1}{4} \frac{\phi _{xx}\phi _{xt}}{\phi ^2_x}, \end{aligned} \end{aligned}$$
(2.2)

and the following nonauto-BT

$$\begin{aligned} \begin{aligned} u&= -\frac{1}{2}\frac{\phi _{xx}}{\phi _x}, \\ v&= \frac{1}{4}\frac{\phi _y + \phi _{xxt}}{\phi _x} - \frac{1}{4} \frac{\phi _{xx}\phi _{xt}}{\phi ^2_x}, \end{aligned} \end{aligned}$$
(2.3)

between the (\(2+1\))-dimensional nmCBS system (1.2) and its Schwarzian form

$$\begin{aligned} S_t + K_x = 0, \quad K \equiv \frac{\phi _y}{\phi _x}, \quad S \equiv \frac{\phi _{xxx}}{\phi _x} - \frac{3}{2}\frac{\phi ^2_{xx}}{\phi ^2_x}. \end{aligned}$$
(2.4)

This form is invariant under the Möbius transformation

$$\begin{aligned} \phi \rightarrow \frac{a + b\phi }{c + d\phi }, \quad (ad \ne bc), \end{aligned}$$
(2.5)

which implies that the Schwarzian equation (2.4) admits the following Möbius transformation symmetry

$$\begin{aligned} \sigma ^\phi = -\phi ^2. \end{aligned}$$
(2.6)

Applying the residual symmetry theorem [13] to the (\(2+1\))-dimensional nmCBS system (1.2), it is inferred that the residual symmetry of system (1.2) is given by

$$\begin{aligned} \big (\sigma ^u,\sigma ^v\big ) = \biggl (\phi _x,-\frac{1}{2}\phi _{xt}\biggr ). \end{aligned}$$
(2.7)

We introduce three functions g, h and p defined as

$$\begin{aligned} g = \phi _x, \quad h = \phi _t, \quad p = g_t. \end{aligned}$$
(2.8)

The nonlocal residual symmetry (2.7) can now be localized to a local Lie point symmetry

$$\begin{aligned} \begin{aligned} \sigma ^u&= g, \quad \sigma ^v = -\frac{1}{2}p, \quad \sigma ^\phi = -\phi ^2, \\ \sigma ^g&= -2\phi g, \quad \sigma ^h = -2\phi h, \quad \sigma ^p = -2(\phi p + gh), \end{aligned} \end{aligned}$$
(2.9)

for the prolonged system (1.2), (2.3) and (2.8). Solving the corresponding initial value problem

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}{\tilde{u}}(\varepsilon )}{\mathrm{d}\varepsilon }&= {\tilde{g}}(\varepsilon ), \quad {\tilde{u}}(0) = u, \\ \frac{\mathrm{d}{\tilde{v}}(\varepsilon )}{\mathrm{d}\varepsilon }&= -\frac{1}{2}{\tilde{p}}(\varepsilon ), \quad {\tilde{v}}(0) = v, \\ \frac{\mathrm{d}{\tilde{\phi }}(\varepsilon )}{\mathrm{d}\varepsilon }&= -{\tilde{\phi }}(\varepsilon )^2, \quad {\tilde{\phi }}(0) = \phi , \\ \frac{\mathrm{d}{\tilde{g}}(\varepsilon )}{\mathrm{d}\varepsilon }&= -2{\tilde{\phi }}(\varepsilon ) {\tilde{g}}(\varepsilon ), \quad {\tilde{g}}(0) = g, \\ \frac{\mathrm{d}{\tilde{h}}(\varepsilon )}{\mathrm{d}\varepsilon }&= -2{\tilde{\phi }}(\varepsilon ) {\tilde{h}}(\varepsilon ), \quad {\tilde{h}}(0) = h, \\ \frac{\mathrm{d}{\tilde{p}}(\varepsilon )}{\mathrm{d}\varepsilon }&= -2({\tilde{\phi }}(\varepsilon ) {\tilde{p}}(\varepsilon ) + {\tilde{g}}(\varepsilon ){\tilde{h}}(\varepsilon )), \quad {\tilde{p}}(0) = p, \end{aligned} \end{aligned}$$
(2.10)

we get the finite symmetry transformation, which is stated in the following theorem.

Theorem 2.1

If \(\{u,~v,~\phi ,~g,~h,~p\}\) is a solution of the prolonged system (1.2), (2.3) and (2.8), then so is \(\{{\tilde{u}}(\varepsilon ),~{\tilde{v}}(\varepsilon ),~{\tilde{\phi }}(\varepsilon ),~{\tilde{g}}(\varepsilon ),~{\tilde{h}}(\varepsilon ),~{\tilde{p}}(\varepsilon )\}\), and it is given by

$$\begin{aligned} \begin{aligned} {\tilde{u}}(\varepsilon )&= u + \frac{\varepsilon g}{1 + \varepsilon \phi }, \quad {\tilde{v}}(\varepsilon ) = v - \frac{\varepsilon p}{2(1 + \varepsilon \phi )} + \frac{\varepsilon ^2gh}{2(1 + \varepsilon \phi )^2}, \\ {\tilde{\phi }}(\varepsilon )&= \frac{\phi }{1 + \varepsilon \phi }, \quad {\tilde{g}}(\varepsilon ) = \frac{g}{(1 + \varepsilon \phi )^2}, \\ {\tilde{h}}(\varepsilon )&= \frac{h}{(1 + \varepsilon \phi )^2}, \quad {\tilde{p}}(\varepsilon ) = \frac{p}{(1 + \varepsilon \phi )^2} - \frac{2\varepsilon gh}{(1 + \varepsilon \phi )^3}, \end{aligned} \end{aligned}$$
(2.11)

where \(\varepsilon \) is an arbitrary group parameter.

Due to the linearity of the symmetry equation and existence of an infinite number of solutions of the Schwarzian equation (2.4), we can obtain an infinite number of residual symmetries

$$\begin{aligned} \sigma ^u_n = \sum _{i=1}^{n}c_i\phi _{i,x}, \quad \sigma ^v_n = -\frac{1}{2}\sum _{i=1}^{n}c_i\phi _{i,xt}, \quad n=1,2,\ldots , \end{aligned}$$
(2.12)

where \(\phi _i~(i=1,\ldots ,n)\) represent different solutions of the Schwarzian equation (2.4). The symmetries (2.12) can be localized in a similar way, the corresponding result is illustrated as follows.

Theorem 2.2

If \(\{u,~v,~\phi _i,~g_i,~h_i,~p_i,~i=1,\ldots ,n\}\) is a solution of the prolonged system

$$\begin{aligned}&u_y + u_{xxt} - 4u^2u_t - 4u_xv = 0, \end{aligned}$$
(2.13a)
$$\begin{aligned}&uu_t - v_x = 0, \end{aligned}$$
(2.13b)
$$\begin{aligned}&u = -\frac{1}{2}\frac{\phi _{i,xx}}{\phi _{i,x}}, \end{aligned}$$
(2.13c)
$$\begin{aligned}&v = \frac{1}{4}\frac{\phi _{i,y} + \phi _{i,xxt}}{\phi _{i,x}} - \frac{1}{4}\frac{\phi _{i,xx}\phi _{i,xt}}{\phi ^2_{i,x}}, \end{aligned}$$
(2.13d)
$$\begin{aligned}&g_i = \phi _{i,x}, \quad h_i = \phi _{i,t}, \quad p_i = g_{i,t}, \end{aligned}$$
(2.13e)

then the symmetries (2.12) are transformed to local Lie point symmetries

$$\begin{aligned} \sigma ^u= & {} \sum _{j=1}^{n}c_jg_j, \nonumber \\ \sigma ^v= & {} -\frac{1}{2}\sum _{j=1}^{n}c_jp_j, \nonumber \\ \sigma ^{\phi _i}= & {} -c_i\phi ^2_i - \sum _{j \ne i}^{n}c_j\phi _i\phi _j,\nonumber \\ \sigma ^{g_i}= & {} -2c_i\phi _ig_i - \sum _{j \ne i}^{n}c_j(\phi _ig_j + \phi _jg_i), \nonumber \\ \sigma ^{h_i}= & {} -2c_i\phi _ih_i - \sum _{j \ne i}^{n}c_j(\phi _ih_j + \phi _jh_i), \nonumber \\ \sigma ^{p_i}= & {} -2c_i(\phi _ip_i + g_ih_i) - \sum _{j \ne i}^{n}c_j(\phi _ip_j + \phi _jp_i + g_ih_j + g_jh_i). \end{aligned}$$
(2.14)

Proof

The linearized system of the prolonged system (2.13) is written as

$$\begin{aligned}&\sigma ^u_y + \sigma ^u_{xxt} - 4u(u\sigma ^u_t + 2u_t\sigma ^u) - 4(v\sigma ^u_x + u_x\sigma ^v) = 0, \end{aligned}$$
(2.15a)
$$\begin{aligned}&u\sigma ^u_t - \sigma ^v_x + u_t\sigma ^u = 0, \end{aligned}$$
(2.15b)
$$\begin{aligned}&\sigma ^u = -\frac{1}{2}\frac{\sigma ^{\phi _i}_{xx}}{\phi _{i,x}} + \frac{1}{2}\frac{\phi _{i,xx}\sigma ^{\phi _i}_x}{\phi ^2_{i,x}}, \end{aligned}$$
(2.15c)
$$\begin{aligned}&\sigma ^v = \frac{1}{4}\frac{\sigma ^{\phi _i}_y + \sigma ^{\phi _i}_{xxt}}{\phi _{i,x}} - \frac{1}{4}\frac{\phi _{i,xx}\sigma ^{\phi _i}_{xt} + \phi _{i,xt}\sigma ^{\phi _i}_{xx} + (\phi _{i,y} + \phi _{i,xxt})\sigma ^{\phi _i}_x}{\phi ^2_{i,x}} + \frac{1}{2}\frac{\phi _{i,xx}\phi _{i,xt}\sigma ^{\phi _i}_x}{\phi ^3_{i,x}}, \end{aligned}$$
(2.15d)
$$\begin{aligned}&\sigma ^{g_i} = \sigma ^{\phi _i}_x, \quad \sigma ^{h_i} = \sigma ^{\phi _i}_t, \quad \sigma ^{p_i} = \sigma ^{g_i}_t, \quad i=1,\ldots ,n. \end{aligned}$$
(2.15e)

Without loss of generality, we fix k, \(c_k \ne 0\) while \(c_j = 0\), \(j \ne k\) in Eq. (2.12). From (2.9) we get

$$\begin{aligned} \sigma ^u&= c_kg_k, \end{aligned}$$
(2.16a)
$$\begin{aligned} \sigma ^v&= -\frac{1}{2}c_kp_k, \end{aligned}$$
(2.16b)
$$\begin{aligned} \sigma ^{\phi _k}&= -c_k\phi ^2_k, \end{aligned}$$
(2.16c)
$$\begin{aligned} \sigma ^{g_k}&= -2c_k\phi _k g_k, \end{aligned}$$
(2.16d)
$$\begin{aligned} \sigma ^{h_k}&= -2c_k\phi _k h_k, \end{aligned}$$
(2.16e)
$$\begin{aligned} \sigma ^{p_k}&= -2c_k(\phi _k p_k + g_kh_k). \end{aligned}$$
(2.16f)

For \(j \ne k\), eliminating u and v through Eqs. (2.13c) and (2.13d) by taking \(i = k\) and \(i = j\), respectively, we deduce that

$$\begin{aligned} \begin{aligned} \phi _{j,xx}&= \frac{\phi _{k,xx}\phi _{j,x}}{\phi _{k,x}}, \\ \phi _{j,y}&= \frac{\phi _{k,y}\phi _{j,x}}{\phi _{k,x}}. \end{aligned} \end{aligned}$$
(2.17)

Substituting (2.16a) and (2.16b) into (2.15c) and (2.15d) with \(i = j\), respectively, and eliminating \(\phi _{j,xx}\) and \(\phi _{j,y}\) by means of (2.17), we find

$$\begin{aligned} \sigma ^{\phi _j} = -c_k\phi _j\phi _k. \end{aligned}$$
(2.18)

Using (2.15e) with \(i=j\), we have

$$\begin{aligned} \begin{aligned} \sigma ^{g_j}&= -c_k(\phi _jg_k + \phi _kg_j), \\ \sigma ^{h_j}&= -c_k(\phi _jh_k + \phi _kh_j), \\ \sigma ^{p_j}&= -c_k(\phi _jp_k + \phi _kp_j + g_jh_k + g_kh_j). \end{aligned} \end{aligned}$$
(2.19)

Taking linear superpositions of the above results for \(k=1,2,\ldots ,n\), the proof of Theorem 2.2 is then completed. \(\square \)

The initial value problem corresponding to Lie point symmetries (2.14) reads

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}{\tilde{u}}(\varepsilon )}{\mathrm{d}\varepsilon }&= \sum _{j=1}^{n}c_j{\tilde{g}}_j(\varepsilon ), \\ \frac{\mathrm{d}{\tilde{v}}(\varepsilon )}{\mathrm{d}\varepsilon }&= -\frac{1}{2}\sum _{j=1}^{n}c_j{\tilde{p}}_j(\varepsilon ), \\ \frac{\mathrm{d}{\tilde{\phi }}_i(\varepsilon )}{\mathrm{d}\varepsilon }&= -c_i{\tilde{\phi }}_i(\varepsilon )^2 - \sum _{j \ne i}^{n}c_j{\tilde{\phi }}_i(\varepsilon ){\tilde{\phi }}_j(\varepsilon ), \\ \frac{\mathrm{d}{\tilde{g}}_i(\varepsilon )}{\mathrm{d}\varepsilon }&= -2c_i{\tilde{\phi }}_i(\varepsilon ){\tilde{g}}_i(\varepsilon ) - \sum _{j \ne i}^{n}c_j\left( {\tilde{\phi }}_i(\varepsilon ){\tilde{g}}_j(\varepsilon ) + {\tilde{\phi }}_j(\varepsilon ){\tilde{g}}_i(\varepsilon )\right) , \\ \frac{\mathrm{d}{\tilde{h}}_i(\varepsilon )}{\mathrm{d}\varepsilon }&= -2c_i{\tilde{\phi }}_i(\varepsilon ){\tilde{h}}_i(\varepsilon ) - \sum _{j \ne i}^{n}c_j\left( {\tilde{\phi }}_i(\varepsilon ){\tilde{h}}_j(\varepsilon ) + {\tilde{\phi }}_j(\varepsilon ){\tilde{h}}_i(\varepsilon )\right) , \\ \frac{\mathrm{d}{\tilde{p}}_i(\varepsilon )}{\mathrm{d}\varepsilon }&= -2c_i\left( {\tilde{\phi }}_i(\varepsilon ){\tilde{p}}_i(\varepsilon ) + {\tilde{g}}_i(\varepsilon ){\tilde{h}}_i(\varepsilon )\right) \\&\quad - \sum _{j \ne i}^{n}c_j\left( {\tilde{\phi }}_i(\varepsilon ){\tilde{p}}_j(\varepsilon ) + {\tilde{\phi }}_j(\varepsilon ){\tilde{p}}_i(\varepsilon ) + {\tilde{g}}_i(\varepsilon ){\tilde{h}}_j(\varepsilon ) + {\tilde{g}}_j(\varepsilon ){\tilde{h}}_i(\varepsilon )\right) , \\ {\tilde{u}}(0)&= u, \quad {\tilde{v}}(0) = v, \quad {\tilde{\phi }}_i(0) = \phi _i, \\ {\tilde{g}}_i(0)&= g_i, \quad {\tilde{h}}_i(0) = h_i, \quad {\tilde{p}}_i(0) = p_i, \quad i=1,\ldots ,n. \end{aligned} \end{aligned}$$
(2.20)

Solving the above initial value problem, we obtain the following result which describes nth BT for the prolonged system (2.13).

Theorem 2.3

If \(\{u,~v,~\phi _i,~g_i,~h_i,~p_i,~i=1,\ldots ,n\}\) is a solution of the prolonged system (2.13), then so is \(\{{\tilde{u}}(\varepsilon ),~{\tilde{v}}(\varepsilon ),~{\tilde{\phi }}_i(\varepsilon ),~{\tilde{g}}_i(\varepsilon ),~{\tilde{h}}_i(\varepsilon ),~{\tilde{p}}_i(\varepsilon ),~i=1,\ldots ,n\}\), and it is given by

$$\begin{aligned} \begin{aligned} {\tilde{u}}(\varepsilon )&= u + (\ln |M|)_x, \quad {\tilde{v}}(\varepsilon ) = v - \frac{1}{2}(\ln |M|)_{xt}, \\ {\tilde{\phi }}_i(\varepsilon )&= \frac{|M_i|}{|M|}, \quad {\tilde{g}}_i(\varepsilon ) = {\tilde{\phi }}_{i,x}(\varepsilon ), \\ {\tilde{h}}_i(\varepsilon )&= {\tilde{\phi }}_{i,t}(\varepsilon ), \quad {\tilde{p}}_i(\varepsilon ) = {\tilde{\phi }}_{i,xt}(\varepsilon ), \end{aligned} \end{aligned}$$
(2.21)

where

$$\begin{aligned} M&= \begin{pmatrix} c_1\varepsilon \phi _1 + 1 &{} c_1\varepsilon \omega _{12} &{} \cdots &{} c_1\varepsilon \omega _{1j} &{} \cdots &{} c_1\varepsilon \omega _{1n} \\ c_2\varepsilon \omega _{12} &{} c_2\varepsilon \phi _2 + 1 &{} \cdots &{} c_2\varepsilon \omega _{2j} &{} \cdots &{} c_2\varepsilon \omega _{2n} \\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ c_j\varepsilon \omega _{1j} &{} c_j\varepsilon \omega _{2j} &{} \cdots &{} c_j\varepsilon \phi _j + 1 &{} \cdots &{} c_j\varepsilon \omega _{jn} \\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ c_n\varepsilon \omega _{1n} &{} c_n\varepsilon \omega _{2n} &{} \cdots &{} c_n\varepsilon \omega _{jn} &{} \cdots &{} c_n\varepsilon \phi _n + 1 \end{pmatrix}_{n\times n}, \quad \omega _{ij} = \sqrt{\phi _i\phi _j}, \\ M_i&= \begin{pmatrix} c_1\varepsilon \phi _1 + 1 &{}\quad c_1\varepsilon \omega _{12} &{}\quad \cdots &{}\quad c_1\varepsilon \omega _{1,i-1} &{}\quad c_1\varepsilon \omega _{1i} &{}\quad c_1\varepsilon \omega _{1,i+1} &{}\quad \cdots &{}\quad c_1\varepsilon \omega _{1n} \\ c_2\varepsilon \omega _{12} &{}\quad c_2\varepsilon \phi _2 + 1 &{}\quad \cdots &{}\quad c_2\varepsilon \omega _{2,i-1} &{}\quad c_2\varepsilon \omega _{2i} &{}\quad c_2\varepsilon \omega _{2,i+1} &{}\quad \cdots &{}\quad c_2\varepsilon \omega _{2n} \\ \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots \\ c_{i-1}\varepsilon \omega _{1,i-1} &{}\quad c_{i-1}\varepsilon \omega _{2,i-1} &{}\quad \cdots &{}\quad c_{i-1}\varepsilon \phi _{i-1} + 1 &{}\quad c_{i-1}\varepsilon \omega _{i-1,i} &{}\quad c_{i-1}\varepsilon \omega _{i-1,i+1} &{}\quad \cdots &{}\quad c_{i-1}\varepsilon \omega _{i-1,n} \\ \omega _{1i} &{}\quad \omega _{2i} &{}\quad \cdots &{}\quad \omega _{i-1,i} &{}\quad \phi _i &{}\quad \omega _{i,i+1} &{}\quad \cdots &{}\quad \omega _{in} \\ c_{i+1}\varepsilon \omega _{1,i+1} &{}\quad c_{i+1}\varepsilon \omega _{2,i+1} &{}\quad \cdots &{}\quad c_{i+1}\varepsilon \omega _{i-1,i+1} &{}\quad c_{i+1}\varepsilon \omega _{i,i+1} &{}\quad c_{i+1}\varepsilon \phi _{i+1} + 1 &{}\quad \cdots &{}\quad c_{i+1}\varepsilon \omega _{i+1,n} \\ \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots \\ c_n\varepsilon \omega _{1n} &{}\quad c_n\varepsilon \omega _{2n} &{}\quad \cdots &{}\quad c_n\varepsilon \omega _{i-1,n} &{}\quad c_n\varepsilon \omega _{in} &{}\quad c_n\varepsilon \omega _{i+1,n} &{}\quad \cdots &{}\quad c_n\varepsilon \phi _n + 1 \end{pmatrix}_{n\times n}. \end{aligned}$$

3 Soliton and soliton-cnoidal wave interaction solutions

We know that the CTE is connected to the truncated Painlevé expansion via the following straightening transformation

$$\begin{aligned} \phi = \frac{d_1}{d_2\tanh (f) + d_3}, \quad (d_1,~d_2 \ne 0). \end{aligned}$$
(3.1)

This transformation allows us to reduce the truncated Painlevé expansion (2.1) and Schwarzian equation (2.4) to the CTE solution

$$\begin{aligned} \begin{aligned} u&= f_x\tanh (f) - \frac{1}{2}\frac{f_{xx}}{f_x}, \\ v&= -\frac{1}{2}f_xf_t{{\,\mathrm{sech}\,}}^2(f) - \frac{1}{2}f_{xt}\tanh (f) + \frac{1}{4}\frac{f_y + f_{xxt}}{f_x} - \frac{1}{4}\frac{f_{xx}f_{xt}}{f^2_x}, \end{aligned} \end{aligned}$$
(3.2)

and a new consistent equation

$$\begin{aligned} \left( \frac{f_{xxx}}{f_x} - \frac{3}{2}\frac{f^2_{xx}}{f^2_x}\right) _t + \left( \frac{f_y}{f_x}\right) _x - 4f_xf_{xt} = 0, \end{aligned}$$
(3.3)

respectively. Once the solution of the consistent equation (3.3) is given, explicit expressions for u and v can be deduced. In the following, we provide two kinds of exact solutions of the (\(2+1\))-dimensional nmCBS system (1.2), including the soliton solution and soliton-cnoidal wave interaction solution.

3.1 Soliton solution

Equation (3.3) has a quite trivial straight-line solution

$$\begin{aligned} f = \kappa _1x + l_1y + \omega _1t + \omega _0, \end{aligned}$$
(3.4)

which results in the following single soliton solution

$$\begin{aligned} \begin{aligned} u&= \kappa _1\tanh (\kappa _1x + l_1y + \omega _1t + \omega _0), \\ v&= -\frac{1}{2}\kappa _1\omega _1{{\,\mathrm{sech}\,}}^2(\kappa _1x + l_1y + \omega _1t + \omega _0) + \frac{l_1}{4\kappa _1}. \end{aligned} \end{aligned}$$
(3.5)

3.2 Soliton-cnoidal wave interaction solution

To construct the soliton-cnoidal wave interaction solution, we take the solution of Eq. (3.3) to be

$$\begin{aligned} f = \kappa _1x + l_1y + \omega _1t + F(\kappa _2x + l_2y + \omega _2t) \equiv \kappa _1x + l_1y + \omega _1t + F(\xi ). \end{aligned}$$
(3.6)

The substitution of (3.6) into the consistent equation (3.3) produces the following elliptic equation

$$\begin{aligned} F_{1,\xi }^2 = a_0 + a_1F_1 + a_2F^2_1 + a_3F^3_1 + 4F^4_1, \quad F_1 \equiv F_\xi , \end{aligned}$$
(3.7)

with

$$\begin{aligned} \begin{aligned} a_0&= \frac{2\kappa ^2_1(C_1 - C_2\kappa _1)}{\kappa _2} - \frac{\kappa _1(\kappa _1l_2 - \kappa _2l_1)}{\kappa ^4_2\omega _2}, \\ a_1&= 2\kappa _1(2C_1 - 3C_2\kappa _1) - \frac{\kappa _1l_2 - \kappa _2l_1}{\kappa ^3_2\omega _2}, \\ a_2&= \frac{2\kappa ^3_2(C_1 - 3C_2\kappa _1) + 4\kappa ^2_1}{\kappa ^2_2}, \quad a_3 = \frac{2(4\kappa _1 - C_2\kappa ^3_2)}{\kappa _2}. \end{aligned} \end{aligned}$$
(3.8)

Then, (3.6) leads to the interaction solution between a soliton and the F function wave solution of system (1.2) of the form

$$\begin{aligned} u= & {} (\kappa _1 + \kappa _2F_1)\tanh (\kappa _1x + l_1y + \omega _1t + F) - \frac{\kappa ^2_2F_{1,\xi }}{2(\kappa _1 + \kappa _2F_1)}, \nonumber \\ v= & {} -\frac{1}{2}(\kappa _1 + \kappa _2F_1)(\omega _1 + \omega _2F_1) {{\,\mathrm{sech}\,}}^2(\kappa _1x + l_1y + \omega _1t + F) \nonumber \\&- \frac{1}{2}\kappa _2\omega _2F_{1,\xi }\tanh (\kappa _1x + l_1y + \omega _1t + F) \nonumber \\&- \frac{\kappa ^3_2\omega _2F^2_{1,\xi } - \kappa _2l_1F_1 - \kappa _1l_1}{4(\kappa _1 + \kappa _2F_1)^2} + \frac{\kappa ^2_2\omega _2F_{1,\xi \xi } + l_2F_1}{4(\kappa _1 + \kappa _2F_1)}. \end{aligned}$$
(3.9)
Fig. 1
figure 1

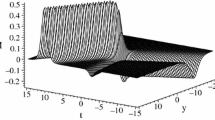
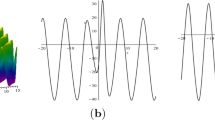
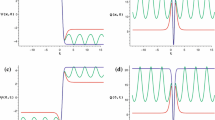
The soliton-cnoidal wave interaction solution (3.12) with the parameters \(\kappa _1 = -1.74\), \(\kappa _2 = 1.2\), \(l_1 = -1.4670776\), \(l_2 = 2\), \(\omega _1 = 1\), \(\omega _2 = 1.5\), \(b_0 = 1\), \(b_1 = 0.135\), \(b_2 = 0.9\), \(m = 0.3\) and \(\gamma = 0\). a, e The profiles at \(t=0\) and \(y=0\), b, f the profiles at \(t=0\) and \(x=0\), c, g the three-dimensional plots, d, h the density plots

Full size image

It is well known that the elliptic equation (3.7) has Jacobi elliptic functions solution. We take only a simple solution of elliptic equation (3.7) as

$$\begin{aligned} F_1 = b_0 + b_1\text {sn}(b_2\xi ,m), \end{aligned}$$
(3.10)

where \(\text {sn}(b_2\xi ,m)\) is the Jacobi elliptic sine function. Substituting (3.10) and (3.8) into (3.7) and vanishing the coefficients of different powers of \(\text {sn}(b_2\xi ,m)\), \(\text {cn}(b_2\xi ,m)\) and \(\text {dn}(b_2\xi ,m)\) give rise to

$$\begin{aligned} C_1= & {} -\frac{4b^2_0 + b_2(4b_0 - 4b_2 + b_2m^2)}{2\kappa _2}, \quad C_2 = \frac{2(2b_0 - b_2)}{\kappa ^2_2}, \nonumber \\ \kappa _1= & {} -\frac{1}{2}\kappa _2(2b_0 + b_2), \quad l_1 = -\frac{1}{2}l_2(2b_0 + b_2) - \kappa ^2_2\omega _2b^3_2(m^2 - 1), \quad b_1 = \frac{1}{2}b_2m.\nonumber \\ \end{aligned}$$
(3.11)

We thus have the following exact soliton-cnoidal wave interaction solution of the (\(2+1\))-dimensional nmCBS system

$$\begin{aligned} u= & {} -\frac{1}{2}\kappa _2b_2(mS - 1)\tanh (X) - \frac{1}{2}\frac{\kappa _2b_2mCD}{mS - 1}, \nonumber \\ v= & {} - \frac{1}{8}\kappa _2b_2(mS - 1)[2\omega _1 + \omega _2(2b_0 + b_2mS)]{{\,\mathrm{sech}\,}}^2(X) + \frac{1}{4}\kappa _2\omega _2b^2_2mCD\tanh (X) \nonumber \\&+ \frac{l_2}{4\kappa _2} - \frac{1}{4}\frac{\kappa ^2_2\omega _2b^2_2mD^2\big [S(mS - 1) + mC^2\big ]}{\kappa _2(mS - 1)^2} - \frac{1}{4}\frac{\kappa _2\omega _2b^2_2(m^3SC^2 + 2m^2 - 2)}{mS - 1},\nonumber \\ \end{aligned}$$
(3.12)

where \(S=\text {sn}(b_2\xi ,m)\), \(C=\text {cn}(b_2\xi ,m)\), \(D=\text {dn}(b_2\xi ,m)\) and \(X = \frac{1}{2}\kappa _2b_2x + \frac{1}{2}b_2[2\kappa ^2_2\omega _2b^2_2(m^2 - 1) + l_2 ]y - (\omega _1 + \omega _2b_0)t - \frac{1}{2}\ln (D - mC) - \gamma \).

We illustrate the interaction solution (3.12) graphically in Fig. 1. As seen in the figure, a soliton propagates on the cnoidal periodic wave background. This kind of interaction exists in some physical systems, such as the Fermionic quantum plasma system, the unmagnetized plasma system and the magnetized electron-positron-ion plasma system [35,36,37,38].

4 Conclusions

In the present paper, we first derive the residual symmetry using the truncated Painlevé expansion. Then by introducing three functions, this residual symmetry is converted into the Lie point symmetry and the finite symmetry transformation is derived. Furthermore, the multiple residual symmetries, which are a linear superposition of residual symmetries with different solutions of the Schwarzian nmCBS equation, are provided. Analogously, they are also transformed to Lie point symmetries through introducing more functions and nth BT in the determinant form is presented. Finally, via a straightening transformation, we directly derive the CTE solution and a new consistent equation, which yield the exact soliton and soliton-cnoidal wave interaction solutions.

It is well known that many physically important systems are connected to negative-order equations via reciprocal transformations, such as the Camassa–Holm equation and the negative-order KdV equation [39], the Degasperis–Procesi equation and the negative-order Kaup–Kupershmidt equation [40], the Novikov equation and the negative-order Sawada–Kotera equation [41]. Whether one can find a physically meaningful system reciprocally linked to the (\(2+1\))-dimensional nmCBS equation (1.1) is a very interesting issue to be clarified by further study.