1 Introduction

Nonlinear evolution equations (NLEEs) and their solutions play an important role in almost all branches of physics [1,2,3,4]. To further understand these nonlinear phenomena, a variety of powerful methods are proposed to look for exact solutions of NLEEs [5,6,7,8,9,10,11,12], such as Hirota direct method [13,14,15,16,17], exp function method [18], three-wave approach [19,20,21], etc.

Recently, the research about lump solutions has become the hot spot since lump solutions were firstly proposed [22, 23], which appeared in a lot of interesting physically relevant situations [24,25,26,27,28,29,30,31,32,33,34,35,36,37,38]. In this paper, by utilizing the Hirota’s bilinear form, we will discuss the following new (3 + 1)-dimensional generalized Kadomtsev–Petviashvili(ngKP) equation [39, 40]:

$$\begin{aligned} u_{ty}+u_{tx}+u_{tz}-u_{zz}+3 (u_x\,u_y)_x+u_{xxxy}=0. \end{aligned}$$
(1)

Wazwaz [39] obtained the multiple soliton solutions of the ngKP equation. Liu [41] presented new exact periodic solitary-wave solutions for the ngKP equation. As far as we know, lump solutions of the ngKP equation have not been discussed.

The organization of this paper is as follows: Sect. 2 obtains the lump solutions of the ngKP equation based on the Hirota’s bilinear form of Eq. (1). Section 3 presents the lump–kink solutions of Eq. (1) and shows the dynamic properties of these obtained solutions described in figures by selecting appropriate parameters. Finally, the conclusions are given.

2 Lump solutions for the ngKP equation

Utilizing the variable substitution \(u=2(ln\xi )_x\), we get the following Hirota’s bilinear form

$$\begin{aligned} (D_t D_x+D_t D_y+D_t D_z+D_x^3 D_y-D_z^2) \xi \cdot \xi =0.\nonumber \\ \end{aligned}$$
(2)

This is equivalent to

$$\begin{aligned}&(\xi _{xxxy}+\xi _{tx}+\xi _{ty}+\xi _{tz}-\xi _{zz})\,\xi -3 \xi _{xxy} \xi _x+3 \xi _{xy}\,\xi _{xx}\nonumber \\&\quad -\,\xi _{y}\,\xi _{xxx}-\xi _t \xi _x-\xi _t \xi _y-\xi _t \xi _z+\xi _z^2=0. \end{aligned}$$
(3)

To look for lump solutions of Eq. (3), we make the following hypothesis

$$\begin{aligned} g= & {} x \alpha _1+y \alpha _2+z \alpha _3+t \alpha _4+\alpha _5,\nonumber \\ h= & {} x \alpha _6+y \alpha _7+z \alpha _8+t \alpha _9+\alpha _{10},\nonumber \\ \xi= & {} g^2+h^2+\alpha _{11}, \end{aligned}$$
(4)

where \(\alpha _i(1\le i \le 11)\) are real constants to be determined later. Substituting Eq. (4) into Eq. (3), we can derive the following form of solutions for the parameters \(\alpha _i(1\le i \le 11)\) by the Mathematical software

Case (1)

$$\begin{aligned} \alpha _4= & {} \frac{\alpha _6 \left( \alpha _6 \alpha _3^2-2 \alpha _1 \alpha _8 \alpha _3-\alpha _6 \alpha _8^2\right) }{\left( \alpha _1+\alpha _2+\alpha _3\right) \left( \alpha _1^2+\alpha _6^2\right) },\quad \alpha _9=\frac{-\alpha _1 \alpha _4}{\alpha _6}, \nonumber \\ \alpha _7= & {} \left[ \alpha _6 \alpha _8^3+[\alpha _6^2-\alpha _1 (\alpha _1\right. \nonumber \\&\quad +\,\alpha _2-\alpha _3)] \alpha _8^2+\alpha _3 \left( 4 \alpha _1+2 \alpha _2+\alpha _3\right) \alpha _6 \alpha _8\nonumber \\&\quad +\,\alpha _3^2 [\alpha _1 \left( \alpha _1+\alpha _2+\alpha _3\right) \nonumber \\&\quad \left. -\,\alpha _6^2]\right] /[\alpha _6 \alpha _3^2-2 \alpha _1 \alpha _8 \alpha _3-\alpha _6 \alpha _8^2],\nonumber \\ \alpha _{11}= & {} \left[ 3 \left( \alpha _1^2+\alpha _6^2\right) ^2 \left[ -\alpha _6^2 \alpha _8^3+\alpha _6 \right. \right. \nonumber \\&\quad \left( \alpha _1 \left( \alpha _1+2 \alpha _2-\alpha _3\right) -\alpha _6^2\right) \alpha _8^2-\alpha _3 [(4 \alpha _1\nonumber \\&\quad + 2 \alpha _2+\alpha _3) \alpha _6^2-2 \alpha _1^2 \alpha _2] \alpha _8\nonumber \\&\quad +\left. \left. \,\alpha _3^2 \alpha _6 \left[ \alpha _6^2-\alpha _1 \left( \alpha _1+2 \alpha _2+\alpha _3\right) \right] \right] \right] \nonumber \\&\quad /\left[ \left( \alpha _1 \alpha _3+\alpha _6 \alpha _8\right) ^2 \left( -\alpha _6 \alpha _3^2+2 \alpha _1 \alpha _8 \alpha _3+\alpha _6 \alpha _8^2\right) \right] ,\nonumber \\ \end{aligned}$$
(5)

where \(\left( \alpha _1 \alpha _3+\alpha _6 \alpha _8\right) ^2 \left( -\alpha _6 \alpha _3^2+2 \alpha _1 \alpha _8 \alpha _3+\alpha _6 \alpha _8^2\right) \ne 0\), \(\alpha _6\ne 0\),\(\left( \alpha _1+\alpha _2+\alpha _3\right) \left( \alpha _1^2+\alpha _6^2\right) \ne 0\).

Case (2)

$$\begin{aligned} \alpha _2= & {} \alpha _1 \left( -\frac{\alpha _1 \alpha _3^2}{\alpha _4 \alpha _6^2}-1\right) -\alpha _3, \alpha _8=-\frac{\alpha _1 \alpha _3}{\alpha _6}, \nonumber \\ \alpha _7= & {} \frac{\alpha _1 \alpha _3 \left( \alpha _4-\alpha _3\right) }{\alpha _4 \alpha _6}-\alpha _6, \nonumber \\ \alpha _{9}= & {} \frac{\alpha _4 \alpha _6}{\alpha _1}, \alpha _{11}=-\frac{3 \left( \alpha _1^2+\alpha _6^2\right) \left( \alpha _1 \alpha _3^2+\alpha _4 \alpha _6^2\right) }{\alpha _3^2 \alpha _4},\nonumber \\ \end{aligned}$$
(6)

where \(\alpha _1 \alpha _6 \alpha _3 \alpha _4\ne 0\).

Case (3)

$$\begin{aligned} \alpha _8= & {} \frac{\alpha _1 \alpha _3 \alpha _6+\epsilon _1 \sqrt{-\alpha _1^2 \left( \left( \alpha _1+\alpha _2+\alpha _3\right) \alpha _4-\alpha _3^2\right) \left( \alpha _1^2+\alpha _6^2\right) }}{\alpha _1^2},\nonumber \\ \alpha _{9}= & {} \frac{\alpha _4 \alpha _6}{\alpha _1},\nonumber \\ \alpha _7= & {} \frac{\epsilon _1 \left( -\alpha _4+2 \alpha _3\right) \sqrt{-\alpha _1^2 \left( \left( \alpha _1+\alpha _2+\alpha _3\right) \alpha _4-\alpha _3^2\right) \left( \alpha _1^2+\alpha _6^2\right) }}{\alpha _1^2 \alpha _4}\nonumber \\+ & {} \frac{-2 \alpha _4 \alpha _6 \alpha _1^2+\left( 2 \alpha _3^2-\left( \alpha _2+2 \alpha _3\right) \alpha _4\right) \alpha _6 \alpha _1}{\alpha _1^2 \alpha _4},\nonumber \\ \alpha _{11}= & {} -[3 \left( \alpha _1^2+\alpha _6^2\right) [\alpha _2 \alpha _4 \alpha _1^3-2 \alpha _4 \alpha _6^2 \alpha _1^2\nonumber \\&+\left( 2 \alpha _3^2-\left( \alpha _2+2 \alpha _3\right) \alpha _4\right) \alpha _6^2 \alpha _1+\epsilon _1 (-\alpha _4\nonumber \\&+2 \alpha _3) \alpha _6 \sqrt{-\alpha _1^2 \left( \left( \alpha _1+\alpha _2+\alpha _3\right) \alpha _4-\alpha _3^2\right) \left( \alpha _1^2+\alpha _6^2\right) }]]\nonumber \\&\quad /[\alpha _1^2 \alpha _4 \left( \left( \alpha _1+\alpha _2+\alpha _3\right) \alpha _4-\alpha _3^2\right) ], \end{aligned}$$
(7)

where \(\epsilon _1=\pm \, 1\), \(\alpha _1 \alpha _4\ne 0\), \(\left( \alpha _1+\alpha _2+\alpha _3\right) \alpha _4-\alpha _3^2 < 0\).

Case (4)

$$\begin{aligned} \alpha _9= & {} \frac{\alpha _3 \alpha _8+\epsilon _2 \sqrt{(\alpha _3^2-(\alpha _1+\alpha _2+\alpha _3) \alpha _4) (\alpha _8^2+(\alpha _1+\alpha _2+\alpha _3) \alpha _4)}}{\alpha _1+\alpha _2+\alpha _3},\nonumber \\ \alpha _7= & {} \frac{\alpha _3 \alpha _8-\epsilon _2 \sqrt{(\alpha _3^2-(\alpha _1+\alpha _2+\alpha _3) \alpha _4) (\alpha _8^2+(\alpha _1+\alpha _2+\alpha _3) \alpha _4)}}{\alpha _4}\nonumber \\ {}- & {} \left( \alpha _6+\alpha _8\right) ,\nonumber \\ \alpha _{11}= & {} -[3 \left( \alpha _1^2+\alpha _6^2\right) [\alpha _1 \alpha _2 \alpha _4+\alpha _6 [\alpha _3 \alpha _8-\alpha _4 \left( \alpha _6+\alpha _8\right) \nonumber \\&\quad -\,\epsilon _2 \sqrt{\left( \alpha _3^2-\left( \alpha _1+\alpha _2+\alpha _3\right) \alpha _4\right) \left( \alpha _8^2+\left( \alpha _1+\alpha _2+\alpha _3\right) \alpha _4\right) }]]]\nonumber \\&\quad /[\alpha _4 \left( \left( \alpha _1+\alpha _2+\alpha _3\right) \alpha _4-\alpha _3^2\right) ], \end{aligned}$$
(8)

where \(\left( \alpha _3^2-\left( \alpha _1+\alpha _2+\alpha _3\right) \alpha _4\right) \big (\alpha _8^2+(\alpha _1+\alpha _2+\alpha _3) \alpha _4\big ) > 0\), \(\epsilon _2=\pm 1\), \(\left( \alpha _1+\alpha _2+\alpha _3\right) \alpha _4\ne 0\).

Substituting Eqs. (5)–(8) into Eq. (4) and the transformation \(u=2(ln\xi )_x\), we can obtain four classes lump solutions of the ngKP equation.

Fig. 1
figure 1

Plots of the lump solution of Eq. (1) for \(\alpha _1=3\), \(\alpha _2=\alpha _3=2\), \(\alpha _5=\alpha _6=0\), \(\alpha _7=1\), \(\alpha _8=-\,2\), \(\alpha _{10}=-\,1\), \(z=0\), when \(t=-10\) in a, d, \(t = 0\) in b, e and \(t = 10\) in c, f

Full size image
Fig. 2
figure 2

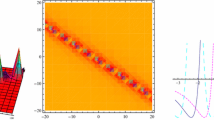
Plots of the lump solution of Eq. (1) for \(\alpha _2=2\), \(\alpha _1=\alpha _3=1\), \(\alpha _5=14\), \(\alpha _6=-\,7\), \(\alpha _7=-\,1\), \(\alpha _8=-\,2\), \(\alpha _{10}=12\), \(z=0\), when \(t=-\,40\) in a, d, \(t = 0\) in b, e and \(t = 40\) in c, f.

Full size image

These obtained lump solutions given from Eqs. (5) to (8) have the equal form but differ from each other only by the coefficients. Therefore, the plots of these solutions also have properties in common with each other. As an example, we will take Case (1) to illustrate their dynamic properties through three-dimensional plots and contour plots (see Figs. 1, 2).

Fig. 3
figure 3

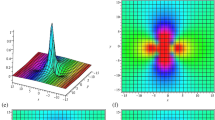
Plots of the lump-link solution of Eq. (1) for \(\alpha _2=2\), \(\alpha _3=25\), \(\alpha _5=-5\), \(k_1=-\,1\), \(k=5\), \(\epsilon _3=1\), \(\epsilon _4=-\,1\), \(\alpha _{10}=10\), \(z=0\), when \(t=-\,2\) in a, d, \(t = 0\) in b, e and \(t = 2\) in c, f

Full size image

3 Lump–kink solutions for the ngKP equation

In this section, we will investigate the interaction solution between the lump solution and exponential function, called a lump–kink solution. Adding the exponential function to Eq. (4)

$$\begin{aligned} g= & {} x \alpha _1+y \alpha _2+z \alpha _3+t \alpha _4+\alpha _5,\nonumber \\ h= & {} x \alpha _6+y \alpha _7+z \alpha _8+t \alpha _9+\alpha _{10},\nonumber \\ l= & {} e^{x k_1+y k_2+z k_3+t k_4} k,\nonumber \\ \xi= & {} g^2+h^2+l+\alpha _{11}, \end{aligned}$$
(9)

where \(\alpha _i(1\le i \le 11)\), k and \(k_i(i=1,2,3,4)\) are real undetermined constant. Substituting Eq. (9) into Eq. (3), we have

$$\begin{aligned} \alpha _1= & {} -\,\alpha _3, \alpha _4=-\frac{\alpha _6^2}{\alpha _2}, \alpha _8=-\alpha _6, \alpha _7=\frac{\alpha _2 \alpha _3}{\alpha _6},\nonumber \\ \alpha _9= & {} -\,\frac{\alpha _3 \alpha _6}{\alpha _2}, \nonumber \\ k_2= & {} \frac{-\,3 \alpha _2^2 k_1^5+2 \left( 3 k_1^2-2\right) \alpha _6^2 k_1+\epsilon _3 \sqrt{9 \left( k_1^2-4\right) \alpha _2^4 k_1^8+4 \left( 3 k_1^2+4\right) \alpha _2^2 \alpha _6^2 k_1^4}}{\left( 2-3 k_1^2\right) ^2 \alpha _6^2-9 k_1^4 \alpha _2^2},\nonumber \\ \alpha _6= & {} \epsilon _4 \frac{3}{2} k_1^2 \alpha _2, k_4=\frac{k_3^2-k_1^3 k_2}{k_1+k_2+k_3}, \alpha _{11}=0, k_3=-\,\frac{3}{2} k_1^2 k_2, \end{aligned}$$
(10)

with the following restrictive conditions

$$\begin{aligned}&(1): \alpha _2 \ne 0, k_1 < 0, k^2_1 \ne \frac{4}{3}, k_1+k_2+k_3\ne 0,\\&\quad \epsilon _3=1, \epsilon _4=\pm 1,\\&(2): \alpha _2 \ne 0, k_1 > 0, k^2_1 \ne \frac{4}{3}, k_1+k_2+k_3\ne 0,\\&\quad \epsilon _3=-1, \epsilon _4=\pm 1. \end{aligned}$$

Substituting Eqs. (9) and (10) into the transformation \(u=2(ln\xi )_x\), the lump–kink solutions of Eq. (1) can be obtained as follows

$$\begin{aligned} u=\frac{2(2 \alpha _1 g+2 \alpha _6 h+l k_1)}{g^2+h^2+l}, \end{aligned}$$
(11)

where g, h, l satisfy Eq. (10) with some restrictive conditions.

Three-dimensional plots and corresponding contour plots of the lump–kink solutions (11) are shown in Fig. 3 when \(t=-2, 0, 2\). Figure 3 describes the interaction between the obtained lump solutions and the exponential function.

4 Conclusion

In this work, by utilizing the Hirota’s bilinear formulation, abundant lump solutions of the ngKP equation are given with some restrictive conditions. By adding an exponential function to Eq. (4), we obtain the lump–kink solutions of the ngKP equation. The dynamic properties of these obtained lump solutions are shown in Figs. 1 and 2 by selecting appropriate parameters. The interaction between the obtained lump solutions and the exponential function is described by some three-dimensional plots and corresponding contour plots in Fig. 3.