1 Introduction

Designing new chaotic systems with interesting features has attracted lots of interest recently. Some of these chaotic systems can be categorized according to their equilibria: chaotic systems with no equilibrium points [1, 2], with only stable equilibria [3, 4], with curves of equilibria [5], with surfaces of equilibria [6, 7] and with non-hyperbolic equilibria [8, 9]. Some other examples unrelated to equilibria are chaotic systems with multiscroll attractors [10,11,12], with multistability [13,14,15], with different kinds of symmetry [16,17,18] and with the algebraically simplest equations [19,20,21,22].

Chua [23] introduced the fourth circuit element, popularly known as memristors, in 1971. Memristors are considered to be highly nonlinear with nonvolatile characteristics and can be implemented with nanoscale technologies [24,25,26,27]. Memristor-based chaotic oscillators have been widely investigated in the recent years. Some examples are circuits with two HP memristors in antiparallel [28], a current feedback op-amp-based memristor oscillators [29] and a practical implementation of memristor-based chaotic circuits with off-the-shelf components [30]. Also memristor-based chaotic circuit for pseudorandom number generation has been analyzed in a cryptography application study [31].

Recently many researchers have discussed about fractional-order calculus and its applications [32,33,34]. For example, fractional-order nonlinear systems with different control approaches have been investigated [35,36,37], and fractional-order memristor-based no equilibrium chaotic and hyperchaotic systems are proposed [38,39,40,41].

Implementation of chaotic and hyperchaotic system using field-programmable gate arrays (FPGAs) has been widely investigated [42,43,44]. Chaotic random number generators have been implemented in FPGA for applications in image cryptography [45] or FPGA-implemented Duffing oscillator-based signal detectors has been proposed [46].

In the next section, we introduce a memcapacitor-based 3D chaotic oscillator with two unstable equilibriums. In Sect. 3, we analyze it carefully through dissipativity, equilibrium points, Lyapunov exponents (LE), Kaplan–Yorke (KY) dimension, bifurcation, and bicoherence in detail. Section 4 deals with the circuit implementation of the memcapacitor chaotic system. In Sects. 5 and 6, fractional-order form of chaotic memcapacitor system and its dynamic analysis are presented. Sections 7 and 8 illustrate a FPGA-based practical application and random number generator design with the fractional-order chaotic system. Finally, conclusions are given in Sect. 9.

2 Problem formulation

Many memcapacitor models with piecewise linear, quadric and cubic functions have been discussed in the literature [47,48,49,50]. Some interesting properties such as hidden attractors [51,52,53,54], coexistence attractors [55,56,57] and extreme multistability [58,59,60,61] were found in the memcapacitor-based chaotic oscillators.

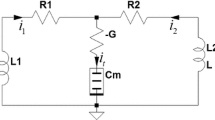
In this study, a novel memcapacitor chaotic oscillator (NMCO) with charge-controlled memcapacitor, discussed in [62], as shown in Fig. 1 is investigated.

Fig. 1
figure 1

Memcapacitor-based chaotic oscillator

Full size image
Fig. 2
figure 2

a \(x-y\) plane, b \(x-z\) plane and c \(y-z\) plane phase portraits of system (3) when \(a_{1} = 1.638\), \(a_2 = -\,0.963\), \(a_3 = 4.5\), \(a_4 = 0.7\), \(a_5 = -\,0.4\) and \(a_6 = -\,1.75\)

Full size image

In Fig. 1 R, L, G and C represent resistance, inductances, conductance and capacitance, respectively. \(C_{m} \)is the memcapacitor as discussed in [62, 63]. The current flowing through the circuit is \(i_G,i_R,i_{C_m},i_L\) applying Kirchhoff’s law to the circuit shown in Fig. 1,

$$\begin{aligned} {\begin{array}{l} {\frac{\mathrm{d}q_{C_m } }{\mathrm{d}t}=\frac{V_C }{R}+\left( {G-\frac{1}{R}} \right) V_{C_m } } \\ {C\frac{\mathrm{d}V_C }{\mathrm{d}t}=\frac{(V_{C_m } -V_C )}{R}-i_L } \\ {L\frac{\mathrm{d}i_L }{\mathrm{d}t}=V_C } \\ \end{array} } \end{aligned}$$
(1)

where \(q_{C_m}\) represents the memcapacitor charge, and \(V_{C}\) and \(V_{Cm}\) represent voltage across capacitor and memcapacitor, respectively. Voltage of a charge-controlled memcapacitor can be written as:

$$\begin{aligned} {\begin{array}{l} {V_{C_m } =(\alpha -\beta \sigma )q_{C_m } } \\ \end{array} } \end{aligned}$$
(2)

where \(\alpha \) and \(\beta \) are memcapacitor parameters such that \(\alpha -\beta \sigma \) is the inverse of memcapacitance (\(C_m^{-1}\)) and \(\sigma =\sigma _0 +\int _t^\smallint {t}_0 (t)\mathrm{d}t\). If Eq. (2) is substituted into Eq. (1), it can be seen that Eq. (1) has four state variables namely: \(q_{C_m},V_C,\sigma \) and \(i_L\). If the initial value of \(\sigma \) is taken very small (i.e., close to zero), then \(\sigma \approx \int _{t_0}^{t}q_{cm}(t)\mathrm{d}t\). By taking time integral of Eq. (1), the number of state variable can be reduced to three. The time integral of Eq. (1) is

$$\begin{aligned} {\begin{array}{l} {\frac{\mathrm{d}\sigma }{\mathrm{d}t}=\frac{\varphi _C }{R}+\left( {G-\frac{1}{R}} \right) \varphi _{C_m } } \\ {C\frac{\mathrm{d}\varphi _C }{\mathrm{d}t}=\frac{\left( {\varphi _{C_m } -\varphi _C } \right) }{R}-q_L } \\ {L\frac{\mathrm{d}q_L }{\mathrm{d}t}=\varphi _C } \\ \end{array} } \end{aligned}$$
(3)

where \(\sigma \approx \int _{t_0}^{t}q_{cm}(t)\mathrm{d}t\), \(\varphi _{c} =\int v_{c}(t)\mathrm{d}t\), \(\varphi c_m =\int v_{m}(t)\mathrm{d}t\) and \(q_L =\int \imath _{L} (t)\mathrm{d}t\).

The time integral of memcapacitor voltage can be written as:

$$\begin{aligned} \varphi {{c}_{m}} =\int v {{c}_{m}}(t)\mathrm{d}t=\alpha \sigma -\frac{1}{2}\beta \sigma ^{2} \end{aligned}$$
(4)

By substituting time integral of memcapacitor voltage given in Eq. (4) into Eq. (3), the following equation system is obtained

$$\begin{aligned} {\begin{array}{l} {\frac{\mathrm{d}\sigma }{\mathrm{d}t}=\frac{\varphi _C }{R}+\left( {G-\frac{1}{R}} \right) (\alpha \sigma -\frac{1}{2}\beta \sigma ^{2})} \\ {C\frac{\mathrm{d}\varphi _C }{\mathrm{d}t}=\frac{\left( {\alpha \sigma -\frac{1}{2}\beta \sigma ^{2}-\varphi _C } \right) }{R}-q_L } \\ {L\frac{\mathrm{d}q_L }{\mathrm{d}t}=\varphi _C } \\ \end{array} } \end{aligned}$$
(5)

The state variables of Eq. (5) are \(\sigma ,\varphi _C\) and \(q_L \). Let us define new state variables as \(x=\sigma ,y=\varphi _c \) and \(z=-Rq_L \) and let us define \(\tau =\frac{t}{RC}\).

$$\begin{aligned} \frac{\mathrm{d}x}{\mathrm{d}\tau }= & {} a_1 x+a_2 x^{2}+a_3 y \nonumber \\ \frac{\mathrm{d}y}{\mathrm{d}\tau }= & {} a_4 x+a_5 x^{2}-y+z \nonumber \\ \frac{\mathrm{d}z}{\mathrm{d}\tau }= & {} a_6 y \end{aligned}$$
(6)

where the parameters are defined as \(a_1 =C\alpha (RG-1),a_2 =-\frac{C\beta }{2}(RG-1),a_3 =C,a_4 =\alpha ,a_5=-\frac{\beta }{2},a_6 =-\frac{R^{2}C}{L}\) and for the values of \(L=0.13H,C=3.57F,G=2.1,?R=211\Omega ,\alpha =0.7F^{-1}\) and \(\beta =0.8F^{-1}c^{-1}s^{-1}\), and the NMCO system shows chaotic oscillations and the corresponding parameter values are derived as, \(a_1 =1.638,a_2 =-\,0.936,a_3 =4.5,a_4 =0.7,a_5 =-\,0.4\) and \(a_6 =-\,1.75\). The initial conditions are chosen as [0.001, 0.001, 0.001]. Figure 2 shows the 2D phase portraits of system (6).

3 Dynamic analysis of hyperchaotic memcapacitor oscillator (NMCO)

The dynamic properties of the NMCO system namely dissipativity, equilibrium points, eigenvalues, Lyapunov exponents (LE) and Kaplan–Yorke (KY) dimension are derived and discussed in this section.

3.1 Dissipativity, equilibrium points, Lyapunov exponents and Kaplan–Yorke dimension

The divergence of Eq. (3) is

$$\begin{aligned} \frac{\partial {{x}}}{\partial x}+\frac{\partial {{y}}}{\partial y}+\frac{\partial {{z}}}{\partial z}=a_1 +2a_2 x-1 \end{aligned}$$
(7)

This shows that it is dissipative if \({<}x{>}\) be smaller than \(\frac{1-a_1 }{2a_2 }\), where \({<}x{>}\) represents the arithmetic average of x. Hence, the system volume is going to be reduced to zero, and the NMCO system (3) converges to a strange attractor of the system asymptotically. By equating\({{X}}=0\), the NMCO system (3) shows two equilibrium points \(E_1 =[0,0,0]\) and \(E_2 =[-a_1 /a_2,0,0]\). By calculating the characteristic equation of the system, it can be seen that both equilibria are unstable. The Jacobian method is employed in calculation of the LEs of the NMCO system. The numerical value of LEs of the NMCO system are

$$\begin{aligned} L_{1} = 0.105, L_{2} = 0, L_{3} = -\,2.1734 \end{aligned}$$
(8)

Since there is a positive LE in (5), the NMCO system (3) has chaotic solutions. The sum of LEs of the NMCO system (3) is given below which is negative.

$$\begin{aligned} L_{1} + L_2 + L_3 = -\,2.065<0 \end{aligned}$$
(9)

The dissipativity of the NMCO system (3) can be shown with Eq. (6). The KY dimension of the NMCO system (3) is

$$\begin{aligned} D_{KY} =2+\frac{L_1 +L_2 }{|L_3 |}=2.048, \end{aligned}$$
(10)

which is fractional.

3.2 Bifurcation

To understand the parameter dependence of the NMCO system, we derive and investigate the bifurcation plots. By changing all of its six parameters, this NMCO system exhibits a familiar period doubling to enter chaos. However, for simplicity, only bifurcation diagram and Lyapunov exponents diagram with changing parameter \(a_1\) are shown in Fig. 3.

Fig. 3
figure 3

a Bifurcation diagram of system (3) with respect to parameter \(a_1\) (\(y_{\mathrm{max}}\) are the local maxima of y signal and the initial values are (0.1, 0.1, 0.1)) and b Lyapunov exponents of system (3) with respect to parameter \(a_1\). The rest of the parameters are \(a_2= -\,0.963\), \(a_3 = 4.5\), \(a_4 = 0.7\), \(a_5 = -\,0.\)4 and \(a_6 = -\,1.75\)

Full size image
Fig. 4
figure 4

Bicoherence plot of NMCO system for state x with sampling frequency of 1.5 KHz

Full size image

3.3 Bicoherence

Higher-order spectra have been used to study the nonlinear interactions between frequency modes [64, 65]. Let x(t) be a stationary random process defined as,

$$\begin{aligned} x(t)=\sum _{n=1}^{N}{A_n} e^{j\omega _n t}+A_n^*e^{-j\omega _n t} \end{aligned}$$
(11)

where w is the angular frequency, n is the frequency modal index and \(A_n \) are the complex Fourier coefficients. The power spectrum can be defined as,

$$\begin{aligned} P(\omega _k )=E[A_{\omega _k } A_{\omega _k }^*] \end{aligned}$$
(12)

and discrete bispectrum can be defined as,

$$\begin{aligned} B(\omega _k,\omega _j )=E[A_{\omega _k } A_{\omega _j } A_{\omega _k +\omega _j }^*] \end{aligned}$$
(13)

If the modes are independent, then the average triple products of Fourier components is zero resulting in a zero bispectrum [64]. The study of bicoherence is to give an indication of the relative degree of phase coupling between triads of frequency components. There are two main reasons to employ bicoherence analysis. The first one is obtaining information about deviations due to Gaussianity and suppressing colored Gaussian noise. The second one is that signals with asymmetric nonlinearities can be detected and identified with bicoherence analysis. It is a third-order spectrum as it can be seen in Eq. (10), while as it can be seen in Eq. (9) power spectrum is a second order. Power spectrum and bispectrum can be defined as \({X}'\left( f \right) *X\left( f \right) \) and \(X\left( {f_j } \right) *X\left( {f_k } \right) *{X}'\left( {f_j +f_k } \right) \), respectively, where \(X\left( f \right) \) represents Fourier transform of x(t) and \({X}'\left( f \right) \) represents Fourier transform of conjugate of x(t). It can be understood that the bispectrum is a complex function of two frequencies \((f_j,f_k )\). Bicoherence is square of amplitude. To calculate the bispectrum, the time series are divided into M parts and each part has length of N. Then, their Fourier transforms and biperiodogram are calculated. Finally, they are averaged over all segments. Although the inputs of bicoherence functions are two different frequencies and their summation, the output of the function is one-dimensional. Hence, bicoherence can be considered as a function of sum of two frequencies. Pezeshki [66] gives autobispectrum of a chaotic system. Autobispectrum is calculated from the Fourier coefficients.

$$\begin{aligned} B(\omega _1,\omega _2 )=E[A(\omega _1 )A(\omega _2 )A^{*}(\omega _1 +\omega _2 )] \end{aligned}$$
(14)

where \(w_n \) is the radian frequency and A is the Fourier coefficients. The square of bicoherence can be written as

$$\begin{aligned} b(\omega _1,\omega _2 )=\left| {B(\omega _1,\omega _2 )} \right| ^{2}/P(\omega _1)P(\omega _2)P(\omega _1 +\omega _2 )\nonumber \\ \end{aligned}$$
(15)

where \(P(\omega _1)\) and \(P(\omega _2)\) are the power spectrums at \(f_1 \) and \(f_2 \).

Figures 4 and 5 show the bicoherence contours of the FONMCO system for state x and all states together, respectively. Yellow-colored parts show the multifrequency components contributing to the power spectrum. As it is shown in Figs. 4 and 5, the cross-bicoherence is nonzero and non-constant; hence, the state relationship is nonlinear. As shown in Fig. 4, the spectral power is very low as compared to the spectral power of all states together (Fig. 5) indicating the existence of multifrequency nodes. Also Fig. 5 shows the nonlinear coupling (straight lines connecting multiple frequency terms) between the states. The yellow shades/lines and non-sharpness of the peaks and the structure around the origin in figures indicate that the nonlinear relation of the states x, y, z is not of the quadratic nonlinearity. The most two dominant frequencies (\(f_1\), \(f_2\)) are selected to obtain bicoherence contour. As a reference frequency, the sampling frequency (\(f_s\)) is selected. To derive the power spectrum for individual frequencies, direct FFT is used and Hankel operator is used as the frequency mask. Hanning window is used as the FIR filter to separate the frequencies [40].

Fig. 5
figure 5

Bicoherence plot of NMCO system for all states with sampling frequency of 1.5 KHz

Full size image

4 Circuit implementation of the memcapacitor chaotic system

There are many works in the literature related to electronic circuit designs [67,68,69,70,71,72,73,74,75,76,77]. In this section, the circuit design of memcapacitor chaotic system (3) is differently implemented in the oscilloscope as real-time engineering application. The chaotic memcapacitor in this work has been exhibited noise-like behaviors because its signal values are very low as shown in Fig. 2. So, chaotic system are firstly scaled to increase the signal values for electronic circuit application.

For scaling process, let \(X = 5x\), \(Y = 5y\), \(Z = 5z\), and then, setting the original state variables x, y, z as X, Y, Z the scaled chaotic memcapacitor system becomes as follows.

$$\begin{aligned}&\left\{ \begin{array}{lll} {{\dot{x}}=a_1 x+a_2 x^{2}+a_3 y}&{} &{} {X=5x} \\ {{\dot{y}}=a_4 x+a_5 x^{2}-y+z}&{} \Rightarrow &{} {Y=5y} \\ {{\dot{z}}=a_6 y}&{} &{} {Z=5z} \\ \end{array}\right\} \Rightarrow \begin{array}{l} x=X/5 \\ y=Y/5 \\ z=Z/5 \\ \end{array}\end{aligned}$$
(16)
$$\begin{aligned}&X=5x,\quad Y=5y,\quad Z=5z \end{aligned}$$
(17)

Finally, scaled chaotic memcapacitor system are given by

$$\begin{aligned} {\dot{X}}= & {} a_1 X+\frac{a_2 X^{2}}{5}+a_3 Y \nonumber \\ {\dot{Y}}= & {} a_4 X+\frac{a_5 X^{2}}{5}-Y+Z \nonumber \\ {\dot{Z}}= & {} a_6 Y \end{aligned}$$
(18)

In Fig. 6 are shown the new phase portraits of scaled memcapacitor oscillator with increased amplitude values. After these processes, we can do electronic circuit design as real-time application.

Fig. 6
figure 6

2D and 3D phase portraits of the scaled memcapacitor oscillator (3): a \(x-y\), b \(x-z\), c \(y-z\), d \(x-y-z\)

Full size image

The designed electronic circuit of the scaled memcapacitor chaotic system is given in Fig. 7. The circuit consists of basic electronic components such as resistors, capacitor, op-amps and multipliers.

Fig. 7
figure 7

Electronic circuit of the scaled chaotic memcapacitor system

Full size image

\(\hbox {R}1=244~\hbox {k}\Omega \), \(\hbox {R}2=213~\hbox {k}\Omega \), \(\hbox {R}3 = 89~\hbox {k}\Omega \), \(\hbox {R}4=\hbox {R}5=100~\hbox {k}\Omega \), \(\hbox {R}6=570~\hbox {k}\Omega \), \(\hbox {R}7=500~k\Omega \), \(\hbox {R}8=\hbox {R}9=400~\hbox {k}\Omega \), \(\hbox {R}10=\hbox {R}11=100~\hbox {k}\Omega \), \(\hbox {R}13=228~\hbox {k}\Omega \), \(\hbox {R}14=\hbox {R}15=100~\hbox {k}\Omega \), \(\hbox {C}1=\hbox {C}2=\hbox {C}3=1~\hbox {nF}\), \(\hbox {Vn}=-\,15~\hbox {V}\), \(\hbox {Vp}=15~\hbox {V}\) were chosen. The oscilloscope outputs of memcapacitor chaotic system are shown in Fig. 8 for \(x-y\), \(x-z\) and \(y-z\) planes.

Fig. 8
figure 8

2D phase portraits of the chaotic memcapacitor on the oscilloscope. The initial conditions and parameter values are taken as in Sect. 2: a \(x-y\), b \(x-z\), c \(y-z\)

Full size image

Also, the experimental circuit of the chaotic memcapacitor circuit is shown in electronic card in Fig. 9 for \(x-z\) plane.

Fig. 9
figure 9

Experimental circuit of the chaotic memcapacitor circuit

Full size image

5 Fractional-order NMCO system (FONMCO)

In this section, modeling of the fractional-order form of the hyperchaotic memcapacitor oscillator (FONMCO) is introduced. Grunwald–Letnikov, Riemann–Liouville and Caputo [32,33,34] are the usually employed methods for the fractional-order differential operator. In the study, Grunwald–Letnikov (GL) method is employed and given as

$$\begin{aligned} _a D_t^q f(t)= & {} \lim \limits _{h\rightarrow 0}\left\{ \frac{1}{h^{q}}\sum _{j=0}^{\left[ \frac{t-q}{h} \right] }(-1)^{j}\left( \begin{array}{l} q \\ j \\ \end{array}\right) f(t-jh) \right\} \nonumber \\= & {} \lim \limits _{h\rightarrow 0} \left\{ \frac{1}{h^{q}}\Delta _h^q f(t) \right\} \end{aligned}$$
(19)

where D refers to the fractional-order generalization, \(\Delta _h^q f(t)\) is generalized difference, h is the step size, a and t are limits, and q is the fractional order of the differential equation.

Equation (16) can be written as

$$\begin{aligned} _{(t-L)} D_t^q f(t)=\mathop {\lim }\limits _{h\rightarrow 0} \left\{ {h}^{-q}\sum _{j=0}^ {N(t)}b_{j} \left( {f(t-jh} \right) \right\} \end{aligned}$$
(20)

where \(b_{j}\) is binomial and given as

$$\begin{aligned} b_j =\left( {1-\frac{a+q}{j}} \right) b_{j-1} \end{aligned}$$
(21)

In theory, calculation of fractional-order differential equation requires use of infinite memory, but in practice, the equation given below is used for the calculation.

$$\begin{aligned} N(t)=\min \left\{ {\left[ {\frac{t}{h}} \right] ,\left[ {\frac{L}{h}} \right] } \right\} \end{aligned}$$
(22)

where L and h represents the memory length sampling time, respectively.

Using (16)–(19), the FONMCO system is derived as,

$$\begin{aligned} \frac{\mathrm{d}^{q_x}x}{\mathrm{d}t^{q_x}}= & {} a_1 x+a_2 x^{2}+a_3 y \nonumber \\ \frac{\mathrm{d}^{q_y}y}{\mathrm{d}t^{q_y}}= & {} a_4 x+a_5 x^{2}-y+z \nonumber \\ \frac{\mathrm{d}^{q_z}z}{\mathrm{d}t^{q_z}}= & {} a_6 y \end{aligned}$$
(23)

where \(q_x,q_y,q_z\) are the fractional orders of the FONMCO system. The 2D phase portraits of the FONMCO system is given Fig. 10. The system parameters and the initial values are as same as in the system discussed in Sect. 2.

Fig. 10
figure 10

2D phase portraits of the FONMCO system, \(q=0.992\)

Full size image

6 Dynamic analysis of the FONMCO chaotic systems

6.1 Bifurcation with fractional order

Some of the FONMCO system dynamic properties such as LEs and bifurcation remain similar to the that of the NMCO chaotic systems [38, 39] if \(q_x,q_y,q_z >0.983\). For a fractional-order system, investigation of bifurcation with fractional order is very important. As shown in Fig. 11, bifurcation of the FONMCO system for change in fractional order shows that the systems’ chaotic oscillations remain if \(q_i >0.983\) and when \(q=0.992\) the largest positive Lyapunov exponent is \(L_1 =0.118\), while for the integer-order case the largest Lyapunov exponent is \(L_1 =0.105\). Figure 12a–f shows the 2D phase portraits in \(X-Y\) plane for different fractional orders.

Fig. 11
figure 11

Fractional-order bifurcation plot

Full size image
Fig. 12
figure 12

2D phase portrait (\(X-Y\) plane) of FONMCO system for different fractional orders a \(q= 0.999\), b \(q=0.995\), c \(q=0.992\), d \(q=0.990\), e \(q=0.985\), f \(q=0.983\)

Full size image

6.2 Stability analysis

6.2.1 Commensurate order

For a q-order commensurate FONMCO system, the system shows chaotic oscillations if

$$\begin{aligned} \left| {\arg (\hbox {eig}(J_E ))} \right| =\left| {\arg (\lambda _i )} \right| >\frac{q\pi }{2} \end{aligned}$$

where \(J_E\) is the Jacobian matrix at the equilibrium E and \(\lambda _i\) are the eigenvalues of the FONMCO system for \(i=1,2,3\). The eigenvalues must be in the unstable region and stability condition for the FONMCO system is \(q>\frac{2}{\pi }\tan ^{-1} \left( {\frac{\left| {\mathrm {Im}}\lambda \right| }{{\mathrm {Re}}\lambda }}\right) \). The NMCO system shows two equilibrium at \(E_1 =[0,0,0]\) and \(E_2 =[-\,1.75,0,0]\), and the characteristic equation for the commensurate orders \(q=0.99\) for the equilibrium point \(E_1\) is given by \(\lambda ^{297}+3\lambda ^{199}+2.638\lambda ^{198}+3\lambda ^{101}+5.276\lambda ^{100}+0.238\lambda ^{99}+\lambda ^{3}+2.638\lambda ^{2}+0.238\lambda +2.8665\) and at \(E_2\) is \(\lambda ^{297}+3\lambda ^{199}-0.638\lambda ^{198}+3\lambda ^{101}-1.276\lambda ^{100}+3.262\lambda ^{99}+\lambda ^{3}-0.638\lambda ^{2}+3.262\lambda -2.8665\).

6.2.2 Incommensurate order

The FONMCO system shows chaotic oscillations for the given condition below.

$$\begin{aligned} \frac{\pi }{2M}-\hbox {min}_{i}\left( {\left| {\arg (\lambda i)} \right| } \right) >0 \end{aligned}$$

where M is the least common multiple (LCM) of the fractional orders. If \(q_x =0.99,q_y =0.99,q_z =0.98,q_w =0.98\), then \(M=100\). The characteristic equation of the system at the equilibriums is \(\det (\hbox {diag}[\lambda ^{Mq_x},\lambda ^{Mq_y},\lambda ^{Mq_z}]-J_E)=0\); then, we get \(\det (\hbox {diag}[\lambda ^{99},\lambda ^{99},\lambda ^{98}]-J_E )=0\) and the characteristic equation at equilibrium point \(E_1\) is \(\lambda ^{296}+\lambda ^{199}+3\lambda ^{198}+1.638\lambda ^{197}+2\lambda ^{101}+4.638\lambda ^{100}+1.876\lambda ^{99}+\lambda ^{3}+2.638\lambda ^{2}+0.238\lambda +2.8665\) and at the equilibrium point \(E_2\) is \(\lambda ^{296}+\lambda ^{199}+3\lambda ^{198}-1.638\lambda ^{197}+2\lambda ^{101}+1.362\lambda ^{100}+1.624\lambda ^{99}+\lambda ^{3}-0.638\lambda ^{2}+3.262\lambda -2.8665\). For the values of parameters mentioned in Sect. 2, the solution of the characteristic equation is approximated to \(\lambda _{296} =1.848\) and whose argument is zero and which is the minimum argument, and hence, the stability necessary condition becomes \(\frac{\pi }{200}-0>0\) which solves for \(0.0157>0\).

7 FPGA implementation of the FONMCO systems

The three main approaches to solve fractional-order chaotic systems are frequency-domain method [78], Adomian decomposition method (ADM) [79] and Adams–Bashforth–Moulton (ABM) algorithm [80]. Among these three methods, ADM is the most advantageous one for obtaining accurate results with less computational power [81, 82]. Hence, the proposed FONMCO system is implemented in FPGA by applying ADM scheme. The most challenging issue in the FPGA realization of the FONMCO system is that there is no available block for the fractional-order integrator in the system generator [39,40,41]. Because the ADM algorithm converges fast [82, 83], for obtaining FONMCO system solution the first 6 terms are taken. For real cases, it is impossible to find the accurate value of x when t takes larger values [84]. Hence, a discretization method in time is designed. That is to say, for a time interval of \(\hbox {ti}\) (initial time) to \(\hbox {tf}\) (final time), we divide the interval into (tn, tn+1) and we get the value of \(x(n + 1)\) at time \(\hbox {tn}+1\) by applying x(n) at time \(t_{n}n \) using the relation \(x(n+1)=F(x(n))\) [84]. We use the ADM method [79, 84] to discretize the fractional-order CA system for implementing in FPGA. The fractional-order discrete form of the dimensionless state equations for the FONMCO system can be given as,

$$\begin{aligned} {x}_{n+1}= & {} \sum _{j=0}^6 p_{1}^{j}\frac{h^{jq}}{\Gamma \left( {jq+1} \right) } \nonumber \\ {y}_{n+1}= & {} \sum _{j=0}^6 p_{2}^{j}\frac{h^{jq}}{\Gamma \left( {jq+1} \right) }\nonumber \\ {z}_{n+1}= & {} \sum _{j=0}^6 p_{3}^{j}\frac{h^{jq}}{\Gamma \left( {jq+1} \right) } \end{aligned}$$
(24)

where \(p_i^j\) are the Adomian polynomials with \(i=1,2,3\) and \(p_1^0 =x_n,p_2^0 =y_n,p_3^0 =z_n\). The Adomian first polynomial is derived as,

$$\begin{aligned} {p}_1^1= & {} a_1 p_1^0 +a_2 p_1^0 p_1^0 +a_3 p_{2^0 } \nonumber \\ {p}_2^1= & {} a_4 p_1^0 +a_5 p_1^0 p_1^0 -p_2^0 +p_{3^0 } \nonumber \\ {p}_3^1= & {} a_6 p_{2^0 } \end{aligned}$$
(25)

The Adomian second polynomial is derived as,

$$\begin{aligned} {p}_1^2= & {} a_1 p_1^1 +a_2 \left[ {p}_1^0 p_1^1 +p_1^1 p_{1^0 } \right] +a_3 p_{2^1 }\nonumber \\ {p}_2^2= & {} a_4 p_1^1 +a_5 \left[ {p}_1^0 p_1^1 +p_1^1 p_{1^0 } \right] -p_2^1 +p_{3^1 } \nonumber \\ {p}_3^2= & {} a_6 +p_{2^1 } \end{aligned}$$
(26)

The Adomian third polynomial is derived as,

Fig. 13
figure 13

RTL schematics of the FONMCO system implemented in Kintex 7 (\(\hbox {Device}=7k160t~\hbox {Package}=\hbox {fbg}484\) S). The sampling time of the system is kept at 0.01 s to minimize the time slack errors. The entire system is configured for a 32-bit operation

Full size image
$$\begin{aligned} {p}_1^3= & {} a_1 p_1^2+a_2 \left[ p_1^0 p_1^2+p_1^2 p_1^0 \nonumber \right. \\&\left. +\frac{\Gamma (2q+1)}{\Gamma ^{2}(q+1)}\left[ {p_1^1 p_1^1 +p_1^1 p_1^1 } \right] \right] +a_3 p_{2^2 } \nonumber \\ {p}_2^3= & {} a_4 p_1^2 +a_5 \left[ p_1^0 p_1^2+p_1^2 p_1^0 \nonumber \right. \\&\left. +\frac{\Gamma (2q+1)}{\Gamma ^{2}(q+1)}\left[ {p_1^1 p_1^1 +p_1^1 p_1^1 } \right] \right] -p_2^2 +p_{3^2 } \nonumber \\ {p}_3^3= & {} a_6 p_{2^2 } \end{aligned}$$
(27)

The Adomian fourth polynomial is derived as,

$$\begin{aligned} {p}_1^4= & {} a_1 p_1^3 +a_2 \left[ {p}_1^0 p_1^3 +p_1^3 p_1^0 \right. \nonumber \\&\left. +\frac{\Gamma (3q+1)}{\Gamma (q+1)\Gamma (2q+1)}\left[ {p}_1^2 p_1^1 +p_1^2 p_{1^1 } \right] \right] \nonumber \\ p_2^4= & {} a_4 p_{1}^{3} +a_5 \left[ p_1^0 p_1^3 +p_1^3 p_1^0\right. \nonumber \\&\left. +\frac{\Gamma (3q+1)}{\Gamma (q+1)\Gamma (2q+1)}\left[ {p}_1^2 p_1^1 +p_1^2 p_{1^1 } \right] \right] \nonumber \\&-~p_2^3 +p_{3^3 } \nonumber \\ {p}_3^4= & {} a_6 p_{2^3 } \end{aligned}$$
(28)

The Adomian fifth polynomial is derived as,

$$\begin{aligned} p_1^5= & {} a_1 p_1^4 +a_2 \left[ {p}_1^4 p_1^0 +p_1^0 p_1^4\right. \nonumber \\&\left. +\frac{\Gamma (4q+1)}{\Gamma (q+1)\Gamma (3q+1)}\left[ {p}_1^3 p_1^1 +p_1^1 p_{1^3 } \right] \right] \nonumber \\&+~a_3 p_{2^4 }\nonumber \\ p_2^5= & {} a_4 p_1^4 +a_5 \left[ p_1^4 p_1^0 +p_1^0 p_1^4 \right. \nonumber \\&\left. +\frac{\Gamma (4q+1)}{\Gamma (q+1)\Gamma (3q+1)}\left[ p_1^3 p_1^1 +p_1^1 p_{1^3 } \right] \right] \nonumber \\&-p_2^4 +p_3^4 \nonumber \\ p_3^5= & {} a_6 p_2^4 \end{aligned}$$
(29)

The Adomian sixth polynomial is derived as,

$$\begin{aligned} {p}_1^6= & {} a_1 p_1^5 +a_2 \left[ p_1^5 p_1^0 +p_1^0 p_1^5\right. \nonumber \\&\left. +\frac{\Gamma (5q+1)}{\Gamma (q+1)\Gamma (4q+1)}\left[ {p_1^4 p_1^1 +p_1^1 p_1^4 } \right] \right] \nonumber \\&+~a_3 p_{2^5 } \nonumber \\ {p}_2^6= & {} a_4 p_1^5 +a_5 \left[ p_1^5 p_1^0 +p_1^0 p_1^5\right. \nonumber \\&\left. +\frac{\Gamma (5q+1)}{\Gamma (q+1)\Gamma (4q+1)}\left[ {p_1^4 p_1^1+p_1^1 p_1^4 } \right] \right] \nonumber \\&-~p_2^5 +p_{3^5 } \nonumber \\ {p}_3^6= & {} a_6 p_{2^5 } \end{aligned}$$
(30)

where \(h =t n+1 - t n \) and \(\Gamma (\dot{)}\) is the gamma function. The fractional-order discretized system (21) is then implemented in FPGA, and the necessary Adomian polynomials are calculated using (22)–(27). For implementing in FPGA, the value of h is taken as 0.001 s and the initial values are fed into the forward register with fractional order \(q=0.992\) for FONMCO system. Figure 13 shows the RTL schematics of the FONMCO system implemented in Kintex 7. Figure 14a shows the power consumed by FONMCO system for order \(q=0.992\), and Fig. 14b shows the power consumed for various fractional orders and it can be seen that maximum power is consumed when the FONMCO system exhibits the largest Lyapunov exponent. Table 1 shows the resources consumed with the consumed clock frequencies, and Fig. 15 shows the 2D phase portraits of the FPGA-implemented FONMCO system.

Fig. 14
figure 14

a Power consumed by FONMCO system for \(q=0.998\), b power consumed by FONMCO system for various fractional orders. It can be seen that maximum power of 0.204 W is consumed for order \(q=0.998\) when the FONMCO system shows the largest Lyapunov exponents

Full size image
Table 1 Resource consumption of FPGA-implemented FONMCO system
Full size table
Fig. 15
figure 15

2D phase portraits of the FPGA-implemented FONMCO system. The initial conditions and parameter values are taken as in Sect. 2, and the order of the system is \(q=0.992\); a X–Y plane, b X–Z plane, c Y–Z plane

Full size image
Table 2 NIST-800-22 test results of 3D memcapacitor chaotic system-based RNG
Full size table

8 Random number generator with FONMCO system

Random numbers are used in many areas, e.g., video games, encryption, drawing of lots and weather forecast simulations [85,86,87]. In the literature, jitter [88], metastable [89] and chaotic systems [70, 72, 76, 90,91,92,93,94,95] are also used as a source of entropy. In the paper, a design of random number generator (RNG) is realized with FONMCO whose entropy source is a chaotic system. The chaotic system used in the paper is fractional order and to the best knowledge of authors there is no this type of study in the literature. The fractional-order chaotic system used in random number generation is as follows.

$$\begin{aligned} \frac{{\mathrm{d}}^{q_{x}}x}{{\mathrm{d}t}^{q_x }}= & {} a_1 x+a_2 x^{2}+{a}_3 y \nonumber \\ \frac{{\mathrm{d}}^{q_{y}}y}{{\mathrm{d}t}^{q_y }}= & {} a_4 x+a_5 x^{2}-{y+z} \nonumber \\ \frac{{\mathrm{d}}^{q_{z}}z}{{\mathrm{d}t}^{q_z }}= & {} a_{6 y} \end{aligned}$$
(31)

\(q_{x},q_{y}\) and \(q_{z}\) values are fractional order of the system and all of these values are taken as 0.992. The phase portraits of the system are shown in Fig. 10. The both parameter values and initial conditions of the system are as same as in the non-fractional-order memcapacitor system.

Random number generator design steps with fractional-order chaotic system are as given in Algorithm 1. As it is given in the algorithm, for random number generation, order of the chaotic system and its parameter and initial values are needed. Any change in these parameters will result in generation of different random numbers. The addition of fractional order to the random number generation is an important factor for security. If the generated random numbers are used in encryption, the fractional order of the chaotic system has to be known exactly to regenerate the same random numbers. As a next step, after entering initial and parameter values, time step is determined in order to discretize time series of the fractional-order chaotic system and then discretized with RK4 which is differential equation solving method.

After the discretization process, the obtained floating-based x, y and z outputs is converted into 32-bit binary number; hence, random number generation process is realized. For the random number generation, the last 16 bits of output x, the last 12 bits of output y and the last 16 bits of output z are taken.

To evaluate the performance of the generated number series, NIST-800-22 tests [96] are employed. The NIST test is the most widely used test to evaluate randomness of the number series. In order to be considered successful in passing the NIST-800-22 tests, the P value must be greater than 0.001 for the all tests. The NIST-800-22 tests results of generated numbers from x, y and z outputs are given in Table 2.

figure a

9 Conclusions

A memcapacitor chaotic oscillator with two unstable equilibrium points is proposed and investigated. Dynamic properties of the proposed system are investigated. The fractional-order model of the proposed chaotic oscillator is derived and analyzed. The largest Lyapunov exponent of the system is found to exist in the fractional order. Adomian decomposition method is used to discretize the fractional-order system for implementing in FPGA. The fractional-order FPGA-implemented chaotic oscillator is investigated, and the power consumption analysis confirms the existence of the systems’ largest Lyapunov exponent in its fractional order.