Complex dynamics of a non-volatile memcapacitor-aided hyperchaotic oscillator

Abstract

To explore memcapacitors and their characteristics in chaotic oscillators, this paper proposes a logarithmic charge-controlled memcapacitor model. Using power-off plot analysis, we show that the memcapacitor possesses continuous non-volatile characteristic. Also, its dynamic route map shows the memcapacitor can rapidly switch from one memcapacitance to another by applying a single voltage pulse. Based on the memcapacitor model, we design a chaotic oscillator, which can exhibit some complex dynamic characteristics, such as chaos, hyperchaos and various coexisting attractors. The multistable coexisting oscillation of the system is further analyzed by using phase portraits, basins of attraction and double-bifurcation diagrams. Symmetric coexistence attractors with infinite homogeneity and heterogeneity are also found, which can evolve into hyperchaos under certain initial conditions. Finally, the chaotic oscillator is verified by numerical simulations and digital signal processor experiments.

1 Introduction

In 1971, Professor Chua proposed the definition of the fourth circuit element, memristor, and in 1976, the concept of the memristive system. Until 2008, the physical implementation of a $\mathrm{TiO}_2$ memristor was firstly reported by HP Labs in Nature. On November 2008, at the International Symposium on Memristors and Memristor Systems held at the University of California at Berkeley, the memcapacitor was defined, and it was pointed out that a memcapacitor lost less data in data reading, writing and storage than a memristor. In 2009, the definitions of memristive systems are extended to the memcapacitor and meminductor, namely a memcapacitor and a meminductor whose memcapacitance and meminductance depend on the state and history of the system. A memcapacitor is actually a nonlinear capacitor whose capacitance depends on its internal state and the input signal. The basic characteristic of a memcapacitor is its non-volatility of memcapacitance, which has great potential in information storage, multiharmonic oscillation, chaotic oscillation and secure communications and so on [1].

Memristors can be used in non-volatile memories, logical circuits, neural networks, chaotic circuits and other fields [2,3,4,5]. The preliminary commercialization of memristors has been realized in 2018 [6], which is of practical significance for the realization and application of new memory components. Under the background that memcapacitors have not been commercialized yet, there is an interest in researching the modeling, characteristics and potential applications of memcapacitors.

It is of theoretical and engineering significance to study the non-volatile characteristics of memcapacitors and their state transition rules. It is also of practical value to explore the characteristics of memcapacitors and their complex behavior in chaotic nonlinear circuits. Compared with memristors, the research on the memcapacitor-based chaotic oscillators is relatively less. In 2016, Ref. [7] proposed a smooth curve-type memcapacitor model and applied it to a chaotic oscillation circuit that was simulated through DSP (digital signal process). In 2018, Ref. [8] introduced a memcapacitor simulator into a multivibrator circuit and proposed a flux-controlled coupled double memcapacitor analog circuit. In addition, the mathematical relationship between its memcapacitance and flux was established theoretically. Karthikeyan et al. proposed a hyperchaotic oscillator based on a charge-controlled memcapacitor and carried out a detailed dynamic analysis, which was verified by FPGA (field-programmable gate array) simulations [9].

Multistability is an intrinsic property of many nonlinear dynamical systems, which reveal the abundant dynamic characteristics of the system, and has attracted much attention in recent years. Specifically, when the parameters of the system are the same, but the initial conditions are different, if the system has several different attractors, the system can be said to have multistability [10], which can be widely used for many information engineering. For example, an improved Chua’s circuit with double stable node-foci is proposed in Ref. [11] and the multistability of this system is analyzed. Ref. [12] proposed a simple chaotic circuit that only contains three memory devices in parallel: a memristor, a memcapacitor and a meminductor. Its complex dynamics, especially multistability, was further observed and investigated. An active BPF-based memristive circuit was established in Ref. [13], and the flux-charge analysis method was used to control the extreme multistability of this circuit in the flux-charge domain.

Most of the existing memcapacitor models are only concerned with the nonlinear constitutive relation ${v_c}\left( t \right) = {C^{ - 1}}\left( x \right) q\left( t \right)$, and there is no attention to its essential memory characteristics and the non-volatility. In addition, the inverse memcapacitance, ${C^{ - 1}}\left( x \right)$, is generally set as the power function of $\sigma = \int {q\mathrm{d}t}$. However, recently, it is found by experiments that the internal particle motion of some memory nanodevices usually obeys the exponential (or logarithmic) laws [14].

In order to conform to the characteristics of actual memory devices, especially to reflect the non-volatility of memcapacitor, this paper proposes a mathematical model with a logarithmic function for a memcapacitor and analyzes its non-volatile characteristics. Based on this model, a hyperchaotic oscillation circuit is designed, whose multistability and complex dynamic characteristics are discovered.

The rest of this paper is organized as follows: Sect. 2 shows the logarithmic memcapacitor model and the state transition characteristics. In Sect. 3, a newly chaotic oscillator is constructed based on this memcapacitor. In Sect. 4, multistable coexisting oscillation and coexisting attractors are studies in detail. In Sect. 5, the logarithmic memcapacitor oscillator is verified by DSP experiment. At last, the main research conclusion is summarized, and a simple outlook for the future research is given.

2 A novel logarithmic memcapacitor (LMC)

2.1 LMC model

The logarithmic charge-controlled memcapacitor proposed in this paper can be described as

$$\begin{aligned} \left\{ \begin{array}{l} {v} = ( - k + \ln (m + n{\sigma ^2}))q\\ \frac{{\mathrm{d}\sigma }}{{\mathrm{d}t}} = q \end{array} \right. \end{aligned}$$

(1)

where v and q are the voltage and charge of the memcapacitor, respectively; $\sigma$ is the integral of q, that is, $\sigma =\int _{{t_0}}^t {q\left( \tau \right) \mathrm{d}} \tau$; ${C^{ - 1}} = - k + \ln \left( {m + n{\sigma ^2}} \right)$ denotes the inverse memcapacitance at time t; k, m and n are all real constants.

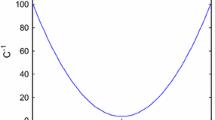
As shown in Fig. 1, the $q{-}v$ curve of the memcapacitor is a pinched hysteresis loop when a sinusoidal signal $q = Q\sin \omega t$ is applied to the memcapacitor. Observe that the area of the pinched hysteresis loops decreases monotonically as the frequency f of the input signal increases or the amplitude Q decreases. In addition, the shape of the pinched hysteresis loops changes as the frequency f varies and will shrink to a single valued function through the origin, as the frequency tends to infinity.

Fig. 1

Pinched hysteresis loops of LMC at $k = 0.01\,{\mathrm{V}}\,{{\mathrm{C}}^{{\mathrm{- 1}}}}$, $m = 0.3\,{\mathrm{V}}\,{{\mathrm{C}}^{{\mathrm{- 1}}}}$, $n = 1.2\,{\mathrm{V}}\,{{\mathrm{C}}^{{\mathrm{- 3}}}}\,{{\mathrm{S}}^{{\mathrm{- 2}}}}$ with a different frequency and b different amplitude

2.2 Non-volatile analyses of the memcapacitor

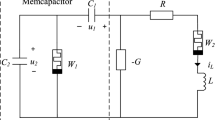
Non-volatility of the logarithmic memcapacitor is further studied by using the charge–discharge characteristic of the memcapacitor. As mentioned above, memcapacitor is a kind of nonlinear capacitor, whose memcapacitance can change with the historical values of the input state variable. The charge–discharge diagram of the memcapacitor is shown in Fig. 2. By controlling the switch K, the memcapacitor and the resistor R are connected in series when charging and in parallel when discharging, where the resistor R can be regarded as a parasitic resistor with a tiny resistance.

Fig. 2

Charge–discharge diagram of LMC

Assume that the initial values of the voltage, charge and charge integral at both ends of the memcapacitor are $v\left( {{t_0}} \right) = 0$, $q\left( {{t_0}} \right) = 0$ and $\sigma \left( {{t_0}} \right) = {\sigma _1}$ at time $t_0$, respectively. When the memcapacitor is connected to the power supply E, it will start to be charged through the series resistor R. From the KVL, the following equations can be obtained:

$$\begin{aligned} \left\{ \begin{array}{l} {{ E}} = R{i_R} + {C^{ - 1}}q\\ {i_R} = \frac{{\mathrm{d}q}}{{\mathrm{d}t}} \end{array} \right. \end{aligned}$$

(2)

where $i_R$ denotes the current flowing through the resistor R while charging. $C^{-1}$ is the inverse memcapacitance defined as

$$\begin{aligned} {C^{ - 1}} = - k + \ln \left( {m + n{\sigma ^2}} \right) \end{aligned}$$

(3)

From Eqs. (1) and (2), we can obtain:

$$\begin{aligned} \left\{ \begin{array}{l} \frac{{\mathrm{d}q}}{{\mathrm{d}t}} = \frac{1}{R}\left( {{ E} - \left( { - k + \ln \left( {m + n{\sigma ^2}} \right) } \right) q} \right) \\ \frac{{\mathrm{d}\sigma }}{{\mathrm{d}t}} = q \end{array} \right. \end{aligned}$$

(4)

If a voltage pulse with the amplitude E and width W is applied to the memcapacitor, the waveforms of voltage v, charge q and charge integral $\sigma$ can be described in Fig. 3c during the memcapacitor charging, where $R = 0.0001\,\Omega$, $k = 0.01\,{\mathrm{V}}\,{{\mathrm{C}}^{{\mathrm{- 1}}}}$, $m = 0.3\,{\mathrm{V}}\,{{\mathrm{C}}^{{\mathrm{- 1}}}}$, and $n = 1.2\,{\mathrm{V}}\,{{\mathrm{C}}^{{\mathrm{- 3}}}}\,{{\mathrm{S}}^{{\mathrm{- 2}}}}$.

Fig. 3

DRM diagram and corresponding switching process of LMC

Because of the tiny parasitic resistance, the charging time constant is very small. Consequently, when charging begins at $t_1$, v and q of the memcapacitor will rise rapidly. When the charging reaches $t_2$, the voltage v of the memcapacitor is equal to the voltage E of the power supply, and the charging stops. At this point, the circuit has no current, and the charge of the memcapacitor stabilizes at $q = q\left( {{t_1}} \right) = {q_1}$.

When $t=t_3$, the voltage pulse jumps to zero and the memcapacitor starts discharging through the resistor R in parallel. According to the KVL, we obtain:

$$\begin{aligned} R{i_R} = {C^{ - 1}}q \end{aligned}$$

(5)

Similarly, it follows from Eqs. (1) and (5) that:

$$\begin{aligned} \left\{ \begin{array}{l} \frac{{\mathrm{d}q}}{{\mathrm{d}t}} = \frac{1}{R}\left( { - k + \ln \left( {m + n{\sigma ^2}} \right) } \right) q\\ \frac{{\mathrm{d}\sigma }}{{\mathrm{d}t}} = q \end{array} \right. \end{aligned}$$

(6)

According to Eq. (6), the change process of voltage v, charge q and charge integral $\sigma$ can be obtained during the memcapacitor discharging, as shown in Fig. 3c. The memcapacitor discharges at $t = t_3$, causing a rapid drop in voltage v and charge q, which then become to zero at time $t_4$. Simultaneously, $\sigma$ increases slowly and stabilizes at $\sigma _2$.

The memcapacitance $(C(\sigma ))$ is controlled by state variable $\sigma$, which is governed by the state equation ${{\mathrm{d}\sigma } / {\mathrm{d}t}} = f\left( q \right)$. The memcapacitor is said to be non-volatile if its state variable or memcapacitance remains unchanged before and after power off. When we switch off the memcapacitor, the ${{\sigma - \mathrm{d}\sigma } / {\mathrm{d}t}}$ curve is called power-off plot (POP). A memcapacitor is non-volatile if, and only if, its POP coincides with the $\sigma$-axis.

By setting $q = 0$, the state equation of the memcapacitor can be described by

$$\begin{aligned} \frac{{\mathrm{d}\sigma }}{{\mathrm{d}t}} = q = 0 \end{aligned}$$

(7)

where ${{\mathrm{d}\sigma } / {\mathrm{d}t}}$ is identically equal zero, independent of the state variable $\sigma$. Observe from Fig. 3b that the POP coincides with the $\sigma$-axis, thereby meaning that the memcapacitor is non-volatile.

When the memcapacitor is charging, the rate of change of the state variable $\sigma$ satisfies the curve parameterized by the memristor charge q$({{\mathrm{d}\sigma } / {\mathrm{d}t}} = q)$. The set of curves corresponding to different charge is defined as dynamical route map (DRM). The DRM of the memcapacitor is shown in Fig. 3b, for five dynamic routes, each parameterized by a value of the memcapacitor charge q. Furthermore, DRM reflects the change tendency of the state variable $\sigma$ on different charges and has non-backtracking property. That is, if a dynamic route is located in the upper (resp., lower) half plane, where ${{\mathrm{d}\sigma } /{\mathrm{d}t}} > 0$ (resp., ${{\mathrm{d}\sigma } /{\mathrm{d}t}} < 0$), the state variable $\sigma$ must move to the right (resp., left) with a rate of ${{\mathrm{d}\sigma } / {\mathrm{d}t}} = q$.

According to the above analysis, it can be found that when the pulse voltage E is applied to the memcapacitor at $t_1$, the charge rises rapidly from zero to $q_1$ at $t_2$. Synchronously, the $\sigma$ of the memcapacitor jumps rapidly from point A on POP to point B on DRM and then moves to the right at the rate of ${{\mathrm{d}\sigma } /{\mathrm{d}t}} = {q_1}$. Until $t_3$, the pulse voltage E jumps to zero, and the memcapacitor is cut off and then discharged through the resistor R. At this point, the charge drops rapidly and became zero at $t_4$. Simultaneously, the $\sigma$ jumps rapidly from point C on DRM to point D on POP and stays in point D, remaining its state values at $\sigma (D)$. Figure 3c shows the change processes of the state variable $\sigma$ and corresponding memcapacitance.

In summary, regardless of the charge values of the memcapacitor when power-off, the state variable $\sigma$ of the memcapacitor can always memory the state before power-off, which proves that the memcapacitor is non-volatile.

3 Hyperchaotic logarithmic memcapacitor oscillator (HLMCO)

3.1 HLMCO and its typical attractors

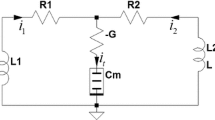
Based on the proposed memcapacitor described by Eq. (1), a HLMCO is designed as shown in Fig. 4, which consists of an inductance (L), a capacitance ($C_2$), two conductance ($G_0$ and $G_1$) and a memcapacitance ($C_\mathrm{M}$).

Fig. 4

Hyperchaotic logarithmic memcapacitor oscillator (HLMCO)

According to Kirchhoff’s laws and volt–ampere relationship between components shown in Fig. 4, the following differential equations can be obtained:

$$\begin{aligned} \left\{ \begin{array}{l} \frac{{\mathrm{d}{i_L}}}{{\mathrm{d}t}} = \frac{1}{L}{v_{C2}}\\ \frac{{\mathrm{d}{v_{C2}}}}{{\mathrm{d}t}} = \frac{{{G_1}}}{{{C_2}}}\left( {v - {v_{C2}}} \right) - \frac{1}{{{C_2}}}{i_L}\\ \frac{{\mathrm{d}q}}{{\mathrm{d}t}} = {G_1}\left( {{v_{C2}} - v} \right) + {G_0}v\\ \frac{{\mathrm{d}\sigma }}{{\mathrm{d}t}} = q \end{array} \right. \end{aligned}$$

(8)

where $v = \left( { - k + \ln \left( {m + n{\sigma ^2}} \right) } \right) q$; k, m and n are all real constants.

With suitable parameters and initial values, the system will exhibit chaotic or hyperchaotic characteristics. For example, when $k =0.01\,{\mathrm{V}}\,{{\mathrm{C}}^{{\mathrm{- 1}}}}$, $m = 0.3\,{\mathrm{V}}\,{{\mathrm{C}}^{{\mathrm{- 1}}}}$, $n = 1.2\,{\mathrm{V}}\,{{\mathrm{C}}^{{\mathrm{- 3}}}}\,{{\mathrm{S}}^{{\mathrm{- 2}}}}$, $L = 0.33\,{\mathrm{mH}}$, ${G_0} = 1.17\,{\mathrm{mS}}$, ${G_1} = 2.69\,{\mathrm{mS}}$, ${C_2} = 3.2\,{\mathrm{nF}}$ and the initial values are (0, 0.01, 0, 0), the Lyapunov exponents of this HLMCO system are calculated as $\mathrm{LE1} = 0.0810$, $\mathrm{LE2} = 0$, $\mathrm{LE3} = -0.0032$, $\mathrm{LE4} = -2.2330$, with the Lyapunov dimension $D_\mathrm{L}= 2.0821$, which shows the HLMCO system is chaotic. The corresponding typical chaotic attractors can be obtained as shown in Fig. 5a–c. Figure 5d–f shows the time-domain waveforms, $i_L-v_{C2}$ plane Poincaré mapping and its three-dimensional attractor, respectively.

When $L = 0.17\,{\mathrm{mH}}$, ${G_0} = 1.12\,{\mathrm{mS}}$, ${G_1} = 2.69\,{\mathrm{mS}}$, ${C_2} = 3.8\,{\mathrm{nF}}$ and initial values (0, 0.01, 0, 0), the HLMCO system Lyapunov exponents are $\mathrm{LE1} = 0.0874$, $\mathrm{LE2} = 0.0215$, ${\mathrm{LE3}} = - 0.0027 \approx 0$, $\mathrm{LE4} = -2.2870$, with the Lyapunov dimension $D_\mathrm{L}= 3.0464$, so exhibiting a weakly hyperchaotic oscillation. The corresponding attractors, time-domain waveforms and $i_L-v_{C2}$ plane Poincaré mapping are displayed in Fig. 6.

Fig. 5

Typical chaotic attractors with its time-domain waveforms and Poincaré mapping, where $L = 0.33\,{\mathrm{mH}}$, ${G_0} = 1.17\,{\mathrm{mS}}$, ${G_1} = 2.69\,{\mathrm{mS}}$, ${C_2} = 3.2\,{\mathrm{nF}}$, and initial values (0, 0.01, 0, 0)

Fig. 6

Typical hyperchaotic attractors with its time-domain waveforms and Poincaré mapping, where $L = 0.17\,{\mathrm{mH}}$, ${G_0} = 1.12\,{\mathrm{mS}}$, ${G_1} = 2.69\,{\mathrm{mS}}$, ${C_2} = 3.8\,{\mathrm{nF}}$, and initial values (0, 0.01, 0, 0)

An appropriate set of initial values are chosen to make the system oscillate chaotically. Note that the initial values of the system should be in its attraction regions, which can include equilibrium points of the system or be close to a bifurcation point. For a fixed set of parameter values of a system, different dynamics such as chaos, limit cycles and fixed points depend on the initial values of the system variables, which is called coexisting oscillation of bifurcation without parameters.

3.2 Dissipativity and stability

The dissipativity of the HLMCO system can be described as

$$\begin{aligned} \mathrm{div}V= & {} \frac{{\partial {{\dot{i}}_L}}}{{{i_L}}} + \frac{{\partial {{\dot{v}}_{C2}}}}{{{v_{C2}}}} + \frac{{\partial \dot{q}}}{q} + \frac{{\partial {\dot{\sigma }} }}{\sigma } \nonumber \\= & {} - \frac{{{G_1}}}{{{C_2}}} + \left( {{G_1} - {G_0}} \right) \left( { - k + \ln \left( {m + n{\sigma ^2}} \right) } \right) \nonumber \\ \end{aligned}$$

(9)

When $\left( {{G_1} - {G_0}} \right) \left( {{\mathrm{- }}k + \ln \left( {m + n{\sigma ^2}} \right) } \right) - {{{G_1}} /{{C_2}}} < 0$, the system is dissipative and converges exponentially,

$$\begin{aligned} \frac{{{\mathrm{d}}V}}{{{\mathrm{d}}t}} = {e^{\left( {{G_1} - {G_0}} \right) \left( {{\mathrm{- }}k + \ln \left( {m + n{\sigma ^2}} \right) } \right) - {{{G_1}} / {{C_2}}}}} \end{aligned}$$

(10)

That is, each volume element containing the system trajectories shrinks to zero at an exponential rate $\left( {{G_1} - {G_0}} \right) \left( {{\mathrm{- }}k + \ln \left( {m + n{\sigma ^2}} \right) } \right) - {{{G_1}} / {{C_2}}}$ when $t \rightarrow \infty$. Hence, all trajectories are eventually confined to a set of zero volumes and fixed on an attractor.

Fig. 7

a Lyapunov exponent spectrum, and b bifurcation diagram with parameter $C_2$, where $L = 0.33\,{\mathrm{mH}},{G_0} = 1.17\,{\mathrm{mS}},{G_1} = 2.69\,{\mathrm{mS}}$ with initial conditions (0, 0.01, 0, 0)

When the parameters are set as in Fig. 5, i.e., $k =0.01\,{\mathrm{V}}\,{{\mathrm{C}}^{{\mathrm{- 1}}}}$, $m = 0.3\,{\mathrm{V}}\,{{\mathrm{C}}^{{\mathrm{- 1}}}}$, $n = 1.2\,{\mathrm{V}}\,{{\mathrm{C}}^{{\mathrm{- 3}}}}\,{{\mathrm{S}}^{{\mathrm{- 2}}}}$, $L = 0.33\,{\mathrm{mH}}$, ${G_0} = 1.17\,{\mathrm{mS}}$, ${G_1} = 2.69\,{\mathrm{mS}}$, ${C_2} = 3.2\,{\mathrm{nF}}$ and $\sigma _0 = 0$, the dissipativity of the HLMCO system can be obtained from Eq. (12)

$$\begin{aligned} \mathrm{div}V = \left( {2.69 - {G_0}} \right) \left( { - 0.01 + \ln 0.3} \right) - 2.69/3.2\nonumber \\ \end{aligned}$$

(11)

Since the dissipativity needs to be less than zero, the value range of parameter $G_0$ is

$$\begin{aligned} {G_0} < 3.3824 \end{aligned}$$

(12)

If the system satisfies both the dissipativity and instability conditions, chaos may occur in the system.

Next, the stability of this system is judged according to the set of its equilibrium points. Let ${\dot{i}_L} = {\dot{v}_{C2}} = \dot{q} = {\dot{\sigma }} = 0$, and the equilibrium equations can be obtained

$$\begin{aligned} \left\{ \begin{array}{l} \frac{1}{L}{v_{C2}} = 0\\ \frac{{{G_1}}}{{{C_2}}}\left( {\left( { - k + \ln \left( {m + n{\sigma ^2}} \right) } \right) q - {v_{C2}}} \right) - \frac{1}{{{C_2}}}{i_L} = 0\\ \left( {{G_0} - {G_1}} \right) \left( { - k + \ln \left( {m + n{\sigma ^2}} \right) } \right) q + {G_1}{v_{C2}} = 0\\ q = 0 \end{array} \right. \nonumber \\ \end{aligned}$$

(13)

That is, the system equilibrium can be calculated as $E = \left\{ {\left. {\left( {{i_L},{v_{C2}},q,\sigma } \right) } \right| {i_L} = } \right.$$\left. {{v_{C2}} = q = 0,\sigma \in R} \right\}$, which indicates this system has infinite numbers of equilibria. According to Routh and Hurwitz’s stability criterion, the stability of this system is discussed as follows.

The Jacobian matrix J at this equilibrium set E is

$$\begin{aligned} J = \left[ {\begin{array}{*{20}{c}} 0&{}{\frac{1}{L}}&{}0&{}0\\ { - \frac{1}{{{C_2}}}}&{}{ - \frac{{{G_1}}}{{{C_2}}}}&{}{\frac{{{G_1}}}{{{C_2}}}W\left( \sigma \right) }&{}0\\ 0&{}{{G_1}}&{}{\left( {{G_0} - {G_1}} \right) W\left( \sigma \right) }&{}0\\ 0&{}0&{}1&{}0 \end{array}} \right] \end{aligned}$$

(14)

where $W\left( \sigma \right) = - k + \ln \left( {m + n{\sigma ^2}} \right)$. The corresponding characteristic equation is

$$\begin{aligned}&{\lambda ^4} + \left[ {\frac{{{G_1}}}{{{C_2}}} - \left( {{G_0} - {G_1}} \right) W\left( \sigma \right) } \right] {\lambda ^3} \nonumber \\&\quad + \left[ {\frac{1}{{{C_2}L}} - \frac{{{G_1}{G_0}}}{{{C_2}}}W\left( \sigma \right) } \right] {\lambda ^2} \nonumber \\&\quad - \frac{{\left( {{G_0} - {G_1}} \right) W\left( \sigma \right) }}{{{C_2}L}}\lambda = 0 \end{aligned}$$

(15)

Let $a_4 = 1$, ${a_3} = {G_1}/{C_2} - \left( {{G_0} - {G_1}} \right) W\left( \sigma \right)$, ${a_2} = 1/\left( {{C_2}L} \right) - {G_1}{G_0}W\left( \sigma \right) /{C_2}$, ${a_1} = - \left( {{G_0} - {G_1}} \right) W\left( \sigma \right) /\left( {{C_2}L} \right)$, $a_0 = 0$. Stability of the system can be obtained according to the necessary conditions of Routh and Hurwitz’s stability criterion, i.e., the coefficients $a_i$ of the characteristic equation are all positive. Observe from Eq. (15) that because the coefficient $a_0$ is zero, the system is in an unstable or critical stable state at the equilibrium set E.

Fig. 8

Corresponding evolution process of the HLMCO system with changing parameter $C_2$

4 Dynamic analysis of the HLMCO

4.1 Evolution of the system under variation of parameters

With the changes of the system parameters, the stability of the system equilibrium point also switches, and so the system orbit will be in different states. If the parameters are set as $L = 0.33\,{\mathrm{mH}}$, ${G_0} = 1.17\,{\mathrm{mS}}$, ${G_1} = 2.69\,{\mathrm{mS}}$ with initial conditions (0, 0.01, 0, 0), the Lyapunov exponent spectrum of the HLMCO system can be obtained when parameter $C_2$ varies in the range of [0, 10], as shown in Fig. 7a. To make the graph more clearly, the fourth Lyapunov exponential curve is not drawn (always less than zero). Figure 7b shows the corresponding bifurcation diagram of the state variable $i_L$ varying with parameter $C_2$.

Fig. 9

Dynamic map with parameters $C_2$ and L, where ${G_0} = 1.17\,{\mathrm{mS}},{G_1} = 2.69\,{\mathrm{mS}}$ with initial conditions (0, 0.01, 0, 0)

Observe from Fig. 7 that the system transforms from the stable points to period doubling bifurcation within ${C_2} \in \left[ {0,1.38} \right]$. Then, at ${C_2} = 1.39\,{\mathrm{nF}}$, the system enters a chaotic state and switches between chaotic and hyperchaotic state. Moreover, the system exhibits a distinct ‘period-three window’ when ${C_2} \in \left[ {3.9,4.55} \right]$. Under the influence of parameter $C_2$, the evolutionary process of the HLMCO system is shown in Fig. 8, which also shows the variation of scroll attractors. That is, the attractor of the system will evolve from the upper single-scroll to the lower single-scroll through some double-scroll, and then back to the double-scroll finally with changing $C_2$.

Next, we change both $C_2$ and L in order to further observe how the dynamic characteristics change with these two parameters. The evolution process of the system can be intuitively observed by the corresponding dynamic map. Fixing the parameters as ${G_0} = 1.17\,{\mathrm{mS}}$, ${G_1} = 2.69\,{\mathrm{mS}}$ with initial conditions (0, 0.01, 0, 0), the dynamic map is shown in Fig. 9 when simultaneously changing parameters $C_2$ and L in the range of [0, 10] and [0, 0.38], respectively. The yellow region, light-blue region and blue region denote periodic, chaotic and hyperchaotic orbit, respectively. Moreover, there is a thin red line close to the vertical axis, which indicates the system is in a stable point state.

Fig. 10

Typical attractors with parameters $C_2$ and L, where initial conditions are (0, 0.01, 0, 0)

Table 1 Corresponding parameters and states of the typical attractors shown in Fig. 10

From Fig. 9, we can obtain the evolution law of the HLMCO system under the changes of parameters $C_2$ and L. As parameter L is close to zero, the system is in a red stable point state and its corresponding attractor is shown in Fig. 10a. As parameter L varies in the range of [0, 0.1], the system keeps in the yellow periodic state, regardless of the effect with parameter $C_2$. Figure 10b shows the corresponding attractor. When parameter L changes within the interval [0.1, 0.38], parameters $C_2$ and L jointly affect the dynamic behaviors of the system, making the system switch between periodic, chaotic and hyperchaotic orbits, where the blue hyperchaotic dots scatter like snowflakes in the light-blue chaotic and yellow periodic regions. The corresponding attractors are shown in Fig. 10c, d. The parameter values of different typical attractors in Fig. 10 are shown in Table 1.

Fig. 11

Lyapunov exponent spectrum with initial value $\sigma _0$, where $L = 0.33\,{\mathrm{mH}},{C_2} = 3.2\,{\mathrm{nF}},{G_0} = 1.17\,{\mathrm{mS}},{G_1} = 2.69\,{\mathrm{mS}}$, and $\left( {{i_{L0}},{v_{C20}},{q_0}} \right) = \left( {0,0.01,0} \right)$

Fig. 12

Corresponding coexisting attractors and their evolutionary process with initial value $\sigma _0$

4.2 Multistable symmetrical coexisting oscillations with initial values

Dynamic behaviors of the HLMCO system are affected not only by the parameters but also by the initial values. Under certain parameters, different combinations of initial values will lead the system in a different state. These different attractors are called coexisting attractors, which can be classified into two categories according to whether they have the same dynamic behavior or not. That is, one is the homogeneous coexisting attractors which have different attractors but with the same dynamics. Another is heterogeneous coexisting attractors with different dynamics [15].

Fig. 13

Basin of attraction under the influence of initial values $q_0$ and $\sigma _0$, where $L = 0.33\,{\mathrm{mH}},{C_2} = 3.2\,{\mathrm{nF}},{G_0} = 1.17\,{\mathrm{mS}},{G_1} = 2.69\,{\mathrm{mS}}$, and $\left( {{i_{L0}},{v_{C20}}} \right) = \left( {0,0.01} \right)$

Fig. 14

Typical coexisting attractors in the attraction basin with respect to $q_0$ and $\sigma _0$, where $L = 0.33\,{\mathrm{mH}},{C_2} = 3.2\,{\mathrm{nF}},{G_0} = 1.17\,{\mathrm{mS}},{G_1} = 2.69\,{\mathrm{mS}}$

By setting the parameters as $L = 0.33\,{\mathrm{mH}},{C_2} = 3.2\,{\mathrm{nF}},{G_0} = 1.17\,{\mathrm{mS}},{G_1} = 2.69\,{\mathrm{mS}}$ with initial values $\left( {{i_{L0}},{v_{C20}},{q_0}} \right) = \left( {0,0.01,0} \right)$, the Lyapunov exponent spectrum is shown in Fig. 11, as changing initial value $\sigma _0$ in the range of $[-1.5, 1.5]$. For the sake of clarity, the fourth Lyapunov exponential curve is not drawn (always less than zero). Observe that with the change of initial condition $\sigma _0$, the system first enters the periodic orbit from the chaotic and hyperchaotic orbits, then returns the periodic orbit, and eventually evolves the hyperchaotic and chaotic orbit, hence showing that the system possesses coexisting attractors and multistability. The corresponding evolutionary attractors of the HLMCO system are shown in Fig. 12.

Table 2 Corresponding initial values, types and colors of coexisting attractors of Fig. 14

As illustrated in Fig. 12, the attractors of the HLMCO system under initial conditions ${\sigma _0} \ge 0$ and ${\sigma _0} < 0$ are represented in red and blue, respectively. From the red orbits in Fig. 12a–d, we can see the evolution process of the system under initial condition ${\sigma _0} \ge 0$. With $\sigma _0$ increases, the system transitions from double-scroll chaotic attractor to single stable point, then enters single-scroll chaotic attractor and finally remains in the double-scroll chaotic state. Similarly, the evolutionary process of the system in ${\sigma _0} < 0$ is shown as the blue orbits in Fig. 12a–d (and not be repeated here).

Furthermore, by combining the exponential spectrum in Fig. 11 and corresponding typical attractors in Fig. 12, it can be found that the attractors of the system will be symmetrical about the origin when initial value $\sigma _0$ is negative, that is, there are symmetrical coexisting attractors. Actually, the system will not change when the initial values transform from $\left( {{i_L},{v_C}_2,q,\sigma } \right)$ to $\left( {{i_L},{v_C}_2,q, - \sigma } \right)$, i.e., the phase space related to the state variable will be symmetric with respect to the origin. That is to say, the symmetric coexisting oscillation of the HLMCO system is caused by the symmetry of the system itself.

Fig. 15

Basin of attraction under the influence of initial values $i_{L0}$ and $\sigma _0$, where $L = 0.33\,{\mathrm{mH}},{C_2} = 3.2\,{\mathrm{nF}},{G_0} = 1.17\,{\mathrm{mS}},{G_1} = 2.69\,{\mathrm{mS}}$, and $\left( {{v_{C20}},{q_0}} \right) = \left( {0.01,0} \right)$

As mentioned above, we can find that the attraction domain of the system will change correspondingly with the convert of the initial values. When initial values $q_0$ and $\sigma _0$ are changed simultaneously, the dynamic behavior of the system can be determined by the basin of attraction. It can be visualized that the various coexisting attractors are identified with different colors in the basin of attraction, according to its gravity center and shape. Fixing the parameters as $L = 0.33\,{\mathrm{mH}},{C_2} = 4.2\,{\mathrm{nF}},{G_0} = 1.17\,{\mathrm{mS}},{G_1} = 2.69\,{\mathrm{mS}}$, and initial values $\left( {{i_{L0}},{v_C}_{20}} \right) = \left( {0,0.01} \right)$, Fig. 13 shows the basin of attraction as changing initial values $q_0$ and $\sigma _0$ in the region of $[-2, 2]$ and $[-5, 5]$, respectively.

Fig. 16

Typical attractors of the $i_{L0} - \sigma _0$ basin of attraction, where $L = 0.33\,{\mathrm{mH}},{C_2} = 3.2\,{\mathrm{nF}},{G_0} = 1.17\,{\mathrm{mS}},{G_1} = 2.69\,{\mathrm{mS}}$

Table 3 Corresponding initial values, types and colors of coexisting attractors of Fig. 16

Fig. 17

Double-bifurcation diagram and Lyapunov exponent spectrum under the co-influence of parameter $C_2$ and initial value $\sigma _0$

Fig. 18

Typical coexisting attractors varying with parameters $C_2$ and initial value $\sigma _0$, where $L = 0.33\,{\mathrm{mH}},{G_0} = 1.17\,{\mathrm{mS}},{G_1} = 2.69\,{\mathrm{mS}}$, and $\left( {{i_{L0}},{v_{C20}},{q_0}} \right) = \left( {0,0.01,0} \right)$

Observed the anti-S-shape $q_0-\sigma _0$ basin of attraction shown in Fig. 13, the HLMCO system has five coexisting attractors with different colors which in different gravity centers or shapes, in which the ivory regions indicate that the system is in a divergent state. Combining with the corresponding typical attractors in Fig. 14, we can see that the type1 and type2 attractors are a pair of symmetrical homogeneous single-scroll coexisting attractors as shown in Fig. 14a. The type3 double-scroll chaotic attractor in Fig. 14b is a combination of type1 and type2 attractors, and the three attractors are all homogeneous coexisting attractors. Moreover, the type4 and type5 attractors in Fig. 14c are a pair of symmetrically homogeneous coexisting stable points, and the corresponding waveforms of type4 attractor are shown in Fig. 14d. Table 2 lists the corresponding initial values, types and colors of these above typical attractors.

Similarly, Fig. 15 shows the S-shape ${i_{L0}} - {\sigma _0}$ basin of attraction as changing initial values $i_{L0}$ and $\sigma _0$ in the ranges of $[-3, 3]$ and $[-4, 4]$, respectively. The corresponding typical attractors are shown in Fig. 16, which indicates some changes compared with the attractors in Fig. 14. That is, the type4 and type5 attractors disappear in the S-shape basin of attraction, while type1, type2 and type3 attractors remain, and six other types of attractors appear.

As shown in Fig. 16, type6 and type7, type8 and type9 attractors are two pairs of symmetric coexistence attractors and homogeneous periodic attractors for each other. Type10 and type11 attractors are a pair of single-scroll chaotic attractors which are different from the type1 and type2 attractors. These four attractors and type3 attractor are all homogenous chaotic attractors. Moreover, the chaotic attractors and periodic attractors are heterogeneous coexisting attractors. The corresponding initial values, types and colors of the above typical attractors are listed in Table 3.

It follows from the above analysis that the HLMCO system has as many as 11 types of attractors, when changing initial values $q_0$, $i_{L0}$, and $\sigma _0$ in the scopes of $[-2, 2]$, $[-3, 3]$ and $[-4, 4]$, respectively. Furthermore, each kind of the coexisting attractors also has a different state like chaotic, periodic and other states, which indicate that the HLMCO system has infinite coexisting attractors under different initial values.

4.3 Dynamics with respect to both parameters and initial values

In this part, the dynamic characteristics of the HLMCO system are further analyzed with changing the parameter and initial value simultaneously. Fix the parameters as $L = 0.33\,{\mathrm{mH}},{G_0} = 1.17\,{\mathrm{mS}},{G_1} = 2.69\,{\mathrm{mS}}$ with initial values $\left( {{i_{L0}},{v_{C20}},{q_0}} \right) = \left( {0,0.01,0} \right)$, and the double-bifurcation diagram is shown in Fig. 17a with changing parameter $C_2$ from 0 to 8.12, where the red bifurcation diagram is at $\sigma _0 = 0.1$ and the blue one is at $\sigma _0 = -0.1$, respectively. The corresponding Lyapunov exponent spectrum with $\sigma _0 = 0.1$ and $\sigma _0 = -0.1$ is shown in Fig. 17b and c, respectively. The fourth Lyapunov exponential curves are not drawn to make the graph clearer (always less than zero). The corresponding typical coexisting attractors are shown in Fig. 18.

Table 4 Corresponding parameter settings, colors, and states of the attractors in Fig. 18

From Figs. 17 and 18, the system will be in different states under the influence of the parameter $C_2$ when the initial values and other parameters are fixed. The corresponding parameter settings, colors and states of the attractors in Fig. 18 are shown in Table 4.

Moreover, observe from Figs. 17 and 18 that the dynamic behavior of the HLMCO system changes consistently no matter $\sigma _0$ is 0.1 or -0.1. That is, the system enters chaotic and hyperchaotic states from the doubling bifurcation periodic state. More detailed, the attraction region of the system will vary according to initial value $\sigma _0$ at parameter ${C_2} \in \left[ {0,3.3} \right]$. For example, the system is in a red attractor with a upper single-scroll at $\sigma _0 = 0.1$, while it has a lower single-scroll attractor in blue at $\sigma _0 = -0.1$, as shown in Fig. 18c. When parameter $C_2$ changes in the region of [3.4, 8.12], the system is always in the double-scroll attractor state at initial value $\sigma _0 = \pm \,0.1$, and the shape of the attractor is basically the same as shown in Fig. 18f. From the above analysis, it can be proved that the HLMCO system has two independent and disconnected basins of attraction under these parameters and initial values, with the attractors in a symmetrical topological structure.

Fig. 19

Evolution of the attraction basin related to $q_0-\sigma _0$ varying with the parameter $C_2$, and corresponding coexisting attractors, where $L = 0.33\,{\mathrm{mH}},{G_0} = 1.17\,{\mathrm{mS}},{G_1} = 2.69\,{\mathrm{mS}}$ , and $\left( {{i_{L0}},{v_{C20}}} \right) = \left( {0,0.01} \right)$

Table 5 Corresponding parameters, types and colors of coexisting attractors of Fig. 19

Now, we further study the dynamic behaviors by using the evolution processes of coexisting attractors and attraction basins when parameter $C_2$ and initial conditions $q_0$, $\sigma _0$ are changed simultaneously. Figure 19 shows the evolution processes of the coexisting attractors and their attraction basins versus $q_0$, $\sigma _0$ and $C_2$. Observe that the shapes of the attraction basins are basically the same, while the color distribution varies greatly with different parameter $C_2$, indicating that the unstable regions of the HLMCO system are basically the same, while the system has unique dynamic behaviors which represented by different colors. Observe from Fig. 19 that the system will be in different states with a fixed set of parameters and different initial values. Figure 19 also shows the corresponding typical attractors. Their parameter settings, types and colors of coexisting attractors are shown in Table 5.

Likewise, when changing parameter L and initial condition $\sigma _0$ simultaneously, the inconsistent dynamics behavior of the HLMCO system can be observed more clearly. As shown in Fig. 20 with parameter L increasing in the scope of [0, 0.38], the red bifurcation is at $\sigma _0 = 0.1$ and the blue one is at $\sigma _0= -0.1$. The corresponding Lyapunov exponent spectrums with $\sigma _0 = 0.1$ and $\sigma _0 = -0.1$ are illustrated in Fig. 20b and c, respectively. For the sake of clarity, the fourth Lyapunov exponential curves are not drawn (always less than zero).

Fig. 20

Double-bifurcation diagram and Lyapunov exponent spectrums with parameter L and initial value $\sigma _0$,  where ${C_2} = 0.3\,{\mathrm{nF}},{G_0} = 1.17\,{\mathrm{mS}},{G_1} = 2.69\,{\mathrm{mS}}$, and $\left( {{i_{L0}},{v_{C20}},{q_0}} \right) = \left( {0,0.01,0} \right)$

According to the double-bifurcation diagram and Lyapunov exponent spectrum in Fig. 20, it can be concluded that the system has the same evolutionary process under the influence of parameter L whether initial value $\sigma _0 = 0.1$ or $\sigma _0 = -0.1$, i.e., the system finally enters chaos with some periodic windows from the period doubling bifurcation in general. To be more detailed, after parameter $L = 0.19$, the trajectory state of the system remains same, that is, the system is in the chaotic state at $L \in \left[ {0.191,0.255} \right] \cup \left[ {0.314,0.38} \right]$ and is in the periodic window at $L \in \left[ {0.256,0.313} \right]$. These typical attractors are presented in Fig. 21c–f. However, the evolutions of trajectories started from different initial values $\sigma _0 = 0.1$ and $\sigma _0 = -0.1$ are not synchronized at $L \in \left[ {0.141,0.19} \right]$, that is, the system with $\sigma _0 = -0.1$ has already entered the chaotic state, but the system with $\sigma _0 = 0.1$ is still in the period doubling bifurcation. This phenomenon indicates that the system is in an asymmetric situation and the corresponding typical attractors are shown in Fig. 21b. The above analysis can be further proved that the HLMCO system has two independent and disconnected attractive domain with the symmetrical topological structure under different parameters and initial values.

Fig. 21

Typical coexisting attractors under the co-influence of the parameters L and initial value $\sigma _0$

5 DSP experiment of the HLMCO system

In this section, we consider the implementation of the HLMCO system by using DSP technology. DSP is a fast processor to realize the digital signal algorithm. In order to realize the continuous chaotic system through digital devices, it is necessary to discretize the chaotic system. Here, the classical Euler algorithm is used to discretize the HLMCO system, which is achieved based on the definition of derivative, that is,

$$\begin{aligned} {f^\prime }\left( x \right) = \mathop {\lim }\limits _{\Delta t \rightarrow 0} \frac{{x\left( {{t_n} + \Delta t} \right) - x\left( {{t_n}} \right) }}{{\Delta t}} = \mathop {\lim }\limits _{\Delta t \rightarrow 0} \frac{{{x_{n + 1}} - {x_n}}}{{\Delta t}}\nonumber \\ \end{aligned}$$

(16)

Equation (16) is approximated to the following formula, while $\Delta t$ tends to zero,

$$\begin{aligned} {f^\prime }\left( x \right) \approx \frac{{{x_{n + 1}} - {x_n}}}{{\Delta t}} = \frac{{x\left( {n + 1} \right) - x\left( n \right) }}{{\Delta t}} \end{aligned}$$

(17)

Substituting Eq. (17) into Eq. (8), we can get

$$\begin{aligned} \left\{ \begin{array}{l} {i_L}\left( {n + 1} \right) = {i_L}\left( n \right) + \Delta t\left[ {\frac{1}{L}{v_{C2}}\left( n \right) } \right] \\ {v_{C2}}\left( {n + 1} \right) = {v_{C2}}\left( n \right) + \Delta t\left[ {\frac{{{G_1}}}{{{C_2}}}\left( {v\left( n \right) - {v_{C2}}\left( n \right) } \right) - \frac{1}{{{C_2}}}{i_L}\left( n \right) } \right] \\ q\left( {n + 1} \right) = q\left( n \right) + \Delta t\left[ {{G_1}\left( {{v_{C2}}\left( n \right) - v\left( n \right) } \right) + {G_0}v\left( n \right) } \right] \\ \sigma \left( {n + 1} \right) = \sigma \left( n \right) + \Delta tq\left( n \right) \end{array} \right. \nonumber \\ \end{aligned}$$

(18)

where $v\left( n \right) = \left( { - k + \ln \left( {m + n{\sigma ^2}\left( n \right) } \right) } \right) q\left( n \right)$. Equation (18) is the discretized chaotic system.

Then, the system (18) is simulated on the DSP platform, and the results are converted by D/A converter to get the analog signal which can be observed on the oscilloscope. Here, the DSP evaluation module ICETEK-VC5509A is employed in this paper. Selecting the same parameter values and initial conditions as in Fig. 5, the typical chaotic attractors can be observed in the oscilloscope as shown in Fig. 22a–c. Similarly, the hyperchaotic attractors are shown in Fig. 22d–f while selecting the same parameter values as in Fig. 6. It follows from Figs. 5, 6 and 22 that the experimental results are agreed well with the numerical simulations.

Fig. 22

Experimental results observed from the oscilloscope of the HLMCO system: a–c chaotic attractors; d–f hyperchaotic attractors

6 Conclusions

We have designed a novel logarithmic charge-controlled memcapacitor. Its continuous non-volatility and switching features have been verified theoretically by using POP and DRM, respectively. Based on the memcapacitor, we also designed a hyperchaotic oscillator, and its complex dynamics have been analyzed via coexisting bifurcation, Lyapunov exponent spectrum, dynamic map and attraction basin.

In this work, it has been found that the proposed memcapacitor has infinite stable equilibria on its POP and thus has continuous non-volatility. By applying an appropriate voltage plus to the memcapacitor, it can be quickly switched from any state to another, which can be used to imitate synaptic properties of neurons and to implement information storage and logic operations. The proposed chaotic circuit has a riddled basin, in which chaos and hyperchaos appear alternately with the changes of parameters $C_2$ and L in the intervals $0< {C_2} < 10$ and $0.1< L < 0.4$. We also proved that the circuit proposes complex multistable symmetrical coexisting oscillation and various homogeneous and heterogeneous coexisting attractors, including coexisting chaotic and hyperchaotic attractors, symmetrical coexisting chaotic attractors and periodic orbits (Type 1–Type 5) with respect to initial values $\sigma _0$ and $q_0$ over the intervals of $-5< {\sigma _0} < 5$ and $-2< {q_0} < 2$; coexisting chaotic and periodic attractors with respect to initial values ${i_{L0}}$ and $\sigma _0$ over the intervals of $-3< {i_{L0}} < 3$ and $-4< {\sigma _0} < 4$. We also proved the coexisting attractors varying with both system parameters and initial values, including coexisting bifurcations with respect to both $C_2$ and $\sigma _0$ in the range of $0< {C_2} < 8$ and the values of ${\sigma _0} = \pm \, 0.1$; riddled basins of coexisting attractors with respect to parameter $C_2$ and initial values $q_0$ and $\sigma _0$ in the range of $-2< {q_0} < 2$ and $-5< {\sigma _0} < 5$, and some typically coexisting chaotic and periodic attractors with ${C_2} = 0.3,1.15,1.46,1.38, 3.6$, and 6.6. We also observed some novel coexisting phenomena of chaotic attractors, hyperchaotic attractors, periodic orbits and stable points, which vary with both parameter L and initial value $\sigma _0$.

The proposed memcapacitor model can serve as models to study memcapacitive memory and memcapacitive synaptic plasticity for memcomputing, which can store and process information on the same physical platform. Furthermore, there is evidence that neural networks can exhibit enhanced computational complexity when operated at the chaotic state. Hence, the proposed memcapacitor-based controllable chaotic oscillator can be incorporated into a memcapacitive neural circuit for optimizing neural computations in a memcomputing scheme. This paper only proposed a memcapacitor model, but its realization is not involved. It will be a challenging task for us to study the realization and applications of the memcapacitor. Furthermore, how to implement memcapacitor-based memcomputing is also one of our future researches.

We end this paper with a DSP experiment, which verifies the dynamics of the memcapacitor-based circuit.