FPGA Implementation of a Real-Time Weak Signal Detector Using a Duffing Oscillator

Abstract

This paper presents an implementation of a weak signal detector using a Duffing oscillator on field programmable arrays (FPGAs) for the real-time detection of weak signals in noisy environments. The proposed implementation has combined the efficiency of weak signal detection by chaotic oscillators in noisy environments with the advantages of hardware implementation to achieve an efficient weak signal detector. To optimize the performance versus area, we have used VHDL. A novel state detector, phase trajectory autocorrelation, has been introduced for the state detection of the Duffing oscillator. As an experiment, the Duffing oscillator has been implemented on a Cyclone IV GX FPGA. In this paper, in addition to the structure and resource utilization of the design, experimental results are presented to demonstrate the effectiveness of the proposed implementation.

1 Introduction

Currently, the real-time detection of weak signals in noisy environments is a growing demand for most of applications that involve certain types of signal detection. Some particular examples of such applications are fault detection, industrial measurements, communications, radar, and sonar [5–8, 12, 20].

Although there are some conventional methods for detecting weak signals [25], immunity to noise has been unsuccessfully sought for decades, as these methods do not offer the expected results in noisy environments. Chaos theory is an approach that can feasibly achieve these demands.

After Edward Lorenz introduced chaos theory [11], it became widespread in many applications. Because of immunity to noise while being sensitive to a special weak signal, chaotic oscillators have been used in applications that involve weak signal detection. Wang [19] proved validity of this method in the presence of strong noise. He obtained experimental results with low SNR and conducted a quantitative study on detection and estimation of weak signals using Duffing oscillators (DUOS) [18].

After proving the validity of this method, more studies were performed on the efficiency of this method in applications that involve weak signal detection. This method was considered for machinery fault detection [12], communications [24], EEG analysis [23], GPS receivers [4], sonar detection and target identification [22], metal detection [21] and much more.

Today, one of the most common chaotic oscillators used in such applications is the DUOS [19], which is a non-linear second-order differential equation. In non-linear dynamic systems, a small change in the parameters of the system or the initial conditions may lead to qualitative changes in the system state [10]. This phenomenon forces the state of the chaotic oscillator to change from the chaotic state to the periodic state by applying a weak signal with a specified frequency that is in the sensitivity range of the oscillator.

The DUOS is sensitive only to a very narrow range of frequencies and phase delays [19], and in most applications, the frequency and phase delay of the weak signal are completely unknown or at least known without sufficient accuracy. Therefore, detecting a weak signal with an unknown frequency and a phase delay requires an array of oscillators.

The software implementation of an array for non-real-time applications or for detection of a weak signal with very low frequency is usually acceptable. However, when the performance is a critical requirement or the weak signal is of high frequency, software-implemented arrays require large amount of computational resources.

In addition to the applications that require real-time execution, there are some applications that require hardware solutions for weak signal detection. All these reasons together justify the hardware implementation of the chaotic oscillators for weak signal detection.

The main goal of this article is to design a practical solution for fault detection in induction motors. In this application, the frequency of target signal, as a fault indicator, depends on the variable slip of the motor. So, its frequency lies in the specified rang and therefore an array of oscillators is required for detecting the fault signal. In this regard, the attempt has been made to implement the DUOS in a way that requires low resources so that it can be useable in the array. Introducing a novel method called phase trajectory autocorrelation (PTA) instead of the largest Lyapunov exponent (LLE) is one of the things that we have done beside other optimizations to approach this goal.

Some related works on the FPGA implementation of chaotic oscillators are: Hardware Implementation of the Rössler Chaotic System for Securing Chaotic Communication [16], Real-time hardware implementation of a new Duffing’s chaotic attractor [15], An FPGA Real-time Implementation of the Chen’s Chaotic System for Securing Chaotic Communications [14].

In References [14] & [16] hardware chaotic oscillators are presented for secure communications based on the single Rossler chaotic and Chen’s chaotic system and Ref. [15] introduces a real-time FPGA implementation of a three-scroll chaotic attractor using Runge–Kutta 4th order (RK4) numerical solver, But these approaches have never been used in any applications.

As is known, there has been no implementations about weak signal detection by chaotic oscillators. Employment of weak signal detection has some important requirements such as high precision of calculation that none of the mentioned implementations has considered it before. Most of the mentioned works have sufficed to implement only a single chaotic oscillator without using it for a special application. Also, they are different in the purpose of implementing, selected chaotic oscillator, methods of implementation and optimizations; overally, the extent of their study is not comparable with that of the current work.

Thus, this paper introduces an FPGA-implemented weak signal detector using a DUOS.

This paper is organised into seven sections, as follows. In Sect. 2, the principles of weak signal detection by DUOS are explained. In Sect. 3, the novel method of state detection is presented with its MATLAB simulation. In Sect. 4, the structure of the proposed hardware-implemented DUOS and the state detection method are explained. In Sect. 5, the structure of the designed PTA block is introduced. The results of the synthesis and experiments are presented in Sect. 6 and finally Sect. 7 gives the conclusions.

2 Principles of Weak Signal Detection Based on DUOS

As mentioned, in non-linear dynamic systems, like chaotic oscillators, a small change in the parameters or conditions may force the system to changes its state. So, any change in the state, which we call state transition, will be the indicator of parameters change. In weak signal detection by chaotic oscillators, a periodic weak signal with special frequency that is buried in large noise is applied to system as a parameter. Although, any changes in parameter leads to state transition, changes due to noise do not change the state while any small change in weak periodic signal lead to state transition. Immunity to noise while being sensitive to a weak signal with special frequency is the most important properties of these method that make it reliable approach for weak signal detection in noisy environments. Figure 1 shows the scheme of weak signal detection by chaotic oscillator.

Fig. 1

Scheme of weak signal detection by Duffing oscillator

Accordingly, in weak signal detection by chaotic oscillators, state transition is the indicator of weak signal. Thus, a high sensitivity and sudden transition due to the change in a parameter of the oscillator are the main requirements for weak signal detection by chaotic oscillators. Accordingly, any chaotic oscillator that fulfils these two requirements can be used for this application. Holmes Duffing equation [19] is the most common chaotic oscillator for weak signal detection because of its popularity and sensitivity [20].

In this work, the single-well and double-well forms of the Duffing equation are considered to select the best chaotic oscillator. For the tested parameters, single-well form of the Duffing equation does not show the expected behaviour. For example, it leads to order by period-halving bifurcations and does not show a sudden transition from the chaotic state to the periodic state, but the double-well form of the Duffing equation presents acceptable behaviour for this purpose. Based on the evaluations and previous related research that was performed in this field [5–7, 12, 18–20], the Holmes Duffing equation has been chosen for the current work. The basic form of the Holmes Duffing equation is given in Eq. (1) [18]:

$$\begin{aligned} x^{\prime \prime }(t)+{bx}^{\prime }(t)-x(t)+{x}^{3}(t)=\gamma \cdot \cos (t) \end{aligned}$$

(1)

In Eq. (1), $\gamma \cdot \cos (t)$ and $bx^{\prime }( t)$ are the driving force and the damping, respectively, to remove energy conservation from the system which is essential for the system to become chaotic.

For weak signal detection, a special form of Eq. (1) is used in which a fixed value of 0.5 is assumed for the parameter $b.$ In this special form of the Duffing equation, the amplitude of the driving force $\gamma$ (while $\omega _0 =1)$ can easily control the state of the Duffing oscillator.

Thus, if $t=\omega _0 \tau$ and $b=0.5$, the Duffing equation can be re-written as Eq. (2) [19], which can be used to detect weak signals at any frequency, such as $\omega _0$.

$$\begin{aligned} \frac{1}{\omega _{0}^2 }x^{\prime \prime }( {\omega _0 \tau })+\frac{0.5}{\omega _0 }x^{\prime }( {\omega _0 \tau })-x( {\omega _0 \tau })+x^{3}( {\omega _0 \tau })=\gamma \cdot \cos ( {\omega _0 \tau }) \end{aligned}$$

(2)

Because Eq. (2) is derived from Eq. (1), the system is seen on another time scale. Therefore, the dynamic properties are not changed, and the difference consists only in the running speed [19]. Thus, the behaviour of the oscillator does not change for different values of $\omega _0$.

In [13] and [19], the state transition of a DUOS due to the input driving force and the other system parameters has been demonstrated by adding an external weak input signal to the driving force, which leads to Eq. (3).

$$\begin{aligned} \frac{1}{\omega _0^2 }x^{\prime \prime }( {\omega _0 \tau })+\frac{0.5}{\omega _0 }x^{\prime }( {\omega _0 \tau })-x( {\omega _0 \tau })+x^{3}( {\omega _0 \tau })=\gamma \cdot \cos ( {\omega _0 \tau })+Input(\tau ), \end{aligned}$$

(3)

where $\omega _0$ is the frequency of the driving force and $Input(\tau )$ is in the form of Eq. (4).

$$\begin{aligned} Input(\tau )=a\cdot \cos ( {(\omega _0 +\Delta \omega )\tau +\varphi })+noise(\tau ) \end{aligned}$$

(4)

In Eq. (4), $a$ is the amplitude of the target signal, $\Delta \omega$ is the difference between the frequencies of the input signal and the driving force, and $noise(\tau )$ is the strong noise of the environment that is assumed to be a normally distributed white noise with 0 mean and variance of $\sigma ^2$.

By assuming $a=0$, the value of $\gamma$ can be set to $\gamma _C$ to force the oscillator to operate in the critical state which means the chaotic state, but on the verge of the transition to the periodic state. In the critical state, very small increases in the amplitude of the driving force cause the oscillator to transition to the periodic state. In this situation, the existence of any weak signal with a frequency identical to the frequency of the driving force (that can play the role of increasing the amplitude of the driving force and cause the oscillator to change its state) will be detected. Therefore, in this method, the state transition from chaotic to periodic is the signature of weak signal detection.

Previous studies have proven the efficiency of this method in many different conditions of SNR, frequency, phase delay and etc., and in most of these studies, signals with very low SNRs have been detected by this method. A behavioural analysis of DUOS against the critical value of $\gamma _C$, SNR and the frequency change are conducted in [19]. Since in this work, no improvement scheme had been introduced to increase the immunity to noise, no great effort was done to prove the efficiency of the method by considering the influence of noise.

Based on our experiment and the study reported in Ref. [19], the Duffing oscillator is able to detect weak signals, the frequency of which are very close to the reference frequency of the oscillator ($\left| {{\Delta \omega }/{\omega _0 }} \right| \le 0.3\,\% )$. This limitation justifies the use of an array of Duffing oscillators to detect a weak signal with an unknown frequency.

Because there is no absolute analytical solution for the Duffing equation, especially with damping and driving forces, a numerical solution of the state equation Eq. (5) based on the RK4 and Euler methods is used in this study.

$$\begin{aligned} \left\{ {\begin{array}{l} x^{\prime }( t)=\omega _0 y( t) \\ y^{\prime }( t)=\omega _0 [x( t)-x^{3}( t)-0.5y( t)+\gamma \cos ( {\omega _0 t})+Input(t)] \\ \end{array}} \right. \end{aligned}$$

(5)

2.1 RK4

The recursive equations used for RK4 are Eqs. (6), (7) and (8):

$$\begin{aligned} \left\{ {\begin{array}{l} k_1 =\frac{h}{2}f( {Y_n }) \\ l_1 =\frac{h}{2}g( {t_n ,X_n ,Y_n }) \\ k_2 =\frac{h}{2}f( {Y_n +l_1 }) \\ l_2 =\frac{h}{2}g( {t_n +\frac{h}{2},X_n +k_1 ,Y_n +l_1 }) \\ k_3 =hf( {Y_n +l_2 }) \\ l_3 =hg( {t_n +\frac{h}{2},X_n +k_2 ,Y_n +l_2 }) \\ k_4 =\frac{h}{2}f( {Y_n +l_3 }) \\ l_4 =\frac{h}{2}g( {t_n ,X_n +k_3 ,Y_n +l_3 }) \end{array}} \right. \end{aligned}$$

(6)

$$\begin{aligned} K&= (k_1 +2k_2 +k_3 +k_4 )/3\end{aligned}$$

(7)

$$\begin{aligned} L&= (l_1 +2l_2 +l_3 +l_4 )/3, \end{aligned}$$

(8)

where

$$\begin{aligned} f( {Y_n })&= \omega _0 Y_n\end{aligned}$$

(9)

$$\begin{aligned} g( {t_n ,X_n ,Y_n })&= \omega _0 [X_n -X_n ^3-0.5Y_n +\gamma \cos ( {\omega _0 t_n })+Input(t_n )] \end{aligned}$$

(10)

and

$$\begin{aligned} \left\{ {\begin{array}{l} X_{n+1} =X_n +K \\ Y_{n+1} =Y_n +L \\ t_{n+1} =t_n +h \end{array}} \right. \end{aligned}$$

(11)

Based on $t_n +\frac{h}{2}$ term in Eq. (6), sampling period of $Input$ signal should be $\frac{h}{2}$.

2.2 Euler Method

In the Euler method, $K$ and $L$ are calculated using Eq. (12) instead of Eqs. (6), (7), (8) and other equations remain unchanged.

$$\begin{aligned} \left\{ {\begin{array}{l} K=h\cdot f( {Y_n }) \\ L=h\cdot g( {t_n ,X_n ,Y_n }) \end{array}} \right. \end{aligned}$$

(12)

3 State Detection Method

In the basic form of weak signal detection by DUOS, the state of the oscillator is determined by observing the phase space trajectory, and the precision of this method depends on human observation [9]. Some methods have been suggested to increase the accuracy of the observation and to automate the process of state detection, including Poincare maps, FFT, the LLE, the 0–1 test, and the correlation dimension [1–3]. The Poincare map is a qualitative method while other methods require great computational resources.

Automatic state detection is an essential requirement for hardware implementation of DUOS; hence, in this section, PTA is introduced as a novel state detection method that requires fewer computational resources than LLE and other mentioned methods.

When the DUOS is in the periodic state, the frequency is equal to the frequency of the driving force; in addition, it includes the odd harmonics of the driving force frequency. However, when the oscillator is in the chaotic state, various frequencies are observed in its output.

Therefore, to detect the periodic state, it is sufficient to compare each period of the phase space variables with their previous period. The similarities between each two consecutive periods of the phase space variables can be compared by means of a correlation function.

The correlation coefficient between two random variables X and Y with expected values $\mu _X$, $\mu _Y$ and standard deviations ${\sigma }_\mathrm{X}$, ${\sigma }_\mathrm{Y}$ is defined in Eq. (13).

$$\begin{aligned} \mathrm{corr}( {\text{ X },\text{ Y }})=\frac{\mathrm{cov}(\text{ X },\text{ Y })}{\sigma _\mathrm{X} \sigma _\mathrm{Y} }=\frac{E[( {\text{ X }-\mu _\mathrm{X} })( {\text{ Y }-\mu _\mathrm{Y} })]}{\sigma _\mathrm{X} \sigma _\mathrm{Y} }, \end{aligned}$$

(13)

where $E$ is the expected value operator and cov is the covariance.

Autocorrelation is the cross-correlation of a signal with itself. Autocorrelation is a time domain function that measures the extent to which a signal’s waveform resembles a delayed version of itself. In other words, it gives a degree of similarity between a signal and a lagged version of itself over successive time intervals.

The lag $k$ autocorrelation coefficient is the simple correlation coefficient of the first $k$ observations, $x_i, i=1, 2,{\ldots },k$ and the next $k$ observations, $x_{i+k}, i= 1, 2,{\ldots },k$. The lag $k$ autocorrelation coefficient is defined in Eq. (14).

$$\begin{aligned} r_x (k)=\frac{E[( {X-\mu _{X} })( {X_k -\mu _{X_k } })]}{\sigma _{X_i } \sigma _{X_k } }, \end{aligned}$$

(14)

where $X_k$ is related to the next $k$ observations of $X$. Eq. (14), which is the lag $k$ autocorrelation function, can be written as Eq. (15):

$$\begin{aligned} r_x ( k)=\frac{\mathop \sum \nolimits _{i=n1}^{i=n1+k} (x_i -\mathop {x_1 }\limits ^- )(x_{i+k} -\mathop {x_2 }\limits ^- )}{\sqrt{\mathop \sum \nolimits _{i=n1}^{i=n1+k} (x_i -\mathop {x_1 }\limits ^- )^2\mathop \sum \nolimits _{i=n1}^{i=n1+k} (x_{i+k} -\mathop {x_2 }\limits ^- )^2} } \end{aligned}$$

(15)

where $\mathop {x_1 }\limits ^-$, $\mathop {x_2 }\limits ^-$ are respectively the mean of the first $k$ samples and the mean of the next $k$ samples and $n1$ is an arbitrary initial point for the autocorrelation.

The mean value of phase state variables in each orbit ($\mathop {x_1}\limits ^-$, $\mathop {x_2 }\limits ^- )$ is zero for the periodic state. Although this value is not zero for the chaotic state, since a threshold value and some windowing processes were used in this method, Eq. (15) can be simplified to Eq. (16) by assuming $\mathop {x_1 }\limits ^- =\mathop {x_2 }\limits ^- =0$.

$$\begin{aligned} r_x ( k)=\frac{\mathop \sum \nolimits _{i=n1}^{i=n1+k} (x_i \cdot x_{i+k} )}{\mathop \sum \nolimits _{i=n1}^{i=n1+k} (x_i )^2} \end{aligned}$$

(16)

Because of the nature of this application, the correlation function is effectively simplified and optimized. This simplification is the main reason that we have introduced PTA method.

To calculate the autocorrelation of each two consecutive periods of the phase space trajectory, the value of $k$ should be equal to the number of samples in one orbit.

$$\begin{aligned} k=\frac{{2\pi } / {\omega _0 }}{h}=\frac{T_0 }{h}, \end{aligned}$$

(17)

where $\omega _0$ and $T_0$ are respectively the frequency and period of the driving force, and $h$ is the step size in the numerical solver.

Figure 2a shows an example of the phase space trajectory during two consecutive cycles of the periodic state and Fig. 2b shows some consecutive cycles of chaotic state.

It should be emphasized that in the PTA method, the continuous autocorrelation should be calculated for each two consecutive periods.

Since in the periodic state all consecutive cycles resemble each other, the result of Eq. 16 is almost above +0.98; on the other hand, in the chaotic state, as indicated in Fig. 2b, although there are some consecutive cycles like 2 & 3 which differ from each other, there are some consecutive cycles like 1 & 2 which resemble each other. So, in autocorrelation result for the chaotic state, there should be some positive values that incorrectly indicate periodic state. In this regard, windowing process with a threshold value is used.

Fig. 2

Examples of phase space trajectory; a in the periodic state, b in the chaotic state

The value of $r_x ( k)$ ranges from $-$1 to +1; +1 and $-$1 indicate perfect correlation and perfect anti-correlation, respectively. In this paper, all un-correlation values are treated as perfect anti-correlation, as shown in Eq. (18). The exact value of 0.98 does not influence the result of PTA method and any other value that lies in the range of 0.80$<$Threshold$<$0.98 can be acceptable.

$$\begin{aligned} \left\{ {{\begin{array}{l} {\text{ if }\; {{r}_{x}} ({k})\ge 0.98 \rightarrow {r}_{x} ({k})=+1} \\ {\mathrm{if}\; {r}_{x} ({k})<0.98\rightarrow {r}_{x} ( {k})=-1}\\ \end{array} }} \right. \end{aligned}$$

(18)

If the percentage of anti-correlation number to the total number of samples in a window exceeds $\text{ s }\,\%$, this window is designated as the chaotic state. The length of the window determines the response time of this method. Although width of the window and parameter s can be calculated to have the best results, we have not investigated in calculation of these parameters.

To study the efficiency of this method in detecting the state of the DUOS, the oscillator was simulated for 36 s by RK4 under four different conditions listed in Table 1.

Table 1 Parameters of the DUOS and four different conditions of the input signal

In all cases, the simulation time was 36 s. During the first 18 s, there were no input signal and in the remaining time, the input signal with the parameters specified in Table 1 was applied to the oscillator. In this paper, the definition used for SNR is according to the definition used in Ref. [19]. In Ref. [19], SNR is defined as the ratio of power spectrum amplitude of the signal to noise according to Eq. (19).

$$\begin{aligned} \left. {\mathrm{SNR}=\frac{H_s (\omega )}{H_n (\omega )}} \right| _{\omega =\omega _0 } \end{aligned}$$

(19)

In Eq. (19), $H_s (\omega )$ and $H_n (\omega )$ are the power spectrum amplitude of the signal and noise, respectively as Eq. (20).

$$\begin{aligned} \begin{array}{l} H_s (\omega )=\left\{ {\begin{array}{l} \frac{a^2}{4}{\begin{array}{ll} &{} \\ \end{array} }\omega =\pm \omega _0 \\ 0{\begin{array}{ll} &{} \\ \end{array} }\omega \ne \pm \omega _0 \\ \end{array}} \right. \\ H_{n} (\omega )=\int _{-\infty }^{+\infty } {\sigma ^{2}\delta (\tau )} e^{-j\omega \tau }\mathrm{d}\tau =\sigma ^{2} \\ \Rightarrow \left. {\mathrm{SNR}=\frac{H_s (\omega )}{H_n (\omega )}} \right| _{\omega =\omega _{0}} =\frac{a^{2}}{4\sigma ^{2}} \\ \end{array} \end{aligned}$$

(20)

In the logarithmic form, (according to Ref. [19]), SNR in Eq. 19 becomes:

$$\begin{aligned} \mathrm{SNR}=20\log \frac{a^2}{4\sigma ^2}(\mathrm{dB}) \end{aligned}$$

(21)

Figure 3a, b show the results of Eq. 16 for Case D of Table 1 respectively before and after applying the threshold value.

Fig. 3

Autocorrelation results before applying windowing process; a before applying threshold, b after applying threshold

According to the chaotic part of Fig. 3b, there are some +1 values in the result of autocorrelation. So, as mentioned before, a counting or averaging method is required to distinguish the state of oscillator from the output of autocorrelation.

In both state detection methods (LLE and PTA), the response time is defined as the duration between the moment the input signal is applied and the moment that it is detected by the state detection methods.

Figure 4a, b show the responses of the LLE and PTA state detection methods to the signals listed in Table 1, respectively. As expected, both methods show that the oscillator is working in the critical state for the first 18 s of the simulation and it changes its state to the periodic state when the input signal is added at the 18th s. In the LLE method, a value greater than 5e$-$3 indicates that the oscillator is in the chaotic state [17]; in the PTA method, a value of zero indicates chaotic motion and a value of +1 indicates the periodic state. Table 2 displays the response times of the LLE and PTA methods in the four studied cases.

Fig. 4

Results of state detection methods; a LLE result; b PTA result (Window size = 25, $s=10$ %)

Table 2 Response time of the LLE and PTA methods to the four cases studied

As Fig. 4 and Table 2 show, the PTA method presents better response times in comparison with LLE.

Simulation results show that the time of transition from chaotic to the periodic state is varying for different cases. The periodic state is started sooner in Cases C and D in comparison with Cases A and B. In this paper, we conclude that the amplitude of the weak signal affects the time of DUOS’s transition significantly and so, the speed of detection. It means that by increasing the amplitude of weak signals, the oscillator needs shorter time to detect it; so it needs fewer cycles for state transition from chaotic to periodic. Although response time of transition slightly depends on the amplitude of weak signal, it does not make any problems for the current work because of consecutive autocorrelation.

4 Structure of the Hardware Implementation

Because the implementation of weak signal detection by the DUOS should be useable to detect weak signals with high frequencies, achieving a higher performance is an important aim for this implementation. Using an array of DUOSs also requires area optimization and low power consumption. All these demands justify using VHDL for the current implementation.

Due to complexity of interconnections between blocks, the structure of implantation is illustrated using block diagrams in all over of the paper. The structure and dataflow diagram of the weak signal detection using the DUOS are shown in Fig. 5.

As shown in Fig. 5, this hardware implementation includes three main parts: 1- Implementing an interface for the system. 2- Implementing the DUOS. 3- Implementing the PTA method.

Fig. 5

Structure and dataflow diagram of weak signal detection using DUOS; a Structure; b Dataflow diagram

4.1 Test Bench and System Interface

In this work, a Cyclone IV GX FPGA development kit running on an EP4CGX150BF14 FPGA was used as a test bench for the implementation. The input signal was applied to the FPGA using a real-time win32 application running on the PC system. The data transfer between the FPGA and the PC was performed via the PCIe hard IP block of the FPGA.

Using this interfacing mechanism, the developed real-time software (DRTS) is able to send or receive any data to or from the FPGA. The mechanism of the DRTS is not discussed in this paper. The DRTS can generate any desired input signal, as in Eq. (22), and write its samples by a virtual sampling frequency rate to the internal registers of the FPGA. In other words, this mechanism simulates the application of an input signal by an ADC.

$$\begin{aligned} Input(t)=A_{m}\cdot \cos ( {\omega _{0}t})+noise(t) \end{aligned}$$

(22)

4.2 Structure of the DUOS Block

The sensitivity of the Duffing equations to the accuracy of calculations made it necessary to use single precision floating-point arithmetic which was implemented by using Altera’s floating-point library. Single precision floating-point arithmetic has a precision of 24 bits (about 7 decimal digits) which is more than enough for the required accuracy.

To implement Eq. (5), the ALTFP_ADD_SUB and ALTFP_MULT megafunctions were used, and the ALTFP_CONVERT megafunction was also used in the construction of a cosine function based on a look-up table to convert the floating-point number into an integer. The used look-up table had 4,096 entries and offered a resolution of $0.0015\;radians$ for the cosine function, which meets the present requirements.

Figure 6 shows the structure of the DUOS block. As is shown, the DUOS consists of some megafunctions (ALTFP_XXX) and some blocks developed using VHDL (e.g., the “Duffing Equation” block).

Fig. 6

Structure of DUOS block

Because the ALTFP_MULT and ALTFP_ADD_SUB megafunctions used a considerable amount of the logic elements of the FPGA, the implementation of the DUOS was serialized so that only one instance of the multiplier and adder/subtractor megafunctions was added to the design. Using one instance of the multiplier and adder/subtractor implies that only one operation of multiplication and one operation of addition/subtraction can be handled at a time. This limitation led to the serialization of the whole process of DUOS. For example, to calculate $y^{\prime }( t)$ in Eq. (5), serialization was performed in five steps, as depicted in Table 3 $\cos (\omega _0 t))$ was calculated separately, and the last step was transferred to the numerical solver block.

Table 3 Example of the serialized form to calculate $y^{\prime }( t)$ in Eq. (5) (the highlighted operations show the operations that are running in the ordered steps)

The same process was performed for the “Numerical solver” block. The number of required steps for the whole process depends on the used numerical solution. For the Euler method, the process was separated into five steps, as shown in Table 4. One of the steps of the Euler method (Step 1 part 2: “$Duffing \, eq. \leftarrow \quad x,y$”) consisted of the five sub-steps mentioned in Table 3. By applying the same process, the RK4 method was separated into 23 steps, and four of its steps themselves consisted of five sub-steps, as mentioned in Table 3.

Table 4 Serialized form of the Euler method (the highlighted operations show the operations that are running in the ordered steps)

In the implementation of the “Duffing equation” and “Numerical solver” blocks, the processes mentioned in Tables 3 and 4 shared the same multiplier and adder/subtractor megafunctions. Thus, as shown in Fig. 6, the controller unit was considered to provide the sharing mechanism.

5 Structure of PTA Block

As in the structure of the DUOS, the calculations of the PTA method were serialized to use only one instance of the multiplier and adder/subtractor megafunctions. Therefore, a controller unit was dedicated to the control of the process. The main steps to compute the PTA are shown in Table 5.

Table 5 Serialized steps of the PTA (the highlighted operations show the operations that were running in the ordered steps)

Figure 7a shows the structure of the PTA block. Similar to the DUOS, it consists of some megafunctions (ALTFP_XXX) and a control unit developed using VHDL. For clarity, the process by which the controller unit of this section was designed is shown in Fig. 7(b).

The input data of this process is the phase space variables, and the output is the result of PTA, which is valid at the end of each orbit. The controller unit has been designed to reset the latches at the beginning of every orbit.

Fig. 7

The structure and calculation process of PTA block; a Structure; b Calculation process

6 Hardware Results

In this section, the hardware output results of the weak signal detection using the DUOS, resource utilization and the maximum operation frequency are presented. Similar to the simulation, the oscillator was configured to operate in the critical state, and the noisy signal was applied to the oscillator. Table 6 summarises the weak signal detector configurations and the input signal specifications.

Table 6 Parameters of the DUOS during the experiments

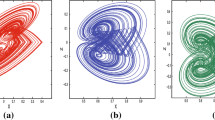
Figure 8 shows the phase trajectory of the DUOS to the applied noisy signal corresponding with Table 6 using the Euler method. Because the phase trajectory obtained for the RK4 method was similar to that obtained for the Euler method, it is not depicted. As Fig. 8a, c indicate, before applying the noisy signal, the DUOS was operating in the chaotic state, and, after application of the signal, the DUOS changed its state to periodic (Fig. 8b, d).

Fig. 8

Experimental results for the phase trajectory of DUOS with Euler method; a Case S from second 0 to 21, b Case S from second 21 to 36, c Case L from second 0 to 19, d Case L from second 19 to 36

The final output of the weak signal detector, which was the output of the PTA, is shown in Fig. 9, which demonstrates that the output results of both the Euler and RK4 numerical solvers used for the oscillators are approximately equal; the time of detection was not a fixed value and varied in each test.

Fig. 9

Result of PTA for both Small (5e$-$4) and Large (1e$-$1) amplitude; a Euler method and b RK4 method

As shown in Fig. 9, the time of detection highly depends on the amplitude of weak signal.

The maximum clock frequency and the resource utilization for weak signal detection are reported for both area and speed optimizations in Table 7. For clarity, Table 8 shows the same values for each block separately.

Table 7 Resource utilization and the maximum clock frequency for weak signal detection

Table 8 Resource utilization and the maximum clock frequency of the DUOS and PTA blocks

Due to the serialization mentioned before, the oscillator and the state detector required a fixed number of clocks to present a valid result. Table 9 summarises the latency and required time for each iteration. The minimum iteration time, which was the smallest step size of the numerical solvers, is calculated by Eq. (23).

$$\begin{aligned} \text{ Minimum } \text{ iteration } \text{ time }\,(\upmu \mathrm{s})=\frac{\text{ Latency }\,(\text{ Clock })}{\text{ FMAX }\,(\text{ MHz })} \end{aligned}$$

(23)

Table 9 The output latency and the minimum required time for each iteration of the DUOS and PTA blocks

Furthermore, the DUOS with the RK4 numerical solver should have better accuracy; however, when using a small step size of $h=5$e$-$5, no differences were observed in the accuracy of detection results between the Euler and RK4 implementations. For larger step sizes used in the numerical solver, this difference in accuracy became significant, but for a small step size achieved in the hardware implementations (a minimum step size of 578 ns), the difference between the accuracy of the Euler and RK4 methods can be neglected. According to the significant differences in the resource utilization, the minimum iteration time between the Euler and RK4 implementations, and equality of the results due to the small step size, it can be concluded that the Euler implementation can be appropriate for most applications, especially when the frequency of the weak signal is low. However, to detect weak signals of high frequency, the RK4 method is more appropriate.

7 Conclusions

In summary, a high-performance FPGA implementation for weak signal detection using a DUOS was presented using VHDL. First, the DUOS was implemented to detect the existence of the weak signal. Then, a novel method was introduced and implemented to detect the state of the DUOS.

The DUOS was implemented by two different numerical methods, the Euler and RK4 methods. The Euler method implementation was more appropriate due to its lower resource utilization and better performance. As an important modification, the whole process was serialized to achieve a lower usage of the FPGA resources, which is essential for hardware implementation.

The efficiency of the weak signal detection by chaotic oscillators and the advantages of hardware implementation make this work a valuable tool for the real-time detection of weak signals in noisy environments.