1 Introduction

The memristor (the acronym of memory resistor) was theoretically described by Chua [1] in 1971 and later implemented (a nanoscale \(TiO_2 \) device) by the Stanley William group from Hewlett Packard (HP) in 2008[2]. It takes its place alongside the rest of more standard circuit elements such as resistor, capacitor and inductor. The characteristic of these four basic elements of electrical circuit theory relates the four variables in electrical engineering, namely voltage, current, flux and charge. The memristor is a two-terminal nonlinear component with variable resistance called memristance which depends on the amount of electric charge that has passed through it in a given direction [3, 4]. More precisely, memristors have the distinctive property to memorize the past quantity of electric charge. The current–voltage (i-v) characteristic curve of a memristor (i.e. its fingerprint) displays a pinched hysteresis loop whose shape varies with frequency and takes the form a straight line as the frequency goes to infinity[3, 4]. Potential applications of such memristors span diverse fields of science and engineering ranging from nonvolatile memories on the nanoscale to modeling neural networks. The intrinsic nonlinearity of memristors is also currently exploited for the design of new chaotic circuits by substituting nonlinear elements in standard chaotic circuits with the memristor, thus giving rise to rich varieties of bifurcation structures [5,6,7,8,9]. Since memristors are commercially unavailable, various memristor emulators have been proposed. Accordingly, several nonlinearities including HP memristor model [10], non-smooth piecewise linearity [11], cubic nonlinearity [12] and smooth piecewise quadratic nonlinearity [13] (just to name a few) are currently utilized to model the relationship between flux and electric charge of the memristors. The main advantage of these memristor emulators is that the corresponding equivalent circuit can be constructed using off-the-shelf components such as resistors, capacitors, operational amplifiers and analog multipliers, which are particularly suited for breadboard experiments. Of particular interest are memristive diode bridge-based circuits [14,15,16] with relatively simple topological structures (involving only elementary electronic circuit elements such as diodes, resistors and capacitors).

Fig. 1
figure 1

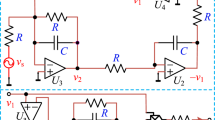
Simple electronic circuit realization (a) of the memristor-based novel jerk circuit. The memristor symbol and the corresponding discrete realization are shown in b. The following values of electronic circuit components are used for the analysis, \(R_m =1\,\hbox {k}\Omega , R_\delta =5\,\hbox {k}\Omega \), \(R=10\,\hbox {k}\Omega \, C_1 =C_2 =C_3 =C=10\,\hbox {nF}\), \(C_m =100\,\hbox {nF}, D_1 =D_2 =D_3 =D_4 \) (1N4148) (\(\eta =1.9, V_T =26\,\hbox {mV}, I_S =2.682\,\hbox {nA})\); \(R_\alpha \) is tuneable resistor

Full size image

In this contribution, we consider the dynamics of a simple autonomous jerk circuit obtained by substituting the single semiconductor diode in the jerk circuit described in [17] with a first-order memristive diode bridge to synthesize a symmetric nonlinearity. Owing to the presence of the memristor in the modified circuit, the new model is highly symmetric [18] and thus is particularly suited to experience multiple coexisting attractors among many other interesting properties such as antimonotonicity, period-doubling, symmetry-recovering crises and chaos. At this point, we would like to recall that jerk systems [19,20,21,22] are third-order differential equations of the form \(\dddot{x}=J\left( {\ddot{x},\dot{x},x} \right) \) where the nonlinear function \(J(\cdot )\) is called the “jerk,” because it denotes the third-time derivative of x, which would correspond to the first-time derivative of acceleration in a mechanical system. Very recently, a series of works dealing with the issue of coexisting multiple attractors in simple jerk dynamical systems have been published [23,24,25]. In Ref. 23, a systematic analysis of a simple autonomous jerk system with cubic nonlinearity [22, 23, 26] is considered. The dynamics of the model is investigated in terms of equilibria and stability, phase portraits, frequency spectra, bifurcation diagrams and Lyapunov exponent plots. A window in the parameter space is found in which the jerk system with cubic nonlinearity experiences the unusual feature of multiple attractors (i.e. coexistence four disconnected periodic and chaotic attractors). Results of theoretical analysis are verified by laboratory experimental measurements. By approximating the cubic nonlinearity with by a hyperbolic sine function (synthesized by two antiparallel diodes) [24], or alternatively by using a memristive diodes bridge [25], novel jerk circuits (with relatively simpler electronic structure) capable of multiple coexisting attractors are obtained. Compared to some few cases of lower-dimensional systems (e.g. Newton–Leipnik system [27, 28]) capable of displaying such type of behavior reported to date, the above-mentioned jerk systems represent the simplest and the most “elegant” paradigms. We would like to point out that all the three jerk circuits studied by Kengne et al. [23,24,25] can be regarded as typical examples of third (or four order, in the case of memristive jerk)-order control systems with nonlinear position feedback showing three rest points. In contrast, the model introduced in this work is an example of fourth-order system with nonlinear velocity feedback having a single rest point located at the origin. The novel memristive jerk circuit shows simpler electronic structure and depicts richer bifurcation scenarios compared to cases of jerk circuits with position feedback. Also, the aim of this paper can be formulated in the following three key points: a) to carry out a systematic analysis of the novel jerk circuit and explain the chaos mechanism; b) to define the domain in the parameter space in which the proposed model experiences multiple coexisting attractors and hysteretic dynamics; c) to carry out an experimental study of the system to validate the theoretical predictions. The overall motivation behind this work is to enrich the literature with a novel chaotic system/circuit with multiple coexisting attractors; in addition, we develop useful tools for the practical circuit design of such types of oscillators. More importantly, a simple conclusion that can be drawn from this work is that the presence of a multitude of fixed points is not a necessary condition for the occurrence of multiple attractors in a jerk system in particular (as the example shows) and nonlinear dynamical systems in general.

The layout of the paper is as follows. Section 2 is concerned with the modeling process. The electronic structure of the novel memristive jerk circuit is described, and a suitable mathematical model is derived to investigate the dynamics of the proposed oscillator. Some basic properties of the model are discussed. The stability of the unique equilibrium point is studied. In Sec. 3, the bifurcation structures of the system are investigated numerically showing period-doubling, periodic windows and symmetry-recovering crises events. Some windows (in the parameter space) corresponding to the occurrence of multiple competing attractors (for the same parameters settings) are depicted. Accordingly, basins of attraction of various coexisting solutions are plotted showing nontrivial basin structures. The experimental study is carried out in Sec. 4. Laboratory experimental measurements show a very good agreement with the theoretical results. Finally in Sec. 5, we summarize our results and draw the conclusion of this work.

2 Description and analysis of the model

2.1 Circuit description

The circuit diagram of the novel memristor-based jerk circuit under investigation is depicted in Fig. 1. The single semiconductor diode of the original circuit [17] is replaced by a memristor diode bridge [14, 16]. The novel memristive jerk oscillator consists of three successive active integrators in a loop, plus a second nonlinear feedback loop involving two integrators and an inverter with a memristor. The following values of electronics components are adopted: \(D_1 =D_2 =D_3 =D_4 \)(1N4148); op. amplifiers (TL084 type) \(C=10\,\hbox {nF};C_m =100\,\hbox {nF}; R=10\,\hbox {k}\Omega ; R_m =0.1\,\hbox {k}\Omega ; R_\alpha \) and \(R_\delta \) are tuneable resistors. These resistors will serve as the main control parameters for the system. Assuming ideal op. amplifiers (working in their linear domain), we would like to point out that the memristor represents the only nonlinear component responsible of the chaotic behavior of the complete electronic oscillator. The generalized memristor consisting of a diode bridge (see Fig. 1b) with a first-order parallel RC filter [14] is employed. Its mathematical description [14] is given by the following equations:

$$\begin{aligned}&i_m =2I_s \exp (-\rho \upsilon _{C_m } )\sinh (\rho \upsilon ) \end{aligned}$$
(1a)
$$\begin{aligned}&\frac{\mathrm{d}\upsilon _{C_m } }{\mathrm{d}t}=\frac{2I_s (\exp (-\rho \upsilon _{C_m } )\cosh (\rho \upsilon )-1)}{C_m }-\frac{\upsilon _{C_m } }{RC_m }\nonumber \\ \end{aligned}$$
(1b)

where \(\rho =1/{2n\upsilon _T }\); \(I_S , n, \upsilon _T \) denote the reverse current, the emission coefficient and the thermal voltage of the diode, respectively [29, 30]. \(\upsilon _{C_m }\) is the voltage of the capacitor \(C_m \) while \(\upsilon \) and \(i_m \) represent the input voltage and current of the generalized memristor. According to Eq. (1a), the generalized memristor is voltage-controlled and its memductance which can be expressed by:

$$\begin{aligned} G_m =\frac{i}{\upsilon }=\frac{2I_s \exp (-\rho \upsilon _{C_m } )\sinh (\rho \upsilon )}{\upsilon } \end{aligned}$$
(2)

depends both on its input and capacitor voltages. The RC memristive diode bridge is implemented using the following nominal values of electronic circuit components: \(C_m =100\,\hbox {nF}, R_m =1\,\hbox {k}\Omega \) and four diodes (1N4148 type) which parameters are \(I_S =2.682\,\hbox {nA}, n=1.9\) and \(\upsilon _T =26\,\hbox {mV}\). Following the works of Bao and colleagues [14, 16], the generalized memristor exhibits the three characteristic fingerprints for identifying a memristor [3]. It should be noted that with the additional memory element brought by the memristor, the novel memristor-based jerk circuit is now a fourth-order dynamical system.

2.2 State equation

Denoting by \(\upsilon _{C_1 } , \upsilon _{C_2 }, \upsilon _{C_3 } \) and \(\upsilon _{C_m } \) the voltage across capacitors \(C_1 , C_2, C_3 \) and \(C_m \), respectively, the Kirchhoff’s electric circuit laws can be applied to the schematic diagram of Fig. 1 to derive the following set of four coupled first-order differential equation describing the novel memristive jerk circuit:

$$\begin{aligned} \left\{ {\begin{array}{l} C_1 \frac{\mathrm{d}\upsilon _{C_1 } }{\mathrm{d}t}=\frac{\upsilon _{C_2 } }{R} \\ C_2 \frac{\mathrm{d}\upsilon _{C_2 } }{\mathrm{d}t}=\frac{\upsilon _{C_3 } }{R_\alpha } \\ C_3 \frac{\mathrm{d}\upsilon _{C_3 } }{\mathrm{d}t}=-\frac{\upsilon _{C_1 } }{R_\delta }-\frac{\upsilon _{C_3 } }{R}-2I_s \exp ({-\upsilon _{C_m } }/{2n\upsilon _T })\\ \qquad \ \ \quad \qquad \times \sinh ({\upsilon _{C2} }/{2n\upsilon _T }) \\ C_m \frac{\mathrm{d}\upsilon _{C_m } }{\mathrm{d}t}=2I_s (\exp ({-\upsilon _{C_m } }/{2n\upsilon _T })\\ \qquad \qquad \qquad \times \cosh ({\upsilon _{C2} }/{2n\upsilon _T })-1)-\frac{\upsilon _{C_m } }{R_m } \\ \end{array}} \right. \end{aligned}$$
(3)

where the nonlinear terms describe the nonlinear characteristics of the memristor as defined above. With the following change of variables and parameters:

$$\begin{aligned}&t=\tau RC,\quad \alpha =R/{R_\alpha },\quad \delta =R/{R_\delta },\quad \eta =R/{R_m }, \nonumber \\&\beta =\frac{2RI_S }{1V}, \quad \varepsilon =C/{C_m }, \quad \rho =\frac{1V}{2n\upsilon _T }, \nonumber \\&1V\times x_1 =\upsilon _{C_1 }, \nonumber \\&1V\times x_2 =\upsilon _{C_2 },\quad 1V\times x_3 =\upsilon _{C_3 } ,\quad 1V\times x_4 =\upsilon _{C_m }\nonumber \\ \end{aligned}$$
(4)

the dimensionless circuit equations (convenient for numerical analyses) are defined by the following smooth nonlinear fourth-order differential equation:

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{x}_1 =x_2 \\ \dot{x}_2 =\alpha x_3 \\ \dot{x}_3 =-\delta x_1 -x_3 -\beta \exp (-\rho x_4 )\sinh (\rho x_2 ) \\ \dot{x}_4 =\varepsilon (\beta (\exp (-\rho x_4 )\cosh (\rho x_2 )-1)-\eta x_4 ) \\ \end{array}} \right. \end{aligned}$$
(5)

where the over dots represent differentiation with respect to the dimensionless time \(\tau \). It can be noticed that only two state variables (namely \(x_2\) and \(x_4\)) are involved in the nonlinearities of model (5). Also, it should be mentioned that all the state variables are real and may be measured in real experiments with a standard oscilloscope (see the model in Ref. [17] for comparison purposes). In the mathematical model (5), six parameters can be found; nevertheless, parameter \(\alpha \) (resistor \(R_\alpha \)) will be considered as the main bifurcation control parameter in this work. The numerical experiment is carried out with the following dimensionless parameters: \(\delta =2,\varepsilon =2\times 10^{-3}, \eta =10,\beta =5.36\times 10^{-5},\rho =10.121\).

2.3 Symmetry and dissipation

One can easily notice that system (5) is invariant under the transformation: \(\left( {x_1 ,x_2 ,x_3 ,x_4 } \right) \Leftrightarrow \left( -x_1 ,-x_2 ,-x_3 ,x_4 \right) \). Therefore, if \(\left( {x_1 ,x_2 ,x_3 ,x_4 } \right) \) is a solution of system (5) for a specific set of parameters, then \(\left( {-x_1 ,-x_2 ,-x_3 ,x_4 } \right) \) is also a solution for the same parameters set. A symmetric solution is a solution of (5) that is invariant under the above transformation; otherwise, it is an asymmetric solution. Consequently, the projections of attractors onto the \(\left( {x_1 ,x_2 ,x_3 } \right) \) subspace have to be symmetric with respect to the origin; otherwise, they must occur in pairs, to satisfy the exact symmetry of the model equations. This exact symmetry may be used to explain the appearance of multiple coexisting attractors in state space. We would like to remark that compared to other types of memristive systems [23, 24] with three rest points, the novel memristive jerk system has the origin \(E_0 \left( {0,0,0,0} \right) \) as the only fixed point.

The rate of volume contraction of system (5) is given by the Lie derivative,

$$\begin{aligned} \nabla V= & {} \frac{\partial \dot{x}_1 }{\partial x_1 }+\frac{\partial \dot{x}_2 }{\partial x_2 }+\frac{\partial \dot{x}_3 }{\partial x_3 }+\frac{\partial \dot{x}_4 }{\partial x_4 }\nonumber \\= & {} -(1+\varepsilon (\beta \rho \exp (-\rho x_4 )\cosh (\rho _1 x_2 )+\eta )) \end{aligned}$$
(6)

This expression shows that the divergence is negative independently of the position \(\left( {x_1 ,x_2 ,x_3 ,x_4 } \right) \) in state space, meaning that the novel memristive jerk circuit is dissipative. Hence, system (5) limit sets are ultimately confined to a specific limit set of zero volume in state space, and the asymptotic motion of the novel memristive jerk circuit settles onto an attractor [31].

2.4 Fixed-point analysis

The preliminary study of the system’s dynamics starts by analyzing possible states of equilibrium (i.e. static solutions). Briefly recall that the fixed points constitute the simplest cases of steady states; thus through the study of their bifurcations, it is possible to detect the existence of other more complicated dynamic regimes [31,32,33] including the possibility of hidden oscillations [34,35,36,37]. In other words, the equilibrium points play a crucial role on the nonlinear dynamics of the circuit. As mentioned above, system (5) has a single equilibrium point located at the origin of the system coordinates independently of the values of control parameters. The Jacobian matrix of system (5) evaluated at any point \(\left( {x_1^0 ,x_2^0 ,x_3^0 ,x_4^0 } \right) \) of the state space is expressed as follows:

$$\begin{aligned} M_j =\left[ {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} 0&{} 1&{} 0&{} 0 \\ 0&{} 0&{} \alpha &{} 0 \\ {-\delta }&{} {-\theta }&{} {-1}&{} \phi \\ 0&{} {\varepsilon \phi }&{} 0&{} {-\varepsilon (\theta +\eta )} \\ \end{array} }} \right] \end{aligned}$$
(7)

where \(\theta =\beta \rho \left( {\exp (-\rho x_4^0 )\cosh (\rho x_2^0 )} \right) \) and \(\phi =\beta \rho \left( {\exp (-\rho x_4^0 )\sinh (\rho x_2^0 )} \right) \). Thus, the Jacobian matrix evaluated at the equilibrium point \(E_0 \left( {0,0,0,0} \right) \) satisfies the following characteristic equation (\(\det \left( {M_J -\lambda I_d } \right) =0)\):

$$\begin{aligned} \lambda ^{{4}}+b_{3} \lambda ^{{3}}+b_{2} \lambda ^{{2}}+b_{1} \lambda +b_{0} =0 \end{aligned}$$
(8a)

where \(I_d\) is the 4x4 identity matrix and the coefficients \(b_i \left( {i=0,1,2,3} \right) \) are defined as:

$$\begin{aligned} b_{0}= & {} \delta \alpha \varepsilon \left( {1+\eta } \right) \end{aligned}$$
(8b)
$$\begin{aligned} b_{1}= & {} \alpha \left( {\varepsilon +\varepsilon \eta +\delta } \right) \end{aligned}$$
(8c)
$$\begin{aligned} b_{2}= & {} \varepsilon +\varepsilon \eta +\alpha \end{aligned}$$
(8d)
$$\begin{aligned} b_{3}= & {} \varepsilon +\varepsilon \eta +1 \end{aligned}$$
(8e)

A set of necessary and sufficient conditions for all the roots of Eq. (8) to have negative real parts is given by the well-known Routh–Hurwitz criterion expressed in the form:

$$\begin{aligned}&b_i >0\left( {i=0,1,2,3} \right) \end{aligned}$$
(9a)
$$\begin{aligned}&b_2 b_3 -b_1 >0 \end{aligned}$$
(9b)
$$\begin{aligned}&b_3 \left( {b_1 b_2 -b_0 b_3 } \right) -b_1 ^{2}>0 \end{aligned}$$
(9c)

Thus, if inequalities (9) are satisfied, the system exhibits a fixed-point motion; otherwise, the equilibrium is unstable and the system experiences an oscillatory behavior. These conditions can be achieved in practice by monitoring some suitable tuneable circuit components. For instance, considering the following set parameters: \(\delta =2, \varepsilon =2\times 10^{-3},\eta =10,\beta =5.36\times 10^{-5},\rho =10.121\), for which the system develops a double scroll attractor (see Sect. 3), we have numerically computed the following eigenvalues for the Jacobian matrix \(M_J \) for \(\alpha =15: \lambda _1 =-3.4788, \lambda _{2} =-1.0001\) and \(\lambda _{3,4} =1.2394\pm \hbox {2.6623}i\). Also, due to the presence of eigenvalues with real parts of different signs, the origin \(E_0 (0,0,0,0)\) is an unstable equilibrium point for system (5) for this particular set of parameters. More generally, in the regime of oscillations, the fixed point \(E_0 \) is always unstable; hence, the system develops self-excited attractors [38, 39] instead of hidden ones [40,41,42,43].

3 Complex dynamics in the novel jerk circuit

3.1 Numerical methods

In order to investigate the rich variety of bifurcation modes which can be observed in the novel memristor-based jerk circuit, system (5) is solved numerically using the classical fourth-order Runge–Kutta integration algorithm. For each set of parameters used in this work, the time step is always \(\Delta t=0.0025\) and the calculations are performed using variables and constants parameters in extended precision mode. The system is integrated for a sufficiently long time, and the transient is cancelled. Two indicators are substantially exploited to define the type of scenario giving rise to chaos, namely the bifurcation diagram and the graph of three largest Lyapunov exponents. Concerning the latter case, the dynamics of the system is classified using its Lyapunov exponents which are computed numerically by exploiting the algorithm described by Wolf and collaborators [44]. Mention that for periodic orbits, \(\lambda _1 =0,\lambda _2 ,\lambda _3 , \lambda _4 <0\), for quasiperiodic orbits \(\lambda _1 =\lambda _2 =0, \lambda _3, \lambda _4 <0\), while for chaotic attractors \(\lambda _1 \ge 0, \lambda _2 =0,\lambda _3 , \lambda _4 <0\) and for hyperchaotic attractors \(\lambda _1 \ge \lambda _2 \ge 0, \lambda _3 =0\), \(\lambda _4 <0\). In particular, the sign of the largest Lyapunov exponent determines the rate of almost all small perturbations to the system’s state, and consequently, the nature of the underlined dynamical attractor. For \(\lambda _1 <0\), all perturbations vanish and trajectories starting sufficiently close to each other converge to the same stable equilibrium point in state space. For \(\lambda _1 =0\), initially close orbits remain close but distinct, corresponding to oscillatory dynamics on a limit cycle or torus. Finally for \(\lambda _1 >0\), small perturbations grow exponentially, and the system evolves chaotically within the folded space of a strange attractor.

Fig. 2
figure 2

Bifurcation diagram (a) showing local maxima of the coordinate \(x_1 \left( \tau \right) \) and the corresponding graph of four largest Lyapunov exponents (b) versus parameter \(\alpha \). Cyan and magenta diagrams correspond, respectively, to increasing and decreasing values of \(\alpha \) plotted in the range \(1\le \alpha \le 34\). The positive value of \(\lambda _1 \) is the signature of chaotic motion. Notice the presence of a window of hysteretic behaviors in the range of \(27.24\le \alpha \le 29.8\) where up to four different attractors coexist. (Color figure online)

Full size image
Fig. 3
figure 3

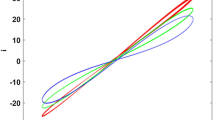
Phase portraits showing routes to chaos in the system for varying \(\alpha \): a period-1 for \(\alpha =4\), b period-2 for \(\alpha =5\), c period-4 for \(\alpha =5.554\), d single-band chaos for \(\alpha =6.5\), e double-band chaotic attractor for \(\alpha =10\), f single-band chaos for \(\alpha =17.7\), g single-band chaos for \(\alpha =28\), period-4 for \(\alpha =32\), period-2 for \(\alpha =35\), period-1 for \(\alpha =35\)

Full size image
Fig. 4
figure 4

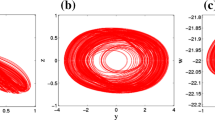
Two-dimensional projections of the double-band chaotic attractor a–d illustrating the complexity of the system, corresponding frequency spectra (e) and corresponding double-sided Poincaré section (f) in the plane \(x_1 =0\). Parameters are those in Fig. 3

Full size image
Fig. 5
figure 5

Bifurcation diagram (a) showing local maxima of the coordinate \(x_2 \left( \tau \right) \) and the corresponding graph of three largest Lyapunov exponents (b) versus parameter \(\delta \). Magenta and cyan diagrams correspond, respectively, to increasing and decreasing values of \(\delta \) plotted in the range \(1\le \delta \le 8\) (see text for detailed procedures). The positive value of \(\lambda _1 \) is the signature of chaotic motion. Notice the presence of a window of hysteretic behaviors in the range of \(2\le \delta \le 2.65\) where up to four different attractors coexist

Full size image
Fig. 6
figure 6

Enlargement of the bifurcation diagram of Figs. 2 and 5 showing the region in which the system exhibits multiple coexisting attractors. This region corresponds to values of a: \(\alpha \) in the range: \(26\le \alpha \le 31\) and b: \(\delta \) in the range \(1\le \delta \le 3\). Two sets of data corresponding, respectively, to increasing and decreasing values of the bifurcation control parameter are superimposed (see text for detailed procedures)

Full size image

3.2 Transitions to chaos

To investigate the sensitivity of the novel jerk system with respect to a single bifurcation control parameter, we fix \(\delta =2; \eta =10\) and vary \(\alpha \) in the range \(1\le \alpha \le 34\). It is observed that the novel memristive jerk system under consideration can experience very rich bifurcation structures when slowly adjusting the bifurcation parameter. Sample results showing the bifurcation diagram for varying \(\alpha \) as well as the corresponding graphs of Lyapunov exponents are provided in Fig. 2a, b, respectively. The bifurcation diagram depicts plots of local maxima of the coordinate in terms of the bifurcation control parameter. In the graph in Fig. 2a, two sets of data (magenta and cyan) are superimposed. The diagram in cyan is obtained for increasing (or decreasing) values of parameter \(\alpha \) starting from the initial condition \(\left( {x_1 (0)=-1.2,x_2 (0)=x_3 (0)=x_4 (0)=0} \right) \); the final state at each iteration of the bifurcation control parameter \(\alpha \) serves as the initial state for the next iteration. In contrast, the one in magenta is obtained by starting the system from the initial conditions \(\left( {x_1 (0)=1.4,x_2 (0)=0.8,x_3 (0)=x_4 (0)=0} \right) \) at each iteration of the control parameter. The four largest Lyapunov exponents are obtained by exploiting the same strategy as that used for the cyan bifurcation diagram (see Fig. 2b). This strategy represents a simple method to uncover the domain in which the novel memristive jerk system exhibits multiple coexisting attractors’ behavior (see Sect. 4). From the graph in Fig. 2a, some striking bifurcation events including period-doubling scenarios to chaos, revere period-doubling, symmetry-recovering crises [45], as well as periodic windows can easily be identified. It can be seen that the bifurcation diagram well matches with the spectrum of the Lyapunov exponents. Note that there is always a single positive Lyapunov exponent, meaning that the system is simply chaotic (and not hyperchaotic), although it is a fourth-order nonlinear system. Using the same values of parameters in Fig. 2, various numerical phase portraits and corresponding frequency spectra were computed to confirm different bifurcation sequences depicted previously (see Fig. 3). Asymmetric attractors pairs are observed in Fig. 3a–e, g–j while a double-band strange attractor is depicted in Fig. 3f. To gain more information about the complexity of the attractor shown in Fig. 3f, we provide in Fig. 4 the related two-dimensional projections, frequency spectrum, as well the double-sided Poincare section projected onto the plane \(x_1 =0\). The shape of this Poincaré section as well as the broad noise like frequency spectrum is characteristics of chaotic attractors.

Using the following set parameters \(\alpha =29.12\); \(\eta =10\), the period-doubling scenario to chaos, the symmetry-recovering crisis phenomenon as well as periodic windows are also found when using \(\delta \) as bifurcation control parameter. The corresponding bifurcation diagram for varying \(\delta \) in the range \(1\le \delta \le 8\) and the graph of Lyapunov exponents are provided in Fig. 5a, b, respectively. In the graph in Fig. 5a, the diagram in cyan is obtained for decreasing values of parameter \(\delta \) starting from the initial conditions \(\left( {x_1 (0)=0.1,x_2 (0)=x_3 (0)=x_4 (0)=0} \right) \) and the final state at each iteration of the bifurcation control parameter \(\alpha \) serves as the initial state for the next iteration. The one in magenta is obtained by starting the system from the same (i.e. fixed) initial conditions \(\left( {x_1 (0)=-0.2,x_2 (0)=0,x_3 (0)=x_4 (0)=0} \right) \) at each iteration of the control parameter. The three largest Lyapunov exponents are obtained by exploiting the same strategy as that used for the cyan bifurcation diagram (see Fig. 5b). Those diagrams are of great utility for a practical circuit design of a physical jerk circuit. In particular, it can be noticed, in both cases, a window of hysteretic dynamics marked by the coexistence of a pair of periodic attractors with a pair of chaotic ones [depending solely on the choice of initial conditions (see Sect. 3.3)]. Also, it should be stressed that the routes to chaos reported in this work have also been found in various other nonlinear systems such as the second-order non-autonomous Duffing oscillator [33] and Chua’s circuit [44].

3.3 Occurrence of multiple attractors

With Reference to the enlargement of the diagram shown in Fig. 6a, a window of hysteretic dynamics can be identified in the range \(27.24\le \alpha \le 29.8\) (see Fig. 6a). In this graph, two sets of data (magenta and cyan) are superimposed. The diagram in cyan is obtained for increasing values of parameter \(\alpha \) starting from the initial point \(\left( \alpha =26,x_1 (0)=0.4,x_2 (0)=x_3 (0)=x_4 (0)=0 \right) \), while the one in magenta is obtained for decreasing values of \(\alpha \) starting from the initial point \(\left( \alpha =29.8,x_1 (0)=0.04,x_2 (0)=x_3 (0)=x_4 (0)=0 \right) \). In both cases, the final state at each iteration of the bifurcation control parameter \(\alpha \) serves as the initial state for the next iteration. Using the same strategy as described above, the diagram of Fig. 6b is obtained. In the graph of Fig. 6b, the diagram in magenta is obtained for increasing values of parameter \(\delta \) starting from the initial point \(\left( \delta =2,x_1 (0)=0.04,x_2 (0)=x_3 (0)=x_4 (0)=0 \right) \) while the one in cyan is obtained for decreasing values of \(\delta \) starting from the initial point \(\left( \delta =3,x_1 (0)=-0.52,x_2 (0)=x_3 (0)=x_4 (0)=0 \right) \). For values of \(\alpha \) within the range \(27.24\le \alpha \le 29.8\), the long-term behavior of the system depends crucially on the choice of initial conditions, thus leading to the interesting and striking phenomenon of coexisting multiple attractors’ behavior. Up to four different solutions can be obtained depending solely on the value of initial conditions (see Fig. 7a, b). For instance, the phase portraits of Fig. 7a(i)–a(ii) can be obtained under the initial conditions \(x_1 (0)=\pm 1.4, x_2 (0)=0, x_3 (0)=0, x_4 (0)=0\) and \(x_1 (0)=\pm 2.4, x_2 (0)=0, x_3 (0)=0, x_4 (0)=0\), respectively, with \(\alpha =29.12\). Similarly, we provide in Fig. 7 the coexistence of four different asymmetric chaotic solutions for different initial conditions for \(\alpha =27.3\). Correspondingly, using the same set of parameters in Fig. 7a and carrying out a scan of initial conditions (see Fig. 8), we have computed the domain of initial conditions in which each attractor can be found. The complex structure of the resulting basin boundaries is clearly visible in Fig. 8 where cross sections of the basins of attraction are provided, respectively, for \(x_1 =0, x_2 =0, x_3 =0\), and \(x_4 =0\) associated with the symmetric pair of limit cycles (blue and yellow) and the pair of chaotic attractors (green and magenta). Red zones denote unbounded motion. It should be mentioned that for all sets of parameters considered in this work, the system has a single equilibrium point \(E_0 \left( {0,0,0,0} \right) \) for which the eigenvalues always have real parts of opposite sign. For instance, considering the following set of parameters: \(\delta =2, \varepsilon =2\times 10^{-3}, \eta =10\), \(\beta =5.36\times 10^{-5}, \rho =10.121\, \alpha =29.12\), for which the system develops a pair of periodic attractors coexisting with a pair of chaotic ones, we have numerically computed the following eigenvalues: \(\lambda _1 =-4.2397, \lambda _{2}=-1.0001\) and \(\lambda _{3,4} =1.6198 \pm \hbox {3.3336i}\). Hence, it is clear that the system always experiences self-excited attractors [46,47,48,49,50,51]. It ought be mentioned that, as far as the authors’ knowledge goes, the striking phenomenon of multiple stability involving four disconnected coexisting attractors is also reported in the Leipnik–Newton system [27] and very recently in a linear transformation of jerk system Models MO5 and MO15 [23, 24]. The case reported in this work is singular in the sense that the novel memristor circuit has a unique fixed point in contrast to the above-mentioned cases. Thus, a simple conclusion that can be drawn from this paper is that the presence of a multitude of equilibrium points is not a necessary condition for the occurrence of multiple coexisting attractors in a jerk system in particular and nonlinear dynamical systems in general. However, we would also like to recall that multiple attractors behavior (involving least than four non-static attractors) is reported in various other nonlinear dynamical systems such as laser [52], biological system [53, 54], Lorenz system [55], electrical circuits [56,57,58,59], smooth 3D and 4D systems [60,61,62], just to name a few. The intriguing situation involving the coexistence of infinitely many attractors also called extreme multistability was recently reported by Hens and co-workers [63] and very recently by [64, 65] in a fourth-order memristor oscillators. It is known that the occurrence of multiple attractors represents an additional form of randomness [66]; also, some obvious potential applications include, for instance, chaos-based secret communication, image encryption as well as random bits generation. However, this singular phenomenon is not desirable in general and thus requires control. Detailed development on this direction is far beyond the scope of this work; also, interested readers would consult profitably the review work on control of multistability described in [67].

Fig. 7
figure 7

Coexistence of four different attractors (a pair of chaotic attractors a(i) and a pair of period-3 limit cycles a(ii)) for \(\alpha =29.12\) and \(\delta =2\). Initial conditions \((x_1 (0),x_2 (0),x_3 (0),x_4 (0))\) are \(\left( {\pm 1.4,0,0,0} \right) \) and \(\left( {\pm 2.4,0,0,0} \right) \), respectively, and coexistence of four different chaotic attractors (a pair of chaotic attractors b(i) and another pair of chaotic attractors b(ii)) for \(\alpha =27.3\) and \(\delta =2\). Initial conditions \((x_1 (0),x_2 (0),x_3 (0),x_4 (0))\) are \(\left( {\pm 1.4,0,0,0} \right) \) and \(\left( {\pm 2.4,0,0,0} \right) \)

Full size image
Fig. 8
figure 8

Cross sections of the basin of attraction for \(x_3 (0)=x_4 (0)=0, x_1 (0)=x_4 (0)=0, x_2 (0)=x_4 (0)=0, x_2 (0)=x_3 (0)=0\), respectively, corresponding to the asymmetric pair of period-3 cycle (blue and yellow) and the pair of chaotic attractors (green and magenta) obtained for \(\alpha =29.12, \delta =2\) et \(\eta =10\)

Full size image
Fig. 9
figure 9

Bifurcation diagrams showing local maxima of the coordinate \(x_2 \left( \tau \right) \) in terms of control parameter \(\delta \) for remerging Feigenbaum tree (bubbling): a primary bubble for \(\alpha =1.6\); b period-4 bubble for \(\alpha =1.75\); c period-8 bubble for \(\alpha =1.82\); d–f full Feigenbaum remerging tree at \(\alpha =1.85, \alpha =1.95\) and \(\alpha =2.2\), respectively. Parameters are: \(\eta =100\) and \(\delta \) in the range \(0\le \delta \le 7\)

Full size image
Fig. 10
figure 10

First-return map of the maxima of the coordinate \(x_2 \). This map is indicative of one-dimensional maps with two critical points confirming the occurrence of antimonotonicity phenomenon in the improved Colpitts oscillator. The parameters are: \(\alpha =3.2\) and \(\eta =100\)

Full size image
Fig. 11
figure 11

The experimental memristor-based novel jerk circuit in operation. The oscilloscope displays the double-band chaotic attractor captured from the experimental circuit mounted on a breadboard

Full size image
Fig. 12
figure 12

Experimental phase portraits (right) obtained from the circuit (with \(R_m =1\,\hbox {k}\Omega , R_\delta =10\,\hbox {k}\Omega \) and \(R=10\,\hbox {k}\Omega )\) using a dual-trace oscilloscope in the XY mode; the corresponding numerical phase portraits are shown in the left. Output voltages \(-X_2 \) and \(X_3 \) are fed to the X and Y input, respectively: a period-1 for \(R_\alpha =185\Omega \), b period-2 for \(R_\alpha =284.56\Omega \), c period-4 for \(R_\alpha =313.65\Omega \), d single-band chaos for \(R_\alpha =357.7\Omega \), e single-band chaos for \(R_\alpha =587.5\,\Omega \), f double-band chaotic attractor for \(R_\alpha =0.9\,\hbox {k}\Omega \), g single-band chaos for \(R_\alpha =1.54\,\hbox {k}\Omega \), h period-4 for \(R_\alpha =1.7\,\hbox {k}\Omega \), i period-2 for \(R_\alpha =2.14\,\hbox {k}\Omega \), j period-1 for \(R_\alpha =2.54\,\hbox {k}\Omega \) The scales are \(X=0.2V{/}\mathrm{div}\) and \(Y={0.5V}{/}\mathrm{div}\)

Full size image
Fig. 13
figure 13

Coexistence of multiple solutions for \(R_\alpha =331\Omega \). Both periodic and chaotic attractors appear randomly in experiment when switching on and off the power supply. The scales are \(X=0.2V{/}\mathrm{div}\) and \(Y={0.5V}{/}\mathrm{div}\) for all pictures

Full size image
Fig. 14
figure 14

Coexistence of multiple solutions for \(R_\alpha =366\Omega \). Four chaotic attractors appear randomly in experiment when switching on and off the power supply. The scales are \(X=0.2V{/}\mathrm{div}\) and \(Y={0.5V}{/}\mathrm{div}\) for all pictures

Full size image

3.4 Antimonotonicity

It is well established that in many nonlinear systems, periodic orbits can be created and then annihilated via reverse period-doubling bifurcation scenarios as a bifurcation control parameter is slowly monitored [68]. This phenomenon is referred to as antimonotonicity and has been reported in various nonlinear systems including the Duffing oscillator [69, 70], Chua circuit [71], laser system [72] and second-order nonlinear non-autonomous MLC circuit [73, 74]. Recall that in order for a nonlinear system to develop forward and reversed period-doubling bifurcations, it is necessary to form periodic islands in the parameter space [68]. Also, in order to demonstrate the phenomenon of antimonotonicity in our model (1), we have produced some bifurcation diagrams as parameter \(\delta \) is varied in the range \(0.1\le \delta \le 7\) for some discrete values of parameter \(\alpha \). Sample results are depicted in Fig. 9. In light of the graphs in Fig. 9, for \(\alpha =1.60\), a period-2 bubble is observed and the branch develops a stable period-4 bubble at \(\alpha =1.75\). Similarly, we have a period-8 bubble at \(\alpha =1.82\). As \(\alpha \) is further increased, more bubbles are created until an infinitely tree (like chaos) finally occurs. In Fig. 10, we provide the first return map of the coordinate \(x_1 \) (\(M_{n+1} \left( {x_1 } \right) =f\left( {M_n \left( {x_1 } \right) } \right) \). This map is typical of one-dimensional maps with two critical points \(P_1 \) and \(P_2 \) which support the occurrence of antimonotonicity in the novel system (1) [68, 75]. Following the work of [75], reverse period-doubling scenarios can occur when a minimum number of conditions are satisfied. The main requirement is that the system of differential equations must remain invariant under the transformation \(\left( {x_1 ,x_2 ,x_3 ,x_4 } \right) \leftrightarrow \left( {-x_1 ,-x_2 ,-x_3 ,-x_4 } \right) \) where \(\left( {x_1 ,x_2 ,x_3 ,x_4 } \right) \) represents the system state vector. System (5) does not remain invariant with respect to the above transformation. However, the phenomenon of antimonotonicity and reverse period doubling do occur (see Fig. 9). Consequently, the above criterion by Bier and Boutis [75] is not a necessary condition for the occurrence of antimonotonicity in a nonlinear system.

4 Experimental study

According to the theoretical analysis developed above, it is predicted that the novel memristive jerk circuit under consideration can experience extremely rich and complex bifurcation structures. This section aims to verify the theoretical results obtained previously by carrying out an experimental study of the real memristive oscillator [76,77,78]. For this purpose, the circuit diagram of Fig. 1 is realized on a breadboard (see Fig. 11). The circuit consists of TL084 op. amplifiers chip powered by a symmetric ±15 V dc voltage supply. The same values of electronics components used for the numerical investigations are kept here to enable the comparison process. The following set of circuit parameters is used: \(R_m =1\,\hbox {k}\Omega , R_\delta =10\,\hbox {k}\Omega , R=10\,\hbox {k}\Omega , C_1 =C_2 =C_3 =C=10\,\hbox {nF}, C_m =100\,\hbox {nF}\) (see caption of Fig. 1). Experimental results are obtained by slowly increasing \(R_\alpha \) (i.e. decreasing parameter \(\alpha )\) and recording phase space trajectories \(\left( {X_1 ,X_2 } \right) \) using a dual-trace oscilloscope in the XY mode. When slowly adjusting the control resistor \(R_\alpha \), various types of bifurcations are observed in the experimental memristive jerk circuit. In particular, for \(R_\alpha =185\Omega \) a period-1 limit cycle is observed. When \(R_\alpha \) is gradually increased, the complete sequence of bifurcation reported during the numerical analysis is observed. Some tiny domains of regular oscillations sandwiched within the chaotic zones are also noted in experiment. This is clearly highlighted by the experimental phase portraits in Figs. 11 and 12 showing the real behavior of the novel memristive jerk circuit proposed in this work. In light of the pictures in Fig. 12, it can be seen that the real memristive jerk circuit experiences the same bifurcation scenarios as predicted during the theoretical analysis.

To experimentally demonstrate the coexistence of multiple attractors in the experimental memristive jerk circuit, the values of the control resistor are fixed to \(R_\alpha =331\Omega \). When switching on and off the power supply (and thereby randomly altering initial conditions), either a regular period-3 limit cycle or a single-band chaotic one can be found. As expected (owing to the fractal structure of basin boundaries), jumps between various competing attractors are observed in experiment. The four experimental coexisting attractors are shown in Fig. 13. Similarly, four different coexisting asymmetric chaotic solutions for \(R_\alpha =366\Omega \) are also depicted in Fig. 14. Once more, a very good similarity can be captured between numerical and experimental results. However, a slight discrepancy that may be attributed to the precision on the values of electronic components as well as the simplifying assumptions considered during the modeling process (i.e. ideal diode model, ideal op. amplifier) can be noted between numerical and experimental results.

5 Conclusions

In summary, the dynamics of a novel memristive jerk circuit obtained by replacing the single semiconductor diode in the original jerk circuit of [17] with a first-order memristive diode bridge has been detailed in this work. The modification yields a relatively simple jerk circuit/system [79] with a symmetric nonlinearity capable of rich and interesting varieties of nonlinear phenomena such as period-doubling bifurcation, antimonotonicity, chaos and coexisting multiple attractors. By exploiting classical nonlinear analysis tools such as bifurcation diagrams, graph of Lyapunov exponents, equilibria and stability, phase space trajectories and frequency spectra, the dynamics of the system has been characterized with respect to its parameters. As a major result of this work, it is shown that the novel proposed memristive jerk circuit exhibits the unusual feature of multiple attractors (i.e. coexistence of four disconnected non-static attractors depending only on the selection of initial sates) for various ranges of circuit parameters. The novel memristive jerk circuit uses only off-the-shelf electronic components and may be re-scaled over a wide range of frequencies. To the best of authors’ knowledge, the jerk circuit introduced in this paper represents one of the simplest electrical circuits reported to date, capable of exhibiting such form of multistability [23,24,25, 41]. A very good agreement is observed between theoretical and experimental results.