1 Introduction

Since Lorenz discovered the first chaotic attractor [1], a series of significant progressive findings have been made on chaos research, such as chaos control [2, 3], chaos generation [4–6], chaos coefficients optimization [7], and chaotic encryption [8–10]. In recent years, by means of numerical calculations and bifurcation analysis, a series of new chaotic systems have been generated, for example, the new chaotic system based on Chen [11], the multi-wing [12, 13] and multi-scroll chaotic attractors [14–16], the hyper-chaotic system [17–20], the fractional-order chaotic system [21, 22], and so on. Due to the great application prospect, the studies on chaotic circuits have been widely concerned, and the analog chaotic circuits [23], integrated chaotic circuit [24, 25], and FPGA chaotic circuit [26, 27] have been realized constantly.

Fig. 1
figure 1

Four-wing chaotic attractor with \(a = 4, b = 6, c = 10, d = 5\), \(k = 1\), a projection on \(x-y\) plane, b projection on \(x-z\) plane

Full size image

So far, the rigorous proof of chaotic characteristics is still a difficult problem. Due to the calculation error, the numerical evidences of chaotic characteristics are insufficient to demonstrate the chaotic characteristics such as Lyapunov exponents and bifurcation diagrams. The topological horseshoe theory is a useful tool which can solve this problem [28–30]. Nonetheless, the topological horseshoe lemma [31–33] provided a practical computer-assisted proof method for rigorous verification of the existence of chaos, which has evolved from the Smale horseshoe map [34] and topological horseshoe theory proposed by Kennedy [35]. Some typical chaotic systems have been rigorously verified by utilizing this method. For example, Jia et al. proved the chaos existence of the Lü system [36]; Ma et al. [37] proved the existence of chaos of a financial system ; and Li et al. [38] founded a 3D topological horseshoe in a memristive system.

For a four-wing chaotic attractor, this paper rigorously verified its chaotic properties from view of mathematics. This paper is organized as follows. In Sect. 1, a brief overview on generation and properties verification of chaos is given. In Sect. 2, the three-dimensional four-wing chaotic attractor is introduced briefly. In Sect. 3, a one-dimensional tensile topological horseshoe in the Poincaré section is discovered by utilizing the topological horseshoe lemma, which verifies the existence of chaos in the four-wing attractor. This four-wing chaotic attractor is physically implemented based on an FPGA chip in Sect. 4. In the end, the research work is summarized in Sect. 5.

Fig. 2
figure 2

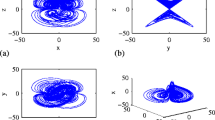
Poincaré section of the system (1), a section in \(x = 0\), b section in \(y= 0\)

Full size image

2 The four-wing chaotic attractor

Recently, a new three-dimensional four-wing chaotic attractor was proposed [39], which can be described as follows:

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{x}=ax-byz, \\ \dot{y}=-cy+xz, \\ \dot{z}=kx-dz+xy. \\ \end{array}} \right. \end{aligned}$$
(1)

The numerical analysis shows that the dynamic behaviors of this system are chaotic with wide parameter a, k ranges. For example, when \(a=4, b=6, c=10, d=5, k=1\), the Lyapunov exponents of the system (1) are \(\lambda _1 =1.038, \lambda _2 =0, \lambda _{3} =-12.045\); the corresponding chaotic attractors are shown in Fig. 1.

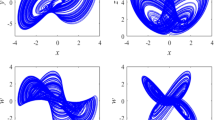
The chaotic characteristics of the system (1) were analyzed by utilizing a numerical bifurcation diagram and Lyapunov exponent spectrum [39]. To rigorously verify the existence of chaos by utilizing the topological horseshoe theory, the Poincaré section, which reflects the global structure of the attractor, should be seriously analyzed. Portions of the Poincaré section of the system (1) on different planes are depicted in Fig. 2.

As Fig. 2 shows, the dense points form a certain hierarchical structure, indicating that the attractor orbits have continuous bifurcation and folding in different directions. System (1) displays complex dynamic behaviors.

3 Topological horseshoe analysis and verification

3.1 Topological horseshoe lemma

The topological horseshoe lemma is a useful theoretical tool which can provide a rigorous computer-assisted verification method for the existence of chaos. The topological horseshoe lemma is introduced as below [16].

Suppose that an f-connected family F exists with respect to disjointed compact subsets \(D_1 ,\ldots ,D_{m-1} \) and \(D_{m }\). Then a compact invariant set \(K\subset D\) exists such that f|K is semi-conjugate to an m-shift map; therefore, its topological entropy satisfies \(ent(f)\ge \log m\). Based on the lemma, the system is chaotic when \(m >1\).

The topological horseshoe theorem cannot be applied in a continuous system directly; however, the Poincaré section and the Poincaré map bridge the gap between them. Therefore, we can select an appropriate Poincaré section and then prove that the corresponding Poincaré map is semi-conjugate to a 2-shift map, which implies that topological entropy of the attractor ent \((f) \ge \) log2, and thus the existence of chaos is verified.

3.2 Selected Poincaré section

Considering the section plane, \(\prod =\left\{ \left( {x,y,z} \right) \in R^{3}:\right. \left. x=0 \right\} \). As shown in Fig. 3, one wing of the attractor was selected as the corresponding cross section, \(\Gamma =\left| {ABCD} \right| \), with its four vertices \(A= \left[ {0, 0, 20} \right] , B= \left[ {0, 20, 20} \right] ,C= \left[ {0, 20, 0} \right] , D= \left[ {0, 0, 0} \right] \) and then choosing a subset \(P= \left| {EFGH} \right| \) in \(\Gamma \), with four vertices \(E= \left[ {0, 3.4, 6} \right] \), \(F= \left[ {0, 4.6, 7.3} \right] \), \(G= \left[ {0, 5.7, 7.8} \right] ,H= \left[ {0, 4.5, 6.2} \right] \). The subset P is shown in Fig. 4.

Fig. 3
figure 3

The selected cross section \(\Gamma =\left| {ABCD} \right| \)

Full size image
Fig. 4
figure 4

The subset \(P=\left| {EFGH} \right| \)

Full size image

3.3 Definition of a Poincaré map

Definition 1

Define a Poincaré map

$$\begin{aligned} \tau :P\rightarrow \Gamma \end{aligned}$$
(2)

For any point \(x\in P\), \(\tau (x)\) is the first return map point in the \(\Gamma \) section of system (1) with the initial condition x. Under the map \(\tau \), the image \(\tau (P)\) is a very thin hook-like strip which is situated wholly across P.

As shown in Fig. 5, enlarging the neighborhood region of EF, \(E^{\prime }F^{\prime }\) (green line) and \(G^{\prime }H^{\prime }\) (red line) cross E H in the enlarged view, where the image \(\tau (P)=\left| {E^{\prime }F^{\prime }G^{\prime }H^{\prime }} \right| \), and \({E}^{\prime }= \left[ {0, 7.8303, 10.9371} \right] \), \({F}^{\prime }= \left[ {0, 11.7420, 14.3876} \right] \), \({G}^{\prime }= \left[ 0, 14.0442,\right. \left. 16.7601 \right] \), \({H}^{\prime }= \left[ {0, 5.5276, 8.2568} \right] \).

Fig. 5
figure 5

The image \(\left| {{E}^{\prime }{F}^{\prime }{G}^{\prime }{H}^{\prime }} \right| \)of the quadrangle \(\left| {EFGH} \right| \) under the map \(\tau \), partially enlarged view under the lower right corner

Full size image
Fig. 6
figure 6

Two mutually disjointed subsets \({\varvec{a}}\) (green section) and \({\varvec{b}}\) (purple section). (Color figure online)

Full size image

3.4 Computer-assisted verification

According to the topological horseshoe lemma, two mutually disjointed compact subsets should be selected. After many numerical calculations, subsets \({\varvec{a}}\) and \({\varvec{b}}\) of subset P are chosen. As shown in Fig. 6, subset \({\varvec{a}} = \left| {EIJH} \right| \), where \(E=\left[ {0, 3.4, 6} \right] ,I=\left[ {0, 3.88, 6.52} \right] \), \(J=\left[ {0, 4.86, 6.68} \right] \), \(H=\left[ {0, 4.5, 6.2} \right] \), and subset \({\varvec{b}} = \left| {KMNL} \right| \), where \(K=\left[ {0, 4, 6.65} \right] ,M=\left[ {0, 4.48, 7.17} \right] \), \(N=\left[ {0, 5.58, 7.64} \right] \), \(L=\left[ 0, 4.98,\right. \left. 6.84 \right] \).

Then, for the first return, the Poincaré map \(\tau :P\rightarrow \Gamma \), \(\tau (a)=\left| {{E}^{\prime }{I}^{\prime }{J}^{\prime }{H}^{\prime }} \right| \), the image \(\left| {{E}^{\prime }{I}^{\prime }{J}^{\prime }{H}^{\prime }} \right| \) is a very thin hook-like strip with EH mapped to \({E}^{\prime }{H}^{\prime }\) and IJ mapped to \({I}^{\prime }{J}^{\prime }\), where \(I^{\prime } =\left[ {0, 2.7768, 4.9288} \right] \), \(J^{\prime } =\left[ {0, 3.1307, 5.3694} \right] \). Figure 7 shows that \({E}^{\prime }{H}^{\prime }\) is above the edge EH and \({I}^{\prime }{J}^{\prime }\) is below the edge IJ. Furthermore, by enlarging the local region in Fig. 7, we can find that \(E^{\prime } I^{\prime }\) (red line) and \(J^{\prime } H^{\prime }\)(green line) are wholly situated across the set \({\varvec{a}}\).

Fig. 7
figure 7

The image \(\left| {E^{\prime } I^{\prime } J^{\prime } H^{\prime } } \right| \) of the quadrangle \(\left| {EIJH} \right| \), partially enlarged view under the lower right corner

Full size image
Fig. 8
figure 8

The image \(\left| {K^{\prime } M^{\prime } N^{\prime } L^{\prime } } \right| \) of the quadrangle \(\left| {KMNL} \right| \), partially enlarged view under the lower right corner

Full size image
Fig. 9
figure 9

Structure model of a discretized chaotic system, a general model of simulation, b substructure of realization of variable x, c substructure of realization of variable y, d substructure of realization of variable z

Full size image
Fig. 10
figure 10

Chaotic attractors generated by the FPGA, a projection on \(x-y\) plane, b projection on \(x-z\) plane, c projection on \(y-z\) plane

Full size image

As shown in Fig. 8, \(\left| {K^{\prime } M^{\prime } N^{\prime } L^{\prime } } \right| \) depicts the image of subset \({\varvec{b}}\) under the Poincaré map \(\tau \), \(\tau (b)=\left| {K^{\prime } M^{\prime } N^{\prime } L^{\prime } } \right| \), where \(K^{\prime } =\left[ {0, 2.1519, 4.1357} \right] ,M^{\prime } =\left[ {0, 9.9891, 12.5830} \right] \), \(N^{\prime } =\left[ {0, 6.1229, 8.5603} \right] \), \(L^{\prime } =\left[ {0, 2.6377, 4.7541} \right] \). From enlarged local region in Fig. 8, it is clear that \({K}^{\prime }{L}^{\prime }\) is above the edge KL, \({M}^{\prime }{N}^{\prime }\) is below the edge MN, the edges KL and MN are mapped to opposite side respectively. It suggested that the image of subset \({\varvec{b}}\) is positioned wholly across the set \({\varvec{b}}\).

Based on the above analysis, it is obvious that the images \(\tau (a)\) and \(\tau (b)\) are wholly situated across P;  so, the following conclusion can be obtained. For each connection \(\xi \) between subset \({\varvec{a}}\) and subset \({\varvec{b}}\) in set P,the images \(\tau (\xi \cap a)\) and \(\tau (\xi \cap b)\) also wholly cross the set P. In other words, the images \(\tau (\xi \cap a)\) and \(\tau (\xi \cap b)\) are still connections between subset \({\varvec{a}}\) and subset \({\varvec{b}}\) in set P. On the basis of Definition 1, an f-connected family of the first return Poincaré map exists. According to the topological horseshoe lemma, the map \(\tau \) is semi-conjugate to an m-shift map; here \(m = 2\); hence the topological entropy \(ent(f)\ge \log 2>0\), which implies that the system (1) has a positive topological entropy with \(a=4, b=6, c=10, d=5, k=1\). The existence of chaos in system (1) was verified.

4 FPGA implementation

Currently, studies on chaotic circuit realization based on the analog devices have attained some achievements. However, due to the factor of parameter drift, signal regeneration in an analog circuit is sensitive to the device error, which suggests that an analog chaotic circuit is difficult to practically apply in secure communications. On the contrary, the chaotic signal is easy to be regenerated in a digital circuit, and the signal precision is controllable. The digital chaotic circuit is more suitable for application in the field of information encryption.

Due to the high logic density, versatility, and other features, the FPGA chip has been widely used. In this section, a digital chaotic circuit is designed and implemented by utilizing the FPGA chip. Firstly, according to Eq. (3), the continuous system (1) is discretized by using the Euler method. Based on Nyquist sampling criteria, sampling frequency should be at least twice of input signal frequency. The discrete chaotic system should follow this rule. By using the pwelch estimate method [40, 41], the cutoff frequency of system (1) is about 18.6 Hz, and sampling rate should be 37.2 Hz at least to assure the chaotic behavior. To keep the smoothness of chaotic trajectories, we fix the sample rate to 1000 Hz in this section.

For the convenience of programming design, the coordinate translation of a discrete chaotic system (3) is executed, which does not change the dynamic behaviors of system (1).

The discretized chaotic system is shown as Eq. (3).

$$\begin{aligned} \left\{ {\begin{array}{l} x(k+1)=x(k)+\Delta t[ax(k)-by(k)z(k)], \\ y(k+1)=y(k)+\Delta t[-cy(k)+x(k)z(k)], \\ z(k+1)=z(k)+\Delta t[kx(k)-dz(k)+x(k)y(k)], \\ \end{array}} \right. \end{aligned}$$
(3)

where the parameters \(a=4, b=6, c=10, d=5, k=1,\Delta t=0.001\).

As shown in Fig. 9, the structure model of Eq. (3) is built by using the System Generator Module.

Subsequently, the discretized model (3) is transformed into VHDL language which is convenient for being compiled and downloaded in an ISE development environment. Then the four-wing chaotic attractor is implemented by using the VIRTEX-II FPGA development board.

For the convenience of the analog oscilloscope observation, the output digital signals of the FPGA are converted into analog signals by using a DAC900 chip. The D/A chip can meet the precision requirement of chaotic signal conversion. The clock frequency of the D/A chip and the FPGA chip is synchronization in 20MHz. The four-wing chaotic attractors generated by the FPGA are illustrated in Fig. 10.

The above experimental results show that the chaotic attractors generated by the FPGA are consistent with the numerical simulations on each phase plane, which verifies the accuracy and validity of the FPGA implementation method. Compared with the analog circuit, the chaotic signal generated by the FPGA chip has obvious advantages in stability, reproducibility, and accuracy. Furthermore, this method is easy to modify and extend, is also suitable for higher-dimensional chaotic systems, and has good versatility.

5 Conclusion

In this paper, a certain three-dimensional four-wing chaotic attractor is comprehensively studied, and its chaotic properties were rigorously verified through the integrated use of the topological horseshoe theory and numerical calculations. The key of this method is defining a first return Poincaré map in a selected Poincaré section, which takes many numerical calculations. Subsequently, a one-dimensional tensile topological horseshoe is discovered, which verifies the existence of chaos in the four-wing attractor. This method is more convenient and practical than the traditional mathematics proof method. In addition, a digital circuit is designed to realize the four-wing chaotic attractor by using the FPGA chip, which provides technical support for the engineering applications of chaos.