1 Introduction

Harvesting of the species and misuse of biological resources are normal in fishery, forestry, agriculture and wildlife management. The pioneering work on this issue was done by Clark [17] Quite a good number of works were published on harvesting in different systems such as fishery [14], prey–predator models, eco-epidemiological models [5] and time delay models [42]. In ecology, control of disease is one of the major challenges, and the harvesting is a common procedure for controlling the disease. A lot of theoretical studies have been carried out on controlling the disease with culling as a harvesting policy. Harvesting can make a system stable or unstable [18]. Chattopadhyay et al. [13] studied a harvested predator–prey model with infection in the prey population and concluded that harvesting on infected prey prevents the limit cycle oscillations and may be used as a biological control. Harvesting in both the susceptible and infected prey species was studied by Bairagi et al. [5]. They concluded that reasonable harvesting can remove the parasite from their hosts The authors also concluded that impulsive harvesting can control the cyclic behavior and obtain stable disease-free equilibrium. However, the optimal harvesting policy in such a situation is very important and cannot be ignored as overexploitation can lead to the extinction of the species. For example, due to overexploitation, the Atlantic cod population collapsed suddenly in 1992. In another example, the giant bird Moa were overexploited to the point of extinction and their predator giant Haast’s eagle also become extinct. These observations motivate us to study the dynamics under the optimal harvesting policy by using the Pontryagin’s maximum principle.

Eco-epidemiological models have received much attention from scientists in recent times. The spread of disease among predator–prey interacting populations was first modeled by Hadeler and Freedman [25]; after that, Chattopadhyay and Arino [11] coined the term eco-epidemiology for such systems. In recent years, researchers are paying more enthusiasm to consolidate these two critical areas of research, i.e., ecology and epidemiology [4, 12, 28, 62] that have significant biological importance in nature. Biological application of such systems in nature was first demonstrated by Gulland [24]. The main motives of eco-epidemiological models are centered around the role of infection on species mortality, reduction in reproduction rate, characteristics of contamination, change in population size, spread of epidemic waves, permanence of the disease and global behavior of the infected species [51].

Recently, substantial research has been done on the development of the concept for Allee effect, which corresponds to the positive correlation between population size/density and per capita growth rate at low population density [1, 38, 46, 48, 59]. Complications in finding mates, reproductive facilitation, predation, environment conditioning, inbreeding depressions, etc. are few well-known mechanisms behind this Allee effect. Allee effects mainly classified into two ways: strong and weak [20]. Ecologists paid significant attention on this topic as it relates to species extinction [22, 56, 58]. Allee effect and disease are both responsible for extinction of species, and if the disease is combined with the Allee effects, the interaction between them has substantial biological significance in nature [29, 34, 53–55, 66]. Many species suffer from the Allee effect and the disease. For example, the combined effects of a disease and the Allee effect have been observed in the African wild dogs [19] and the island fox [3]. As a consequence, researchers have paid significant attention on Allee effect in eco-epidemiology [7, 8, 10, 52].

Exploitations in multispecies system are interesting phenomena but not easy to solve both theoretically and practically. On the other hand, time delay may arise in many ecological systems and man-made activities in biology, medicine and other areas (for details see [35] and the references therein). Ignoring time delay means ignoring reality; thus, without delays, dynamical models become a worse conjecture of reality. Various biological reasons lead to the introduction of time delays in models of disease transmission. Time delays used to model the mechanisms in the disease dynamics [30, 44] described a simple HIV/AIDS model with a single class of infective, which incorporates a time delay due to the long incubation period of the disease. Incubation period is the period from the point of infection to the appearance of symptoms of the disease. Time delay plays an important role in biological systems and network of neurons. Propagation time delay (between nodes or in neurons), intrinsic time delay or response time delay that neuron needs to give the response to external forcing. For example, appropriate time delay in autapse of neuron and network can produce complex biological function such as the pacemaker in a network [21, 41, 49, 67]. Kuang [35] concluded that for digesting food, the predator requires some time as time delay. There are numerous research articles on dynamical behaviors such as periodic oscillation, persistence, bifurcation, chaos of population with delayed prey–predator systems [9, 39, 43, 47, 57, 60, 63]. To our knowledge, there are very few works on time delayed population dynamics in the presence of Allee effect [7, 10, 65]. According to the authors, this is the first noble attempt of considering the time delay effects for eco-epidemic models under the influence of Allee effect and harvesting simultaneously in the prey population.

The combined effect of Allee and harvesting in a delayed eco-epidemiology may provide some interesting results. To study the dynamics of such complex system under the optimal harvesting strategy is also another interesting issue. The rest of the article is organized as follows: Sect. 2 deals with the development of the model. In Sect. 3, we have analyzed the non-delayed model. In Sect. 4, detailed mathematical analysis of our time delayed model has been presented. In this section, we have discussed many important issues such as boundedness of delayed model, uniform persistence, permanence, direction and stability of Hopf bifurcation. The time delayed model shows the chaotic behavior; the existence of chaotic dynamics has been discussed in Sect. 5. In Sect. 6, we have discussed the effect of three important parameters: time lag, inverse of individual searching efficiency and harvesting effort. In Sect. 7, we have discussed the optimal harvesting policy for the time delayed model, to maximize the profit earned by harvesting the prey species (both susceptible and infected) only. The article ends with a discussion.

2 The model

In this section, we develop a delayed eco-epidemiological model with Allee effects and the disease in the prey population.

2.1 General eco-epidemiological model with disease and weak Allee in prey

We start from the assumption that the disease infects the prey population and divides it into two disjoint classes, viz. susceptible (S) and infected (I), so that the total population at any time t is \(N = S+I\). Susceptible population is only capable of reproducing, and the infected population dies before having the capacity of reproduction. We also assume that the disease is not vertically transmitted, but it is untreatable and causes an additional death.

We assume that the prey population follows the logistic dynamics with a weak Allee effect in the absence of disease and predation, and can be described by the following single species population model \(\frac{\mathrm{d}S}{\mathrm{d}t} = S(1-S)\frac{S}{S+\theta },\) where S denotes the normalized healthy prey population. The term \(\frac{S}{S+\theta }\) represents the Allee effect function (known as the weak Allee function), which is the probability of finding a mate and \(\theta \) is the inverse of the individuals searching efficiency [20]. No mating occurs at zero population size, and mating is guaranteed when the population is large (i.e., \(\frac{S}{\theta +S}\rightarrow 1\) as \(S\rightarrow +\infty \)). For small prey population density, bigger values of \(\theta \) strengthen the Allee effect and slow down the per capita growth rate of the prey.

A general predator–prey model where prey is subjected to the weak Allee effects and the disease is given by the following set of nonlinear differential equations:

$$\begin{aligned} \begin{array}{lcl} \frac{\mathrm{d}S}{\mathrm{d}t} &{}=&{} S\left( 1-S-I\right) \frac{S}{S+\theta } - \phi (N) \frac{I}{N} S - g(S, N)P, \\ \frac{\mathrm{d}I}{\mathrm{d}t} &{}=&{} \phi (N) \frac{I}{N} S- g(I, N)P - \mu I, \\ \frac{\mathrm{d}P}{\mathrm{d}t} &{}=&{} P\left[ c g(S,N)+\gamma g(I,N)-d\right] . \end{array} \end{aligned}$$
(1)

where all parameters are non-negative: The parameter d represents the natural death rate of predator; the parameter \(c\in (0,1]\) is the conversion rate of susceptible prey biomass into predator biomass; and \(\gamma \) indicates that the effects of the consumption of infected prey on predator. The functions \(\phi (N)\) and g(S / I, N) are the general forms of disease transmission function and functional responses, respectively.

2.2 Model with gestation delay

Next, we include two important biological components in the model (1). First, after consumption of prey by predator, some amount of energy in the form of prey biomass is converted into predator biomass through a very complicated internal digestion process of the predator. This bio-physiological procedure is not basic; the transformation of prey energy to predator energy is not immediate, and few procedures are included in this complex mechanism. To start with, the portion of prey biomass goes into the digestive system of predator. Digestion is a convoluted process; a few proteins are emitted in the digestive system which act one by one and the prey foods such as starch, protein and fat are processed and changed into monosaccharide, amino acids, fatty acids and glycerol. The digested foods are absorbed in the digestive system of the predator, and the prey food is assimilated into the predator’s protoplasm, i.e., transformed into the predator’s energy in the form of biomass. The whole transformation process requires time; thus, we have considered a constant time lag \(\tau ({>}0)\) for the gestation of predator [15, 35, 40, 64]. The model becomes

$$\begin{aligned} \frac{\mathrm{d}S}{\mathrm{d}t}= & {} S\frac{S}{S+\theta }\left( 1-S-I\right) - \phi (N) \frac{I}{N} S - g(S, N)P, \nonumber \\ \frac{\mathrm{d}I}{\mathrm{d}t}= & {} \phi (N) \frac{I}{N} S- g(I, N)P - \mu I, \nonumber \\ \frac{\mathrm{d}P}{\mathrm{d}t}= & {} P\left[ c g(S(t-\tau ),N(t-\tau ))\right. \nonumber \\&\left. +\,\gamma g(I(t-\tau ),N(t-\tau ))-d\right] . \end{aligned}$$
(2)

2.3 Model with predation only on infected prey

We have neglected the predation on susceptible prey by the predator population and considered that the predator feeds only on infected prey. This assumption supports the experimental evidence provided by Lafferty and Morris [37]. They evaluated that the predation rate on infected fish, on an average, is 31 times higher than the predation rate on susceptible fish. In addition, we have assumed that the consumption of infected prey contributes positive growth to the predator population.

Therefore, a predator–prey model with the above assumptions can be described by the following set of nonlinear differential equations:

$$\begin{aligned} \begin{array}{lll} \frac{\mathrm{d}S}{\mathrm{d}t} &{}=&{} S\left[ (1-S-I)\frac{S}{S+\theta }-\beta I\right] \\ \frac{\mathrm{d}I}{\mathrm{d}t} &{}=&{} I\left[ \beta S-a P -\mu \right] \\ \frac{\mathrm{d}P}{\mathrm{d}t} &{}=&{} \gamma a P(t-\tau ) I(t-\tau )-d P \\ &{}=&{} \alpha P(t-\tau )I(t-\tau ) -d P. \end{array} \end{aligned}$$
(3)

For our current study, we have considered disease transmitted through mass action law and predator follows Holling type I functional response, where \(\beta \) is the disease transmission rate and a is the predation rate.

2.4 Model with harvesting effort

In this study, we have considered harvesting on the prey populations (both on susceptible and infected prey), while the predator population is excluded from the harvesting process. The lack of economic viability of such harvesting, predator conservation, etc. is various reasons for such exclusions. In effect, both the predator and the harvester are competing for the same resource, namely the prey population. Considering the harvesting effects in (3), we get

$$\begin{aligned} \frac{\mathrm{d}S}{\mathrm{d}t}= & {} S\left[ (1-S-I)\frac{S}{S+\theta }-\beta I-q_1 E\right] \nonumber \\ \frac{\mathrm{d}I}{\mathrm{d}t}= & {} I\left[ \beta S-a P -\mu -q_2 E\right] \nonumber \\ \frac{\mathrm{d}P}{\mathrm{d}t}= & {} \alpha P(t-\tau )I(t-\tau ) -d P \end{aligned}$$
(4)

where E is the harvesting effort, \(q_1\) and \(q_2\) are the catchability coefficients of the susceptible and infected preys, respectively. All the variables and parameters are positive. The variables and parameters used in the model (4) are presented in Table 1.

The initial conditions for the system (4) take the form

$$\begin{aligned}&S(\phi ) = \psi _{1}(\phi ),~~~ I(\phi )= \psi _{2}(\phi ),~~~ \\&\quad P(\phi )= \psi _{3}(\phi ),~~~~ -\tau \le \phi \le 0, \end{aligned}$$

where \(\psi =(\psi _{1}, \psi _{2}, \psi _{3})^\mathrm{T}\in {\mathcal {C}}_{+} \) such that \(\psi _{i}(\phi )\ge 0 \) \((i=1, 2, 3)\), \(\forall \) \( \phi \in [-\tau , 0 ] \), and \({\mathcal {C}}_{+}\) denotes the Banach space \({\mathcal {C}}_{+}\left( [-\tau , 0 ],{\mathbb {R}}^{3}_{+}\right) \) of continuous functions mapping the interval \([-\tau , 0 ]\) into \({\mathbb {R}}^{3}_{+}\) and denotes the norm of an element \(\psi \) in \({\mathcal {C}}_{+}\) by

$$\begin{aligned} \displaystyle {\Vert \psi \Vert =\sup _{-\tau \le \phi \le 0}\Big \{\mid \psi _{1}(\phi )\mid , \mid \psi _{2}(\phi )\mid , \mid \psi _{3}(\phi )\mid \Big \}}. \end{aligned}$$

For biological feasibility, we further assume that \(\psi _{i}(0)> 0\), for \(i=1, 2, 3\).

Table 1 Variables and parameters used in the model (4)
Full size table

3 Mathematical analysis of the system (4) with no time lag \(\left( \tau = 0\right) \)

In this section, we have analyzed our model without the time delay effect. The system (4) without time delay can be written as

$$\begin{aligned} \begin{array}{lll} \frac{\mathrm{d}S}{\mathrm{d}t} &{}=&{} S\left[ (1-S-I)\frac{S}{S+\theta }-\beta I-q_1 E\right] , \\ \frac{\mathrm{d}I}{\mathrm{d}t} &{}=&{} I\left[ \beta S-a P -\mu -q_2 E\right] , \\ \frac{\mathrm{d}P}{\mathrm{d}t} &{}=&{} P\left[ \alpha I -\mathrm{d}\right] . \end{array} \end{aligned}$$
(5)

The system (5) has the following boundary equilibria:

$$\begin{aligned} E^0= & {} (0, 0, 0),~~~E^1_i = (S_i, 0, 0),\\ E^{2}= & {} \left( \frac{\mu +q_2 E}{\beta },\frac{\left( \frac{\mu +q_2 E}{\beta }\right) \left( 1-\frac{\mu +q_2 E}{\beta }\right) -q_1 E\frac{\mu +q_2 E}{\beta }-q_1 E \theta }{\frac{\mu +q_2 E}{\beta }+\beta \theta +\mu +q_2 E}, 0\right) =(S_2,I_2,0). \end{aligned}$$

where \(S_i\) are the roots of

$$\begin{aligned} S_i^2 +S_i(q_1 E-1)+q_1 E \theta =0. \end{aligned}$$

\(S_i\) exists, if \(1>q_1 E\) and \(S_{1}{=}\frac{(1-q_1 E) +\sqrt{(1-q_1 E)^2-4q_1 E \theta )}}{2},~ S_{2}=\frac{(1-q_1 E) -\sqrt{(1-q_1 E)^2-4q_1 E \theta )}}{2}\).

The system (5) has two interior equilibria \(E_1^* = \left( S_1^*, I_1^*, P_1^*\right) \) and \(E_2^* = \left( S_2^*, I_2^*, P_2^*\right) \), where \(I_2^* = \frac{d}{\alpha }=I_1^*\), \(P_1^* = \frac{1}{a}\left( \beta S_1^* - \mu -q_2 E\right) \), \(P_2^* = \frac{1}{a}\left( \beta S_2^*\right. \left. - \mu -q_2 E\right) \) and \(S_1^*,~S_2^*\) are the roots of the quadratic equation

$$\begin{aligned}&\left( S^*\right) ^2 + S^*\left( (\beta +1)\frac{d}{\alpha }+q_1 E -1\right) \\&\quad + \left( \beta \theta \frac{d}{\alpha }+ q_1 E \theta \right) = 0. \end{aligned}$$

The interior equilibria exist if \(1-(\beta +1)\frac{d}{\alpha }-q_1 E>0\) and both of the solutions satisfy \(S_1^* > \frac{\mu +q_2 E}{\beta }\), \(S_2^* > \frac{\mu +q_2 E}{\beta }\). Now,

$$\begin{aligned} \begin{array}{lll} S_1^* = \frac{B_{11}-\sqrt{B_{11}^2-4C_{11}}}{2} \text{ and } S_2^* = \frac{B_{11}+\sqrt{B_{11}^2-4C_{11}}}{2}, \end{array}\nonumber \\ \end{aligned}$$
(6)

where \(B_{11} = \left( 1-(\beta +1)\frac{d}{\alpha }-q_1 E\right) \) and \(C_{11} = \left( \beta \theta \frac{d}{\alpha }+q_1 E \theta \right) \).

Proposition 1

(Local stability of equilibria for the model (5)) The local stability of equilibria for the Model (5) is summarized in Table 2.

Table 2 Local stability of equilibria for the model (5)
Full size table

Proof

We have not given the detailed proof in this manuscript (our analysis is similar to the analysis given in [10]). \(\square \)

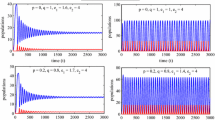
For the set of parameter values in Table 1, we obtain the interior equilibrium point \(E_1^*=(0.0056,0.1176,0.0121)\) which is an unstable equilibrium and \(E_2^*=(0.8303,0.1176,3.2696)\) is a stable focus as we see that all the trajectories initiating inside the region of attraction approach toward the equilibrium point \(E_2^*=(0.8303,0.1176,3.2696)\) (see Fig. 1). Different initial values are chosen as [0.3, 0.1, 0.2], [0.25, 0.2, 0.7], [0.22, 0.40, 1], [0.75, 0.05, 1.2] and [0.1, 0.60, 2] and draw the phase portrait of the system (4) in Fig. 1.

Fig. 1
figure 1

Stability of the interior equilibrium for the non-delayed model (5), with default parameter values as in Table 1, with different initial conditions

Full size image
Fig. 2
figure 2

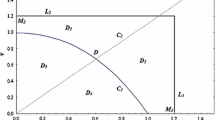
Bistability region of the system (5). The magenta region shows the bistability of \(E^0\) and \(E_2^*\), the yellow region shows the bistability of \(E^0\) and \(E^2\), and the red region indicates the bistability of \(E^0\) and \(E_1^1\). In the white region, only \(E^0\) is stable. (Color figure online)

Full size image
Table 3 Sufficient condition for bistability for system (5)
Full size table

3.1 Saddle node bifurcation

Both \(S_{1}\) and \(S_{2}\) exist if \((1-q_1 E)^2-4q_1 E \theta >0\). For \((1-q_1 E)^2-4q_1 E \theta <0\), \(E_1 ^1\) and \(E_2^1\) vanishes. So, we can say that depending on the values of E and \(\theta \) both of these equilibria exist. For

$$\begin{aligned} \frac{\left( \frac{1}{\sqrt{(}q_1 E)}-\sqrt{(}q_1 E)\right) ^2}{4}=\theta , \end{aligned}$$

we observe saddle node bifurcation for the equilibria \(E_1 ^1\) and \(E_2^1\).

Similarly, saddle node bifurcation between two interior equilibria \(E_1^*\) and \(E_2^*\) exists for

$$\begin{aligned} \frac{\left( 1-(\beta +1)\frac{d}{\alpha }-q_1 E\right) }{\left( \beta \frac{d}{\alpha }+ q_1 E \right) }=\theta . \end{aligned}$$

3.2 Bistability

In this subsection, we investigate the possibility of multistability of our model system. We see that the model may be bistable with or without the interior equilibrium. Bistability is a phenomenon where the system converges to two different equilibria for the same parametric region based on the variation of the initial conditions. Here we observe that the system (5) shows three types of bistability (see Fig. 2): one is in the presence of interior equilibrium, and the other two are in the absence of interior equilibrium. Any trajectory starting from the interior of \({\mathbb {R}}^3_+\) either converges to \(E^2\), \(E_1^1\) or \(E^0\) when interior equilibrium does not exist (depending on the parameter space), or converges to \(E_0\) or \(E_2^*\) when interior equilibrium exists. We summarize the bistability criterion of the system (5) as follows (also see Table 3).

Fig. 3
figure 3

a Bistability between \(E^0\) and \(E_1^1\), b bistability between \(E^0\) and \(E^2\) and c bistability between \(E^0\) and \(E_2^*\)

Full size image

Note: Role of Allee effect on the existence of interior attractor of (5): Without Allee effect, the system (5) has one interior equilibria which is always stable (proof is not given), while in the presence of the Allee effect the system (5) can have either two interior equilibria or no equilibria, depending on the Allee parameter \(\theta \). So, from the above-described dynamics, we can conclude that Allee effect can generate or destroy interior attractors.

4 Mathematical analysis of the time delayed model (4)

In this section, we have analyzed the model (4). Here, we have performed permanence, local stability analysis of equilibria, the direction and stability of Hopf bifurcation of the delay differential Eq. (4).

4.1 Uniform persistence of the system

We first present the conditions for uniform persistence of the system (4). We denote by \({\mathbb {R}}^3_+ = \{(S, I, P)\in {\mathbb {R}}^3 : S\ge 0,I\ge 0, P\ge 0\}\) the non-negative quadrant and by \(\hbox {int}({\mathbb {R}}^3_+) = \Big \{(S, I, P)\in {\mathbb {R}}^3: S>0, I>0, P>0\Big \}\).

Definition

System (4) is said to be uniformly persistent if a compact region \(D \subset \text{ int } ({\mathbb {R}}^3_+)\) exists such that every solution \(\varXi (t) = \left( S(t), I(t), P(t)\right) \) of the system (4) with initial conditions eventually enters and remains in the region D.

4.2 Boundedness of the solution of the delayed system (4)

The first equation of the system (4) can be written as

$$\begin{aligned} \begin{array}{lll} \frac{\mathrm{d}S}{S}= & {} \left[ \left( 1-S-I\right) \frac{S}{S+\theta } - \beta I-q_1 E\right] \mathrm{d}t. \end{array} \end{aligned}$$

Integrating between the limits 0 and t, we have

$$\begin{aligned} \begin{array}{lll} &{}S(t) = S(0)\exp \\ &{}\Big \{\int ^t_0\left[ \left( 1-S-I\right) \frac{S}{S+\theta } - \beta I-q_1 E\right] \mathrm{d}s\Big \}. \end{array} \end{aligned}$$

Similarly from the second and the third equation of the system, we have

$$\begin{aligned} \begin{array}{lll} I(t) = I(0)\exp \Big \{\int ^t_0\left[ \beta S- a P- \mu -q_2 E\right] \mathrm{d}s\Big \} \end{array} \end{aligned}$$

and

$$\begin{aligned} \begin{array}{lll} &{}P(t) = P(0)\exp \\ &{}\Big \{\int ^t_0\left[ \alpha I(s-\tau )P(s-\tau )\frac{1}{P(s)} - \mathrm{d}\right] \mathrm{d}s\Big \} \end{array} \end{aligned}$$

where \(S(0)= S_0 > 0\), \(I(0)= I_0 > 0\) and \(P(0)= P_0 > 0\). Therefore, \(S(t) > 0\), \(I(t) > 0\) and \(P(t) > 0\).

Proposition 2

All the solutions of the system (4) starting in int\(({\mathbb {R}}^3_+)\) are uniformly bounded with an ultimate bound.

For detailed proof see “Appendix.”

4.3 Permanence

We use the uniform persistence theory for infinite dimensional systems [26], to prove permanence of the system (4). Let X be a complete metric space. Suppose that \(X^{0}\) is open and dense in X and \(X^{0}\cap X_{0}=\varPhi \). Assume that T(t) is a \(C^{0}\) semigroup on X satisfying

$$\begin{aligned} \begin{array}{lll} T (t) : X^{0}\rightarrow X^{0} ,\,T (t) : X_{0}\rightarrow X_{0}. \\ \end{array} \end{aligned}$$
(7)

Let \(T_{b}(t) = T (t)\big |_{X_{0}}\) and let \(A_{b}\) be the global attractor for \(T_{b}(t)\). To investigate the permanence of the system (4), the following lemmas are useful.

Lemma 1

[26] If T(t) satisfies (7) and we have the following:

  • (i) there is a \(t_{0}\ge 0\) such that T (t) is compact for \( t \ge t_{0}\);

  • (ii) T (t) is a point dissipative in X;

  • (iii) \(\widehat{A_{b}}=\cup _{x\in A_{b}} \omega (x) \) is isolated and thus has an acyclic covering \(\widehat{M}\), where \(\widehat{M}= \{M_{1},M_{2}, \ldots ,M_{n}\}\);

  • (iv) \(W^{s}( M_{i} ) \cap X^{0} = \varPhi \) for \(i = 1, 2, \ldots , n.\)

Then \(X_{0}\) is a uniform repeller with respect to \(X^{0}\), i.e., there is an \(\epsilon > 0\) such that for any \(x \in X^{0}\), \(\displaystyle {\lim _{t\rightarrow \infty }inf \ d(T(t)x, X_{0} )\ge \epsilon }\), where d is the distance of T(t)x from \(X_{0}\).

Lemma 2

[62] Consider the following differential equation:

$$\begin{aligned} \dot{x}(t) = A x(t-\tau )-B x(t) \end{aligned}$$

where \(A,~ B,~ \tau > 0\); \(x(t) > 0\), for \(-\tau \le t\le 0\). Then we have

  • (i) if \(A < B\), then \(\displaystyle {\lim _{t\rightarrow \infty } x(t)} = 0;\)

  • (ii) if \(A > B\), then \(\displaystyle {\lim _{t\rightarrow \infty } x(t)} = + \infty .\)

Theorem 1

(Permanence of the model (4)) System (4) is permanent provided

  • (i) \(\frac{\mu +q_2 E +a\epsilon _1}{\beta }(1-\frac{\mu +q_2 E +a\epsilon _1}{\beta })>q_1 E\frac{\mu +q_2 E+a\epsilon _1}{\beta }+q_1 E \theta ,\) where \(\epsilon _{1}\) is sufficiently small and

  • (ii) \(\alpha (I_2-\epsilon _2)>d\)  where \(I_2=\frac{\left( \frac{\mu +q_2 E}{\beta }\right) \left( 1-\frac{\mu +q_2 E}{\beta }\right) -q_1 E\frac{\mu +q_2 E}{\beta }-q_1 E \theta }{\frac{\mu +q_2 E}{\beta }+\beta \theta +\mu +q_2 E}.\)

Proof

We have not given the detailed proof in this manuscript (our analysis is similar to the analysis given in [10]). \(\square \)

4.4 Local stability analysis

Let \(\widetilde{E} = \left( \widetilde{S},~\widetilde{I},~\widetilde{P}\right) \) be any equilibrium point of the system (4). The linearized system of the system (4) at \(\widetilde{E} = \left( \widetilde{S},~\widetilde{I},~\widetilde{P}\right) \) is

$$\begin{aligned} \begin{array}{lll} \dot{x}(t) &{} = &{} \frac{(\beta \theta \widetilde{I}-\widetilde{S}^2)}{\widetilde{S}+\theta } x(t) -\frac{\widetilde{S}}{\widetilde{S}+\theta }(\beta \theta +\widetilde{S}(1+\beta )) y(t),\\ \dot{y}(t) &{} = &{} \beta \widetilde{I} x(t)- a\widetilde{I}z(t),\\ \dot{z}(t) &{} = &{} y\left( t-\tau \right) \alpha \widetilde{P}+z\left( t-\tau \right) \alpha \widetilde{I}-d z(t). \end{array} \end{aligned}$$
(8)

So, the characteristic equation of the delayed system (4) around any equilibrium point \(\widetilde{E} = (\widetilde{S}, \widetilde{I}, \widetilde{P})\) is given by

$$\begin{aligned}&\det \left[ \begin{array}{ccc} \frac{(\beta \theta \widetilde{I}-\widetilde{S}^2)}{\widetilde{S}+\theta }-\lambda &{} -\frac{\widetilde{S}}{\widetilde{S}+\theta }(\beta \theta +\widetilde{S}(1+\beta )) &{} 0 \\ \\ \beta \widetilde{I} &{} -\lambda &{} -a\widetilde{I} \\ \\ 0&{} e^{-\lambda \tau } \alpha \widetilde{P} &{} e^{-\lambda \tau } \alpha \widetilde{I}-d -\lambda \\ \end{array} \right] \nonumber \\&\quad =0. \end{aligned}$$
(9)

In previous section, we observe that in the absence of the delay, the interior equilibrium \(E_1^*=(S_1^*, I_1^*, P_1^*)\) is unstable, while the other interior equilibria \(E_2^*=(S_2^*, I_2^*, P_2^*)\) is locally stable. Hence, in the present section, we study the stability analysis of the delayed system around the interior equilibria \(E_2^*\).

The following transcendental equation represents the characteristic equation at the interior equilibrium \(E_2^* = \left( S_2^*, I_2^*, P_2^*\right) \) of the dynamical system (4).

$$\begin{aligned} \begin{array}{lll} \lambda ^{3}+B_{1}\lambda ^{2}{+}B_{2}\lambda +B_{3} {=} \left[ B_{4}\lambda ^{2}+B_{5}\lambda +B_{6}\right] \text {e}^{-\lambda \tau }. \end{array}\nonumber \\ \end{aligned}$$
(10)

where

$$\begin{aligned} B_{1}= & {} -\frac{(\beta \theta I_2{^*}-S_2{^*}^2)}{S_2{^*}+\theta } +d,\nonumber \\ B_{2}= & {} - \frac{(\beta \theta I_2{^*}-S_2{^*}^2)}{S_2{^*}+\theta }d\nonumber \\&+\,\beta I_2{^*} \frac{S_2{^*}}{S_2{^*}+\theta }(\beta \theta +S_2{^*}(1+\beta )),\nonumber \\ B_{3}= & {} \beta I_2{^*} \frac{S_2{^*}}{S_2{^*}+\theta }(\beta \theta +S_2{^*}(1+\beta )) d,\nonumber \\ B_{4}= & {} \alpha I_2{^*},\nonumber \\ B_{5}= & {} -\alpha I_2{^*}\frac{(\beta \theta I_2{^*}-S_2{^*}^2)}{S_2{^*}+\theta } -a\alpha I_2{^*}P_2{^*},\nonumber \\ B_{6}= & {} \beta \alpha I_2{^*} I_2{^*} \frac{S_2{^*}}{S_2{^*}+\theta }(\beta \theta +S_2{^*}(1+\beta ))\nonumber \\&+\, a \alpha I_2{^*}P_2{^*}\frac{(\beta \theta I_2{^*}-S_2{^*}^2)}{S_2{^*}+\theta }. \end{aligned}$$
(11)

For the delay induced system (4), it is known that if all the roots of the corresponding characteristic equation (10) have negative real part, then the equilibrium point \(E_2{^*}\) will be asymptotically stable. The classical Routh–Hurwitz criterion cannot be used to determine the stability of the dynamical system as the characteristic equation (10) is a transcendental equation and has infinitely many roots. We need the sign of the real parts of the roots of the characteristic equation (10), to investigate the nature of the stability.

Let \(\lambda (\tau )=\zeta (\tau )+i\rho (\tau )\) be the eigenvalue of the characteristic equation (10); substituting this value in Eq. (10), we obtain real and imaginary parts, respectively, as

$$\begin{aligned}&\zeta ^{3} - 3\zeta \rho ^{2} + B_{1}\left( \zeta ^{2}-\rho ^{2}\right) +B_{2}\zeta +B_{3} \nonumber \\&\quad = \left[ \Big \{B_{4}(\zeta ^{2}-\rho ^{2}) +B_{5}\zeta +B_{6}\Big \}\right. \nonumber \\&\quad \left. \cos \rho \tau \left( 2B_{4}\zeta \rho +\rho B_{5}\right) \sin \rho \tau \right] \text {e}^{-\zeta \tau }, \end{aligned}$$
(12)

and

$$\begin{aligned}&3\zeta ^{2}\rho -\rho ^{3}+2B_{1}\zeta \rho +B_{2}\rho \nonumber \\&\quad = \left[ \left( 2B_{4}\zeta \rho +B_{5}\rho \right) \cos \rho \tau \right. \nonumber \\&\quad \left. -\{\left( \zeta ^{2}-\rho ^{2}\right) B_{4}\zeta B_{5}+B_{6}\}\sin \rho \tau \right] \text {e}^{-\zeta \tau }. \end{aligned}$$
(13)

A necessary condition to change the stability of \(E_2{^*}\) is that the characteristic equation (10) should have purely imaginary solutions. We set \(\zeta =0\) in (12) and (13). Then we get,

$$\begin{aligned} B_{3}-B_{1}\rho ^{2}= & {} \left( -B_{4}\rho ^{2}+B_{6}\right) \cos \rho \tau +\rho B_{5}\sin \rho \tau ,\nonumber \\ \end{aligned}$$
(14)
$$\begin{aligned} B_{2}\rho - \rho ^{3}= & {} B_{5}\rho \cos \rho \tau -\left( -B_{4}\rho ^{2}+B_{6}\right) \sin \rho \tau .\nonumber \\ \end{aligned}$$
(15)

Eliminating \(\tau \) by squaring and adding the equations (14) and (15), we get the algebraic equation for determining \(\rho \) as

$$\begin{aligned}&\rho ^{6}+\left( B_{1}^{2}-2B_{2}-B_{4}^{2}\right) \rho ^{4}\nonumber \\&\quad +\left( B_{2}^{2}-2B_{1}B_{3}-B_{5}^{2} +2B_{4}B_{6}\right) \rho ^{2}\nonumber \\&\quad +\left( B_{3}^{2}-B_{6}^{2}\right) = 0. \end{aligned}$$
(16)

Substituting \(\rho ^{2} = \theta \) in Eq. (16), we obtain a cubic equation given by

$$\begin{aligned} k(\theta )=\theta ^{3}+\sigma _{1}\theta ^{2}+\sigma _{2}\theta +\sigma _{3} = 0, \end{aligned}$$
(17)

where

$$\begin{aligned} \sigma _{1}= & {} \left( B_{1}^{2}-2B_{2}-B_{4}^{2}\right) ,~~\sigma _{2}\\= & {} \left( B_{2}^{2}-2B_{1}B_{3}-B_{5}^{2} +2B_{4}B_{6}\right) ,~~\sigma _{3}\\= & {} \left( B_{3}^{2}-B_{6}^{2}\right) . \end{aligned}$$

Now \(\sigma _{3}<0\) implies that (17) has at least one positive root. The following theorem gives a criterion for the switching in the stability behavior of \(E_2{^*}\).

Theorem 2

Suppose that \(E_2{^*}\) exists and is locally asymptotically stable for (4) with \(\tau =0\). Also let \(\theta _{0}=\rho ^{2}_{0}\) be a positive root of (17).

  1. 1.

    Then there exists \(\tau = \tau ^{*}\) such that the interior equilibrium point \(E_2{^*}\) of the delay system (4) is asymptotically stable when \(0\le \tau <\tau ^{*}\) and unstable for \(\tau >\tau ^{*}\).

  2. 2.

    Furthermore, the system will undergo a Hopf bifurcation at \({E_2{^*}}\) when \(\tau =\tau ^{*}\), provided \(Z(\rho )X(\rho )-Y(\rho )W(\rho )>0\).

Proof

The proof is similar to the analysis given in [10].

\(\square \)

Fig. 4
figure 4

Waveform plot and phase plane for the delayed system (4), with the time delay \(\tau = 1 ({<} \tau _{*} = 3.2)\) and the other parameter values are fixed as in Table 1. The first row left figure is the time series for the susceptible prey; the first row right figure is the 3D phase portrait of the stable interior of (4)

Full size image

4.5 The direction and stability of Hopf bifurcating periodic solutions

We already know that the system (4) will undergo Hopf bifurcation at endemic equilibrium \(E_{*} = \left( S_*,I_*,P_*\right) \) when \(\tau \) passes through \(\tau ^{*}\) (for our convenience we assume that \(E_{*} = E_2^*\)). In this section, we investigate the direction, stability and period of Hopf bifurcating solutions at \(\tau = \tau ^{*}\) for system (4) by using the techniques of normal form theory and center manifold theorem introduced by [27].

We have not given the detailed analysis for the direction and stability of the Hopf bifurcation in this manuscript (our analysis is similar to the analysis given in [10]). From the detailed analysis, we can compute the following quantities, which determine the direction, stability and the periods of the bifurcating periodic solutions of Hopf bifurcation.

$$\begin{aligned} C_{1}(0)= & {} \frac{i}{2\rho _{0}\tau ^{*}}\left( g_{20}g_{11}{-}2|g_{11}|^2{-}\frac{1}{3}|g_{02}|^2\right) {+}\frac{1}{2}g_{21}, \\ \mu _{2}= & {} -\frac{Re\{C_{1}(0)\}}{Re\{\acute{\lambda }(\tau ^{*})\}}, \\ \beta _{2}= & {} 2Re\{C_{1}(0)\}, \\ \tau _{2}= & {} -\frac{Im\{C_{1}(0)\}+\mu _{2}Im\{\acute{\lambda }(\tau ^{*})\}}{\rho _{0}\tau ^{*}}. \end{aligned}$$

It is well known that \(\mu _{2}\) and \(\beta _{2}\) determine the direction of Hopf bifurcation and stability of bifurcating periodic solutions. If \(\mu _{2}>0\) \(({<}0)\), and \(\beta _{2}<0\) \(({>}0)\), then the Hopf bifurcation is supercritical (subcritical), bifurcating periodic solutions exist for \(\tau >\tau ^{*}\) (\(\tau < \tau ^{*}\)) and are orbitally stable (unstable). \(\tau _{2}\) determines the periods of the bifurcating periodic solutions and the period increases (decreases) if \(\tau _{2}>0 ({<}0)\).

From our analytical findings, it is observed that \(E_2^*\) is locally asymptotically stable for \(\tau <\tau ^{*}=3.20\). Figure 4 shows that the system (4) is stable focus for \(\tau =1<\tau ^{*}\). Interior equilibrium point \(E_2^*\) looses its stability as \(\tau \) passes through its critical value \(\tau ^{*}\) and the system (4) experiences Hopf bifurcation. From 4.5, the nature of the stability and direction of the periodic solution bifurcating from the interior equilibrium \(E_2^*\) at the critical point \(\tau ^{*}\) can be computed. Through simulations, we compute that

$$\begin{aligned}&C_1(0)= -3.4661 - 0.9500i,~\mu _2= 588.89,\\&\quad \beta _2= -6.9323,~\tau _2=11.972. \end{aligned}$$

It shows the existence of bifurcating periodic solution, and it is supercritical and stable as evident from Fig. 5. Figure 5 shows that the limit cycle is stable around the coexisting equilibrium point \(E_2^*\). The solutions starting from two different initial values converge to the limit cycle oscillation for \(\tau =3.28\).

Fig. 5
figure 5

The system (4) shows Hopf bifurcation behavior and existence of stable supercritical bifurcating periodic solution around the interior equilibrium \(E_2^*\) at \(\tau =3.28\). The other parameter values are kept same as in Table 1

Full size image

5 Chaotic behavior in our model dynamics (4)

In this section, the time series diagram, phase plane diagram and bifurcation diagram of the system (4) are drawn to describe the feasibility of different complex dynamical behaviors such as one periodic and two periodic limit cycles and chaos.

We fix the parameter values as in Table 1 and vary the time delay parameter to investigate the different complex dynamics of our model (4). For our model (4), the equilibrium \(E^*_2\) is locally asymptotically stable for the delay parameter \(\tau < 3.20 ~(=\tau ^*)\). If we increase the parameter beyond \(\tau ^*\), then at \(\tau =4>\tau _{*}\), the system (4) shows the limit cycle oscillation of period one (see Fig. 6). If we further increase the time delay parameter \(\tau \), then the system (4) will show the limit cycle oscillation of period two for \(\tau = 11.2\) (see Fig. 7).

We observe that system (4) shows the chaotic behavior for \(\tau = 18\) (see Fig. 8). To establish the chaotic dynamics, we have plotted the maximum Lyapunov exponent with time in Fig. 9a, corresponding to Fig. 8. We use Wolf algorithm [61] to calculate maximum Lyapunov exponents. A Poincare map of a typical chaotic regime is shown in Fig. 9b. The scattered distribution of the sampling points implies the chaotic behavior of the system.

Fig. 6
figure 6

Waveform plot and phase plane for the delayed system (4), with the time delay \(\tau =4\) and the other parameter values are fixed as in Table 1. Figure indicates the existence of limit cycle

Full size image
Fig. 7
figure 7

Existence of two periodic solutions around the interior equilibrium \(E_2^*\) for the system (4), with the time delay \(\tau =11.4 ({>}\tau ^{*} = 3.2)\), where the other parameter values are same as in Table 1

Full size image
Fig. 8
figure 8

Solution curves and the phase plane showing chaotic attractor at \(\tau =18\) for the model (4) and the other parameter values are fixed as in Table 1

Full size image
Fig. 9
figure 9

Maximum Lyapunov exponents and Poincare section to show the chaotic behavior of the system (4). a Chaotic behavior of the system (4). b Poincare plot {S=0.83} in the I–P plane for the system (4)

Full size image

6 Effects of the time delay \((\tau )\), inverse of individual searching efficiency \((\theta )\) and harvesting effort (E)

In this section, we will discuss the effects of the three important model parameters: (a) effects of time lag \(\tau \), (b) effects of the inverse of individual searching efficiency \(\theta \) and (c) the effects of the harvesting effort. We produce three bifurcation diagrams with respect to \(\tau \), \(\theta \) and E for our model (4) to clearly depict our results, by fixing the other parameter values as in Table 1.

6.1 Effect of time lag

First we draw the bifurcation diagram with respect to time delay \(\tau \) for \(0 < \tau \le 18.5\), with the parameter values \(\theta = 0.1\), \(E = 0.01\) and the remaining parameters are fixed as in Table 1. The bifurcation diagram with respect to time delay \(\tau \) drawn in Fig. 10 reports the complex dynamical behavior of the model (4) with period doubling bifurcation. The system (4) undergoes from stable focus to limit cycle oscillation, limit cycle oscillation to chaotic oscillation for further increase the delay parameter. Figure 10 shows that for \(\tau \in [0,3.2)\) the interior equilibrium \(E_2^*\) is stable, for \(\tau \in [3.2,11.2)\) it shows limit cycle oscillations, and for \(\tau \in [11.2,18.5]\) it exhibits higher periodicity and chaotic oscillations.

6.2 Effect of Allee parameter

Next, we draw the bifurcation diagram with respect to the parameter \(\theta \) for \(\theta \in (0,1.28]\) where \(\tau \) is fixed at 18, \(E = 0.01\) and the remaining parameters are fixed as above. The complex dynamic behavior including chaos of the delayed system with respect to \(\theta \) is evident from Fig. 11. We observe that for \(\theta \in (0,0.05)\), system exhibits limit cycle and for \(\theta \in [0.05,0.44)\) the system (4) shows higher periodicity and chaotic oscillations through quasi-periodicity route. For further increasing the strength of Allee parameter invokes a period-halving bifurcation and controls the chaotic oscillations. The system (4) shows two-period oscillation and limit cycle behavior for \(\theta \in (0.44,0.78)\), and \(\theta \in (0.78,1.28]\), respectively. Further increment of \(\theta \) results extinction of all the species.

6.3 Effect of harvesting effort

We fix the parameter values \(\tau = 18\), \(\theta = 0.1\) and the other parameters are fixed as above and vary the parameter E. For the gradual increase of the parameter E, the system (4) switches its stability from chaotic oscillation to limit cycle oscillation, limit cycle oscillation to stable focus through the period-halving bifurcation. When \(E\in [0,0.04)\), we observe higher periodicity and chaotic oscillations. For \(E\in [0.04,0.1)\), we notice limit cycle behavior. Figure 12 shows that the system is stable for \(E\in [0.10,0.15]\).

For clear visualization, we draw the stability region for the model (4), with respect to \(\theta \) and E when \(\tau =18\). In Fig. 13, the whole region is divided into several distinct parts where we observe that the system (4) is stable in the green region; black region shows limit cycle oscillation, period doubling in the yellow region, chaotic oscillation in the blue region; predator extinction in the red region, infected prey and predator extinction in the cyan region and white region shows the extinction of all species.

Fig. 10
figure 10

Bifurcation diagrams with respect to \(\tau \) for the system (4), when the other parameters are fixed as in Table 1. a Bifurcation diagram for the susceptible prey; b bifurcation diagram for the infected prey; and c bifurcation diagram for the predator

Full size image
Fig. 11
figure 11

Bifurcation diagrams with respect to \(\theta \) for the system (4). When the other parameters are fixed as in Table 1 and \(\tau = 18\). a Bifurcation diagram for the susceptible prey; b bifurcation diagram for the infected prey; and c bifurcation diagram for the predator

Full size image
Fig. 12
figure 12

Bifurcation diagrams with respect to E for the system (4). When the other parameters are fixed as in Table 1 and \(\tau = 18\). a Bifurcation diagram for the susceptible prey; b bifurcation diagram for the infected prey; and c bifurcation diagram for the predator

Full size image
Fig. 13
figure 13

Stability region of the system (4) when \(\tau =18\). The system is stable in the green region, black region shows limit cycle oscillation, period doubling in the yellow region, chaotic oscillation in the blue region, predator extinction in the red region, infected prey and predator extinction in the cyan region and white region shows the extinction of all species

Full size image

7 Optimal harvesting policy

In this section, we study the optimal harvesting policy for both the non-delayed and delayed model. Exploitation can change the behavior of the system in several ways. It can reduce population size or density to a level close to or below an Allee threshold or increases the Allee effect strength. For example, in an Irish sea, at least four species of skate and shark have been exploited to extinction [6]. Naturally optimal harvesting policy is very much needed for such system. So, we formulate an optimal harvesting policy which ensures species conservation and maximizes the profit [23, 33, 36].

Here, we study the optimal harvesting policy by considering the profit earned by harvesting with conservation of prey population. We assume that price function is inversely proportional to the available prey population. Let c be the constant harvesting cost per unit effort, \(p_1\) and \(p_2\) are constant price per unit biomass of the S and I species, \(v_1\) and \(v_2\) are economic constraints and \(\delta \) denotes the continuously compounded annual rate of discount. Infected prey (I) has less demand, so we assume that \(p_2<p_1\).

We now formulate the problem of optimal harvesting policy for

$$\begin{aligned} J(E)= & {} \int _0^\mathrm{T}[(p_1-v_1 q_1 E S)q_1 E S \\&+ (p_2-v_2 q_2 E I)q_2 E I -c E] e^{-\delta t}\mathrm{d}t, \end{aligned}$$

subject to the system (4) and the effort constraint \(0\le E\le E_{\max }\). Here, \(E_{\max }\) is the maximum effort capacity of the harvesting industry. The objective of the problem is to find the optimal harvesting effort \(E^*\) such that

$$\begin{aligned} J(E^*)=\max _{E \in U}J(E) \end{aligned}$$

where U is the control set defined by

$$\begin{aligned} U=\{E: E ~\mathrm{is}\,\,\mathrm{measurable}~\mathrm{and} ~0\le E\le E_{\max }\}. \end{aligned}$$

To find the maximum value of J(E), we set \(x(t) = (S(t), I(t),P(t))\) and \(x_\tau (t) = (S_\tau (t), I_\tau (t),P_\tau (t))\), where \(S_\tau (t)= S(t - \tau ), I_\tau (t) := I(t - \tau ), P_\tau (t) := P(t - \tau )\), and define the Hamiltonian \(H(t) = H(x, x_\tau , E,\lambda )(t)\) for the control problem as follows:

$$\begin{aligned} H= & {} \left[ (p_1{-}v_1 q_1 E S)q_1 E S {+} (p_2{-}v_2 q_2 E I)q_2 E I {-}c E\right] \\&+\lambda _S \left[ S\left[ (1-S-I)\frac{S}{(S+\theta )}-\beta I-q_1 E\right] \right] \\&+ \lambda _I \left[ I\left[ \beta S-a P -\mu -q_2 E\right] \right] \\&+ \lambda _P\left[ \alpha P(t-\tau )I(t-\tau ) -d P\right] . \end{aligned}$$

The variables \(\lambda _S, \lambda _I, \lambda _P \) are adjoint variables and the transversality conditions are \(\lambda _S (T)=0\), \(\lambda _I (T)=0\) and \(\lambda _P (T)=0\).

Theorem 3

There exists an optimal control \(E^*\) for \(t\in [0,T]\) such that

$$\begin{aligned} J(S(t), I(t), P(t), E^* )=\max _{E \in U} J(S(t), I(t), P(t), E) \end{aligned}$$

subject to the differential equation (4) and there exists adjoint variables \(\lambda _S, \lambda _I, \lambda _P \) with the transversality conditions as \(\lambda _S (T)=0\), \(\lambda _I (T)=0\), \(\lambda _P (T)=0\).

Proof

For details, see [23, 32, 33, 36]. \(\square \)

7.1 Characterization of the optimal control

In order to derive the necessary condition for the optimal control, Pontryagin’s maximum principal with delay given in [68] was used. The state equations are given by:

$$\begin{aligned} x(t) = H(x, x_\tau , E,\lambda )(t), \end{aligned}$$

the optimality condition is

$$\begin{aligned} 0 = H_E(x, x_\tau , E,\lambda )(t), \end{aligned}$$

and the adjoint equation is

$$\begin{aligned}&-\frac{\mathrm{d}\lambda }{\mathrm{d}t} (t) = H_x(x, x_\tau , E,\lambda )(t) \\&\quad + \chi _{[0~T-\tau ]} \lambda (t + \tau )H_{x_\tau } (x, x_\tau , E,\lambda )(t), \end{aligned}$$

where \(H_E, H_x\) and \(H_{x_\tau }\) denote the derivative with respect to E, x and \(x_\tau \), respectively. Now we apply the necessary conditions to the Hamiltonian H.

The condition for the optimal control can be obtained from the relation \(E_\delta =\frac{p_1 q_1 S + p_2 q_2 I -c- \lambda _S q_1 S - \lambda _I q_2 I }{2(v_1 q_1^2 S^2+v_2 q_2^2 I^2)}\). The adjoint equations are

$$\begin{aligned} \frac{\mathrm{d} \lambda _S}{\mathrm{d}t}= & {} \lambda _S(t) \delta \nonumber \\&-[p_1 q_1 E - 2v_1 q_1^2 E^2 S ]\nonumber \\&- \lambda _S(t) \left[ S(1-S-I)\frac{(S+2 \theta )}{(S+\theta )^2} \right. \nonumber \\&\left. - \frac{S^2}{S+\theta }-\beta I-q_1 E \right] \nonumber \\&- \lambda _I(t) \beta I \nonumber \\ \frac{\mathrm{d} \lambda _I}{\mathrm{d}t}= & {} \lambda _I(t) \delta -[p_2 q_2 E - 2v_2 q_2^2 E^2 I]\nonumber \\&+\, \lambda _S(t) \beta S -\lambda _I(t) \left[ \beta S-a P -\mu -q_2 E\right] \nonumber \\&-\chi _{[0~T-\tau ]} \lambda _P(t+\tau ) \alpha P(t-\tau )\nonumber \\ \frac{\mathrm{d} \lambda _P}{\mathrm{d}t}= & {} \lambda _P(t) \delta - \lambda _P(t) d\nonumber \\&+\,\lambda _I(t) a I -\chi _{[0~T-\tau ]}\lambda _P(t+\tau ) \alpha I(t-\tau ). \end{aligned}$$
(18)

The optimal harvesting effort at any time t is given by

$$\begin{aligned} \begin{array}{lcl} E^*={\left\{ \begin{array}{ll} E_{\min }, ~~~~\frac{\mathrm{d} H}{\mathrm{d} E}< 0\\ E_\delta ,~~~~~~~\frac{\mathrm{d} H}{\mathrm{d} E}= 0\\ E_{\max }, ~~~~\frac{\mathrm{d} H}{\mathrm{d} E}> 0.\\ \end{array}\right. } \end{array} \end{aligned}$$
(19)

The numerical solutions of the considered optimal problem completely determined using Runge–Kutta fourth-order forward–backward procedure. The successive steps are displayed as follows:

Let there exists a step size \(h > 0\) and \(\tau =mh\), \(T=nh\). We obtain the following partition: \(t_{-m}<-\tau<\cdots .<t_0<\cdots \cdots<T\cdots \cdots <t_{n+m}\). Then we have \(t_i=t_0+ih\).

  1. 1.

    For \(i=-m,\ldots .,0\) do \(S_i=S_0;I_i=I_0;P_i=P_0;E{^*}_i=0\)   End for

    For \(i=n,\ldots .,n+m\) do \(\lambda _S=0;\lambda _I=0;\lambda _P=0\)   End for

  2. 2.

    For \(i=0,\ldots .,n-1\) using the initial condition \(S_0,I_0,P_0\) solve the state equation according to the DDE with the values for \(E^*\) forwardly.

    Using the transversality condition \(\lambda _S (T)=0\), \(\lambda _I (T)=0\), \(\lambda _P (T)=0\), with the computed values of state variables and \(E^*\) evaluate the values of adjoint variables \(\lambda _S,\lambda _I,\lambda _P\).

  3. 3.

    Update \(E^*\) using the rule \(E^*=\min \{E_{\min },\max \{E_\delta ,E_{\max }\}\}\).

  4. 4.

    If the solutions of the variables (excluding the control variable) are convergent then the last iteration is the complete solution. Otherwise, return to step 2.

We illustrate this with a numerical example. For this purpose, we choose the parameter values to be \(\beta =0.75;~ \mu =0.001;~ d=0.1;~ a=0.4;~ \theta =0.1;~ \alpha =0.2;~ T=10;~ \epsilon =0.05;~ p1=1.2;~ p2=0.1;~ q1=1;~ q2=1;~ v1=2;~ v2=2;~ c=0.1;~ S(0)=1;~ I(0)=0.05;~ P(0)=1.\) We assume that \(0\le E\le 1\). Now we solve the optimal control problem numerically using Runge–Kutta fourth-order iterative method. For the state variables, first we solve the system (5) by forward Runge–Kutta fourth-order procedure and then using that state values we solve the system (18) by using the backward fourth-order Runge–Kutta procedure (when \(\tau =0\)).

In Fig. 14, we represent the solution curves of the three state variables in the presence of the harvesting. Figure 15 represents the variation of adjoint variables. Final values of the adjoint variables are 0. As harvesting effort increases, the biomass of prey and predator population decreases. From Fig. 16, we observe that the optimal harvesting effort is maximum when \(\theta =0.5.\) The optimal effort \(E_\delta \) varies with \(\theta \). Biologically, we can say that if \(\theta \) increases, then numerically \(\frac{S}{S+\theta }\) decreases and as a result maximum optimal harvesting effort increases.

Fig. 14
figure 14

Diagrams for the state variables with control for the system (5). a Diagram for the susceptible prey; b diagram for the infected prey; and c diagram for the predator

Full size image
Fig. 15
figure 15

Figures for the adjoint variables of the system (5)

Full size image
Fig. 16
figure 16

Variation of the optimal effort E with respect to time with different \(\theta \) for the system (5)

Full size image

Next, we assume the same parameter values as Fig. 14 and \(0\le E\le 1\). Using the above-described method in subsection 7.1, we investigate optimal harvesting policy for the model (4). For \(\tau =1\), the optimal trajectories for the system (4) with initial population densities (S(0), I(0), P(0)) are shown in Fig. 17. The variations of adjoint variables are also drawn in Fig. 18. Optimal harvesting effort is hugely dependent on gestation delay \(\tau \) which is evident from Fig. 19. Maximum value of optimal harvesting increases as gestation delay \(\tau \) increases. The optimal harvesting effort increases monotonically and assumes it’s maximum value in each case.

8 Discussion

The model (4) has two interior equilibria \(E_1^*\) and \(E_2^*\), in which first one is always unstable and the another one is stable. We discuss the saddle node bifurcation and bistability between different equilibria for the model (5). For our model (4), the delay parameter (\(\tau \)) plays an important role. Time delay can switch the stability of the equilibrium point form stable to unstable; that is, for some critical value \(\tau ^*\), the positive equilibrium \(E_2^*\) is stable when \(\tau <\tau ^*\), and it becomes unstable as \(\tau \) crosses through its critical magnitude from lower to higher values. It is demonstrated that the model (4) encounters the Hopf bifurcation as the delay parameter \(\tau \) crosses the critical value \(\tau ^*\). Further increasing of the delay parameter beyond the bifurcation point leads to complex dynamic behavior, including chaos. The explicit formulae which determine the stability, direction and other properties of bifurcating periodic solution are investigated, by using normal form and center manifold theorem. Finally, by using numerical simulations, we illustrate our analytical results. We also draw the various stability regions for the model (4), with respect to \(\theta \) and E when \(\tau =18\).

Fig. 17
figure 17

Diagrams for the state variables with control for the system (4). a Diagram for the susceptible prey; b diagram for the infected prey; and c diagram for the predator

Full size image
Fig. 18
figure 18

Figures for the adjoint variables of the system (4) when \(\tau =1\)

Full size image
Fig. 19
figure 19

Variation of the optimal effort E with respect to time with different \(\tau \) for the system (4)

Full size image

From environmental perspective, chaos has the most extreme natural significance. Numerous hypothetical studies uncover essential biological community’s highlight, for example, consistency, species constancy [2] and bio-differences [31] can be influenced by chaos. Different chaos control plans have been investigated, till now. In [34, 53, 69], the authors concluded that Allee effect may be a destabilizing force in prey–predator systems. We have shown that higher values of time delay make the system chaotic, and chaos can be controlled by the harvesting effort E. In our model (4), the non-linearity induced by Allee effect can produce chaotic oscillations but the changes in the strength of \(\theta \) may reduce/remove the chaotic behavior of the system. The dynamical behavior of \(\theta \) is not same as in [10]. Clearly, if the Allee parameter increases, the system loses stability and becomes chaotic. It is worth noting that we draw the bifurcation diagram by plotting the maximum and minimum values of the time series solutions of the system (4). We observe that the system (4) enters into the chaotic regime through quasi-periodicity route [50]. The impact of the Allee effect on the stability of population models show a diverse effect which entirely relies on the assumption of the relating model. Harvesting makes the coexistence equilibria stable for the system (4) and can control chaotic dynamics of the system. Continuous harvesting will make the system disease-free (also predator-free). The system has the ability to recover if P-class are not made extinct by excessive exploitation of their food supply.

We assume that the selling price of the infected prey (I) is less than the price of susceptible fish (S). Large amount of infected prey is harmful for the economic condition of harvesters. Also if \(q_1\) and \(q_2\) increase with the advancement of technology, while the remaining parameters are fixed, then the density of prey population shifts to a lower level. Further increment of \(q_1\) and \(q_2\) makes the prey population extinct. In this article, we consider the economic loss of harvesters due to the unwilling harvesting of infected prey species. Using the Pontryagin’s maximum principle, the optimal harvesting policy has been discussed. We find that optimal harvesting policy is dependent on both gestation delay and Allee effect.

A large number of empirical evidences for drastic global reduction of valuable fish stocks are available. In fisheries, undisciplined harvesting diminish the population at the point where depensatory process dominates. Long ago fishery scientists are acquainted with the possibility of Allee effects (depensatory) in marine populations [45] and demanded enquiry of the “depensatory process.” In fisheries, strong and weak Allee effects are known as critical and pure depensation, respectively [16]. First time we develop a management problem considering an eco-epidemiological model with weak Allee effect and harvesting in prey population. One practical example for our model (4) is Antarctic krill-whale community. The Antarctic krill population is being increasingly harvested and the prime source of food of whales is krill. We use gestation delay to make our model (4) more realistic. Exploitation can affect system with Allee effects in several ways. It can reduce population density to a level close to or below an Allee threshold or increase the Allee effect strength [6]. We observe that, for our model (4), prey density should be greater than \(\frac{\mu +q_2 E}{\beta }\) for existence of all the species. Effective harvesting helps to protect biological balance within the ecosystem which is our prime goal. Optimal harvesting policy is an important tool to maximize the profit earned by exploitation while ensuring the existence of all the species. Figures 14 and 17 indicate the existence of all the species with optimal harvesting policy. Our findings indicate that over exploitation implies the extinction of the population, and a proper harvesting policy should ensure the feasibility of the biomass which is in line with reality.