Complex dynamics of ecological systems under nonlinear harvesting: Hopf bifurcation and Turing instability

Abstract

In this paper, we study the complex dynamics of a spatial nonlinear predator-prey system under harvesting. A modified Leslie–Gower model with Holling type IV functional response and nonlinear harvesting of prey is considered. We perform a detailed stability and Hopf bifurcation analysis of the spatial model system and determine the direction of Hopf bifurcation and stability of the bifurcating periodic solutions. Numerical simulations were performed to figure out how Turing patterns evolve under nonlinear harvesting. Simulation study leads to a few interesting sequences of pattern formation, which may be relevant in real world situations.

1 Introduction

Alan Turing’s idea that diffusion can destabilize an otherwise stable system of reactants has been explored in several context; an explanation of spatial patterns on animal skin is an example. Molecular analysis of hair follicle formation provides evidence to support biological pattern formation through diffusion-driven instability [19]. Diffusion-driven instability can lead to spatial concentration patterns of fixed characteristic length from an arbitrary initial configuration [30]. Spatial patterns in early embryo development, which emerges from single cell to skeletal patterns such as hair, teeth, feather and coat markings have been explained on the basis of the mechanism of pattern formation suggested by Turing [4]. Three-dimensional Turing patterns have been observed in aqueous nano-droplets much smaller than the scale of the stationary patterns [3]. Spatial pattern of ecological interactions are considered to be an important factors how real world ecological communities are shaped. Inhomogeneous distribution of nutrients and processes; e.g., migration, etc. can have important impact on the dynamics of biological populations. Alonso and collaborators have explored the possibility of Turing spatial patterns generated by mutual interference [1]. Perfecto and Vandermeer [21] have shown self-organized spatial patterns in Coffee Agro-forestry system. Authors examined the consequences of the stability of spatial patterns for the stability of predator-prey systems, for a key Coccinelid beetle preying on the scale insects and a phorid fly parasitoid parasitizing on the ant. Diffusion-driven spatial patterns have been observed in patterns of insect outbreak [13]. Spatial pattern formations have also been observed in patterning of spruce budworm [18], in an insect host-parasitoid system [20] and in North Sea plankton [25]. Guan et al. [9] investigated the spatiotemporal dynamics of a modified Leslie–Gower predator-prey model incorporating a prey refuse. They studied the Turing bifurcation which determines the Turing space in spatial domain and numerically illustrated five categories of Turing bifurcation close to the onset of Turing bifurcation. Camara and Aziz-Alaoui [5] studied how diffusion affects the stability of positive equilibrium of a Leslie–Gower type predator-prey model and derived the conditions for Hopf and Turing bifurcation in spatial domain. Li et al. [17] studied the Hopf bifurcation and Turing instability in a spatial Holling–Tanner model with Neumann type boundary condition. Authors also identify the parameter ranges of stability and instability of spatially homogeneous equilibrium solutions and bifurcating periodic orbits. Recently, Wang [28] studied the pattern formation in a spatial epidemic model with nonlinear incidence rate and presented Hopf and Turing bifurcation. Zhang et al. [32] investigated the spatiotemporal dynamics of a reaction-diffusion system with hyperbolic mortality rate and find the Turing space in which Turing instability occurs.

The study of population dynamics with harvesting is a vital topic of mathematical bioeconomics and is related to the optimal management of renewable resources. The management of renewable resources is based on the concept of maximal sustainable yield, which suggests exploiting the surplus production on the basis of biological growth model. Clark [7] reviewed the effect of harvesting on fisheries management using ecological and economic models. There are mainly three types of harvesting reported in the literature: (i) constant rate of harvesting $h(x)=h$, where a fixed number of individuals are harvested per unit time, (ii) proportionate harvesting $h(x)= qEx$, that is, the catch is proportional to the stock and effort [8], where $q$ is called the catchability coefficient, $E$ is effort used for harvesting (number of boats, fishing nets etc) and $qE$ is the fishing mortality, and (iii) nonlinear harvesting $h(x)= qEx/(m_1E+m_2x)$ (Holling type II), where ${m_1},{m_2}$ are suitable positive constants. $m_1$ is proportional to the ratio of the stock-level to the harvesting rate (catch-rate) at high levels of effort and $m_2$ is proportional to the ratio of the effort-level to the harvesting rate at higher stock-levels. Lan and Zhu [16] studied the phase portraits, Hopf bifurcation and limit cycles of Leslie–Gower (LG) model with constant harvesting in prey. Gupta and Chandra [10] studied the modified LG model with nonlinear prey harvesting and observed that the nonlinear harvesting in prey significantly modifies the dynamics of the model system with proportionate harvesting in prey. Recently, Huang et al. [14] studied the effect of constant yield predator harvesting on the dynamics of a Leslie–Gower type model. It has been shown that the model has a Bogdanov–Takens singularity of codimension 3 or a weak focus of multiplicity two for some parameter values. As the parameters varies, the model exhibit saddle-node bifurcation, repelling and attracting Bogdanov–Takens bifurcations, supercritical, subcritical and degenerate Hopf bifurcation. Saleh [24] discussed the dynamical properties of a modified Leslie–Gower model with quadratic predator harvesting. Rao [23] investigated the spatiotemporal complexity of a ratio-dependent spatially extended food chain model. Baek [2] investigated the pattern formations of a ratio-dependent predator-prey system with linear harvesting rate. Sun et al. [26] studied the spatiotemporal complexity in a Holling–Tanner model and investigated how directed movement (migration) and random movement (diffusion) affect predator-prey dynamics. Rai et al. [22] investigated the effects of random and directed animal movements of a 1D spatial nonlinear coupled reaction-diffusion system with a Holling type IV functional response.

The ever growing demand of food and other natural resources leads to an exploitation of several biological resources which badly affect the ecosystem. Also there is a global concern to protect the natural resources/ecosystem at large. For facing these two opposite situations, we are looking for an optimal management policy which is necessary for a scientific management of commercial exploitation of the biological resources. The main motive of the optimal management of renewable resources (like forestry, fishery and wildlife) is to determine how much one can harvest without altering critically the harvested population and conserving it for the benefits of humanity and future generations. For instant, let us think about an outbreak of algal bloom caused by plankton population. In this case, harvesting the populations of phytoplankton or zooplankton is one of simple ways to control the algal bloom. Truly speaking, the management of renewable resource is complicated and constructing an accurate mathematical model is even more complicated. To gain insight in the scientific management of renewable resources, bioeconomic modeling is widely used. In our work, we have tried to address this issue with the help of a designed model system and determine how the nonlinear harvesting affects the dynamics which is more efficient and economic than the constant and proportionate harvesting. Such harvesting activity has an effect on both prey and predator species. Leslie–Gower spatial model under nonlinear harvesting on prey species with Holling type IV functional response has not been studied so far. In this paper, we have designed a two-dimensional modified Leslie–Gower predator-prey diffusive model system with nonlinear harvesting in prey population. The Leslie–Gower model leads to asymptotic solutions tending to stable equilibrium, which is independent of initial conditions and depends on the intrinsic factors governing the biology of the system. The interaction between prey and predator is modeled with Holling type IV functional response. Andrews investigated a function of the form $f(x)=\frac{mx}{\frac{x^2}{i}+x+a}$ and called it Holling type IV functional response or Monod–Haldane function, which is similar to the Monod (i.e., the Michaelis–Menten) function for low concentration but includes the inhibitory effect at high concentrations. This functional response was first introduced by Haldane [11] for enzymology. The parameter $m$ and $a$ can be interpreted as the maximum per capita predation rate and the half-saturation constant in the absence of any inhibitory effect. The parameter $i$ is a measure of the predator’s immunity from the prey. As the value of the parameter $i$ decrease’s, the predator’s foraging efficiency decreases. In the limit of large $i$, it reduces to a type II functional response. This immunity of the predator exists in the circumstances when group defense is operational [27]. We have also studied the existence of Hopf bifurcation and Turing instability in this spatial model with nonlinear harvesting.

2 The mathematical model

The modified Leslie–Gower type model described by the autonomous two-dimensional system of differential equations with Holling type IV functional response is given by

$$\begin{aligned} \frac{\hbox {d}x}{\hbox {d}T}&= \Big (r\left( 1-\frac{x}{K}\right) -\frac{my}{\frac{x^2}{i}+x+a}\Big )x, \nonumber \\ \frac{\hbox {d}y}{\hbox {d}T}&= s\Big (1-\frac{ny}{x}\Big )y, \end{aligned}$$

(1)

subjected to positive initial conditions $x(0)>0, y(0)>0$. Here $x\equiv x(T)$ and $y\equiv y(T)$ are the prey and predator population densities, respectively.

Model system (1) is defined on the set:

$$\begin{aligned} \varOmega = \{(x,y)\in \mathbf R ^2| x\ge 0,y\ge 0\}, \end{aligned}$$

(2)

with all the parameters $r,K,m,i,s,a$ and $n$ being positive. Further, the parameters have the following biological meanings:

• (i) $~r$ and $s$ are intrinsic growth rates or biotic potential of the prey and predators, respectively.

• (ii) $~K$ is the carrying capacity of the environment for prey.

• (iii) $~m$ is the maximum per capita predation rate.

• (iv) $~i$ is a direct measure of, the predator’s immunity from, or tolerance of the prey.

• (v) $~a$ is the half-saturation constant in the absence of any inhibitory effect.

• (vi) $~n$ is number of prey required to support one predator at equilibrium.

Here, the interaction between prey and predator is expressed by the Holling type IV functional response that is $f(x) = \frac{mx}{\frac{x^2}{i}+x+a}$ [27]. Now, we introduce the nonlinear harvesting $H(x) = \frac{qEx}{(m_1E+m_2x)}$ in model system (1). Therefore, the modified system of differential equations are

$$\begin{aligned} \frac{\hbox {d}x}{\hbox {d}T}&= \Big (r\left( 1\!-\!\frac{x}{K}\right) -\frac{my}{\frac{x^2}{i}\!+\!x\!+\!a}-\frac{qE}{(m_1E\!+\!m_2x)}\Big )x, \nonumber \\ \frac{\hbox {d}y}{\hbox {d}T}&= s\Big (1-\frac{ny}{x}\Big )y, \end{aligned}$$

(3)

subjected to positive initial condition $x(0)=x_0>0$ and $y(0)=y_0 > 0$. The parameter $r,K,m,i,s,a$ and $n$ have the same biological meaning as in model (1), $q$ is the catchability coefficient, $E$ is the effort applied to harvest individuals and $m_1,m_2$ are suitable constants. All parameters are assumed to be positive. The system (3) is defined on the set $\varOmega$.

We introduce the following substitutions and notations to bring the system of equations into non-dimensional form

$$\begin{aligned} x&= Ku, t = rT, h = \frac{qE}{rm_2K}, c = \frac{m_1E}{m_2K}, y = \frac{rKv}{m},\\ \alpha&= \frac{i}{K}, \gamma = \frac{a}{K}, \delta = \frac{s}{r}, \beta = \frac{nr}{m}. \end{aligned}$$

Constants $m_1$ and $m_2$ are chosen in such a way that $\big (\frac{m_1}{m_2}\big )E<x$, where $x$ is the prey biomass at a given instant of time.

The model system in dimensionless form can be written as

$$\begin{aligned} \frac{\hbox {d}u}{\hbox {d}t}&= u(1-u)-\frac{uv}{\frac{u^2}{\alpha }+u+\gamma }-\frac{hu}{c+u}, \nonumber \\ \frac{\hbox {d}v}{\hbox {d}t}&= \delta v\Big (1-\beta \frac{v}{u}\Big ). \end{aligned}$$

(4)

Now we present the result which states that the model system (4) is well behaved as one intuits from the biological/ecological problem.

Lemma 1

The solutions of system (4) are positive and eventually bounded, i.e., there exists $T\ge 0$ such that $u(t)<M_1,v(t)<M_2$ for $t\ge T$.

Proof

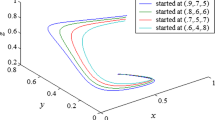
The phase portrait of (4) is shown in Fig. 1. The nullclines of the systems are: $C_1:v=(1-u-\frac{h}{c+u})(\frac{u^2}{\alpha }+u+\gamma )$, on which $\frac{\hbox {d}u}{\hbox {d}t}=0;$ and $C_2: v=\frac{u}{\beta },$ on which $\frac{\hbox {d}v}{\hbox {d}t}=0$. The first quadrant is divided into four parts $D_1,D_2,D_3$ and $D_4$ by $C_1$ and $C_2$. The intersection of $C_1$ and $C_2$ is the positive equilibrium point $(u^*,v^*)$. Set $L_1=\{(u,v):u=M_1,0\le v\le M_2\}$ and $L_2=\{(u,v):0\le u\le M_1, v= M_2\}$. Denote $D$ as the rectangular region whose boundary consists of $L_1, L_2, u$-axis and $v$-axis. Clearly $D$ is an invariant set and attracts any trajectory starting in the first quadrant. Hence, the solutions are eventually bounded.

Next, we prove the positivity of the solutions by showing that trajectories starting from first quadrant cannot reach the $v$-axis. To this end, we only need to prove that trajectories cannot arrive the $v$-axis in $D_2$.

Fig. 1

Phase portrait of model system (4) in $u-v$ plane with $h = 0.01,c = 1,\alpha = 3,\beta = 0.9$

From a given point $(u_0,v_0)\in D_2$, denote $T_1$ as the time of the trajectory running from $(u_0,v_0)$ to $C_1$ and $T_2(N)$ as the time of the trajectory running from $(u_0,v_0)$ to the line $u=u_0/N,N\in \mathbf {N}$ and ${N}\ge 2$. We estimate the time $T_1$ and $T_2$.

$$\begin{aligned} T_1&\le \int _{v_0}^1 \frac{1}{\delta v \Big (1-\beta \frac{v}{u} \Big ) } \hbox {d}v \le \int _{1}^{v_0} \frac{1}{\delta v \Big (\beta \frac{v}{u_0}-1 \Big )} \hbox {d}v\\&= \frac{1}{\delta } ln \Big (\frac{\beta -\frac{u_0}{v_0}}{\beta -u_0}\Big ). \end{aligned}$$

Hence $T_1$ is finite. Now,

$$\begin{aligned} T_2(N)&= \int _{u_0}^{u_0/N} \frac{1}{u(1 - u)-\frac{u v}{((u^2/\alpha )+u+\gamma )}- \frac{hu}{(c+u)}} \hbox {d}u\\&\ge \int _{u_0}^{u_0/N} \frac{1}{u(u+h+v-1)}\hbox {d}u\\&= \frac{1}{h+v-1} ln \Bigg (\frac{u_0+N(h+v_0-1)}{h+u_0+v_0-1}\Bigg ). \end{aligned}$$

Since

$$\begin{aligned} \hbox {lim}_{N\rightarrow +\infty } \frac{1}{h\!+\!v-1} \hbox {ln} \Bigg (\frac{u_0\!+\!N(h+v_0-1)}{h+u_0+v_0-1}\Bigg )=+\infty \end{aligned}$$

there exists an $N_0\in \mathbf {N}$ such that

$$\begin{aligned}&\frac{1}{h+v-1} \hbox {ln} \Big (\frac{u_0+N_0(h+v_0-1)}{h+u_0+v_0-1}\Big )\\&\quad >\frac{1}{\delta } \hbox {ln} \Big (\frac{\beta -\frac{u_0}{v_0}}{\beta -u_0}\Big ), \end{aligned}$$

hence, $T_2(N_0)>T_1$. This shows that the time of the trajectory running to the $v$-axis is far longer than that to $C_1$, that is the trajectory runs into $D_3$ before it reaches the $v$-axis. From the properties of the vector field shown in Fig. 1, the trajectories cannot reach the $v$-axis in $D_3$, therefore any trajectories starting in the first quadrant cannot reach the $v$-axis.

From the above discussion, we know that there is no homoclinic or heteroclinic orbit in the domain $D$. Hence, it is proved.

Now we consider the populations in the spatial domain and the dispersal of species is assumed to be random, so that the Fick’s law holds, and it leads to the following diffusion model in non-dimensionalized form as

$$\begin{aligned} \frac{\partial u}{\partial t}&= d_1\varDelta u+u(1-u)-\frac{uv}{\frac{u^2}{\alpha }+u+\gamma }-\frac{hu}{c+u}, \nonumber \\ \frac{\partial v}{\partial t}&= d_2\varDelta v+\delta v\Big (1-\beta \frac{v}{u}\Big ). \end{aligned}$$

(5)

with the initial condition

$$\begin{aligned} u(0,x,y)&= u_0(x,y)>0,\nonumber \\ v(0,x,y)&= v_0(x,y)>0 \end{aligned}$$

(6)

and the boundary condition

$$\begin{aligned} \partial _{\nu }u = \partial _{\nu }v = 0, \end{aligned}$$

(7)

where $u$ and $v$ denote the population densities of prey and predator population at time $t$ and in space $(x,y)$, respectively; the positive constants $d_1$ and $d_2$ represents the diffusion rates of prey and predator species, respectively; The parameter $\alpha$ is a measure of the predator’s immunity from, or tolerance of, the prey. $\gamma$ is the half-saturation constant in the absence of any inhibitory effect; $\beta$ is conversion coefficient from prey into predator; $\delta$ denotes the growth rate of predator species; $h$ and $c$ are positive constants.$\square$

3 Analysis of the spatial model system

In order to deal with the stability and bifurcation analysis of the spatiotemporal system (5), we linearize the dynamical system (5) around the spatially homogeneous fixed point $E^*(u^*,v^*)$ for small space and time fluctuations. To accomplish this purpose, we assume that

$$\begin{aligned} u(\varvec{x},t)\approx u^*e^{\varvec{\lambda } t}e^{i\varvec{k}.\varvec{x}}, \nonumber \\ v(\varvec{x},t)\approx v^*e^{\varvec{\lambda } t}e^{i \varvec{k}.\varvec{x}}, \end{aligned}$$

(8)

where $\varvec{x}=(x,y)$ and $\varvec{k}.\varvec{k}=k^2, \varvec{k}$ and $\lambda$ are the wave number vector and frequency, respectively. Then we can obtain the corresponding characteristic equation $\left| J_k-\lambda I\right| =0$, where $J_k=J-k^2D$ and $D=\hbox {diag}(d_1,d_2)$ is the diffusion matrix and Jacobian matrix $J$ is given by

$$\begin{aligned} J=\begin{pmatrix}_{\displaystyle {\frac{\partial F}{\partial u}}} &{}_{\displaystyle {\frac{\partial F}{\partial v}}}\\ _{\displaystyle {\frac{\partial G}{\partial u}}} &{}_{\displaystyle {\frac{\partial G}{\partial v}}} \end{pmatrix}, \end{aligned}$$

(9)

where $F=u(1-u)-\frac{uv}{\frac{u^2}{\alpha }+u+\gamma }-\frac{hu}{c+u}$ and $G=\delta v\big (1-\beta \frac{v}{u}\big )$. From an elementary calculation, we obtain

$$\begin{aligned} J= \begin{pmatrix}_{\displaystyle {F_u}} &{}_{\displaystyle {F_v}}\\ _{\displaystyle {\delta /\beta }} &{}_{\displaystyle {-\delta }} \end{pmatrix} \end{aligned}$$

where $F_u={1-2u^*-\frac{c h}{(c+u^*)^2} +\frac{ (\alpha (-\alpha \gamma + {u^*}^2) v^*)}{({u^*}^2 +\alpha (\gamma +u^*))^2}},$ and $F_v={-\frac{\alpha u^*}{({u^*}^2+\alpha (\gamma +u^*))}}$.

The characteristic equation of $J_k$ is

$$\begin{aligned} \lambda ^2-\hbox {tr}(J_k) \lambda +\hbox {det}(J_k)=0, \quad k=0,1,2, \ldots \end{aligned}$$

(10)

where

$$\begin{aligned}&\hbox {tr}(J_k)=F_u-\delta -k^2(d_1+d_2), \nonumber \\&\hbox {det}(J_k)=k^4d_1 d_2\!+\!k^2(\delta d_1\!-\!F_u d_2)-\delta \left( F_u \!+\!\frac{F_v}{\beta }\right) .\nonumber \\ \end{aligned}$$

(11)

Then the solutions of the characteristic Eq. (10) yield the dispersion relation as

$$\begin{aligned} \lambda _k^{\pm }=\frac{1}{2}(\hbox {tr}(J_k)\pm \sqrt{(\hbox {tr}(J_k))^2-4\hbox {det}(J_k)}). \end{aligned}$$

(12)

By analyzing the distribution of roots of (10), we obtain the following results.

Theorem 1

Suppose that $E^*(u^*,v^*)$ is locally asymptotically stable equilibrium for model system (4) and $\delta >F_u$. Then $E^*(u^*,v^*)$ is locally asymptotically stable equilibrium solution of system (5) if and only if one of following is satisfied

• (i) $d_1\ge F_u,$

• (ii) $d_1\ge \frac{d_2 F_u}{\delta },$

• (iii) $d_1<min\big \{F_u,\frac{d_2 F_u}{\delta }\big \}$ and $\delta >\frac{\beta d_2 k^2(F_u-d_1 k^2)}{\beta d_1 k^2-(\beta F_u+F_v)}$, for all $k\ge 1$ satisfying $k<\sqrt{\frac{F_u}{d_1}}.$

Proof

First, it is clear that $\hbox {tr}(J_{k+1})<\hbox {tr}(J_{k})$ for $k \ge 0$ from the definition of $\hbox {tr}(J_{k})$, and $\hbox {tr}(J_{0})<0$. So $\hbox {tr}(J_{k})<0$, for all $k \ge 0.$ Hence, the signs of the real parts of roots of (10) are determined by the signs of $\hbox {det}(J_k),$ respectively. We regard $\hbox {det}(J_k)$ as a quadratic function about $k^2$ denoted by $\hbox {det}(k^2)$, that is, $\hbox {det}(k^2)=k^4d_1 d_2+k^2(\delta d_1-F_u d_2)-\delta (F_u +\frac{F_v}{\beta }), k \in \mathbf {N}$. The symmetry axis of the graph of $(k^2,\hbox {det}(k^2))$ is $l(\delta )=(d_2 F_u-d_1 \delta )/2d_1d_2$.

Assumption (i) implies that $d_1 k^2-F_u\ge 0$ for all $k\ge 1$, that means $\hbox {det}(J_k)=k^4d_1 d_2+k^2(\delta d_1-F_u d_2)-\delta \left( F_u +\frac{F_v}{\beta }\right) >0$ for all $k~\ge ~0$.

Assumption (ii) implies that $l(\delta )< 0$, then we can conclude that $\hbox {det}(J_k)>0$ for all $k \ge 0$ since $\hbox {det}(J)~>~0$.

Clearly, (iii) implies that $\hbox {det}(J_k)>0$ for all $k\ge 0$. So all the roots of (10) will have negative real parts under any one of assumptions (i), (ii) and (iii).$\square$

4 Stability of steady state and existence of Hopf Bifurcation

From the biological point of view, the properties of positive constant steady-state solution are important and interesting. Therefore, in the following, we shall focus on the stability of $E^*(u^*,v^*)$ and the existence of Hopf bifurcation. We first translate the equilibrium $E^*(u^*,v^*)$ of system (5) to the origin using the transformation $\hat{u}=u-u^*$ and $\hat{v}=v-v^*$. Then system (5) in a neighborhood of the origin can be written as

$$\begin{aligned} \frac{\partial \hat{u}}{\partial t}&= d_1\varDelta \hat{u}(t,x)+(\hat{u}+u^*)(1-\hat{u}-u^*)\nonumber \\&-\,\frac{(\hat{u}+u^*)(\hat{v}+v^*)}{\frac{(\hat{u}+u^*)^2}{\alpha }+(\hat{u}+u_*)+\gamma }-\frac{h(\hat{u}+u^*)}{c+\hat{u}+u^*}, \nonumber \\ \frac{\partial \hat{v}}{\partial t}&= d_2\varDelta \hat{v}(t,x)+\delta (\hat{v}+v^*)\Bigg (1-\frac{\beta (\hat{v}+v^*)}{(\hat{u}+u^*)}\Bigg ).\nonumber \\ \end{aligned}$$

(13)

Using the Taylor series expansion at $(u,v)=(0,0)$, system (13) can be expressed as

$$\begin{aligned} \frac{\partial \hat{u}}{\partial t}&= d_1\varDelta \hat{u}(t,x) + (1-2u^*- a_1)\hat{u} + a_2\hat{v}\nonumber \\&\quad +\,f(\hat{u},\hat{v},\theta ),\nonumber \\ \frac{\partial \hat{v}}{\partial t}&= d_2\varDelta \hat{v}(t,x)+b_1\hat{u}+(\delta -b_2)\hat{v}+g(\hat{u},\hat{v},\theta ),\nonumber \\ \end{aligned}$$

(14)

where

$$\begin{aligned} f(\hat{u},\hat{v},\theta )&= (a_3 - 1)\hat{u}^2 + a_4\hat{u}\hat{v} + a_5\hat{v}^2 +a_6\hat{u}^3 \\&\quad +\, a_7\hat{u}^2\hat{v} +\cdots , \\ g(\hat{u},\hat{v},\theta )&= b_3\hat{u}^2 +b_4\hat{u}\hat{v} +b_5\hat{v}^2 + b_6\hat{u}^3 +\cdots , \end{aligned}$$

and

$$\begin{aligned} a_1&= \frac{ch}{(c+u^*)^2 }+(\alpha \gamma - {u^*}^2) \theta ,\\ a_2&= -\frac{\alpha u^*}{{u^*}^2+\alpha u^*+\alpha \gamma },\\ a_3&= \frac{ch}{(c+u^*)^3}+\frac{(\alpha ^2 \gamma + 3 \alpha \gamma u^* - {u^*}^3) \theta }{({u^*}^2+\alpha (\gamma + {u^*}^2))} ,\\ a_4&= \frac{(-\alpha \gamma + {u^*}^2)\theta }{v^*},\\ a_5&= 0,a_6=\frac{-c h}{(c + u^*)^4 }\\&+\,\frac{(-\alpha ^3 \gamma + \alpha ^2 \gamma (\gamma -4u^*) - 6 \alpha \gamma {u^*}^2 + {u^*}^4) \theta }{({u^*}^2+\alpha (\gamma + {u^*}^2))^2},\\ a_7&= \frac{(\alpha ^2 \gamma +3\alpha \gamma u^*-{u^*}^3) \theta }{v^*({u^*}^2+\alpha (\gamma + {u^*}^2))},\\ b_1&= \frac{ \delta }{\beta }, b_2 =2 \delta , b_3=-\frac{\beta \delta {v^*}^2}{{u^*}^3},\\ b_4&= \frac{2\beta \delta v^*}{{u^*}^2},b_5=-\frac{\beta \delta }{u^*},\\ b_6&= \frac{\beta \delta v_*^2}{u_*^4},\theta = \frac{\alpha v^*}{({u^*}^2+\alpha (\gamma + {u^*}^2))^2}. \end{aligned}$$

In the following, we use $\theta$ as the bifurcation parameter. The variance of $\theta$ plays an important role in determining the stability of positive constant steady-state solution and for the existence of Hopf bifurcation.

Now, we introduce new variables $U_1(t ),U_2(t)$ and $U(t)$ by

$$\begin{aligned}&U_1(t) = \hat{u}(t,.), \quad U_2(t) = \hat{v}(t,.), \\&U(t) = (U_1(t),U_2(t))^T. \end{aligned}$$

Then model system (14) can be transformed into an abstract differential equation

$$\begin{aligned} \dot{U(t)} = L(U)+G(U) \end{aligned}$$

(15)

where,

$$\begin{aligned} L=\left( \begin{array}{ll} (1-2u^*- a_1)+d_1\varDelta &{} \quad a_2 \\ b_1 &{} \quad \delta -b_2+d_2\varDelta \\ \end{array} \right) \end{aligned}$$

and

$$\begin{aligned} G(U) = (f,g)^T \end{aligned}$$

Let

$$\begin{aligned} K=\left( \begin{array}{ll} (1-2u^*- a_1) &{} \quad a_2 \\ b_1 &{} \quad \delta -b_2 \\ \end{array} \right) ,\quad D=\left( \begin{array}{ll} d_1 &{} \quad 0 \\ 0 &{} \quad d_2 \\ \end{array} \right) \end{aligned}$$

then $L = K+D\left( \begin{array}{ll} \varDelta &{} \quad 0 \\ 0 &{} \quad \varDelta \\ \end{array} \right)$ and

$$\begin{aligned}&\hbox {det} K =\delta \left( 2u^*\!-\!1\!+\! \frac{c h}{(c \!+\! u^*)^2} \!+\! \frac{u^*\alpha }{(\beta ({u^*}^2 \!+\!\alpha (\gamma \!+\! u^*)))}\right. \\&\left. \qquad \quad +\,\frac{\alpha ^2 \!\gamma v^*}{({u^*}^2\!+\!a(\gamma \!+\!u^*))^2}\!-\!\frac{\alpha {u^*}^2 v^*}{({u^*}^2\!+\!\alpha (\gamma \!+\!u^*))^2}\right) \!>\!0, \end{aligned}$$

if $u^*>1/2$ and $\alpha \gamma \ge {u^*}^2$.

Now, linearizing system (15) at the origin (0,0), one can obtain that

$$\begin{aligned} \dot{U}(t) = L(U). \end{aligned}$$

(16)

The characteristic equation of system (16) is

$$\begin{aligned} \lambda y-D\left( \begin{array}{ll} \varDelta &{} \quad 0 \\ 0 &{} \quad \varDelta \\ \end{array} \right) y - K(y) = 0, \end{aligned}$$

(17)

where $y\in \hbox {dom}\Big (D\Big ( \begin{array}{ll} \varDelta &{} \quad 0 \\ 0 &{} \quad \varDelta \\ \end{array} \Big )\Big )\backslash \{0\}.$

It is well known that the stability of trivial solution of (15) depends on the locations of roots of (17), when all roots of (17) have negative real parts, the trivial solution of (15) is stable; otherwise, it is unstable.

Clearly, the eigenvalue problem

$$\begin{aligned} -\varDelta \phi =\lambda \phi ,\quad x\in \varOmega , \qquad \partial \phi _{\nu }=0, \quad x\in \partial \varOmega , \end{aligned}$$

has eigenvalues $0 = \lambda _0 <\lambda _1 < \cdots <\lambda _k < \cdots$ , and the corresponding eigenfunctions are

$$\begin{aligned} \gamma _k=\phi _k(x), k\in \mathbf N _0 = \{0,1,2,\ldots \}. \end{aligned}$$

Let $\beta _k^1 = \Big ( \begin{array}{ll} \gamma _k \\ 0 \\ \end{array} \Big ), ~\beta _k^2 = \Big ( \begin{array}{ll} 0 \\ \gamma _k \\ \end{array} \Big )$. Then $B_k = \{(\beta _k^1,\beta _k^2)\}_{k=0}^{\infty }$ construct a basis of the phase space of system (15) and $y\in dom\Big (D\Big ( \begin{array}{ll} \varDelta &{} \quad 0 \\ 0 &{} \quad \varDelta \\ \end{array} \Big )\Big )\backslash \{0\}$ can be decomposed as

$$\begin{aligned} y&= \sum _{k=0}^{\infty }\left( \left\langle y,\beta _k^1\right\rangle \beta _k^1 + \left\langle y,\beta _k^2\right\rangle \beta _k^2\right) ,\nonumber \\&= \sum _{k=0}^{\infty }(\beta _k^1,\beta _k^2)\left( \begin{array}{ll} \left\langle y,\beta _k^1\right\rangle \\ \left\langle y,\beta _k^1\right\rangle \\ \end{array} \right) . \end{aligned}$$

(18)

Thus, the characteristic Eq. (17) is equivalent to

$$\begin{aligned}&\hbox {det }\left[ \left( \begin{array}{ll} \lambda +d_1\lambda _k &{} \quad 0 \\ 0 &{} \quad \lambda +d_2\lambda _k \\ \end{array} \right) \right. \\&\qquad \left. -\left( \begin{array}{ll} (1-2u^*- a_1) &{} \quad a_2 \\ b_1 &{} \quad \delta -b_2 \\ \end{array} \right) \right] \\&\quad = 0,\hbox { for some }k\in \mathbf {N}_0 \end{aligned}$$

that is,

$$\begin{aligned}&\lambda ^2((d_1+d_2)\lambda _k+b_2-\delta -1+2u^*+a_1)\lambda \nonumber \\&\quad +(d_1d_2\lambda _k^2-(1-2u^*-a_1)d_2\lambda _k-(\delta -b_2)d_1\lambda _k\nonumber \\&\quad +(1-2u^*-a_1)(\delta -b_2)-b_1a_2)=0. \end{aligned}$$

(19)

Let $J_k := K-\lambda _kD$, then

$$\begin{aligned} \hbox {tr}J_k =\hbox {tr}K -(d_1+d_2)\lambda _k = -(d_1+d_2)\lambda _k + \theta ^* - \theta \end{aligned}$$

and

$$\begin{aligned} \hbox {det}J_k&= d_1d_2\lambda _k^2-[d_1(\delta -b_2)\\&+\,d_2(1-2u^*- a_1)]\lambda _k+ \hbox {det}K, \end{aligned}$$

where

$$\begin{aligned} \theta ^*&= 1-\delta -2u^*\!-\!\frac{ch}{(c + u^*)^2}+\frac{\alpha v^*}{({u^*}^2+\alpha (\gamma + u^*))^2}\nonumber \\&-\,\frac{\alpha (\alpha \gamma - {u^*}^2) v^*}{({u^*}^2 + \alpha (\gamma + u^*))^2}.\nonumber \end{aligned}$$

Thus, the characteristic Eq. (19) can be denoted simply as

$$\begin{aligned} \lambda ^2-\lambda \hbox {tr}J_k+\hbox {det}J_k = 0. \end{aligned}$$

(20)

According to (20) and det$K >0$, it is easy to know that under the condition that $u^* \ge 1/2$ and $\alpha \gamma \ge 1+{u^*}^2$, if $\theta > \theta ^*-(d_1+d_2)\lambda _k$ for every $k\in \mathbf {N}_0$, then the positive constant steady-state solution $E^*(u^*,v^*)$ is stable; if there exists certain $k\in \mathbf {N}_0$ such that $\theta < \theta ^*-(d_1+d_2)\lambda _k$, then the positive constant steady-state solution $E^*(u^*,v^*)$ is unstable.

Suppose that $i\omega$ is a pure imaginary root of (20). Substituting $i\omega$ into (20), we have

$$\begin{aligned} -\omega ^2-\hbox {tr}J_k\omega i + \hbox {det}J_k = 0. \end{aligned}$$

(21)

Separating the real and imaginary parts of the above equation, one can obtain

$$\begin{aligned} \omega ^2 = \hbox {det}J_k>0, \hbox {tr}J_k = \hbox {tr}K -(d_1+d_2)\lambda _k = 0. \end{aligned}$$

Let

$$\begin{aligned} \theta _j = \theta ^* -(d_1+d_2)\lambda _j \qquad (j\in \text {N}_0). \end{aligned}$$

(22)

Then, the only value of $\theta$ at which the homogeneous Hopf bifurcation occurs is $\theta = \theta _0$. Near $\theta _0$, substituting $\lambda = p_1 + q_1i$ into (20) and separating the real and imaginary parts, one can get that

$$\begin{aligned}&p_1^2-q_1^2-p_1\hbox {tr}J_k +\hbox {det}J_k = 0,\end{aligned}$$

(23)

$$\begin{aligned}&2p_1q_1 -q_1\hbox {tr}J_k = 0. \end{aligned}$$

(24)

Differentiating two sides of (24) with respect to $\theta$, we get

$$\begin{aligned} \hbox {sgn}\Big [\frac{\hbox {d}p_1}{\hbox {d}\theta }\Big ]_{\theta = \theta _0} = -\frac{1}{2}\ne 0. \end{aligned}$$

(25)

Therefore, the transversality condition holds. According to the Hopf bifurcation theorem for differential Eq. [6], we have the following result.

Theorem 2

Suppose that $u^* \ge 1/2$ and $\alpha \gamma \ge 1+{u^*}^2$. Then

• (i) If $\theta > \theta _0$, then the positive constant steady-state solution $E^*(u^*,v^*)$ of system (5) is asymptotically stable and unstable when $\theta < \theta _0$;

• (ii) System (5) can undergo a Hopf bifurcation at the positive constant steady-state solution $E^*(u^*,v^*)$ when $\theta = \theta _j, j\in \mathbf N _0$.

The model system (5) is integrated numerically using Runge-Kutta Method. For parameter values $\alpha = 0.05,~\beta =0.02,~c=1,~\delta =0.12,~\gamma =.5,~h=0.01,~d_1=0.005,~d_2=0.0001$, a limit cycles appears in a small neighborhood of the equilibrium point (see Fig. 2).

Fig. 2

The figure shows that the limit cycle have created around the equilibrium point

5 Stability of spatially homogeneous periodic orbits

In Sect. 4, we have obtained the conditions under which a family of periodic solutions bifurcate from the positive constant steady-state solution $E^*(u^*,v^*)$ of system (5) when the parameter $\theta$ crosses through the critical value $\theta _j$. In this section, we study the direction of Hopf bifurcations and stability of bifurcated periodic solutions arising through Hopf bifurcations by applying the center manifold theorem and normal form theory introduced by Hassard et al. [12].

To determine the stability of bifurcated periodic solutions, we need to know the restriction of the system to its center manifold at $\theta _0$. Denote by $L^*$ the conjugate operator

$$\begin{aligned} \left( \begin{array}{ll} u \\ v \\ \end{array} \right) \rightarrow L^*\left( \begin{array}{ll} u \\ v \\ \end{array} \right) , \end{aligned}$$

(26)

with domain

$$\begin{aligned} \{(u, v)\in H^2(\varOmega )\times H^2(\varOmega )|\partial u_{\nu } \!=\! \partial v_{\nu } = 0, x\in \partial \varOmega \}, \end{aligned}$$

where the $H^2(\varOmega )$ is the standard Sobolev space and

$$\begin{aligned} L^*=\left( \begin{array}{ll} (1-2u^*- a_1)+d_1\varDelta &{} \quad a_2 \\ b_1 &{} \quad \delta -b_2+ d_2\varDelta \\ \end{array} \right) .\nonumber \\ \end{aligned}$$

(27)

In fact, we choose

$$\begin{aligned}&q=\left( \begin{array}{ll} 1 \\ \frac{i\omega -(1-2u^*- a_1)}{a_2} \\ \end{array} \right) ,\quad q^*\!=\!D^*\left( \begin{array}{ll} \frac{\omega -(1-2u^*- a_1)i}{a_2} \\ -i \\ \end{array} \right) ,\\&D^* = \frac{a_2}{2\omega }. \end{aligned}$$

For all $\alpha \in D_{L^*}, \beta \in D_{L}$, it is not difficult to verify that

$$\begin{aligned}&\left\langle L^*\alpha ,\beta \right\rangle = \left\langle \alpha ,L\beta \right\rangle ,Lq = i\omega q,\\&L^*q^* = -i\omega q^* ,\left\langle q^*,q\right\rangle = 1,\left\langle q^*,\bar{q}\right\rangle = 0, \end{aligned}$$

where $\left\langle \alpha ,\beta \right\rangle = \int _{\varOmega }{\bar{\alpha }^T\beta \hbox {d}x }$ denotes the inner product in $L^2(\varOmega )\times L^2(\varOmega )$.

Following Hassard et al. [12], we decompose $X=X^C\oplus X^S$ with $X^C:=\{zq+\bar{z}\bar{q}:z\in C\}$,

$X^S:=\{W \in X:\langle q^*,W\rangle =0\}$. For any $(x,y)\in X,$ there exists $z \in C$ and $W=(W_1,W_2)\in X^S$ such that

$$\begin{aligned} (u,v)^T = zq+\bar{z}\bar{q}+(W_1,W_2)^T, \quad z=\left\langle q^*,(u,v)^T\right\rangle , \end{aligned}$$

then

$$\begin{aligned} u&= z+\bar{z}+W_1,\nonumber \\ v&= z\Big (\frac{i\omega }{a_2}-\frac{(1-2u_*- a_1)}{a_2}\Big )\nonumber \\&+\bar{z}\Big (\frac{-i\omega }{a_2}-\frac{(1-2u_*- a_1)}{a_2}\Big )+W_2. \end{aligned}$$

(28)

System in $(z,W)$ coordinates becomes

$$\begin{aligned}&\frac{\hbox {d}z}{\hbox {d}t} = i\omega z+ \left\langle q^*,\tilde{f}\right\rangle ,\nonumber \\&\frac{\hbox {d}W}{\hbox {d}t} = LW + [\tilde{f} - \left\langle q^*,\tilde{f}\right\rangle q-\left\langle \bar{q^*},\tilde{f}\right\rangle \bar{q}], \end{aligned}$$

(29)

where $\tilde{f} = (f,g)^T,$ and $f,g$ are defined by Eq. (14).

Then, the calculations show that

$$\begin{aligned}&\left\langle q^*,\tilde{f}\right\rangle = D^*\Big [\frac{\omega }{a_2}f-\frac{(1-2u_*- a_1)}{a_2}fi-gi\Big ],\\&\left\langle \bar{q^*},\tilde{f}\right\rangle = D^*\Big [\frac{\omega }{a_2}f+\frac{(1-2u_*- a_1)}{a_2}fi+gi\Big ],\\&\left\langle q^*,\tilde{f}\right\rangle q \\&\quad =D^*\left( \begin{array}{ll} \frac{\omega }{a_2}f\!-\!\frac{(1\!-\!2u_*\!-\! a_1)}{a_2}f\!-\!gi\\ \frac{\omega ^2}{a_2^2}fi\!+\!\frac{(1\!-\!2u_*\!-\! a_1)^2}{a_2^2}fi\!+\!\frac{\omega }{a_2}g\!+\!\frac{(1\!-\!2u_*\!-\! a_1)}{a_2}gi \\ \end{array} \right) ,\\&\left\langle q^*,\tilde{f}\right\rangle \bar{q}\\&\quad =D^*\left( \begin{array}{ll} \frac{\omega }{a_2}f\!+\!\frac{(1\!-\!2u_*\!-\! a_1)}{a_2}f\!+\!gi\\ -\frac{\omega ^2}{a_2^2}fi\!-\!\frac{(1\!-\!2u_*\!-\! a_1)^2}{a_2^2}fi\!+\!\frac{\omega }{a_2}g\!-\!\frac{(1\!-\!2u_*\!-\! a_1)}{a_2}gi \\ \end{array} \right) . \end{aligned}$$

Notice that

$$\begin{aligned} H&= \frac{H_{20}}{2}z^2+H_{11}z\bar{z}+ \frac{H_{02}}{2}\bar{z}^2+O(\left| {z}\right| ^3),\\ W&= \frac{W_{20}}{2}z^2+W_{11}z\bar{z}+ \frac{W_{02}}{2}\bar{z}^2+O(\left| {z}\right| ^3). \end{aligned}$$

On the center manifold, we have

$$\begin{aligned}&(2i\omega - L)W_{20} = H_{20},\\&(- L)W_{1} = H_{11},\\&W_{02} = \bar{W}_{20}. \end{aligned}$$

and

$$\begin{aligned}&\left\langle q^*,\tilde{f}\right\rangle q+\left\langle \bar{q^*},\tilde{f}\right\rangle \bar{q} =D^*\left( \begin{array}{ll} \frac{2\omega }{a_2}f\\ \frac{2 \omega }{a_2}g \\ \end{array} \right) = (f,g)^T,\\&H(z,\bar{z},W):= \tilde{f}-\left\langle q^*,\tilde{f}\right\rangle q-\left\langle \bar{q^*},\tilde{f}\right\rangle \bar{q} = (0,0)^T. \end{aligned}$$

Fig. 3

Space series generated at different time level at (i) $t=600$ in a–c , (ii) $t=1{,}500$ in d–f and for different values of $d_1=0.009, 0.025,$ and $0.5$ showing the effect of prey diffusivity constant $d_1$ on dynamics of the model system (5). Other parameters were fixed at $\alpha =0.2,h=0.02,\beta =0.15,c=0.6,\delta =0.09,d_2=5$

This implies that

$$\begin{aligned} W_{20} = W_{02} = W_{11} = 0. \end{aligned}$$

Therefore

$$\begin{aligned} \frac{\hbox {d}z}{\hbox {d}t}&= i\omega z+\frac{1}{2}g_{20}z^2+g_{11}z\bar{z}+\frac{1}{2}g_{02}\bar{z}^2\\&+\,\frac{1}{2}g_{21}z^2\bar{z}+O(\left| {z}\right| ^4), \end{aligned}$$

where

$$\begin{aligned} g_{20}&= \frac{1}{2}\left[ -2 +2 \Big (\frac{c h}{(c + u^*)^3} + \frac{\alpha (\alpha ^2 \gamma + 3 \alpha \gamma u^*- {u^*}^3) v^*}{({u^*}^2 +\alpha (\gamma + u^*))^3 }\Big )\right. \\&\left. \quad \, - \frac{2 (-\alpha \gamma + {u^*}^2) (-1 + 2 u^* + \frac{(c h)}{(c + u^*)^2} + \frac{(\alpha (\alpha \gamma - {u^*}^2) v^*)}{({u^*}^2 + \alpha (\gamma + u^*))^2 }+ i w)}{(u^* ({u^*}^2 + \alpha (\gamma +u^*)))}\right] ,\\ g_{11}&= \frac{1}{2} \left[ -2 +2 \Big (\frac{c h}{(c + u^*)^3} + \frac{\alpha (\alpha ^2 \gamma + 3 \alpha \gamma u^*- {u^*}^3) v^*}{({u^*}^2 +\alpha (\gamma + u^*))^3 }\Big )\right. \\&\left. \quad \, - \frac{(2 (-\alpha \gamma + {u^*}^2) (-1 + 2 u^* + \frac{(c h)}{(c + u^*)^2} + \frac{(\alpha (\alpha \gamma - {u^*}^2) v^*)}{({u^*}^2 + \alpha (\gamma + u^*))^2 })}{(u^* ({u^*}^2 + \alpha (\gamma +u^*)))}\right] ,\\ g_{02}&= \frac{1}{2}\left[ -2 +2 \Big (\frac{c h}{(c + u^*)^3} + \frac{\alpha (\alpha ^2 \gamma + 3 \alpha \gamma u^*- {u^*}^3) v^*}{({u^*}^2 +\alpha (\gamma + u^*))^3 }\Big )\right. \\&\left. \quad \, - \frac{(2 (-\alpha \gamma + {u^*}^2) (-1 + 2 u^* + \frac{(c h)}{(c + u^*)^2} + \frac{(\alpha (\alpha \gamma - {u^*}^2) v^*)}{({u^*}^2 + \alpha (\gamma + u^*))^2 }- i w))}{(u^* (u1^2 + \alpha (\gamma +u^*)))}\right] ,\\ g_{21}&= \frac{1}{2}\left[ 6 \Big (-\frac{c h}{(c + u^*)^4} +\frac{\alpha (-\alpha ^3 \gamma + \alpha ^2 \gamma (\gamma -4 u^*) - 6 \alpha \gamma {u^*}^2 + {u^*}^4) v^*\Big )}{({u^*}^2 +\alpha (\gamma + u1))^4)}\right. \\&\left. \quad \, -\frac{\left( 2 \left( a^2 \gamma + 3 \alpha \gamma u^* -{u^*}^3\right) \Big (3 \left( -1 + 2u^*+ \frac{ch}{(c + u^*)^2}+\frac{ \alpha (\alpha \gamma \!-\! {u^*}^2) v^*}{({u^*}^2 + \alpha (\gamma + u^*))^2}\right) + i w\Big )\right) }{u^*({u^*}^2 +\alpha (\gamma +u^*))^2)}\right] , \end{aligned}$$

According to Hassard et al. [12], we can obtain

$$\begin{aligned}&C_1(0) = \frac{i}{2\omega }\Big (g_{20}g_{11} - 2\left| g_{11}\right| ^2 - \frac{\left| g_{02}\right| ^2}{3}\Big )+\frac{g_{21}}{2},\\&\mu _2 = -\frac{Re\{C_1(0)\}}{Re\{\lambda '(\theta )\}},\\&\beta _2 = 2Re\{C_1(0)\}. \end{aligned}$$

Therefore, we have the following results:

Theorem 3

Suppose $\mu _2$ determines the directions of Hopf bifurcation. If $\mu _2 > 0 (< 0)$, then the Hopf bifurcation is supercritical (subcritical); $\beta _2$ determines the stability of bifurcated periodic solutions. If $\beta _2<0(>0)$, the bifurcated periodic solutions are stable (unstable).

Fig. 4

Space series generated at different time level at (i) $t=600$ in a–c, (ii) $t=1{,}500$ in d–f, and for different values of $d_2=1, 15,$ and $30$ showing the effect of predator diffusivity constant $d_2$ on dynamics of the model system (5). Other parameters were fixed at $\alpha =0.2,h=0.02,\beta =0.15,c=0.6,\delta =0.09,d_1=0.065$

Fig. 5

Spatial distribution of population showing the effect of harvesting $(h)$ on the dynamics of the model systems (5) at (i) $h=0.02$ in  a–c ,(ii) $h=0.05$ in  d–f , (iii) $h=0.09$ in  g–i and for parameter values $\alpha =0.2,h=0.02,\beta =0.15,c=0.6,\delta =0.09,d_1=0.055,d_2=5$ , and at time $t=200, 600, 1{,}000$, respectively

6 Numerical simulations

In this section, we perform numerical simulations of model (5) in one and two-dimensional space. To solve differential equations by computer, one has to discretize the problem in space and time. The continuous problem defined by the reaction-diffusion system in two-dimensional space is solved in a discrete domain with $M\times N$ lattice sites. The spacing between the lattice points is defined by the lattice constant $\varDelta h$. In the discrete system the Laplacian describing diffusion is calculated using finite differences, i.e., the derivatives are approximated by differences over $\varDelta h$. The time evolution is also discrete, i.e., the time goes in steps of $\varDelta t$. The time evolution can be solved using the Euler method. In the present paper, we set $\varDelta h=1, \varDelta t = 0.1$ and $M = N = 200$. All of our numerical simulations employ the Neumann boundary conditions. It is checked that a further decrease of the step values does not lead to any significant modification of the results. Then we use the standard five-point approximation for the 2D Laplacian with the zero-flux boundary conditions. The concentration at mesh point $(x_i,y_j)$ at the moment $(n + 1)\tau$ is denoted by $(u^{n+1}_{i,j}, v^{n+1}_{i,j})$ is given by

$$\begin{aligned} u^{n+1}_{i,j}&= u^n_{i,j}+\tau d_1 \varDelta _h u^n_{i,j}+\tau f(u^n_{i,j},v^n_{i,j}),\\ v^{n+1}_{i,j}&= v^n_{i,j}+\tau d_2 \varDelta _h v^n_{i,j}+\tau g(u^n_{i,j},v^n_{i,j}), \end{aligned}$$

with the Laplacian defined by

$$\begin{aligned} \varDelta _h u^n_{i,j}=\frac{u^n_{i+1,j}+u^n_{i-1,j}+u^n_{i,j+1}+u^n_{i,j-1}-4u^n_{i,j}}{h^2}. \end{aligned}$$

6.1 The spatiotemporal dynamics in one-dimensional case

In this subsection, the plots (space vs. population densities) are obtained to study the spatial dynamics of the model systems. In one-dimensional case, we assume the domain of size $7000$. From a realistic biological point of view, we consider a non-monotonic form of initial condition which determine the initial spatial distribution of the species in the real community as

$$\begin{aligned} u(x,0)&= u^*+\epsilon (x-x_1)(x-x_2),\\ v(x,0)&= v^*, \end{aligned}$$

where $E^*(u^*,v^*)$ is the non-trivial state for coexistence of prey and predator and $\epsilon =10^{-8},x_1=1{,}200, x_2=2{,}800$ is the parameter affecting the system dynamics. The dynamics of the prey and predator is observed at the parameter values $\alpha =0.2,h=0.02,\beta =0.15,c=0.6,\delta =0.09,d_2=5$, and at time level $t=600$ and $1{,}500$ for different diffusivity constant, i.e., $d_1=0.009,0.025$ and $0.5$ as shown in Fig. 3. Figure 3 shows the onset of chaotic phase for $d_1=0.009$. But when we increase the value of diffusivity constant for prey population, the dynamics becomes cyclic. As we increase the time level from $t = 600$ to $t =1{,}500$, it is observed that the jagged pattern representing chaotic behavior of the system grows steadily with time. The size of the domain occupied by the irregular chaotic patterns slowly grows with time in both directions displacing the regular pattern (characterized by a stable limit cycle in the phase plane of the system) with chaotic dynamics. The chaotic dynamics is observed only for $d_1=0.009$ and $d_1=0.025$. For $d_1=0.5$ system becomes stable in the long range.

The dynamics of the model system in one-dimensional case is also observed at the same time level $t=600$ and $1{,}500$ for the same set of parameter values but with fixed parameter $d_1=0.065$ and for different values of $d_2=1,15$ and $30$ as shown in Fig. 4. In Fig. 4, we observe the effect of diffusivity constant $d_2$ on the dynamics of the model system (5). Changing the value of parameter $d_2$, and other parameter fixed as above, we observe limit cycle in the first column and onset of chaos in second and third columns of Fig. 4. Wave of chaos phenomena is observed as we increase the diffusivity constant $d_2$ and time level.

The dynamics of the model system in one-dimensional case is observed at the time level $t=200,600$ and $1{,}000$, at the fixed value of diffusivity constant $d_1=0.055, d_2=5$ and for different values of harvesting rate, $h=0.02,0.05$ and $0.09$ as shown in Fig. 5. In Fig. 5, we observe the effect of harvesting on dynamics of the model system. As we increase the value of $h$ , at same time level, the cyclic and chaotic patterns becomes stable regular patterns. At $h=0.05$ for the time level $t=600$ and $t=1{,}000$, the cyclic and chaotic patterns is observed in the region $500\le x\le 5{,}000$ and $0\le x\le 3{,}000$, respectively. Now we increase the value of $h$ to $0.09$ and find that the previously observed cyclic and chaotic patterns settled at stable regular pattern in the regions $100 \le x\le 4{,}500$. Thus, we can say that increased value of harvesting is stabilizing the system.

7 Turing instability of coexistence equilibrium point

Turing bifurcation is sometimes called Turing instability or diffusion-driven instability. It is well known that Turing bifurcation breaks spatial symmetry, leading to the formation of patterns that are stationary in time and oscillatory in space. Moreover, since this instability occur only if the prey$(u)$ diffuses more slowly than predator$(v)$the condition $d_1<<d_2$ is assumed.

Turing bifurcation occurs when the positive steady state $E^*(u^*,v^*)$ for the non-spatial system (4) is stable and it is unstable for the diffusive system (5). The condition for steady state $E^*(u^*,v^*)$ of system (5) to be stable is discussed in previous Sect. 3.

Theorem 4

The equilibrium $E^*(u^*,v^*)$ is an unstable solution of spatial model (5) if

• (i) $d_1<\hbox {min}\left\{ F_u,\frac{d_2 F_u}{\delta }\right\}$ and

• (ii) $\delta <\frac{\beta d_2 k^2(F_u-d_1 k^2)}{\beta d_1 k^2-(\beta F_u+F_v)}$, for some $k \in \mathbf {N}$ satisfying $k<\sqrt{\frac{F_u}{d_1}}.$

Thus, the equilibrium $E^*(u^*,v^*)$ is Turing unstable if $\delta$ belongs to the interval:

$$\begin{aligned} I_k=\left\{ \delta : F_u<\delta <\frac{\beta d_2 k^2(F_u-d_1 k^2)}{\beta d_1 k^2-(\beta F_u+F_v)}\right\} . \end{aligned}$$

That is, if $\delta \in I_k$, then $E^*(u^*,v^*)$ is locally asymptotically stable with respect to the model dynamics of system (4), and it is unstable with respect to spatial model (5).

Proof

Since $\hbox {tr}(J_0)<0, \hbox {tr}(J_k)$ is always negative and hence the two roots of the characteristic Eq. (10) cannot be positive at the same time. Therefore, Turing instability can happen only if $\hbox {det}(J_k)<0$ because the stationary state is unstable to spatial perturbation for $\lambda _k\ne 0$, i.e.,

$$\begin{aligned} \hbox {det}(J_k)&= H(k^2)=(k^2)^2 d_1 d_2+k^2(\delta d_1-F_u d_2)\nonumber \\&-\delta (F_u +\frac{F_v}{\beta })<0. \end{aligned}$$

(30)

Fig. 6

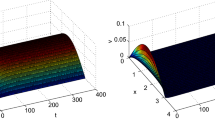
An illustration of the dispersion relation ($Re(\lambda _k)$ vs. $k$). Green, red and black lines are corresponding to the $h = 0.12$ , $h=0.19$ and $h=0.25$, respectively, and other parameter parameters were fixed at $\alpha =0.2,\gamma =1,\delta =0.09,c=0.6,\beta =0.15$ and $d_1=0.025,d_2=10$ . (Color figure online)

When (i) and (ii) holds, $\hbox {det}(J_k)<0$ , Eq. (10) has at least one root with positive real part. Hence, $E^*(u^*,v^*)$ is an unstable equilibrium solution of model system (5).

However, the condition (30) is necessary, not a sufficient condition. For $H(k^2)$ to be negative for some non-vanishing $k$, the minimum of $H(k^2)$ must be negative. Actually, $\hbox {det}(J_k)$ has the minimum value at some value of $k_\mathrm{T}^2$.

$$\begin{aligned} {k_\mathrm{T}^2} = \frac{1}{2d_1d_2}[d_2 F_u-d_1\delta ], \end{aligned}$$

(31)

which is called the wave number. Therefore, the condition $H(k_\mathrm{T}^2)<0$ gives

$$\begin{aligned} (d_2 F_u-d_1\delta )^2> 4 d_1 d_2\left( -\delta F_u- F_v \frac{\delta }{\beta }\right) . \end{aligned}$$

(32)

Fig. 7

Snapshots of pattern formation for the time evolution of the prey and predator at different instants with $\alpha =0.2,\gamma =1,\delta =0.09,c=0.6,\beta =0.15,d_1=0.025,d_2=10$ and taking $h=0.12$, which are in Turing space at time level at (i) $t = 200$ in a, b, (ii) $t = 1{,}000$ in c, d

This implies that the diffusive instability to small perturbation of the form (8) will take place.

In order to obtain the threshold of Turing bifurcation, let the inequality in (32) be the equality. Then we have the critical value of the bifurcation parameter $h$ for which Turing instability occurs as:

$$\begin{aligned} h=h_\mathrm{T}. \end{aligned}$$

(33)

At the Turing threshold $h_\mathrm{T}$, the spatial symmetry of the system is broken and the patterns are stationary in time and oscillatory in space with the wavelength

$$\begin{aligned} \lambda _\mathrm{T}=\frac{2\pi }{k_\mathrm{T}}. \end{aligned}$$

(34)

Fig. 8

Snapshots of pattern formation for the time evolution of the prey and predator at different instants with $\alpha =0.2,\gamma =1,\delta =0.09,c=0.6,\beta =0.15,d_1=0.025,d_2=10$ and taking $h=0.19$, which are in Turing space at time level at (i) $t = 200$ in a, b (ii) $t = 1{,}000$ in c, d

Fig. 9

Snapshots of pattern formation for the time evolution of the prey and predator at different instants with $\alpha =0.2,\gamma =1,\delta =0.09,c=0.6,\beta =0.15,d_1=0.025,d_2=10$ and taking $h=0.25$, which are in Turing space at time level at (i) $t = 200$ in a, b (ii) $t = 1{,}000$ in c, d

Only for a finite number of eigen modes $k$, the interval $I_k$ is non-trivial and it is empty if $k^2\ge F_u/d_1$. Now for fixed $d_1$, we can select a large enough $d_2$ to guarantee that $I_k$ is non-empty for $k^2<F_u/d_1$. Following Yi et al. [31], we find that when these conditions are met and certain transversality conditions are satisfied, a pitchfork bifurcation for the non-constant equilibrium solutions occurs at $\delta =\delta _k=\frac{\beta d_2 k^2(F_u-d_1 k^2)}{\beta d_1 k^2-(\beta F_u+F_v)}$. For decreasing $\delta$, the constant equilibrium $E^*(u^*,v^*)$ loses stability to a non-constant equilibrium before Hopf bifurcation at $\delta =\delta _0<\delta _k$. The first such bifurcation point is

$$\begin{aligned} \delta _*=\hbox {max}_{k\in \mathbf {N}}= \frac{\beta d_2 k^2(F_u-d_1 k^2)}{\beta d_1 k^2-(\beta F_u+F_v)}. \end{aligned}$$

When $\delta >\delta _*, E^*(u^*,v^*)$ is locally asymptotically stable for the spatial model system (5), and it is unstable if $\delta \le \delta _*.$ $\square$

Fig. 10

Equidensity contours for varying $d_1$ at $t=1{,}000$ days (i) $d_1= 0.009$ in a, b (ii) $d_1= 0.025$ in c, d (iii) $d_1=0.055$ in e, f. Other parameters are fixed at $\alpha =0.2,\gamma =1,\delta =0.09,c=0.6,\beta =0.15,d_2=5$

Fig. 11

Equidensity contours for varying $d_2$ at $t = 1{,}000$ days (i) $d_2=5$ in a, b (ii) $d_2=10$ in c, d (iii) $d_2=15$ in e, f. Other parameters are fixed at $\alpha =0.2,\gamma =1,\delta =0.09,c=0.6,\beta =0.15,d_1=0.045$

7.1 The evolutionary process of Turing pattern formation

In this section, we see that the small random perturbation of the stationary solution $u^*$ and $v^*$ leads to the formation of a strongly irregular transient pattern in the domain when the parameter values are in the domain of Turing space (see Fig. 6). In Turing pattern formation, there are mainly three categories of patterns: holes, stripes and spots patterns. Next, we show the evolutionary process of Turing pattern formation. System parameters were fixed at $\alpha =0.2,\gamma =1,\delta =0.09,c=0.6,\beta =0.15$ and $d_1=0.025,d_2=10.$ Different spatial patterns emerge for different values of the harvesting rate of prey.

In Fig. 7, when $h=0.12$, starting with a homogeneous state $E^*=(0.128381,0.85587)$, random perturbation leads to the formation of spots and stripes.

In Fig. 8, when $h=0.19$, starting with a homogeneous state $E^*=(0.109208,0.728056),$ random perturbation leads to formation of spots which give way to strip in the long run.

In Fig. 9, when $h=0.25$, starting with a homogeneous state $E^*=(0.0931094,0.620729)$, random perturbation leads to formation of different spatiotemporal patterns like strip, spot and strip-spot mixtures with time. Thus we can summarize that the prey has a tendency to take group defense against its harvesting and greater the harvesting rate, the stronger the group defense of the prey. We can also observe that the prey population is decreasing accordingly as the harvesting rate of the prey is increasing. Figures 7, 8, 9 display evolution of equi-density contours when $h$ is increased.

7.2 Species spread with varying $d_1$ and fixed $d_2$

In this case, we consider spatiotemporal dynamics of model (5) with fixed parameter values $\alpha =0.2,\gamma =1,\delta =0.09,c=0.6,\beta =0.15,d_2=5$ and varying parameter $d_1$. Parameter values are chosen from Turing space. Turing patterns are shown in Fig. 10. Figure 10 display equi-density contours which select spatial patterns with spots as $d_1$ increases. Spot patterns for prey and predator population are distributed over the whole domain are discernible in Fig. 10 e, f. When $d_1$ varies from $0.009$ to $0.055$, a sequence strip $\rightarrow$ strip-spot mixture $\rightarrow$ spots is observed. Biologically, we can say that the prey and predator populations are flocking together as $d_1$ is increased.

7.3 Species spread with fixed $d_1$ and varying $d_2$

Next, we consider the spatiotemporal dynamics of model (5) at fixed parameter values $\alpha =0.2,\gamma =1,\delta =0.09,c=0.6,\beta =0.15,d_1=0.045$. Parameter $d_2$ is varied. Turing patterns are shown in Fig. 11. When $d_2$ varies from $5$ to $15$, a sequence of patterns spots$\rightarrow$spot-stripe mixture$\rightarrow$ strip patterns emerges. From these figures, we observe that the prey will ungroup or distribute over the whole domain with increase of $d_2$ , i.e., spread of prey population within the given domain and same time will increase along with increase of $d_2$.

8 Discussions and conclusions

In this paper, we have investigated the complex dynamics of a diffusive Leslie–Gower type model with Holling type IV functional response and with nonlinear harvesting (Holling type II). We have also investigated the distribution of the roots of the characteristic equation of the linearized system of the spatial model at the steady-state solution and discussed its stability. It has been shown that the system under consideration can undergo Hopf bifurcation under certain conditions, and we further studied the stability of bifurcated periodic solutions by applying the central manifold theorem and normal form theory.

It has been shown from the bifurcation analysis that the system has Turing and Hopf bifurcations. Furthermore, we also studied the conditions under which the model undergoes diffusion-driven instability. Numerical simulations show that our model can exhibit different patterns such as stripes, spots and strip-spot mixture patterns. Further, stable Turing pattern form, which implies that both prey and predator population persist in space and it has ecological implication as spots patterns are assumed as a predator defense function and strips patterns are related to the social communication and predator defense [15].

We have illustrated that this system has typical Turing patterns such as spotted, stripe-like, or spot-stripe mixtures patterns which are similar to those obtained by Wang et al. [29]. Moreover, we can infer from Figs. 7,  8, 9 that the presence of nonlinear harvesting rate $h$ dramatically changes the spatial patterns from spotted patterns to the stripe patterns or coexistence of spotted pattern and stripe pattern of the prey. Biologically, we can conclude that if the prey is harvested, it has an opportunity to be centralized or assembled. From this, we could summarize that the prey has a tendency to take group defense against its harvest, the stronger group defense of the prey is observed at greater harvesting rate similar to the result obtained by Baek [2]. In Figs. 8 and 9, contours for prey and predator appear similar. Equi-density contours of the model system evolve with time (cf. Figs. 7,  8, 9) and is different for different value of $h$ at $t=200$. As $h$ increases, spatial patterns change and both prey and predator have similar pattern at $t=200$. At $t=1{,}000$ , prey and predator redistribute themselves. When $h$ is further increased, prey and predator equi-density contour acquire same spatial patterns. Spatial patterns are selected in such a way that condition $\left( \frac{m_1}{m_2}\right) E<u$ always holds. If the ecological system is harvested at a rate which does not honor this condition, then there is a danger of system collapse. Spatial patterns selected by the system (e. g., Fig. 11) at $t=1{,}000$ honor this condition. Therefore, if one can monitor the population dynamics of prey and predator, it has been observed that nonlinear harvesting control method is more reasonable and realistic than linear and constant harvesting control method.