Effect of harvesting and infection on predator in a prey–predator system

Abstract

In this article, we propose and analyze a mathematical model of a prey–predator system where infection spreads among the predators and predator is subject to harvesting. Dynamical behavior of the system is studied, and the consequences of harvesting on the long-run equilibrium fish biomass are evaluated. Optimal control theory has been used to determine the optimal harvesting policy for fish stocks to maximize the discounted utility of harvesting over time, employing a constant time discount rate. Some simulation works are given to verify our analytic results.

1 Introduction

Mathematical models have recently been heavily used to describe different ecological systems and their dynamical behaviors. Interaction between prey and their predators is one of the ecological problems in which not only theoretical ecologists but also applied mathematicians have shown their interests. Also rapid development of computing techniques enables the simulation works and model predictions in a quite better way than the earlier stages. Ecological models are characterized by interactions among all the species present in the environment. In ecology, predation is one of the most important interactions among different population species. Throughout their works, the researchers like Das et al. [6], Gao et al. [7], Jana et al. [16], Jana and Kar [15, 17], Kar [18], Kuang and Takeuchi [24], Song and Guo [29], Venturino [30], Xu and Ma [36], Yongzhen et al. [37], Zhang et al. [38], and references therein have obtained many new and interesting results on the dynamics of prey–predator systems.

Mathematical modeling is a good and important tool for the study of epidemiological problems. Classical predator–prey models formed with the help of the system of differential equations take more complex forms if either one or both of the two species are subject to infections. There are a number of good works considering infection within the prey species in predator–prey interactions. These types of prey–predator models with infection in prey species can be observed in agricultural pest control, phytoplankton–zooplankton system where phytoplankton are attacked by some viral infections, etc. The works of Venturino [31], Shi et al. [28], Jana and Kar [15, 17], and others describe interactions of a prey– predator system where prey populations are affected by some diseases. In pest management policy, some researchers like Bhattacharyya and Bhattacharya [1], Ghosh et al. [8], Wang and Song [34], and Kar et al. [23] have also used mathematical models to control the pest by infection and predators. But the infection may also spread among the predator species with or without affecting prey populations. Hseih and Hsiao [14] considered a prey–predator model where both the populations are attacked by same parasite of disease. But in reality, it may not be possible that the same parasite can spread the disease between the prey and their predator. For example, if we consider the fish population as a predator population and their live food like earthworms, sludge worms, water fleas (Daphnia and cyclops), bloodworms, feeder fish, infusoria (protozoa and different microorganisms) as a prey population, then it can be easily claimed that the parasites which are the cause for the infection of the fish population (e.g., Henneguya salminicola causes disease for salmon fish and Aeromonas salmonicida causes the disease in marine and freshwater fish) do not infect those live food of fish. Thus, it is an explicit example of prey–predator ecological system where predators are affected by infection. Some authors (e.g., [11–13, 32, 33]) have already investigated the dynamics of prey–predator system with predator infections although they avoid the dynamics of the system subject to effect of harvesting of either species or both the species. As here we intend to study a live food-fish system with infection in the fish populations, harvesting of fish population must be a common and important phenomenon. The main reason for harvesting of fish populations is that both of marine and fresh water fishes are very popular food to human beings. The subject of harvesting in predator–prey systems has recently combined area of research involving ecologists, economists, mathematicians, and sociologists. The effect of harvesting at a constant rate on the predator–prey models has been investigated successfully by some researchers like Dai and Tang [5], Myerscough et al. [25], Xiao and Ruan [35], and references therein. Optimal steady-state harvesting on multispecies fishery system has been investigated by Clark [3], Hannesson [10], and Ragozin and Brown [27]. Kar and Chaudhuri [19, 20] describe a mathematical model for non-selective harvesting in a multispecies fishery system. In his book, Clark [4] describes the optimal harvesting policies corresponding to different ecological systems. In our present work, we consider a live food (prey) and fish (predator) model and here we use the word ‘harvesting’ as fishing. Here, we consider only the selective harvesting of predator species which is generally done by common fishermen.

Now to describe the system mathematically, let the biomass of prey species be $x(t)$ and divide the predator into two classes, namely the susceptible predator (to whom the infection may be spread) $y(t)$ and the infected predator $z(t)$. The prey population grows logistically with intrinsic growth rate $r$ and environmental carrying capacity $K$. Let the susceptible predator population consumes prey population with Holling type I functional response (i.e., the predator do not need any handling time or saturation time to catch prey) at a rate $a$ and the conversion rate of the biomass from the prey populations to the healthy predator is taken as $m$. The susceptible predator becomes infected due to their direct contact with the infected predator, and $\alpha$ is taken as the product of contact rate with the disease transmission. Also let the death rate of the susceptible predator and infected predator be, respectively, $d$ and $\delta$. The predator species is harvested with harvesting effort $E(t)$ ($E(t)$ is taken time dependent only when the optimal control policy is discussed). Further, we take $q_1$ and $q_2$ as the catchability coefficients for $y(t)$ and $z(t)$, respectively. An important assumption for the present model is that the infected predator $z(t)$ has no catching power to the prey populations.

With the help of the above assumptions, we construct our proposed model as follows:

$$\begin{aligned} \frac{\hbox {d}x}{\hbox {d}t}= & {} r x\left( 1-\frac{x}{K}\right) -a x y,\nonumber \\ \frac{\hbox {d}y}{\hbox {d}t}= & {} \max {y}- \hbox {d} y- \alpha y z -q_1 E y, \nonumber \\ \frac{\hbox {d}z}{\hbox {d}t}= & {} \alpha y z-\delta z -q_2 E z, \end{aligned}$$

(1)

subject to the initial conditions

$$\begin{aligned} x(0)\ge 0,\quad y(0)\ge 0,\quad z(0)\ge 0. \end{aligned}$$

(2)

The rest of the paper is organized as follows: In the next section, we describe the dynamical behavior of the above formulated system. In Sect. 3, we modify our model system (1), and its dynamical behavior is discussed in Sect. 4. In Sect. 5, we formulate the optimal control problem by choosing effort as the control variable, and then, we discuss the numerical procedure to solve the optimal control problem in Sect. 6. In the last section we present some of the key findings obtained throughout the analysis of this work.

2 Analysis of the model system

In this section, we now describe the dynamical behavior of the model system (1). It can be shown that all the solutions of system (1) have nonnegative solutions and mathematical details regarding nonnegativity of the solutions are given in “Appendix 1.” Next, we find all the possible equilibria of the system and discuss their stability criteria.

2.1 Equilibria

The possible equilibria of the system (1) are:

• (i) The trivial or vanishing equilibrium $E_{01}(0,0,0)$,

• (ii) The predator-free equilibrium $E_{K1}(K,0,0)$,

• (iii) The infection-free equilibrium $E_{xy}(x^1,y^1,0)$ where $x^1=\frac{d_1}{am},\,y^1=\frac{r \left( a K m-d_1\right) }{a^2 K m},\,\,d_1=d+q_1 E$ and this equilibrium is feasible if $K>d_1/(ma)$, and

• (iv) The interior equilibrium $E_{*}\left( x_*,y_*,z_*\right)$,

where $x_*=\frac{K}{\alpha r}\left( \alpha r-a \delta _1\right) ,\,y_*=\frac{\delta _1}{\alpha }$ and $z_*=\frac{m a x_* - d_1}{ \alpha }$ with $\delta _1=\delta +q_2 E$, which is feasible provided $\alpha r>a \delta _1$ and $K>\left( \frac{d_1}{ma}+\frac{a \delta _1}{\alpha r}\right) \,\,=K_1$ (say).

In the following theorem, we give the local stability criteria of the system around different equilibria, and their proofs are given in “Appendix 2.”

Theorem 1

The system (1) is

• (i) always unstable around the trivial equilibrium $E_{01}(0,0,0)$,

• (ii) locally asymptotically stable around the predator-free equilibrium $E_{K1}$ if $K<d_1/(am)$.

• (iii) locally asymptotically stable around the infected predator-free equilibrium $E_{xy}$ if $K<K_2$ where $K_2=\frac{d_1}{am}/\left( 1-\frac{a\delta _1}{\alpha r}\right)$ and

• (iv) the interior equilibrium is always locally asymptotically stable if it is feasible.

Here, we see that for the model system (1), the parameter $K$ (environmental carrying capacity) plays a crucial role on the dynamical behavior of the system. Feasibility of the infection-free equilibrium and interior equilibrium as well their stability including predator-free equilibrium depends explicitly on $K$. It is evident that if $K<d_1/(am)$, then obviously $K<K_2$. Thus, for $K\in \left( d_1/(am),K_2\right)$, the equilibrium $E_{xy}$ is feasible and locally asymptotically stable. With similar arguments, we can describe the feasibility and stability of other equilibria. Therefore, we have the following range of $K$ regarding the feasibility and stability of the system (1) assuming that $K_1>K_2$.

Range	Feasible equilibrium (s)	LAS equilibrium (s)
$K<d_1/(am)$	$E_{01},E_{K1}$	$E_{K1}$
$d_1/(am)<K<K_2$	$E_{01},E_{K1},E_{xy}$	$E_{xy}$
$K_2<K<K_1$	$E_{01},E_{K1},E_{xy}$	–
$K>K_1$	$E_{01},E_{K1},E_{xy},E_{*}$	$E_*$

Next, suppose that $K_1<K_2$, in this case, we have the following range for the feasibility and stability of the different equilibria:

Range	Feasible equilibrium (s)	LAS equilibrium (s)
$K<d_1/(am)$	$E_{01},E_{K1}$	$E_{K1}$
$d_1/(am)<K<K_1$	$E_{01},E_{K1},E_{xy}$	$E_{xy}$
$K_1<K<K_2$	$E_{01},E_{K1},E_{xy},E_{*}$	$E_*,E_{xy}$
$K>K_2$	$E_{01},E_{K1},E_{xy},E_{*}$	$E_*$

The main interesting observations from the above two tables are that when $K_2<K_1$, then for $K\in (K_2,K_1)$, there is no stable equilibrium, whereas if $K_1<K_2$, then for $K\in (K_1,K_2)$, there occurs bistability of the equilibria $E_*$ and $E_{xy}$. Further at the boundary of each range, bifurcation occurs and it is studied in in the next subsection.

2.2 Bifurcation analysis

It is observed that for $m=d_1/(a x_*)$, the interior equilibrium $E_*$ reduces to the infection-free equilibrium $E_{xy}$ and at $m=d_1/(a K)$ the infection-free equilibrium $E_{xy}$ reduces to the predator-free equilibrium $E_{K1}$. Also it is shown that the equilibrium $E_{K1}$ is locally asymptotically stable for $m<d_1/(a K)$ and $E_{xy}$ is feasible for $m>d_1/(a K)$. Therefore, at $m=d_1/(a K)$, the system (1) undergoes a transcritical bifurcation from $E_{xy}$ to $E_{K_1}$. By similar argument, we may conclude that, around the equilibrium $E_{xy}$, the system (1) undergoes a transcritical bifurcation at $m=d_1/(a x_*)$ from the equilibrium $E_*$. Here, we omit the details of mathematical proof which is available in Guckenheimer and Holmes [9] and Kar and Mondal [22]. Therefore, we can treat the infection transmission rate $m$ as one of the important parameters as it deals with the stability and bifurcation of different equilibria of system (1).

3 Model with predation power of infected predator

In model system (1), we consider that only the susceptible predators have predation power on the basis of the assumptions that either infected predators survive for very small period of time or infection makes them so weak that they are unable to predate. In this section, we assume that, instead of their weakness due to the infection, infected predators have some predation power. But, realistically the predation rate of infected predator should be fewer when compared to that of susceptible predator. The infected predator should need some searching period and handling time in the predation period. Therefore, the functional response for the infected predator is taken in Holling type II form to consider the handling time and searching period. Quite similar assumptions are made by some other researchers like Yongzhen et al. [37] and references therein. Therefore, we modify model (1) by considering a Holling type II functional response for the infected predator. We consider $b$ and $c$, respectively, as the capturing rate and the half-saturation constant due to the handling period and $n$ be the conversion factor contributed to the growth of the infected predator from predation. Therefore, the system (1) is modified as follows:

$$\begin{aligned} \frac{\hbox {d}x}{\hbox {d}t}= & {} r x\left( 1-\frac{x}{K}\right) -a x y-\frac{b x z}{c+x},\nonumber \\ \frac{\hbox {d}y}{\hbox {d}t}= & {} m a x y- d y- \alpha y z -q_1 E y, \nonumber \\ \frac{\hbox {d}z}{\hbox {d}t}= & {} \frac{n b x z}{c+x}+\alpha y z-\delta z -q_2 E z, \end{aligned}$$

(3)

subject to the initial conditions

$$\begin{aligned} x(0)\ge 0,\quad y(0)\ge 0,\quad z(0)\ge 0. \end{aligned}$$

(4)

4 Dynamical behavior of the model (3)

In this section, we study the system in (3) with constant harvesting effort. Like system (1), the system (3) with initial conditions (4) has all its solution nonnegative (see “Appendix 1” for mathematical details).

4.1 Equilibria and their stability

The system (3) has following five possible equilibria:

• (i) The trivial equilibrium $E_0(0,0,0)$.

• (ii) The boundary equilibrium $E_1(K,0,0)$.

• (iii) The infection-free equilibrium $E_2(x_2,y_2,0)$, where $x_2=(d_1)/(ma)$ and $y_2=r(1-x_2/K)/a$ with $d_1=d+q_1 E$. This equilibrium is feasible if $K>d_1/(am)$.

• (iv) The healthy predator-free equilibrium $E_3(x_3,0,z_3)$ where $z_3=r(c+x_3)(1-x_3/K)/b$ and $x_3=c\delta _1/(nb-\delta _1 )$ with $\delta _1=\delta +q_2 E$ and this equilibrium is feasible if $nb>\delta _1$ and $K>x_3$.

• (v) Lastly, the interior equilibrium $E^*(x^*,y^*,z^*)$,

where $x^*$ is the positive root of the following equation

$$\begin{aligned}&r \alpha x^2 + \left( a b K m +c r \alpha +a K \delta _1 - a b K n -K r \alpha \right) x \\&\quad -\, K \left( b d_1+c r\alpha -a c \delta _1 \right) =0, \end{aligned}$$

$y^*= \frac{-b n x^*+c \delta _1+x^* \delta _1}{(c+x^*) \alpha }$ and $z^*= \frac{-d_1+a m x^*}{\alpha }$. This interior equilibrium $E^*$ will be unique and feasible if $a<\frac{b d_1 + c r \alpha }{c \delta _1}$ and $x^* \in \left( \frac{d_1}{am},\frac{c \delta _1}{bn-\delta _1}\right)$, i.e., $x^*\in \left( x_2,x_3\right)$ provided $bn>\delta _1$ (i.e., if the reproduction rate of the infected predator exceeds its mortality). However, if $bn <\delta _1$ (i.e., if the growth of the infected predator from the prey populations is less than their total death), then this interior equilibrium $E^*$ will be feasible if $x^*>x_2$. Now let us denote the equilibrium biomass of prey $x^*$ as $\xi$. So with more convenient way, it may be described that $E^*$ will be both unique and feasible if $a<\frac{b d_1 + c r \alpha }{c \delta _1}$ (uniqueness condition) and $x_2<\xi <x_3$ (existence condition) provided $bn>\delta _1$. If $bn<\delta _1$, then $E_3$ is infeasible but $x_3$ would be negative. So $E^*$ is positive if $\xi >\xi _1$ where $\xi _1=\max \{x_2,-x_3\}$. Further at $bn=\delta _1,\,E^*$ would be feasible if $\xi >x_2$, and in this case, let us denote $x_2$ as $\xi _1$. Therefore, if $bn \le \delta _1$, then $E^*$ will be both unique and feasible if $\xi >\xi _1$ and $a<\frac{b d_1 + c r \alpha }{c\delta _1}$.

Next, we discuss local asymptotic stability of the system (3) around different equilibria. As expected, around the trivial equilibrium $E_0$ all the species go to extinction and all the solutions repel from that point. Therefore, this trivial equilibrium $E_0$ is unstable. So we are now interested about the rest of the equilibria. In the next theorem, we give the stability criteria of the equilibrium $E_1(K,0,0)$.

Theorem 2

The predator-free equilibrium $E_1$ of the system (3) is locally asymptotically stable if $K<\min \{x_2,\,x_3\}$.

Proof

The characteristic equation of the system around the equilibrium $E_1$ is given by:

$$\begin{aligned}&\!\!\!(\lambda +r ) \left( \lambda +d-a K m +E q_1\right) \left( \lambda \right. \\&\!\!\!\quad \left. -\,\frac{b K n}{c+K}+\delta +E q_2\right) =0. \end{aligned}$$

It is obvious that if $K<x_2(=d_1/(am))$ and $K<x_3\left( =c\delta _1/\{nb-\delta _1 \}\right)$, then all the eigenvalues at $E_1$ of (3) are negative and the system will be locally asymptotically stable. Hence the theorem.

Note If $K<\min \{x_2,\,x_3\}$, then both the $E_2$ and $E_3$ do not exist. Hence, the local asymptotic stability of $E_1$ implies the nonexistence $E_2$ and $E_3$.

Theorem 3

The equilibrium $E_2$ is locally asymptotically stable if $E_3$ does not exist.

Proof

Two eigenvalues of the system (3) at the equilibrium $E_2$ are imaginary with real part $-\left( r x_2)/(2 K \right)$, and the third eigenvalue which is of course real is negative if $a K m<d_1$ (existence condition of $E_2$) and $n b<\delta _1$ (nonexistence condition of $E_3$).

Theorem 4

The susceptible predator-free equilibrium $E_3$ is locally asymptotically stable if $K<\frac{c\left( bn+\delta _1\right) }{bn-\delta _1}$ and $x_3<\left( d_1+\alpha z_3\right) /(am)$.

Proof

The characteristic equation of the system at $E_3$ is given by:

$$\begin{aligned}&\!\!\!\left( \lambda +d-a m x_3+ \alpha z_3 +E q_1\right) \left( \lambda ^2\right. \\&\!\!\!\quad \left. +\,\left( \frac{r}{K}-\frac{bz_3}{\left( c+x_3\right) ^2}\right) x_3 \lambda +\frac{b^2cnx_3z_3}{\left( c+x_3\right) ^2}\right) =0. \end{aligned}$$

So all the eigenvalues of the system will be either negative or having negative real part if $\frac{r}{K}>\frac{b z_3}{\left( c+x_3\right) ^2}$, i.e., if $K<\frac{c\left( bn+\delta _1\right) }{bn-\delta _1}$ and $x_3<\left( d_1+\alpha z_3\right) /(am)$. Hence the theorem.

Next, we describe the dynamical behavior of the system around its interior equilibrium $E^*$. Now we state one sufficient condition for which the system (3) would be locally asymptotically stable around $E^*$ (the details are given in “Appendix 3”). Actually if $bn>\delta _1$, then $E^*$ is feasible for $\xi \in (x_2,x_3)$, whereas if $bn \le \delta _1$, then $E^*$ is feasible for $\xi \in (\xi _1,\infty )$. In the following theorem, we state the local asymptotic stability condition of the system (3) around $E^*$ for $bn>\delta _1$.

Theorem 5

Suppose that $K<\frac{r \alpha (a+\xi )^2}{b(am \xi -d_1)}$ hold. Then,

• (i) if both of $\phi \left( x_2\right) \,\left[ or, \phi (\xi _1)\right]$ and $\phi \left( x_3\right) \,\left[ or, \phi (\infty )\right]$ are positive and there is no $\eta \in \left( x_2, x_3\right) \,[or, \eta \in \left( \xi _1,\infty \right) ]$ such that $\phi (\eta ) \le 0$, then the system is always locally asymptotically stable around $E^*$.

• (ii) suppose that $\phi \left( x_2\right) . \phi \left( x_3\right) < 0\,\left[ or, \phi (\xi _1).\phi (\infty )\right. \left. <0\right]$. Then, if $\xi$ belongs to that(those) subinterval(s) of $\left( x_2, x_3\right) \,[or, \left( \xi _1,\infty \right) ]$ where the function $\phi$ is positive, then the system (3) would be locally asymptotically stable around the interior equilibrium and the point(s) where the function $\phi$ vanishes are the Hopf bifurcation point(s) of $\xi$, provided there is no multiple zeros of $\phi (x)$ within the interval $\left( x_2, x_3\right) \,[or, \left( \xi _1,\infty \right) ]$.

• (iii) if both of $\phi \left( x_2\right) \left[ or, \phi \left( \xi _1\right) \right]$ and $\phi \left( x_3\right) \left[ or, \phi \left( \infty \right) \right]$ are negative, then the system is always unstable at the interior equilibrium $E^*$.

In the next theorem, we describe some interesting features of some particular parametric values around the equilibria $E_1,\,E_2$, and $E_3$.

Theorem 6

The system (3) undergoes a transcritical bifurcation

• (i) from $E_1$ to $E_2$ at $K=d_1/(am)$ provided $nb<\delta _1$ and

• (ii) from $E_2$ to $E_3$ at $bn=\delta _1$ provided $E_2$ is feasible and $\Lambda (K)>0$ where $\Lambda (K)=bd_1n+\alpha n r c^2 \left( 1-\frac{c \delta _1}{K\left( bn-\delta _1\right) }\right) -\delta _1\left( d_1+amc\right)$.

Proof

Let $bn<\delta _1$ holds. Then, the parametric condition $K<d_1/(am)$ is the local asymptotic stability condition of the system (3) around the predator-free equilibrium $E_{1}$ but in this case, $E_2$ does not exist. On the other hand for $K>d_1/(am)$, the equilibrium $E_{1}$ is unstable, but the equilibrium $E_{2}$ is locally asymptotically stable. Hence, a change in feasibility occurs at $K=d_1/(am)$. This type of phenomenon is known as the transcritical bifurcation (for mathematical details, see Kar and Jana [21], Kar and Mondal [22], and Gukenheimer and Holmes [9]). To prove the second part, let us assume that $\Lambda (K)>0$ holds. Now for $nb<\delta _1$, $E_2$ is locally asymptotically stable and the infection-free equilibrium $E_3$ is unstable. Again for $nb>\delta _1$, $E_2$ is unstable and $E_3$ is locally asymptotically stable. Therefore, there will occur a change in stability from the equilibrium $E_2$ to $E_3$ at $bn=\delta _1$ through the transcritical bifurcation.

It is observed that like system (1), the environmental carrying capacity $K$ has a great influence on system. It is also interesting to observe that there exists one extra equilibrium for the system (3) where infected predators remain in the system but the susceptible predator goes to extinction and these phenomenon is possible if the infected predators are able to capture the prey populations in a sufficient amount and the carrying capacity of the prey is greater than some threshold. However, the local stability of that equilibrium $E_3$ is possible if $K\in \left( \frac{c\delta _1}{bn-\delta _1},\frac{c\left( bn+ \delta _1\right) }{bn-\delta _1}\right)$ and the equilibrium biomass of the prey population is less than some threshold. Actually in physical sense, local stability of $E_3$ implies the sufficient recruitment of infected predators and large death rates of the susceptible predators. Obviously, if $E_3$ becomes locally asymptotically stable, then $E_2$ never be stable, and this phenomenon is observed here. But for economic perspective, this situation is never beneficial as the infected fish has negligible selling price and we discuss it in the latter section.

On the contrary, if $E_2$ is locally asymptotically stable, then the infected predator goes to extinction. Therefore, as expected, it is observed that when $E_2$ is locally asymptotically stable, $E_3$ would be infeasible. Similarly, at the equilibrium $E_1$, both the classes of the predator populations go to extinction. Therefore, local asymptotic stability of $E_1$ imply higher death of predator classes. In these situations, neither classes of the predator populations can exist and we theoretically proved that if $E_1$ is locally asymptotically stable, then not only $E_2$ and $E_3$ but also $E^*$ does not exist.

Lastly, the unique interior equilibrium $E^*$ may be either locally asymptotically stable or unstable, or it may be stable for some parametric space and unstable at another parametric space. In the later section, we verify our theoretical observations numerically.

4.2 Comparison between two models

For obvious reason, we pay more attention to study the behavior around the interior equilibrium of the system. In system (1), we see that the equilibrium biomass of infected predator $(z_*)$ depends on the equilibrium biomass of prey $(x_*)$ although the infected predator has no direct relation with the prey. This phenomenon occurs since here we consider both the disease transmission coefficient and the functional response for predation rate by healthy predator as linear type. Furthermore, if $K>K_1$ (i.e., if coexisting equilibrium $E_*$ is feasible), then equilibrium biomass of healthy predator $y_*$ always remains constant, and more importantly, it is independent of predation rate although equilibrium biomass of prey $x_*$ is affected by predation rate $(a)$. The biomass of healthy predator depends on the infection rate as well as death rate of infected predator, and therefore, we may conclude that the infection rate has more effect than the predation rate of the susceptible predator. But for model (3), we see that at interior equilibrium, although the equilibrium biomass of infected predator $z^*$ does not directly depend on equilibrium biomass of healthy predator $y^*$, but that of susceptible predator depends on both the infection transmission and predation rate. Therefore, for model (3), both of the predation and infection have great effects on the equilibrium biomass of healthy predator.

4.3 Numerical simulation

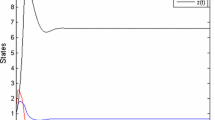
Here, we check the validity of our theoretical explanations by numerical simulations. First, we give simulation to the model system (1). For this purpose, we take the parameters as $r=0.5,\,K=10,\,a=0.5,\,m=0.6,\,d=0.4,\,\alpha =1.3,\,q_1=1.5,\,E=0.4,\,\delta =0.2,\,q_2=0.4$ in appropriate units. For this set of parameters, we see that the system (1) is locally asymptotically stable around the equilibria $E_*$ and $E_{xy}$ (see Fig. 1).

Fig. 1

Bistability of the system (1) around the equilibria $E_*$ and $E_{xy}$

Next, we give some numerical results to support our theoretical works of the model system (3). Let us take the following parameter set $P_1=\{r,\,K,\,a,\,b,\,c,\,m,\,d,\,\alpha ,\,n,\,\delta \}\,=\{2.1,\,100,\,0.91,\,0.08,\,0.05,\,0.95,\,0.01,\,0.72,\,0.95,\,0.1,\,1\}$. It should be noted that for the parameter set $P_1$, we always have $bn<\delta _1$ for all values of $q_1$ and $q_2$. Therefore, the interior equilibrium will be feasible for $\xi >x_2$. We assume that $\breve{E}=q_1 E$ is the per unit harvesting rate of healthy predator and $\tilde{E}=q_2 E$ is the per unit harvesting rate for the infected predator. For the parameter set $P_1$ and in the absence of harvesting, i.e., for $\breve{E}=\tilde{E}=0$, the total number of harvesting predator populations is zero and the system will be locally asymptotically stable around $E_3$, which is presented in following Fig. 2. Now if predators are subject to harvesting, using the parameter set $P_1$ along with $\breve{E}=\tilde{E}=1.5$, it is shown that the interior equilibrium is feasible but unstable (see Fig. 3). But further increment of healthy predator harvesting effort makes $E^*$ locally asymptotically stable (see Fig. 4 with $\breve{E}=2.5$ and $\tilde{E}=1.5$). Moreover, it is also observed that if we increase the harvesting rate $\tilde{E}$ of the infected predator, from $1.5$ to $2.5$, then the infected predators go to extinction due to their high death rate and the system becomes locally asymptotically stable around $E_2$ (see Fig. 5).

Fig. 2

Solution curves for the parameter set $P_1$ with $\breve{E}=\tilde{E}=0$

Fig. 3

Solution curves for the parameter set $P_1$ with $\breve{E}=\tilde{E}=1.5$

Fig. 4

Solution curves for the parameter set $P_1$ with $\breve{E}=2.5,\,\tilde{E}=1.5$

Fig. 5

Solution curves for the parameter set $P_1$ with $\breve{E}=\tilde{E}=2.5$

Thus, it is observed that increasing total harvesting of predators in a certain level can transform the stable equilibrium $E_3$ to the stable equilibrium $E^*$. However, if the total harvest of the infected predator increases, then infected predator goes to extinction.

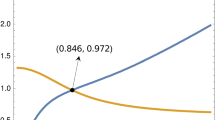
In Fig. 6, we show the graph of $\phi (\xi )$ versus $\xi$ for the parameter set taken to draw Fig. 3. Obviously, the interior equilibrium $E^*$ is feasible if $\xi >2.9034(=x_2)$. We see that if $\xi \in (2.9034,5.4816)$, then the system is unstable around $E^*$, for $\xi > 5.4816$, the system is locally asymptotically stable around $E^*$, and at $\xi =5.4816$, the system (3) undergoes a Hopf bifurcation.

Fig. 6

Variation of $\phi (\xi )$ with respect to $\xi$

Now let us take another parameter set $P_2=\{r,\,K,\,a,\,b,\,c,\,m,\,d,\,\alpha ,\,n,\,\delta \}\,= \{3.1,\,100,\,0.2,\,0.08,\,0.05,\,0.95,\,0.01,\,0.01,\,0.9,\,0.1\}$. The parameter set $P_2$ with $\breve{E}=\tilde{E}=0$ gives the unstable interior equilibrium (see Fig. 7). Thus, in the absence of harvesting, the system may be unstable around the interior equilibrium point. Next in Fig. 8, it is shown that the interior equilibrium is asymptotically stable for the parameter set $P_2$ along with the harvesting efforts $\breve{E}=2$ and $\tilde{E}=0.1$. Further, in Fig. 9, it is shown that if harvesting effort for the infected predator $\tilde{E}$ increases from $0.1$ to $0.25$, then the system will be infection free and it is locally asymptotically stable there.

Fig. 7

Interior equilibrium is unstable for the parameter set $P_2$ with $\breve{E}=\tilde{E}=0$

Fig. 8

Interior equilibrium is asymptotically stable for the parameter set $P_2$ with $\breve{E}=2,\,\tilde{E}=0.1$

Fig. 9

Infection-free equilibrium is asymptotically stable for the parameter set $P_2$ with $\breve{E}=2,\,\tilde{E}=0.25$

Now we would like to describe what would happen if $bn>\delta _1$. In this case, the interior equilibrium $E^*$ of the system (3) exists if $\xi \in (x_2,x_3(={c\delta _1}/(\delta _1-bn)))$. Again, if we take another parameter set $P_3=\{r,\,K,\,a,\,b,\,c,\,m,\,d,\,\alpha ,\,n,\,\delta ,\,E,\,q_1,\,q_2\}\,=\{1.5,\,100,\,0.91,\,3.2,\,1.25,\,0.95,\,0.01,\,0.72,\,0.95,\,0.1,\,1,\,2.5,\,2.5\}$, a very simple calculations show that the system has a unique interior equilibrium if $\xi \in (2.90341,\,7.38636)$. In Fig. 10, we show the curve of $\phi (\xi )$ with respect to $\xi$. From the figure, it is observed that for $\xi \in (2.90341,\,2.942)$, the system is locally asymptotically stable around $E^*$, whereas in the interval $\xi \in (2.942,\,7.38636)$, the system (3) is unstable and at $\xi =2.942$, the system (3) undergoes a Hopf bifurcation.

Fig. 10

$\phi (\xi )$ versus $\xi$ for the parameter set $P_3$

Figure 11 shows the equilibrium phase portrait of the system (3) for different $b$ [obviously for $b=0$, it represents system (1)].

Fig. 11

Phase portrait of the system by varying the parameter $b$

Due to unavailability of real-world data, our numerical simulation is based on some simulated values of parameters. However, we choose our parameter set in such a way that it can be compared with realistic system. Moreover, as we study only the qualitative behavior of the system, our simulation work will remain quite same for real-world data.

5 The optimal control problem: effect of harvesting

In commercial exploitation of renewable resources, the main objective of the exploitation of renewable resources is to determine the optimal trade-off between the present and future harvests. Since here we consider predator populations as the fish populations, the optimal net profit is to be determined from the fishing. In this section, we study the optimal harvesting policy by considering the profit earned by harvesting, focusing on quadratic costs and conservation of fish population. Here, it is assumed that price is a function which is inversely proportional to the available biomass of fish (predator), i.e., the price function decreases when biomass of fish increases (see [2]). Let $\breve{c}$ be the constant harvesting cost per unit effort, and $p_1$ and $p_2$ be, respectively, the constant price per unit biomass of the susceptible and infected predator. Thus, to maximize the total discounted net revenues from the fishery, the optimal control problem can be formulated as:

$$\begin{aligned} J(E)= & {} \int \limits _{t_0}^{t_1}e^{-\epsilon t}\left[ \left( p_1 - v_1 q_1 E y\right) q_1 E y\right. \nonumber \\&\left. +\,\left( p_2 - v_2 q_2 E z\right) q_2 E z-\breve{c} E\right] \hbox {d}t, \end{aligned}$$

(5)

subject to the system of differential Eqs. (3) and the initial conditions (4). $v_1$ and $v_2$ are economic constants, and $\epsilon$ is the instantaneous discount rate.

Now if we look at the socioeconomic context, we observe that the infected predator has generally less demand and are sold in reduced price. In fact, it would not be any wrong if we assume that the selling price for infected predator $p_2=0$. So we modify the total discounted net revenues from (5) as follows:

$$\begin{aligned} J(E)= & {} \int \limits _{t_0}^{t_1}e^{-\epsilon t}\left[ \left( p_1 - v_1 q_1 E y\right) q_1 E y \right. \nonumber \\&\left. - \,v_2 q_2 E zq_2 E z-\breve{c} E\right] \hbox {d}t, \end{aligned}$$

(6)

subject to the system of differential equations (3) with the initial conditions (4).

Here, the control $E$ is bounded in $0\le E\le E_{\max }$, and our object is to find an optimal control $E_o$ such that

$$\begin{aligned} J\left( E_o\right) =\max _{E\in U} J(E) \end{aligned}$$

where $U$ is the control set defined by

$$\begin{aligned} U= & {} \{E : E \, \hbox {is measurable and }\,0 \\&\quad \le E\le E_{\max },\, \hbox {for all }\,t\}. \end{aligned}$$

Here, the convexity of the objective functional with respect to the control variable $E$ along with the compactness of the range values of the state variables can be combined to give the existence of the optimal control $E_o$. Now the optimal control can be found by using Pontryagin’s maximum principle ([26]). To optimize the objective functional $J(E)$, we construct the Hamiltonian $H$ of the system as follows:

$$\begin{aligned} H= & {} \left( p_1-v_1 q_1 Ey\right) q_1 E y-v_2q_2^2E^2z^2\\&\quad -\,\breve{c}E+\lambda _1\left( r x\left( 1-\frac{x}{K}\right) -a x y-\frac{bxz}{c+x}\right) \\&\quad +\,\lambda _2\left( m a x y- d y- \alpha y z -q_1 E y\right) \\&\quad +\, \lambda _3\left( \frac{nbxz}{c+x}+\alpha y z-\delta z -q_2 E z\right) . \end{aligned}$$

Here, the variables $\lambda _1,\,\lambda _2$, and $\lambda _3$ are adjoint variables, and the transversality conditions are:

$$\begin{aligned} \lambda _i(t_1)=0,\quad i=1,2,3 \end{aligned}$$

(7)

First, we use the optimality condition $\partial H/\partial E=0$ to obtain the optimal effort which is as follows:

$$\begin{aligned} E_{\epsilon }=\frac{p_1 q_1 y-\breve{c}-q_1 \lambda _2 y-q_2 \lambda _3 z}{2\left( v_1 q_1^2 y^2+v_2 q_2^2 z^2\right) }. \end{aligned}$$

The adjoint equations are

$$\begin{aligned} \frac{\hbox {d} \lambda _1}{\hbox {d}t}= & {} \epsilon \lambda _1- \frac{\partial H}{\partial x}\nonumber \\= & {} \left( ay+\frac{bcz}{(c+x)^2}-r\left( 1-\frac{2x}{K} \right) +\epsilon \right) \lambda _1\nonumber \\&-\,may \lambda _2 -\frac{bcnz}{(c+x)^2}\lambda _3,\nonumber \\ \frac{\hbox {d} \lambda _2}{\hbox {d}t}= & {} \epsilon \lambda _2- \frac{\partial H}{\partial y}\nonumber \\= & {} 2v_1 q_1^2 E^2 y-p_1 q_1 E+x a \lambda _1\nonumber \\&-\,\left( \max -d -\epsilon -\alpha z-q_1 E\right) \lambda _2 -\alpha z \lambda _3,\nonumber \\ \frac{\hbox {d}\lambda _3}{\hbox {d}t}= & {} \epsilon \lambda _3- \frac{\partial H}{\partial z}\nonumber \\= & {} 2v_2 q_2^2 E^2 z+\left( \frac{b x}{c+x}\right) \lambda _1+\alpha y \lambda _2\nonumber \\&-\,\left( \frac{nbx}{c+x}+\alpha y -\delta -q_2 E-\epsilon \right) \lambda _3. \end{aligned}$$

(8)

Therefore, we have the following theorem regarding the optimal value of the harvesting effort

Theorem 7

There exists an optimal control $E_{\epsilon }$ (explicit value of $E_{\epsilon }$ has already presented) corresponding to optimal solutions for the state variables such as $x_{\epsilon },\,y_{\epsilon }$ and $z_{\epsilon }$ which optimize the objective functional $J$ over the region $U$. Moreover, there exist adjoint variables $\lambda _1,\,\lambda _2$, and $\lambda _3$ which satisfy the first-order differential equations given in (8) with the transversality conditions given in (7), where at the optimal harvesting level, the values of the state variables $x,\,y$ and $z$ are, respectively, $x_{\epsilon },\,y_{\epsilon }$ and $z_{\epsilon }$.

6 Numerical simulation to the optimal control problem

In this section, we numerically illustrate the solutions obtained for optimal control problem. First, we use fourth-order Runge–Kutta forward iterative method to solve the state variables of the Eq. (3) with initial conditions (4), and then, we solve the Eq. (8) for the adjoint variables by backward fourth-order Runge–Kutta iterative method with the final value conditions (7). For simulation works, we have taken the time interval for which the effort is applied optimally is 1000 units. Next, we have taken the biomass of the prey, susceptible predator, and infected predator, respectively, as 50, 10, and 5 units and the bounds of the effort $E$ as zero and $0.01$, i.e., $0\le E \le 0.01$. In Fig. 12, we show the results of the state variables when optimal harvesting is done. Next in Fig. 13, we show the variation for the optimal effort $E$, and it is observed that initially for about one-fourth of total time duration, the effort $E$ assumes it highest possible value, then it reduces, and at last the final value of that control $E$ becomes zero. In the next Fig. 14, we show the graphs for adjoint variables $\lambda _1,\,\lambda _2$, and $\lambda _3$, respectively, when the harvesting is done according to optimal control policy. It is interesting to observe that all the adjoint variables are monotone with respect to time ($\lambda _1$ and $\lambda _2$ are monotonicaly decreasing, whereas $\lambda _3$ monotonicaly increasing) and final values are zero, as expected.

Fig. 12

Figures for the state variables with controls

Fig. 13

Variation of the effort $E$ with respect to time

Fig. 14

Graph for the adjoint variables

7 Concluding remarks

In this paper, we have studied a prey–predator type ecological model where the predator species are attacked by some infection and subject to harvesting. In particular, our model can be considered as a live food-fish model where the live food is taken as the prey and the fish are predators with infection spreading among fishes. In the literature review, it can be found that there are several articles on theoretical studies on prey–predator type ecological systems with predator infections, but it is very rare to observe harvesting phenomenon there. Venturino [32] and Haque et al. [13] describes some predator–prey models with infection in predator populations, but they do not present any effect on harvesting phenomenon. On the other hand, Chakraborty et al. [2] studied a prey–predator type ecological model with harvesting, but they do not consider any infection in their model.

We describe the dynamical behavior of the system for both the cases when the infected predators have no predation power and have some predation power. For the constant effort case, it is observed that the environmental carrying capacity $K$ has a huge impact on the stability of the model system around different equilibria. But the harvesting should be time dependent and so we consider effort as the control variable to solve the optimal control problem.

Fishing is required for the fishermen to improve their economic conditions, but it may not be always economically beneficial for them. The selling price of the infected fish obviously is negligible in comparison with the price of healthy fish. Also the infected fish cannot be separated from healthy fish in the time of catching because there is no isolation between healthy fish and infected fish. Therefore, huge amount of infected fish not only damages the balance in ecology of water but also directly affects the fishermen’s economic condition. According to our best knowledge, there are not so many model-based works on optimal harvesting policy for harvesting of fish populations by considering the loss occurring due to the infected fish harvesting. In this paper, we take a sound approach on considering the economic loss of fishermen due to the unwilling harvesting of infected predator species.

We use numeric analysis due to the complexity of the analytical solutions. With the help of simulation works, we describe the whole system and its dynamical status. It may also be noted that the simulations presented in the present work should be considered from a qualitative, rather than a quantitative point of view. However, if the real-world data are available, then through our analysis, we can describe these complex types of ecological systems presented here.

Appendices

Appendix 1

We can write the system (3) with the initial conditions given in (4) as follows:

$$\begin{aligned} x= & {} x(0) \exp \int \limits _0^t\{r(1-x/K)\nonumber \\&-\,\alpha y-b z/(c+x)\}\hbox {d}t\,(\ge 0),\nonumber \\ y= & {} y(0) \exp \int \limits _0^t\{\max -d-\alpha x -q_1 E\}\hbox {d}t\,(\ge 0),\nonumber \\ z= & {} z(0) \exp \int \limits _0^t\{n b x/(c+x)+\alpha y-\delta \nonumber \\&-\,q_2 E\}\hbox {d}t\,(\ge 0). \end{aligned}$$

(9)

So it can be concluded that all the solutions of the system (3) with nonnegative initial conditions are nonnegative. Again the result obtained in (9) remains unchanged for $b=0$. Since for $b=0$, the system (3) reduces to (1), we may also conclude that the system (1) with initial conditions (2) has all its solutions nonnegative.

Appendix 2

The characteristic equation of the system (1) at the trivial equilibrium $E_{01}$ is given by

$$\begin{aligned} (\lambda -r ) \left( \lambda +d +E q_1\right) \left( \lambda +\delta +E q_2\right) =0 \end{aligned}$$

with an eigenvalue $r>0$. Hence, the system (1) is unstable around $E_{01}$.

Again, the characteristic equation of the system (1) around $E_{K1}$ is

$$\begin{aligned} (\lambda +r ) \left( \lambda +d_1-a K m\right) \left( \lambda +\delta +E q_2\right) =0. \end{aligned}$$

The above characteristic equation shows that if $d_1>a K m$, i.e., if $K<d_1/(a m)$, then all the roots of that equation are negative. Therefore, we may conclude that for $K<d_1/(a m)$, the system (1) is locally asymptotically stable at $E_{K1}$. Next, the characteristic equation of the system (1) at $E_{xy}$ is

$$\begin{aligned} \left( \lambda ^2 +\frac{r x^1}{K} \lambda +a^2 m x^1 y^1\right) \left( \lambda +\delta _1 -\alpha y^1 \right) =0. \end{aligned}$$

From the above characteristic equation, it can be easily concluded that if $\delta _1>\alpha y^1$, then all the eigenvalues have negative real parts and so the system becomes locally asymptotically stable.

Lastly, the characteristic equation of the system (1) at the interior equilibrium $E_*(x_*,y_*,z_*)$ can be written as

$$\begin{aligned}&\lambda ^3+\frac{r x_* }{K} \lambda ^2 +\left( a^2 m x_* y_*+y_* z_* \alpha ^2\right) \lambda \nonumber \\&\quad +\,\frac{r x_* y_* z_* \alpha ^2}{K}=0. \end{aligned}$$

Applying the Routh–Hurwitz criteria, we may say that all the roots of the above characteristic equation have negative real parts, and therefore, the system is locally asymptotically stable around $E_*$.

Appendix 3

The characteristic equation of the system at the equilibrium $E^*(x^*,y^*,z^*)$ is

$$\begin{aligned} \lambda ^3+b_1\lambda ^2+b_2 \lambda +b_3=0, \end{aligned}$$

where, $b_1=\left( \frac{r \xi }{K}-\frac{b \xi z^*(\xi )}{(c+\xi )^2}\right) ,\,b_2=\left( a^2 m \xi y^*(\xi )\right. \left. +\,\frac{b^2 c n \xi z^*(\xi )}{(c+\xi )^3}+y^*(\xi ) z^*(\xi ) \alpha ^2\right)$ and $b_3=\frac{\alpha \xi y^*(\xi ) z^*(\xi )\left( a b c K (m-n)+r (c+\xi )^2 \alpha +b K d_1\right) }{\left( K (c+\xi )^2\right) }$.

From the above expressions, it is clear that both $b_2$ and $b_3$ are always positive. Therefore, using Routh–Hurwitz criteria, we may conclude that the system will be locally asymptotically stable if $b_1>0$ and $b_1 b_2-b_3>0$, i.e., if $K<\frac{r \alpha (a+\xi )^2}{b(am \xi -d_1)}$ and the following condition holds

$$\begin{aligned}&\left[ \frac{b^2 c n \xi z^*(\xi ) \left( \frac{r (c+\xi )^2}{K}-b z^*(\xi )\right) }{(c+\xi )^5}\right. \\&\quad +\,a^2 m \xi y^*(\xi ) \left( \frac{r}{K}-\frac{b z^*(\xi )}{(c+\xi )^2}\right) \\&\quad \left. -\,\frac{a b (c (m-n)+m \xi ) y^*(\xi ) z^*(\xi ) \alpha }{(c+\xi )^2}\right] >0. \end{aligned}$$

That is, if $\phi (\xi )>0$ where

$$\begin{aligned}&\!\!\!\phi (\xi )=c_0 \xi ^6+c_1 \xi ^5 +c_2 \xi ^4+c_3 \xi ^3 +c_4 \xi ^2+c_5 \xi +c_6, \\&\!\!\!c_0=\frac{a^2 m r \left( -b n+\delta _1\right) }{K}\\&\!\!\!c_1=\frac{a^2 m \left( b n (a b K m+b K m \alpha -4 c r \alpha )-(a b K m+b K m \alpha -5 c r \alpha ) \delta _1\right) }{K \alpha }\\&\!\!\!c_2=\frac{1}{K \alpha }a m \biggr (-b K (a+\alpha ) d_1 \left( b n-\delta _1\right) +\,c \biggr (b n \left( 2 a^2 b K m+b r \alpha \right. \\&\!\!\!\quad \left. +\,a (b K (3 m-n)-6 c r) \alpha \right) +\,a (-3 a b K m+(b K (-4 m+n)\\&\!\!\!\quad +\,10 c r) \alpha ) \delta _1\biggr )\biggr )\\&\!\!\!c_3=-\frac{1}{K \alpha }c \biggr (b d_1 \left( b n \left( 2 a^2 K m+a K (3 m-n) \alpha \right. \right. \\&\!\!\!\!\!\quad \left. \left. +\,r \alpha \right) +a K (-3 a m+(-4 m+n) \alpha ) \delta _1\right) \\&\!\!\!\quad +\,a m (b n \left( -a^2 b c K m-2 b c r \alpha \right. \\&\!\!\!\quad \left. +\,a \left( b^2 K m+b c K (-3 m+2 n) \alpha +4 c^2 r \alpha \right) \right) +\, a c (3 a b K m\\&\!\!\!\quad +\,(6 b K m-3 b K n-10 c r) \alpha ) \delta _1)\biggr )\\&\!\!\!c_4=-\frac{1}{K \alpha }c \biggr (b d_1 \left( b n \left( a^2 c K m+2 c r \alpha \right. \right. \\&\!\!\!\quad \left. +\,a K (-2 b m+3 c m \alpha -2 c n \alpha )\right) \left. -\,3 a c K (a m+2 m \alpha -n \alpha ) \delta _1\right) \\&\!\!\!\quad +\,a c^2 m \left( b n (-b r+a (b K (-m+n)+c r)) \alpha \right. \\&\!\!\!\quad \left. +\,a (a b K m+(b K (4 m-3 n)-5 c r) \alpha ) \delta _1\right) \biggr )\\&\!\!\!c_5=\frac{1}{K \alpha }\biggr (-b^3 c K n d_1^2+a^2 c^4 m (b K (-m+n)\\&\!\!\!\quad +\,c r) \alpha \delta _1+b c^3 d_1 (b n (a K (-m+n)-r) \alpha \\&\!\!\!\quad +\,a K (a m+4 m \alpha -3 n \alpha ) \delta _1)\biggr )c_6+a b c^4 (m-n) d_1 \delta _1. \end{aligned}$$

Let for $\xi =\eta$ we have $b_1b_2-b_3=0$, and thus at this parametric condition, the system (3) has a pair of purely imaginary eigenvalues. Thus, for $\xi =\eta$, the system undergoes a bifurcation around its interior equilibrium $E^*$, and our aim is to show that this type of bifurcation is Hopf bifurcation. Obviously at $\xi =\eta ,\,b_1b_2-b_3=0$. Next to show that the transversality condition holds good for this system, we assume that at $\xi =\eta$, the eigenvalues are of the form $\lambda _1$ and $\lambda _{2,3}=\mu \pm i\omega$. Now differentiating the characteristic equation with respect to $\xi$, we get

$$\begin{aligned}&3\lambda ^{2}\frac{\hbox {d}\lambda }{\hbox {d}\xi }+2b_{1}\lambda \frac{\hbox {d}\lambda }{\hbox {d}\xi }+b_{2}\frac{\hbox {d}\lambda }{\hbox {d}\xi } +\lambda ^{2}\frac{db_{1}}{\hbox {d}\xi } +\lambda \frac{db_{2}}{\hbox {d}\xi }\nonumber \\&\quad +\,\frac{db_{3}}{\hbox {d}\xi }=0. \end{aligned}$$

(10)

Since one value of $\lambda$ is $\mu +i\omega$, then substituting $\lambda =\mu +i\omega$ in (B1) and separating real and imaginary part, we have

$$\begin{aligned} L\frac{\hbox {d}\mu }{\hbox {d}\xi }-N\frac{\hbox {d}\omega }{\hbox {d}\xi }= & {} \Lambda _{1},\nonumber \\ L\frac{\hbox {d}\mu }{\hbox {d}\xi }+N\frac{\hbox {d}\omega }{\hbox {d}\xi }= & {} \Lambda _{2}. \end{aligned}$$

(11)

Now solving (B2) for $\hbox {d}\mu /\hbox {d}\xi$, it is easy to show that

$$\begin{aligned} \frac{\hbox {d}\mu }{\hbox {d}\xi }=\frac{L\Lambda _{1}+N\Lambda _{2}}{L^{2} +N^{2}}\mid _{\xi =\eta }\ne 0. \end{aligned}$$

Hence, we have for $\xi =\eta ,\,\mu =0$ and $\frac{\hbox {d}\mu }{\hbox {d}\xi }\mid _{\xi =\eta }\ne 0$. Thus, the transversality condition for the Hopf bifurcation is satisfied.