New approach for stability and bifurcation analysis on predator–prey harvesting model for interval biological parameters with time delays

Abstract

This paper presents a prey–predator harvesting model with time delay for bifurcation analysis. We consider the parameters of the proposed model with imprecise data as form of interval in nature, due to the lack of precise numerical information of the biological parameters such as prey population growth rate and predator population decay rate. The interaction between prey and predator is assumed to be governed by a Holling type II functional response and discrete type gestation delay of the predator for consumption of the prey under impreciseness of the biological parameters. Parametric functional form of interval number with two parameters is introduced. This study reveals that not only delay and harvesting effort play a significant role on the stability on the system but also interval parameters play a crucial role on the stability of the system. Computer simulations of numerical examples are given to explain our proposed imprecise model. We also address critically the biological implications of our analytical findings with proper numerical example.

1 Introduction

There has been a great interest during the past few decades in dynamical characteristics of population models (Kot 2001; Murray 1993) and among these models, predator–prey systems play an important role in population dynamics. Also over the past few decades, mathematics plays an important role to understand biological phenomena. Most of the biological phenomena such as prey–predator harvesting model (Hoekstra and van den Bergh 2005; Palma and Olivares 2012; Gupta and Chandra 2013; Pal et al. 2012; Duncan et al. 2011; Anita et al. 2009), prey–predator refuge model (Chen et al. 2012, 2013; Wang et al. 2009; Rebaza 2012), prey–predator disease model (Das et al. 2009; Bairagi et al. 2009; Hethcote et al. 2004; Pal and Samanta 2010), etc. can be represented by the set of nonlinear differential equations. But in most of the models on ecosystem, the population of one species does not respond instantly to the interactions with other species. These types of model can be handled by incorporating time lag in the differential equations of the models. In population dynamics, a time delay is introduced when the rate of change of population not only depends on the function of the present population, but also depends on the past population. Therefore, time delay can be included in the mathematical population model due to various factors such as maturation time, capturing time and other reasons. Moreover, the existence of time delays is frequently a source of instability in some ways. To make a more realistic biological mathematical model, many researchers (Gopalsamy 1983; Kar 2003; Yongzhen et al. 2011; Qu and Wei 2007; Shao 2010; Jiao et al. 2009) introduced time delay in their respective model. In reality, time delays occur in almost every biological situation (MacDonald 1989) and assumed to be one of the reasons of regular fluctuations in population density. Misra and Dubey (2010) proposed a prey–predator model with discrete delay and ratio-dependent functional response. Zhang (2012) presented prey–predator delay model using a modified Holling–Tanner functional response with delay as the bifurcation parameter. Bandyopadhyay and Banerjee (2006) introduced a stage-structured predator–prey model with gestation as the delay and switching of stability due to variation of delay. On the other hand, two species models with different functional responses are extensively studied in ecological literature. The Lotka–Volterra functional response (Holling type I functional response) (Kot 2001; Murray 1993) is of the form $p( x) =ex$ and the Holling type II functional response (Kot 2001; Murray 1993) is of the form $p( x) =\frac{ex}{( f+x) }$, where x is the population density of prey, e is the maximum rate of predation, i.e., the maximum number of prey that can be eaten by a predator in unit a time, f is the half-saturation constant, i.e., the number of prey necessary to achieve one-half of the maximum rate e. With the help of such functional responses, many researchers have concentrated their study on the stability of the predator–prey systems.

So far most of the above researchers considered their models in a precise environment but in reality, data cannot be recorded or collected precisely due to several reasons. The impreciseness of the bio-mathematical model is caused by environmental fluctuations or imprecise biological phenomenon. Therefore, there are many cases where the parameters of bio-mathematical model cannot be presented in a precise manner. So, mathematical modelling of the biological phenomenon through the deterministic approach is subject to inaccuracies due to the nature of the state variables involved, by parameters as coefficients of the model and by the initial conditions. There are few approaches such as fuzzy approach, stochastic approach and fuzzy stochastic approach to handle these types of imprecise models. Bassanezi et al. (2000) put a foundation stone to apply fuzzy differential equations in population dynamics to study the stability of fuzzy dynamical systems. After that, Barros et al. (2000), Peixoto et al. (2008), Tuyako et al. (2009), Pal et al. (2013a) and few more researchers used the concepts of fuzziness in biomathematical model. Again stochastic prey–predator model was enormously studied by Abundo (1991), Rudnicki (2003), Liu and Wang (2012), Vasilova (2013), and Aguirre et al. (2013). However, there are some difficulties in handling the imprecise biological parameters by fuzzy approach as well as stochastic approach. In fuzzy approach, the imprecise parameters are replaced by fuzzy sets with known membership function or by fuzzy numbers. But it is very difficult to construct a suitable membership function for the imprecise biological parameters. In stochastic approach, the imprecise parameters are assumed to be a random variable with known probability distributions. But to identify the suitable probability distribution for a stochastic approach is a very tough one. Keeping in mind such difficulties Pal et al. (2013b) first introduced the concept of interval number to present imprecise prey–predator model. They used parametric functional form of interval number with one parameter to illustrate different aspects of the model. After that many researchers (Zhang and Zhao 2014; Pal et al. 2014; Pal and Mahapatra 2014) were attracted by this new approach to use parametric functional form with single parameter in their respective models. However, according to the information available, until now no one has considered prey–predator system with interval biological parameter using parametric functional form with two parameters to illustrate dynamical behaviour of the model.

In this paper, we present an imprecise prey–predator harvesting model with discrete type gestation delay of predators, where the prey-specific growth rate, predator decay rate in the absence of prey species are in interval in nature. We consider the intrinsic growth rate of the prey species and decay rate of predator species (in the absence of prey species), as interval in nature. We transform the imprecise prey–predator delay model to a parametric prey–predator delay model (PPPDM) with two parameters (p and q ) using the functional form of the interval number to make the model more realistic. The dynamical behaviour of the parametric model is investigated for different values of the parameters $p\in [ 0,1]$ and $q\in [ 0,1]$. We study the combined effects of harvesting and delay as well as impreciseness on the dynamics of the model. Our aim was to obtain some interesting and new results due to the presence of impreciseness in the model. The construction of our imprecise model system is sketched in Sect. 3. In Sect. 4, positivity, permanence and persistence of the solutions and stability of different types of equilibrium points are discussed. The analysis of the delayed model is described in Sect. 5. This analysis shows that there is a critical value of delay $( \tau _{0}^{+})$ based on the parameters p and q below which the system is stable and above which the system becomes unstable at the interior equilibrium $P_{3}( x^{*},y^{*})$. The system undergoes Hopf-bifurcation around $P_{3}( x^{*},y^{*})$ when the value of the delay $\tau =\tau _{0}^{+}$. In Sect. 6 we have estimated the length of delay to preserve the stability around $P_{3}( x^{*},y^{*})$. All our analytical results are numerically verified and presented graphically in Sect. 7. Finally, Sect. 8 contains the general discussions of the paper and biological implications of our mathematical findings.

2 Prerequisite mathematics

In this section, we discuss some preliminary mathematics which we use to study the imprecise prey–predator delay model.

Definition 1

(Interval number) An interval number B is represented by closed interval $[ b_{l},b_{u}]$ and defined by $B=[ b_{l},b_{u}] =\{ y:b_{l}\le y\le b_{u},y\in R\}$, where R is the set of real numbers and $b_{l},b_{u}$ are the left and right limits of the interval number, respectively.

Now we define interval-valued function (Pal et al. 2013b, 2014; Zhang and Zhao 2014; Pal and Mahapatra 2014; Mahapatra and Mandal 2012) which will be used to present an interval number.

Definition 2

(Interval-valued function) Let $c,d>0$ and consider the interval is of the form [c, d] ; the interval-valued function of the interval is represented as $h( p) =c^{1-p}d^{p}$ for $p\in [ 0,1]$.

Now we present some arithmetic operations on interval-valued functions. Let $A=[ a_{l},a_{u}]$ and $B=$ $[ b_{l},b_{u}]$ be two interval numbers so that $a_{l}$, $b_{l}>0$.

Addition: $A+B=[ a_{l},a_{u}] +[ b_{l},b_{u}] =[ a_{l}+b_{l},a_{u}+b_{u}]$. The interval-valued function for the interval $A+B$ is given by $h( p) =a_{L}^{1-p}a_{U}^{p}$ where $a_{L}=a_{l}+b_{l}$ and $a_{U}=a_{u}+b_{u}$.

Subtraction: $A-B=[ a_{l},a_{u}] -[ b_{l},b_{u}] = [ a_{l}-b_{u},a_{u}-b_{l}]$. provided $a_{l}-b_{u}>0$. The interval-valued function for the interval $A-B$ is given by $h( p) =b_{L}^{1-p}b_{U}^{p}$ where $b_{L}=a_{l}-b_{u}$ and $b_{U}=a_{u}-b_{l}$.

Scalar multiplication: $\beta A=\beta [ a_{l},a_{u}] =\left\{ \begin{array}{l} [ \beta a_{l},\beta a_{u}] \text {, if }\beta \ge 0 \\ \left[ \beta a_{u},\beta a_{l}\right] \text {, if }\beta <0 \end{array}\right.$, provided $a_{l}>0$. The interval-valued function interval $\beta A$ is given by $h( p) =c_{L}^{1-p}c_{U}^{p}$ if $\beta \ge 0$ and $h( p) =-d_{U}^{1-p}d_{L}^{p}$ if $\beta <0$, where $c_{L}=\beta a_{l}$, $c_{U}=\beta a_{u}$, $d_{L}=\vert \beta \vert a_{l}$ and $d_{U}=\vert \beta \vert a_{u}$.

3 Mathematical form of prey–predator model with time delay

In this section, we present mathematical form of a prey–predator harvesting model with a time delay due to gestation. First, we present the concept behind the construction of the model which will specify its biological significance of it. We assume that in the absence of predators, the prey population grows according to a logistic low of growth with intrinsic growth rate r and carrying capacity k. Further, it is inherently assumed that the metabolic energy a predator obtains through its food is used for growth, which ultimately enhances the predator population. The predator population consumes the prey population at a constant rate $\alpha$ but the reproduction of predators after predating the prey population is not instantaneous. It will be incorporative by some time lag required for gestation of predators. Suppose that the time interval between the moments when an individual prey is killed and the corresponding biomass is added to predator population is considered as time delay $\tau$. Here, we also assume that both the prey and predator species are continuously harvested by the harvesting agencies. Therefore, the mathematical form of our proposed prey–predator model with Michaelis–Menten–Holling type functional response, delay in predator response function and subject to harvesting efforts $E_{1}$ and $E_{2}$ of prey and predator species, respectively, is as follows:

$$\begin{aligned} \frac{\mathrm{d}x}{\mathrm{d}t}&=rx\left( 1-\frac{x}{k}\right) -\frac{\alpha xy}{m+x} -q_{1}E_{1}x \nonumber \\ \frac{\mathrm{d}y}{\mathrm{d}t}&=-\delta y+\frac{\beta x( t-\tau ) y}{m+x( t-\tau ) }-q_{2}E_{2}y \end{aligned}$$

(1)

with initial conditions

$$\begin{aligned} \left. x( \theta ) =\phi _{1}(\theta ), y( \theta ) =\phi _{2}(\theta ),\quad \text {such that }\; \phi _{i}(\theta )\ge 0\text { } (i=1,2)\text {, }\quad \forall \text { }\theta \in [ -\tau ,0], \right. \end{aligned}$$

where $\phi _{i}(\theta )\ge 0$ $(i=1,2)$ are non-negative continuous functions on $\theta \in [ -\tau ,0]$. For a biological meaning, we further assume that $\phi _{i}(\theta )>0$ $(i=1,2)$.

Here x(t) and y(t) stand for prey and predator density, respectively, at time t. Also r, $\delta ,$ k,  $\alpha$, m, $\beta$, $q_{1}$ and $q_{2}$ are positive constants that stand for prey intrinsic growth rate, predator death rate, carrying capacity, capturing rate, half-saturation constant, conversion rate, catchability coefficient of prey and catchability coefficient of predator, respectively. $\tau \ge 0$ is a constant representing the delay that prey species takes $\tau$ unit of time to become mature. Also, the conversion of prey biomass to predator biomass takes $\tau$ unit of time. Our proposed mathematical model fits well in fishery industry. The real-life example of our proposed model is Antarctic Krill–Whale community where Krill is the main resource of food for whales and the Antarctic Krill is being increasingly harvested. On the contrary, the moratorium imposed by the International Whaling Commission (IWC) on killing of Whales continues. Large catches from the lower trophic level (Krill) make a serious impact on lower trophic level (Krill) and higher trophic level (Whale). Therefore, a harvesting plan is recommended to keep the ecological balance. Also, the conversion of Krill biomass to Whale biomass is not instantaneous and eventually takes some time. This required time is known as discrete time delay or discrete time lag. Again we are completely unaware of the nature of biological phenomenon of both species; these are based on survey data so they are not precise in nature. Therefore, the imprecise model is more powerful than the precise one to present bio-mathematical model.

3.1 Imprecise prey–predator delay model

All the biological coefficients of the prey–predator model are positive in nature. Consequently in model (1), all the biological parameters are considered positive and precise. But in reality, they are not always precise due to lack of proper information or the data of our ecosystem. Therefore, there are many cases in which the biological parameters may not be presented in a precise manner. Intuitively, if any of the parameters is imprecise then the model presented in (1) becomes an imprecise one. Furthermore, when right-hand side of the model becomes an interval number rather than a single value, then there does not exist so straightforward rule to convert the model to the standard form like model (1). So, for an imprecise parameter, we present our proposed model with an interval parameter.

Let $\widehat{r}$ and $\widehat{\delta }$ be the interval counterparts of r (${>}0$) intrinsic growth rate of the prey species and $\delta$ (${>}0$) predator death rate, respectively; then the imprecise prey–predator delay model with prey harvesting effort E is in the following form:

$$\begin{aligned} \frac{\mathrm{d}x}{\mathrm{d}t}&=\widehat{r}x\left( 1-\frac{x}{k}\right) -\frac{\alpha xy}{m+x} -q_{1}E_{1}x \nonumber \\ \frac{\mathrm{d}y}{\mathrm{d}t}&=-\widehat{\delta }y+\frac{\beta x( t-\tau ) y}{ m+x( t-\tau ) }-q_{2}E_{2}y, \end{aligned}$$

(2)

where $\widehat{r}$ $\in [ r_{l},r_{u}]$, $\widehat{\delta }\in [ \delta _{l},\delta _{u}]$. Also $r_{l}>0$ and $\delta _{l}>0$ for all time t.

The delay model (2) can be written in parametric form with two parameters as follows:

$$\begin{aligned} \left. \begin{array}{l} \frac{\mathrm{d}x( t;p) }{\mathrm{d}t}=r_{l}^{1-p}r_{u}^{p}x\left( 1-\frac{x}{k} \right) -\frac{\alpha xy}{m+x}-q_{1}E_{1}x \\ \frac{\mathrm{d}y( t;q) }{\mathrm{d}t}=-\delta _{u}^{1-q}\delta _{l}^{q}y+\frac{ \beta x( t-\tau ) y}{m+x( t-\tau ) }-q_{2}E_{2}y \end{array} \right. \text { for }p\in [ 0,1]\quad \text { and }\quad q\in [ 0,1] \end{aligned}$$

(3)

with initial conditions

$$\begin{aligned}&x( \theta ;p) =\phi _{1}(\theta ), y( \theta ;q) =\phi _{2}(\theta ),\quad \text {such that }\quad \phi _{i}(\theta )>0\text { } (i=1,2),\nonumber \\&\quad \text { for all }\quad \theta \in [ -\tau ,0] \end{aligned}$$

(4)

The following Lemma gives the concept that the parametric form of model (2) is possible with two different parameters p and q is possible when $\widehat{r}$ and $\widehat{\delta }$ are interval numbers.

Lemma 1

The following differential equation with interval-valued coefficient

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}x}{\mathrm{d}t}&=\widehat{r}_{0}x\left( 1-\frac{x}{k}\right) -\frac{\alpha xy}{ m+x}-q_{1}E_{1}x \\ \frac{\mathrm{d}y}{\mathrm{d}t}&=-\widehat{\delta }_{0}y+\frac{\beta x( t-\tau ) y}{ m+x( t-\tau ) }-q_{2}E_{2}y, \end{aligned} \end{aligned}$$

(5)

where $\widehat{r}_{0}$ $\in [ r_{l},r_{u}]$ and $\widehat{ \delta }_{0}\in [ \delta _{l},\delta _{u}]$ with $r_{l}$, $\delta _{l}>0$ given has the corresponding interval-valued function coefficients form representation with two different parameters p and q by the following differential equation:

$$\begin{aligned} \left. \begin{array}{l} \frac{\mathrm{d}x( t;p) }{\mathrm{d}t}=r_{l}^{1-p}r_{u}^{p}x\left( 1-\frac{x}{k} \right) -\frac{\alpha xy}{m+x}-q_{1}E_{1}x \\ \frac{\mathrm{d}y( t;q) }{\mathrm{d}t}=-\delta _{u}^{1-q}\delta _{l}^{q}y+\frac{ \beta x( t-\tau ) y}{m+x( t-\tau ) }-q_{2}E_{2}y \end{array} \right. \quad \text { for }\; p\in [ 0,1]\quad \text { and }\; q\in [ 0,1] \end{aligned}$$

Proof

The differential equation (5) can be written as

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}x}{\mathrm{d}t}&=[r_{l},r_{u}]x\left( 1-\frac{x}{k}\right) -\frac{\alpha xy}{m+x }-q_{1}E_{1}x \\ \frac{\mathrm{d}y}{\mathrm{d}t}&=-[\delta _{l},\delta _{u}]y+\frac{\beta x( t-\tau ) y}{m+x( t-\tau ) }-q_{2}E_{2}y \end{aligned} \end{aligned}$$

(6)

Let $r_{1}\in [ r_{l},r_{u}]$ and $\delta _{1}\in [ \delta _{l},\delta _{u}],$ respectively. Following the interval arithmetic operations and properties equation (6) reduce to

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}x}{\mathrm{d}t}&=r_{1}x\left( 1-\frac{x}{k}\right) -\frac{\alpha xy}{m+x} -q_{1}E_{1}x \\ \frac{\mathrm{d}y}{\mathrm{d}t}&=-\delta _{1}y+\frac{\beta x( t-\tau ) y}{m+x( t-\tau ) }-q_{2}E_{2}y \end{aligned} \end{aligned}$$

(7)

For fixed n and m, let us consider interval-valued functions $h_{n}( p) =a_{n}^{1-p}b_{n}^{p}$ for $p\in [ 0,1]$ and $h_{m}( \mathbf {q}) =a_{m}^{1-\mathbf {q}}b_{m}^{\mathbf {q}}$ for $q\in [ 0,1]$ for the intervals $\beta _{n}\in [ a_{n},b_{n}]$ and $\beta _{m}\in [ a_{m},b_{m}]$. Since $h_{n}( p)$ and $h_{m}( \mathbf {q})$ are strictly increasing and continuous functions, the Eq. (7) reduces to

$$\begin{aligned} \frac{\mathrm{d}x}{\mathrm{d}t}&=r_{1}^{\prime }x\left( 1-\frac{x}{k}\right) -\frac{\alpha xy}{ m+x}-q_{1}E_{1}x \nonumber \\ \frac{\mathrm{d}y}{\mathrm{d}t}&=-\delta _{1}^{\prime }y+\frac{\beta x( t-\tau ) y}{ m+x( t-\tau ) }-q_{2}E_{2},y, \end{aligned}$$

where $r_{1}^{\prime }\in r_{l}^{1-p}r_{u}^{p}$, $\delta _{1}^{\prime }\in \delta _{u}^{1-q}\delta _{l}^{q}$, $p\in [ 0,1]$ and $q\in [ 0,1]$. Therefore, the parametric form of the differential equation (5) with two different parameters p and q is given by

$$\begin{aligned} \left. \begin{array}{l} \frac{\mathrm{d}x( t;p) }{\mathrm{d}t}=r_{l}^{1-p}r_{u}^{p}x\left( 1-\frac{x}{k} \right) -\frac{\alpha xy}{m+x}-q_{1}E_{1}x \\ \frac{\mathrm{d}y( t;q) }{\mathrm{d}t}=-\delta _{u}^{1-q}\delta _{l}^{q}y+\frac{ \beta x( t-\tau ) y}{m+x( t-\tau ) }-q_{2}E_{2}y \end{array} \right. \quad \text { for }\; p\in [ 0,1]\quad \text {and }\; q\in [ 0,1] \end{aligned}$$

$\square$

4 Dynamical behaviour of the proposed delay prey–predator model

System (3) has three non-negative equilibria, namely $P_{1}( 0,0)$, $P_{2}( k,0)$ and $P_{3}( x^{*},y^{*})$ for all $p\in [ 0,1]$ and $q\in [ 0,1 ]$, where $x^{*}$ and $y^{*}$ are the solution of the equations

$$\begin{aligned} \left. \begin{array}{l} r_{l}^{1-p}r_{u}^{p}\left( 1-\frac{x}{k}\right) -\frac{\alpha y}{m+x} -q_{1}E_{1}=0 \\ -\delta _{u}^{1-q}\delta _{l}^{q}+\frac{\beta x}{m+x}-q_{2}E_{2}=0 \end{array} \right\} \end{aligned}$$

(8)

Solving (8) we get $x^{*} \,{=}\, \frac{\big ( \delta _{u}^{1-q}\delta _{l}^{q}+q_{2}E_{2}\big ) m}{\beta -\delta _{u}^{1-q}\delta _{l}^{q}-q_{2}E_{2}}$ and $y^{*}\,{=}\, \frac{\beta m}{\alpha \big ( \beta -\delta _{u}^{1-q}\delta _{l}^{q}-q_{2}E_{2}\big ) }\left[ r_{l}^{1-p}r_{u}^{p}-q_{1}E_{1}-\frac{\big ( \delta _{u}^{1-q}\delta _{l}^{q}+q_{2}E_{2}\big ) m}{k\big ( \beta -\delta _{u}^{1-q}\delta _{l}^{q}-q_{2}E_{2}\big ) }\right]$ for all $p\,{\in }\, [ 0,1]$ and $q\,{\in }\, [ 0,1]$. The nontrivial equilibrium point $P_{3}( x^{*},y^{*})$ exists only if (i) $E_{2}<\frac{1}{q_{2}} \big ( \beta -\delta _{u}^{1-q}\delta _{l}^{q}\big )$ and (ii) $E_{1}< \frac{r_{l}^{1-p}r_{u}^{p}}{q_{1}}\left[ 1-\frac{\big ( \delta _{u}^{1-q}\delta _{l}^{q}+q_{2}E_{2}\big ) m}{k\big ( \beta -\delta _{u}^{1-q}\delta _{l}^{q}-q_{2}E_{2}\big ) }\right]$. From $y^{*}$, we observe that as the harvesting effort $E_{1}$ of the prey species increases, $y^{*}$ gradually decreases. This situation is natural because predator species suffers for adequate food as the harvesting rate of the prey species increases which causes a slump in predator survival rate.

4.1 Stability analysis of the model

Stability of the equilibrium points is discussed in two cases: first we consider delay $\tau =0$ and in the second case we consider delay $\tau$ $\ne 0$. The characteristic equation about an arbitrary equilibrium point $( x^{*},y^{*})$ of (3) is given by

$$\begin{aligned} \Delta ( \lambda ,\tau ) =\vert A+Be^{-\lambda \tau }-\lambda I\vert =0, \end{aligned}$$

(9)

where $A=( a_{ij}) _{2\times 2}$, $a_{11}=\frac{\alpha x^{*}y^{*}}{( m+x^{*}) ^{2}}-\frac{r_{l}^{1-p}r_{u}^{p}x^{ *}}{k}$, $a_{12}=-\frac{\alpha x^{*}}{m+x^{*}}$, $a_{21}=0$, $a_{22}=0$, $B=( b_{ij}) _{2\times 2}$, $b_{11}=0$, $b_{12}=0$, $b_{21}=\frac{\beta my^{*}}{( m+x^{*}) ^{2}}$ and $b_{22}=0$. After some algebraic calculation, the characteristic equation ( 9) reduces to

$$\begin{aligned} \Delta ( \lambda ,\tau ) =\lambda ^{2}+a_{1}\lambda +a_{2}e^{-\lambda \tau }=0, \end{aligned}$$

(10)

where $a_{1}=-\left( \frac{\alpha x^{*}y^{*}}{( m+x^{*}) ^{2}}-\frac{r_{l}^{1-p}r_{u}^{p}x^{*}}{k}\right)$ and $a_{2}= \frac{\alpha \beta mx^{*}y^{*}}{( m+x^{*}) ^{3}}$.

5 Analysis of the prey–predator model without time delay

In this section, we discuss the existence and uniqueness solution of our proposed prey–predator system (3) in the absence of delay with the given initial condition. We present persistence and permanence, which play an important role to describe long-term behaviour of the system.

5.1 Positivity and boundedness

Let $\mathbb {R} _{+}$ denote the set of all non-negative real numbers and $\mathbb {R} _{+}^{n}=\{ x\in \mathbb {R} ^{n}:x=( x_{1},x_{2},\ldots x_{n}),$ where $x_{i}\in \mathbb {R} _{+}\text {,}\forall i=1,2,\ldots n\}$. If we denote the function on the right-hand side of system (3) in the absence of delay, by $f=( f_{1},f_{2})$ clearly $f\in C^{1}( \mathbb {R} _{+}^{2})$. Hence, $f: \mathbb {R} _{+}^{2}\rightarrow \mathbb {R} ^{2}$ is locally lipschitz on $\mathbb {R} _{+}^{2}=\{ ( x,y) :x>0,y>0\}$. Thus the fundamental theorem of existence and uniqueness assures existence and uniqueness of solution of system (3) in the absence of delay with the given initial condition. The state space of aforesaid system is the non-negative cone, $\mathbb {R} _{+}^{2}=\{ ( x,y) :x>0,y>0\}$.

Theorem 1

Every solution of system (3) in the absence of delay with initial conditions x(0; p), $y(0;q)>0$ exists in the interval $[ 0,\infty )$ and x(t; p), $y(t;q)>0$ for all $t\ge 0$, $p\in [ 0,1]$ and $q\in [ 0,1]$.

Proof

Since the right-hand side of system (3) in the absence of delay (i.e., $\tau =0$) is completely continuous and locally Lipschitzian on $C^{1}$, the solution (x(t; p) , y(t; q) ) of system (3) in the absence of delay with given initial condition exists and is unique on $[ 0,\xi ),$ where $0\le \xi <+\infty$. From system (3) with $\tau =0$ and given initial condition, we have

$$\begin{aligned} x( t;p)&=x( 0;p) \exp \left[ \int _{0}^{t}\left\{ r_{l}^{1-p}r_{u}^{p}\left( 1-\frac{x( s;p) }{k}\right) -\frac{ \alpha y( s;q) }{m+x( s;p) }-q_{1}E_{1}\right\} \mathrm{d}s \right]>0 \nonumber \\ y( t;q)&=y( 0;q) \exp \left[ \int _{0}^{t}\left\{ \frac{ \beta x(s;p)}{m+x(s;p)}-\delta _{u}^{1-q}\delta _{l}^{q}-q_{2}E_{2}\right\} \mathrm{d}s\right] >0, \end{aligned}$$

which completes the proof. $\square$

To prove the boundedness of system (3) in the absence of delay, we need to recall the following result, whose proof can be found in Brikhoff and Rota (1982) and Abbas et al. (2010)):

Lemma 2

If $a,b>0$ and $\frac{\mathrm{d}u}{\mathrm{d}t}=u( t) ( a-bu( t) )$, along with initial condition $u( 0) >0$, then for all $t\ge 0$, $u( t) \le \frac{a}{b-ce^{-at}}$ with $c=b-\frac{a}{ u( 0) }$. In particular, $u( t) \le \max \left\{ u( 0), \frac{a}{b}\right\}$ for all $t\ge 0$.

Theorem 2

Let S be the set defined by $S=\{ ( x,y) :0\le x\le M_{1},0\le y\le M_{2}\},$ where $M_{1}=\max \{ x( 0;p) ,k\}$, $M_{2}=k_{2}$ and $k_{2}=y( 0;q) \exp \left[ -\delta _{u}^{1-q}\delta _{l}^{q}-q_{2}E_{2}+\frac{\beta M_{1}}{m} \right]$. Then S is positively invariant.

Proof

If we take $( x( 0;p) ,y( 0;q) ) \in S$, from the Theorem 1, it is obvious that (x(t; p) , y(t; q) ) remains non-negative. To show that $( x( t;p) ,y( t;q) ) \in S$ for all $t\ge 0$, we need to prove that $x( t;p) \le M_{1}$ and $y( t;q) \le M_{2}$. We first show that $x( t;p) \le M_{1}$. Under positivity of the variables x and y (see Theorem 1) from first equation of system (3), we can write

$$\begin{aligned} \frac{\mathrm{d}x( t;p) }{\mathrm{d}t}\le r_{l}^{1-p}r_{u}^{p}x\left( 1-\frac{x}{k} \right) \end{aligned}$$

(11)

From Eq. (11) and using Lemma 2, we get $x( t;p) \le \max \{ x( 0;p) ,k\} =M_{1}$ for all $t\ge 0$. Further, from second equation of system (3) in the absence of delay, we obtain

$$\begin{aligned}&\frac{\mathrm{d}y( t;q) }{\mathrm{d}t}\le y( t;q) \left( -\delta _{u}^{1-q}\delta _{l}^{q}-q_{2}E_{2}+\frac{\beta M_{1}}{m}\right) \nonumber \\&\quad \Rightarrow y( t;q) \le y( 0;q) \exp \left[ -\delta _{u}^{1-q}\delta _{l}^{q}-q_{2}E_{2}+\frac{\beta M_{1}}{m}\right] =M_{2} \end{aligned}$$

(12)

This completes the proof. $\square$

In other words, we can say that all trajectories of system (3) in the absence of delay initiating from any point in $\mathbb {R} _{+}^{2}$ ultimately lies in fixed bounded region defined by S: Hence, the flow/dynamical systems associated with system (3) in the absence of delay is dissipative.

5.2 Permanence and persistence

A system analytically is said to be persistent if it persists for each population, i.e., ${\lim \nolimits {t\rightarrow \infty } }\inf x( t) >0$ (stronger case) or ${\lim \nolimits {t\rightarrow \infty } }\sup x( t) >0$ (weaker case) for each of the population x(t) of the system. Again geometrically, persistence means that trajectories that initiate in a positive cone are eventually bounded away from coordinate planes. On the contrary, permanent coexistence (uniformpersistence) implies the existence of a region in the phase space at a non-zero distance from boundary, in which all the population vectors must lie ultimately. To show the persistence for the non delay system (3) we need the following definitions and Lemma (Chen 2005; Chen et al. 2007):

Definition 3

Persistence: Prey–predator system (3) in the absence of delay is said to be weakly persistent if every solution (x(t; p) , y(t; q) ) satisfies two conditions for all $p\in [ 0,1]$ and $q\in [ 0,1]$: (i) $x( t;p) \ge 0$ and $y( t;q) \ge 0$. (ii) ${\lim \nolimits _{t\rightarrow \infty } }\sup x( t;p) >0$ and ${\lim \nolimits {t\rightarrow \infty } }\sup y( t;q) >0$. On the other hand, Model system (3) in the absence of delay is strongly persistent if every solution (x(t; p) , y(t; q) ) satisfies two conditions for all $p\in [ 0,1]$ and $q\in [ 0,1]$: (i) $x( t;p) \ge 0$ and $y( t;q) \ge 0$. (ii) ${\lim \nolimits { t\rightarrow \infty } }\inf x( t;p) >0$ and ${\lim \nolimits { t\rightarrow \infty } }\inf y( t;q) >0$.

Definition 4

Permanence: The prey–predator system (3) in the absence of delay is said to be permanent if there exist positive constants $\xi _{1}$ and $\xi _{2}$ $( 0<\xi _{1}<\xi _{2})$ such that each solution $( x( t;p,x_{0},y_{0}) ,y( t;q,x_{0},y_{0}) )$ for all $p\in [ 0,1]$ and $q\in [ 0,1]$ with initial condition $( x_{0},y_{0}) \in \mathrm{Int}( \mathbb {R} _{+}^{2})$ satisfies the following: (i)  $\min \{{\lim \nolimits { t\rightarrow \infty } }\inf x( t;p,x_{0},y_{0}), {\lim \nolimits { t\rightarrow \infty } }\inf y( t;p,x_{0},y_{0}) \} \ge \xi _{1}$ (ii) $\max \{ {\lim \nolimits {t\rightarrow \infty } }\sup x( t;p,x_{0},y_{0}), {\lim \nolimits {t\rightarrow \infty } }\sup x( t;p,x_{0},y_{0}) \} \le \xi _{2}$.

Lemma 3

If $L>0,M>0$ and $\frac{\mathrm{d}u}{\mathrm{d}t}\le ( \ge ) u( t) ( M-Lu( t) )$, $u( t_{0}) >0$, then we have ${\lim \nolimits _{t\rightarrow \infty } }\sup u( t) \le \frac{ M}{L}$ $\Big ( {\lim \nolimits _{t\rightarrow \infty } }\inf u( t) \ge \frac{M}{L}\Big )$.

Theorem 3

The system (3) is said to be permanent if $r_{l}^{1-p}r_{u}^{p}> \frac{\alpha k_{2}}{m}+q_{1}E_{1}$ for all $p\in [ 0,1]$ and $q\in [ 0,1]$.

Proof

From Eq. (11) and Lemma 2, it is clear that $0<x( t;p) <k$ for sufficiently large t. Also from Eq. (12) and Lemma 2, we obtain $0<y( t;q) <M_{2}$ for sufficiently large t. Using the positivity of variables x,  y and the first equation of system (3) in the absence of delay, we have

$$\begin{aligned} \frac{\mathrm{d}x( t;p) }{\mathrm{d}t}= & {} x( t;p) \left( r_{l}^{1-p}r_{u}^{p}-\frac{r_{l}^{1-p}r_{u}^{p}x}{k}-\frac{\alpha y( t;q) }{m+x}-q_{1}E_{1}\right) \\\ge & {} x( t;p) \left[ r_{l}^{1-p}r_{u}^{p}-\frac{ r_{l}^{1-p}r_{u}^{p}x}{k}-\frac{\alpha M_{2}}{m}-q_{1}E_{1}\right] =x( t;p) \left[ a_{1}-\frac{r_{l}^{1-p}r_{u}^{p}x( t;p) }{k} \right] \end{aligned}$$

for sufficiently large t, where $a_{1}=r_{l}^{1-p}r_{u}^{p}-\frac{\alpha M_{2}}{m}-q_{1}E_{1}$. If $a_{1}>0$, i.e., $r_{l}^{1-p}r_{u}^{p}>\frac{\alpha M_{2}}{m}+q_{1}E_{1}$, then from Lemma 3, we have ${\lim \nolimits _{t\rightarrow \infty } }\inf x( t;p) \ge \frac{a_{1}k}{ r_{l}^{1-p}r_{u}^{p}}\equiv \omega _{1}$. So for arbitrary, $\in _{1}>0$ there exists a positive real number $T_{1}$ such that $x( t;p) \ge \omega _{1}-$ $\in _{1}$ for all $t>T_{1}$. In the similar fashion, using the positivity of variables x, y and the second equation of system (3), we have

$$\begin{aligned} \frac{\mathrm{d}y( t;p) }{\mathrm{d}t}= & {} y( t;q) \left( -\delta _{u}^{1-q}\delta _{l}^{q}+\frac{\beta x( t;p) }{m+x( t;p) }-q_{2}E_{2}\right) \\\ge & {} y( t;q) \left( -\delta _{u}^{1-q}\delta _{l}^{q}+\frac{ \beta \left( \frac{\beta x( t;p) }{m+x( t;p) }-\in _{1}\right) }{m+k}-q_{2}E_{2}\right) \end{aligned}$$

As $\in _{1}>0$ is arbitrary, we can write

$$\begin{aligned} \frac{\mathrm{d}y( t;p) }{\mathrm{d}t}\ge y( t;q) \left( -\delta _{u}^{1-q}\delta _{l}^{q}+\frac{\beta a_{1}k}{r_{l}^{1-p}r_{u}^{p}( m+k) }-q_{2}E_{2}\right) ; \end{aligned}$$

therefore, ${\lim \nolimits {t\rightarrow \infty } }\inf y( t;q) \ge y( 0;q) \exp \big [ \big ( -\delta _{u}^{1-q}\delta _{l}^{q}+\frac{\beta a_{1}k}{r_{l}^{1-p}r_{u}^{p}( m+k) }-q_{2}E_{2}\big ) \big ] \equiv \omega _{2}$ for sufficiently large t. Also from inequalities (11) and (12) together with Lemma 3, we have ${\lim \nolimits _{t\rightarrow \infty } } \sup x( t;p) \le k$, ${\lim \nolimits _{t\rightarrow \infty } }\sup y( t;q) \le M_{2}$. Now, choosing $\xi _{1}=\min ( \omega _{1},\omega _{2})$ and $\xi _{2}=\max ( k,M_{2})$, we obtain the permanence of system (3) for all $p\in [ 0,1]$ and $q\in [ 0,1]$. $\square$

5.3 Stability of equilibrium points

For $\tau =0$, the characteristic Eq. (10) reduces to

$$\begin{aligned} \Delta ( \lambda ,0) =\lambda ^{2}+a_{1}\lambda +a_{2}=0 \end{aligned}$$

(13)

Theorem 4

The trivial equilibrium point $P_{1}( 0,0)$ is stable if $E_{1}>( BTP) _{x},$ where $( BTP) _{x}=$ $\frac{ r_{l}^{1-p}r_{u}^{p}}{q_{1}}=$ Biotechnical Productivity $=\frac{\text { Biotic\,potential}}{\text {Catchability coefficient}}$ of the prey species.

Proof

The eigenvalues corresponding to the equilibrium point $P_{1}( 0,0)$ are $r_{l}^{1-p}r_{u}^{p}-q_{1}E_{1}$ and $-( \delta _{u}^{1-q}\delta _{l}^{q}+q_{2}E_{2})$ for all $p\in [ 0,1]$ and $q\in [ 0,1]$. Since $( \delta _{u}^{1-q}\delta _{l}^{q}+q_{2}E_{2}) >0$ for all $q\in [ 0,1]$, $P_{1}( 0,0)$ is asymptotically stable if $r_{l}^{1-p}r_{u}^{p}-q_{1}E_{1}<0\Rightarrow E_{1}>\frac{r_{l}^{1-p}r_{u}^{p} }{q_{1}}$, i.e., $E_{1}>( BTP) _{x}$ for all $p\in [ 0,1 ]$ and $q\in [ 0,1]$.

Theorem 5

The equilibrium point $P_{2}( k,0)$ is asymptotically stable if the condition $E_{2}>\frac{1}{q_{2}}\left( \frac{\beta k}{m+k}-\delta _{u}^{1-q}\delta _{l}^{q}\right)$ for all $p\in [ 0,1]$ and $q\in [ 0,1]$ holds.

Proof

The eigenvalues corresponding to the equilibrium point $P_{2}( k,0)$ are $-( r_{l}^{1-p}r_{u}^{p}+q_{1}E_{1}) <0$ and $-\delta _{u}^{1-p}\delta _{l}^{p}+\frac{\beta k}{m+k}-q_{2}E_{2}$. Therefore, the equilibrium point $P_{2}( k,0)$ is asymptotically stable if $-\delta _{u}^{1-p}\delta _{l}^{p}+\frac{\beta k}{m+k} -q_{2}E_{2}<0$, i.e., $E_{2}>\frac{1}{q_{2}}\left( \frac{\beta k}{m+k} -\delta _{u}^{1-q}\delta _{l}^{q}\right)$ for all $p\in [ 0,1]$ and $q\in [ 0,1]$. $\square$

Theorem 6

The interior equilibrium point $P_{3}( x^{*},y^{*})$ is asymptotically stable if

$$\begin{aligned} \left. \begin{array}{l} ( BTP) _{x}\left[ 1-\frac{m\big (\beta +\delta _{u}^{1-q}\delta _{l}^{q}+q_{2}E_{2}\big )}{k\big (\beta -\delta _{u}^{1-q}\delta _{l}^{q}-q_{2}E_{2}\big )} \right]<E_{1}<( BTP) _{x}\left[ 1-\frac{\big ( \delta _{u}^{1-q}\delta _{l}^{q}+q_{2}E_{2}\big ) m}{k\big (\beta -\delta _{u}^{1-q}\delta _{l}^{q}-q_{2}E_{2}\big )}\right] \quad \text {and} \\ \text { }E_{2}<\frac{1}{q_{2}}\big ( \beta -\delta _{u}^{1-q}\delta _{l}^{q}\big )\quad for\, all \, p\in [ 0,1]\quad \text { and }\quad q\in [ 0,1]. \end{array} \right. \end{aligned}$$

Proof

The roots of the characteristic equation (13) corresponding to the equilibrium point $P_{3}( x^{*},y^{*})$ is given by

$$\begin{aligned} \lambda =-\frac{1}{2}a_{1}\pm \frac{1}{2}\sqrt{a_{1}^{2}-4a_{2}} \end{aligned}$$

(14)

From Eq. (14), the roots of the characteristic equation are negative or complex with negative real part if $a_{1}>0$ and $a_{2}>0$. As $a_{2}$ is always positive, the condition is satisfied only if $a_{1}>0$. Now $a_{1}>0$ implies the condition $E_{1}>( BTP) _{x}\left[ 1- \frac{m\big (\beta +\delta _{u}^{1-q}\delta _{l}^{q}+q_{2}E_{2}\big )}{k\big (\beta -\delta _{u}^{1-q}\delta _{l}^{q}-q_{2}E_{2}\big )}\right]$. Again the equilibrium point exists if $E_{1}<( BTP) _{x}\left[ 1-\frac{\big ( \delta _{u}^{1-q}\delta _{l}^{q}+q_{2}E_{2}\big ) m}{k\big (\beta -\delta _{u}^{1-q}\delta _{l}^{q}-q_{2}E_{2}\big )}\right]$and $E_{2}<\frac{1}{q_{2}} \big ( \beta -\delta _{u}^{1-q}\delta _{l}^{q}\big )$ for all $p\in [ 0,1]$ and $q\in [ 0,1]$. Hence, the interior equilibrium point $P_{3}( x^{*},y^{*})$ exists and is asymptotically stable if $( BTP) _{x}\left[ 1-\frac{m\big (\beta +\delta _{u}^{1-q}\delta _{l}^{q}+q_{2}E_{2}\big )}{k\big (\beta -\delta _{u}^{1-q}\delta _{l}^{q}-q_{2}E_{2}\big )}\right]<E_{1}<( BTP) _{x} \left[ 1-\frac{\big ( \delta _{u}^{1-q}\delta _{l}^{q}+q_{2}E_{2}\big ) m}{ k\big (\beta -\delta _{u}^{1-q}\delta _{l}^{q}-q_{2}E_{2}\big )}\right]$ and $E_{2}< \frac{1}{q_{2}}\big ( \beta -\delta _{u}^{1-q}\delta _{l}^{q}\big )$ for all $p\in [ 0,1]$ and $q\in [ 0,1]$. $\square$

Now we investigate the global stability of the interior equilibrium. The following theorem gives the condition of global stability:

Theorem 7

The interior equilibrium point $P_{3}( x^{*},y^{*})$ is globally asymptotically stable if

$$\begin{aligned} \left. \begin{array}{l} ( BTP) _{x}\left[ 1-\frac{m\big (\beta +\delta _{u}^{1-q}\delta _{l}^{q}+q_{2}E_{2}\big )}{k\big (\beta -\delta _{u}^{1-q}\delta _{l}^{q}-q_{2}E_{2}\big )} \right]<E_{1}<( BTP) _{x}\left[ 1-\frac{\big ( \delta _{u}^{1-q}\delta _{l}^{q}+q_{2}E_{2}\big ) m}{k\big (\beta -\delta _{u}^{1-q}\delta _{l}^{q}-q_{2}E_{2}\big )}\right] \quad \text { and} \\ \text { }E_{2}<\frac{1}{q_{2}}\big ( \beta -\delta _{u}^{1-q}\delta _{l}^{q}\big )\quad for\, all\, p\in [ 0,1]\quad \text { and } q\in [ 0,1]. \end{array} \right. \end{aligned}$$

Let us consider the system

$$\begin{aligned} \left. \begin{array}{l} \frac{\mathrm{d}x}{\mathrm{d}t}=xa( x) -yb( x) \\ \frac{\mathrm{d}y}{\mathrm{d}t}=y[ -\gamma +c( x) ] \end{array} \right\} , \end{aligned}$$

(15)

where x(0) ,  $y( 0) >0$. Then by a theorem given in Kuang and Freedman (1988) the system (15) has exactly one limit cycle which is globally asymptotically stable with respect to the set {$( x,y) \mid x>0,$ $y>0$}$\smallsetminus P_{3}( x^{*},y^{*})$ if $\frac{d}{\mathrm{d}x}\left\{ \frac{xa^{\prime }( x) +a( x) -xa( x) \frac{b^{\prime }( x) }{b( x) }}{ -\gamma +c( x) }\right\} \le 0$, in $0\le x\le x^{*}$ and $0<x^{*}\le k$. In our system $a( x) =r_{l}^{1-p}r_{u}^{p}x\left( 1-\frac{x}{k}\right) -q_{1}E_{1}$, $b( x) =\frac{\alpha x}{m+x}$, $c( x) =\frac{\beta x}{m+x},$ and $\gamma =( \delta _{u}^{1-q}\delta _{l}^{q}+q_{1}E_{2})$. In that case $\left. \frac{d}{\mathrm{d}x}\left\{ \frac{xa^{\prime }( x) +a( x) -xa( x) \frac{b^{\prime }( x) }{ b( x) }}{-\gamma +c( x) }\right\} \right| _{x=x^{*}}\le 0$ implies

$$\begin{aligned} \left. E_{1}\le ( BTP) _{x}\left[ 1-\frac{m\big (\beta +\delta _{u}^{1-q}\delta _{l}^{q}+q_{2}E_{2}\big )}{k\big (\beta -\delta _{u}^{1-q}\delta _{l}^{q}-q_{2}E_{2}\big )}\right] \quad {\mathrm{for}} \, {\mathrm{all}} \,\, p\in [ 0,1]\quad \text { and }\quad q\in [ 0,1] \right. \end{aligned}$$

(16)

Now if the condition (16) is satisfied, then the proposed parametric delay model (3) has a globally stable limit cycle. Again if a equilibrium point $P_{3}( x^{*},y^{*})$ exists and is stable and if the system has no limit cycle, the equilibrium point is globally asymptotically stable. Hence, the interior equilibrium point $P_{3}( x^{*},y^{*})$ is globally asymptotically stable if

$$\begin{aligned} \left. \begin{array}{l} ( BTP) _{x}\left[ 1-\frac{m\big (\beta +\delta _{u}^{1-q}\delta _{l}^{q}+q_{2}E_{2}\big )}{k\big (\beta -\delta _{u}^{1-q}\delta _{l}^{q}-q_{2}E_{2}\big )} \right]<E_{1}<( BTP) _{x}\left[ 1-\frac{\big ( \delta _{u}^{1-q}\delta _{l}^{q}+q_{2}E_{2}\big ) m}{k\big (\beta -\delta _{u}^{1-q}\delta _{l}^{q}-q_{2}E_{2}\big )}\right] \quad \text { and} \\ \text { }E_{2}<\frac{1}{q_{2}}\big ( \beta -\delta _{u}^{1-q}\delta _{l}^{q}\big )\quad \mathrm{for}\, \mathrm{all}\, p\in [ 0,1]\quad \text { and }\quad q\in [ 0,1]. \end{array} \right\} \nonumber \\ \end{aligned}$$

(17)

From Theorems 6 and 7, we observe that if the harvesting efforts $E_{1}$ and $E_{2}$ satisfy the above inequalities , then the local stability of the interior equilibrium point $P_{3}( x^{*},y^{*})$ implies global asymptotic stability. It is also observable that the range of the harvesting effort $E_{1}$ and $E_{2}$ as given in (17) depends upon the parameters p and q, i.e., the imprecise nature of parameters. Therefore, we may conclude that stability of the system may be hampered due to imprecise nature of the biological parameters. Also, the resource manager should plan harvesting effort within the range of the interval (17) for the sustainable progress of ecosystem.

6 Stability analysis of time delay model

In this section, we discuss the existence and uniqueness solution of our proposed model system (3) with delay and given initial condition.

6.1 Positivity

Theorem 8

Every solution of system (3) with initial condition (4) exists in the interval $[ 0,\infty )$ and x(t; p), $y(t;q)>0$ for all $t\ge 0$, $p\in [ 0,1]$ and $q\in [ 0,1]$.

Proof

Since the first equation of the system (3) is completely continuous and locally Lipschitzian on $C^{1}$, the solution x(t; p) of system (3) with given initial conditions (4) exists and is unique on $[ 0,\xi _{1})$ where $0\le \xi _{1}<+\infty$. From the first equation of the system (3) with given initial condition, we have

$$\begin{aligned} x( t;p) =x( 0;p) \exp \left[ \mathop {\displaystyle \int }\limits _{0}^{t}\left\{ r_{l}^{1-p}r_{u}^{p}\left( 1-\frac{x( \eta ;p) }{k}\right) - \frac{\alpha y( \eta ;q) }{m+x( \eta ;p) } -q_{1}E_{1}\right\} \mathrm{d}\eta \right] >0 \end{aligned}$$

To show that y(t; q) is positive on $[ 0,\infty )$, suppose that there exists $t_{1}>0$ such that $y( t_{1};q) =0$ and $y( t;q) >0$ for $t_{1}\in$ $[ 0,t_{1})$. Then $\frac{\mathrm{d}y( t_{1};q) }{\mathrm{d}t}<0$. From the second equation of the system (3), we have $\frac{\mathrm{d}y( t_{1};q) }{\mathrm{d}t}=-\delta _{u}^{1-q}\delta _{l}^{q}y( t_{1};q) +\frac{\beta x( t-\tau ) y( t_{1};q) }{m+x( t-\tau ) } -q_{2}E_{2}y( t_{1};q) =0$, which is contradictory. Therefore, x(t; p), $y(t;q)>0$ for all $t\ge 0$, $p\in [ 0,1]$ and $q\in [ 0,1]$. $\square$

6.2 Stability and bifurcation analysis

Here, we discuss the effects of time delay to the system (3) for different values of the parameters p.

Let $\lambda =iw$, ($w>0$) is a root of the Eq. (10); then we have

$$\begin{aligned} -w^{2}+ia_{1}w+a_{2}e^{-iw\tau }=0 \end{aligned}$$

(18)

Equating real and imaginary parts of the Eq. (18) we have

$$\begin{aligned} -w^{2}+a_{2}\cos w\tau =0\quad \text { and }\quad a_{1}w-a_{2}\sin w\tau =0 \end{aligned}$$

(19)

Squaring both the equations of (19) and adding, we get the following fourth-degree polynomial

$$\begin{aligned} w^{4}+a_{1}^{2}w^{2}-a_{2}^{2}=0 \end{aligned}$$

(20)

Solving the above quadratic equation in $w^{2},$ we get $w^{2}=-\frac{1}{2} a_{1}^{2}\pm \frac{1}{2}\sqrt{a_{1}^{4}+4a_{2}^{2}}$. Since $a_{1}^{4}+4a_{2}^{2}>a_{1}^{4}$, the Eq. (20) has only one positive solution $w_{+}^{2}$ . Therefore, the characteristic equation (10) has a pair of purely imaginary roots $\pm iw_{+}$ for all values of the parameter $p\in [ 0,1]$ and $q\in [ 0,1]$. Putting the value of $w_{+}^{2}$ in both the equations of (19) and solving for $\tau$ we get

$$\begin{aligned} \tau _{i}^{+}=\frac{1}{w_{+}}\arctan \left( \frac{a_{1}}{w_{+}}\right) + \frac{2i\pi }{w_{+}},\quad i=0,1,2\ldots . \end{aligned}$$

(21)

From the above discussion, we have the following lemma:

Lemma 4

For $\tau =\tau _{0}^{+}$ the Eq. (10) has a pair of imaginary roots $\pm iw_{+}$ for all $p\in [ 0,1]$ and $q\in [ 0,1 ]$.

Theorem 9

Let $\tau _{i}^{+}$ be defined by (21) and the condition (17) is satisfied; then the equilibrium point $P_{3}( x^{*},y^{*})$ of the system (3) is asymptotically stable for $\tau<$ $\tau _{0}^{+}$ and unstable for $\tau>$ $\tau _{0}^{+}$. Further, as $\tau$ increases through $\tau _{0}^{+}$, $P_{3}( x^{*},y^{*})$ bifurcates into small amplitude periodic solutions, where $\tau _{0}^{+}=$ $\tau _{i}^{+}$ for $i=0$ and for all values of $p\in [ 0,1]$ and $q\in [ 0,1]$.

Proof

For $\tau =0$, the equilibrium point $P_{3}( x^{*},y^{*})$ is asymptotically stable if the condition (17) is satisfied based on the Theorem 6. Hence, by Butler’s lemma (Freedman and Sree 1983), $P_{3}( x^{*},y^{*})$ remains stable for $\tau<$ $\tau _{0}^{+}$ for all $p\in [ 0,1]$ and $q\in [ 0,1]$. Now we have to show that $\left. \frac{d\left( \mathrm{Re}\lambda \right) }{\mathrm{d}t} \right| _{\tau =\tau _{0}^{+},w=w_{+}}>0$. This indicates that there exists at least one eigenvalue with positive real part for $\tau>$ $\tau _{0}^{+}$ and for all $p\in [ 0,1]$ and $q\in [ 0,1]$ . Also, the conditions for Hopf-bifurcation are satisfied yielding the required periodic solution for all $p\in [ 0,1]$ and $q\in [ 0,1]$. Now differentiating (10) with respect to $\tau$, we get $[ 2\lambda +a_{1}-a_{2}e^{-\lambda \tau }] \frac{\mathrm{d}\lambda }{ \mathrm{d}\tau }=a_{2}\lambda e^{-\lambda \tau }$. This implies

$$\begin{aligned} \left( \frac{\mathrm{d}\lambda }{\mathrm{d}\tau }\right) ^{-1}=\frac{2\lambda +a_{1}}{ a_{2}\lambda e^{-\lambda \tau }}-\frac{\tau }{\lambda } \end{aligned}$$

(22)

Since $e^{-\lambda \tau }=-\frac{\lambda ^{2}+a_{1}\lambda }{a_{2}}$, the Eq. (22) becomes $\left( \frac{\mathrm{d}\lambda }{\mathrm{d}\tau }\right) ^{-1}=-\frac{2\lambda +a_{1}}{\lambda ( \lambda ^{2}+a_{1}\lambda ) }-\frac{\tau }{\lambda }$. Thus

$$\begin{aligned} \left. \text {sign}\left\{ \frac{d}{\mathrm{d}t}\left( \mathrm{Re}\lambda \right) \right\} \right| _{w=iw_{+}}&=\left. \text {sign}\left\{ \mathrm{Re}\left( \frac{\mathrm{d}\lambda }{\mathrm{d}\tau }\right) ^{-1}\right\} \right| _{w=iw_{+}}\nonumber \\&=\mathrm{ Si}gn\mathrm{Re}\left[ -\frac{2\lambda +a_{1}}{\lambda ( \lambda ^{2}+a_{1}\lambda ) }-\frac{\tau }{\lambda }\right] _{w=iw_{+}} \end{aligned}$$

Therefore, $\left. \text {sign}\left. \left\{ \frac{d\left( \mathrm{Re}\lambda \right) }{\mathrm{d}t}\right\} \right| _{w=iw_{+}}=\text {sign}\left\{ \frac{ a_{1}^{2}+2w_{+}^{2}}{w_{+}^{4}+a_{1}^{2}w_{+}^{2}}\right\} \right.$.

So $\left. \frac{d\left( \mathrm{Re}\lambda \right) }{\mathrm{d}t}\right| _{\tau =\tau _{0}^{+},w=w_{+}}>0$; therefore, the transversality condition holds and hence Hopf-bifurcation occurs at $w=w_{+}$, $\tau =\tau _{0}^{+}$ for all $p\in [ 0,1]$ and $q\in [ 0,1]$. This completes the proof. $\square$

6.3 Estimation of the length of delay to preserve stability

We consider the prey–predator delay system (3) and the space of all real-valued continuous functions defined on $[ -\tau ,\infty )$ satisfying the initial conditions on $[ -\tau ,0)$. We initialize the prey–predator system (3) about its interior equilibrium $P_{3}( x^{*},y^{*})$ and we get

$$\begin{aligned} \left. \begin{array}{l} \frac{\mathrm{d}x_{1}( t;p) }{\mathrm{d}t}=a_{11}x_{1}+a_{12}y_{1} \\ \frac{\mathrm{d}y_{1}( t;q) }{\mathrm{d}t}=b_{21}x_{1}( t-\tau ) \end{array} \right\} \quad \text { for }\;\; p\in [ 0,1]\quad \text { and }\quad q\in \left[ 0,1 \right] , \end{aligned}$$

(23)

where $x_{1}( t;p) =x( t;p) +x^{*}$ and $y_{1}( t;q) =y( t;q) +y^{*}$.

Taking Laplace transform of the system (23), we get

$$\begin{aligned}&( s+a_{11}) \overline{x}_{1}( s;p) =a_{12}\overline{y} _{1}( s;q) +x_{1}( 0;p) \nonumber \\&s\overline{y}_{1}( s;q) =b_{21}e^{-s\tau }\overline{x}_{1}( s;p) +b_{21}e^{-s\tau }k_{1}( s) +y_{1}( 0;q), \end{aligned}$$

(24)

where

$$\begin{aligned} k_{1}( s) =\mathop {\displaystyle \int }\limits _{-\tau }^{0}e^{-s\tau }x_{1}( t;p) \mathrm{d}t \end{aligned}$$

and $\overline{x}_{1}( s;p)$ and $\overline{y}_{1}( s;q)$ are the Laplace transform of $x_{1}( t;p)$ and $y_{1}( t;q)$, respectively.

Now, we will use the “Nyquist theorem” which states that if s is the arc length along a curve encircling the right half of the plane, then a curve $\overline{x}_{1}( s;p)$ will encircle the origin a number of times equal to the difference between the number of poles and the number of zeros of $\overline{x}_{1}( s;p)$ in the right half of the plane. From Erbe et al. (1986) and using “Nyquist theorem”, it can be shown that the conditions for local asymptotic stability of $P_{3}( x^{*},y^{*})$ are given by

$$\begin{aligned} \mathrm{Im}H( iw_{0})> & {} 0 \end{aligned}$$

(25)

$$\begin{aligned} \mathrm{Re}H( iw_{0})= & {} 0, \end{aligned}$$

(26)

where $H( s) =s^{2}+a_{1}s+a_{2}e^{-s\tau }$ and $w_{0}$ is the smallest positive root of the Eq. (26).

We have already shown that $P_{3}( x^{*},y^{*})$ is stable in the absence of delay. Hence, by continuity all eigenvalues will continue to have negative real parts for sufficiently small $\tau >0$, provided one can guarantee that no eigenvalue with positive real parts bifurcates from infinity as $\tau$ increases from zero. This can be proved by using Bulter’s lemma (Erbe et al. 1986).

In this case, conditions (25) and (26) give

$$\begin{aligned} a_{1}w_{0}-a_{2}\sin w_{0}\tau> & {} 0 \end{aligned}$$

(27)

$$\begin{aligned} -w_{0}^{2}+a_{2}\cos w_{0}\tau= & {} 0 \end{aligned}$$

(28)

Now, the sufficient conditions to guarantee stability if (27) and ( 28) satisfy simultaneously. We shall utilize them to get an estimate on the length of delay. Our aim was to find an upper bound $w_{+}$ on $w_{0}$, independent of $\tau$ so that (27) holds for all values of w, $0\le w\le w_{+}$ and hence in particular at w $=$ $w_{0}$. We rewrite the Eq. (28) as

$$\begin{aligned}&-w_{0}^{2}+a_{2}\cos w_{0}\tau =0 \nonumber \\&\Rightarrow w_{0}^{2}=a_{2}\cos w_{0}\tau \end{aligned}$$

(29)

Maximizing $a_{2}\cos w_{0}\tau$ subject to $\vert \cos w_{0}\tau \vert \le 1$, we obtain

$$\begin{aligned} w_{0}^{2}\le \vert a_{2}\vert \end{aligned}$$

(30)

Hence, if

$$\begin{aligned} w_{+}=\sqrt{\vert a_{2}\vert }, \end{aligned}$$

(31)

then clearly from (31), we have $w_{0}$ $\le w_{+}$. From the inequality (27) we get

$$\begin{aligned}&a_{1}w_{0}>a_{2}\sin w_{0}\tau \nonumber \\&\Rightarrow a_{1}w_{0}^{2}>a_{2}w_{0}\sin w_{0}\tau \end{aligned}$$

(32)

As $P_{3}( x^{*},y^{*})$ is locally asymptotically stable for $\tau =0$, for sufficiently small $\tau >0$ the Eq. (32) will continue to hold. Substituting (29) into (32) and rearranging, we get

$$\begin{aligned} a_{2}w_{0}\sin w_{0}\tau -a_{1}a_{2}\cos w_{0}\tau <0 \end{aligned}$$

(33)

Using the bounds, we obtain

$$\begin{aligned} a_{2}w_{0}\sin w_{0}\tau \le a_{2}w_{+}^{2}\tau \quad \text { and }\quad a_{1}a_{2}\cos w_{0}\tau \le a_{1}a_{2} \end{aligned}$$

(34)

Now, from (33) and (34) we get

$$\begin{aligned} l_{1}\tau -l_{2}<0, \end{aligned}$$

(35)

where $l_{1}=a_{2}w_{+}^{2}$ and $l_{2}=a_{1}a_{2}$. Hence, if

$$\begin{aligned} \tau _{+}=\frac{l_{2}}{l_{1}}, \end{aligned}$$

(36)

then the stability is preserved for $0\le \tau <\tau _{+}$. Summarizing the above discussions we come to the following result:

Theorem 10

The delayed model (3) will be locally asymptotically stable at $P_{3}( x^{*},y^{*})$ if the delay $\tau$ lies within the interval $( 0,\tau _{+})$ where $\tau _{+}$ is given by (36).

7 Numerical illustrations and biological interpretations

Analytical studies can never be completed without numerical verification of the derived results. Beside verification of our analytical findings, numerical solutions are very important from practical point of view. For this purpose, in this section we demonstrate the analytical results that we establish in the previous sections using numerical simulations instead of real-world data, which of course would be of great interest and has the advantage that it is easy to isolate the effects of the interactions between the different classes. With the real-world data, the prices, costs and technological factors are likely to vary from one epidemic system to other, and it would be harder to assign the causes for different results. However, numerous scenarios covering the breath of the biological feasible parameter space were conducted and the results display the range of dynamical results collected from all the scenarios tested. For the purpose of simulation experiments we mainly use the software MATLAB R2008a and Wolfram Mathematica 8. As the problem is not a case study for a particular species, here some hypothetical data are taken for the sole purpose of illustrating the analytical results of the previous sections. Moreover, it may be noted that as the parameters of the model are not based on real-world observations, the main features described by the simulations presented in this section should be considered from a qualitative, rather than a quantitative point of view. Numeric results of the proposed imprecise delay model are illustrated through proper numerical example in the absence of delay and with delay. For the purpose of simulation we consider the hypothetical values of the parameters such as the following: $[r_{l},r_{u}]=[0.4,0.6]$, $[ d_{l},d_{u}] =[ 0.1,0.3]$, $\alpha =0.9$, $\beta =0.9$, $k=200$, $q_{1}=0.2$, $q_{2}=0.1$ and $m=12.3794$ in appropriate units. We study numerically the basic dynamics between prey–predator (Krill–Whale) interaction responses by discrete time delay due to gestation of predators under interval environment. We observe the effects of variation of the parameters p and q on the parametric prey–predator delay model (3). In order to study the effects of parameters p and q on the parametric prey–predator delay model (3), we run simulations separately in two different cases ($\tau =0$ and $\tau \ne 0$) using the standard matlab differential integrator.

7.1 Simulation of the proposed model in the absence of time delay

For the above values of the biological parameters it is found that the non trivial equilibrium point exists and globally asymptotically stable if the harvesting efforts of two species ($E_{1}$and $E_{2}$) lie in the specified interval (see Theorem 6) for different choices of the two distinct parameters p and q. If we take the harvesting effort outside the interval, the predator–prey system becomes unstable.

The interval of the harvesting effort $E_{2}$ for different values of the parameter are given in Table 1 in which the non trivial equilibrium point exists and is globally asymptotically stable.

Table 1 Interval of the harvesting effort of predator species ($E_{2}$) for different p and q

Now depending on the values of $E_{2}$ (here we consider $E_{2}=4$ which belongs to the respective interval for different combinations of the parameter) the interval of $E_{1}$ where the non trivial equilibrium point globally asymptotically stable is given in Table 2.

Table 2 Interval of the harvesting effort of prey species ($E_{1}$) for different p and q

It is clearly observed from Tables 1 and 2 that when functional parameters p and $\ q$ increase through zero, the intervals of the harvesting efforts are changing and hence the stability of model at the interior equilibrium point $( x^{*},y^{*})$ changes from being stable to unstable or vice versa. The stable (taking harvesting effort within the specified interval) equilibrium points for different values of the parameter p and q are given in Table 3.

Table 3 Equilibrium point when harvesting efforts lies within specified intervals for different p and q

From Table 3 we observe that whatever be the values of the parameters p and q if the harvesting efforts of two species lie within the specified intervals, then the system has a unique positive equilibrium point which is globally asymptotically stable or converges to a unique globally stable limit cycle. Again, in reality to increase the profit the fishermen will harvest both the species. Also, harvesting of predator species is very costly and sometimes difficult. However, in the case of prey species fishermen will not get that much profit when compared to predators. However, some fishermen concentrate their attention to harvest the prey species, since prey fishes (like Goldband small fishes) play a vital role for curing eye related diseases.Therefore, we take the harvesting effort of the predator species within the specified interval ($E_{2}=4$) and taking the harvesting efforts of the prey species outside the specified intervals of the harvesting of the prey species ($E_{1}$) for different values of the functional parameters p and q. In that case we see that the system becomes unstable. The unstable nature of the equilibrium point is found for different values of the parameters p and q if we take the harvesting effort of the prey species outside the specified interval. The specified interval for the harvesting effort of the prey species for different values of parameters p and q is given in Table 4.

Table 4 Equilibrium point when harvesting efforts of prey lies outside the specified intervals for different p and q

The variation of population against time depending on the above result, as shown in Tables 1 and 2, is clearly shown in Figs. 1, 2 and 3 with $x( 0) =1$ and $y( 0) =5$ for different p and q.

Fig. 1

Time evolution of species when harvesting efforts lie within and outside the specified interval for $p=0$, $q=1$ and $p=0.2$, $q=0.8$

Fig. 2

Time evolution of species when harvesting efforts lie within and outside the specified interval for $p=0.4,$ $q=0.6$ and $p=0.6$, $q=0.4$

Fig. 3

Time evolution of species when harvesting efforts lie within and outside the specified interval for $p=0.8,$ $q=0.2$ and $p=0$, $q=1$

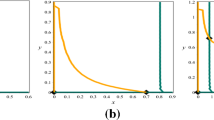
Also the phase plane trajectories of the system biomass beginning with different initial levels when the harvesting efforts of prey and predator species lies within and outside the specified interval with different values of the functional parameter are depicted through Figs. 4, 5 and 6. Here, different colour shows different initial levels.

Fig. 4

Phase trajectories of biomass for $p=0,$ $q=1$ and $p=0.2$, $q=0.8$

Fig. 5

Phase trajectories of prey–predator biomass for $p=0.4,$ $q=0.6$ and $p=0.6$, $q=0.4$

Fig. 6

Phase trajectories of prey–predator biomass for $p=0.8,$ $q=0.2$ and $p=0$, $q=1$

From Tables 1 and 2 we observe that the interval of the harvesting efforts and the level of both the populations at the equilibrium stage changes depending upon the values of the parameters p and q.

Figures 1, 2, 3, 4, 5 and 6 show the consistency with the result obtained in Table 4. Therefore, in the absence of delay, the dynamical behaviour of the model has great impact due to imprecise nature of some biological parameters of the model. Therefore, the imprecise modelling is more realistic than the precise one.

7.2 Simulation of the proposed model in the presence of time delay

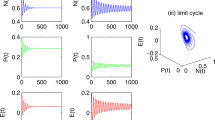
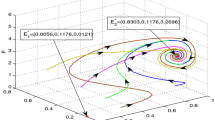
It is mentioned before that the stability criteria in the absence of delay ($\tau =0$) will not necessarily guarantee the stability of the system in the presence of delay ($\tau \ne 0$). Let us choose the parameters of the system same as previous section. It is already seen in Table 3 that for such choices of parameters (taking the harvesting efforts within the specified interval) the obtained equilibrium $( x^{*},y^{*})$ for different values of the parameters p and q is locally asymptotically stable in the absence of delay. Now for these choices of parameters and depending on the values of p and q it is seen from Lemma 4 and Theorem 8 that there is a unique positive root $( w_{+})$ of the Eq. (20) and critical value of $\tau =\tau _{0}$ from Eq. (21) which is given in Table 5. Here, $x( 0) =1$ and $y( 0) =5,$ for a particular value of p and q, if the value of $\tau$ is below the critical value $\tau _{0}$, then Figs. 7, 8 and 9 show that the nontrivial equilibrium point $( x^{*},y^{*})$ is asymptotically stable and both prey and predator species converge to their steady states in finite time and the xy-plane projections of the solution (presented in Fig. 10) being stable spiral. Keeping other parameters fixed, if we take $\tau >\tau _{0}$ for all values of p and q in each case (presented in Figs. 7, 8, 9) for $x( 0) =1$ and $y( 0) =5,$ it is seen that $( x^{*},y^{*})$ is unstable which is the case of Hopf-bifurcation and there is a bifurcating periodic solution near $( x^{*},y^{*})$ (see Fig. 11).

Table 5 Values of $w_{+}$ and critical values of time delay ($\tau _{0}$) for different p and q

Fig. 7

Populations approach their equilibrium values in finite t if $\tau <\tau _{0}$ and become unstable if $\tau >\tau _{0}$ for $p=0,$ $q=1$ and $p=0.2$, $q=0.8$

Fig. 8

Populations approach their equilibrium values in finite t if $\tau <\tau _{0}$ and become unstable if $\tau >\tau _{0}$ for $p=0.4,$ $q=0.6$ and $p=0.6$, $q=0.4$

Fig. 9

Populations approach their equilibrium values in finite t if $\tau <\tau _{0}$ and become unstable if $\tau >\tau _{0}$ for $p=0.8,$ $q=0.2$ and $p=0$, $q=1$

Fig. 10

Phase portrait of system 3 showing that $( x^{*},y^{*})$ is locally asymptotically stable when $\tau$ $<\tau _{0}$

Fig. 11

Phase portrait of the system 3 showing a limit cycle which grows out of $( x^{*},y^{*})$ when $\tau$ $>\tau _{0}$

Again if we increase delay $\tau$ from its threshold value for different p and q ($\in [ 0,1]$) then we get the presentation of the dynamical behaviour of the model through Figs. 12, 13 and 14.

Fig. 12

Unstable solution of growing oscillation of imprecise delayed system as $\tau$ increases from the threshold value $\tau _{0}$ for $p=0$, $q=1$

Fig. 13

Unstable solution of growing oscillation of imprecise delayed system as $\tau$ increases from the threshold value $\tau _{0}$ for $p=0.6$, $q=0.4$

Fig. 14

Unstable solution of growing oscillation of imprecise delayed system as $\tau$ increases from the threshold value $\tau _{0}$ for $p=1$, $q=0$

8 Discussion and conclusion

It is a well-known fact that the oceans and their living resources are in alarming condition. Significant numbers of marine organisms, including mammals, birds and turtles as well as some commercially harvested fish and shellfish are now threatened or endangered. Clearly mathematical approaches are considered to stem the damage and ensure that ecosystems and their unique features are protected and restored. To construct the mathematical model, researchers or mathematicians consider some parameters on the basis of their requirement. But the sensitive parameters of the model system fluctuate above their average values due to random fluctuations of nature. Mathematics has so far made a considerable impact to model and understand complicated interaction. Most of the research work in this area have focused on predator–prey models in precise environment. A little attention has been paid on the models with imprecise environment. To tackle imprecise parameters most of the researchers have opted fuzzy approach, stochastic approach and fuzzy stochastic approach. But all the mentioned approaches pose little bit difficulties which we have already discussed in the Introduction section. In this paper, we study the complex dynamics of a prey–predator system with discrete time delay due to gestation under imprecise biological parameters. We analyse the dynamical behaviour of an imprecise prey–predator model system incorporating a discrete time delay as bifurcation mechanism using parametric functional form of the interval number with two distinct parameters. Boundedness of the system in the presence and absence of the time delay is discussed. Stability analysis of the trivial, axial and nontrivial equilibrium is presented with different values of parameters p and q. The criterion for stable coexistence of the prey and predator in the absence of delay due to imprecise biological parameters is given in Theorem 6. The theoretical results are illustrated numerically in Sect. 5.1 and strongly supported by Figs. 1, 2, 3, 4, 5 and 6. Here it is established that when time delay is zero then the interior equilibrium $P_{3}( x^{*},y^{*})$ is asymptotically stable, provided the harvesting effort of both the species must lie in the certain interval depending on the values of the parameters p and q.

Again it is mentioned by several researchers that the effect of time delay is an important factor to construct a biological useful mathematical model. Here, to make the model more sensible and acceptable, we consider the time delay as well as the imprecise biological parameters as interval number to construct model 2. Here, we consider the time delay due to gestation period for predators. In general, delay differential equations exhibit much more complicated dynamics than the ordinary differential equation and due to inserting the imprecise parameters, the model becomes more complicated. But we suitably handled the delay differential equation by unique approach, known as functional parametric approach with two different parameters for two different intervals. We know that a time delay could cause a locally stable equilibrium to become unstable and cause the populations to fluctuate. We formulate the model 2 where the delay may be looked upon as gestation time for predators. Then a rigorous analysis in interval environment leads us to Theorem 8 which mentions that the stability criteria in absence of delay are no longer enough to guarantee the stability in the presence of delay, rather than there is a critical value $\tau _{0}^{+}$ of the delay $\tau$ (depending on the values of the parameters p and q) the system is locally stable for $\tau <\tau _{0}^{+}$ and unstable when $\tau$ just exceeds $\tau _{0}^{+}$ which is shown numerically in Sect. 7.2 and strongly supported by Figs. 7, 8, 9, 10 and 11. Thus using the time delay and functional parameters p and q as control, it is possible to break the stable behaviour of the system and derive unstable state. Also it is possible to keep the populations at a desired level using the above-stated control. Such regulatory impact of delay is also illustrated elaborately through computer simulation in Sect. 5.2.

It is well known that natural populations of plants and animals neither increase indefinitely to blanket the world nor become extinct except in some rare cases due to some rare reasons. Hence in practice, we often want to reduce the predator to an acceptable level in finite time. In order to accomplish this, we strongly suggest that in realistic field situations (where effect of time delays can never be violated) the biological parameters of the system should be regulated in such a way that they are imprecise in nature and $0<\tau <\tau _{0}^{+}$.

We have not made any case studies, but a good example of our presented imprecise model is Antartic Krill–Whale fishery. The ultimate objective is to maintain the ecological balance between prey and predator. It is deemed important to undertake this type of imprecise model for the purpose of investing the impact of imprecise biological parameters, harvesting efforts on the species as well as time delay so that sustainability of the ecosystem may be resumed through achieving the commercial purpose of the fishery. Hence, the results of our new proposed model are not only useful for assessing the biological, social and economic impact of existing resources but also provide appropriate measures to maintain long-term sustainability of the resource.

From the analysis of the proposed model, it may be concluded that the interval model has high movement probabilities to explain easily the different characteristic of the model than the other imprecise one. An imprecise prey–predator interval model with parametric functional form is generally utilised to investigate the critical dynamical behaviour of the model for different values of the functional parameter. Therefore, the functional parameters play an important role to incorporate impreciseness to the model parameters. Thus for a sustainable ecosystem, interval model of population is an important modelling approach which ensures the presence of random fluctuation of the modelling parameters. The delay model can be made more realistic when incorporated with impreciseness in the delay term it makes the model more complicated and is left for future work consideration.