Introduction

Pests and diseases are integral components of natural environment. For a sustainable system there should be a balance between predators and pests. The pests are harmful to agriculture as they affect the crop yields by means of feeding on crop or parasitizing livestock. One must need to take care of controlling any harm that will come along the way such as the infestation of pests. It is very difficult to control the damage of crop if the pest or disease starts attacking the crop at large scale. Sometimes it is also observed that, pests (prey) are affected by some disease [5, 17]. In such cases, disease induced pests are more exposed to predator and such viral infection is used in pest control management to reduce the level of pests. But, this may be harmful to the natural predator and may destroy the biological balance of natural system.

There are several methods that are applied to control the pest populations, viz. use of sterile adults, plant resistance, use of pheromones, and other chemicals. For example, integrated pest management (IPM) is a popular pest control method among farmers, researchers and policy makers [42]. In IPM, several methods are integrated for pest control. In general, IPM minimizes the reliance on pesticides by putting emphasize on the contribution of other control methods, that include biological control, host-plant resistance breeding, cultural techniques, etc. Among them the use of viruses, fungi and bacteria are the most effective biological methods for controlling pests [5]. In biological control, living organisms are used to control pest. These living organisms are called natural enemies. Apart from birds, mammals and reptiles, the most important group of natural enemies are insects that feed on other insects. Of all methods, chemical pesticides are used widely, because they can quickly eradicate a considerable fraction of a pest population. However, chemical pesticides are recognized as major health problems to human beings and several beneficial insects. In addition, overuse of chemical pesticides not only develop resistance of the pest population but also increase the agricultural cost tremendously [26]. It is important to recognize that the sole purpose of biological control is not to eradicate the pest population completely, but to maintain them at levels where they cause no substantial harm. In fact, a successful biological control can be guaranteed, if a small population of pests are always available for the sustainability of natural enemies. The main objective of our study is to examine the basic dynamical behavior of the system consisting of a susceptible pest exhibiting Allee effect, infected pest and their predators.

The Allee effect, named after ecologist W. C. Allee is an important biological concept, corresponds to density mediated drop in population fitness when they are small in numbers [1, 39, 40]. A species exhibits an Allee effect when certain component of individual fitness (e.g. litter size, juvenile survival, adult mortality etc.) is reduced with decrease in population size (mainly due to difficulty in finding mates), known as component Allee effect [39]. When two or more component Allee act together and result in lowering the overall mean individual fitness, is known as demographic Allee effect [39, 12]. Sometime demographic Allee effect may become so severe that below a threshold population size growth rate is negative that eventually lead to extinction of species. This is known as strong Allee effect and the threshold population size is known as Allee threshold. In the other hand a demographic Allee effect without this Allee threshold is known as weak Allee effect. Empirical evidence of the Allee effect has been reported in many natural populations including plants [15, 18], insects [28], marine invertebrates [41], birds and mammals [13]. Without going into meticulous details of the Allee effects we suggest the reader to see the review [12] and other references therein.

The evidence of Allee effect was first demonstrated in the confused flour beetle (Tribolium confusum, a type of darkling beetle). Practical applications of the mate-finding Allee effect in pest control programs include pheromone-baited traps and the sterile insect technique (e.g. [27, 32, 20]). Additional impose of component Allee effect might be efficient to control the pest species that also suffers from mating failure. Boukal and Berec [6] discussed the impact of two commonly considered strategies in biological control, viz. culling based on constant effort and inundative release of pheromones. They also discussed the usefulness of component Allee effect in combination with mate limitation, giving rise to multiple Allee effect viz., release of generalist enemies that attack pest with type II functional response [16] and mass release of sterile individuals [43]. Then combination of two strategies were analyzed to demonstrate the effect of triple Allee effect. Using single population model of pest they predicted that, if males, females or both sexes are driven below a threshold density, a complete eradication of pest can be achieved.

In this investigation we propose and analyze an eco-epidemiological model with weak Allee effect on susceptible pest. We use Rosenzweig and Mac-Arthur modeling formulation which integrates logistic self-limitation, and nonlinearity in the density or consumption relationship. The use of functional response is a debatable issue. We use three types of Holling functional responses with an aim to find a suitable functional which can adequately represent disease eradication. We shall discuss the following biological control strategies in the light of mathematical modeling: (1) Control of pest by releasing natural predator with an appropriate functional response; (2) Control of pest population by using viral infection; (3) Conservation of natural predators while adopting an optimal pest control strategies; (4) How the Allee effects in pest population change the system dynamics in pest control. The rest of the paper is organized as follows: Development of mathematical model is elaborated in “Development of the Model” section. In “Linear mass-action functional response”, “Hyperbolic Functional Response”, Sigmoidal Functional Response” sections stability analysis of the model systems are presented considering linear mass-action law, hyperbolic and sigmoidal respectively as predator functional response. Numerical simulations with discussion is presented in the “Numerical Simulation” section. The paper ends with a conclusion.

Development of the Model

In this section we will discuss the development of eco-epidemiological model with Allee effect in pest. We start with the assumptions that in the natural predator–pest interaction, the pest population is facing a viral disease that can be captured with an SI (Susceptible-Infected) framework.

SI Epidemic Model

A typical SI model with an open system of variable size can be written as follows:

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}S}{\mathrm{d}t}=&S\varPhi (S) - \varPsi (S,I),\\ \frac{\mathrm{d}I}{\mathrm{d}t} =&\,\, \varPsi (S,I) - \mu I, \end{aligned} \end{aligned}$$
(1)

where S and I are the densities of susceptible pest and infected pest population respectively, \(\varPhi (S)\) is the per capita growth function of the susceptible pest population, \(\varPsi (S,I)\) is the incidence function of the disease i.e. the rate at which infections occur and \(\mu \) is the sum of death rate due to disease and the natural death. It is assumed that all susceptible and infected pest populations are equally susceptible and infectious respectively. It is also assumed that the disease transmission follows the simple law of mass action, i.e. \(\varPsi (S,I) = \lambda SI\), where \(\lambda \) is the rate of infection per susceptible and per infective.

Predator–Pest Model with Mate-Finding Allee Effect on Pest

A natural predator–pest model with mate-finding Allee effect on pest in its classical form is represented by

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}N}{\mathrm{d}t}=&Nf(N)A(N) - Ph(N), \\ \frac{\mathrm{d}P}{\mathrm{d}t}=&\,\,\theta Ph(N) - \delta P, \end{aligned} \end{aligned}$$
(2)

where N and P are, respectively, the densities of pest and predator population. \(f(N)\) is the per capita growth rate of pest in the absence of predation which we assume logistic with intrinsic growth rate r and carrying capacity K so that \(f(N) = r\left( 1-\frac{N}{K}\right) \). Here \(h(N)\) is the functional response and the term \(\theta h(N)\) is the numerical response of the predator, \(\theta \) being the conversion efficiency and \(\delta \) is the predator mortality, which is assumed to be constant. \(A(N)\) is the positive density dependent factor i.e. the Allee function. \(A(N)\) is considered as the probability that a female finds and mates with at least one male during the reproductive period [8] and satisfy the following conditions:

  • No mating occurs at zero population size, \(A(0) = 0\).

  • \(A'(N)>0\) i.e. the population size increases the probability that, a female will find a mate increases.

  • Mating is guaranteed when the population is large, that is \(A(N) \rightarrow 1\) and \(N\rightarrow +\infty \).

Now we are in a position to formulate the basic eco-epidemiological model combining the \(SI\) epidemic model (1) and the Predator–pest model (2) with mate-finding Allee effect on pest.

Eco-epidemiological Model with the Allee Effect on Pest

The following assumptions are made in formulating the basic eco-epidemiological model:

  • In the absence of infection and predation, the pest population grows logistically. In the presence of infection, the pest population are divided into two disjoint classes, namely, susceptible S and infected I. Therefore at any time t, the total number of pest population is \(N(t) = S(t) + I(t)\).

  • It is assumed that only susceptible pest population, S, are capable of reproducing with logistic law and the infective pest population dies out before having the capability of reproducing individuals. However, the infective population, still contributes with S to population growth towards the carrying capacity.

  • The disease transmission is captured by the law of mass-action [9, 10]. The disease is spread among the pest population only and the disease is not genetically inherited. The infected population do not recover or become immune.

  • It is assumed that predator cannot distinguish the infected and healthy pest, they consume both the susceptible and infected pest at the rates \(h(S)\) and \(g(I)\), respectively. Consumption of infected pest will contribute negative growth in the predator population [11, 4], whereas feeding on susceptible pest enhances the growth rate of predator population.

  • The predation term for infected pest follows a linear mass-action functional response [19] because infected pest are weakened and easier to catch [33, 34, 23, 22], for simplicity we assume \(g(I) = \beta I\), \(\beta \) is the attack rate on infected pest. In particular, we assume the predator response function, \(h(S)\), for susceptible pest as linear, hyperbolic and sigmoid. Although \(S\) and \(I\) are indistinguishable, the choice of functional response differs from the fact that, infected prey are easier to catch.

  • We incorporate the Allee effect \(A(S)\) = \(\frac{S}{w+S}\) on susceptible pest population only due to limitations in finding mates (which is known as weak Allee effect function). This function \(A(S)\), be the probability of finding a mate where \(w\) is the individuals searching efficiency [14, 36, 36]. The bigger \(w\) is the stronger Allee effect and as a result the per capita growth rate of the susceptible pest is reduced from

    $$\begin{aligned} rS\left( 1-\frac{S}{K}\right) \quad \mathrm{to} \quad rS\left( 1-\frac{S}{K}\right) \frac{S}{w + S}, \end{aligned}$$

    especially when \(S\) is small.

  • \(I\)-class does not contribute to the reproduction of newborns but they are compete for resource with susceptible pest. Then in the presence of infected pest and absence of predator susceptible pest dynamics can be described by the following equation

    $$\begin{aligned} \frac{dS}{dt} = rS\left( 1-\frac{S+I}{K}\right) \frac{S}{w+S}. \end{aligned}$$
Table 1 Variables and parameters used in the models of susceptible pest-infected pest-predator population interaction
Full size table

Based on the above assumptions we have the following equations as our eco-epidemiological model with weak Allee effect on susceptible pest:

$$\begin{aligned} \frac{\mathrm{d}S}{\mathrm{d}t}= & {} rS \left( 1- \frac{S+I}{K}\right) \frac{S}{w+S} - \lambda SI - h(S)P, \nonumber \\ \frac{\mathrm{d}I}{\mathrm{d}t}= & {} \lambda SI - \beta IP - \mu I, \\ \frac{\mathrm{d}P}{\mathrm{d}t}= & {} \theta \left( h(S) - \beta I \right) P - \delta P.\nonumber \end{aligned}$$
(3)

System (3) has to be analyzed with the initial conditions \(S(0) > 0\), \(I(0) > 0\), \(P(0) > 0\), and with three different functional forms of \(h(S)\) viz. linear, hyperbolic and sigmoid. The biological significance of the parameters used in this model is provided in Table 1.

Note:

  1. 1.

    The carrying capacity is shared by both infective and susceptible individuals. Infective competes for resources but does not contribute to reproduction.

  2. 2.

    Infected pest population dies out before having the capability of reproducing new offsprings. So they are not susceptible to the Allee effect due to mate finding limitation.

The right-hand side of Eq. (3) are smooth functions of the variables \(S\), \(I\), \(P\) and parameters, as long as these quantities are nonnegative, so local existence, uniqueness and continuation properties hold in the positive octant for some time interval \((0, t_{f})\). In the next theorem we show that the linear combination of susceptible pest, infected pest and predator population is less than a finite quantity, the solution of system (3) is bounded.

Theorem 1

The solution \(y(t)\) of (3), where \(y = (S, I, P)\), is uniformly bounded for \(y_{0} \in \mathbb R^{3}_{0,+}\).

Stability Analysis of Model (3) with Different Functional Responses

In this section we will discuss the stability of model (3) with different functional responses. In the next subsection we first consider the commonly used linear mass-action functional response.

Linear Mass-Action Functional Response

We first consider the equilibria of system (3), and discuss their local stability properties in terms of linearization of system (3) near each equilibrium. Next, we consider global asymptotic properties for the solutions of system. For mass-action response function, system (3) takes the following form:

$$\begin{aligned} \frac{\mathrm{d}S}{\mathrm{d}t}= & {} rS\left( 1-\frac{S+I}{K}\right) \frac{S}{w+S} - \lambda SI - \alpha SP, \nonumber \\ \frac{\mathrm{d}I}{\mathrm{d}t}= & {} \lambda SI - \beta IP - \mu I, \\ \frac{\mathrm{d}P}{\mathrm{d}t}= & {} \theta \left( \alpha S - \beta I \right) P - \delta P \nonumber . \end{aligned}$$
(4)

Applying the transformations \(s = \frac{S}{K}\), \(i = \frac{I}{K}\), \(p = \frac{P}{K}\), \(\tau = \lambda Kt\) we have the following dimensionless form of the model equation (4). Now, we will replace \(\tau \) by \(t\) for notational convenience.

$$\begin{aligned} \frac{\mathrm{d}s}{\mathrm{d}t}= & {} bs(1-(s+i))\frac{s}{v+s} - si - m_{1}sp, \nonumber \\ \frac{\mathrm{d}i}{\mathrm{d}t}= & {} si - dip - ei, \\ \frac{\mathrm{d}p}{\mathrm{d}t}= & {} \theta \left( m_{1}s - d i \right) p - gp \nonumber . \end{aligned}$$
(5)

where \(b = \frac{r}{\lambda K}\), \(m_{1} = \frac{\alpha }{\lambda }\), \(d = \frac{\beta }{\lambda }\), \(e = \frac{\mu }{\lambda K}\), \(g = \frac{\delta }{\lambda K}\) and \(v = \frac{w}{K}\).

Equilibria and Local Stability

The model equations of system (5) has the following equilibria: (a) trivial equilibria \(E^{I}_{0} = (0,0,0)\), (b) infection and predator free axial equilibrium \(E^{I}_{1} = (1,0,0)\), (c) predator-free planner equilibrium

$$\begin{aligned} E^{I}_{2} = \left( e, \frac{be(1-e)}{v+e+be}, 0 \right) , \end{aligned}$$

(d) infection-free planner equilibrium

$$\begin{aligned} E^{I}_{3} = \left( \frac{g}{\theta m_{1}}, 0, \frac{bg(\theta m_{1}-g)}{\theta m_{1}^2(v\theta m_{1} +g)}\right) \end{aligned}$$

and (e) interior equilibrium \(E^{I}_{*} = (s^{*}, i^{*}, p^{*})\), where, \(s^{*}\) is the unique positive root of the quadratic equation \(As^{*2} + Bs^* + C = 0\) and

$$\begin{aligned} i^{*} = \frac{\theta m_{1} s^{*} - g}{\theta d},~~~~ p^{*} = \frac{s^{*} - e}{d} \quad \mathrm{and} \quad s^{*} + i^{*} \le 1. \end{aligned}$$
(6)

with

$$\begin{aligned} A = \theta (bd + bm_{1} + 2m_{1}) (> 0), \quad B = \theta \left( 2v-e\right) \left( m_1-T\right) , \quad C = -v(m_{1}\theta e +g) (< 0), \end{aligned}$$

and

$$\begin{aligned} T =\frac{bd\theta + g(1-b)}{\theta (2v-e)}. \end{aligned}$$

The unique interior equilibrium exists if \(s^*>\max \left\{ e,\frac{g}{\theta m_1}\right\} \), which is always unstable (see Table 2 and Theorem (6).

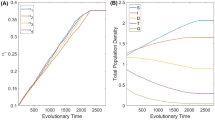
Note: The last condition of (6) is due to the fact that at any time point \(t\), sum of susceptible and infected pest population can not exceed the environmental carrying capacity. It has been emphasized in the model formulation that both the populations compete for same resource determined by the carrying capacity. It is interesting to note that due to Allee effect in susceptible pest population, there is a reduction in the equilibrium population sizes in both the infectives and the predators as compared to the case when there is no Allee effect in susceptible pest (see Fig. 1).

The equilibria \(E^{I}_{0}\) and \(E^{I}_{1}\) exist for all parameter values. \(E^{I}_{2}\) exists if \(e < 1\). \(E^{I}_{3}\) exists if \(m_{1} > \frac{g}{\theta }\). The interior equilibrium \(E^{I}_{*}\) exists if

$$\begin{aligned} e < 1, \quad m_{1} > \frac{g}{\theta } \quad \mathrm{and} \quad \max \left( e, \frac{g}{m_{1}\theta } \right) < s^{*} < \frac{g+d\theta }{\theta (m_{1}+d)}. \end{aligned}$$
Fig. 1
figure 1

a Describes the density of susceptible pest with respect to Allee effect, for \(\alpha =0.002\) and \(\lambda =0.005\). b Describes the density of infected pest with respect to Allee effect, for \(\alpha =0.004\) and \(\lambda =0.01\). c Describe the density of predator with respect to Allee effect, for \(\alpha =0.008\) and \(\lambda =0.005\). All the other parameter values are defined in Table (1)

Full size image

Observe that \(E^{I}_{2}\) arises from \(E^{I}_{1}\) for \(e = 1\) and persists for all \(e < 1\), whereas \(E^{I}_{3}\) arises from \(E^{I}_{1}\) for \(m_{1} = \frac{g}{\theta }\) and persists for all \(m_{1} > \frac{g}{\theta }\). If \(e = 1\) and \(m_{1} = \frac{g}{\theta }\), then \(E^{I}_{2}\) and \(E^{I}_{3}\) will approach \(E^{I}_{1}\). This means eventual eradication of infected pest population and predator population. The variational matrix for the system (5) about any arbitrary equilibrium point \((s^*, i^*, p^*)\) is given by

$$\begin{aligned} \left[ \begin{array}{ccc} \displaystyle \frac{vbs^*(2-3s^*-2i^*)\,+\,bs^{*2}(1-2s^*-i^*)}{(v+s^*)^2} - i^* - m_{1}p^* &{}\displaystyle -\frac{bs^{*2}}{v\,+\,s^*} - s^* &{} -m_{1}s^* \\ \displaystyle i^* &{} s^*-\mathrm{d}p^*-e &{} -\mathrm{d}i^* \\ \displaystyle m_{1}\theta p^* &{} -\mathrm{d}\theta p^* &{} -\mathrm{d}\theta i^* -g + m_{1}\theta s^* \end{array} \right] . \end{aligned}$$

We now state and prove the following theorems:

Theorem 2

Trivial equilibrium point \(E^{I}_{0}\) is a saddle-node equilibrium with two stable eigenvalues, of the system (5) for all parametric values.

Proof

From the variational matrix of the system (5), it is easy to verify that the system has three eigenvalues \(\xi ^I_{1,0} = 0\), \(\xi ^I_{2,0} = -e\) and \(\xi ^I_{3,0} = -g\) for the trivial equilibrium point \(E^{I}_{0}\). Eigenvectors corresponding to these three eigenvalues are (1,0,0), (0,1,0) and (0,0,1) respectively. So there is a one-dimensional central manifold tangent to the eigenvector (1,0,0) and the ip-plane is the stable manifold of the system for \(E_{0}\). Theoretically the stable set \(W^s(E_0)\) is the half-space \(\left\{ S \le 0 \right\} \), within which the majority of the orbits tend to the equilibrium tangent to the s-axis, but \(S\) can not be negative. So the stable set is \(\left\{ (0,I,P) : I,P \ge 0\right\} \) and the unstable set \(W^u(E_0)\) is the half-space \(\left\{ S > 0\right\} \). Therefore \(E_{0}\) is a saddle-node equilibrium point (see [29]) with two stable eigenvalues. \(\square \)

Theorem 3

System (5) is locally asymptotically stable around \(E^{I}_{1}\) if \(e > 1\) and \(m_{1} < \frac{g}{\theta }\).

Proof

The characteristic roots corresponding to \(E^{I}_{1}\) are given by \(\xi ^{I}_{1,1} = - \frac{b}{v+1}\), \(\xi ^{I}_{2,1} = 1- e\) and \(\xi ^{I}_{3,1} = m_{1} \theta - g\). Thus \(E^{I}_{1}\) is stable if \(e > 1\) and \(m_{1} < \frac{g}{\theta }\). Here stability conditions of \(E^{I}_{1}\) eliminate the existence of \(E^{I}_{2}\), \(E^{I}_{3}\), \(E^{I}_{*}\). In this case, all solutions initiating on the \(ip\)-plane approach \(E_0^I\) and all other solutions with initial values \(\mathbb {R}^3_{0,+}\)-\(ip\)-plane will approach \(E^I_1\) as we have \(\frac{\mathrm{d}i}{\mathrm{d}t}<0\) and \(\frac{dp}{dt}<0\), whenever conditions of Theorem (3) hold. \(\square \)

Observation 1 (a) System without infected pest: The relation \(e>1\) implies \(\lambda K < \mu \) i.e. the maximum renewal rate of infected pest is less than their natural mortality rate, then the infection can not spread and eventually infected pest will die out.

(b) System without predator: The relation \(m_1 < \frac{g}{\theta }\) implies \(\left( \theta \alpha \right) K < \delta \) i.e. the maximum renewal rate of predator by consuming the susceptible pest is less than their natural mortality rate, hence the predator population will die out. Thus in this case neither infection nor predator persist, only susceptible pest settles down at their own carrying capacity (see Fig. 2a).

Fig. 2
figure 2

a–d depict the time series solution of the model equation (4), with initial values [30,10,15], [15,20,10] and [10,5,5] for the parameters as in table (1). a Disease and predation free boundary equilibrium \(E^I_1\) is locally asymptotically stable for \(\alpha =0.004\) and \(\lambda =0.003\). b Predation free planner equilibrium \(E^I_2\) is locally asymptotically stable for \(\alpha =0.005\) and \(\lambda =0.015\). c Infection free planner equilibrium \(E^I_3\) (at low infection rate) is locally asymptotically stable for \(\alpha =0.007\) and \(\lambda =0.003\). d Infection free planner equilibrium \(E^I_3\) (at high infection rate) is locally asymptotically stable for \(\alpha =0.009\) and \(\lambda =0.008\)

Full size image
Table 2 Interior equilibrium and local stability for system (5)
Full size table

Theorem 4

System (5) is locally asymptotically stable around \(E^{I}_{2}\) if

$$\begin{aligned} m_{1} < \frac{1}{\theta e} \left[ g + \frac{bd\theta e(1-e)}{v+e+be}\right] , \end{aligned}$$

\(e < 1\) and \(e^3(1+b) > v(v+e-2ve-3e^2-be^2)\).

Proof

Observe that when \(\xi ^{I}_{2,1} > 0\) (i.e. \(e < 1\)) and \(\xi ^{I}_{3,1} < 0\) (i.e. \(m_{1} < \frac{g}{\theta }\)), then system (5) admits \(E^{I}_{0}\), \(E^{I}_{1}\) and \(E^{I}_{2}\) as its equilibrium points. Clearly, \(E^{I}_{0}\) is always unstable and \(E^{I}_{1}\) is unstable with sp-plane and i-axis as its stable and unstable manifolds respectively.

From the variational matrix corresponding to \(E^{I}_{2}\) one can observe that the eigenvalue in the p-direction is given by

$$\begin{aligned} \xi ^{I}_{3,2} = m_{1}\theta e - g - \frac{bd\theta e(1-e)}{v+e+be}, \end{aligned}$$

which is negative if

$$\begin{aligned} m_{1} < \frac{1}{\theta e} \left[ g + \frac{bd\theta e(1-e)}{v+e+be} \right] . \end{aligned}$$

Other two eigenvalues are the roots of the quadratic equation

$$\begin{aligned} \xi ^2 + \left[ \frac{be^4(1+b) - vbe \left( v+e-2ve-3e^2-be^2 \right) }{\left( v+e+be \right) \left( v+e \right) ^2} \right] \xi + \frac{be^2\left( 1-e\right) }{v+e} = 0. \end{aligned}$$

Obviously, both the roots of this quadratic equation are real negative or complex conjugate with negative real parts if \(e^3(1+b) > v(v+e-2ve-3e^2-be^2)\). Hence \(E^{I}_{2}\) is locally asymptotically stable if

$$\begin{aligned} m_{1} < \frac{1}{\theta e} \left[ g + \frac{bd\theta e(1-e)}{v+e+be} \right] , \quad e < 1 \end{aligned}$$

and \(e^3(1+b) > v(v+e-2ve-3e^2-be^2)\) hold.

Note that when \(E^{I}_{1}\) becomes unstable with i-axis as its unstable manifold and sp-plane as its stable manifold, then still \(\xi ^{I}_{3,2} < 0\), \(E^{I}_{2}\) becomes locally asymptotically stable if conditions of Theorem (4) are satisfied. Since \(\xi ^{I}_{3,1} < 0\) (i.e. \(m_{1} < \frac{g}{\theta }\)) implies \(\frac{\mathrm{d}p}{\mathrm{d}t} < 0\), from the third equation of (5), hence all solutions initiating in the interior of the positive octant will approach si-plane. \(\square \)

Observation 2 (a) Requirement for better yield: The relation \(e<1\) implies \(\lambda K > \mu \) i.e. the maximum renewal rate of infected pest is greater than their natural mortality, hence infection persists in the pest population. In this case predation rate to susceptible pest is not so high that directs the predator population to die out. Hence, the system goes to the stable state where susceptible pest and infected pest coexist as a stable equilibrium (see Fig. 2b). To obtain better yield it is required to reduce the equilibrium size of the pest. For low values of Allee parameter, equilibrium value of the infected pest increases and at the same time equilibrium value of the susceptible pest decreases (by virtue of the relation \(s^*+i^* \le 1\)) assuring better yield (Fig. 3). But this sort of control mechanism has a problem. In such case, as the predator consumes infected pest, it enhance risk of extinction of natural predator. This is elaborately discussed in next theorem with a mechanism to overcome this problem.

Fig. 3
figure 3

Change in equilibrium density of infected pest in \(\alpha -\lambda \) parameter space, a for the Allee parameter \(w=10\) and b for the Allee parameter \(w=30\), for the linear mass-action functional response (model (4)). It is interesting to note that, \(i^*\) assumes high values with change in \(\lambda \), if \(w\) is small. Since, \(s^*+i^* \le 1\), when \(i^*\) increases \(s^*\) decreases. Hence when the effect of Allee is small, control of pests via viral infection will be effective in a predator free environment. Here, blue region is for the density of infected pest at the equilibrium \(E^I_1\), yellow region is for the density at \(E^I_2\) and green region is for the density at \(E^I_3\). Here, \(\alpha \in [0, 0.01]\), \(\lambda \in [0.005, 0.02]\) and other parameters are same as in Table (1). (Color figure online)

Full size image

(b) It is interesting to note that, if we increase the value of Allee parameter, then the equilibrium value of the infected pests decreases at high infection rate (see Fig. 3). Thus in a predator free environment, the application of Allee effect (for example, use of sterile insects) and use of viral infection together is not helpful to control the pest populations.

If \(\xi ^{I}_{2,1} < 0\) (i.e. \(e > 1\)) and \(\xi ^{I}_{3,1} > 0\) (i.e. \(m_{1} > \frac{g}{\theta }\)) then system (5) admits three equilibria viz. \(E^{I}_{0}\), \(E^{I}_{1}\) and \(E^{I}_{3}\). In this case \(E^{I}_{1}\) is saddle with si-plane as its stable manifold and p-axis as unstable manifold, whereas \(E^{I}_{0}\) is always unstable saddle.

Theorem 5

The sufficient conditions for asymptotic stability of equilibria \(E^{I}_{3}\) are \(2vg\theta m_{1} + g^2 > v\theta ^{2}m_{1}^{2}\) and \(m_{1} > \frac{g}{e\theta }\) or \(m_{1} > \frac{g}{\theta }\) according as \(e < 1\) or \(e > 1\).

Proof

The characteristic equation corresponding to \(E^{I}_{3}\) is given by

$$\begin{aligned} (s - d p - e - \xi ) \left( \xi ^2 + \frac{bs(2vs + s^2 - v)}{(v + s)^2} \xi + m_{1}^{2}\theta s p \right) = 0. \end{aligned}$$

The eigenvalue in the i-direction is

$$\begin{aligned} \xi ^{I}_{2,3} = s - d p -e = \frac{g}{\theta m_{1}} - e - \frac{bdg(\theta m_{1} - g)}{\theta m_{1}^{2}(v\theta m_{1} + g)}. \end{aligned}$$

The sufficient condition for \(\xi ^{I}_{2,3}\) to be negative is \(m_{1} > \frac{g}{e \theta }\). The other eigenvalues \(\xi ^{I}_{1,3}\) and \(\xi ^{I}_{3,3}\) are the roots of the quadratic equation

$$\begin{aligned} \xi ^2 + \frac{bs \left( 2vs + s^2 - v \right) }{ \left( v + s \right) ^2} \xi + m_{1}^{2}\theta s p = 0. \end{aligned}$$

The roots of this equation are either real negative or complex conjugate with negative real parts if \((2vs + s^2 - v) > 0\) i.e. \(2vg\theta m_{1} + g^2 > v\theta ^{2}m_{1}^{2}\). Also, the existence condition of \(E^{I}_{3}\) is \(m_{1} > \frac{g}{\theta }\). Hence the sufficient condition for the stability of \(E^{I}_{3}\) are \(m_{1} > \max \left\{ \frac{g}{e\theta }, \frac{g}{\theta } \right\} \) and \((2vs + s^2 - v) > 0\) i.e. \(2vg\theta m_{1} + g^2 > v\theta ^{2}m_{1}^{2}\). Note that \(\max \left\{ \frac{g}{e\theta }, \frac{g}{\theta } \right\} \) = \(\frac{g}{e\theta }\) or \(\frac{g}{\theta }\) according as \(e < 1\) or \(e > 1\). Since \(\xi ^{I}_{2,1} < 0\) (i.e. \(e > 1\)), we have \(\frac{di}{dt} < 0\). Hence all solutions initiating in the interior of the positive octant will be drawn towards the sp-plane and eventually approach \(E^{I}_{3}\). Hence the theorem. \(\square \)

Observation 3: Necessity for additional predator depending on predational threshold

Fig. 4
figure 4

Stability regions of the boundary equilibria \(E^I_1\), \(E^I_2\) and \(E^I_3\) in \(\alpha \)-\(\lambda \) parameter space. Here, \(\alpha \in [0, 0.01]\) and \(\lambda \in [0.005, 0.02]\). We fix the other parameter values as in Table (1). Here (i) yellow region is for the basin of attraction of the equilibrium \(E^I_2\); (ii) green region is for the basin of attraction of the equilibrium \(E^I_3\); (iii) blue region is for the basin of attraction of the equilibrium \(E_1^{I}\). (Color figure online)

Full size image
Fig. 5
figure 5

Equilibrium density of the susceptible pest population at different levels of \(\alpha \) and \(\lambda \), for the linear mass-action functional response (model (4)). Here, \(\alpha \in [0, 0.01]\) and \(\lambda \in [0.005, 0.02]\) and other parameters are same as in Table 1. Here, blue region is for the density of susceptible pest at the equilibrium \(E^I_1\), yellow region is for the density at \(E^I_2\) and green region is for the density at \(E^I_3\). (Color figure online)

Full size image

(a) If the rate of infection is high (\(\lambda K>\mu \)), the disease will persist. It is already stated that, consumption of infected pest is harmful to the natural predator and eventually may go to extinction. Such a situation is not at all desirable. To overcome such situation, the predation rate of natural predator should be above a threshold determined by the relation \(\alpha >\frac{\lambda \delta }{\theta \mu }\), the disease will die out and the predator will persist (green region in Fig. 4). Naturally to conserve the natural predator, introduction of natural predator is necessary in such occasion.

(b) When the infection rate is low i.e. \(\lambda K < \mu \), then the maximum renewal rate of infected pest is less than their mortality rate, infection will die out. Simultaneously for \(m_1>\frac{g}{\theta }\) i.e. \((\theta \alpha )K > \delta \) i.e. the maximum renewal rate of predator by consuming the susceptible pest is higher than the mortality rate, the predator population coexists with susceptible pest (see Fig. 2c). From Fig. 5 we observe that for small \(\lambda \), as \(\alpha \) increases the equilibrium density of pest decreases (green dots). Thus when the pest is at an advanced harmful stage, mass release of natural enemies will be helpful with a threshold predation rate determined by the relation \(\alpha > \frac{\delta }{\theta K}\). This will ultimately reduce the equilibrium size of the pest and as a result natural predator will sustain.

It is to be noted that in case of higher infection, the predational threshold will be higher (\(\frac{\lambda \delta }{\theta \mu }\)) than the predational threshold for lower infection (\(\frac{\delta }{\theta K}\)). Hence more additional predator is required in case of high infection.

Theorem 6

System (5) is always unstable around \(E^{I}_{*}\) for all parametric values.

Proof

Observe that from first two equations of system (5), we always have

$$\begin{aligned} \frac{d(s+i)}{dt}= & {} \frac{bs^2}{a+s}(1 - (s + i)) - m_{1}sp - dip - ei \\< & {} bs(1 - (s+i)) - m_{1}sp - dip - ei \\< & {} b(s+i)(1-(s+i)). \end{aligned}$$

Hence from [30], we have \(\lim _{t \rightarrow \infty } \left\{ s(t) + i(t)\right\} < 1\). Thus we have \(s^{*} + i^{*} < 1\) and the last condition of (6) is always satisfied. It is also true for hyperbolic and sigmoidal response functions also. The variational matrix corresponding to \(E^{I}_{*}\) is

$$\begin{aligned} V(E^I_*) = \left[ \begin{array}{ccc} m^{I}_{11} \,&{}\quad m^{I}_{12} \,&{}\quad m^{I}_{13}\\ m^{I}_{21} \,&{}\quad 0 \,&{}\quad m^{I}_{23}\\ m^{I}_{31} \,&{}\quad m^{I}_{32} \,&{}\quad 0 \end{array} \right] , \end{aligned}$$

where

$$\begin{aligned} m^{I}_{11} = \frac{vbs^{*}(2\mathrm{d}\theta - 3\mathrm{d}\theta s^{*} - 2\theta m_{1} s^{*} + 2g) + b(s^{*})^{2}(\mathrm{d}\theta - 2\mathrm{d}\theta s^{*} - \theta m_{1}s^{*} + g) - (v + s^{*})^2(2\theta m_{1}s^{*} - g - m_{1}\theta e)}{d\theta (v + s^{*})^2}, \end{aligned}$$
$$\begin{aligned} m^{I}_{12}= & {} -s^{*}\left( \frac{bs^{*}}{v+s^{*}} + 1 \right) (< 0), \quad m^{I}_{13} = -m_{1}s^{*} (< 0), \quad m^{I}_{21} = i^{*} (> 0),\\ m^{I}_{23}= & {} -\mathrm{d}i^{*} (< 0), \quad m^{I}_{31} = m_{1}\theta p^{*} (> 0), \quad m^{I}_{32} = -\mathrm{d}\theta p^{*} (< 0) \end{aligned}$$

The characteristic equation corresponding to this variational matrix can be put in the form

$$\begin{aligned} \lambda ^3 + A_1\lambda ^2 + A_2\lambda + A_3 = 0, \end{aligned}$$

where

$$\begin{aligned} A_{1} = - \mathrm{tr}[V(E^I_*)] = - m^{I}_{11}, \quad A_{2} = - (m^{I}_{23}m^{I}_{32} + m^{I}_{31}m^{I}_{13} + m^{I}_{12}m^{I}_{21}) \end{aligned}$$

and

$$\begin{aligned} A_{3} = -\mathrm{det}[V(E^I_*)] = m^{I}_{11}m^{I}_{23}m^{I}_{32} - m^{I}_{12}m^{I}_{31}m^{I}_{23} - m^{I}_{13}m^{I}_{21}m^{I}_{32}. \end{aligned}$$

From \(Routh{-}Hurwitz\) criterion, \(E^{I}_{*}\) is locally asymptotically stable if and only if

$$\begin{aligned} A_{1} > 0, ~~~~ A_{3} > 0, ~~~~ A_{1}A_{2} - A_{3} > 0. \end{aligned}$$

Now \(A_{1} > 0 \Leftrightarrow m^{I}_{11}\) must be negative.

Again from the signs of those defined, \(m^{I}_{ij}, i, j = 1, 2, 3\), it is easy to verify that \(A_{3} < 0\) for all parametric values. Thus system (5) is always unstable around \(E^{I}_{*}\). This completes the theorem. \(\square \)

Note: Here, coexistence of the three populations viz. susceptible pest, infected pest and natural predator is not possible because of the assumption that growth rate of natural predator is negative by consuming the infected pest [24, 35]. If growth rate of the predator is positive by consuming the infected pest then \(m^I_{32}=\mathrm{d}\theta p^* > 0\) and other \(m^I_{i,j}, i,j = 1,2,3\) are same as defined earlier. Thus, \(A_1>0\) if \(m^I_{11}<0\), \(A_3>0\) if \(m^I_{11}m^I_{23}m^I_{32}>m^I_{12}m^I_{31}m^I_{23} +m^I_{13}m^I_{21}m^I_{32}\) and \(A_1A_2-A_3\) is always greater than zero. Thus in this case, coexistence of all the three populations is possible if \(m^I_{11}<0\) and \(m^I_{11}m^I_{23}m^I_{32}>m^I_{12}m^I_{31}m^I_{23} +m^I_{13}m^I_{21}m^I_{32}\).

In this case (i.e. \(A_1 > 0\), \(A_3 < 0\) and \(A_2\) become positive or negative, then sum of eigenvalues become negative and one eigenvalue must be positive, which imply that other two eigenvalues become real negative or complex conjugate with negative real parts), one can observe that at interior equilibrium \(E^I_*\), the system (5) has one positive eigenvalue and other two eigenvalues become real negative or complex conjugate with negative real parts. Eventually the unstable equilibrium \(E^I_*\) becomes saddle or outward spiral respectively. The magnitude of a positive eigenvalue characterizes the level of repulsion along the corresponding eigenvector. Similarly, magnitude of negative eigenvalues characterizes the level of attraction along the corresponding eigenvectors. The number of interior equilibria and their stability are listed in Table 2.

For numerical example, we consider the values of parameters as \(r = 3\) day\(^{-1}\), \(K = 45\) unit (designated area)\(^{-1}\), \(w = 10\) unit (designated area)\(^{-1}\), \(\beta = 0.05\) day\(^{-1}\), \(\mu = 0.24\) day\(^{-1}\), \(\theta = 0.7\) day\(^{-1}\), \(\delta = 0.09\) day\(^{-1}\), \(\alpha = 0.006\) day\(^{-1}\), \(\lambda = 0.03\) day\(^{-1}\), the interior equilibrium \(E^I_*\) become \(\left( S^*, I^*, P^*\right) = \left( 2.5826, 0.2528, 1.4429\right) \). The eigenvalues corresponding to this interior equilibrium are \(\xi _{1,2} = -8.8861 \pm 1.0415 i\) and \(\xi _3 = 1.8556\) and eventually the interior equilibrium in this case becomes outward spiral.

Observation 4 Non-existence of predator–pest coexistence: Ecologically, instability of the interior equilibrium is attributed to the harmful effect of the infected pest on the predator. The predator population will not coexist with the infected population. As the derivative of the right hand side of the second equation of system (3) with respect to \(P\) is always negative for all three functional responses, ensures the interior equilibrium to be unstable for all parametric values.

When \(\xi ^{I}_{2,1} > 0\) (i.e. \(e < 1\)) and \(\xi ^{I}_{3,1} > 0\) (i.e. \(m_{1} > \frac{g}{\theta }\)), then system (5) admits all the five equilibria \(E^{I}_{0}\), \(E^{I}_{1}\), \(E^{I}_{2}\), \(E^{I}_{3}\) and \(E^{I}_{*}\). Here \(E^{I}_{0}\), \(E^{I}_{1}\) and \(E^{I}_{*}\) are all unstable. Hence all solutions initiating in the interior of the positive octant will approach either towards the si-plane and eventually approach \(E^{I}_{2}\) or towards the sp-plane and eventually approach \(E^{I}_{3}\) depending on whether the initial value of the system is contained in the invariant set which contain the equilibrium point \(E^{I}_{2}\) or \(E^{I}_{3}\), respectively.

Hyperbolic Functional Response

The objective of this subsection is to introduce the eco-epidemiological model with hyperbolic functional response to observe the dynamics of the system. For hyperbolic response function, system (3) takes the following form:

$$\begin{aligned} \frac{\mathrm{d}S}{\mathrm{d}t}= & {} rS\left( 1-\frac{S+I}{K}\right) \frac{S}{w+S} - \lambda SI - \frac{\alpha SP}{a + S}, \nonumber \\ \frac{\mathrm{d}I}{\mathrm{d}t}= & {} \lambda SI - \beta IP - \mu I, \\ \frac{\mathrm{d}P}{\mathrm{d}t}= & {} \theta \left( \frac{\alpha S}{a + S} - \beta I \right) P - \delta P.\nonumber \end{aligned}$$
(7)

\(\alpha \) denotes the effective search rate, \(a\) denotes the handling time of predators, and \(\theta \) denotes the conversion efficiency of ingested pest into new predators. The product, \(\frac{\alpha SP}{a + S}\), represents the predators hyperbolic functional response. All the parameters are positive constants. Applying the same transformations as before we have the following dimensionless form of the model equation (7).

$$\begin{aligned} \frac{\mathrm{d}s}{\mathrm{d}t}= & {} bs(1-(s+i))\frac{s}{v+s} - si - \frac{m_{2}sp}{1 + ls}, \nonumber \\ \frac{\mathrm{d}i}{\mathrm{d}t}= & {} si - \mathrm{d}ip - ei, \\ \frac{\mathrm{d}p}{\mathrm{d}t}= & {} \theta \left( \frac{m_{2}s}{1 + ls} - \mathrm{d}i \right) p - gp,\nonumber \end{aligned}$$
(8)

where \(m_{2} = \frac{\alpha }{\lambda a}\) and \(l = \frac{K}{a}\). Note that \(l\), the ratio of the carrying capacity to the half-saturation constant, will be assumed to be greater than unity in the future study.

Equilibria and Local Stability

System (8) has the following equilibria: (a) trivial equilibria \(E^{II}_{0} = \left( 0 ,0, 0 \right) \), (b) infection and predator free axial equilibrium \(E^{II}_{1} = \left( 1, 0, 0 \right) \), (c) predator-free planner equilibrium

$$\begin{aligned} E^{II}_{2} =\left( e, \frac{be\left( 1-e\right) }{be+v+e}, 0 \right) , \end{aligned}$$

(d) infection-free planner equilibrium

$$\begin{aligned} E^{II}_{3} = \left( \frac{g}{\theta m_{2} - gl}, 0, \frac{bg\theta \left( \theta m_{2} - gl -g \right) }{\left( v\theta m_{2} - vgl + g \right) \left( \theta m_{2} - gl \right) ^2} \right) \end{aligned}$$

and (e) interior equilibrium \(E^{II}_{*} = (s^{*}, i^{*}, p^{*})\), where

$$\begin{aligned} i^{*} = \frac{1}{\mathrm{d}\theta }\left( \frac{\theta m_{2}s^{*}}{1 + ls^{*}} - g \right) , \quad p^{*} = \frac{s^{*} - e}{d} \quad \mathrm{and} \quad s^* + i^* \le 1. \end{aligned}$$

Note that \(p^{*} > 0\) as \(s^{*} > e\), otherwise \(i \rightarrow 0\) from the second equation of (8) and \(i^{*} > 0\) as \(\frac{\theta m_{2}s^{*}}{1 + ls^{*}} > g\), otherwise \(p \rightarrow 0\) from the third equation of (8). \(s^{*}\) is the positive root of the cubic equation

$$\begin{aligned} As^{*3} + Bs^{*2} + Cs^{*} + D = 0 \end{aligned}$$

where \(A = bd\theta l (\,{>}\,0)\), \(B \,{=}\, \theta \left( b+2\right) \left( m_2-T_1\right) \), \(C \,{=}\, 2v\theta \left( m_2-T_2\right) \), \(D \,{=}\, - v( g+ m_{2}l\theta ) (< 0)\),

$$\begin{aligned} T_1 = \frac{gl(b+1)+bd\theta (l-1)}{\theta (b+2)} \quad \mathrm{and} \quad T_2 = \frac{g(b+1)+bd\theta + vgl}{2\theta v}. \end{aligned}$$

Here, \(s^*\) and \(i^*\) must satisfy the inequality \(s^{*} + i^{*} \le 1\). The interior equilibrium \(\left( s^{*}, i^{*}, p^{*}\right) \) exists if

$$\begin{aligned} m_{2} > \frac{g(l+1)}{\theta }, \quad s^{*} > \max \left\{ e, \frac{g}{m_{2}\theta - gl} \right\} \quad \mathrm{and} \quad e < 1. \end{aligned}$$

Now the sufficient conditions on the existence of the number of interior equilibria and their stability for system (8), are listed in Table 3, where, \(\Delta = 18ABCD - 4B^3D + B^2C^2 - 4AC^3 - 27A^2D^2\).

Table 3 Sufficient conditions for the existence and local stability of interior equilibrium for system (8)
Full size table

The equilibria \(E^{II}_{0}\) and \(E^{II}_{1}\) exist for all parameter values. \(E^{II}_{2}\) exists if \(e < 1\) and \(E^{II}_{3}\) exists if \(m_{2} > \frac{g(l + 1)}{\theta }\). Observe that \(E^{II}_{2}\) arises from \(E^{II}_{1}\) for \(e = 1\) and persists for all \(e < 1\), whereas \(E^{II}_{3}\) arises from \(E^{II}_{1}\) for \(m_{2} = \frac{g(l+1)}{\theta }\) and persists for all \(m_{2} > \frac{g(l+1)}{\theta }\). Also observe that the existence of \(E^{II}_{*}\) implies the existence of the equilibria \(E^{II}_{2}\) and \(E^{II}_{3}\). Variational matrix studies around each equilibrium point, as in the previous section, lead to the following theorem.

Theorem 7

System (8) around

  • \(E^{II}_{0}\) is a saddle-node equilibrium for all parametric values,

  • is locally asymptotically stable around \(E^{II}_{1}\) if \(e > 1\) and \(m_{2} < \frac{g(l + 1)}{\theta }\),

  • is locally asymptotically stable around \(E^{II}_{2}\ { if}\ m_{2} < \frac{1 + le}{\theta e} \left[ g + \frac{bd\theta e(1-e)}{v + e(b+1)} \right] , \quad e < 1\) and \(e^3(1+b) > v(v+e-2ve-3e^2-be^2)\),

  • is asymptotically stable around \(E^{II}_{3}\) if

    $$\begin{aligned} m_{2} > \frac{g(1+l)}{\theta }, T\left( vT+g\right) \left( g-eT\right) < bdg\theta \left( T-g\right) \end{aligned}$$

    and \(\theta m_2\left( 2vT^2-gT\left( 3v-1\right) -2g^2\right) < T\left( vT+g\right) \left( T-g\right) \), where \(T = \theta m_2-gl\),

  • is unstable around \(E^{II}_{*}\) for all parametric values.

The interior equilibrium is always unstable. For interior equilibrium, one eigenvalue becomes positive and other two eigenvalues become real negative or complex conjugate with negative real parts (same as linear mass-action functional response case). Eventually the interior equilibrium becomes saddle or outward spiral respectively. For numerical example, we have considered the parameter values \(r = 3\) day\(^{-1}\), \(K = 45\) unit (designated area)\(^{-1}\), \(w = 10\) unit (designated area)\(^{-1}\), \(a = 12\) unit (designated area)\(^{-1}\), \(\beta = 0.05\) day\(^{-1}\), \(\mu = 0.15\) day\(^{-1}\), \(\theta = 0.8\) day\(^{-1}\), \(\delta = 0.07\) day\(^{-1}\), \(\alpha = 0.15\) day\(^{-1}\) and \(\lambda = 0.004\) day\(^{-1}\). For this set of parameter values there is a unique interior equilibrium point given by \(E^{II}_{*}\) become \(\left( S^*, I^*, P^*\right) = \left( 0.9848, 0.0136, 0.0121\right) \). The eigenvalues corresponding to this interior equilibrium are \(\xi _1 = -0.0614\), \(\xi _2 = -0.1467\) and \(\xi _3 = 0.4963\) that implies that the interior equilibrium is a saddle point. For difficulty we skip the case when there exists three interior equilibrium points.

Sigmoidal Functional Response

The objective of this subsection is to introduce the eco-epidemiological model with sigmoidal functional response and summarize its dynamical behaviors. For sigmoidal response function, system (3) takes the following form:

$$\begin{aligned} \frac{\mathrm{d}S}{\mathrm{d}t}= & {} rS(1-\frac{S+I}{K})\frac{S}{w+S} - \lambda SI - \frac{\alpha S^2P}{a^2 + S^2}, \nonumber \\ \frac{\mathrm{d}I}{\mathrm{d}t}= & {} \lambda SI - \beta IP - \mu I, \\ \frac{\mathrm{d}P}{\mathrm{d}t}= & {} \theta \left( \frac{\alpha S^2}{a^2 + S^2} - \beta I \right) P - \delta P.\nonumber \end{aligned}$$
(9)

Applying the same transformations as before we have the following dimensionless form of the model equation (7).

$$\begin{aligned} \frac{\mathrm{d}s}{\mathrm{d}t}= & {} bs(1-(s+i))\frac{s}{v+s} - si - \frac{m_{3}s^2p}{1 + l^2s^2}, \nonumber \\ \frac{\mathrm{d}i}{\mathrm{d}t}= & {} si - \mathrm{d}ip - ei, \\ \frac{\mathrm{d}p}{\mathrm{d}t}= & {} \theta \left( \frac{m_{3}s^2}{1 + l^2s^2} - \mathrm{d}i\right) p - gp,\nonumber \end{aligned}$$
(10)

where \(m_{3} = \frac{\alpha K}{\lambda a^2}\).

Equilibria and Local Stability

System (10) has the following equilibria: (a) trivial equilibria \(E^{III}_{0} = (0, 0, 0)\), (b) infection and predator free axial equilibrium \(E^{III}_{1} = (1, 0, 0)\), (c) predator-free planner equilibrium

$$\begin{aligned} E^{III}_{2} = \left( e, \frac{be\left( 1-e \right) }{be + v + e}, 0 \right) , \end{aligned}$$

(d) infection-free planner equilibrium

$$\begin{aligned} E^{III}_{3} = \left( A, 0, \frac{b\theta A^2\left( 1 - A\right) }{g\left( v + A\right) } \right) , \end{aligned}$$

where

$$\begin{aligned} A = \sqrt{\frac{g}{\left( \theta m_{3} - g l^2\right) }} \end{aligned}$$

and (d) interior equilibrium \(E^{III}_{*} = \left( s^{*}, i^{*}, p^{*} \right) \), where

$$\begin{aligned} i^{*} = \frac{1}{d\theta }\left[ \frac{m_{3}\theta s^{*2}}{1 + l^2s^{*2}} - g \right] , ~~~~ p^{*} = \frac{s^{*} - e}{d}\quad \text{ and } \quad s^*+i^* \le 1. \end{aligned}$$

Note that \(p^{*} > 0\) as \(s^{*} > e\), otherwise \(i \rightarrow 0\) from the second equation of (10) and \(i^{*} > 0\) as

$$\begin{aligned} \frac{m_{3}\theta s^{*2}}{1 + l^2s^{*2}} > g, \end{aligned}$$

otherwise \(p \rightarrow 0\) from the third equation of (10). \(s^{*}\) is determined from the biquadratic equation

$$\begin{aligned} Ps^{*4} + Qs^{*3} + Rs^{*2} + Ss^{*} + T = 0, \end{aligned}$$

where \(P = bd\theta l (> 0)\), \(Q = \theta \left( b+2\right) \left( m_3-T_1\right) \), \(R = \theta \left( 2v-e\right) \left( m_3-T_2\right) \), \(S = -\left[ \theta \left( bd + m_{3} ve \right) + g \left( b+1 \right) \right] (< 0)\), \(T = - gv (< 0)\),

$$\begin{aligned} T_1=\frac{\left[ bd\theta + g\left( b+1\right) \right] l^2}{\theta \left( b+2\right) } \quad \mathrm{and} \quad T_2 = \frac{gvl^2-bd\theta }{\theta \left( 2v-e\right) }. \end{aligned}$$

Here, \(s^*\) and \(i^*\) must satisfy the inequality \(s^{*} + i^{*} \le 1\). The interior equilibrium \((s^{*}, i^{*}, p^{*})\) exists if

$$\begin{aligned} m_{3}>\frac{g(1+l^2)}{\theta }, \quad s^{*} > \max \left\{ e, \sqrt{\frac{g}{\theta m_{3}-gl^2}} \right\} \quad \mathrm{and} \quad e < 1. \end{aligned}$$

Reduced the above biquadratic equation to its standard form we get

$$\begin{aligned} x^4 + Ux^2 + Vx + W = 0, \end{aligned}$$

where

$$\begin{aligned} U = \frac{8PR-3Q^2}{8P^2}, \quad V = \frac{Q^3-4PQR+8P^2S}{8P^3} \end{aligned}$$

and

$$\begin{aligned} W = \frac{256P^3T-64P^2QS+16PQ^2R-3Q^4}{256P^4}. \end{aligned}$$

Now sufficient conditions on the existence of the number of interior equilibrium and their stability for system (10), are listed in Table 4, where, \(\Delta = 256W^3-128U^2W^2+16U(U^3+9V^2)W-V^2(4U+27V^2)\).

Table 4 Sufficient conditions for the existence and local stability of interior equilibrium for system (10)
Full size table

The equilibria \(E^{III}_{0}\) and \(E^{III}_{1}\) exist for all parameter values. \(E^{III}_{2}\) exists if \(e < 1\) and \(E^{III}_{3}\) exists if \(m_{3} > \frac{g(1 + l^2)}{\theta }\). We state the following theorem to summarize the above discussion:

Theorem 8

System (10) around

  • \(E^{III}_{0}\) is a saddle-node equilibrium for all parametric values,

  • is locally asymptotically stable around \(E^{III}_{1}\) if \(e > 1\) and \(g > \frac{\theta m_{3}}{1+l^2}\),

  • is locally asymptotically stable around \(E^{III}_{2}\) if

    $$\begin{aligned} m_{3} < \frac{1 + l^2e^2}{e^2\theta } \left[ g + \frac{bd\theta e (1-e)}{be + v + e} \right] , \quad e < 1, \end{aligned}$$

    and \(be^4(1+b) > vbe(v+e-2ve-3e^2-be^2)\),

  • is asymptotically stable around \(E^{III}_{3}\) if \(g(v + A)(A-e) < bd\theta A^2(1-A)\), \(\theta m_{3} > g(1+l^2)\) and \(2\theta m_{3} A^2 (1-A)(v+A) > g(1+l^2A^2)^2(2v+A(1-3v)-2A^2)\)

  • is unstable around \(E^{III}_{*}\) for all parametric values.

The interior equilibrium is always unstable. For interior equilibrium, one eigenvalue is positive and other two eigenvalues are real negative or complex conjugate with negative real parts (same as linear mass-action functional response case). Eventually the interior equilibrium becomes saddle or outward spiral respectively. For numerical example, we have considered the parameter values \(r = 3\) day\(^{-1}\), \(K = 45\) unit (designated area)\(^{-1}\), \(w = 10\) unit (designated area)\(^{-1}\), \(a = 12\) unit (designated area)\(^{-1}\), \(\beta = 0.053\) day\(^{-1}\), \(\mu = 0.243\) day\(^{-1}\), \(\theta = 0.43\) day\(^{-1}\), \(\delta = 0.013\) day\(^{-1}\), \(\alpha = 0.13\) day\(^{-1}\) and \(\lambda = 0.13\) day\(^{-1}\). For this set of parameter values there is a unique interior equilibrium point given by \(E^{III}_{*}\), \(\left( S^*, I^*, P^*\right) = \left( 3.1033, 0.0330, 6.1000\right) \). The eigenvalues corresponding to this interior equilibrium are \(\xi _1 = -3.3321\), \(\xi _2 = -0.1711\) and \(\xi _3 = 0.1210\) which imply that the interior equilibrium is a saddle point also. For difficulty we skip the case when there exists three interior equilibrium points.

Note: For all the three functional responses, it is observed that the trivial equilibrium is always unstable saddle for all parametric values. When \(\lambda < \frac{\mu }{K}\), \(E_{1}\) is locally asymptotically stable if

$$\begin{aligned} \alpha < \frac{\delta }{K\theta }, \quad \alpha < \frac{\delta (K+a)}{K\theta }\quad \mathrm{and}\quad \alpha < \frac{\delta (a^2+K^2)}{\theta K^2} \end{aligned}$$

for linear, hyperbolic and sigmoidal functional responses, respectively. These conditions are independent of the Allee parameter.

Fig. 6
figure 6

Parameter regions for the global stability of the equilibrium \(E_{1}\) in \(\alpha -\lambda \) parameter space, for different functional responses. All the other parameters are same as in Table 1. In \(R_{1} = \left\{ (\lambda ,\alpha )/ \lambda < \frac{\mu }{K}, \alpha < \frac{\delta }{K\theta }\right\} \), \(E^{I}_{1}\) attracts all positive solutions (for linear functional response). In \(R_{2} = \left\{ (\lambda ,\alpha )/\lambda < \frac{\mu }{K}, \alpha < \frac{\delta (a+K)}{K\theta }\right\} \), \(E^{II}_{1}\) attracts all positive solutions (for hyperbolic functional response). In \(R_{3} = \left\{ (\lambda ,\alpha )/\lambda < \frac{\mu }{K},\alpha < \frac{\delta (a^2+K^2)}{K^2\theta }\right\} \), \(E^{III}_{1}\) attracts all positive solutions (for sigmoidal functional response)

Full size image
Fig. 7
figure 7

Parameter regions for the local stability of the equilibrium \(E_{2}\) in \(\alpha -\lambda \) parameter space, for different functional responses. All the other parameters are same as in Table 1. In \(R_{1} = \{(\lambda ,\alpha )/\lambda > \frac{\mu }{K}, \alpha _1=\alpha < \frac{1}{\mu \theta }[\delta \lambda + \frac{r\beta \mu \theta (\lambda K-\mu )}{w\lambda ^2 K+\mu \lambda K+r\mu }]\}\), \(E^{I}_{2}\) attracts all positive solutions (for linear). In \(R_2 = \{(\lambda ,\alpha )/\lambda > \frac{\mu }{K}, \alpha _2 = \alpha < \frac{\lambda a+\mu }{\lambda \mu \theta }[\delta \lambda + \frac{r\beta \mu \theta (\lambda K-\mu )}{w\lambda ^2 K+\mu \lambda K+r\mu }]\}\), \(E^{II}_{2}\) attracts all positive solutions (for hyperbolic). In \(R_{3} = \{(\lambda ,\alpha )/\lambda > \frac{\mu }{K}, \alpha _3 = \alpha < \frac{\lambda ^2 a^2+mu^2}{\mu ^2 \lambda \theta }[\delta \lambda + \frac{r\beta \mu \theta (\lambda K-\mu )}{w\lambda ^2 K+\mu \lambda K+r\mu }]\}\), \(E^{III}_{2}\) attracts all positive solutions (for sigmoidal)

Full size image
Fig. 8
figure 8

a In \(R_{1} = \{(\lambda , \alpha )/\lambda < \frac{\mu }{K}, \alpha _1 = \frac{\delta }{K\theta } < \alpha < \delta /(w\theta K)(w+\surd (w^2+wK)) = \alpha _2\}\), \(E^{I}_{3}\) attracts all positive solutions. In \(R_{2} = \{(\lambda ,\alpha )/\lambda < \frac{\mu }{K}, \alpha _3 = \frac{\delta (K+a)}{K\theta } < \alpha < \frac{\delta (2K+3a)}{2K\theta } = \alpha _4\}\), \(E^{II}_{3}\) attracts all positive solutions. In \(R_{3} = \{(\lambda , \alpha )/ \lambda < \frac{\mu }{K}, \alpha > \frac{\delta (a^2+K^2)}{K^2\theta } = \alpha _5\}\), \(E^{III}_{3}\) attracts all positive solutions. Parameters are as in Table 1. b In \(R_{1} = \{(\lambda , \alpha )/\lambda > \frac{\mu }{K}, \alpha _{1} = \frac{\delta \lambda }{\mu \theta } < \alpha < \delta /(w\theta K)(w+\surd (w^2+wK)) = \alpha _2\}\), \(E^{I}_{3}\) attracts all positive solutions. In \(R_{2} = \{(\lambda , \alpha )/\frac{\mu }{K} < \lambda < \frac{3\mu }{2K}, \alpha _3 = \frac{\delta (a\lambda +\mu )}{\mu \theta } < \alpha < \frac{\delta (2K+3a)}{2\theta K} = \alpha _4\}\), \(E^{II}_{3}\) attracts all positive solutions. In \(R_{3} = \{(\lambda ,\alpha )/ \lambda > \frac{\mu }{K}, \alpha _5 = \alpha > \frac{\delta }{\theta } + \frac{a^2\delta \lambda ^2}{\theta \mu ^2}\}\), \(E^{III}_{3}\) attracts all positive solutions. Parameters are as in Table 1

Full size image

Observation 5 Usefulness of sigmoidal type interaction

(a) Figure 6 illustrates the parameter regions for the asymptotic stability of the axial equilibrium \(E_{1}\) in \(\lambda -\alpha \) parameter plane. Regions \(R_{1}\), \(R_{2}\), \(R_{3}\) depict the stability areas of \(E_{1}\) corresponding to linear, hyperbolic and sigmoidal response functions. It is to be noted that the stability region increases gradually as we pass from linear mass-action response function to hyperbolic through sigmoidal. This indicates that the stability of the equilibrium \(E_{1}\) is stronger for hyperbolic functional response compared to other two responses. It may be used as a possible control measure to save small group of endangered species (may be due to the Allee effect) by culling its predators which is in well agreement with the observations of [38]. Another study by [7] also revealed that culling predators with a hyperbolic functional response may save the pest from extinction when they become small in numbers.

(b) Figure 7 illustrates the parameter regions for the asymptotic stability of the planner equilibrium \(E_2\) in \(\alpha -\lambda \) parameter plane. In this case also, the parameter regions for the asymptotic stability of the predator-free equilibrium \(E_{2}\) increases as we pass from linear response to hyperbolic through sigmoidal. \(R_1\), \(R_2\) and \(R_3\) are the parameter regions for which \(E_2\) is locally asymptotically stable for linear, hyperbolic and sigmoidal respectively. It is observed that in both the cases hyperbolic functional response has larger stability regions in parameter space compared to the other two functional responses.

(c) Figure 8a, b illustrate the parametric regions for the stability of the disease-free equilibrium, \(E_3\), in \(\alpha -\lambda \) parameter space for lower and higher infection rates, respectively. \(R_1\), \(R_2\) and \(R_3\) are the parameter regions for which \(E_3\) is locally asymptotically stable for linear, hyperbolic and sigmoidal respectively. It is observed that in both the cases sigmoidal functional response has larger stability regions compared to other two. In a predator–pest interaction, sigmoidal response behaves as if there are some pest refuges. This pest refuges reduce predation rates by decreasing encounter rates between predator and pest and thereby stabilize the predator–pest interaction for a wide range of parameter values [2, 37]. Therefore, the stability of the equilibrium \(E_3\) is much stronger in case of sigmoidal response function compared to the other two. Please note that such a situation is desirable from ecological point of view where susceptible pest and predator coexist. In the above two observations (a) and (b) hyperbolic functional response demonstrates larger stability for the equilibrium \(E_1\)and \(_2\), which is not a desirable control mechanism at all for a biological system, because the natural predator go to extinction in such occasion.

If we see, that the interactions between predator and pest is of sigmoidal type, the region of stability increases and as such no precaution measure is necessary at that moment. It can be concluded that this situation is more robust one.

Table 5 Comparison table for stability of the equilibria in original parameters
Full size table

Numerical Simulation

In this section, we will present some numerical simulation results to validate our analytical findings. From the existence conditions and stability analysis of the equilibria, the parameters \(e\) and \(m_{i}\), \(i = 1, 2, 3\) are recognized to be important. But, we cannot compare the dynamics of the model (3) in the \(e-m_{i}\) parameter plane as \(m_{i}\) are different for different \(i\). So, we first rewrite all the conditions of different theorems in the original system parameters in Table 5 and compare the result in the \(\alpha -\lambda \) parameter plane and observe the changes in stability regions due to presence of the Allee effect.

By reduction in population stability we mean destabilization of competitive predator–prey systems [12], extended time in reaching stable equilibrium [44], prevention from exhibiting sustained cycle [25, 7] and reduction of equilibrium population size. In the following we shall measure the stability of an equilibrium point by the region in the parameter space (\(\lambda \), epidemiological - \(\alpha \), ecological) for which the system is stable, hence larger stability region implies stronger stability.

Stability of \(E_1(1,0,0)\)

We choose fixed parameter values as described in Table 1 and vary only one ecological parameter \(\alpha \), predators attack rate on susceptible pest, and one epidemiological parameter \(\lambda \), the rate of infection. For the above set of parameter values we observe that \(E_{1}\) will be stable if \(\alpha \) is less than 0.005, 0.3 and \(0.25\) day\(^{-1}\) for linear, hyperbolic and sigmoidal, respectively when \(\lambda < 0.0053\) day\(^{-1}\). A simple conclusion is that the Allee effect has no effect on infected and predator free equilibria (see Fig. 1a). We select the parameter values \(\lambda = 0.003\) day\(^{-1}\) and \(\alpha =0.004\) day\(^{-1}\), for linear functional response. We observe that all the trajectories with different initial conditions [(30, 10, 15), (15, 20, 10), (10, 5, 5)] converge to the equilibrium where susceptible pest, \(S\), exists in the form of a stable equilibrium (see Fig. 2a, the figures for hyperbolic and sigmoidal functional responses are qualitatively similar with linear, hence omitted). This indicates that equilibrium \(E_{1}\) is locally asymptotically stable for all three functional responses. It is quite natural that in absence of predation and infection the equilibrium density of the susceptible population will approach to its carrying capacity (\(K\)) asymptotically which is not affected by the Allee constant.

Stability of \(E_2(S^*,I^*,0)\)

The net reproductive ratio \(R_0\) of an infectious disease, is defined as the number of secondary infections produced by a single infected individual over his/her entire infectious period when the susceptible population is at a fixed demographic equilibrium (level \(S^*\)). Note that the net reproductive ratio, \(R_{0}\), for all three cases, is given by

$$\begin{aligned} R_{0} = \frac{\lambda S^*}{\mu }. \end{aligned}$$

The numerator is the number of secondary infections \(\lambda S^*\) per unit of time while the denominator denotes the inverse of the average infectious period. If \(R_{0} < 1\), the disease dies out, but if \(R_{0} > 1\), it remains endemic in the host population. Also observe that the net reproductive ratio increases in direct proportion to susceptible population, \(S\). Thus, if the basic reproductive ratio be less than 1 even at maximum host level \(K\) (i.e. \(\frac{\lambda K}{\mu } < 1\) or \(\lambda < \frac{\mu }{K}\)), the infection cannot spread in the susceptible population. Biologically, it implies that if the infection rate is smaller than the average infectious period, the infected population can not survive and the system converge to the equilibrium where only healthy pest exists.

From Table 5 one can observe, if the infection rate is very high and the search rate of susceptible population be moderate then the predator population cannot survive and the system converges to the equilibrium where susceptible pest and infected pest coexist in the form of a stable equilibrium. For the above set of parameter values ( see Table 5) we observe that for the stability of \(E_{2}\) the value of \(\lambda \) should be greater than \(0.0053\) day\(^{-1}\). Choosing \(\lambda = 0.015\) day\(^{-1}\), we observe that \(\alpha \) should less than \(0.166\) day\(^{-1}\), \(5.165\) day\(^{-1}\) and \(5.008\) day\(^{-1}\) for linear, hyperbolic and sigmoidal response functions, respectively. Thus, for \(\lambda = 0.015\) day\(^{-1}\) and \(\alpha = 0.005\) day\(^{-1}\), we observe that all trajectories converge to the predator-free equilibrium \(E_{2}\) where susceptible pest and infected pest coexist in the form of a stable equilibrium (see Fig. 2b, similar conclusion holds for other two functional responses). The density of infected pests decreases due to the Allee effect while density of susceptible pest remains unchanged (see Fig. 1b). Thus the equilibrium \(E_{2}\) is locally asymptotically stable for all three response functions. A simple conclusion is that the equilibrium density of infected pest decreases at high infection rate as Allee parameter increases (see Fig. 3).

From ecological point of view, when density of susceptible population is high, parasite can infect them quickly on a per capita basis as infection rate is high (i.e. \(\lambda > \frac{\mu }{K}\)). As a result, the parasite quickly spreads and \(S\) decreases when \(I\) increases. This result is also reflected in Fig. 2b. Note that, the qualitative behavior of the solutions are same in all three response functions.

Stability of \(E_3(S^*,0,P^*)\)

One can observe from Table 5 that the system can be stable around \(E_{3}\) when infection rate is low or high and accordingly the predation rate must be low or high. For convenience we tabulate (see Table 6) the corresponding numerical ranges of \(\lambda \) and \(\alpha \) for \(E_{3}\) for the parameter values as in Table 5. In case of lower infection rate, we observe that all trajectories with default values as in Table 6 converge to the disease-free equilibrium \(E_3\) where susceptible pest and predator population coexist in the form of a stable equilibrium (see Fig. 2c). Again observe that all trajectories with the default values in case of higher infection rate converge to the disease-free equilibrium \(E_3\) where susceptible pest and predator population coexist in the form of a stable equilibrium (see Fig. 2d). This indicates that the equilibrium \(E_3\) is locally asymptotically stable for all three response functions with different infection and attack rates. A simple conclusion is that the equilibrium density of natural predator decreases at high predation rate as Allee parameter increases (see Fig. 9).

Table 6 Parameter ranges and default values for lower and higher infection rate
Full size table

Stability of \(E^*(S^*,I^*,P^*)\)

For all three functional responses it is observed that the interior equilibrium, where all three species exist, is unstable for all parametric values. The interior equilibrium becomes saddle or outward spiral with stable manifold of dimension two. This stable manifold separates the domains of attraction of the SI and SP equilibrium points. Thus, if the initial value of the system is contained in the invariant domain which contains the equilibrium point \(E_2\), the solution will eventually approach \(E_2\) under suitable parametric conditions and if the initial value of the system is contained in the invariant domain which contains the equilibrium point \(E_3\), the solution will eventually approach \(E_3\) under suitable parametric conditions.

Fig. 9
figure 9

Change in equilibrium density of natural predator in \(\alpha -\lambda \) parameter space, a for the Allee parameter \(w=10\) and b for the Allee parameter \(w=30\), for the linear mass-action functional response (model (4)). Here, blue region is for the density of natural predator at the equilibrium \(E^I_1\), yellow region is for the density at \(E^I_2\) and green region is for the density at \(E^I_3\). Here, \(\alpha \in [0, 0.01]\), \(\lambda \in [0.005, 0.02]\) and other parameters are same as in Table (1). (Color figure online)

Full size image

In a disease free system, when pest exhibits a weak Allee effect and predators have hyperbolic functional response, the populations can cycle for a larger range of pest carrying capacities and predator mortality rates [7]. On the contrary, if pest is subjected to the disease induced mortality, then stable coexistence of all three populations (susceptible, infected, predator) is not possible neither as a stable equilibrium state nor as a limit cycle oscillations. It depends on the conservation managers to adopt management actions based on the situation of disease driven extinction or predator driven extinction of pest populations. Our model may provide solutions in such conservation problem because, both disease-free and predator-free boundary equilibria is to be locally asymptotically stable under certain range of ecological and epidemiological parameter values. Thus tuning the ecological and epidemiological conditions artificially, one can prevent the extinction of pest populations in either cases.

Conclusion

The basic goal of this paper is to address some meaningful management aspects to save the population from disease induced eradication. An eco-epidemiological model with weak Allee effect is proposed and analyzed with Holling type functional responses. The reason for using different types of Holling’s functional response is to observe which functional response would be a suitable candidate to represent disease eradication. The question may arise why Rosenzweig - MacArthur formulation and why only Holling type functional responses? Eco-epidemiological models under the influence of Allee effect is still in its infancy stage and needs in depth study. Moreover, the use of functional response is also a debatable issue. To start such study we follow the general advice espoused by Anderson [3], to explore fundamental components, before increasing model complexity (i.e. “learning to walk before we run”).

Biological controls are often specific for a particular pest because other helpful insects, animals or people can go unaffected or disturbed by their use and less dangerous on the environment. This study may help better to explain the interactions of different management goals while applying management strategies in pest control program so that the biological balance of nature is conserved. The role of Allee effect plays a significant role to determine the optimal control strategy for the pest, so that the natural predator survives. Future endeavor to explore the effects of Allee effect in IPM would be more informative in decision making having well defined biological objectives, for instance, efficient use of strong Allee effect may be required for a complete eradication of the pest when a complete eradication of pest is necessary. One can easily see that, the modeling framework in this study is built on a general eco-epidemiological systems, hence may have wider range of applications across disciplines.

If the pest becomes dominant, then crop will be affected heavily with economic loss. Also, if the prey becomes extinct, then the natural predator will die out, that may affect the biological balance of the ecosystem. Thus, it is very important to maintain the biological balance of the ecosystem in such a way so that in one hand crop yield will be maximized and predators also survive. As already discussed that, if the pest population becomes abundant and natural predators are small in numbers, then the pest can be controlled through viral infection. However, in application of virus based control, a potential problem is that, infected pests may be harmful to the predators. If the abundance of infected pest becomes high, predator will be washed away by consuming the infected pests, although, crop yield will may be maximized by use of virus control. Hence introduction of viral infection should be done at an optimal level so that the conservation of natural predator is preserved.

Especially, our analysis can have an important message for management actions to save a species populations from disease induced extinction. If a pest disease would have advanced towards an endemic state in absence of predators, an introduction of predators/ natural enemies with a sigmoidal functional response would be most effective to eradicate the disease in pest. One should also stress that, such management strategies does not depend only on the traits of the natural enemies, but also on the quantities released [7]. Thus use of predators as disease control agents may not be always useful if there is limitations in finding mates among predator populations [21]. Future endeavor along this direction by considering the Allee effect in predator may provide helpful insight in management strategies in disease eradication and preservation of biological populations.

Before ending the article we like to mention that existing functional responses are categorized mostly mechanistically by most of the work, which corroborates the vast amount of literature from \(1989\) onwards after the initiation of Ratio-dependent theory. Taking account of the mechanistic functional form may be justified as it is mathematically simpler to incorporate, but it lacks reliability for some predators in justifying their population dynamics in the light of their evolutionary adaptation based on prey dynamics. Naturally, the choice of functional response is a big issue in population biology. Should we look forward to frame a new functional response model or should continue with its old mechanistic counterparts?