Stick–slip vibration of an oscillator with damping

Abstract

This paper proposes a new criterion for the occurrence of stick–slip vibration in an oscillator excited by a moving belt. Equations of motion were derived for a single-degree-of-freedom oscillator excited by the friction between the oscillator mass and a moving belt, considering two types of velocity-dependent friction models: exponential and polynomial. Based on the derived equations, dynamic responses were analyzed for various damping values, and it was found that the damping value determines the classification of oscillator motion among stick–slip, pure slip, and damped slip motions. Furthermore, a criterion for the occurrence of stick–slip motion, expressed in an integral form, was derived in terms of friction and damping forces. Using the least squares method, closed forms for the damping values to determine the occurrence of stick–slip vibration were obtained as functions of normal force, relative speed between contact surfaces, and friction parameters. In addition, the effects of the belt speed and of friction parameters on the occurrence of stick–slip vibration were also investigated.

1 Introduction

Stick–slip vibration, a repetitive behavior of relatively fixed motion (called stick motion) and sliding motion (called slip motion) between contact surfaces, is one of the most interesting problems for mechanical engineers because stick–slip vibration induces dynamic instabilities and leads to complicated difficulties in mechanical systems. Stick–slip vibration usually occurs in manufacturing machines, affecting their machining accuracy [1, 2]. It is also considered as an important factor contributing to unpleasant mechanical noise (chatter, squeal, squeak, etc.) which is a growing issue in industrial field [3, 4].

Many researchers have attempted to understand stick–slip vibration problems by using the model of a simple oscillator excited by a moving base, specifically a mass-spring-damper system supported by a moving belt that exerts a frictional force. Some have reported adaptable descriptions for the friction force that generates a stick–slip motion in the oscillator and to explain how stick–slip vibration occurs [5–7]. Others have reported on the dynamic responses of stick–slip vibration, including time histories, frequency spectra, and oscillation patterns [8–14]. According to these previous reports, stick–slip vibration is associated with the difference between the static and kinetic frictions, and a typical feature of stick–slip vibration is the appearance of a specific state of zero relative velocity between contact surfaces.

From an engineering point of view, some researchers have focused on the occurrence of stick–slip vibration in oscillators. Ding et al. [15] and Li et al. [16] introduced criterion conditions for stick–slip vibration by analyzing a general solution for stick–slip motion. However, these criteria are applicable to only the Coulomb model because these analyses are difficult to adopt when the kinetic friction force varies dynamically. Their general solutions for stick–slip motion can be obtained only if the kinetic friction force is constant. On the other hand, Thomsen and Fidlin [17] presented an analytical prediction for the occurrence of stick–slip by assuming that the steady-state response with pure slip has a harmonic motion. The presented prediction can be applied to only the case that the kinetic friction force can be expressed as a polynomial function of relative velocity between contact surfaces. They applied a straightforward perturbation method to obtain an approximate solution for stick–slip motion, and their approach seems to be suitable as long as the difference between static and kinetic friction forces is relatively small. The drawback of this approach is that the occurrence criterion for the stick–slip motion cannot be obtained when the kinetic friction force is not a polynomial function of the relative velocity or when the force is an exponential function. Some researchers [18–22] also presented the occurrence criteria of the stick–slip motion for single-degree-of-freedom oscillators, which are expressed in terms of system parameters. Le Rouzic et al. [18], Galvanetto and Bishop [19], Nakano and Maegawa [20], Liu and Chang [21] presented criteria for damped oscillators, while Kang et al. [22] presented a criterion for undamped oscillators. However, their criteria were derived from the stability analyses around the equilibrium positions of the oscillators; therefore, they may have some errors in predicting the stick–slip occurrence of oscillators with considerable vibration amplitudes. Stark et al. [23] classified the conditions for stick–slip occurrence in parameter planes to investigate the dynamics of an atomic force microscope (AFM). They executed only numerical simulations and performed phase path analysis to observe stick–slip occurrence. They did not present an analytical form of the occurrence criterion for the stick–slip motion. Different from the criterion for the stick–slip motion, Abdo and Abouelsoud [24] presented alternative approximate techniques to determine the amplitudes of the limit cycles that evolve from stick–slip vibrations based on a mass-on-moving-belt model.

Even though the occurrence of stick–slip vibration has been studied in several ways, it is our carefully considered opinion that the existing analytical approaches are not sufficient to become established as common solutions. Although numerical solutions may provide fine results, mathematical solutions are also required to analyze the physical meanings of stick–slip occurrence. In particular, because the kinetic friction force can take a variety of forms depending upon the normal load, relative velocity between contact surfaces, material combination, lubrication, etc., it is useful and interesting to examine the contribution of friction parameters to the occurrence of stick–slip. Therefore, a practical and analytical formulation is desirable that can predict the occurrence of stick–slip with no restriction on the form of kinetic friction force.

The purpose of the present study is to propose a new criterion for the occurrence of stick–slip vibration in an oscillator excited by a moving belt. Herein, the dynamic state of the oscillator is separated into the stick state and the slip state, and equations are established for both. To analyze the occurrence of stick–slip motion, dynamic responses of the oscillator mass are computed. Employing the principle of work and energy, criterion equations are derived for the occurrence of stick–slip motion. Kinetic friction forces are linearized using a least squares method to obtain closed-form solutions of the criterion equations. The obtained solutions yield regions of stick–slip occurrence in parameter planes of damping coefficient and belt speed. Validity of the presented results is evaluated by comparing them with the results of numerical simulations. Finally, the aspects of stick–slip occurrence are investigated corresponding to various values of the friction parameter.

2 Equations of motion

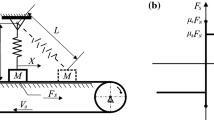
An oscillator excited by a moving base, the subject of our investigation, is illustrated in Fig. 1a. The oscillator is composed of a mass m connected to a fixed frame through a spring of stiffness k and a viscous damper of damping coefficient c. The mass is placed on a moving belt that is driven at the constant speed V. In this system, a normal force N causes a reaction force N as a contact force, which induces a friction force f on the mass (Fig. 1b). Denoting the displacement of mass as x, the relative velocity between the mass and the belt can be expressed as $v_r=\dot{x}-V$, where the superposed dot represents differentiation with respect to time t.

Fig. 1

Self-excited oscillator placed on a moving belt: a dynamic model and b free-body diagram

The oscillator has two kinds of dynamic states depending on the relative velocity $v_r$. In the stick state, the relative velocity is equal to zero ($v_r =0)$, meaning that the mass and the belt move together. In the stick state, the net force on the mass is zero, and this state persists as long as the static friction force does not exceed the maximum static friction force. Thus, the equation of motion and the static friction force for the stick state can be written as

$$\begin{aligned} \dot{x}=V, \quad f=c\dot{x}+kx, \quad \left| f \right| \le \mu _s N \quad \hbox {when} \quad v_r =0\nonumber \\ \end{aligned}$$

(1)

where $\mu _s$ is the maximum static friction coefficient. In the slip state, the relative velocity is not equal to zero ($v_r \ne 0)$, meaning that the mass slides on the belt. In the slip state, the kinetic friction force acts in the direction opposite to the relative velocity. Thus, the equation of motion and the kinetic friction force can be written as

$$\begin{aligned}&m\ddot{x}+c\dot{x}+kx=f, \quad f=-\mathrm{sgn}(v_r )\mu (v_r )N \quad \hbox {when} \nonumber \\&\quad v_r \ne 0 \end{aligned}$$

(2)

where $\mu$ is a coefficient of kinetic friction, which is a function of the relative velocity $v_r$.

Fig. 2

Friction coefficient versus relative velocity in the two friction models considered: a exponential-type and b polynomial-type

Actually, because kinetic friction can have several forms under different circumstances [7], two types of velocity-dependent friction models are considered in the present study. In the first model, herein called the exponential-type friction model, friction asymptotically decreases as the relative velocity increases (Fig. 2a). This type of friction model is commonly used for contact between solid surfaces in dry conditions, and its coefficient function (as introduced in [7]) can be expressed as

$$\begin{aligned} \mu (v_r )=\mu _m +(\mu _s -\mu _m )\hbox {e}^{-\alpha \left| {v_r } \right| } \end{aligned}$$

(3)

where $\mu _m$ is the minimum kinetic friction coefficient and $\alpha$ is a tuning parameter used to control the negative slope of the coefficient curve. In the second model, herein called the polynomial-type friction model, friction continuously decreases and then increases as the relative velocity increases (Fig. 2b). The decreasing region, i.e., the dynamic softening region, corresponds to solid friction whereby the contact surfaces slide under a dry condition, whereas the increasing region, i.e., the dynamic stiffening region, corresponds to liquid friction whereby a viscous fluid separates the contact surfaces. Considering the characteristics of both solid friction and liquid friction, a coefficient function for the second model (as introduced in [17]) can be given by

$$\begin{aligned} \mu (v_r )=\mu _s -\frac{3(\mu _s -\mu _m )}{2v_m }\left| {v_r } \right| +\frac{(\mu _s -\mu _m )}{2v_m^3 }\left| {v_r } \right| ^{3} \end{aligned}$$

(4)

where $v_m$ is the relative velocity corresponding to the minimum kinetic friction coefficient $\mu _m$.

3 Dynamic response analysis

It is interesting to analyze the dynamic responses of the oscillator as the damping coefficient varies. To compute the dynamic responses, the following formulas and properties were used in the present work unless noted otherwise. Using the Newmark time integration method [25] with the time step size of $\Delta t=10^{-4}\,\hbox { s}$, the dynamic responses were computed using the equations of motion corresponding to the conditions of relative velocity and friction force as mentioned in Sect. 2. In particular, because the relative velocity $v_r$ could not be equal to zero numerically, the relative velocity conditions of $v_r =0$ and $v_r \ne 0$ were changed into $\left| {v_r } \right| \le 10^{-4}\,\hbox { m/s}$ and $\left| {v_r } \right| >10^{-4}\,\hbox { m/s}$, respectively. The following physical parameters were used: $m=1\,\hbox { kg}$, $k=100\,\hbox { N/m}$, $V=0.5\,\hbox { m/s}$, $N=9.81\,\hbox { N}$, $\mu _s =0.5$, $\mu _m =0.2$, $\alpha =3\,\hbox { s/m}$, and $v_m =1\,\hbox { m/s}$. The initial displacement and velocity of the mass were $x(0)=0\,\hbox { m}$ and $\dot{x}(0)=V\,\hbox { m/s}$, respectively.

Fig. 3

Dynamic response of the velocity of mass m when the exponential-type friction model is adopted with $V\,=\,$0.5 m/s, for various values of c: a 0 kg/s, b 1 kg/s, c 2 kg/s, d 2.574 kg/s, and e 3.5 kg/s

First, dynamic responses were analyzed for various values of the damping coefficient. Time histories of the velocity of the mass are shown for $c=0$, 1, 2, 2.574, and 3.5 kg/s, when the exponential-type friction model was applied to the oscillator (Fig. 3). The damping ratios corresponding, respectively, to these damping coefficients are $\zeta =0$, 0.05, 0.1, 0.1287, and 0.175. As the damping coefficient was increased from 0 to 2.574 kg/s, the interval of the constant-velocity state (i.e., the stick state) and the oscillation period both decreased gradually; for each of these coefficients, the velocity response was of constant amplitude (Fig. 3a–c). When the damping coefficient reached the critical value of 2.574 kg/s, the stick state disappeared, whereas the response amplitude remained constant. For the greatest damping coefficient input, 3.5 kg/s, the stick state clearly disappeared and the response amplitude decayed (Fig. 3e). Herein, the repetitive motion of stick state and slip state is called stick–slip motion, the stationary slip state motion with constant amplitude is called pure slip motion, and the stationary slip state motion with decaying amplitude is called damped slip motion.

Fig. 4

Dynamic response of the velocity of mass m when the polynomial-type friction model is adopted with $V\,=\,$0.5 m/s, for various values of c: a 0 kg/s, b 1 kg/s, c 2 kg/s, d 3.038 kg/s, and e 3.5 kg/s

The critical damping coefficient corresponding to pure slip motion depended on the type of friction model used. Time histories of the velocity of the mass are shown for $c=0$, 1, 2, 3.038, and 3.5 kg/s, when the polynomial-type friction model was applied to the oscillator (Fig. 4). In this case, although the transition of dynamic responses was similar to that in the case of the exponential-type friction model, the critical damping value corresponding to pure slip motion was greater: 3.038 kg/s. In addition, these damping values varied depending on the speed of the moving belt. Note that the critical values given here for the two models both corresponded to $V=0.5\,\hbox { m/s}$. If the belt speed is changed, the corresponding critical values that yield pure slip motion vary consequently.

Fig. 5

Phase plots of the motion of mass m when the exponential-type friction model is adopted with V = 0.5 m/s: a stick–slip motion when $c\,=\,$2 kg/s, b pure slip motion when $c\,=\,$2.574 kg/s, and c damped slip motion when $c\,=\,$3.5 kg/s

Phase plots may facilitate the understanding of stick–slip vibration. Phase plots of displacement versus velocity of the mass are shown in Fig. 5; Fig. 5a–c, respectively, represents stick–slip motion, pure slip motion, and damped slip motion, and thus, respectively, corresponds to the dynamic responses shown in Fig. 3c–e. In the case of stick–slip motion, the amplitudes of displacement and velocity do not change; the constant velocity interval for the stick state and the oscillatory velocity interval for the slip state are sequentially repeated (Fig. 5a). In the case of pure slip motion, the amplitudes of the responses are maintained even though the mass oscillates in a slip state after an initial transition from a stick state at a point P (Fig. 5b). In the case of damped slip motion, the amplitudes of both displacement and velocity decay while the mass oscillates in a slip state (Fig. 5c). Overall, the results show that the amplitudes of responses decrease as damping increases. Similar trends can be observed for the case of the polynomial-type friction model.

4 Criterion for stick–slip motion

It is valuable to investigate the critical damping coefficient that determines whether stick–slip motion occurs. Recall that the point P, plotted in Fig. 5, maintains its position and velocity for the first transition from the stick state to the slip state. Then, suppose that a point Q has the same position as point P and represents the position and velocity of the mass after a cycle. As marked in Fig. 5, in the cases of stick–slip motion and pure slip motion, points P and Q can coincide, whereas in the case of damped slip motion, points P and Q cannot coincide. As introduced in Sect. 3, because pure slip motion separates the regimes of stick–slip motion and damped slip motion, the condition of pure slip motion represents a criterion for stick–slip motion.

The criterion for stick–slip motion can be derived based on the principle of work and energy. During the oscillation of the mass from point P to point Q, the relation between the work performed by applied forces and the variation in the kinetic energy of the mass can be expressed according to the principle of work and energy as follows:

$$\begin{aligned} \int _{\mathrm{P}\rightarrow Q} {(f-c\dot{x}-kx)\hbox {d}x} =\frac{1}{2}m\left( {V_{Q}^2 -V_{P}^2 } \right) \end{aligned}$$

(5)

where $V_{P}$ and $V_{Q}$ indicate the velocities of the mass at points P and Q, respectively. Denoting T as the time interval during which the mass travels from point P to Q, in the cases of stick–slip motion and pure slip motion, $V_{P}$ and $V_{Q}$ are equal (recall Fig. 5a, b); thus, (5) can be written as

$$\begin{aligned} \int _T {(f-c\dot{x})\dot{x}\hbox {d}t} =0 \end{aligned}$$

(6)

where the friction force f for stick–slip motion is the sum of the static friction force expressed in (1) and the kinetic friction force expressed in (2), whereas the friction force for pure slip motion is purely the kinetic friction force. In the case of damped slip motion, though the positions of points P and Q are same, $V_{Q}$ is less than $V_{P}$ (recall Fig. 5c); thus, (5) becomes

$$\begin{aligned} \int _T {(f-c\dot{x})\dot{x}\hbox {d}t} <0 \end{aligned}$$

(7)

where the friction force is the kinetic friction force only. Therefore, the boundary of the stick–slip regime corresponds to those conditions for which the relation of work and energy satisfies (6) with the kinetic friction force only.

To derive the criterion for stick–slip motion from (6) in closed form, it is necessary that the kinetic friction coefficient be expressed as a linear function of relative velocity. If the kinetic friction coefficient is a nonlinear function of relative velocity, the kinetic friction force in (6) also becomes a nonlinear function, since it is proportional to the kinetic friction coefficient and normal force as given in (2). Thus, the criterion of stick–slip motion cannot be derived in closed form, for a reason that will be explained later.

Let us consider the linearization of the kinetic friction coefficients introduced in (3) and (4), and the derivation of a criterion for stick–slip motion in closed form. Assume that the kinetic friction coefficient is a linearized function of relative velocity $\mu _L$ as follows:

$$\begin{aligned} \mu _L (v_r )=-a\left| {v_r } \right| +b \end{aligned}$$

(8)

where a and b are constants to be determined by linearization. As illustrated in Fig. 5, because the velocities of the mass during pure slip motion and damped slip motion are less than or equal to the belt speed V, the relative velocity defined as is negative or zero; i.e., $v_{r}\le 0$. Thus, for the criterion Eq. (6), the kinetic friction force f in the nonlinear function given by (2) can be expressed in the form of a linearized function as

$$\begin{aligned} f=N[a(\dot{x}-V)+b] \end{aligned}$$

(9)

Substituting (9) into (6) and then rearranging yields

$$\begin{aligned} (b-aV)N\left( {x_Q -x_P } \right) +(aN-c)\int _T {\dot{x}^{2}\hbox {d}t} =0\nonumber \\ \end{aligned}$$

(10)

where $x_{P}$ and $x_{Q}$ represent the displacements of the mass at points P and Q, respectively. Because these are equal for pure slip motion, the first term of (10) becomes zero, and because the integral of squared velocity cannot be zero, (10) is true if and only if

$$\begin{aligned} c=aN \end{aligned}$$

(11)

Herein, the damping coefficient represented by (11) is called the pure slip damping coefficient because it is necessary to determine the pure slip condition. However, the above derivations cannot be carried out if the kinetic friction force f is a nonlinear function; this is the reason why the kinetic friction coefficient should be linearized when it is expressed as a nonlinear function of relative velocity.

To obtain a linearized function $\mu _L$ that reflects the characteristics of the nonlinear kinetic friction, the least squares method was employed. While the mass undergoes pure slip motion as illustrated in Fig. 5b, the dissipative energy due to the viscous damping is supplemented by friction-induced energy on the mass during a cycle. This means that the work done by non-conservative forces over a period are equivalent, and thus, the pure slip motion can be approximated as a simple harmonic motion. Under these conditions, the velocity of mass seems to be bounded in the range of $-V$ to V and the magnitude of relative velocity $|v_r|$ is regarded to vary between 0 and 2V in this paper.

Motivated by the consideration that integration of $(f-c\dot{x})\dot{x}$ over a period should be zero for pure slip motion, as presented in (6), linearization conditions for the kinetic friction coefficient were obtained by minimizing the following equation using the least squares method:

$$\begin{aligned} S=\int _{-V}^V {\left[ {\mu (v_r )-\mu _L (v_r )} \right] ^{2}\dot{x}^{2}\hbox {d}\dot{x}} \end{aligned}$$

(12)

Substituting (8) into (12) and then substituting based on the definition of relative velocity, (12) can be rewritten as

$$\begin{aligned} S=\int _0^{2V} {\left[ {\mu (v_r )+a\left| {v_r } \right| -b} \right] ^{2}\left( {V-\left| {v_r } \right| } \right) ^{2}\hbox {d}\left| {v_r } \right| } \end{aligned}$$

(13)

The linearization constants a and b that minimize S are those such that

$$\begin{aligned} \frac{\partial S}{\partial a}=0, \quad \frac{\partial S}{\partial b}=0 \end{aligned}$$

(14)

(13) and (14) lead to the following solutions for a and b:

$$\begin{aligned} a= & {} \frac{5}{2V^{5}}\int _0^{2V} {\mu (v_r )\left( {V-\left| {v_r } \right| } \right) ^{3}\hbox {d}\left| {v_r } \right| } ,\nonumber \\ b= & {} \frac{1}{2V^{4}}\int _0^{2V} {\mu (v_r )\left( {V-\left| {v_r } \right| } \right) ^{2}\left( {8V-5\left| {v_r } \right| } \right) \hbox {d}\left| {v_r } \right| }\nonumber \\ \end{aligned}$$

(15)

By substituting (15) into (11), the damping coefficient to determine the pure slip motion, i.e., the pure slip damping coefficient c, can be expressed in terms of belt speed, normal force, and kinetic friction coefficient as

$$\begin{aligned} c=\frac{5N}{2V^{5}}\int _0^{2V} {\mu (v_r )\left( {V-\left| {v_r } \right| } \right) ^{3}\hbox {d}\left| {v_r } \right| } \end{aligned}$$

(16)

From the form of (16), it can be seen that the mass m and the spring stiffness k do not affect the pure slip damping coefficient.

The above derivations allow pure slip damping coefficients subjected to the exponential-type and polynomial-type friction models to be found that correspond to given system parameters. Substituting (3) into (16) and then integrating the resulting equation, the pure slip damping coefficient for the exponential-type friction model can be obtained in closed form as

$$\begin{aligned} c=\frac{5N(\mu _s -\mu _m )\hbox {e}^{-\alpha V}\left[ {\left( {6\alpha V+\alpha ^{3}V^{3}} \right) \hbox {cosh}\alpha V-\left( {6+3\alpha ^{2}V^{2}} \right) \hbox {sinh}\alpha V} \right] }{V^{5}\alpha ^{4}} \end{aligned}$$

(17)

Similarly, substituting (4) into (16) and then integrating the resulting equation gives the pure slip damping coefficient for the polynomial-type friction model in closed form as

$$\begin{aligned} c=\frac{(\mu _s -\mu _m )N\left( {21v_m^2 -26V^{2}} \right) }{14v_m^3 } \end{aligned}$$

(18)

From the forms of (17) and (18), it can be seen that the pure slip damping coefficient is determined by the belt speed V, the normal force N, and the friction parameters $\mu _s$, $\mu _m$, $\alpha$, and $v_m$.

5 Validation and discussion

To validate the pure slip damping coefficients obtained above, the solutions of (17) and (18) were compared with pure slip damping coefficients obtained by means of numerical computation, and they were also compared with the damping coefficients obtain in previous studies. To facilitate comparison, the physical parameters and initial conditions used for the numerical computation were the same as those given in Sect. 3. First, analytical solutions for the pure slip damping coefficients were obtained using (17) and (18). Then, numerical solutions for the pure slip damping coefficients were obtained by calculating dynamic responses over the range of damping coefficient c from 0 to 6 kg/s, in increments of 0.001 kg/s, and then finding the damping coefficient that yielded pure slip motion. Furthermore, the pure damping coefficients obtained analytically and numerically were also compared with the coefficients of Thomsen and Fidlin [17] and Galvanetto and Bishop [19]. As discussed in the Introduction, since the coefficient of Thomsen and Fidlin [17] cannot be applied to the exponential-type friction model, this coefficient was compared with those for only the polynomial-type friction model. The study results of [18–21] have no intrinsic difference from each other, so only the results of Galvanetto and Bishop [19] were included in the comparison.

Fig. 6

Critical damping coefficients of the exponential-type friction model in the parameter plane of damping coefficient and belt speed

Figure 6 illustrates the pure slip damping coefficients versus belt speed V for the exponential-type friction model. Pure slip damping coefficients are represented by the solid and dashed lines and circle symbols, corresponding, respectively, to the analytical solutions of this study and Galvanetto and Bishop [19] and a numerical result. For this numerical computation, belt speed was varied over the range from 0 to 1 m/s in increments of 0.01 m/s. The analytical and numerical results agreed well, validating the proposed analytical method to determine the criterion corresponding to the occurrence of stick–slip motion. However, the coefficients obtained by Galvanetto and Bishop [19] show large difference from the coefficients by this study. The critical damping coefficients for the polynomial-type friction model were compared between the present and previous studies and a numerical result, in Fig. 7, where the dotted line represent the coefficient obtained by Thomsen and Fidlin [17]. This figure shows that the result of the study closer than the numerical result than the previous studies [17, 19].

Fig. 7

Critical damping coefficients of the polynomial-type friction model in the parameter plane of damping coefficient and belt speed

The relationships between the pure slip damping coefficients and the belt speed were similar when the exponential-type and polynomial-type friction models were used. In both cases, the pure slip damping coefficient decreased as the belt speed increased. That is to say, for a specified damping coefficient, stick–slip motion is replaced by damped slip motion as the belt speed is increased. With reference to Figs. 6 and 7, the left region represents the parametric area for stick–slip motion, i.e., the stick–slip region, and the right region represents the parametric area for damped slip motion, i.e., the damped slip region; these regions are separated by a solid line corresponding to conditions that yield pure slip motion. For better understanding, phase plots illustrating the behavior of parameter sets marked with points A and B in Fig. 6 are shown in Fig. 8 for the exponential-type friction model; similarly, plots for points C and D in Fig. 7 are shown in Fig. 9 for the polynomial-type friction model. The damping coefficient and belt speed corresponding to points A and C are c = 2 kg/s and V = 0.5 m/s, and the damping coefficient and belt speed corresponding to points B and D are c = 2 kg/s and V = 0.8 m/s; in these examples, only the belt speed is changed while the damping coefficient is held constant. Figures 8 and 9 convincingly show that the stick–slip motion is replaced by damped slip motion when the belt speed exceeds a critical speed corresponding to the pure slip state.

Fig. 8

Phase plots when adopting the exponential-type friction model for points A and B in Fig. 6: a point A ($c\,=\,$2 kg/s, $V\,=\,$0.5 m/s), b point B ($c\,=\,$2 kg/s, $V\,=\,$0.8 m/s)

It is quite interesting to compare the transition speeds for the exponential-type and polynomial-type friction models. The transition speeds for the two friction models distinctly differ as the damping coefficient approaches zero. In the case of the exponential-type friction model as illustrated in Fig. 6, as the damping coefficient approaches zero, the transition speed approaches infinity, and thus, the belt speed is unbounded in the stick–slip region. In other words, for very low damping coefficients, the oscillator cannot escape from stick–slip vibration once it occurs. On the other hand, when the polynomial-type friction model is applied as illustrated in Fig. 7, even when the damping coefficient is equal to zero, the transition speed is bounded at $\sqrt{21/26}v_m \approx 0.9v_m$, as obtained from (18), meaning that the belt speeds corresponding to stick–slip motion are those such that $V<0.9v_m$. Thus, regardless of the damping coefficient, stick–slip vibration cannot occur in the oscillator if the belt moves faster than $0.9v_m$.

Fig. 9

Phase plots when adopting the polynomial-type friction model for points C and D in Fig. 7: a point C ($c\,=\,$2 kg/s, $V\,=\,$0.5 m/s), b point D ($c\,=\,$2 kg/s, $V\,=\,$0.8 m/s)

As can be seen from the forms of (17) and (18), the mass and the spring stiffness do not influence the pure slip damping coefficient. In other words, the natural frequency of the oscillator has no direct relevance to the occurrence of stick–slip vibration. However, similar to the belt speed, the normal force and the friction parameters are also related to the occurrence of stick–slip vibration. Using the same parameters and conditions as presented previously, the changes in the stick–slip transition arising from the use of the different minimum friction coefficients $\mu _m$ of 0.2, 0.3, and 0.4 were examined on the parametric plane of belt speed and damping coefficient for both friction models (Fig. 10). The results indicate that the stick–slip region diminishes as the minimum friction coefficient $\mu$ $_{m}$ approaches the static friction coefficient ($\mu _s\,=\,$0.5). In other words, stick–slip vibration can easily occur when the difference between the maximum and minimum friction coefficients is large.

Fig. 10

Pure slip damping coefficient curves for various values of $\mu _m$ when $\mu _s =0.5$, for the two friction models: a exponential-type and b polynomial-type

6 Conclusions

A criterion for the occurrence of stick–slip vibration in an oscillator excited by a moving base has been studied. Whether stick–slip vibration occurs is determined by friction and damping forces. We have derived criterion equations for the occurrence of stick–slip based on the principle of work and energy. To obtain solutions for the criterion equations in closed form, a proposed least squares linearization method has been applied to two friction coefficient functions, an exponential-type friction model and a polynomial-type friction model. The obtained solutions allow us to predict whether given sets of parameters fall within the regime of stick–slip vibration, without requiring the use of time-consuming simulations.

According to the analysis of the occurrence of stick–slip vibration in the present study, we present two significant results. First, the occurrence of stick–slip vibration depends upon the damping coefficient and the belt speed; stick–slip vibration disappears when the damping coefficient or the belt speed exceed a range of transition values. Second, the occurrence of stick–slip vibration is influenced by the form of the friction model used and its relevant parameters. The two friction models considered in our study had similar aspects with regard to increases in the damping coefficient or belt speed; however, if the damping coefficient is close to zero, stick–slip vibration persists only when the exponential-type friction model is applied; this model yields only negative slope with respect to the increment of relative velocity. The difference between the static friction coefficient and the minimum coefficient also affects the stick–slip transition. The stick–slip region in the parameter plane of damping coefficient and belt speed is reduced as the difference between maximum friction coefficient $\mu$ $_{s}$ and minimum friction coefficient $\mu$ $_{m}$ decreases. Hence, it is sufficient to say that reducing the difference between the minimum and maximum friction coefficients is advantageous to avoid stick–slip vibration. All these consequences can be considered useful when engineers design or operate mechanical systems.