The effect of dynamic normal force on the stick–slip vibration characteristics

Abstract

In the experiment, we observed such a phenomenon: the alternating normal force changes the vibration state of a friction system. A single-degree-of-freedom mathematical model was used in this paper to discuss the effects of a constant and alternating normal force on the stick–slip vibration characteristics for different dynamic and static friction coefficients. Under the condition that the applied constant normal force continues to increase, the vibration amplitude of the system, the amplitude of the limit cycle, and the adhesion time of the system increase. When the difference between the dynamic and static friction coefficients (DSFCs) is small, the system has a complete and clear limit cycle. When the dynamic friction coefficient is reduced, the difference between DSFCs increases, and the limit cycle of the system is deformed. The friction system has more abundant dynamic vibration characteristics under an alternating normal force than a constant normal force. The vibration state of the system presents a single-cycle stick–slip vibration when the alternating normal force excites the multi-order harmonic response of the friction system, and the excitation frequency of the alternating normal force is the same as the main response frequency of the system with the highest energy or the low-order even-order main frequency. In contrast, the system exhibits various vibration modes when the excitation frequency of the alternating normal force is dissimilar to the main frequency of the system's highest energy response or is consistent with the odd-order main frequency. In addition, increasing the difference between DSFCs or using very high excitation frequencies and excitation amplitudes increases the likelihood of the system entering a chaotic vibration state.

1 Introduction

As a vibration phenomenon with significant nonlinear characteristics, stick–slip is an important aspect of friction-induced vibration [1,2,3]. For a single-degree-of-freedom (DoF) system, the stick–slip phenomenon occurs when the coefficient of static friction is higher than the coefficient of kinetic friction [4, 5]. Stick–slip vibration can have positive effects, i.e., the stick–slip vibration of a string instrument can produce beautiful music [6], or a friction damper can help reduce vibration [7]. However, stick–slip vibration typically has adverse effects, such as the groaning noise of a brake system [8, 9].

In recent years, many scholars have carried out multi-angle studies on the stick–slip phenomenon. Popp et al. [10] used a discrete model with low degrees of freedom and discovered the potential bifurcation and chaos of the stick–slip system. Velde et al. [11] proposed a mathematical model of the stick–slip phenomenon caused by deceleration. They verified that deceleration motion caused stick–slip and analyzed the influence of different parameter combinations, e.g., the damping coefficient, deceleration, stiffness, on predicting the occurrence of stick–slip. Li et al. [12] used the mass–damper–spring system to study the influence of the lateral runout of the elastic disk on the in-plane stick–slip vibration characteristics. Numerical simulation results showed that the contact separation of the disk and the slider significantly affected the stick–slip vibration and exhibited nonlinear dynamic behavior. Lisowski et al. [13] studied a two-degree-of-freedom nonlinear torsional model with elastic barriers. They showed that this torsional friction behavior can affect the characteristics of the friction system.

And Pascal et al. [14] established a two-DoF model considering dry friction and harmonic loads and discussed the stability of the three motion trajectories. Wang et al. [15] experimentally analyzed the influence of different damping alloys as friction pair materials on stick–slip vibration; the results showed that Mn–Cu damping alloys and aluminum alloys provided the best suppression of stick–slip oscillations. The study also revealed different wear behaviors and clarified the correlation between different wear behaviors and the stick–slip oscillations. Nakano [16] examined the conditions for stick–slip occurrence based on a single-DoF system with Coulomb friction and expressed the difficulty of stick–slip occurrence by two dimensionless parameters. These results show that velocity, damping coefficient, stiffness, load and other parameters can affect the stick–slip vibration.

The use of low-DoF models to explore the effects of various parameters on system vibration characteristics has been widely adopted in previous studies [10, 17,18,19,20,21,22]. McMillan [17] explored the effects of conveyor belt speed and initial conditions on the induced squeal by using a spring–mass–conveyor belt single-DoF model. Marin et al. [18] studied the effects of some main parameters on the phase-plane and phase-space motion states of the stick–slip vibration of the single-DoF and two-DoF models through standard circuit simulation software. Oestreich et al. [19] studied the effect of simple harmonic excitation frequency on system bifurcation and chaos through a single-DoF model. The results showed that changing external excitation frequency changed the dynamics of period-doubling bifurcation to chaos.

Both numerical simulation and experimental studies have shown that the difference between DSFCs is related to the unstable mechanism of frictional motion [23,24,25,26,27,28]. Ozaki et al. [23] carried out a numerical analysis of stick–slip instability using a single-DoF model. The authors verified that a change in the friction coefficient had a substantial impact on stick–slip instability and discussed the system’s dynamic characteristics, such as the quality, stiffness, and driving speed. On the other hand, Lee et al. [24] experimentally investigated the effects of tangential contact stiffness, volume stiffness, relative sliding velocity, and the difference between DSFCs on the intensity and frequency of stick–slip. The test results showed that the intensity and frequency of stick–slip during low-speed braking were substantially affected by all factors.

Researchers have discussed the stick–slip vibration mechanism and the influence of various factors on stick–slip vibration using theoretical analyses and experimental studies. However, most of these studies used the ideal state of the friction system variables, whereas the parameters change in real time under actual working conditions. For example, the external load of the friction system changes dynamically [29]. Simplifying the variables to the ideal state is convenient for research, and the results are more consistent. However, the conclusions are only suitable for guiding theoretical research and may not be applicable to practical conditions.

The normal force is the excitation input of frictional self-excited vibration and has a crucial influence on the vibration characteristics [30,31,32,33,34]. And any slight changes of normal force may cause changes in the vibration characteristics. Maegawa et al. [35] studied the effects of non-uniform normal loads on the precursory events of stick–slip vibration by means of experiments and numerical simulation. Pilipchuk et al. [36] designed a two-degree-of-freedom experimental device considering the effects of gravity and geometric nonlinearity and established a corresponding mathematical model. The influence of the normal force and the speed of the moving belt on the dynamic characteristics of the system during the braking process were explored. The experimental results showed that under the influence of the above two factors, the dynamic response of the system underwent a qualitative transition, namely the appearance of the densifying spectral bend in the final stages of the deceleration process, and this phenomenon could be regarded as an indicator of the appearance of squeal. The results calculated by the mathematical model had a good qualitative match with the experimental results. Liu and Ouyang [37] designed a two-degree-of-freedom test rig too in which the varying normal force was coupled with the tangential friction-induced vibration of a pin in sliding contact with a rotating disc. The disc surface was treated to possess sectors of different friction properties, and this was found to be capable of reducing the stick–slip vibration of the pin.

And Krallis et al. [38], Papangelo et al. [39] and Pasternak et al. [40] investigated the impact of changing normal forces on stick–slip vibration through a single-DoF mathematical model. To expand, Krallis et al. [38] and Papangelo et al. [39] discussed the critical conditions for the transition between general sliding friction vibration and stick–slip vibration of the friction system on the basis of keeping the static friction coefficient equal to the dynamic friction coefficient. And the influence of parameters such as the amplitude and frequency of the normal force on the critical conditions for the transition of these two states was studied. Pasternak et al. [40] were more inclined to explore how to apply alternating normal forces to eliminate or reduce stick–slip vibration, that is, to change from a stick–slip vibration state to a general sliding friction state. The scope of these papers is between the general sliding friction vibration state and the stick–slip vibration state, and does not consider that the application of alternating normal force will cause the stick–slip vibration to evolve into a more complex vibration of multiple vibrations state and chaotic vibration state.

Few studies have reported the stick–slip vibration characteristics of friction systems under dynamic loads. Therefore, research on the influence and mechanism of an alternating normal force on the stick–slip vibration characteristics can provide theoretical support and guidance for minimizing the damage caused by stick–slip vibration under actual working conditions. Therefore, this paper uses a discrete mathematical model to investigate the effect of real-time varying dynamic loads and different friction coefficients on the stick–slip vibration characteristics. The results are compared with the stick–slip vibration behavior of a system under a constant force. The dynamic load is designed as a normal force that changes according to the sine law, and different amplitudes and frequencies of the normal force are evaluated in the simulation. The time-domain and frequency-domain characteristics of the stick–slip vibration of the friction system under an alternating normal force are evaluated using bifurcation diagrams, phase-space diagrams, spectrograms, and Poincaré diagrams for different excitation amplitudes and excitation frequencies to determine the potential vibration states of the system.

2 Single-degree-of-freedom mathematical model

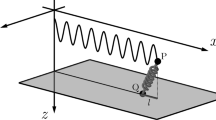
This paper uses the classic undamped single-DoF lumped-mass model to analyze the influence of the alternating normal force on stick–slip vibration. A qualitative analysis is carried out of the dynamic characteristics of the system's stick–slip vibration under an alternating normal force. It should be pointed out that the friction disk in the test equipment (Fig.1) is in rotation and thus the motion of the mass block is largely in one (circumferential) direction, which can be modeled as a translation. As shown in Fig. 2, the concentrated mass m is connected to the fixed wall by a spring of stiffness k₁ and is simultaneously subjected to the normal force F_N and the frictional force between the rigid conveyor belt and the mass moving at a constant speed v₀. It is assumed that the mass and the conveyor belt remain in contact without separation. Since this article focuses on the influence of the alternating normal force on the stick–slip vibration performance of the friction system, the basic parameters in the single-DoF model are set to constants (m = 1 kg, k₁ = 1 N/m, v₀ = 1 mm/s) except the normal loading force F_N. The parameters were selected based on theoretical research [10]. The Coulomb friction model with constant dynamic and static friction coefficients is used to determine the influence of the alternating normal force on the stick–slip motion. Among various influencing factors, the friction coefficient has the most considerable effect on the vibration behavior [23,24,25,26,27,28]. Since it is impossible to evaluate if the friction coefficient has a considerable effect on the vibration behavior of the system under an alternating normal force, we select two groups of dynamic and static friction coefficients. The first group includes the static friction coefficient μ_s = 0.4 and the dynamic friction coefficient μ_k = 0.2; the second group consists of the static friction coefficient u_s = 0.4 and the dynamic friction coefficient μ_k = 0.1. The simulation calculation is conducted using MATLAB software. The influences of the excitation amplitude (F_ω) and the excitation frequency (ω) of the alternating normal force on the stick–slip vibration are investigated.

Fig. 1

The test device: a object picture and b schematic diagram

Fig. 2

The single-DoF mathematical model

According to Newton's second law, the dynamic equation of a single-DoF system in the x-direction is expressed as:

$$ m\ddot{x}{ + }k_{1} x{ = }F_{f} $$

(1)

The friction force F_f is the product of the friction coefficient and the normal contact force F_N between the mass m and the conveyor belt, where F_f = μF_N

$$ F_{N} = F_{0} + F_{\omega } \sin (\omega t) $$

(2)

The ode45 solver in MATLAB is used to solve the time-domain response signal of the system. Due to the interface stick–slip dynamic behavior of the system, the switch model algorithm [41] is used to solve the response of the non-smooth system. It is assumed that the relative speed between the mass and the conveyor belt is v_r; its expression is shown in Eq. (3):

$$ v_{r} { = }v_{0} - \dot{x} $$

(3)

If $\left| {v_{r} } \right| > \varsigma$, where $\varsigma$ is the set minimum error value (10^–6), relative sliding occurs between the friction block and the conveyor belt, and the system is in the slip state. The expression of the dynamic friction force F_f-slip is shown in Eq. (4):

$$ F_{f - slip} = \mu_{k} F_{N} $$

(4)

If $\left| {v_{r} } \right| < \varsigma$ and the spring force is less than the friction force, the mass and the conveyor belt remain relatively static, and the friction system is in the stick state. The static friction force F_f-stick is the combination of the spring force and the maximum static friction force F_mf-stick. Two conditions can occur, as shown in Eq. (5):

$$ F_{{f - {\text{stick}}}} = \left\{ {\begin{array}{*{20}l} {k_{1} x} \hfill & {{\text{Spring}}\;{\text{force}} \le F_{{{\text{mf}} - {\text{stick}}}} } \hfill \\ { - \mu _{s} F_{N} \text{sgn} (v_{r} )} \hfill & {{\text{Spring}}\;{\text{force}} > F_{{{\text{mf}} - {\text{stick}}}} } \hfill \\ \end{array} } \right. $$

(5)

3 Test equipment, results and discussion

3.1 Test equipment and parameters

The experiment is conducted on the CETR-UMT-3 multifunctional friction and wear testing machine using a typical pin-disk surface contact mode. The equipment consists of a test device and a signal acquisition device. The friction block sample and the friction disk sample are attached to the test device with a friction block clamp and friction disk clamp, respectively. The friction block consists of composite material, with dimensions of 9 mm × 9 mm × 15 mm and roughness of 0.4 μm. The friction disc is forged steel with a diameter of 25 mm, a thickness of 3 mm, and roughness of 0.06 μm. The friction radius between the friction block and the friction disc, i.e., the distance between the two components, is 6.1 mm. The normal force and friction force during the test are measured by the built-in two-dimensional force sensor (sensitiveness: 0.025 N; range 5 ~ 500 N) inside the CETR, and the data are stored in the computer that controls the CETR machine. The tangential vibration velocity of the friction block is measured by a laser vibrometer (model: Polytec PDV-100; sensitivity: 8 mv/mm/s; range: ± 500 mm/s; frequency response: 0.5 ~ 22 kHz). The measured data are collected by an 8-channel data acquisition instrument (DH5922N), and the sampling frequency is 10 kHz. The normal, tangential, and radial vibration acceleration signals of the friction block are measured by a three-dimensional acceleration sensor (model: KISTLER 8688A50; sensitiveness: 100 mV/g; frequency response: 0.5 ~ 5 kHz), and the measured data are collected by the 8-channel data acquisition instrument; the sampling frequency is 10 kHz. The test is conducted in a dry environment under standard atmospheric pressure (room temperature: 24 ~ 27°C relative humidity: 60 ± 10%).

The test is divided into two parts. First, a constant normal force of 160 N, 180 N, and 200 N is applied. Second, an alternating normal force is applied with the following parameters: median force F₀ = 180 N, amplitude F_ω = 20 N, and excitation frequencies of 0.25 Hz, 0.5 Hz, 1 Hz, and 2 Hz (the relationship between the excitation frequency f and the excitation angular frequency ω is: f = ω/2π). In the process of test, the rotation speed of the friction disc remains constant at 2.5 rpm, the duration of each group of tests is 2 min, and each set of tests is repeated 3 times.

3.2 Test results and discussion

The tangential velocity signal measured by the laser vibrometer is integrated in the frequency domain to obtain the tangential displacement signal. Figure 3 shows the phase diagrams of the system in the stable phase of 50 s–52 s under three constant normal forces. The velocity in the stick stage is not constant, but there are slight fluctuations due to the inevitable jitter of the test equipment during the test. Under the condition that the applied constant normal force continues to increase, the displacement of the system in the stick state increases. After the displacement reaches the maximum value, it decreases, and with the rapid decrease in speed, the displacement increases rapidly. Since the rotation speed of the friction disc is constant, the greater the normal force, the greater the frictional force of the friction interface is. Thus, the system must accumulate more tangential elastic potential energy to overcome the frictional force. Therefore, since the maximum static friction of the interface has not been exceeded by the elastic potential energy, the tangential displacement of the system continues to increase, and more kinetic energy is accumulated for release in the slip phase. As a result, the speed amplitude of the system increases in the slip phase, corresponding to an increase in the amplitude of the middle limit cycle, as shown in Fig. 3.

Fig. 3

The phase diagram of the system under a constant force a 160 N, b 180 N, c 200 N ^[42]

Figure 4 shows the tangential vibration acceleration signal and the root-mean-square (RMS) value of the system in the stable phase of 50 s–52 s under the constant normal force. The tangential acceleration signal of the system exhibits periodic relatively constant values and peaks. When the acceleration is zero, the friction block and the friction disc are in a relatively static state, and a sudden change in acceleration means that the friction block and the friction disc are in a sliding state. Under the constant normal force, the acceleration amplitude depends on the magnitude of the applied normal force. The greater the applied normal force is, the greater the acceleration amplitude is, i.e., the system is transitioning to a more intense stick–slip vibration state. The acceleration RMS increases with an increase in the normal force.

Fig. 4

a Acceleration signal and b acceleration RMS value of the system under a constant force

Figure 5 exhibits the phase diagram in the stable phase of 50 s–55 s under the four excitation frequencies. The amplitude of the limit cycle of the system is significantly lower under the alternating normal force than the constant normal force, and the shapes of the limit cycle are different. Limit cycles exist in the system at excitation frequencies of 0.25 Hz, 0.5 Hz, and 1 Hz, but the form is different. This result shows that the system exhibits periodic stick–slip motion in these three states, but the motion patterns are different. There is no limit cycle at an excitation frequency of 2 Hz, and the motion trajectories are complex. Figure 5 exhibits that the motion state changes from stable periodic stick–slip vibration to irregular vibration as the frequency of the applied alternating force increases.

Fig. 5

The phase diagram of the system under an alternating force a 0.25 Hz, b 0.5 Hz, c 1 Hz, d 2 Hz

Figure 6 shows the tangential vibration acceleration signal and the RMS value of the acceleration when the system is in the stable phase of 50 s–55 s under the four excitation frequencies. At excitation frequencies of 0.25 Hz, 0.5 Hz, and 1 Hz, a phenomenon similar to that of applying a constant normal force is observed, i.e., the tangential acceleration signal of the system exhibits relatively constant values interrupted by periodic peaks, and the system is in the stick–slip–stick vibration state. However, the difference is that the stick–slip vibration period becomes shorter, and the magnitude of the vibration reduces with an enlargement in the excitation frequency. The RMS values are similar at excitation frequencies of 0.25 Hz, 0.5 Hz, and 1 Hz (Fig. 6b), indicating similar vibration intensities of the system. In contrast, the tangential vibration acceleration signal of the system is more complex at an excitation frequency of 2 Hz, exhibiting a more chaotic vibration signal. Thus, the acceleration of RMS value is significantly higher at 2 Hz than at the other three excitation frequencies, indicating that the vibration intensity and shape of the system are not solely stable stick–slip vibrations. Figure 6 indicates that increasing the excitation frequency of the alternating normal force causes the system to change from stable stick–slip vibration to unstable friction vibration.

Fig. 6

a Acceleration signal and b acceleration RMS value of the system under the alternating force

4 The stick–slip vibration characteristics obtained from a single-degree-of-freedom theoretical model

4.1 The stick–slip vibration characteristics of the system under a constant normal force

The first set of dynamic and static friction coefficients (μ_s = 0.4, μ_k = 0.2) is selected to research the stick–slip vibration characteristics of the system under a constant normal force. Figure 7 exhibits the phase diagram and bifurcation diagram under different constant normal forces. The external normal force gradually increases from 10 to 40 N in steps of 5 N. As the constant normal force increases, stick–slip vibration appears in the system, and the amplitude of the limit cycle of the stick–slip vibration increases sequentially. It is manifest from Fig. 7b that under the condition that the normal force keeps increasing, the balance point of the mass block produces a slight offset, whose value is calculated according to Eq. 6. Under the condition that the normal force keeps increasing, the offset and the amplitude of the mass increase. The reason is that an increase in the normal force increases the maximum static friction force, inducing the system to generate a greater spring force to get over the static friction force. The force ultimately promotes an increase in the adhesion time of the mass, which stores and releases more energy in a single cycle.

$$ x_{s} = \mu_{k} F_{N} {/}k_{1} $$

(6)

Fig. 7

a Phase diagram and b bifurcation diagram of the system under different constant forces

The differential equations of the system are solved by MATLAB's ode45 solver. The initial parameter values are different; therefore, the system requires a different number of steps to reach a stable state. In this paper, the duration of each calculation is 100π s, and the results of the first 300 s are shown in the graph. Only the data after t₁ (62.8 s) are selected for the frequency-domain analysis to prevent an influence of the initial value on the analysis of the system motion state. Figure 8 exhibits the time-domain and frequency-domain signals of the stick–slip vibration of the friction system under normal forces of 20 N and 25 N.

Fig. 8

a Vibration velocity time-domain signal and b FFT analysis results of the friction system under constant forces of 20 N and 25 N

Under a constant normal force, the time–velocity curve of the mass shows a constant single-periodic motion state, and as the normal force increases, the amplitude and period of the system vibration increase. The frequency spectrum of the vibration velocity in t₁ ~ 300 s exhibits that the fundamental frequency of the system response reduces with an increase in the normal force. When the normal force is 20 N (25 N), the system produces a multi-order harmonic response with a fundamental frequency of 0.0855 Hz (0.0738 Hz). Table 1 lists the fundamental frequencies of the system responses under different constant normal forces. As the normal force increases, the fundamental frequency of the vibration response decreases, and the vibration period of the system increases.

Table 1 The basic frequency of the stick–slip vibration response of the friction system under different constant normal forces

Figure 9 shows the displacement–velocity two-dimensional phase diagram of the mass, the three-dimensional phase-space diagram expanded according to the motion cycle (the polar diameter and polar angle of the two-dimensional polar coordinate system, respectively, represent the displacement and the motion period, and the Z axis represents the speed), and the Poincaré cross-section based on the projection of the three-dimensional phase-space trajectory on a plane with a polar angle of π and parallel to the Z-axis (O in the figure represents the pole of the polar coordinates, and θ represents the polar angle). The Poincaré cross-section diagram is used to distinguish the periodic motion, quasi-periodic motion, chaotic motion, and other motion behaviors of the system according to the dynamic differential equations of nonlinear systems. Under the constant normal force, the motion state of the system shows stable single-periodic stick–slip vibration. The two-dimensional phase diagram indicates a single-periodic limit cycle, which is expanded in the three-dimensional phase-space with only one motion trajectory; thus, only one point is shown in the Poincaré cross-section in Fig. 9c. Therefore, under the constant forces of 20 N and 25 N, the mass exhibit single-periodic stick–slip motion.

Fig. 9

a Phase diagram, b phase-space diagram, and c Poincaré cross-section diagram of the system under different normal forces

4.2 The stick–slip vibration characteristics of the system under an alternating normal force

Figure 10 shows the bifurcation and corresponding Lyapunov exponent of the displacement of the mass with the frequency of excitation at a median alternating normal force of F₀ = 25 N and an amplitude of F_ω = 5 N. As the excitation frequency increases, the mass exhibits multiple motion states, such as chaos, single-periodic vibration, and multi-periodic vibration. According to the criterion of Lyapunov exponent for periodic, chaotic, and other forms of motion of the system [43, 44], the bifurcation diagram is divided into seven regions. In regions 'I', 'III' and 'V', the motion state of the system is disordered; in regions 'II', 'IV', and 'VI', the system is in a single-periodic motion state; in region 'VII', the system exhibits multiple motion states. Bifurcation phenomena are observed near critical points, such as sudden boundary changes and jumps. For example, when the excitation frequency is 0.62 rad/s (the critical point of regions 'II' and 'III'), the single-periodic motion state of the mass block suddenly changes.

Fig. 10

a Bifurcation diagram and b corresponding Lyapunov exponent diagram of the system displacement with the excitation frequency at an excitation amplitude of 5 N

Further, we discuss the stick–slip vibration characteristics of the friction system for different frequencies. An excitation frequency of ω = 0.27 rad/s is selected in the chaotic stage, and ω = 0.5 rad/s is selected in the single-periodic stage, and ω = 0.69 rad/s and ω = 1.65 rad/s are chosen in multiple vibration stage.

Figure 11 displays the phase diagram, phase-space diagram, and Poincaré cross-section diagram of the stick–slip vibration of the friction system at different frequencies. At ω = 0.27 rad/s, a single limit cycle with multiple loops is observed in the phase diagram. As the calculation time increases, the number of loops increases, and the phase-space trajectory becomes more chaotic. Multiple discrete points are observed, and the system is in chaotic stick–slip motion at this time. At ω = 0.5 rad/s, the phase diagram exhibits a single-periodic limit cycle, the phase-space diagram has only one trajectory, and only one point is visible in the Poincaré cross-section diagram. Under these circumstances, the system is in a single-periodic stick–slip motion state. At ω = 0.69 rad/s, the system is in a two-periodic vibration state. The phase diagram and phase-space diagram show an additional trajectory, and the Poincaré cross-section diagram exhibits two discrete points. At ω = 1.65 rad/s, the Poincaré cross-section depicts a straight line, and the system is in a quasi-periodic stick–slip state.

Fig. 11

a Phase diagram, b phase-space diagram, and c Poincaré cross-section diagram of the system for different excitation frequencies

Figure 12 shows the external excitation signal, vibration velocity signal, and fast Fourier transform (FFT) analysis results of the system for four excitation frequencies. The value of t₁ is the same in Fig. 12 and Fig. 8. In Fig. 12c, the left Y-axis depicts the FFT results of the speed signal, and the right Y-axis shows the stress vibration frequency (dashed line). The friction system produces multiple main response frequencies at an excitation frequency of 0.27 rad/s and a frequency of 0.0430 Hz. The highest response frequency of the system is 0.0725 Hz, and the vibration behavior of the mass is complex. At 0.5 rad/s, the friction system produces a multi-order harmonic response with a fundamental frequency of 0.0796 Hz. At this time, the excitation frequency is consistent with the response frequency of the system with the highest energy, and the system is in a single-cycle stick–slip state (Fig. 10). At 0.69 rad/s, the excitation frequency is 1.5 times of the response frequency of the system with the highest energy. At this time, the system is in a two-periodic stick–slip state. At 1.65 rad/s, the excitation frequency is in keeping with the third-order vibration frequency component of the system’s response fundamental frequency, and the system is in a quasi-periodic stick–slip motion state.

Fig. 12

a Normal force time-domain diagram, b velocity time-domain diagram, and c frequency spectrum diagram of the system for different excitation frequencies

Further, we select an excitation frequency in each region in Fig. 10 and calculate the response frequency of the system with the highest energy. The frequency data are exhibited in Table 2. The excitation frequency of 0.67 rad/s in area 'III is greater than the highest response frequency but less than the second-order response frequency of the system. The value is three-half of the main frequency of the highest response of the system. At this time, area 'III' is the transition area between the single-periodic stick–slip motion areas 'II' and 'IV'. In area 'IV', the excitation frequency is 1 rad/s, which is consistent with the second-order response frequency of the system. The system is in a single-periodic stick–slip state. In region 'V', the excitation frequency is 1.7 rad/s, which is consistent with the third-order response frequency of the system. However, Fig. 10 exhibits that the system is in a multi-periodic stick–slip motion state at this time. In area 'VI', the excitation frequency is 2.25 rad/s, which is consistent with the fourth-order response frequency of the system; the system is still in a single-periodic stick–slip motion state. In area 'VII', the excitation frequency is 3.15 rad/s, which is equal to the fifth-order response frequency of the system. As the excitation frequency increases, the system goes through different vibration states, including single cycle, multi-periodic, quasi-periodic, and chaotic vibration states.

Table 2 Response frequency of the system for different excitation frequencies

These results show that the condition of the system is chaotic vibration when the excitation magnitude is constant, the excitation frequency does not cause a harmonic response of the system, and the excitation frequency is not a multiple of the main frequency of the system with the highest energy response. When the excitation frequency causes a harmonic response of the system, the system is in a single-cycle motion state if the excitation frequency is in keeping with the main frequency of the system with the highest energy response or an even-order multiple (second-order, fourth-order) of the main frequency. The system can have various vibration states if the frequency is the same as the dominant frequency of the highest odd-order (third-order) of the system, or the excitation frequency is greater than the dominant frequency of the higher-order (fifth-order) response of the system.

Figure 13 shows the bifurcation and corresponding Lyapunov exponent of the displacement with the excitation frequency for an excitation amplitude of F_ω = 10 N. Increasing the excitation amplitude increases the displacement extremum of the bifurcation diagram of the system, which agrees with the results in Fig. 7. The bifurcation diagram is divided into three regions, and the main frequency of the system response at different excitation frequencies is analyzed. The results are listed in Table 3. In area 'I', the excitation frequency is selected as 0.15 rad/s for analysis. This excitation does not cause a harmonic response of the system and is less than the main frequency response of the system with the highest energy. The motion state of the system is disordered. In area 'II', the excitation frequency is selected as 0.55 rad/s for analysis. The excitation frequency is in keeping with the dominant frequency of the system’s highest energy response, and the system is in a single-periodic stick–slip state. Two excitation frequencies (1.35 rad/s and 4.15 rad/s) are selected in area 'III' for analysis. At 1.35 rad/s, the excitation frequency is equal to the third-order response frequency of the system; at 4.15 rad/s, the excitation frequency is in keeping with the seventh-order response frequency of the system. In area 'III', the motion state of the system changes from the stable single-periodic motion in the previous stage to a variety of motion states including chaotic motion. The periodic motion regions and the chaotic regions can also be clearly distinguished from the Lyapunov exponent diagram (Fig. 13). These results indicate that an increase in the excitation amplitude of the alternating normal force increases the area where the system is in multiple vibration states; the system is more likely to be in a state of chaotic motion.

Fig. 13

a Bifurcation diagram and b corresponding Lyapunov exponent diagram of the system displacement with the excitation frequency at an excitation amplitude of 10 N

Table 3 Response frequency of the system for different excitation frequencies

The influence of the excitation amplitude value on the system motion state is analyzed for an excitation frequency of 0.5 rad/s. The bifurcation diagram of the mass displacement response is shown in Fig. 14. The bifurcation graph is divided into two regions. In region 'I', the system is in a multi-periodic stick–slip motion state, and the excitation frequency does not cause a higher energy response frequency of the system. In region 'II', the system is in a single-periodic stick–slip motion status, and the excitation frequency is in keeping with the response frequency of the system with the highest energy (see Table 4 for the details).

Fig. 14

Bifurcation diagram of the system displacement with the excitation amplitude value at an excitation frequency of 0.5 rad/s

Table 4 Response frequency of the system for different excitation amplitudes

Figure 15 exhibits the bifurcation diagram of the displacement response of the mass with the excitation amplitude at an excitation frequency of 1.65 rad/s. Similarly, the bifurcation graph is divided into three regions. The vibration form of the friction system is more complex for the excitation frequency of 1.65 rad/s than of 0.5 rad/s. In area 'I', the system is in a state of multi-periodic stick–slip motion. At this time, the external excitation frequency does not cause a multi-order harmonic response of the system and a higher energy response of the main frequency. In area 'II', the system is in a single-periodic stick–slip state, and the excitation frequency is equal to the fourth-order response frequency of the system. The displacement response of the mass undergoes abrupt changes and increases at the critical points of regions 'II' and 'III'. In area 'III', the system is in a variety of vibration states prior to a normal force of 13.1 N. Subsequently, the system begins to bifurcate into two motion states, which can be approximated as a combination of two multi-periodic motions.

Fig. 15

Bifurcation diagram of the system displacement with the excitation amplitude at an excitation frequency of 1.65 rad/s

Different excitation amplitude values in area 'III' are chosen to calculate the response frequency of the system, as listed in Table 5. A state of motion exists where the excitation frequency stimulates the harmonic response of the system and is in keeping with the third-order response frequency. A harmonic response whose excitation frequency does not affect the system is also observed, resulting in a state of motion in keeping with the highest response frequency of the system. In addition, the friction system also has a two-periodic-like motion state in which two multi-periodic motions are combined, and the excitation frequency of the system is in keeping with the second-order response frequency of the system. At the same excitation amplitude, increasing the excitation frequency complicates the system's vibration form, and it becomes more difficult to transition to a single-periodic stick–slip state.

Table 5 Response frequency of the system for different excitation amplitudes

5 Influence of an alternating normal force on the system vibration characteristics for different friction coefficients

5.1 The stick–slip vibration characteristics of the system under a constant normal force

Figure 16 exhibits the phase diagram and bifurcation diagram of the vibration response of the friction system under different constant normal forces for the coefficients μ_s = 0.4 and μ_k = 0.1. As the normal force increases, a slight deviation of the system equilibrium point occurs in the positive tangential direction, and the vibration amplitude of the mass limit cycle increases. In addition, the displacement of the mass shows a significant increase in the negative tangential direction (minimum point of displacement). It is manifest from Fig. 16(a) that the vibration form of the friction system does not change significantly when the constant normal force is changed. However, the motion form of the mass of the friction system changes after increasing the difference between the dynamic and static friction coefficients from (μ_s = 0.4, μ_k = 0.2) to (μ_s = 0.4, μ_k = 0.1). The reason is that an increment in the difference between DSFCs increases the negative displacement of the mass, affecting the compression state of the tangential spring as the mass changes from the slip state to the stick state. When the external force generated by the spring is much greater than the dynamic friction force, the mass has faster acceleration in the positive tangential direction, increasing the speed of the mass, as shown in Fig. 16(a).

Fig. 16

a Phase diagram and b bifurcation diagram of the system vibration response under different constant normal forces

Figure 17 exhibits the time-domain diagram and frequency-spectrum diagram of the vibration velocity of the friction system at normal forces of 20 N and 25 N. Increasing the difference between DSFCs does not change the motion state; the system has the stick and slip motion states. At a normal force of 20 N (25 N), the system’s vibration response frequency is a multi-order harmonic response with a fundamental frequency of 0.0738 Hz (0.0637 Hz). Figure 18 shows the phase diagram, phase-space diagram, and Poincaré cross-section diagram of the vibration response of the friction system under the two normal forces. The phase diagram exhibits a single limit cycle, and the phase-space diagram depicts a single motion trajectory, but the limit cycle and phase-space trajectory are slightly deformed. The Poincaré cross-section diagram shows only one discrete point.

Fig. 17

a Time-domain diagram and b frequency spectrum diagram of the system vibration response under a constant normal force

Fig. 18

a Phase diagram, b phase-space diagram, and c Poincaré cross-section diagram of the system under a constant normal force

5.2 The stick–slip vibration characteristics of the system under an alternating normal force

Figure 19 shows the bifurcation and corresponding Lyapunov exponent of the vibration response of the mass of the friction system with the excitation frequency for coefficients μ_s = 0.4 and μ_k = 0.1. The median force is F₀ = 25 N, and the excitation amplitude is F_ω = 5 N. When the difference between DSFCs (μ_s = 0.4, μ_k = 0.1) is increased, the vibration state of the system is similar to that at μ_s = 0.4 and μ_k = 0.2, exhibiting periodic motions and chaotic vibration states. However, the chaotic vibration range is significantly increased, and this phenomenon can be seen more clearly from the Lyapunov exponent diagram. In Fig. 10b, there are regions where the Lyapunov exponent is continuously equal to zero, while in Fig. 19b there are only a few points where the Lyapunov exponent is equal to zero, that is, most of the frequency range under study leads to a Lyapunov exponent greater than zero. When the excitation frequency is in the range of 0.32 rad/s–0.78 rad/s, the system exhibits two distinct regions of vibration magnitudes. When the excitation frequency is within the range of 0 rad/s–0.32 rad/s and 0.78 rad/s–5 rad/s, the range of the vibration magnitude changes slightly. The excitation frequencies of 0.51 rad/s, 1.25 rad/s, and 3.98 rad/s are selected for further analysis.

Fig. 19

a Bifurcation diagram and b corresponding Lyapunov exponent diagram of the vibration displacement of the friction system with the excitation frequency at an excitation amplitude of 5 N

Figure 20 shows the phase diagram, phase-space diagram, and Poincaré cross-section diagram of the mass motion of the friction system for excitation angular frequencies of 0.51 rad/, 1.25 rad/s, and 3.98 rad/s. At 0.51 rad/s, a single limit cycle with multiple loops occurs in the phase diagram, and the phase-space trajectory shows very chaotic conditions. The Poincaré cross-section diagram shows irregularly distributed points. Under these circumstances, the system is in a chaotic vibration state. At 1.25 rad/s, there is a stable three-loop limit cycle in the phase diagram of the friction system; correspondingly, there are three motion trajectories in the phase-space diagram and three discrete points on the Poincaré cross-section diagram. At this time, the system is in a three-periodic vibration state. The vibration type of the friction system at 3.98 rad/s is similar to that at 0.51 rad/s. There is a single limit cycle with multiple loops in the phase diagram, and the phase-space trajectory is chaotic. Multiple discrete points are randomly distributed in the Poincaré cross-section diagram, and the system is in a state of chaotic vibration.

Fig. 20

a Phase diagram, b phase-space diagram, and c Poincaré cross-section diagram of the system for different excitation frequencies

Figure 21 shows the normal force time-domain diagram of the friction system, the vibration velocity time-domain signal, and the FFT analysis results for excitation frequencies of 0.51 rad/s, 1.25 rad/s, and 3.98 rad/s. The meaning of t₁ in Fig. 21 is consistent with that in Fig. 8, and the details of the graph in Fig. 21c are consistent with that in Fig. 8c. At an excitation frequency of 0.51 rad/s, the excitation frequency does not cause a harmonic response of the system, and the system has multiple response main frequencies. At 1.25 rad/s, the excitation frequency stimulates a multi-order harmonic response of the system and is consistent with the third-order response frequency of the friction system. At 3.98 rad/s, although the excitation frequency stimulates a multi-order harmonic response of the system, it is equal to the high-order response of the system, and the vibration state of the system is disordered. Increasing the difference between the friction coefficients from (μ_s = 0.4, μ_k = 0.2) to (μ_s = 0.4, μ_k = 0.1) results in the deformation of the limit cycle of the mass movement and an increase in the range in which the system is in a state of chaotic vibration.

Fig. 21

a Normal force time-domain diagram, b velocity time-domain diagram, and c frequency spectrum diagram of the system for different excitation frequencies

Figure 22 shows the bifurcation diagram of the displacement response of the mass with the excitation amplitude at an excitation frequency of 0.5 rad/s. The bifurcation graph is decomposed into four sections: 'I', 'II', 'III', and 'IV'. In area 'I', the system diverges from a single cycle to multiple cycles and finally enters a chaotic state as the excitation amplitude enhances. The excitation amplitude values of 1.8 N, 2.8 N, and 3.6 N are chosen to calculate the response frequency of the system. In area 'I', the external excitation frequency does not cause a higher response frequency of the system (see Table 6), and the system remains in a state of chaotic motion. In area 'II', the system has a smaller vibration amplitude. The excitation amplitude values of 5.8 N, 6.9 N, and 7.8 N are chosen to calculate the response frequency of the system. At this time, the external excitation frequency does not produce a harmonic response and a higher energy response frequency (see Table 6) of the system. In area 'III', the system enters a single-cycle motion state, and the external excitation frequency is consistent with the response frequency of the system with the highest energy (see Table 6). As the excitation amplitude value further increases, the system bifurcates into a two-period motion state in area 'IV', and the external excitation frequency remains the same as the response frequency of the system with the highest energy. These results show that increasing the difference between DSFCs increases the likelihood of the system being in a multi-period vibration state or chaotic motion state. When the excitation amplitude value is very large, the system may branch into a multi-periodic vibration state, even if the external excitation frequency is consistent with the main response frequency of the system with the highest energy.

Fig. 22

Bifurcation diagram of the system displacement with the excitation amplitude at an excitation frequency of 0.5 rad/s

Table 6 Main response frequency of the system for different excitation amplitudes

Further, we discuss the influence of the change of friction coefficient on the stick–slip vibration characteristics of the system under the action of alternating normal force, and select F₀ = 25 N, the excitation amplitude F_ω = 5 N, the excitation frequency ω = 2.5 rad/s. The static friction coefficient is kept constant at 0.4, and the kinetic friction coefficient increases from 0.05 to 0.4. The bifurcation diagram of the system vibration displacement response with the dynamic friction coefficient is shown in Fig. 23. It can be seen that with the increase in the kinetic friction coefficient, the vibration displacement response of the system gradually evolves from an irregular chaotic motion state to a periodic motion state, and the larger the kinetic friction coefficient is, the more obvious this periodicity is. In the region where the coefficient of kinetic friction is less than 0.077, the fluctuation range of the displacement response is much larger than in other regions. These results show that increasing the difference between DSFCs increases the likelihood of the system being in chaotic motion state.

Fig. 23

Bifurcation diagram of system displacement response with dynamic friction coefficient

6 Conclusion

The experiments demonstrated that an alternating normal force changed the vibration state of the system. We selected two sets of dynamic and static friction coefficients and used a single-DoF model to investigate the influence of the normal force on the vibration characteristics of the system. The system had more abundant dynamic vibration characteristics under an alternating normal force than a constant normal force. Furthermore, the effects of different excitation amplitudes and excitation frequencies on the alternating normal force on the system’s vibration characteristics were obtained. The main conclusions are as follows:

• 1. For both sets of dynamic and static friction coefficients, as the constant normal force increased, the vibration amplitude of the system, the amplitude of the limit cycle, and the adhesion time of the system increased. When the difference between DSFCs was small, the system had a complete and clear limit cycle. Reducing the coefficient of dynamic friction led to an increase in the difference between DSFCs, and the limit cycle of the system was deformed.

• 2. Under the influence of changing excitation frequency and excitation amplitude, the system might be in a single-periodic, multi-periodic, and chaotic stick–slip vibration state. When the external excitation frequency caused a harmonic response of the system and was consistent with the system's highest energy response frequency or coincided with the low-order even-order (second-order, fourth-order) main frequency, the system was in a single-cycle stick–slip vibration state. When the excitation frequency was different from the system's highest energy response frequency, or when the excitation frequency was in keeping with the odd-order main frequency of the system, the system could enter various vibration states. In addition, when the excitation frequency and excitation amplitude were very too high, the system could enter multiple vibration states earlier.

• 3. Under the influence of changing excitation frequency and excitation amplitude, the system was more likely to enter a chaotic vibration state or period-doubling bifurcation state when there was a large difference between DSFCs.