1 Introduction

Friction is a very complicated dynamics phenomenon and plays a crucial role in various engineering systems, such as mechanical engineering, civil engineering and seismology [1,2,3]. Moreover, it is a typically nonsmooth factor that may induce self-excited vibration in extensive engineering systems, such as brake systems [4], bearing systems [5], rotating drilling systems [6], rotor rubbing systems [7], and so on. A great number of comprehensive models have been established, such as Coulomb friction model, Dahl model, Sribeck friction, Karnopp model and LuGre model [8, 9]. Among them, the Coulomb friction model is the simplest one and has been extensively adopted.

Friction induced self-excited vibration, also known as stick-slip vibration, often cause some undesired effects observed in everyday life as well as engineering applications, including noise of a squeaking door, squeaky chalk on a blackboard, brake squeal, rattling joints of a robot, chattering machine tools and others. The self-excited vibrations between contact interfaces may lead to wear and damage of a machinery or a failure of a mechanical system. Scholars have done a variety of theoretical and experimental research on the related problems caused by the stick-slip vibration [10,11,12]. Many researchers have attempted to understand stick-slip vibrations by using a simple oscillator excited by a moving belt that exerts a friction force. Majority of these investigations in literature have focused on the occurrence of stick-slip vibration [13, 14], stick-slip periodic solution [15, 16], asymmetric non-sticking solutions [17], stick-slip amplitudes [18, 19] and stick-slip chaos [20,21,22]. However, stick-slip vibrations are sensitive to material properties, such as physical and mechanical properties of the materials between the two surfaces in contact, stiffness of the components, surface topography, system damping, working environment and so on. Until to now, there is no an efficient and feasible method which can fully explain the stick-slip vibration phenomenon. Thus, it is quite important to comprehensively understand the conversion mechanism between the stick motion and the slip motion, which may provide some guidance to reduce the harmful influences of the stick-slip motion on mechanical components and improve the operating performance.

At present, there are numerous nonlinear friction systems characterized by geometry nonlinearities of elastic large deformation or large displacement in mechanical engineering, seismology and climatostratigraphy, such as the geometric friction-induced vibration between the brake plate and pad in a brake system [23], the motion between the moving tectonic plates in an earthquake fault moving across each other [24], the stick-slip phenomenon of the Whillans Ice Stream (WIS) as the climate changes [25]. Therefore, it is of great practical significance to study the mechanism of stick-slip vibrations of friction systems with geometry nonlinearity.

Recently, a self-excited SD oscillator with geometric nonlinearity was proposed in [26] based upon the SD oscillator [28,29,30,31] mounted on a moving belt, which is characterized by the multiple stick zones, hyperbolic structure transition and friction-induced asymmetry phenomenon. The threshold of multiple stick-slip chaos for the perturbed self-excited SD oscillator has been studied in [32]. The local and global bifurcation behaviors including Hopf bifurcation, double tangency bifurcation, grazing bifurcation, sliding homoclinic bifurcation of the self-excited SD oscillator with Stribeck friction characteristic were investigated in [33]. Stochastic P-bifurcations of self-excited SD oscillator under the effects of periodic impulse and random force were studied, see [34] for details. The research on the stick-slip vibration theory of the friction system with geometry nonlinearity is very limited. The most of existing studies regarding the aspect of stick-slip vibration for geometry nonlinear system with friction resort to the numerical simulation. It is necessary to develop some analytical procedures for evaluating the stick-slip vibrations of friction systems with geometry nonlinearity.

The motivation of this paper is to investigate the stick-slip vibrations of the self-excited SD oscillator with Coulomb friction. By employing the Hamilton function, the closed-form solutions can be derived and utilized to examine the influence of the moving belt speed on the steady state of this system. Furthermore, the evolution of sliding regions and the collision of trajectories in stick-slip motion with sliding region for the forced self-excited system can be demonstrated. These investigations on the stick-slip vibrations of the self-excited SD oscillator can lead to a deeper understanding of stick-slip vibration mechanism for friction systems with the geometric nonlinearity in mechanical engineering.

2 The governing equation

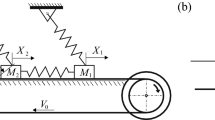
In this section, a self-excited SD oscillator is studied, as shown schematically in Fig. 1a. This system is composed by a mass M, supported by a non-deformable moving belt with a constant velocity \(V_0\), connected to a fixed support by a inclined linear spring of stiffness coefficient K, which is capable of resisting both compression and tension. The contact surface between the mass and the belt is rough so that the belt exerts a friction force \(F_S\) on the mass. It is supposed that the mass moves on the moving belt horizontally without loss of contact with the belt. The position and velocity of the mass over the belt are represented by X and \(\dot{X}\).

Fig. 1
figure 1

The mechanical model. a The dynamical model of a self-excited SD oscillator, b Coulomb friction law

Full size image

The equation of motion for this self-excited system is written as the following

$$\begin{aligned} M\ddot{X}+KX\Big (1-\displaystyle \frac{L}{\sqrt{X^{2}+H^2}}\Big )+F_S=0, \end{aligned}$$
(1)

where the dot denotes the derivative with respect to \(\tau \), L is the original length of the spring, H is the distance between the fixed point and the belt, and the friction \(F_S\) between the mass and the belt is modeled as the Coulomb friction (Fig. 1b).

The stick and slip motions are depended on the relative velocity \(V_{rel}=\dot{X}-V_0\). In the stick state, the relative velocity is equal to zero (\(V_{rel}=0\)), that is the mass and the belt move together and the static friction will take the value necessary to balance the forces, which implies that it is necessary to keep the contacting surfaces from sliding. Furthermore, the mass acceleration is equal to zero, i.e., \({\ddot{X}}=0\). Thus, the static friction can be written as

$$\begin{aligned} -\mu _s F_N\le & {} F_S=-KX(t)\Big (1-\displaystyle \frac{L}{\sqrt{X^{2}(t)+H^2}}\Big )\nonumber \\\le & {} \mu _s F_N, \end{aligned}$$
(2)

where \(\mu _s\) represents the maximum static friction coefficient, \(F_N=Mg-KH(1-{L}/{\sqrt{X^2+H^2}})\) is the total force of the gravity of the mass and vertical component of the spring force to be assumed that \(F_N>0\). Only if the spring force exceeds the peak force \(\mu _s F_N\), the mass begins to slide.

In the slip state, the relative velocity is not equal to zero (\(V_{rel}\ne 0\)), that is the mass slides on the belt and the kinetic friction acts on the direction opposite to the relative velocity. The kinetic friction is given by

$$\begin{aligned} F_S=\mu _k F_N \text {sign}(\dot{X}-V_0), \end{aligned}$$
(3)

where \(\mu _k\) is the coefficient of kinetic friction.

Because the friction \(F_S\) between the mass and the belt is discontinuous and multivalued at \(V_{\mathrm{rel}}=0\), which can be described in the form of the differential inclusion of Filippov type [35] as

$$\begin{aligned} F_S\in \mu (V_{\mathrm{rel}}) F_N \text {Sign}(\dot{X}-V_0), \end{aligned}$$
(4)

where

$$\begin{aligned} \text {Sign}(V_{\mathrm{rel}})=\left\{ \begin{array}{ll} 1 &{}\quad \hbox {if}\quad V_{\mathrm{rel}}> 0,\\ {[}-1,1] &{}\quad \hbox {if} \quad V_{\mathrm{rel}}= 0, \\ -1 &{}\quad \hbox {if}\quad V_{\mathrm{rel}}< 0, \end{array} \right. \end{aligned}$$

\(\mu (V_{\mathrm{rel}})\) is the friction coefficient of contacting surfaces and assumed to have two discrete values, defined as

$$\begin{aligned} \mu (V_{\mathrm{rel}})=\left\{ \begin{array}{ll} \mu _k &{}\quad \hbox {if}\quad V_{\mathrm{rel}}\ne 0,\\ \mu _s &{}\quad \hbox {if}\quad V_{\mathrm{rel}}= 0. \end{array}\right. \end{aligned}$$
(5)

Equation (1) can be made dimensionless by letting \(x={X}/{L}\), \(\omega _{0}^{2}={K}/{M}\), \(\alpha ={H}/{L}\), \(g_1={g}/({L\omega _{0}^2}\)), \(v_0={V_0}/({L\omega _0})\), \(v_{\mathrm{rel}}=\dot{x}- v_0\) and \(t=\omega _0 \tau \), together with Eq. (4), and written as:

$$\begin{aligned}&\ddot{x}+x\Big (1-\displaystyle \frac{1}{\sqrt{x^{2}+\alpha ^2}}\Big )\in -\mu (v_{\mathrm{rel}})\nonumber \\&\quad \Big [g_{1}-\alpha \Big (1-\displaystyle \frac{1}{\sqrt{x^{2}+\alpha ^2}}\Big )\Big ]\text {Sign}(\dot{x}-v_0), \end{aligned}$$
(6)

where the dot denotes the derivative with respect to t.

It is worth noting that the system (6) is strongly geometric nonlinear, having an irrational restoring force \(f(x)=x(1-1/\sqrt{x^2+\alpha ^2})\) due to the geometrical configuration, and a nonlinear friction force \(f_s=\mu (v_{\mathrm{rel}})f_n\) \( \text {Sign}(v_{\mathrm{rel}})\) due to variation of normal contact force \(f_n=g_1-\alpha (1-1/\sqrt{x^2+\alpha ^2})\).

3 Equilibrium bifurcation

In paper [26], the equilibrium and its bifurcation of the self-excited SD oscillator were studied by assuming a constant coefficient of friction, i.e., \(\mu _k=\mu _s=\mu \). In this paper, under the assumption of Coulomb friction, including a static coefficient different from the kinetic one, stick-slip vibrations of a self-excited SD oscillator will be analyzed, which is one of some follow-up work for the self-excited SD oscillator. In this section, we firstly investigate the equilibria and their stability for this system. Equation (6) can be written as following generic planar Filippov system by letting \(\dot{x}=y\),

$$\begin{aligned} \left\{ \begin{array}{ll} \dot{x}=y, \\ \dot{y}\in -x\Big (1-\displaystyle \frac{1}{\sqrt{x^{2}+\alpha ^2}}\Big )-\mu (v_{\mathrm{rel}})\Big [g_{1}-\alpha \Big (1-\displaystyle \frac{1}{\sqrt{x^{2}+\alpha ^2}}\Big )\Big ]\text {Sign}(y-v_0), \end{array} \right. \end{aligned}$$
(7)

which follows the equilibria determined by the following

$$\begin{aligned}&x\Big (1-\displaystyle \frac{1}{\sqrt{x^{2}+\alpha ^2}}\Big )\nonumber \\&\quad -\mu _k \Big [g_{1}-\alpha \Big (1-\displaystyle \frac{1}{\sqrt{x^{2}+\alpha ^2}}\Big )\Big ]=0,\nonumber \\ \end{aligned}$$
(8)

or equivalently, it follows

$$\begin{aligned}&x^4+2\mu _k(\alpha -g_1)x^3+[\alpha ^2-1+\mu _k^2(\alpha -g_1)^2]x^2\nonumber \\&\quad +2\mu _k\alpha (\alpha ^2-g_1\alpha -1)x+\mu _k^2\alpha ^2[(\alpha -g_1)^2-1]=0.\nonumber \\ \end{aligned}$$
(9)

After some calculations, the solutions to Eq. (9) are

$$\begin{aligned} \begin{array}{ll} x_0=\displaystyle \frac{1}{2}\mu _k(g_1-\alpha )-\displaystyle \frac{1}{2}\sqrt{\varUpsilon _1+\varDelta }+\displaystyle \frac{1}{2}\sqrt{2\varUpsilon _1-\varDelta -\varUpsilon _2},\\ \\ x_1=\displaystyle \frac{1}{2}\mu _k(g_1-\alpha )-\displaystyle \frac{1}{2}\sqrt{\varUpsilon _1+\varDelta }-\displaystyle \frac{1}{2}\sqrt{2\varUpsilon _1-\varDelta -\varUpsilon _2},\\ \\ x_2=\displaystyle \frac{1}{2}\mu _k(g_1-\alpha )+\displaystyle \frac{1}{2}\sqrt{\varUpsilon _1+\varDelta }+\displaystyle \frac{1}{2}\sqrt{2\varUpsilon _1-\varDelta +\varUpsilon _2}, \end{array} \end{aligned}$$
(10)

where

$$\begin{aligned} \varUpsilon _1= & {} \frac{1}{3}\mu _k^2(\alpha -g_1)^2-\displaystyle \frac{2}{3}(\alpha ^2-1),\\ \varUpsilon _2= & {} \frac{8\mu _k^3(g_1-\alpha )^3-16\mu _k\alpha (\alpha ^2-g_1\alpha -1)+8\mu _k(\alpha -g_1)[\mu _k^2(\alpha - g_1)^2+\alpha ^2-1]}{4\sqrt{\varUpsilon _1+\varDelta }},\\ \varDelta= & {} \frac{\root 3 \of {2}\varDelta _1}{3\root 3 \of {\varDelta _2+\sqrt{-4\varDelta _1^3+\varDelta _2^2}}}+\displaystyle \frac{\root 3 \of {\varDelta _2+\sqrt{-4\varDelta _1^3+\varDelta _2^2}}}{3\root 3 \of {2}},\\ \varDelta _1= & {} 12\mu _k^2\alpha ^2[(g_1-\alpha )^2-1]-12\mu _k^2(\alpha -g_1)(\alpha ^3-\alpha ^2g_1-\alpha )+[\mu _k^2(\alpha -g_1)^2+\alpha ^2-1]^2,\\ \varDelta _2= & {} 108\mu _k^4\alpha ^2(\alpha - g_1)^2[(\alpha -g_1)^2-1]-72\mu _k^2\alpha ^2[(\alpha -g_1)^2-1][\mu _k^2(\alpha - g_1)^2+\alpha ^2-1]\\&-36\mu _k^2(\alpha -g_1)(\alpha ^3-\alpha ^2g_1-\alpha )[\mu _k^2(\alpha -g_1)^2+\alpha ^2-1]+108\mu _k^2(\alpha ^3-\alpha ^2g_1-\alpha )^2\\&+2[\mu _k^2(\alpha -g_1)^2+\alpha ^2-1]^3. \end{aligned}$$
Fig. 2
figure 2

a Equilibrium surface in \((\alpha , \mu _k, x)\) space and section \(\beta _1\) and \(\beta _2\). b Equilibrium bifurcation in \(x-\alpha \) plane for \(\mu _k\)=0.1. c Equilibrium bifurcation in \(x-\mu _k\) plane for \(\alpha \)=0.4. Dashed and solid lines display the saddle and center, respectively

Full size image
Fig. 3
figure 3

The centre-saddle bifurcation for belt velocity \(v_0=1\). a \(\alpha =0.4\), b \(\alpha =0.4955\), c \(\alpha =0.55\). The black, green and blue dots denote the centres, the saddle point and the centre-saddle point, respectively

Full size image

The equilibria of system (7) are \((x_0, 0)\), \((x_1, 0)\) and \((x_2, 0)\), and their stability can be determined by Jacobian of equilibria of the system (7), where the Jacobian matrix, J, can be written as

$$\begin{aligned} J_{(x_i, 0)}=\left[ \begin{array}{cc} 0 &{} \quad 1 \\ \displaystyle \frac{\alpha ^2-\alpha \mu _k x_i}{(x_i^2+\alpha ^2)^{3/2}} &{} \quad 0 \end{array}\right] , \quad i=0, 1, 2, \end{aligned}$$
(11)

with the characteristic equation written as

$$\begin{aligned} \lambda ^2-\big [\displaystyle \frac{\alpha ^2-\alpha \mu _k x_i}{(x_i^2+\alpha ^2)^{3/2}}-1\big ]=0, \quad i=0, 1, 2, \end{aligned}$$
(12)

where \(x_0\), \(x_1\) and \(x_2\) have been given by Eq. (10).

Eigenvalues, \(\lambda \), of the Jacobian matrix can reflect the features of local stability at the equilibrium point. Therefore, the equilibrium \((x_0,0)\) is a hyperbolic saddle with the eigenvalues \(\lambda _{1{,}2}|_{(x_0{,}0)}{=}\pm \sqrt{\frac{\alpha ^2{-}\alpha \mu _k x_0}{(x_0^2{+}\alpha ^2)^{3/2}}{-}1}\), and the equilibria \((x_{1}{,}0)\) and \((x_{2}{,}0)\) are the pair of centers with the eigenvalues \(\lambda _{1{,}2}|_{(x_1{,}0)}{=}\pm i\sqrt{\frac{\alpha \mu _k x_1{-}\alpha ^2}{(x_1^2{+}\alpha ^2)^{3/2}}{+}1}\) and \(\lambda _{1{,}2}|_{(x_2,0)}=\pm i\sqrt{\frac{\alpha \mu _k x_2-\alpha ^2}{(x_2^2+\alpha ^2)^{3/2}}+1}\), respectively, for the parameters \(\alpha \) and \(\mu _k\) satisfying

$$\begin{aligned} 2\varUpsilon _1(\alpha ,\mu _k)-\varDelta (\alpha ,\mu _k)-\varUpsilon _2(\alpha ,\mu _k)>0. \end{aligned}$$
(13)

Clearly, the equilibria of system (7) depend on the values of \(\alpha \) and \(\mu _k\). To examine the influence of parameters \(\alpha \) and \(\mu _k\) on the dynamics of system (7), the equilibrium surface in \((\alpha , \mu _k, x)\) space from Eq. (8) is shown in Fig. 2a for \(g_1=2\), which clearly shows the equilibrium bifurcations of the self-excited SD oscillator with the variation of parameters \(\alpha \) and \(\mu _k\).

To get a better understanding of the bifurcation process, we investigate the structure of the equilibrium surface by introducing two planes \(\beta _1: \mu _k=0.1\) and \(\beta _2: \alpha =0.4\), in order to cut the equilibrium surface in two different directions and two intersections are obtained in the following:

$$\begin{aligned} \varepsilon _1= & {} \left\{ (x,\alpha )|x-\mu _k\alpha \right. \\= & {} \left. \left[ x-\mu _k(g_1-\alpha )\right] \sqrt{x^2+\alpha ^2},\quad g_1=2, \mu _k=0.1 \right\} ,\\ \varepsilon _2= & {} \left\{ (x,\mu _k)|x-\mu _k\alpha \right. \\= & {} \left. [x-\mu _k(g_1-\alpha )]\sqrt{x^2+\alpha ^2}, \quad g_1=2, \alpha =0.4 \right\} . \end{aligned}$$

The equilibrium bifurcation with the variation of \(\alpha \) for \(\mu _k=0.1\) has been shown in Fig. 2b, meanwhile the equilibrium bifurcation with the variation of \(\mu _k\) for \(\alpha =0.4\) is presented in Fig. 2c, where the dashed and solid curves represent the saddle and the center, respectively. It is clearly seen that the centre-saddle bifurcations occur at \(\alpha ^*=0.4955\) in Fig. 2b, and \(\mu ^*_k=0.1331\) in Fig. 2c, respectively. This process of topological change for the centre-saddle bifurcation is shown in Fig. 3 with the variation of parameter \(\alpha \) for belt velocity \(v_0=1\). The black and green dots denote the centres and the saddle point connecting two homoclinic orbits, respectively, as shown in Fig. 3a for \(\alpha =0.4\). With the increase of \(\alpha \), the centre-saddle bifurcation occurs at \(\alpha =0.4955\) in Fig. 3b, where a blue dot denote the centre-saddle point connecting one homoclinic orbit. In Fig. 3c, the homoclinic orbit vanishes and there is only a centre for \(\alpha =0.55\).

4 Sliding behaviors induced by Coulomb friction

In this section, the stick-slip and pure slip motions induced by Coulomb friction for the self-excited SD oscillator are investigated. Note that, for \(\dot{x}>v_0>0\), there is no equilibrium for this system, and no close orbits exist as known from Fig. 3. We will analyze the sliding behaviors of this system by assuming \(\dot{x}<v_0\), then system (6) can be rewritten into a Hamiltonian system as follows

$$\begin{aligned} \left\{ \begin{array}{ll} \dot{x}=\displaystyle \frac{\partial H}{\partial y}=y, \\ \dot{y}=-\displaystyle \frac{\partial H}{\partial x}=-x\Big (1-\displaystyle \frac{1}{\sqrt{x^{2}+\alpha ^2}}\Big )+\mu _k \Big [g_{1}-\alpha \Big (1-\displaystyle \frac{1}{\sqrt{x^{2}+\alpha ^2}}\Big )\Big ], \end{array} \right. \end{aligned}$$
(14)

from which the Hamiltonian can be obtained as follows

$$\begin{aligned} H(x, y)&{=}H(x, \dot{x}){=}\displaystyle \frac{1}{2}\dot{x}^2+\displaystyle \frac{1}{2} x^2{-}\sqrt{x^{2}+\alpha ^2}\nonumber \\&\quad -\mu _k (g_1{-}\alpha )x{-}\mu _k\alpha \ln \Big (x{+}\sqrt{x^{2}{+}\alpha ^2}\Big ). \nonumber \\ \end{aligned}$$
(15)

Since

$$\begin{aligned} \displaystyle \frac{\mathrm{d}H}{\mathrm{d}t}=\displaystyle \frac{\mathrm{d}H}{\mathrm{d}x}\dot{x}+\displaystyle \frac{\mathrm{d}H}{\mathrm{d}y}\dot{y}=\displaystyle \frac{\mathrm{d}H}{\mathrm{d}x}\displaystyle \frac{\mathrm{d}H}{\mathrm{d}y}-\displaystyle \frac{\mathrm{d}H}{\mathrm{d}y}\displaystyle \frac{\mathrm{d}H}{\mathrm{d}x}\equiv 0, \nonumber \\ \end{aligned}$$
(16)

the level curves \(H(x, \dot{x})\)=constant are solution curves for the system (14). The critical points of \(H(x, \dot{x})\) correspond to the fixed points of the flow of Hamilton’s Eq. (14). For the saddle point \((x_0, 0)\), we can get

$$\begin{aligned} H(x_0, 0)= & {} \displaystyle \frac{1}{2} x_0-\sqrt{x_0^{2}+\alpha ^2}-\mu _k (g_1-\alpha )x_0\nonumber \\&-\mu _k\alpha \ln \Big (x_0+\sqrt{x_0^{2}+\alpha ^2}\Big )=h_0. \end{aligned}$$
(17)

For convenience, a new Hamiltonian can be obtained by introducing a transformation

$$\begin{aligned} \begin{array}{ll} E&{}=\tilde{H}(x, \dot{x})={H}(x, \dot{x})-h_0 =\displaystyle \frac{1}{2}\dot{x}^2+\displaystyle \frac{1}{2} x^2\\ {} &{}\quad -\sqrt{x^{2}+\alpha ^2}-\mu _k (g_1-\alpha )x -\mu _k\alpha \ln \Big (x+\sqrt{x^{2}+\alpha ^2}\Big )-h_0, \end{array} \end{aligned}$$
(18)

where \(x_0\) is the abscissa of the saddle point \((x_0, 0)\) with standard hyperbolic structure, thus \(\tilde{H}(x_0, 0)=0\). With the help of the Hamiltonian (18), the trajectories can be classified and analyzed. Different stationary dynamic behaviours are exhibited as the parameter \(v_0\) varies by numerical analysis, as shown in Figs. 4, 5 and 6 for \(g_1=2\), \(\mu _s=0.1\) and \(\mu _k=0.05\).

When \(\alpha =0.4\), the phase portraits of system (6) are plotted for different values of the Hamiltonian \(\tilde{H}(x,\dot{x})=E\), as shown in Fig. 4a for \(v_0=0.9\). When \(E<0\), there exists two families of periodic orbits inside the homoclinic orbits with asymmetry, respectively. When \(E>0\), there exists another family of periodic orbits outside the homoclinic orbits, where the outermost periodic orbit is a stick-slip motion and the short horizontal part (marked with green) corresponds to the stick locus, as shown in Fig. 4a.

Fig. 4
figure 4

Dynamical behaviour of the system (6) for \(\alpha =0.4\) and \(v_{0}=0.9\). a Phase portraits of the system, b the curves of Hamiltonian \(\tilde{H}(x, \dot{x})\) versus displacement x

Full size image

For a given belt speed \(v_0\), a particular region \(\chi _{s1}\) (shaded in Fig. 4a) in the phase plane is defined by the following inequality [36]:

$$\begin{aligned}&\chi _{s1}: \quad \displaystyle \frac{1}{2}\dot{x}^2+\displaystyle \frac{1}{2} x^2-\sqrt{x^{2}+\alpha ^2}-\mu _k (g_1-\alpha )x\nonumber \\&\quad -\mu _k\alpha \ln \Big (x+\sqrt{x^{2}+\alpha ^2}\Big )-h_0 \le E_{b}, \end{aligned}$$
(19)

where

$$\begin{aligned} E_{b}= & {} \displaystyle \frac{1}{2}v_0^2+\displaystyle \frac{1}{2} x_2^2-\sqrt{x_2^{2}+\alpha ^2}-\mu _k (g_1-\alpha )x_2\nonumber \\&-\mu _k\alpha \ln \Big (x_2+\sqrt{x_2^{2}+\alpha ^2}\Big )-h_0, \end{aligned}$$
(20)

\(x_2\) is the abscissa of the right-hand centre \((x_2, 0)\). The boundary of \(\chi _{s1}\) is a circumference being tangent to the stick locus (marked with green) and the tangent point is \((x_2, v_0)\).

For an initial point \(P_0=(x_p, \dot{x}_p)\) in Fig. 4a, if \(P_0\in \chi _{s1}\), the periodic motion starting from \(P_0\) do exist in a pure slip mode as the following

$$\begin{aligned}&\displaystyle \frac{1}{2}\dot{x}^2+\displaystyle \frac{1}{2} x^2-\sqrt{x^{2}+\alpha ^2}-\mu _k (g_1-\alpha )x\nonumber \\&\quad -\mu _k\alpha \ln \Big (x+\sqrt{x^{2}+\alpha ^2}\Big )-h_0= E_p, \end{aligned}$$
(21)

where \(E_p=\displaystyle \frac{1}{2}\dot{x}_p^2+\displaystyle \frac{1}{2} x_p^2-\sqrt{x_p^{2}+\alpha ^2}-\mu _k (g_1-\alpha )x_p-\mu _k\alpha \ln \Big (x_p+\sqrt{x_p^{2}+\alpha ^2}\Big )-h_0\). The mass will rest if \(P_0\) coincides with the three equilibria of the system (6).

If \(P_0 \not \in \chi _{s1}\), the trajectory starting from \(P_0\) is attracted by a stick-slip motion located in the outermost periodic orbit in Fig. 4a, which is defined as

$$\begin{aligned} \varGamma _s: \quad \left\{ \begin{array}{ll} \displaystyle \frac{1}{2}\dot{x}^2+\displaystyle \frac{1}{2} x^2-\sqrt{x^{2}+\alpha ^2}-\mu _k (g_1-\alpha )x\\ mu_k\alpha \ln \Big (x+\sqrt{x^{2}+\alpha ^2}\Big )-h_0= E_s, \quad \dot{x}<v_0,\\ x_{r1}\le x \le x_{r2}, \quad \dot{x}=v_0, \end{array} \right. \end{aligned}$$
(22)

where

$$\begin{aligned} \begin{array}{ll} E_s=\displaystyle \frac{1}{2} v_0^2+\displaystyle \frac{1}{2} x_{r2}^2-\sqrt{x_{r2}^{2}+\alpha ^2}-\mu _k (g_1-\alpha )x_{r2}\\ \quad \qquad -\mu _k\alpha \ln \Big (x_{r2}+\sqrt{x_{r2}^{2}+\alpha ^2}\Big )-h_0,\\ \\ x_{r2}=\displaystyle \frac{1}{2}\mu _s(g_1-\alpha )+\displaystyle \frac{1}{2}\sqrt{\varUpsilon _1(\mu _s)+\varDelta (\mu _s)}\\ \qquad \quad +\displaystyle \frac{1}{2}\sqrt{2\varUpsilon _1(\mu _s)-\varDelta (\mu _s)+\varUpsilon _2(\mu _s)}, \end{array} \end{aligned}$$
(23)

and \(x_{r1}\) and \(x_{r2}\) are the smallest and largest roots of the equation

$$\begin{aligned}&\displaystyle \frac{1}{2} x^2-\sqrt{x^{2}+\alpha ^2}-\mu _k (g_1-\alpha )x\\&\quad -\mu _k\alpha \ln \Big (x+\sqrt{x^{2}+\alpha ^2}\Big )+\displaystyle \frac{1}{2}v_0^2-h_0= E_s. \end{aligned}$$

The curves of Hamiltonian \(\tilde{H}(x, \dot{x})\) versus displacement x mentioned in [37] for pure-slip periodic motion and stick-slip periodic motion shown in Fig. 4a have been depicted in Fig. 4b, where the potential function V(x) (marked by blue)

$$\begin{aligned} V(x)= & {} \displaystyle \frac{1}{2} x^2-\sqrt{x^{2}+\alpha ^2}\\&-\mu _k (g_1-\alpha )x-\mu _k\alpha \ln \Big (x+\sqrt{x^{2}+\alpha ^2}\Big )-h_0 \end{aligned}$$

is characteristic in asymmetric potential wells. Two centres are the minima of V(x), while the saddle is the local maximum, and it separates the two asymmetric potential wells.

It is observed that the level of Hamiltonian \(\tilde{H}(x, \dot{x})\) is unchanged during the pure-slip motion when \(E\le E_b\) marked with shaded area in Fig. 4b. The Hamiltonian \(\tilde{H}(x, \dot{x})=E_s\) denotes the slip stage of the stick-slip periodic motion \(\varGamma _s\), while the Hamiltonian \(\tilde{H}(x, \dot{x})=E_k\) (depicted with green) represents the stick stage of the stick-slip periodic motion \(\varGamma _s\), which is defined as

$$\begin{aligned} E_k= & {} \displaystyle \frac{1}{2} x^2-\sqrt{x^{2}+\alpha ^2}-\mu _k (g_1-\alpha )x\nonumber \\&-\mu _k\alpha \ln \Big (x+\sqrt{x^{2}+\alpha ^2}\Big )\nonumber \\&+\displaystyle \frac{1}{2}v_0^2-h_0, \quad x\in [x_{r1}, x_{r2}]. \end{aligned}$$
(24)

From the discussion above, we know that the system has three equilibria, a pair of centers and a saddle point with a hyperbolic structure connecting two asymmetric homoclinic branches on both sides under \(\dot{x} < v_0\) with a relatively large belt speed, as shown in Fig. 4a. From some numerical investigations, it is found that there exists two critical belt speeds \(v^*_0\) and \(v^{**}_0\) which can be calculated from the equation \(E=0\), one can get

$$\begin{aligned} v^*_0= & {} \sqrt{2h_0-x_2^2+2\sqrt{x_2^{2}+\alpha ^2}+2\mu _k (g_1-\alpha )x_2}\nonumber \\&\sqrt{+2\mu _k\alpha \ln \Big (x_2+\sqrt{x_2^{2}+\alpha ^2}\Big )}, \end{aligned}$$
(25)
$$\begin{aligned} v^{**}_0= & {} \sqrt{2h_0-x_1^2+2\sqrt{x_1^{2}+\alpha ^2}+2\mu _k (g_1-\alpha )x_1}\nonumber \\&\sqrt{+2\mu _k\alpha \ln \Big (x_1+\sqrt{x_1^{2}+\alpha ^2}\Big )}, \end{aligned}$$
(26)

where \(x_1\) and \(x_2\) is the abscissa of two centres \((x_1, 0)\) and \((x_2, 0)\), respectively.

When \(v_0>v^*_0\), there exists two homoclinic branches connecting the saddle point with a hyperbolic structure. While \(v^{**}_0<v_0 < v^*_0\), the homoclinic orbit on the left-hand remains, and the other homoclinic branch breaks, meanwhile the unstable manifold of the saddle point enters into a stick-slip periodic motion after passing along a stick stage denoted by the segment marked green, as shown in Fig. 5a.

Fig. 5
figure 5

Dynamical behaviour of the system (6) for \(\alpha =0.4\) and \(v_{0}=0.5\). a Phase portraits of the system, b the curves of Hamiltonian \(\tilde{H}(x, \dot{x}) \) versus displacement x

Full size image

For a given belt speed satisfying \(v^{**}_0<v_0<v^{*}_0\), a particular region \(\chi _{s2}\) (shaded in Fig. 5a) in the phase plane is defined by the following inequality:

$$\begin{aligned} \chi _{s2}: \quad \left\{ \begin{array}{ll} \displaystyle \frac{1}{2}\dot{x}^2+\displaystyle \frac{1}{2} x^2-\sqrt{x^{2}+\alpha ^2}-\mu _k (g_1-\alpha )x\\ \quad -\mu _k\alpha \ln \Big (x+\sqrt{x^{2}+\alpha ^2}\Big )-h_0 \le 0, \quad x \le x_0,\\ \displaystyle \frac{1}{2}\dot{x}^2+\displaystyle \frac{1}{2} x^2-\sqrt{x^{2}+\alpha ^2}-\mu _k (g_1-\alpha )x\\ \quad -\mu _k\alpha \ln \Big (x+\sqrt{x^{2}+\alpha ^2}\Big )-h_0 \le E_b, \quad x>x_0. \end{array}\right. \nonumber \\ \end{aligned}$$
(27)

As shown in Fig. 5a, if \(P_0\in \chi _{s2}\), the steady motion from \(P_0\) is a pure-slip periodic motion. If \(P_0 \not \in \chi _{s2}\), the trajectory from \(P_0\) except for the point from the stable manifold of the saddle point is attracted by a stick-slip periodic motion in the right half of a plane in Fig. 5a, as defined in Eq. (22) for \(\varGamma _s\). The curves of Hamiltonian \(\tilde{H}(x, \dot{x})\) versus displacement x corresponding to pure-slip periodic motion and stick-slip periodic motion in Fig. 5a have been shown in Fig. 5b for \(v_0=0.5\). The expressions of \(E_b\), \(E_s\) and \(E_k\) for the Hamiltonian \(\tilde{H}(x, \dot{x})\) have been presented in Eqs. (20), (23) and (24), respectively.

When \(v_0<v^{**}_0\), both two homoclinic orbits break. In this case, a particular region \(\chi _{s3}\) (shaded in Fig. 6a) in the phase plane is defined by the following inequality:

$$\begin{aligned} \chi _{s3}: \quad \left\{ \begin{array}{ll} \displaystyle \frac{1}{2}\dot{x}^2+\displaystyle \frac{1}{2} x^2-\sqrt{x^{2}+\alpha ^2}-\mu _k (g_1-\alpha )x\\ \quad -\mu _k\alpha \ln \Big (x+\sqrt{x^{2}+\alpha ^2}\Big )-h_0 \le E'_b, \quad x < x_0,\\ \displaystyle \frac{1}{2}\dot{x}^2+\displaystyle \frac{1}{2} x^2-\sqrt{x^{2}+\alpha ^2}-\mu _k (g_1-\alpha )x\\ \quad -\mu _k\alpha \ln \Big (x+\sqrt{x^{2}+\alpha ^2}\Big )-h_0 \le E_b, \quad x > x_0, \end{array}\right. \nonumber \\ \end{aligned}$$
(28)

where the \(E_b\) is defined by Eq. (20) and

$$\begin{aligned} E'_{b}= & {} \displaystyle \frac{1}{2}v_0^2+\displaystyle \frac{1}{2} x_1^2-\sqrt{x_1^{2}+\alpha ^2}-\mu _k (g_1-\alpha )x_1\nonumber \\&-\mu _k\alpha \ln \Big (x_1+\sqrt{x_1^{2}+\alpha ^2}\Big )-h_0. \end{aligned}$$
(29)
Fig. 6
figure 6

Dynamical behaviour of the system (6) for \(\alpha =0.4\) and \(v_{0}=0.2\). a Phase portraits of the system, b the curves of Hamiltonian \(\tilde{H}(x, \dot{x})\) versus displacement x

Full size image

As depicted in Fig. 6a, if \(P_0\in \chi _{s3}\), the steady motion from \(P_0\) is a pure-slip periodic motion. If \(P_0 \not \in \chi _{s3}\), and except for the point from the stable manifold of the saddle point, the trajectory from \(P_0\) is attracted by a right or a left stick-slip periodic motion in Fig. 6a, as defined in Eq. (22) for \(\varGamma _s\) and

$$\begin{aligned} \varGamma '_s: \quad \left\{ \begin{array}{ll} \displaystyle \frac{1}{2}\dot{x}^2+\displaystyle \frac{1}{2} x^2-\sqrt{x^{2}+\alpha ^2}-\mu _k (g_1-\alpha )x\\ \quad -\mu _k\alpha \ln \Big (x+\sqrt{x^{2}+\alpha ^2}\Big )-h_0= E'_s, \quad \dot{x}<v_0, \\ x_{l1}\le x \le x_{l2}, \quad \dot{x}=v_0, \end{array}\right. \nonumber \\ \end{aligned}$$
(30)

respectively, where

$$\begin{aligned} \begin{array}{ll} E'_s=\displaystyle \frac{1}{2} v_0^2+\displaystyle \frac{1}{2} x_{l2}^2-\sqrt{x_{l2}^{2}+\alpha ^2}-\mu _k (g_1-\alpha )x_{l2}\\ \quad \qquad -\mu _k\alpha \ln \Big (x_{l2}+\sqrt{x_{l2}^{2}+\alpha ^2}\Big )-h_0,\\ \\ x_{l2}=\displaystyle \frac{1}{2}\mu _s(g_1-\alpha )-\displaystyle \frac{1}{2}\sqrt{\varUpsilon _1(\mu _s)+\varDelta (\mu _s)}\\ \qquad \quad -\displaystyle \frac{1}{2}\sqrt{2\varUpsilon _1(\mu _s)-\varDelta (\mu _s)+\varUpsilon _2(\mu _s)}, \end{array} \end{aligned}$$
(31)

and \(x_{l1}\) and \(x_{l2}\) are the smallest and largest roots of the equation

$$\begin{aligned}&\displaystyle \frac{1}{2} x^2-\sqrt{x^{2}+\alpha ^2}-\mu _k (g_1-\alpha )x\\&\quad -\mu _k\alpha \ln \Big (x+\sqrt{x^{2}+\alpha ^2}\Big )+\displaystyle \frac{1}{2}v_0^2-h_0= E'_s. \end{aligned}$$

The curves of Hamiltonian \(\tilde{H}(x, \dot{x})\) versus displacement x corresponding to a pure slip periodic motion and stick-slip periodic motion in Fig. 6a have been plotted in Fig. 6b for \(v_0=0.2\). The expressions of \(E_b\), \(E_s\) and \(E_k\) for the Hamiltonian \(\tilde{H}(x, \dot{x})\) can be found in Eqs. (20), (23) and (24) above, and the expressions of \(E'_b\) and \(E'_s\) have been described in Eqs. (29) and (31), respectively. While \(E'_k\) is given by

$$\begin{aligned} E'_k= & {} \displaystyle \frac{1}{2} x^2-\sqrt{x^{2}+\alpha ^2}-\mu _k (g_1-\alpha )x\nonumber \\&-\mu _k\alpha \ln \Big (x+\sqrt{x^{2}+\alpha ^2}\Big )\nonumber \\&+\displaystyle \frac{1}{2}v_0^2-h_0, \quad x\in [x_{l1}, x_{l2}]. \end{aligned}$$
(32)

The above results can be particularized to the case of \(\mu _s=\mu _k\): it should be noted that \(\varGamma _s\) coincides with \(\partial \chi _{s1}\) (\(E_s=E_b\)), \(\varGamma '_s\) coincides with \(\partial \chi _{s3}\) in \(x<x_0\) (\(E'_s=E'_b\)), and the steady stick motion reduces to one point (\(E_k=0\)), more details can be seen in [26].

As mentioned in [27], a vector field of the system (6) in the neighborhood of a periodic stick-slip orbit \(\varGamma _s\) defined in Eq. (22) has been shown in Fig. 7 for \(v_0=0.8\). Outsides of \(\varGamma _s\), the vector fields can cross the discontinuous surface \(\dot{x}=v_0\) several times, and enter into the periodic orbit \(\varGamma _s\) finally, e.g., the trajectory (red dotted line) starting from the initial conditions \(p_0=\)(-1.5, 0) is attracted to the periodic orbit \(\varGamma _s\) (blue line). Inside of \(\varGamma _s\), the structure of asymmetric double well is demonstrated.

5 Sliding regions and the associated dynamics

In this section, the sliding regions of stick-slip motion are demonstrated, especially, the collision of the orbits in the stick-slip periodic motion with the sliding region of the system can be presented.

Now suppose system (1) is perturbed by a viscous damping C and an external harmonic excitation of amplitude F and frequency \(\varOmega \), and described by the following

$$\begin{aligned} M\ddot{X}+C\dot{X}+KX\left( 1-\displaystyle \frac{L}{\sqrt{X^{2}+H^2}}\right) \in F\cos \varOmega \tau -\mu (v_{\mathrm{rel}})\nonumber \\ \left[ Mg-KH\Big (1-\displaystyle \frac{L}{\sqrt{X^{2}+H^2}}\Big )\right] \text {Sign}(\dot{X}-V_0),\nonumber \\ \end{aligned}$$
(33)

which can be made dimensionless by letting \(x={X}/{L}\), \(c={C}/{M\omega _0}\), \(\omega _{0}^{2}={K}/{M}\), \(\alpha ={H}/{L}\), \(g_1={g}/{L\omega _{0}^2}\), \(v_0={V_0}/{L\omega _0}\), \(f={F}/{KL}\), \(\omega ={\varOmega }/{\omega _0}\) and \(t=\omega _0 \tau \),

$$\begin{aligned} \ddot{x}+c\dot{x}+x\Big (1-\displaystyle \frac{1}{\sqrt{x^{2}+\alpha ^2}}\Big )\in f\cos \omega t-\mu (v_{\mathrm{rel}})\nonumber \\ \Big [g_{1}-\alpha \Big (1-\displaystyle \frac{1}{\sqrt{x^{2}+\alpha ^2}}\Big )\Big ]\text {sign}(\dot{x}-v_0), \nonumber \\ \end{aligned}$$
(34)

where the \((\cdot )\) denotes the differentiation with respect to the non-dimensional time t.

5.1 Sliding regions

The switching surface of the friction system is determined by the belt speed \(v_0\) at which the friction force changes sign, i.e., \(\dot{x}-v_0=0\). If the friction force on switching surface can balance the external forces and the inertia of the mass then the mass sticks to the surface, which is mathematically the sliding region [38], also known as stick zone [39]. Otherwise, the mass leaves the stick phase and starts to slip. Note that this led to an unavoidable linguistic ambiguity; Physically the mass stick to the surface, yet mathematically it is said to be sliding.

The sliding regions of system (34) are characterized by an extended state space (\(\mathbb {R}^2 \times \mathbb {S}\)) with a new coordinate \(\mathbf{x} =(x,\dot{x}, t)\). The switching surface is now defined as

$$\begin{aligned} \varSigma = \{\mathbf{x }\in {\mathbb {R}}^{2} \times {\mathbb {S}}: h(\mathbf{x })=0\}, \end{aligned}$$
(35)

which depends on the belt velocity physically, and \(h(\mathbf{x} )=v_{\mathrm{rel}}=\dot{x}-v_0\) and divides the system into two parts such that

$$\begin{aligned} {\dot{\mathbf{x }}=} {\left\{ \begin{array}{ll} {f_1(\dot{\mathbf{x }}):=\left( \begin{array}{c} \dot{x}\\ -c\dot{x} -x\Big (1-\displaystyle \frac{1}{\sqrt{x^{2}+\alpha ^2}}\Big )-\mu _s\Big [g_{1}\\ -\alpha \Big (1-\displaystyle \frac{1}{\sqrt{x^{2}+\alpha ^2}}\Big )\Big ]+f\cos (\omega t)\\ 1 \end{array}\right) , \quad \dot{x} > v_0, }\\ {f_2(\dot{\mathbf{x }}):=\left( \begin{array}{c} \dot{x}\\ -c\dot{x}-x\Big (1-\displaystyle \frac{1}{\sqrt{x^{2}+\alpha ^2}}\Big )+\mu _s\Big [g_{1}\\ alpha\Big (1-\displaystyle \frac{1}{\sqrt{x^{2}+\alpha ^2}}\Big )\Big ]+f\cos (\omega t)\\ 1 \end{array}\right) , \quad \dot{x} < v_0, } \end{array}\right. } \end{aligned}$$
(36)

which is continuous and analytic in

$$\begin{aligned} \left\{ \begin{array}{ll} G_1=\big \{(x,\dot{x},t)\in \mathbb {R}^2 \times \mathbb {S}\mid \dot{x}>v_0 \big \}, \\ G_2=\big \{(x,\dot{x},t)\in \mathbb {R}^2 \times \mathbb {S}\mid \dot{x}<v_0 \big \}. \end{array} \right. \end{aligned}$$
(37)

Equation (36) defines a Filippov system which exhibits sliding motion along \(\varSigma \). According to Filippov system’s definition, sliding dynamics is obtained as the following

$$\begin{aligned} \dot{\mathbf{x }}=f_{sl}=\lambda f_1(\mathbf{x} )+(1-\lambda ) f_2(\mathbf{x} ), \end{aligned}$$
(38)

where \(0\le \lambda \le 1\). Since the motion is constrained to the sliding surface \(\varSigma \), \(f_{sl}\) is tangent to \(\varSigma \), i.e., \(\langle \nabla h, f_{sl}\rangle =0\), which yields

$$\begin{aligned} \lambda (\mathbf{x} )= & {} \displaystyle \frac{1}{2\mu _s f_n}\bigg [-c\dot{x}-x\Big (1-\displaystyle \frac{1}{\sqrt{x^{2}+\alpha ^2}}\Big )\nonumber \\&+\mu _s f_n+f\cos (\omega t)\bigg ], \end{aligned}$$
(39)

where \(f_n=g_{1}-\alpha \Big (1-\displaystyle \frac{1}{\sqrt{x^{2}+\alpha ^2}}\Big )\). If there is no such \(\lambda \) at a point in \(\varSigma \), then the corresponding trajectory crosses \(\varSigma \) transversally.

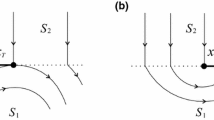
The switching surface \(\varSigma \) can be split into three regions depicted in Fig. 8 as the following

  1. 1.

    Crossing region pointing upwards:

    $$\begin{aligned} \varSigma _c^{+}= & {} \Big \{(x,\dot{x},t)\in \mathbb {R}^2 \times \mathbb {S}\mid f\cos (\omega t)\nonumber \\&-c\dot{x}-x\Big (1-\displaystyle \frac{1}{\sqrt{x^{2}+\alpha ^2}}\Big )> \mu _s f_n \Big \}, \end{aligned}$$
    (40)

    where the flow points away from \(\varSigma \) in \(G_1\) and toward \(\varSigma \) in \(G_2\).

  2. 2.

    Sliding region:

    $$\begin{aligned} \varSigma _s= & {} \Big \{(x,\dot{x},t)\in \mathbb {R}^2 \times \mathbb {S}\mid -\mu _s f_n \nonumber \\< & {} f\cos (\omega t)-c\dot{x}-x\Big (1-\displaystyle \frac{1}{\sqrt{x^{2}+\alpha ^2}}\Big )< \mu _s f_n \Big \}, \nonumber \\ \end{aligned}$$
    (41)

    where the flow points toward \(\varSigma _s\) in both \(G_1\) and \(G_2\).

  3. 3.

    Crossing region pointing downwards:

    $$\begin{aligned} \varSigma _c^{-}= & {} \Big \{(x,\dot{x},t)\in \mathbb {R}^2 \times \mathbb {S}\mid f\cos (\omega t)+\mu _s f_n \nonumber \\< & {} c\dot{x}+x\Big (1-\displaystyle \frac{1}{\sqrt{x^{2}+\alpha ^2}}\Big ) \Big \}, \end{aligned}$$
    (42)

    where the flow points toward \(\varSigma \) in \(G_1\) and away from \(\varSigma \) in \(G_2\).

Fig. 7
figure 7

A vector field of the system (6) in the neighborhood of a periodic stick-slip orbit \(\varGamma _s\) marked with blue line

Full size image
Fig. 8
figure 8

Schematic of the flows of the system (34)

Full size image
Fig. 9
figure 9

Schematic of the phase space of the system (34)

Full size image
Fig. 10
figure 10

Evolution of the sliding regions for the system (34). a \(f=0\), b \(f=0.05\), c \(f=0.1\), d \(f=0.5342\), e \(f=0.5535\), f \(f=0.6\)

Full size image

It is noted that the sliding vector field \(f_{st}=(v_0, 0, 1)^T\) is constant, from the physics point of view: when the mass sticks to the belt, it moves with the same constant speed \(v_0\) as the belt. The boundary of the sliding region is defined as follows

$$\begin{aligned} \mathcal {L}_1=\partial \varSigma _c^{+}=\Big \{(x,\dot{x},t)\in \mathbb {R}^2 \times \mathbb {S}\mid \lambda (\mathbf{x} )=0 \Big \}, \end{aligned}$$
(43)

and

$$\begin{aligned} \mathcal {L}_2=\partial \varSigma _c^{+}=\Big \{(x,\dot{x},t)\in \mathbb {R}^2 \times \mathbb {S}\mid \lambda (\mathbf{x} )=1 \Big \}. \end{aligned}$$
(44)

In this case, the boundaries of the sliding regions are given by

$$\begin{aligned}&\mathcal {L}_1:~\displaystyle f\cos (\omega t)-cv_0-x\Big (1-\displaystyle \frac{1}{\sqrt{x^{2}+\alpha ^2}}\Big )\nonumber \\&\quad =\mu _s \Big [g_{1}-\alpha \Big (1-\displaystyle \frac{1}{\sqrt{x^{2}+\alpha ^2}}\Big )\Big ], \end{aligned}$$
(45)

and

$$\begin{aligned}&\mathcal {L}_2:~\displaystyle f\cos (\omega t)-cv_0-x\Big (1-\displaystyle \frac{1}{\sqrt{x^{2}+\alpha ^2}}\Big )\nonumber \\&\quad =-\mu _s \Big [g_{1}-\alpha \Big (1-\displaystyle \frac{1}{\sqrt{x^{2}+\alpha ^2}}\Big )\Big ]. \end{aligned}$$
(46)

A schematic illustration of phase space with a typical trajectory marked with red is shown in Fig. 9, where the sliding region is plotted in light green, and the boundary of sliding region is formed by the two curves \(\mathcal {L}_1\) with blue and \(\mathcal {L}_2 \) with green. A typical trajectory marked red with a sliding segment starting from initial point O in \(G_2\) reaches A in \(\varSigma _s\), slides continuously to B in \(\mathcal {L}_1\) along segment \(\overline{AB}\) in \(\varSigma _s\), and then begins to slip from the tangential point B. Finally, the trajectory returns back to point C and slides to D along the sliding segment \(\overline{CD}\) in \(\varSigma _s\) and enters into \(G_2\), as shown in Fig. 9 for example.

The sliding regions marked grey are displayed in Figs. 10a–f in plane (x, t) for \(\alpha =0.4\), \(v_0=0.2\), \(g_1=2\), \(\omega =1.08\) as the increase of f, which are determined by the boundary \(\mathcal {L}_1\) given by Eq. (45) and the boundary \(\mathcal {L}_1\) given by Eq. (46). Different types of sliding boundaries are possible due to the amplitude f of external excitation. The sliding region, as shown in Fig. 10a, consists three separated parallel strips if the amplitude of external excitation \(f= 0\), that is, there is no external excitation. The sliding regions may bend with an increase of f, taking Fig. 10b for \(f=0.05\) as an example, even the region strips are bent, the strips are kept separately yet.

Very interesting phenomena appear with the increase of f, three separated sliding strips join into a multiple connected area with some irregular ovals as the increase of bending, as shown in Fig. 10c for \(f=0.1\), where the white irregular ovals represent the crossing regions. The ovals gradually increase as f increases, the multiple connected sliding region becomes a single ribbon type strip, as represented in Figs. 10d–f for \(f=0.5342\), \(f=0.5535\) and \(f=0.6\), respectively.

Finally, as f increases, the sliding ribbon like strip region involutes into a narrowed fluctuation sliding region, as shown in Fig. 11 for \(f=1\) (black), \(f=2\) (red) and \(f=4\) (blue), respectively.

Fig. 11
figure 11

Evolution of the sliding regions for \(f=1\), \(f=2\) and \(f=4\), plotted with black, red and blue lines, respectively

Full size image
Fig. 12
figure 12

Bifurcation diagram of displacement x versus external amplitude f for \(\alpha =0.4\), \(v_0=0.2\), \(g_1=2\), \(\omega =1.08\) and \(c=0.048\)

Full size image
Fig. 13
figure 13

a The stick-slip period-1 motion with slip trajectory below the switching surface for \(f=0.06\). b The corresponding trajectory in the \((x, \dot{x}, t)\) state space

Full size image
Fig. 14
figure 14

a The stick-slip period-1 motion with slip portion crossing the switching surface for \(f=0.12\). b The corresponding trajectory in the \((x, \dot{x}, t)\) state space

Full size image
Fig. 15
figure 15

a The pure slip period-2 motion for \(f=0.35\). b The corresponding trajectory in the \((x, \dot{x}, t)\) state space

Full size image
Fig. 16
figure 16

a The stick-slip period-4 motion for \(f=0.372\). b The corresponding trajectory in the \((x, \dot{x}, t)\) state space

Full size image
Fig. 17
figure 17

a The stick-slip period-8 motion for \(f=0.3734\). b The corresponding trajectory in the \((x, \dot{x}, t)\) state space

Full size image
Fig. 18
figure 18

a The stick-slip chaotic motion for \(f=0.42\). b The chaotic attractor. c The corresponding portion of trajectory in the \((x, \dot{x}, t)\) state space

Full size image
Fig. 19
figure 19

a The stick-slip chaotic motion for \(f=0.7\). b The chaotic attractor. c The corresponding portion of trajectory in the \((x, \dot{x}, t)\) state space

Full size image
Fig. 20
figure 20

a The pure-slip period-1 motion with a large amplitude for \(f=1.3\). b The corresponding trajectory in the extended \((x, \dot{x}, t)\) state space

Full size image

5.2 Dynamics associated with sliding regions

In this subsection, the complicated dynamics associated with sliding region are investigated for the self-excited SD oscillator excited by external excitation \(f\cos {\omega t}\) and damping of coefficient c. Bifurcation diagram for displacement x versus amplitude f of external excitation is constructed with initial condition \((x_0, y_0)=(0.12,0.01)\) for parameters \(\alpha =0.4\), \(v_0=0.2\), \(g_1=2\), \(\omega =1.08\) and \(c=0.048\), as shown in Fig. 12, which shows the periodic windows of period-one, period-two period-four and so on, and a path to chaos from a periodic doubling.

The trajectories of some periodic and chaotic motions for the system (34) are depicted as f varies, as shown in Figs. 13, 14, 15, 16, 17, 18, 19 and 20. All the short horizontal lines marked with green in phase portraits in the following figures correspond to the sticking during the motion.

When f=0.06, a stick-slip period-1 motion and its attractor are shown in Fig. 13a, where a slip trajectory is always below the stick trajectory. In \((x,\dot{x}, t)\) state space, a trajectory approaching switching surface \(\varSigma \) from the subspace governed by vector field \(f_2\) returns back after sliding a short time on the sliding region, and stick trajectories lie in the same sliding region as time t varies, as shown in Fig. 13b.

With the increase of f, there exists a stick-slip period-1 motion crossing switching surface for \(f=0.12\), as shown in Fig. 14a, the trajectory consists of a stick phase, a slip phase above the stick trajectory (\(\dot{x}>v_0\)) and a slip phase below the stick trajectory (\(\dot{x}<v_0\)). In \((x,\dot{x}, t)\) state space, the shape of sliding regions have changed, and a trajectory passes from the lower sub-space governed by vector field \(f_2\) to the upper sub-space governed by vector field \(f_1\), unless it collides with the sliding region. After a finite time, the trajectory hits the switching surface \(\varSigma \) within the sliding region. Then, it evolves according to the sliding flow until crossing the boundary of sliding region, where it finally leaves switching surface \(\varSigma \) toward \(G_2\) (see Fig. 14b).

When \(f=0.35\), a pure slip period-2 motion is found, the corresponding trajectory and the Poincaré section are shown in Fig. 15a. In the extended space \((x, \dot{x}, t)\), the orbit starting from subspace \(G_2\) reaches the switching surface \(\varSigma \), and crosses it into subspace \(G_1\) without colliding with the sliding region. Finally, it returns back to subspace \(G_2\) crossing switching surface \(\varSigma \) again (see Fig. 15b).

A stick-slip period-4 motion and its periodic attractor are presented for \(f=0.372\) in Fig. 16a. In \((x,\dot{x}, t)\) state space, a orbit starting from subspace \(G_2\) into subspace \(G_1\) after crossing switching surface \(\varSigma \), collides with the sliding region and evolves in it until crossing the boundary of sliding region, as shown in Fig. 16b. As f varies, period doubling bifurcation occurs and there exists a stick-slip period-8 motion for \(f=0.3734\), as shown in Fig. 17a. In \((x,\dot{x}, t)\) state space, a trajectory passes from lower subspace \(G_2\) to upper subspace \(G_1\), unless it collides with a sliding region \(\varSigma _s\), and it evolves according to the sliding flow until crossing the boundary of sliding region. After a finite time, it returns back to lower subspace \(G_2\) from upper subspace \(G_1\), as shown in Fig. 17b.

Similarly, a period doubling leading to chaos can be observed as shown in Fig. 12, with the details see from period-2 motion (Fig. 15a) bifurcating to period-4 motion (Fig. 16a), period-8 motion (Fig. 17a), and the chaotic motion (Fig. 18a). The system is transformed from periodic motion to chaotic motion by periodic doubling bifurcation with the increasing of excitation amplitude f. As f further increases, the regular motion vanishes and the stick-slip chaotic motion follows when \(f=0.42\), as shown in Fig. 18a. The corresponding chaotic attractor with stick-slip structure and a part of orbit of chaotic motion in extended state space (\(x, \dot{x} , t\)) are depicted in Fig. 18b and c.

When \(f=0.7\), there exists still a stick-slip chaotic motion, as shown in Fig. 19a, where the stick portion become less. The corresponding chaotic attractor and a part of trajectory in the \((x, \dot{x}, t)\) state space are depicted in Fig. 19b and c. In the extended \((x, \dot{x}, t)\) state space, the shape of the sliding region have changed again, which is shaped like a curved ribbon, as can be seen in Fig. 19c.

Finally, a pure slip period-1 motion with large amplitude occurs when \(f=1.3\), as shown in Fig. 20a. In the extended \((x, \dot{x}, t)\) state space presented in Fig. 20b, a trajectory passes through the switching surface from one subspace to the other without any sticking portion.

It is clear from the above descriptions, for large amplitudes f of the external excitation shortening (see Figs. 16a and 17a) or disappearance (see Fig. 20a) of sliding mode becomes possible. The reason is that the sliding region becomes narrowed with the increasing of the f, as shown in Figs. 10 and 11, and the probability of collision of a trajectory with the sliding region becomes little (see Fig. 20c).

6 Summary and conclusion

In this paper, we have investigated the stick-slip vibrations of a self-excited smooth and discontinuous (SD) oscillator with Coulomb friction. The equilibrium states of this friction system are obtained to shown the complex equilibrium bifurcations. Closed-form solutions for both stick-slip motion and pure slip motion have been obtained by using Hamilton function. Furthermore, the influence of the belt speed on the steady states of the system has been examined by defining two critical values of belt speed. Under the perturbation, different shapes of the sliding regions have been demonstrated with the variation of amplitude of external excitation. The collision of trajectories of the periodic motions and the chaotic motions with the sliding regions have manifested in the \((x,\dot{x},t)\) state space by means of numerical simulations. Phase portraits have been depicted for the better understanding of the dynamical behaviors of the stick-slip vibration of the system. Further research is required to carefully consider the dynamics of the stick-slip vibration for the multiple degree of freedom friction system with geometry nonlinearity arising in mechanical engineering.