Periodic Motions of Coupled Oscillators Excited by Dry Friction and Harmonic Force

Abstract

Vibrating systems excited by dry friction are frequently encountered in technical applications. These systems are strongly nonlinear, and they are usually modeled as spring-mass oscillators. One of the most popular models of stick-slip oscillators consists of several masses connected by linear springs; one (or more) of the masses is in contact with a driving belt moving at a constant velocity. In the past, several authors investigated the behavior of this system, with different friction laws and with or without external actions and damping. In this work, we consider a system composed of two masses connected by linear springs. One of the mass is in contact with a driving belt moving at a constant velocity. Friction force, with Coulomb’s characteristics, acts between the mass and the belt. Moreover, it is assumed that the mass is also subjected to a harmonic external force. Several periodic orbits including stick phases and slip phases are obtained in closed form. In particular, the existence of periodic orbits including an overshooting part is proved. In the case of a nonmoving belt, a set of nonsticking periodic solutions is obtained, and we prove that these orbits are symmetrical in space and in time.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

This paper is a continuation of several investigations [5–7, 10] related to vibrating systems excited by dry friction. One of the most popular models of stick-slip oscillators consists of several masses connected by linear springs; one (or more) of the masses is in contact with a driving belt moving at a constant velocity. In the past, several authors investigated the behavior of this system, with different friction laws and with or without external actions and damping [1, 2, 4, 11], mainly via the numerical approach. However, assuming Coulomb’s laws of dry friction, the corresponding dynamical model is a piecewise linear system, and even for multi-degree-of-freedom cases, some analytical results about the existence and the stability of periodic orbits including stick-slip phases have been obtained [5–7]. One interesting phenomenon is the existence, inside periodic orbits with stick and slip parts, of an “overshooting” slip phase. During this part of the orbit, the mass in contact with the belt moves in the same direction at a higher speed than the belt itself. In this work, we consider the same model of dry friction oscillator subjected to a harmonic external force. Several periodic orbits including stick phases and slip phases are obtained in closed form. In particular, the existence of periodic orbits including an overshooting part is proved. In the case of a nonmoving belt, a set of nonsticking periodic solutions is obtained, and we prove that these orbits are symmetrical in space and in time.

2 Problem Formulation

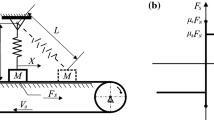
The system (Fig.1) is composed of two masses $m_{1},m_{2}$ connected by two linear springs of stiffness $k_{1},k_{2}$. The second mass is in contact with a belt moving at a constant velocity ν ₀. A friction force $\tilde{F}$ acts between the mass and the belt. Moreover, the second mass is also subjected to a driving force $\tilde{R} =\tilde{ p}\;\cos \left (\omega t+\varphi \right )$ ($\tilde{p},\omega,\varphi$ are constant parameters). The motion of this system are given by equations

$$\displaystyle{ x_{1}'' + x_{1} -\chi x_{2} = 0,\quad x_{2}'' +\chi \eta \left (x_{2} - x_{1}\right ) =\eta u + p\cos \left (\omega t+\varphi \right ), }$$

(1)

$$\displaystyle{\begin{array}{c} \eta = \frac{m_{1}} {m_{2}},\;\;\chi = \frac{k_{2}} {k_{1} + k_{2}},\;\;u = \frac{\tilde{F}} {k_{1} + k_{2}},\;\;p = \frac{\tilde{p}} {k_{1} + k_{2}}, \\ t =\varOmega \; t',\;\;\varOmega = \sqrt{\frac{k_{1 } + k_{2 } } {m_{1}}},\;\;\left (O\right )' = \frac{d\left (O\right )} {dt}, \\ \end{array} }$$

$x_{1},x_{2}$ are the displacements of the masses.

Fig. 1

Dry friction oscillator

The dry friction force u is obtained from Coulomb’s laws:

$$\displaystyle{\begin{array}{ll} u = u_{s}\,\text{sign}\left (V - x'_{2}\right ), &\text{if}\;\;V - x'_{2}\neq 0, \\ u =\chi \left (x_{2} - x_{1}\right ) - r(t),&\text{if}\;\;V - x_{2}' = 0,\;\;\left \vert \chi \left (x_{2} - x_{1}\right ) - r(t)\right \vert < u_{r}, \\ u = u_{s}, &\text{if}\;\;V - x'_{2} = 0,\;\;\;\chi \left (x_{2} - x_{1}\right ) - r(t) > u_{r}, \\ u = -u_{s}, &\text{if}\;\;V - x'_{2} = 0,\;\;\;\chi \left (x_{2} - x_{1}\right ) - r(t) < -u_{r},\\ \\ \\ \end{array} }$$

$$\displaystyle{0 < u_{s} < u_{r},\quad V = \frac{\nu _{0}} {\varOmega },\quad r(t) = \frac{p} {\eta } \cos \left (\omega t+\varphi \right ),}$$

u _r is the static friction force, and u _s is the dynamic friction force.

3 Three Modes of Motion Exhibited by the System

The dynamical behavior of this oscillator includes several phases of slip and stick motion of m ₂. For each kind of motion, the closed form solution is available.

3.1 Slip Motion of m ₂ with x′₂ < V

The solution is obtained from a modal analysis of (1) where u = u _s

$$\displaystyle{\begin{array}{c} Z\left (t\right ) = H\left (t\right )\left (Z_{0} - F_{0}\right ) + F\left (t\right ),\quad F\left (t\right ) = \left (\begin{array}{l} R\left (t\right )\\ R'\left (t\right ) \\ \end{array} \right ), \\ R(t) = Q\cos (\omega t+\varphi ),\quad F_{0} = F(0), \\ Z = \left (\begin{array}{l} z\\ z'\\ \end{array} \right ),\quad Z_{0} = Z(0),\quad Z = X - d_{0},\quad X = \left (\begin{array}{l} x_{1} \\ x_{2}\\ \end{array} \right ), \\ H\left (t\right ) = \left (\begin{array}{l} H_{1}\left (t\right )\;\;H_{2}\left (t\right ) \\ H_{3}\left (t\right )\;\;H_{1}\left (t\right )\\ \end{array} \right ),\quad d_{0} = \left (\begin{array}{l} d_{01} \\ d_{02}\\ \end{array} \right ),\quad d_{01} = \frac{u_{s}} {1-\chi },\quad d_{02} = \frac{d_{01}} {\chi }, \\ Q = \left (\begin{array}{l} q_{1} \\ q_{2}\\ \end{array} \right ),\quad q_{1} = \frac{p\chi } {(\omega ^{2} -\omega _{ 1}^{2})(\omega ^{2} -\omega _{ 2}^{2})},\quad q_{2} = q_{1}\frac{p(1 -\omega ^{2})} {\chi }. \\ \end{array} }$$

The two-by-two matrices $H_{i}\left (t\right )\;\left (i = 1,2,3\right )$ and the natural frequencies ω ₁, ω ₂ are obtained in analytical form [5].

3.2 Slip Motion of m ₂ with x′₂ > V (Overshooting)

The solution is obtained from (1) where $u = -u_{s}$

$$\displaystyle{Z\left (t\right ) = H\left (t\right )\left (Z_{0} - F_{0}\right )+F\left (t\right )+2L\left (t\right )d_{0}\quad L\left (t\right ) = \left (\begin{array}{l} H_{1}\left (t\right ) - I \\ H_{3}\left (t\right )\\ \end{array} \right ),\quad I = \left (\begin{array}{l} 1\;0\\ 0\;1\\ \end{array} \right ).}$$

3.3 Stick Motion of m ₂ (x ₂′ = V )

This motion is related to the dynamical system

$$\displaystyle{ x_{1}'' + x_{1} -\chi x_{2} = 0,\;\quad x_{2}'' = 0. }$$

(2)

The solution [5] is given by

$$\displaystyle{Z\left (t\right ) =\varGamma \left (t\right )Z_{0},\quad \varGamma \left (t\right ) = \left (\begin{array}{l} \varGamma _{1}\left (t\right )\;\;\varGamma _{2}\left (t\right ) \\ \varGamma _{3}\left (t\right )\;\;\varGamma _{1}\left (t\right )\\ \end{array} \right ).}$$

$\varGamma _{i}\left (t\right )\;\left (i = 1,2,3\right )$ are obtained from a modal analysis of the system (2). Moreover, during all this kind of motion, the following constraint holds:

$$\displaystyle{\;\left \vert \chi \eta \left (x_{2} - x_{1}\right ) - p\cos \left (\omega t+\varphi \right )\right \vert <\eta u_{r}.}$$

4 Periodic Orbits Including an Overshooting Part

Several periodic orbits including stick phases and slip phases have been obtained [7]. Among these orbits, a set of periodic orbits including an overshooting part is found. For each period $\left (0 < t < 2\pi /\omega \right )$, the motion is composed of three parts. The first one $\left (0 < t <\tau \right )$ is a slip motion of m ₂ with x ₂′ < V, the next part (0 < t −τ < τ ₁) is an overshooting slip motion of the mass (x′₂ > V ), and the last part ($0 < t -\tau -\tau _{1} < T,\;\;T = 2\pi /\omega -\tau -\tau _{1}$) is a stick motion of m ₂. At the beginning of the motion for t = 0, we assume that

$$\displaystyle{x_{2}'\left (0\right ) = V,\quad \chi \eta \left (x_{2}\left (0\right ) - x_{1}\left (0\right )\right ) = p\cos \varphi +\eta u_{r}}$$

and at t = τ, we assume the conditions

$$\displaystyle{ x_{2}'\left (\tau \right ) = V,\quad \chi \eta \left (x_{2}\left (\tau \right ) - x_{1}\left (\tau \right )\right ) - p\cos \left (\omega \tau +\varphi \right ) +\eta u_{r} < 0. }$$

(3)

The last condition leads to an overshooting motion for t > τ.

An example of a periodic orbit with an overshooting part is obtained for the set of data

$$\displaystyle{\chi = 0.2,\;\eta = 3.8,\;u_{s} = 0.059,\;u_{r} = 0.5347,\;V = 1,\;\omega = 0.6\;,p = 0.1,\;\varphi = 0.}$$

The other parameters are computed:

$$\displaystyle{\tau = 4.775,\;\tau _{1} = 2.65,\;T = 3.047,\;z_{1}\left (0\right ) = 1.1471,\;z_{2}\left (0\right ) = 3.6572,\;z'_{1}\left (0\right ) = -0.7281.}$$

The phase portraits of the system are shown in Fig. 2. The solid lines show slip motion (thick black lines correspond to the overshooting motion); the dotted lines are related to the stick motion.

Fig. 2

Phase portrait of the overshooting periodic solution

5 Nonsticking Periodic Solutions

In industrial applications, avoiding sticking phases of motion is sometimes necessary. In the past, several authors [3, 8] investigated the existence of periodic nonsticking solutions of a one-degree-of-freedom oscillator subjected to simple harmonic loading. The mass is in contact with a fixed surface and a dry friction force acts between the mass and the surface. The aim of these works is to obtain some estimates of the minimum external force amplitude needed to prevent this sticking motion. The nonsticking orbit involves for each period a slip motion with a negative mass velocity and a slip motion with a positive mass velocity (overshooting motion). Moreover, the authors assumed that the motion is symmetrical in space and time [3, 8].

In the following, this problem is revisited for the two-degree-of-freedom oscillator considered in this work. Let us consider the system described in Fig.1 with initial conditions

$$\displaystyle{ x_{20}' = V,\quad \chi \eta \left (x_{20} - x_{10}\right ) > p\cos \varphi +\eta u_{r}. }$$

(4)

The nonsticking periodic orbit is composed of two parts: for 0 < t < τ the system undergoes a slip motion (x′₂ < V ); the second part for τ < t < 2π∕ω is an overshooting motion (x′₂ > V ). At t = τ the conditions (3) are fulfilled. We prove [7] that this kind of periodic orbits exists only if

$$\displaystyle{V = 0,\;\tau =\pi /\omega,\;x\left (0\right ) = -x\left (\tau \right ),\;x'\left (0\right ) = -x'\left (\tau \right ).}$$

The nonsticking periodic orbits are symmetrical in space and time.

A numerical computation is performed for the parameters

$$\displaystyle{\chi = 0.3,\;\eta = 4,\;\omega =.6,\;p = 1,\;u_{s} = 0.1,\;u_{r} = 0.2996\;.}$$

The corresponding values of the initial conditions and of the time lag $\varphi$ are obtained:

$$\displaystyle{x_{10} = 1.5608,\;x_{20} = 3.3295,\;x'_{10} = 0.1523,\varphi = 0.3925\;.}$$

The phase portraits $\left (x_{i},x'_{i}\right ),\;i = \left (1,2\right )$ of the two masses are shown in Fig. 3 (the thick black parts of the curves are related to the overshooting motion). These curves are symmetrical with respect to the origin.

Fig. 3

Phase portrait of the nonsticking orbit

6 Periodic Orbits with Abnormal Stops

The nonsticking orbit investigated in the last paragraph involves for each period two normal stops

$$\displaystyle{x_{2}'\left (0\right ) = x_{2}'\left (\tau \right ) = 0.}$$

These stops occur when the displacement of the second mass reaches a local extremum and the mass reverses its direction of motion at the turning point. In [9], for a one-degree-of-freedom oscillator, with dry friction and harmonic load, a set of periodic orbits including abnormal stops have been obtained. Abnormal stops occur when at the turning point the mass moves in the same direction as its motion prior to the stop. The same phenomenon can be observed for the two-degree-of-freedom oscillator investigated in this paper. At t = 0 the initial conditions (4) are assumed and for 0 < t < τ, the system undergoes a slip motion (x′₂ < 0). Let us assume that at t = τ

$$\displaystyle{x_{2}'\left (\tau \right ) = 0,\;\;\chi \eta \left (x_{2}\left (\tau \right ) - x_{1}\left (\tau \right )\right ) - p\cos \left (\omega \tau +\varphi \right ) -\eta u_{r} > 0.}$$

A new phase of slip motion occurs. This motion ends at $t =\tau +\tau _{1}$ if at this time

$$\displaystyle{x'_{2}\left (\tau +\tau _{1}\right ) = 0,\quad \chi \eta \left (x_{2}\left (\tau +\tau _{1}\right ) - x_{1}\left (\tau +\tau _{1}\right )\right ) - p\cos \left (\omega \left (\tau +\tau _{1}\right )+\varphi \right ) +\eta u_{r} < 0.}$$

For t > τ +τ ₁ the system undergoes an overshooting motion (x′₂ > 0). A periodic orbit of period 2π∕ω is obtained, but due to the symmetry in space and in time of this nonsticking orbit, the overshooting motion ($\tau +\tau _{1} < t < 2\pi /\omega$) involves another abnormal stop for $t =\tau +\tau _{1} + T$, with the conditions

$$\displaystyle{x_{2}'\left (\tau +\tau _{1} + T\right ) = 0,}$$

$$\displaystyle{\chi \eta \left (x_{2}\left (\tau +\tau _{1} + T\right ) - x_{1}\left (\tau +\tau _{1} + T\right )\right ) - p\cos \left (\omega \left (\tau +\tau _{1} + T\right )+\varphi \right ) +\eta u_{r} < 0.}$$

Due to the symmetrical property we obtain

$$\displaystyle{\tau +\tau _{1} =\pi /\omega,\;\;T =\tau,\;\;x\left (\tau +\tau _{1}\right ) = -x\left (0\right ),\;\;x'\left (\tau +\tau _{1}\right ) = -x'\left (0\right ).}$$

This kind of orbit exists only if u _s  = u _r .

An example of periodic orbits with abnormal stops is obtained for the data

$$\displaystyle{\chi = 0.7,\;\eta = 3.8,\;\omega = 2\pi /11,\;p = 1,\;u_{r} = u_{s} = 0.1717,\;\varphi = 2.6455\;.}$$

The other parameters are computed:

$$\displaystyle{\tau = T = 4,\;\tau _{1} = 1.5,\;x_{1}\left (0\right ) = 2.1249,\;x_{2}\left (0\right ) = 2.0451,\;x_{1}'\left (0\right ) = -0.7267\;.}$$

The phase portrait of the system is shown in Fig. 4 (the thick black parts of the curves are related to the overshooting motion).

Fig. 4

Phase portrait of the orbit with abnormal stops