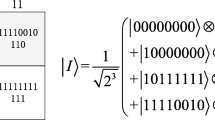1 Introduction

As the advantages of quantum physics, the idea to simulate physics with computers is put forward [1]. Quantum image processing (QIP) is a young emerging cross-discipline of image processing and quantum mechanics. From 1996, QIP gradually comes into our sight. It is primarily devoted to utilizing quantum computing technologies to capture, manipulate, and recover quantum images in different formats and for different purposes [2, 3]. Reference [4] describes the “analogue” quantum computers to discuss image analysis. Besides, references [5, 6] design algorithms based on unstructured picture (data set). Due to some of the astounding properties inherent to quantum computation, the quantum computer has demonstrated a bright prospect over the classic computer, particularly in Feynman’s computation model [1], Deutsch’s quantum parallelism assertion [7], Shor’s integer factoring algorithm [8] and Grover’s database searching algorithm [9].

In terms of applications, available literature on quantum image processing can be broadly classified into two groups: quantum-inspired image processing and classically inspired quantum image processing [10,11,12], respectively. The first step of quantum image processing thatis to store imagesin a quantum computer through quantum image representation. Consequently, several representative models aredeveloped and the pioneering work is the quantum image model of Qubit Lattice [13]. Following that, entangled images, in which geometric shapes are encoded in quantum states [14]; and Real Ket, where the images are quantum states having gray levels as coefficients of the states [15], were proposed by Venegas-Andraca and Latorre, respectively. More recently, Le et al. [16] proposed a flexible representation of quantum image (FRQI) using quantum superposition state to store the colors and the corresponding positions of an image. Years later, more quantum image representations [17,18,19,20] were proposed, which includes: a novel enhanced quantum representation (NEQR) [17] used q qubits encoding the gray-scale values. Thus make the NEQR could perform the complex and elaborate color operations more conveniently than FRQI.

Then, based on the work of quantum image representation models, there are many quantum image processing algorithms, in which includes quantum image geometric transformation [21,22,23,24]; quantum image scaling [25,26,27,28,29]; quantum image scrambling [30,31,32]; quantum image watermarking [33,34,35,36,37]; quantum image steganography based on least significant bit (LSB) [38, 39]; quantum image morphological operation [40,41,42]; quantum image edge detection [43, 44]; quantum image feature point extraction [45]; quantum image matching [46].

This paper is organized as follows. Section 2 briefly introduces the quantum image model NEQR and the classical morphology operations for the grayscale image. A series of specific quantum circuit are constructed to realize a certain function in Section 3. The specific quantum circuit realization morphological gradient for quantum gray-scale image is proposed. Section 5 analyses the circuit’s complexity and experimental results. The conclusions and future work is drawn in section 5.

2 Preliminaries

In this paper, the quantum image NEQR (i.e. a novel enhanced quantum representation of digital images) model is introduced first. Then, the morphology operations for the grayscale image that includes the flat grayscale dilation, erosion and their combination operation of morphology gradient are illustrated in detail.

2.1 Quantum Image Model NEQR and Circuit Complexity

2.1.1 The Novel Enhanced Quantum Representation (NEQR)

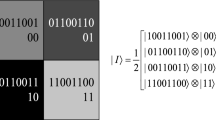
As for an2n × 2nimage with grayscale range[0, 2q − 1], NEQR uses q qubits to represent color information and 2n qubits to represent position information. But for a binary image, the color information just includes two values 0 and 1 (therein q = 1). Thus, the gray-scale value CYXof the pixel coordinate (Y, X) can be expressed by Eq. (1).

$$ {C}_{YX}={{\mathrm{C}}_{\mathrm{YX}}}^0{{\mathrm{C}}_{\mathrm{YX}}}^1\cdots {C_{YX}}^{q-2}{C_{YX}}^{q-1},{C_{YX}}^k\in \left\{0,1\right\},{C}_{YX}\in \left[0,{2}^q-1\right] $$
(1)

Therefore, the NEQR quantum image representation can be written as Eq. (2) for an2n × 2nimage with grayscale range[0, 2q − 1].

$$ \mid I\left\rangle =\frac{1}{2^n}\sum \limits_{Y=0}^{2^n-1}\sum \limits_{X=0}^{2^n-1}\mid {C}_{YX}\right\rangle \mid Y\left\rangle \mid X\right\rangle =\frac{1}{2^n}\sum \limits_{YX=0}^{2^{2n}-1}\underset{k=0}{\overset{q-1}{\otimes }}\mid {C}_{YX}^k\left\rangle \mid YX\right\rangle $$
(2)

Figure 1 shows an image and the corresponding NEQR state is on the right.

Fig. 1
figure 1

An 2 × 2 NEQR image and its quantum state is on the right

Full size image

2.1.2 Simple Quantum Gates and circuit’s Complexity

Quantum Gates

In the quantum circuitmodel, a complex transformation can be broken down into universal quantum logic gates [47], i.e., single-qubit gate, two-qubit and three-qubit gates, such as NOT, Controlled-V gate, Controlled-V+ gate, Feynman gate (FG) [48],Toffoli gate [49] and Peres gate [50] and Thapliyal Ranganathan gate [51] which are shown in Fig. 2.

Fig. 2
figure 2

Some single-qubit gate, two-qubit and three-qubit gates

Full size image

Therein, V is a square-root-of NOT gate and V+ is its Hermittian. Thus, VV or V+V+ creates a unitary matrix of NOT gate and VV+ = V+V = I (an identity matrix), which can be described as Eq. (3).

$$ {\displaystyle \begin{array}{l}V\times V={V}^{+}\times {V}^{+}=X\\ {}V\times {V}^{+}={V}^{+}\times V=I\end{array}} $$
(3)

As shown in Fig. 2, the FG can accomplish XOR function. It is easy to conclude that when cascades (n-1) FG gates we can realize n-bit XOR operation. The concrete quantum circuit realization and corresponding block diagram are shown in Fig. 3.

Fig. 3
figure 3

a The quantum circuit realization of n-bit XOR operation, b the block diagram of n-bit XOR operation

Full size image

Quantum circuit’s Complexity

In the quantum circuit model, a complex transformation can be broken down into simpler gates, i.e., single-qubit gate, two-qubit and three-qubit gates. Therefore, the circuit complexity of anysingle-qubit gate, two-qubit and three-qubit gatesare taken as unity. The circuit’s complexity is determined by the number of these simpler gates. Based on this principle, it is obvious that the NOT gate, FG, Controlled-V gate, Controlled-V+gate and TG can take as unity 1. The PG is composed by 2 Controlled-V gates,1 Controlled-V+gate and 1 FG, therefore, the circuit complexity of PG is 4. As shown in Fig. 3, the n-bit XOR operation is constructed by cascading (n-1) FG, thus the circuit complexity of n-bit XOR module is (n-1).

2.2 Classical Grayscale Morphology Operations

The grayscale morphology is built on binary morphological. In this section, we focus on flat grayscale quantum dilation and erosion operations which are defined in terms of minima and maxima of pixel neighborhoods [52]. Then, based on the flat grayscale dilation and erosion operations, we further introduce the conception of morphological gradient.

2.2.1 The Classical Flat Grayscale Dilation Operation

A function is used to represent the grayscale dilation operation of image F by structuring element B as denoted by

$$ \left(F\oplus B\right)\left(s,t\right)=\max \left\{F\left(s-x,t-y\right)+B\left(x,y\right)|\left(x,y\right)\in {D}_B\right\} $$
(4)

where DB is the domain of b and F(x, y)is assumed to equal−∞outside the domain of F.

Actually, the grayscale dilation operation always done by the flat structuring element, in which means that the value of B is 0 at all coordinates over DB definition. That is,

$$ B\left(x,y\right)=0,\left(x,y\right)\in {D}_B $$
(5)

In this case, the max operation is specified completely by the value of 0 and 1 in binary matrixDB, and the grayscale dilation equation is simplified to

$$ \left(F\oplus B\right)\left(s,t\right)=\max \left\{F\left(s-x,t-y\right)|\left(x,y\right)\in {D}_B\right\} $$
(6)

Thus, flat grayscale dilations are a local-maximum operator, where the maximum is taken over a set of pixel neighbors determined by the shape ofDB.

An example, asshown in Fig. 4, illustrates that the flat grayscale dilation is a local-maximum operator.

Fig. 4
figure 4

The flat grayscale dilation is a local-maximum operator

Full size image

2.2.2 The Classical Grayscale Erosion Operation

A function is used to represent the grayscale erosion operation of image F by structuring element B as denoted by

$$ \left( F\varTheta B\right)\left(s,t\right)=\min \left\{F\left(s+x,t+y\right)-B\left(x,y\right)|\left(x,y\right)\in {D}_B\right\} $$
(7)

where DBis the domain of b and F(x, y)is assumed to equal+∞outside the domain of F.

Conceptually, we again can think of translating the structuring element to all locations in the image. At each translated location, the structuring element values are subtracted to the image pixel values and the minimum is computed.

As with dilation, grayscale erosion is most often performed using flat structuring elements. The equation for flat grayscale erosion can then be simplified to

$$ \left( F\varTheta B\right)\left(s,t\right)=\min \left\{F\left(s+x,t+y\right)|\left(x,y\right)\in {D}_B\right\} $$
(8)

Thus, flat grayscale erosion is a local-minimum operator, in which the minimum is taken over a set of pixel neighbors determined by the shape of DB. So, the erosion problem transfers to search for minimum.

An example, shown in Fig. 5, illustrates that the flat grayscale erosion is a local-minimum operator.

Fig. 5
figure 5

The flat grayscale erosion is a local-minimum operator

Full size image

2.2.3 The Classical Morphological Gradient for Grayscale Image

Dilation and erosion can be used in combination, subtracting the eroded image from the dilated image can produce a morphological gradient, which is a measure of the local gray level change in the image. Thus, the function of morphological gradient based on the flat element can be written as follows.

$$ {\displaystyle \begin{array}{l} MF=\left(F\oplus B\right)\left(s,t\right)-\left( F\varTheta B\right)\left(s,t\right)\\ {}\kern0.84em =\left[\max \left\{F\left(s+x,t+y\right)\right\}-\min \left\{F\left(s-x,t-y\right)\right\}\right],\left(x,y\right)\in {D}_B\end{array}} $$
(9)

3 Quantum Circuit Design

In this section, a series of specific quantum circuit are designed to realize a certain function, which includes special add one operation UA1(n), special subtract one operation US1(n), quantum unitary operator UCand the parallel full subtractor PS. All of the mentioned quantum circuit will be used in the proposed morphology operations.

3.1 Special Add One Operation

The quantum circuit realization of special add one operation UA1(n)for an n-length qubits sequence is shown in Fig. 6. When UA1(n) works on the n qubits quantum state ∣xn − 1xn − 2⋯x1x0〉(Input), the result (Output) will be the∣xn − 1xn − 2⋯x1x0 + 1〉if and only if xn − 1 × xn − 2 × ⋯ × x1 × x0 ≠ 1. Otherwise, the n qubits quantum state∣xn − 1xn − 2⋯x1x0〉will not be changed. The function of UA1(n) can be expressed by Eq. (10).

$$ U{A}_1(n)\mid {x}_{n-1}\cdots {x}_1{x}_0\left\rangle =\right\{{\displaystyle \begin{array}{l}\mid {x}_{n-1}\cdots {x}_1{x}_0+1\Big\rangle, {x}_{n-1}\times {x}_{n-2}\times \cdots \times {x}_1\times {x}_0\ne 1\\ {}\mid {x}_{n-1}\cdots {x}_1{x}_0\Big\rangle, {x}_{n-1}\times {x}_{n-2}\times \cdots \times {x}_1\times {x}_0=1\end{array}} $$
(10)

therein, n is a positive natural number, n ≥ 2, x0, x1, ..., xn − 1 ∈ {0, 1}.

Fig. 6
figure 6

a Quantum circuit realizations of UA1(n), b the block diagram of UA1(n)

Full size image

3.2 Special Subtract One Operation

The quantum circuit realization of special subtract one operation US1(n)for an n-length qubits sequence is shown in Fig. 7. When US1(n) works on the n qubits quantum state ∣xn − 1xn − 2⋯x1x0〉 (Input), the result (Output) will be the∣xn − 1xn − 2⋯x1x0 − 1〉if and only if xn − 1 × xn − 2 × ⋯ × x1 × x0 ≠ 0. Otherwise, the n qubits quantum state∣xn − 1xn − 2⋯x1x0〉will not be changed. The function of US1(n) can be expressed by Eq. (11).

$$ U{S}_1(n)\mid {x}_{n-1}{x}_{n-2}\cdots {x}_1{x}_0\left\rangle =\right\{{\displaystyle \begin{array}{l}\mid {x}_{n-1}{x}_{n-2}\cdots {x}_1{x}_0-1\Big\rangle, {x}_{n-1}\times {x}_{n-2}\times \cdots \times {x}_1\times {x}_0\ne 0\\ {}\mid {x}_{n-1}{x}_{n-2}\cdots {x}_1{x}_0\Big\rangle, {x}_{n-1}\times {x}_{n-2}\times \cdots \times {x}_1\times {x}_0=0\end{array}} $$
(11)

therein, n is a positive natural number, n ≥ 2, xn − 1xn − 2⋯x1x0 ∈ {0, 1}.

Fig. 7
figure 7

a Quantum circuit realizations of US1(n), b the block diagram of US1(n)

Full size image

3.3 Quantum Unitary OperationU C

The quantum unitary operationUCas defined in Eq. (12) can copy the q-length qubit sequence information of∣C〉 =  ∣ cq − 1cq − 2⋯c0〉 into the q ancillary qubits∣0〉⊗q. The quantum circuit realization of UCis shown in Fig. 8.

$$ {U}_C\left(|C\Big\rangle |0\Big\rangle {}^{\otimes n}\right)=\mid {C}_{YX}\left\rangle \mid {C}_{YX}\right\rangle $$
(12)
Fig. 8
figure 8

a Quantum circuit for unitary operation UC, b the simplified graph of UC

Full size image

3.4 Quantum Comparator Circuit

In this section, the n-bit reversible comparator is designed through the 1-bit reversible comparator, in which a series of basic quantum gates (NOT, CNOT, PG and Toffoli gate) are used to construct the synthetic circuit.

3.4.1 1-Bit Reversible Comparator

The result of 1-bit compares shown in Table 1. From the truth table of connectional comparator in Table 1, the logical expressions of 1-bit comparator is as follows:

$$ {\displaystyle \begin{array}{l}{F}_{A>B}=A\overline{B}\\ {}{F}_{A=B}=\overline{A\oplus B}\\ {}{F}_{A<B}=\overline{A}B\end{array}} $$
(13)
Table 1 The truth table of 1-bit comparator
Full size table

According to the logical expression of Eq. (13), the quantum circuit realization 1-bit reversible comparator as illustrated in Fig. 9.

Fig. 9
figure 9

Quantum circuit realization of 1-bit reversible comparator

Full size image

The conventional n-bit comparator is used for comparing two n-bit numbers likeA = aq − 1aq − 2⋯a1a0 and B = bq − 1bq − 2⋯b1b0. The logical expression of n-bit comparator can be written as Eq. (14).

$$ {\displaystyle \begin{array}{l}{F}_{A>B}=\left({a}_{q-1}>{b}_{q-1}\right)\oplus \left({a}_{q-1}={b}_{q-1}\right)\left({a}_{q-2}>{b}_{q-2}\right)\oplus \cdots \\ {}\kern1.2em \oplus \left({a}_{q-1}={b}_{q-1}\right)\left({a}_{q-2}={b}_{q-2}\right)\cdots \left({a}_2={b}_2\right)\left({a}_1={b}_1\right)\left({a}_0>{b}_0\right)\\ {}{F}_{A=B}=\left({a}_{q-1}={b}_{q-1}\right)\left({a}_{q-2}={b}_{q-2}\right)\oplus \cdots \oplus \left({a}_1={b}_1\right)\left({a}_0={b}_0\right)\\ {}{F}_{A<B}=\left({a}_{q-1}<{b}_{q-1}\right)\oplus \left({a}_{q-1}={b}_{q-1}\right)\left({a}_{q-2}<{b}_{q-2}\right)\oplus \cdots \\ {}\kern1.2em \oplus \left({a}_{q-1}={b}_{q-1}\right)\left({a}_{q-2}={b}_{q-2}\right)\cdots \left({a}_2={b}_2\right)\left({a}_1={b}_1\right)\left({a}_0<{b}_0\right)\end{array}} $$
(14)

According to logical expression of q-bit conventional binary comparator, equation of FA < B also can be obtained as followed:

$$ {F}_{A<B}=\overline{F_{A>B}\oplus {F}_{A=B}} $$
(15)

Combine the principle illustrated in Eq. (14) and Eq. (15) that the comparative resultsof FA < B for q-bit A and B can be deduced from the corresponding results of FA > B and FA = B. Thus, the basic quantum comparator for 1-bit module (QC1) that deduces from the 1-bit reversible comparatorcan be rebuilt as illustrated in Fig. 10, which would be used to build the integrate quantum comparator and output the large and small circuits for q-bit in latter.

Fig. 10
figure 10

a The QC1 module, b quantum circuit for the QC1 module

Full size image

3.4.2 Q-Bit Reversible Comparator and Output the Large

Combine the logical value described in Eq. (14) and Eq. (15), the circuit realization of q-bit reversible comparator and output the large (QCOL) is constructed through the QC1 module, n-bit xor gate, PG gate and FG gate, as shown in Fig. 11.

Fig. 11
figure 11

q-bit reversible comparator and output the large

Full size image

3.4.3 Q-Bit Reversible Comparator and Output the Small

Similar to quantum circuit for QCOL, the circuit realization of q-bit reversible comparator and output the small (QCOS) is constructed through the QC1 module, n-bit xor gate, PG gate and FG gate, as shown in Fig. 12.

Fig. 12
figure 12

q-bit reversible comparator and output the small

Full size image

For convenience, Fig. 13 gives the simplified block diagram QCOL and QCOS modules, which omits the constant inputs and garbage outputs.

Fig. 13
figure 13

a The block diagram of QCOL, b the block diagram of QCOS

Full size image

As shown in Fig. 13, A = aq − 1aq − 2⋯a1a0and B = bq − 1bq − 2⋯b1b0. In QCOL module, ifA ≥ B, the large = A; Otherwise, the large = B. In QCOS module, ifA ≥ B, the small = B; Otherwise, the small = A.

3.5 The Parallel Subtractor (PS) Circuit

Thapliyal H. and Ranganathan N. [51] designed subtractor using the TR gate and further realized optimization in terms of quantum cost and delay in [53]. Here, the concrete design of parallel subtractor circuit is given.

  1. (a)

    Reversible half subtractor (RHS)

The RHS can be used to calculate two 1-bit numbers difference, where the corresponding truth value of RHS is shown in Table 2. Therein, the inputs of a0 andb0 are 1-bit binary number whiled0 and b0 denote the corresponding difference and borrow of b0– a0, respectively. The simplified graph of RHS module and its quantum circuit realization are illustrated in Fig. 14, where ∣a0 ⊕ b0〉 represents the difference of ∣b0 − a0〉, and \( \mid {a}_0\overline{b_0}\Big\rangle \) generates the corresponding borrow bit.

Table 2 The truth table of RHS
Full size table
Fig. 14
figure 14

a The block diagram of RHS module, b quantum circuit realization of RHS module

Full size image
  1. (b)

    Reversible fullsubtractor (RFS)

The RFS can be used to calculatethree 1-bit numbers difference, where the corresponding truth value of RFS is shown in Table 3. Therein, the inputs of a0,b0 and c0 are 1-bit binary number while d0 and b0 denote the corresponding difference and borrow of a0–b0– c0, respectively. The simplified graph of RFS module and its quantum circuit realization are illustrated in Fig. 15, where ∣a0 ⊕ b0 ⊕ c0〉represents the difference of ∣a0 − b0 − c0〉, and \( {a}_0\overline{\left({b}_0\oplus {c}_0\right)}\oplus {b}_0\overline{c_0} \) generates the corresponding borrow bit.

Table 3 The truth table of RFS
Full size table
Fig. 15
figure 15

a The simplified graph of RFS module, b quantum circuit for RFS module

Full size image
  1. (c)

    Parallel subtractor (PS)

The parallel subtractor (PS) is used to compute the difference of two n-bit numbers X and Y, whereinX = xn − 1…x0, Y = yn − 1…y0. Assume thatwe define the difference of X − Y isdndn − 1…d1d0. Because of the highest bit dn is a sign bit, i.e., if dn = 1, then X < Y; otherwise, dn = 0 and X ≥ Y. The PS module are designed using 1 RHS and (n-1) RFS as shown in Fig. 16(a). For convenience, the block diagram of PS omits the constant ancillary bit 0 and the other unmarked garbage outputs as shown in Fig. 16(b).

Fig. 16
figure 16

a quantum circuit realization of PS module, b thesimplified graph of PS module

Full size image

4 Circuit Realization Morphological Gradient for Quantum Gray-Scale Image

In this section, the quantum circuit for quantum gray-scale image dilation and erosion are constructed first. Then, based on the results of quantum dilation and erosion, thequantum morphological gradientoperation is done through the PS module, whichsubtracts the eroded image from the dilated image. Finally, through the quantum measurement, the classical morphological gradient can be obtained.

4.1 Workflow of Quantum Grayscale Image Morphological Gradient Operation

The whole procedure ofquantum morphological gradient operationis shown in Fig. 17, which is divided into many steps more specifically.

Fig. 17
figure 17

Whole procedure of quantum morphological gradient operation

Full size image

Here, the working principle of the whole procedure is introduced briefly. The first step in thiswhole procedure is to quantize the classical image into to aquantum image based on NEQR expression model. Following that, A series of modules UA1(n) and US1(n) are implemented in a certain order to shift the quantum image based on the specific shape of structuring element and the quantum unitary operation UC modules to copy the corresponding the pixel information of the shifted quantum image into prepared extra ancillary qubit sequences. Thus, we can obtain the quantum image sets, which is associated with the specific shape of the structuring element. And now, based on these quantum image sets, the QCOL modules is used to find the local-maximum (the quantum dilation result) and the QCOS modules is used to find the local-minimum (the quantum erosion result), respectively. Finally, the quantum morphological gradientcan be obtained by subtracting the eroded image from the dilated image through PS module.

4.2 Quantum Circuit Realization Quantum Dilation and Erosion Operations

Suppose that there adigital image is quantized into a NEQR quantum image with size 2n × 2nand gray range[0, 2q − 1], which is expressed by Eq. (2). The flat structuring element B as shown in Fig. 18 is a 3 × 31-matric including 9 neighbor pixels.

Fig. 18
figure 18

Structuring element B

Full size image

Through the analysis of classical grayscale morphology operations in subsection 2.2.1 and 2.2.2, it is easy to find that the result of the flat grayscale image dilation and erosion are the local-maximum and local minimum operators, respectively. Therein, the maximum and minimum values are taken over a set of neighbor pixels determined by the exact shape of structuring element. Based on this principle, the integrated quantum circuit design is divided into two steps as shown in Fig. 19 and Fig. 20.

Fig. 19
figure 19

Quantum circuit realization obtaining 9 neighbor pixels according to structuring element B

Full size image
Fig. 20
figure 20

Finding the local-maximum and local-minimum in any 3 × 3neighbor window

Full size image

  • Step 1. Firstly, prepare the eight extra qubits∣0〉⊗8qsequences as defined in Eq. (16), which is in a tensor product with the original quantum image state. Then, implement the special add one operation UA1(n), special subtract one operation US1(n) and quantum unitary operation UCin a certain order on the original quantum image, we can get the 9 qubits information of the neighbor pixels of the whole image and store them into the prepared qubit sequences. The concrete circuit realization of this step is shown in Fig. 19.

$$ \frac{1}{2^n}\sum \limits_{Y=0}^{2^n-1}\sum \limits_{X=0}^{2^n-1}\mid 0\left\rangle {}^{\otimes 8q}\mid {C}_{YX}\right\rangle \mid Y\left\rangle \mid X\right\rangle =\frac{1}{2^n}\sum \limits_{YX=0}^{2^{2n}-1}\mid 0\left\rangle {}^{\otimes 8q}\underset{k=0}{\overset{q-1}{\otimes }}\mid {C}_{YX}^k\right\rangle \mid YX\Big\rangle $$
(16)

Therefore, we can get therelative color qubits of the neighbor pixels of the whole image, i.e., the quantum image sets where all the pixels share the same position state as defined in Eq. (17).

$$ \frac{1}{2^n}\sum \limits_{Y=0}^{2^n-1}\sum \limits_{X=0}^{2^n-1}\mid {C}_{YX}\left\rangle \mid {C}_{Y-1X}\right\rangle \mid {C}_{Y-1X+1}\left\rangle \mid {C}_{YX+1}\right\rangle \mid {C}_{Y+1X+1}\left\rangle \mid {C}_{Y+1X}\right\rangle \mid {C}_{Y+1X-1}\left\rangle \mid {C}_{YX-1}\right\rangle \mid {C}_{Y-1X-1}\left\rangle \mid Y\right\rangle \mid X\Big\rangle $$
(17)

  • Step 2. Eight QCOL and Eight QCOS modules are cascaded for finding the local-maximum pixel and local-minimum pixel in quantum image sets, respectively. The specific circuit design is shown in Fig. 20.

Therefore, though the above two steps, we can obtain the quantum dilation and erosion results, which can be expressed Eq. (18)

$$ \mid results\left\rangle =\frac{1}{2^n}\sum \limits_{Y=0}^{2^n-1}\sum \limits_{X=0}^{2^n-1}\mid {D}_{YX}\right\rangle \mid {E}_{YX}\left\rangle \mid Y\right\rangle \mid X\Big\rangle $$
(18)

therein, the qubit sequence ∣DYX〉 and ∣EYX〉 are entangled with each other and share the same position coordinates.

4.3 Quantum Circuit Realization Quantum Morphological Gradient Operation

According to principle of the classical morphological gradient in subsection 2.2.3,we know that the morphological gradient operation can be done through thedilation and erosion operations. Based on this principle, Fig. 21 provides the concrete quantum circuit realization of the morphological gradient, which a single PS module is used to subtract quantum erosion result ∣EYX〉from the quantum dilation result ∣DYX〉.

Fig. 21
figure 21

Subtract the eroded image from the dilated image to produce the morphological gradient

Full size image

Thus, we obtain the quantum morphological gradient as Eq. (19)

$$ \mid G\left\rangle =\frac{1}{2^n}\sum \limits_{Y=0}^{2^n-1}\sum \limits_{X=0}^{2^n-1}\mid {G}_{YX}\right\rangle \mid Y\left\rangle \mid X\right\rangle $$
(19)

5 Circuit Complexity and Experiment Analyses

In this section, the circuit complexity of morphological gradient operation for quantum grayscale image discussed firstly, which includes three figures (Fig. 19, Fig. 20 and Fig. 21). Then, the experiment results aresimulated based onthe classical computer’s MATLAB software.

5.1 Circuit Complexity Analysis

Here consider a size of 2n × 2n quantum image with grayscale range[0, 2q − 1]as an example. Similarly, the circuit’s complexity analysis is divided into three steps according to the circuit realization three steps.

  • Step 1. The quantum circuit realization as shown in Fig. 19, therein, 5 UA1(n) modules and 5 US1(n) modules both are for an n-length qubits sequence, and 8 UCmodules. The single UCmodule is constructed by q FG gates (shown in Fig. 8), thus its circuit’s complexity is q. As shown in Fig. 6 and Fig. 7, the single UA1(n) and US1(n) module both are comprised by (n-1) multi-CNOT (which means the circuit’s control qubits not just one)ofCNOT, 2 − CNOT⋯(n − 2) − CNOT, (n − 1) − CNOTand two n − CNOT.According to analysis of [44, 54], a K-CNOT quantum gate (where K represents the number of control qubits, K ≥ 3) can be constructed by (4 K-8) 2-CNOT gates (TG) and (K-3) assistant qubits. Therefore, the circuit’s complexity of single UA1(n) or US1(n) module is\( 1+\sum \limits_{K=3}^{n-1}\left(4K-8\right)+2\left(4n-8\right)=2{n}^2-2n+5 \). Thus, the circuit’s complexity in step 1 is10 × (2n2 − 2n + 5) + 8q = 20n2 − 20n + 8q + 50.

  • Step 2.The quantum circuit realization as shown in Fig. 20, therein, 8QCOL modules and 8 QCOS modules both are for an q-length qubits sequence. The single QCOL and QCOS modules are shown in Fig. 11 and Fig. 12, respectively, which both are composed by q QC1 modules, 2(q-1) PG gates, 2 FG gates and 2q 2-CNOT gates. Therein, QC1 module is shown in Fig. 10, which circuit’s complexity is 6, and the PG gate and FG gate are shown in Fig. 2 of which circuit’s complexity are 4 and 2, respectively. Thus, we can calculate that the single QCOL or QCOS module is 6q + 4 ⋅ 2(q − 1) + 2 + 2q. Therefore, the circuit’s complexity in this step is16 × (6q + 4 ⋅ 2(q − 1) + 2 + 2q) = 256q − 96.

  • Step 3.The quantum circuit realization is shown in Fig. 21. Therein, just only one PS module for a q-length qubits sequence is used to calculate the difference of the local-maximum and local-minimum. Thus the PS module can be constructed by 1 RHS module and (q-1) RFS module. As shown in Fig. 14 and Fig. 15, single RHS module and single RFS module circuit’s complexity are 4 and 6, respectively. Thus the circuit’s complexity of this step is6(q − 1) + 4 = 6q − 2.

According to thecircuit’s complexity analysis in abovethree steps, we can conclude that the integrated circuit complexity is equal to the sum of the three steps, that is

$$ {\displaystyle \begin{array}{l}\left(20{n}^2-20n+8q+50\right)+\left(256q-96\right)+\left(6q-2\right)\\ {}=20{n}^2+270q-20n-48\\ {}\approx O\left(20{n}^2+270q\right)\end{array}} $$

For classical dilation and erosion operations, the complexity is Ο(m222n) where the size of structuring element and original image are m × mand 2n × 2n, respectively. Therefore, our proposed quantum circuit scheme has a very lower complexity to the classical one.

5.2 Simulation Analysis

All the experiments are simulated by MATLAB 2014 on the classical computer. Two common test images Lena and Rice were chosen, and the structuring element is a 3 × 3 1-matric. The experiment results are shown in Fig. 22.

Fig. 22
figure 22

(a) grayscale image Lena. (b) flat structuring element B. (c) the flat grayscale dilation of Lena by B. (c) the flat grayscale erosion of Lena by B. (e) the morphological gradient producing by (c) and (d); (f) grayscale image Rice. (g) the flat grayscale dilation of Rice by B. (h) the flat grayscale erosion of rice by B. (e) the morphological gradient producing by (g) and (h)

Full size image

6 Conclusions

Morphology provides an approach to the processing of digital images based on shape. In this paper, quantum implementation circuits of flat dilation and erosion of grayscale images are constructed based on NEQR. Then,the circuit realization of morphological gradient for grayscale imageshas been designed.

According to the characteristic of operations of the classical flat grayscalemorphology, the quantum circuit realization mainly are divided into three steps:(1) Obtain the quantum image sets of neighborhood window pixels based on the shape of structuring element using a sequence of UA1(n), US1(n), and UC modules; (2) Finding the local-maximum and local-minimum through a series of QCOLand QCOS modules; (3) Using the PS module to subtract the local-minimum from the local-maximum.

Due to the unique advantages of parallel computing, entanglement, superposition, quantum computer brings bright prospect. Therefore, the quantum versions of erosion and dilation algorithms have been studied, the complexity of which is greatly reduced. Our future work will focus on the application of quantum morphology, such as quantum edge detection, noise reduction, feature detection, and image recognition.