Well behaved anisotropic compact star models in general relativity

Abstract

Anisotropic compact star models have been constructed by assuming a particular form of a metric function $e^{\lambda}$. We solved the Einstein field equations for determining the metric function $e^{\nu}$. For this purpose we have assumed a physically valid expression of radial pressure ($p_{r}$). The obtained anisotropic compact star model is representing the realistic compact objects such as PSR 1937 +21. We have done an extensive study about physical parameters for anisotropic models and found that these parameters are well behaved throughout inside the star. Along with these we have also determined the equation of state for compact star which gives the radial pressure is purely the function of density i.e. $p_{r}=f(\rho)$.

1 Introduction

The strong gravity is a very interesting field in the astrophysics and responsible for several fundamental phenomena. These phenomenons give the features of diverse characters of the gravitating stars. The simplest equation of state $\rho=3p+B$, where $B=2.28\times10^{14}$ has been considered by Brecher and Caporaso (1976) for constructing the first model of quark star. A star forms strange quark matter having surface density $2.28\times10^{14}~\mbox{gm/cm}^{3}$ with the maximum mass $M=2.8M_{\odot}$, which was much higher than the equation of state for baryon matter. Witten (1984) also obtained the strange star models with maximum mass $M=2 M_{\odot}$ and radius $R=11.1~\mbox{km}$ having bag constant $B=57.5~\mbox{MeV}\,\mbox{fm}^{-3}$. The first model with realistic equation of state for strange quark matter was proposed by Haensel et al. (1986). He has also given the specific property of accretion on strange stars. In addition, Alcock et al. (1986) discussed about the creation of strange stars and compared them with the normal curst. Recently Rahaman et al. (2012) have determined the strange star models of the equation of state $p_{r}=\frac{1}{3}(\rho -4B_{g})$ with mass $M=1.4M_{\odot}$, radius $R=6.88~\mbox{km}$ and surface density $\rho_{R}=1.43\times10^{15}~\mbox{gm/cm}^{3}$ for the bag constant $B_{g}=202.275~\mbox{MeV}\,\mbox{fm}^{-3}$. In recent years, it has been shown that there is no astrophysical object which is entirely a perfect fluid. The theoretical investigations of Ruderman (1972) about more realistic stellar object shows that the nuclear matter may be locally anisotropic at least in very high density ranges ($\rho>10^{15}~\mbox{gm/cm}^{3}$).

In this situation the anisotropy factor can divide the pressure inside the fluid sphere into two different pressures as radial pressure and transverse pressure which are orthogonal to each other. Therefore,the pressure anisotropy is quite reasonable inside any compact stellar model to consider more realistic objects. In this connection, Gokhroo and Mehra (1994) have shown that due to anisotropic fluid case the existence of repulsive force helps to construct compact objects. On the other hand Kippenhahn and Weigert (1990) have argued that anisotropy could be introduced due to the existence of solid core or due to the presence of type 3A-superfluid. Also the existences of anisotropy in fluid spheres which is due to different kind of phase transitions (Sokolov 1980), pion condensation (Sawyer 1972) and effects of slow rotation inside the star (Silva et al. 2014). It is noted by Bowers and Liang (1917) that anisotropy might have non-negligible effects on such parameters like equilibrium mass and surface redshift. The theoretical investigations about the anisotropic compact star models are available in the literature (Herrera et al. 2004; Herrera and Santos 1997; Varela et al. 2010; Rahaman et al. 2015; Komathiraj and Maharaj 2007, 2011; Murad 2016; Malaver 2014, 2015a,b; Maurya and Gupta 2012a, 2013, 2014). In addition, Maurya et al. (2015a,b,d, 2016a,b,c) and Singh et al. (2016a,b), Singh and Pant (2016a,b) have obtained several anisotropic compact star models in different approach. However some other important solutions for compact star with electric charge are obtained by several authors (Maurya et al. 2011, 2015c; Maurya and Gupta 2011, 2012b; Pant and Maurya 2012; Ivanov 2010) In this context, the algorithm for generating all spherical symmetric anisotropic solution has been given by Herrera et al. (2008) and for charged anisotropic case by Maurya et al. (2015b). Recently Bhar and Ratanpal (2015) have obtained the anisotropic model for Matese-Whitman mass function. In this solution we have noted that the tangential pressure is not always greater than the radial pressure i.e. $p_{t} < p_{r}$ inside the star at some points. As the existence of a repulsive force (in the case in which $p_{t} > p_{r}$) allows the construction of more compact objects while using anisotropic fluid than using isotropic fluid (Gokhroo and Mehra 1994). For this purpose, we have started with a physically valid metric function $\lambda(r)=\ln(1+br^{2})-\ln(1+ar^{2})$ to obtain the solution for the anisotropic compact stars. Next, we have discussed several physical properties like tangential pressure, anisotropy factor, casuality condition, TOV equation and red-shift etc. It is noted by Fig. 8 that the anisotropic factor is always positive and finite everywhere inside the star. However, the central density of the compact star PSR 1937 +21 is $1.3347\times10^{15}~\mbox{gm/cm}^{3}$. On the other hand, we have also done important investigation about the equation of state in present solution. In this regard, we have determined the EOS for the anisotropic compact star in Sect. 3.2. As we can see from Eq. (15), the radial pressure ($p_{r}$) is purely the function of density ($\rho$). So this relation of pressure and density can represent the equation of state for present anisotropic compact star models.

The structure of the paper as follows: in Sect. 2, the spherically symmetric metric and Einstein’s field equation for anisotropic fluid distribution are discussed. Section 3 includes three subsections (Sects. 3.1, 3.2 and 3.3). In Sect. 3.1, we proposed new solution for anisotropic compact star and the equation of state to represent the realistic matter in Sect. 3.2. However in Sect. 3.3, we have determined the arbitrary constants and mass function ($M$) by using the boundary conditions. Some physical features of the solution like as equation of state parameters, energy conditions, Tolman-Oppenheimer-Volkoff (TOV) equation and effective mass-radius relation with surface red-shift are given in Sect. 4. At last in Sect. 5, we have presented the physical analysis and conclusion.

2 The spherical symmetric metric and Einstein’s field equation for anisotropic fluid distribution

We assume the static spherically symmetric metric of the form:

$$ ds^{2} = e^{\nu(r)} dt^{2}- r^{2} \bigl(d\theta^{2} + \sin^{2}\theta d \phi^{2} \bigr)- e^{\lambda(r)} dr^{2}. $$

(1)

The energy momentum tensor (${T^{i}}_{j}$) for the anisotropic fluid distribution is defined as (Dionysiou 1982):

$$ {T^{i}}_{j} = \bigl[(p_{r} - p_{t}) \theta^{i} \theta_{j}- p_{t}{\delta^{i}}_{j} +(\rho+ p_{r})v^{i}v_{j} \bigr], $$

(2)

where $\theta^{i}\theta_{j}=-v^{i}v_{j}=-1$ and $v^{i}\theta_{j}=0$. $\theta^{i}$ is the unit space like vector in the direction of radial vector and $v^{i}$ is the four-velocity, $p_{r}$ and $p_{t}$ correspond to radial pressure and tangential pressure respectively.

Then the Einstein’s field equations are given as:

$$ {R^{i}}_{j} - \frac{1}{2} R {g^{i}}_{j} =-8\pi{T^{i}}_{j} $$

(3)

where we suppose $G=1=c$ in relativistic geometrized units. However $G$ and $c$ respectively being the Newtonian gravitational constant and velocity of photon in vacua.

In view of metric (1), the Einstein field equations (3) can be expressed in the following system of ordinary differential equations as (Dionysiou 1982):

$$\begin{aligned}& \biggl[ \frac{{\lambda}^{\prime}}{r}-\frac{1}{r^{2}}\biggr] e^{-\lambda } + \frac{1}{r^{2}} = 8\pi\rho \end{aligned}$$

(4)

$$\begin{aligned}& \biggl[\frac{{\nu}^{\prime}}{r}+\frac{1}{r^{2}}\biggr] e^{-\lambda} - \frac{1}{r^{2}} = 8\pi p_{r}, \end{aligned}$$

(5)

$$\begin{aligned}& \biggl[\frac{{\nu}^{\prime\prime}}{2} - \frac{{\lambda}^{\prime}{\nu }^{\prime}}{4} + \frac{{{\nu}^{\prime}}^{2}}{4} + \frac{{\nu}^{\prime} - {\lambda}^{\prime}}{2r} \biggr]e^{-\lambda} = 8\pi p_{t}, \end{aligned}$$

(6)

where the prime denotes differential with respect to $r$.

3 New anisotropic solution, equation of state and boundary conditions

3.1 New anisotropic solution

To determine the anisotropic solution, we suppose the metric potential $\lambda(r)$ of the form:

$$ \lambda(r)=\ln \bigl(1+br^{2} \bigr)-\ln \bigl(1+ar^{2} \bigr) $$

(7)

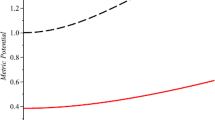
where $a$ and $b$ are constants with $a\neq b\neq0$. However for the physical validity of metric function $e^{\lambda}$, it should be 1 at centre and monotonically increasing with increase of $r$. For this purpose the constant $b$ should be positive and $a$ should be negative.

We have noted that the metric potential $e^{\lambda}$ is 1 at the centre and monotonically increasing away from the centre. The behaviour of $e^{\lambda}$ can be seen in Fig. 1.

Fig. 1

Metric function $e^{\lambda}$ verses fractional radius $r/R$ for the compact star PSR 1937 +21. We have employed the data values in this figure as: $a=-0.000591$, $b = 0.007694$ and $R=11.4005~\mbox{km}$

The expressions for energy density and metric function $\nu$ are given by Eqs. (4) and (5) respectively as:

$$\begin{aligned}& 8\pi\rho=\frac{(b-a)(3+br^{2})}{(1+br^{2})^{2}} \end{aligned}$$

(8)

Then from Eq. (8), $\rho_{r=0}=3(b-a)/8\pi$. Since the density should be positive at the centre this imply that $b>a$. It is clear from Fig. 2, the density is positive everywhere within stellar model and maximum at centre. However it is monotonically decreasing away from centre.

$$\begin{aligned}& \nu^{\prime}=\frac{8\pi rp_{r}(1+br^{2})}{1+ar^{2}}+\frac {(b-a)r}{1+ar^{2}}. \end{aligned}$$

(9)

Fig. 2

Energy density ($8\pi\rho$) verses to fractional radius $r/R$ for the compact star PSR 1937 +21. The data values of the constants $a$, $b$ and $a_{0}$ in this figure is same as in Fig. 1

To find the metric function ‘$\nu$’, we suppose the expression for radial pressure as:

$$ 8\pi p_{r}=\frac{a_{0}(1-br^{2})}{(1+br^{2})^{2}}. $$

(10)

where, $a_{0}$ is positive constant. We can see that the radial pressure $p_{r}$ is physically valid, singularity free and positive finite everywhere inside the star (Fig. 3). However it is monotonically decreasing away from centre. It also vanishes at $r=\frac{1}{\sqrt {b}}$, which gives the radius of the anisotropic star.

Fig. 3

Radial pressure $8\pi p_{r}$ verses fractional radius $r/R$ for the compact star PSR 1937 +21 with the values of the constants and parameters as: $a=-0.000591$, $b = 0.007694$, $a_{0} =0.0037$ and $R = 11.4005~\mbox{km}$

By plugging the value of radial pressure from Eq. (10) into in Eq. (9), we get $\nu^{\prime}$ as:

$$ \nu^{\prime}=\frac{a_{0}r(1-br^{2})}{(1+ar^{2}) (1+br^{2})}+\frac{r(b-a)}{(1+ar^{2})}. $$

(11)

After integration of the above equation w.r. to $r$, we get the metric function $\nu$ of the form as:

$$ e^{\nu}=C \bigl(1+br^{2} \bigr)^{A} \bigl(1+ar^{2} \bigr)^{B} $$

(12)

where, $A=\frac{a_{0}}{(b-a)}$, $B=\frac{(b-a)^{2}-a_{0}(b+a)}{2a(b-a)}$ and $C$ is arbitrary positive constants of integration. The metric function $e^{\nu}$ should be free from singularity and positive, finite within the stars. From Eq. (12), $e^{{\nu}(0)}=C$, which imply that $e^{\nu}$ is positive and finite at centre due to $C$ is a positive. Figure 4 indicates that the metric function is satisfying the required physical conditions.

Fig. 4

Metric function $e^{\nu}$ verses fractional radius $r/R$ for the compact star PSR 1937 +21. For the purpose of plotting this graph, we have employed same data values for the arbitrary constants as in Figs. 1, 2 and 3

Next we obtained the expression for tangential pressure ($p_{t}$) by putting the value of $\lambda$ and $\nu$ into Eq. (6):

$$ 8\pi p_{t}=\frac{bp_{1}+a^{2}r^{2}p_{2}+ap_{3}}{(1+ar^{2})(1+br^{2})^{3}} $$

(13)

where,

$$\begin{aligned} p_{1} =&\bigl[-1-br^{2}+bA^{2}r^{2}+A(2-br^{2})\bigr],\\ p_{2} =&\bigl[1+A^{2}b^{2}r^{4}+b(1+3A)r^{2}\\ &{}+B(1+br^{2})(1+2Abr^{2})+B^{2}(1+br^{2})^{2}\bigr],\\ p_{3} =&1+5Abr^{2}+b^{2}(-1-A+2A^{2})r^{4}\\ &{}+B(1+br^{2})\bigl[2+(1+2A)br^{2}\bigr]. \end{aligned}$$

We have shown the behaviour of tangential pressure in Fig. 5 and conclude that $p_{t}$ is maximum at centre however it is decreasing monotonically throughout the star. Also $p_{t}$ and $p_{r}$ are equal at centre.

Fig. 5

Tangential pressure ($8\pi p_{t}$) verses fractional radius $r/R$ for the compact star PSR 1937 +21 with the values of the constants: $a=-0.000591$, $b = 0.007694$, $a_{0} =0.0037$ and $R = 11.4005~\mbox{km}$

Now the pressure anisotropy factor ($\Delta=p_{t}-p_{r}$) can be determined by using the pressure isotropy condition as:

$$ 8\pi\Delta=\frac{bp_{1}+a^{2}r^{2}p_{2}+ap_{3}-a_{0} (1+ar^{2})(1-b^{2}r^{4})}{(1+ar^{2})(1+br^{2})^{3}} $$

(14)

From Fig. 6, it is clear that the anisotropic factor is zero at the centre and monotonically increasing with increase of ‘$r$’.

Fig. 6

Anisotropic factor ($8\pi\Delta$) verses fractional radius $r/R$ for the compact star PSR 1937 +21. For this figure, we have taken the same values of the constants $a$, $b$ and $a_{0}$ as in Fig. 5

3.2 Equation of state for compact star

For realistic matter, there should be an equation of state for constructing the compact star models. This implies that radial pressure must be purely the function of density i.e. $p_{r}=f(\rho)$. In our present solution we have determined the relation between pressure and density by eliminating $r$ from Eqs. (8) and (10), which is given as:

$$ p_{r}=\frac{a_{0}(1-\rho_{1})}{8\pi(1+2\rho_{1}+{\rho_{1}}^{2})} $$

(15)

where, $\rho_{1}=\frac{b-a-16\pi\rho+\sqrt{(b-a)(b-a+64\pi\rho )}}{16\pi\rho}$.

It clear from the above equation that radial pressure is purely the function of density i.e. $p_{r}=f(\rho)$. This implies that Eq. (15) can represent the equation of state (EOS) for present compact star models.

3.3 Boundary conditions

For determining the arbitrary constants, we should join smoothly the interior of metric (1) for anisotropic matter distribution to the exterior of Schwarzschild solution which can be given by:

$$\begin{aligned} ds^{2} =& \biggl(1-\frac{2M}{r} \biggr) dt^{2} -r^{2} \bigl(d\theta^{2} + \sin^{2} \theta d\phi^{2} \bigr) \\ &{}- \biggl(1- \frac{2M}{r} \biggr)^{-1} dr^{2}. \end{aligned}$$

(16)

For the Continuity of the metric, we must join the metric potentials $e^{\nu}$ and $e^{\lambda}$ at the boundary of the star $r=R$ between the interior and the exterior regions of the star. The above system of equations is also solved subject to boundary condition that the radial pressure $p_{r}$ should be zero at surface of the star $r=R$, whose mass $m(r=R)=M$ is same as Schwarzschild mass $M$ (Misner and Sharp 1964):

The following boundary condition can be expressed as:

$$\begin{aligned}& e^{-\lambda(R)}=1-\frac{2M}{R} \end{aligned}$$

(17)

$$\begin{aligned}& e^{\nu(R)}=1-\frac{2M}{R} \end{aligned}$$

(18)

$$\begin{aligned}& p_{r}=0, \quad r=R \end{aligned}$$

(19)

So from Eq. 10, $p_{r}(R)=0$ gives,

$$ R=\frac{1}{\sqrt{b}}. $$

(20)

Now from (17) and (18), $e^{-\lambda(R)}=e^{\nu(R)}$ gives:

$$ C=\frac{(1+aR^{2})^{1-B}}{(1+bR^{2})^{1+A}} $$

(21)

The total mass $M$ can be determined by using the condition (17) as:

$$ M=\frac{R}{2} \biggl[\frac{(b-a)R^{2}}{1+bR^{2}} \biggr] $$

(22)

4 Some physical features of the anisotropic models

4.1 The variation of ratio of pressure and density

We suppose the radial and tangential pressure are related to the matter density by the parameters $\omega_{r}$ and $\omega_{t}$ as: $p_{r}=\omega_{r} \rho$ and $p_{t}=\omega_{t}\rho$.

Then it can be defined as:

$$\begin{aligned}& w_{r}=\frac{a_{0}(1-br^{2})}{(b-a)(3+br^{2})}, \end{aligned}$$

(23)

$$\begin{aligned}& w_{t}=\frac{bp_{1}+a^{2}r^{2}p_{2}+ap_{3}}{(b-a)(1+ar^{2})(3+4br^{2}+b^{2}r^{4})} \end{aligned}$$

(24)

We have observed that $\omega_{r}$ and $\omega_{t}$ are less than 1 throughout inside the star (Fig. 7). This implies that density is dominating pressures everywhere inside the star. However the decreasing nature of $\omega_{r}$ and $\omega_{t}$ also represents that the temperature is decreasing outward.

Fig. 7

Behaviour of parameters $w_{r}$ and $w_{t}$ verses fractional radius $r/R$ for the compact star PSR 1937 +21. The values of the constants $a$, $b$ and $a_{0}$ involved in this figure is same as of the Figs. 5 and 6

4.2 Energy conditions

The anisotropic fluid models must be satisfy the following energy conditions: (i) Null energy condition (NEC), (ii) Weak energy condition (WEC) and (iii) Strong energy condition (SEC). Then for satisfying the above energy conditions, the anisotropic models should satisfy the following inequalities everywhere inside the compact star (Fig. 8):

• (i) NEC: $\rho\ge0$,

• (ii) $\mathrm{WEC}_{r}$: $\rho-p_{r} \ge0$,

• (iii) $\mathrm{WEC}_{t}$: $\rho-p_{t} \ge0$,

• (iv) SEC: $\rho-p_{r} -2p_{t} \ge0$.

Fig. 8

Energy conditions verses fractional radius $r/R$ for the compact star PSR 1937 +21. For this figure, we have employed the values of the constants as: $a=-0.000591$, $b = 0.007694$, $a_{0} =0.0037$ and radius $R = 11.4005~\mbox{km}$

4.3 Causality condition

The anisotropic models should satisfy the causality conditions, i.e. $0\leq V_{r}=\sqrt{\frac{dp_{r}}{d\rho}}<1$ and $0\leq V_{t}=\sqrt{\frac {dp_{t}}{d\rho}}< 1$, at all points inside the star. As from Fig. 9, we can see that our model is satisfying above these causality conditions. However we note from this figure that $V_{r}$ and $V_{t}$ are monotonically decreasing throughout from the centre to boundary of the star. So our anisotropic solution is well behaved.

Fig. 9

Behaviour of radial and tangential velocity verses fractional radius $r/R$ for the compact star PSR 1937 +21. For the purpose of the plotting this figure, we have employed the same data values of the constants $a$, $b$ and $a_{0}$ as in Fig. 8

4.4 Generalized Tolman-Oppenheimer-Volkoff equation

The generalized (TOV) equation for anisotropic fluid distribution is given by the expression as (Tolman 1939; Oppenheimer and Volkoff 1939):

$$ e^{\frac{\lambda-\nu}{2} }\frac{M_{G} (\rho+p_{r} )}{r^{2} } +\frac {2}{r} (p_{r} -p_{t} )+\frac{dp_{r}}{dr}=0; $$

(25)

Where $M_{G}$ is the effective gravitational mass given by

$$ M_{G} (r)=\frac{1}{2} r^{2} e^{\frac{\nu-\lambda}{2} } \nu' $$

(26)

Equation (25) together with Eq. (26) gives:

$$ -\frac{1}{2}\nu'(\rho+p_{r} ) + \frac{2}{r} (p_{t} -p_{r} )-\frac {dp_{r} }{dr}=0; $$

(27)

Equation (27) describes the equilibrium condition for an anisotropic fluid distribution subject to gravitational force ($F_{g}$), hydrostatic force ($F_{h}$) and anisotropic stress ($F_{a}$) so that (Fig. 10):

$$ F_{g} +F_{h} +F_{a} =0, $$

(28)

where, $F_{g}$, $F_{h}$, and $F_{a}$ can be defined as:

$$\begin{aligned}& F_{g} =-\frac{1}{2} \nu' ( \rho+p_{r} ) \end{aligned}$$

(29)

$$\begin{aligned}& F_{h} =-\frac{dp_{r} }{dr} \end{aligned}$$

(30)

$$\begin{aligned}& F_{a} =\frac{2}{r} (p_{t} -p_{r} ) \end{aligned}$$

(31)

The explicit form of $F_{g}$, $F_{h}$ and $F_{a}$ can be written as:

$$\begin{aligned} F_{g} =&\frac{r}{16\pi} \biggl[\frac{a_{0}r(1-br^{2})+r (b-a)(1+br^{2})}{(1+ar^{2})(1+br^{2})} \biggr] \\ &{}+\frac {r}{16\pi} \biggl[\frac{a_{0}+b^{2}r^{2}-a(3+br^{2})+b(3-a_{0} r^{2})}{(1+br^{2})^{2}} \biggr] \\ \end{aligned}$$

(32)

$$\begin{aligned} F_{h} =&\frac{r}{4\pi} \biggl[\frac{a_{0}b(3-br^{2})}{(1+br^{2})^{3}} \biggr] \end{aligned}$$

(33)

and

$$ F_{a}= \biggl[\frac{bp_{1}+a^{2}r^{2}p_{2}+ap_{3}-a_{0} (1+ar^{2})(1-b^{2}r^{4})}{4\pi r(1+ar^{2})(1+br^{2})^{3}} \biggr] $$

(34)

Fig. 10

Behaviour of different forces $F_{i}$ verses fractional radius $r/R$ for the compact star PSR 1937 +21. For plotting this figure, we have taken the values of constants as $a=-0.000591$, $b = 0.007694$, $a_{0} =0.0037$

4.5 The effective mass radius relation and surface red-shift

The effective mass of the star can be defined as:

$$ \frac{M_{eff}}{R}=\frac{e^{\lambda(R)}-1}{2e^{\lambda(R)}}=\frac{4\pi }{R} \int_{0}^{R}{\rho r^{2} dr}. $$

(35)

For above mass-radius ratio, the compactness of the star can written as:

$$ u= \frac{M_{eff}}{R}= \frac{1}{2} \bigl[1-e^{-\lambda(R)} \bigr]= \frac{1}{2} \biggl[\frac{(b-a)R^{2}}{1+bR^{2}} \biggr]. $$

(36)

The red-shift corresponding to above compactness $u$ can be defined as:

$$ Z = e^{\lambda(R)/2} - 1 = \frac{1-\sqrt{1-2u}}{\sqrt{1-2u}}. $$

(37)

The above equation (37) implies that red shift of the compact star can not be arbitrary large as it depends upon the compactness $u$, i.e. if $u$ is increasing then corresponding surface red shift will increase. In other order words the surface red shift is decreasing with increase of radius $R$.

5 Conclusion

In the present investigation, we have obtained anisotropic solution by considering the anisotropic matter distribution and spherical symmetric space time. The obtained compact star is same as like PSR 1937 +21. However we have introduced the standard values of G and c in the appropriate equations for obtaining the numerical result of physical quantities. The anisotropic compact star PSR 1937 +21 has central density of order $10^{15}~\mbox{gm/cm}^{3}$ which is reliable for the realistic compact star model.

The physical nature of anisotropic solution can be stated as follows.

Regularity of metric functions at centre: The metric functions $e^{\lambda}$ and $e^{\nu}$ are finite and positive inside the star with values 1 and $C$ at the centre respectively. It is observed that the metric functions are also non-singular at the centre (Figs. 1 and 4).

Anisotropy factor: The anisotropy factor should be positive and finite everywhere inside the star to represent the realistic compact star i.e. the tangential pressure ($p_{t}$) should always greater than the radial pressure ($p_{r}$) everywhere inside the star. From Fig. 6, it clear that the anisotropy is monotonically increasing throughout the star. This features of anisotropy implies that $p_{t} > p_{r}$ at each inside point of star.

Energy conditions: In the present solution, the energy conditions are satisfying everywhere inside the compact objects (Fig. 8).

TOV equation: We studied the equilibrium condition through the generalized Tolman-Oppenheimer-Volkoff equation for the anisotropic star. From Fig. 11, the gravitational force is counter balance by the joint action of hydrostatic force and anisotropic stress. Also it is observed that this action keeps the system is in static equilibrium.

Fig. 11

Red-shift ($Z$) verses fractional radius $r/R$ for the compact star PSR 1937 +21. For purpose of plotting this graph, we have employed the data values of the constants same as in Fig. 8

Mass-radius relation: We define the effective mass-radius relation for the compactness $u$ of the star. In our proposed model, the ratio of effective mass—radius is 0.2692 which satisfy the Buchdahl (1959) condition. However the red-shift of the star is determined by using above compactness $u$. The surface red-shift turns out to be 1.0425. This implies that red-shift of our model is in good agreement for the compact star (Böhmer and Harko 2007; Straumann 1984; Böhmer and Harko 2006; Ivanov 2002).

Causality condition for well behaved nature: We observed that $V_{r}$ and $V_{t}$ both are lies between 0 and 1. However Both velocities are monotonically decreasing throughout inside the star from centre to boundary (Figs. 9 and 10). This nature of $V_{r}$ and $V_{t}$ implies that our solution is well behaved.

Moreover the numerical values of all the physical quantities for the star PSR 1937 +21 are given in Tables 1 and 2.

Table 1 Values of different physical parameters of PSR 1937 +21 for $a=-0.000591$, $b = 0.007694$, $a_{0} =0.0037$, $M = 2.0833M_{\odot}$, $R = 11.4005~\mbox{km}$, $P_{r}=8\pi p_{r}$, $P_{t}=8\pi p_{t}$, $D=8\pi \rho$, $\Delta_{i}=8\pi\Delta$

Table 2 Central density, surface and central pressure for PSR 1937 +21 for the above parameter values of Table 1