1 Introduction

The non-zero anisotropy is an important component in relativistic stellar systems in the absence of an electric field. Bowers and Liang (1974) highlighted the anisotropic sphere in general relativity. There has been many work done the physical related to anisotropic pressure. Dev and Gleiser (2002, 2003) have discussed that pressure anisotropy influence the mass, structure and physical properties of compact sphere. Also it was shown by Herrera and Santos (1997) that the effect of anisotropy in pressure. They have proposed physical mechanism in low and very high density system for astrophysical compact objects. Böhmer and Harko (2006) derived upper and lower limits for the basic physical parameters viz. mass-radius ratio, anisotropy, redshift and total energy for arbitrary anisotropic general relativistic matter distributions in the presence of cosmological constant. They have shown that anisotropic compact stellar type objects can be much more compact than the isotropic ones, and their radii may be close to their corresponding Schwarzschild radii.

Anisotropy in fluid pressure usually arise due to presence of mixture of different types of fluids, magnetic field or external field, rotation, existence of super-fluid, viscosity and phase transitions etc. Ruderman (1972) has studied the stellar models and argued that the nuclear matter at very high densities of the order \(10^{15}~\mbox{g}/\mbox{cm}^{3}\) may have anisotropic features and their interactions are relativistic. The paper of many authors (Maurya and Gupta 2013; Maurya et al. 2015) suggest that the anisotropic is a crucial component in the description of dense objects with nuclear matter. Here we would like to mention that Mak and Harko (2003), and Sharma et al. (2001) suggest that anisotropy is a sufficient condition in the study of dense nuclear matter with strange star. In fact, several kinds of literature (Bhar 2015; Bhar et al. 2016; Maurya et al. 2015; Singh et al. 2016b; Singh and Pant 2016a, 2016b; Singh et al. 2016c; Flanagan and Hinderer 2008; Abbott et al. 2018; Sennett et al. 2017; Rahaman et al. 2010) can be referred to understand the effects of the anisotropy on the relativistic compact stellar system. In a more widely context, charged self-gravitating anisotropic fluid spheres have been extensively investigated in general relativity. In an earlier work De Leon (1993) obtained two new exact analytical solutions to Einstein’s field equations for a static fluid sphere with anisotropic pressures. Many studies show that the Einstein field equations play an important role in gravitational matter and relativistic compact star such as neutron stars, gravastar, dark energy star, black holes and quark stars. Neutron stars and white dwarfs are in hydrostatic equilibrium so that inside the star gravity is balanced by degenerate pressure, as described mathematically by the Tolman-Oppenheimer-Volkoff equation (Tolman 1939; Oppenheimer and Volkoff 1939). A detailed study specifically shows that the model actually corresponds to strange stars in terms of their mass and radius. Models with a matter tensor containing anisotropy have been discussed by Maurya et al. (2016a) using the functional form of the pressure anisotropy proposed by Lake which is consistent with physical requirements for astrophysical applications. Maurya et al. (2017a) further suggested pressure anisotropy proposed by Lake, to discuss the probability of having anisotropy is considerably higher in compact stars due to the relativistic interaction among the particles and throughout the region, to conserve any uniform motion they become too random. These investigations have been completed by considering an anisotropic internal configuration that has been handled by the metric assumption by utilizing embedding class one condition. Many authors (Elebert et al. 2009; Abubekerov et al. 2008; Rawls et al. 2011; Demorest et al. 2010; Guver et al. 2010) estimated the masses for the stars SAX J1808.43658, Her X-1, 4U 1538-52, Cen X-3, SMC X-4, PSR J1614-2230, 4U 1608-52, LMC X-4, RX J1856-37, Vela X-1, EXO 1785-248, PSR J1903+327 and 4U 1820-30. Many authors (Elebert et al. 2009; Abubekerov et al. 2008; Rawls et al. 2011; Demorest et al. 2010; Guver et al. 2010) estimated the masses for the stars SAX J1808.43658, Her X-1, 4U 1538-52, Cen X-3, SMC X-4, PSR J1614-2230, 4U 1608-52, LMC X-4, RX J1856-37, Vela X-1, EXO 1785-248, PSR J1903+327 and 4U 1820-30.

In this work we have obtained a new anisotropic compact star model by solving embedding class one condition in static spherical space time. There are two types of solutions of the Karmarkar condition one is the interior Schwarzschild (1916), which has invalid causality condition and other is cosmological. Recently, many relativistic solutions for anisotropic fluid have been found. The following authors Singh et al. (2016a, 2016b), Singh and Pant (2016a), Maurya et al. (2016b, 2017b, 2018) have chosen the generating metric component in a polynomial form, while others Bhar et al. (2017), Bhar (2017), Singh et al. (2017) have chosen generating metric function in a rational form. The exponential generating metric components are taken by following researchers Maurya et al. (2016a, 2017c). Recent study, the authors Kumar et al. (2018, 2018), Kumar and Gupta (2013, 2014) have investigated the isotropic interior solutions of gravitational field equation which are satisfying the required physical conditions inside the star. In our work we assume a very specific form of metric potential with hyperbolic function. This is acceptable with physical condition in astrophysical model. Arising solutions can be used to describe a physically reasonable astrophysical matter distribution. We have also analyzed all physical features in details and provided sample figures to support our data. We have discuss the basic field equations with Karmakar condition in Sect. 2, the field equations have been solved by assuming a physically reasonable new form of the metric potential in Sect. 3. The Sect. 4 is focused on matching conditions between interior and exterior space time regions. In Sect. 5 we discuss stability of the model. Finally Sect. 6 contains the conclusion part.

2 Einstein’s field equations and Karmarkar condition

Let us consider the static spherically symmetric anisotropic distribution of matter in curvature coordinates, described by Schwarzschild line element

$$ ds^{2} = - e^{\lambda ( r )} dr ^{2} - r ^{2} \bigl(d\theta^{2} + \sin^{2} \theta d \phi^{2} \bigr) + e ^{\nu ( r )} dt ^{2} $$
(1)

where \(\lambda ( r ) \) and \(\nu ( r ) \) are the functions of radial coordinate only. Now assuming the interior matter distribution is anisotropic in nature and correspondingly the energy momentum tensor can be expressed as

$$ T_{\mu \nu } = ( \rho + p_{r} ) u_{\mu } u_{\nu } - p _{t} g_{\mu \nu } +( p_{r} - p_{t} ) \chi _{\mu } \chi _{\nu } $$
(2)

where the vectors \(u_{\mu }\) and \(\chi _{\mu } \) represent four-velocity and the unit space like vector in the radial direction with \(- u^{\mu } u_{\mu } = \chi ^{\mu } \chi _{\mu } =1\). \(\rho , p_{r}\) and \(p_{t}\) represents the matter density, radial and transverse pressure of the matter distribution respectively.

The Einstein tensor for this space time is

$$ {R \mu \nu -} \frac{1}{2} {R} g_{\mu \nu } = - \kappa T_{ \mu \nu } $$
(3)

where \(\kappa = \frac{8 \pi G}{C^{4}}\). Here we assume the relativistic geometrized units \(G = c =1\), Eqs. (1) and (3) reduce to Einstein’s field equations as follows

$$\begin{aligned}& 8 \pi p_{r} = \frac{\nu '}{r} e^{-\lambda } - \frac{ ( 1 - e^{- \lambda } )}{r^{2}} \end{aligned}$$
(4)
$$\begin{aligned}& 8 \pi p_{t} = \biggl( \frac{\nu ^{\prime \prime }}{2} - \frac{\lambda ' \nu '}{4} + \frac{\nu ^{\prime \, 2}}{4} + \frac{\nu ' - \lambda '}{2 r} \biggr) e^{- \lambda } \end{aligned}$$
(5)
$$\begin{aligned}& 8 \pi \rho = \frac{\lambda '}{r} e^{-\lambda } + \frac{ ( 1 - e ^{-\lambda } )}{r^{2}} \end{aligned}$$
(6)

where ‘′’ prime denotes the differentiation with respect to the radial coordinate \(r\).

Using Eqs. (4) and (5) we get the anisotropic factor

$$\begin{aligned} \Delta =&8 \pi ( p_{t} - p_{r} ) \\ =& e^{-\lambda } \biggl( \frac{ \nu ^{\prime \prime }}{2} - \frac{\lambda ' \nu '}{4} + \frac{\nu ^{\prime \, 2}}{4} - \frac{ \nu ' + \lambda '}{2 r} \biggr) + \frac{(1- e^{-\lambda } )}{r^{2}} \end{aligned}$$
(7)

If the metric (1) satisfies the Karmarker condition (1948)

$$ R_{1414} = \frac{R_{1212} R_{3434} + R_{1224} R_{1334}}{R_{2323}} $$
(8)

with \(R_{2323} \neq 0\) (Pandey and Sharma 1981), it represents embedding class-one space-time.

For Eq. (8), the line elements of Eq. (1) leads to a following differential equation

$$ \frac{ \nu ^{\prime \prime }}{\nu '} + \nu ' = \frac{\lambda ' e^{\lambda }}{e^{ \lambda } - 1} $$
(9)

Now integrating Eq. (9), we get the following relation between \(\nu \) and \(\lambda \)

$$ e^{\nu } = \biggl( A+B \int \sqrt{ \bigl( e^{\lambda } - 1 \bigr)} dr \biggr)^{2} $$
(10)

where \(A\) and \(B\) are constants of integration. Using Eq. (10) in Eq. (7), we get

$$ 8\pi \Delta = \frac{\nu '}{4 e^{\lambda }} \biggl[ \frac{2}{r} - \frac{ \lambda '}{e^{\lambda } - 1} \biggr] \biggl[ \frac{\nu ' e^{\nu }}{2 B^{2} r} - 1 \biggr] $$
(11)

Here \(\Delta = ( p_{t} - p_{r} )\). It will be attractive in nature if \(p_{t} > p_{r}\) and repulsive if \(p_{t} < p_{r}\).

3 A well behaved anisotropic solution of embedding class one

Now to finding the anisotropic solution, let us assume the metric potential \(g_{rr}\) as follows

$$ e^{\lambda } =1+ a^{2} r^{2} \mathrm{csch}^{2} \bigl( b r^{2} +C \bigr) $$
(12)

where \(a\neq 0,b\neq 0 \) or \(C\neq 0\). If \(a=b=C=0\), then reduced space time is not a space time of class one (Pandey and Sharma 1981). As Bhar (2017) suggested, for all well-behaved model, the metric function \(e^{\lambda }\) should be monotonically increasing and satisfy the conditions \(e^{\lambda (0)} =1\) and \(((e^{\lambda } ) ' )_{r=0} =0\). It is observed that our metric function \(e^{\lambda }\) is increasing function and satisfy the above mentioned conditions. This implies that \(e^{\lambda }\), given by Eq. (12), is physically acceptable.

Solving Eqs. (10) and (12), we get the metric potential \(e^{\nu }\) as

$$ e^{\nu } = \biggl[ A+ \frac{Ba}{2b} \ln \biggl( \frac{e^{ ( b r ^{2} +C )} -1}{e^{ ( b r^{2} +C )} +1} \biggr) \biggr] ^{2} $$
(13)

Using Eqs. (12) and (13), in Eqs. (4), (5), (6) and (7), we obtain the expression of energy density \(( \rho )\) radial pressure \(( p_{r} )\), tangential pressure \(( p_{t} )\) and anisotropic factor \(( \Delta ) \) as,

$$\begin{aligned}& 8\pi \rho = \frac{1}{1+ a^{2} r^{2} \mathrm{csch}^{2} ( b r^{2} +C )} \\& \phantom{8\pi \rho =\,\,}{}\times \biggl[ \frac{2 a^{2} [ \sinh ( b r^{2} +C ) -2b r^{2} \cosh ( b r ^{2} +C ) ]}{\sinh ^{3} ( b r^{2} +C ) + a ^{2} r^{2} \sinh ( b r^{2} +C )} \\& \phantom{8\pi \rho =\,\,}{} + a^{2} \mathrm{csch} ^{2} \bigl( b r^{2} +C \bigr) \biggr] \end{aligned}$$
(14)
$$\begin{aligned}& 8\pi p_{r} = \frac{1}{1+ a^{2} r^{2} \mathrm{csch}^{2} ( b r ^{2} +C )} \\& \phantom{8\pi \rho =\,\,}{}\times\biggl[ \frac{4aB e^{ ( b r^{2} +C )}}{ ( e^{2 ( b r^{2} +C )} -1 ) [ A+ \frac{Ba}{2b} \ln ( \frac{e^{ ( b r^{2} +C )} -1}{e ^{ ( b r^{2} +C )} +1} ) ]} \\& \phantom{8\pi \rho =\,\,}{} - a^{2} \mathrm{csch}^{2} \bigl( b r^{2} +C \bigr) \biggr] \end{aligned}$$
(15)
$$\begin{aligned}& 8\pi \Delta \\& \quad = \frac{\Delta _{1} (r)}{\Delta _{2} (r)} \\& \quad \ \ {} \times \biggl[ \frac{2a e^{2 ( b r^{2} +C )} [ A+ \frac{Ba}{2b} \ln ( \frac{e^{ ( b r^{2} +C )} -1}{e^{ ( b r ^{2} +C )} +1} ) ] - e^{2 ( b r^{2} +C )} +1}{ [ A+ \frac{Ba}{2b} \ln ( \frac{e^{ ( b r^{2} +C )} -1}{e^{ ( b r^{2} +C )} +1} ) ]} \biggr] \end{aligned}$$
(16)
$$\begin{aligned}& p_{t} = p_{r} +\Delta \end{aligned}$$
(17)

where

$$\begin{aligned} \Delta _{1} ( r ) =& 2a e^{2 ( b r^{2} +C )} \bigl( a^{2} r^{2} \mathrm{csch}^{2} ( b r^{2} +C ) \\ &{}+ 2b r^{2} \cosh ( b r^{2} +C ) \bigr),\\ \Delta _{2} (r) =& \bigl( e^{2 ( b r^{2} +C )} -1 \bigr) ^{2} \bigl( 1+ a^{2} r^{2} \mathrm{csch}^{2} ( b r^{2} +C ) \bigr)\\ &{}\times \bigl( \sinh \bigl( b r^{2} +C \bigr) + a^{2} r ^{2} \mathrm{csch}^{2} \bigl( b r^{2} +C \bigr) \bigr) \end{aligned}$$

4 Boundary conditions

It is necessary that the interior solution should connect smoothly with vacuum exterior Schwarzschild solution which is given by

$$\begin{aligned} ds^{2} =&- \biggl( 1- \frac{2M}{r} \biggr)^{-1} dr^{2} - r^{2} \bigl( d\theta ^{2} + \sin ^{2} \theta d\phi ^{2} \bigr) \\ &{}+ \biggl( 1- \frac{2M}{r} \biggr) dt^{2} \end{aligned}$$
(18)

Using Eqs. (1) and (18) at the boundary \(r=R\) we get

$$\begin{aligned}& e^{-\lambda } =1- \frac{2M ( R )}{R} \end{aligned}$$
(19)
$$\begin{aligned}& e^{\nu } =1- \frac{2M ( R )}{R} \end{aligned}$$
(20)
$$\begin{aligned}& p_{r} ( R ) =0 \end{aligned}$$
(21)

From Eqs. (19)–(21), we get

$$\begin{aligned}& \frac{A}{B} = \frac{4 e^{b R^{2} +C} - \frac{a^{2}}{2b} \mathrm{csch} ^{2} ( b R^{2} +C ) ( e^{2 ( b R^{2} +C )} -1 ) \ln ( \frac{e^{ ( b R^{2} +C )} -1}{e^{ ( b R^{2} +C )} +1} )}{a \mathrm{csch}^{2} ( b R^{2} +C ) ( e^{2 ( b R^{2} +C )} -1 )} \\& \end{aligned}$$
(22)
$$\begin{aligned}& A= \frac{1}{\sqrt{1+ a^{2} R^{2} \mathrm{csch}^{2} ( b R^{2} +C )}} - \frac{Ba}{2b} \ln \biggl( \frac{e^{ ( b R^{2} +C )} -1}{e^{ ( b R^{2} +C )} +1} \biggr) \\& \end{aligned}$$
(23)

Now differentiating Eqs. (14)–(17) we get the density and pressure gradient as

$$\begin{aligned}& 8\pi \frac{d\rho }{dr} = f_{1} ( r ) \biggl[ \frac{f_{2} ( r )}{f_{3} ( r )} + a^{2} \mathrm{csch} ^{2} \bigl( b r^{2} +C \bigr) \biggr] \\& \phantom{8\pi \frac{d\rho }{dr} =\,\,}{}+ \frac{1}{1+ a^{2} r^{2} \mathrm{csch}^{2} ( b r^{2} +C )} \\& \phantom{8\pi \frac{d\rho }{dr} =\,\,}{}\times \biggl[ \frac{f_{3} ( r ) \times f_{4} ( r ) - f_{2} ( r ) \times f_{5} ( r )}{f_{3} ( r )^{2}} \\& \phantom{8\pi \frac{d\rho }{dr} =\,\,}{}- \frac{4 a^{2} br \cosh ( b r^{2} +C )}{ \sinh ^{3} ( b r^{2} +C )} \biggr] \end{aligned}$$
(24)
$$\begin{aligned}& 8\pi \frac{d p_{r}}{dr} = f_{1} ( r ) \biggl[ \frac{4aB e ^{ ( b r^{2} +C )} - a^{2} \mathrm{csch}^{2} ( b r ^{2} +C ) f_{6} ( r )}{f_{6} ( r )} \biggr] \\& \phantom{8\pi \frac{d p_{r}}{dr} =\,\,}{}+ \frac{1}{1+ a^{2} r^{2} \mathrm{csch}^{2} ( b r^{2} +C )} \\& \phantom{8\pi \frac{d p_{r}}{dr} =\,\,}{}\times\biggl[ \frac{f_{7} ( r ) - f_{8} ( r )}{f _{6} ( r )^{2}} - \frac{4 a^{2} br \cosh ( b r^{2} +C )}{\sinh ^{3} ( b r^{2} +C )} \biggr] \end{aligned}$$
(25)
$$\begin{aligned}& 8\pi \frac{d \Delta }{dr} = \frac{H_{1} ( r ) H_{4} ( r ) ( H_{2} ( r ) G_{3} ( r ) + H_{3} ( r ) G_{2} ( r ) ) }{ ( H_{1} ( r ) H _{4} ( r ) )^{2}} \\& \phantom{8\pi \frac{d \Delta }{dr} =\,\,}{}- \frac{H_{2} ( r ) H_{3} ( r ) ( H_{1} ( r ) G_{4} ( r )+ H_{4} ( r ) G_{1} ( r ) )}{ ( H_{1} ( r ) H _{4} ( r ) )^{2}} \end{aligned}$$
(26)
$$\begin{aligned}& \frac{d p_{t}}{dr} = \frac{d p_{r}}{dr} + \frac{d \Delta }{dr} \end{aligned}$$
(27)

where

$$\begin{aligned}& f_{1} ( r ) = \frac{2 a^{2} r ( 2b r^{2} \cosh ( b r^{2} +C ) - \sinh ( b r^{2} +C ) )}{ \sinh ^{3} ( b r^{2} +C ) ( 1+ a^{2} r^{2} \mathrm{csch}^{2} ( b r^{2} +C ) )^{2}} \\& f_{2} ( r ) =2 a^{2} \bigl[ \sinh \bigl( b r^{2} +C \bigr) -2b r^{2} \cosh \bigl( b r^{2} +C \bigr) \bigr] \\& f_{3} ( r ) = \sinh ^{3} \bigl( b r^{2} +C \bigr) + a ^{2} r^{2} \sinh \bigl( b r^{2} +C \bigr) \\& f_{4} ( r ) =-4abr \bigl( \cosh \bigl( b r^{2} +C \bigr) -b r^{2} \sinh \bigl( b r^{2} +C \bigr) \bigr) \\& f_{5} ( r ) =2br \cosh \bigl( b r^{2} +C \bigr) \bigl[ 3 \sinh ^{2} \bigl( b r^{2} +C \bigr) + a^{2} r^{2} \bigr] \\& \phantom{f_{5} ( r ) =\,\,}+2 a ^{2} r \sinh \bigl( b r^{2} +C \bigr) \\& f_{6} ( r ) = \bigl( e^{2 ( b r^{2} +C )} -1 \bigr) \biggl[ A+ \frac{Ba}{2b} \ln \biggl( \frac{e^{ ( b r ^{2} +C )} -1}{e^{ ( b r^{2} +C )} +1} \biggr) \biggr] \\& f_{7} ( r ) =8abr f_{6} ( r ), \\& f_{8} ( r ) =8ar e^{2 ( b r^{2} +C )} \biggl[ 2b e^{ ( b r^{2} +C )}\\& \phantom{f_{8} ( r ) =\,\,}{}\times \biggl[ A+ \frac{Ba}{2b} \ln \biggl( \frac{e^{ ( b r^{2} +C )} -1}{e^{ ( b r^{2} +C )} +1} \biggr) \biggr] +a \biggr] \\& H_{1} ( r ) = \bigl( e^{2 ( b r^{2} +C )} -1 \bigr)^{2} \bigl[ 2 a^{2} r^{2} + \sinh ^{2} \bigl( b r^{2} +C \bigr)\\& \phantom{H_{1} ( r ) =\,\,}{} + a^{4} r^{4} \mathrm{csch}^{2} \bigl( b r^{2} +C \bigr) \bigr] \\& H_{2} ( r ) =2a e^{ ( b r^{2} +C )} \bigl( a ^{2} r^{2} +b r^{2} \sinh 2 \bigl( b r^{2} +C \bigr) \bigr) \\& G_{1} ( r ) =8br e^{2 ( b r^{2} +C )} \bigl( e^{2 ( b r^{2} +C )} -1 \bigr) \bigl[ 2 a^{2} r^{2} \\& \phantom{G_{1} ( r ) =\,\,}{}+ \sinh ^{2} \bigl( b r^{2} +C \bigr) + a^{4} r^{4} \mathrm{csch}^{2} \bigl( b r^{2} +C \bigr) \bigr]\\& \phantom{G_{1} ( r ) =\,\,}{} + G_{3} ( r ) \\& G_{3} ( r ) =4 \bigl( e^{2 ( b r^{2} +C )} -1 \bigr)^{2} \bigl[ a^{2} r+br \sinh 2 \bigl( b r^{2} +C \bigr)\\& \phantom{G_{1} ( r ) =\,\,}{} + a^{4} r^{3} \mathrm{csch} \bigl( b r^{2} +C \bigr) \bigl( 1-b r ^{2} \coth \bigl( b r^{2} +C \bigr) \bigr) \bigr] \\& G_{2} ( r ) =2a e^{ ( b r^{2} +C )} \bigl[ 2 \bigl( a^{2} r+br \sinh 2 \bigl( b r^{2} +C \bigr) \bigr) \bigl( b r^{2} +1 \bigr) \\& \phantom{G_{1} ( r ) =\,\,}{}+4 b^{2} r^{3} \cosh 2 \bigl( b r^{2} +1 \bigr) \bigr] \\& H_{3} ( r ) =2a e^{ ( b r^{2} +C )} \biggl[ \frac{A}{B} + \frac{a}{2b} \ln \biggl( \frac{e^{ ( b r^{2} +C )} -1}{e^{ ( b r^{2} +C )} +1} \biggr) \biggr] \\& \phantom{H_{3} ( r ) =\,\,}{}- e^{2 ( b r^{2} +C )} +1, \\& H_{5} ( r ) = \frac{2ar e^{ ( b r^{2} +C )}}{e ^{2 ( b r^{2} +C )} -1} \\& H_{4} ( r ) = \biggl[ \frac{A}{B} + \frac{a}{2b} \ln \biggl( \frac{e^{ ( b r^{2} +C )} -1}{e^{ ( b r^{2} +C )} +1} \biggr) \biggr] \\& G_{5} ( r ) =4abr e^{ ( b r^{2} +C )} H_{4} ( r ) -4br e^{2 ( b r^{2} +C )} \\& \phantom{G_{5} ( r ) =\,\,}{}+2a e^{ ( b r^{2} +C )} H_{5} ( r ) \end{aligned}$$

5 Stability analysis of the compact star model

5.1 Causality condition

Anisotropic fluid stellar model will be physically acceptable, if the velocity of sound will be less than the velocity of light. By the causality condition the radial and transverse velocity of sound is less than 1, this implies that \(0< V_{r} = \sqrt{\frac{d p_{r}}{d\rho }} <1\), \(0< V_{t} = \sqrt{\frac{d p_{t}}{d\rho }} <1\). In Fig. 4 we observe that velocity of sound lies within the expected range. Now we use the concept of cracking proposed by Herrera (1992) to determine the stability of anisotropic star model under the radial perturbations and Abreu et al. (2007) proved that the region of an anisotropic star model is potentially stable if the radial velocity of sound is greater than the transverse velocity of sound.

Fig. 1
figure 1

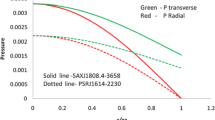
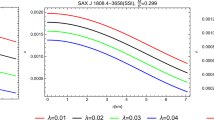
Variation of radial pressure (\(P_{r} =8 \pi p_{r} \) left), transverse pressure (\(P_{t} =8 \pi p_{t} \) right) and density (\(D =8 \pi \rho \) bottom) with respect to fractional radius (\(r/R\)). For plotting this figure the numerical values of constants are as follows: (i) \(a=0.086\), \(C=1\), \(b=-0.0013 \) for S1 (Her X-1), (ii) \(a=0.095\), \(C=1\), \(b=-0.00104\) for S2 (4U 1538-52), (iii) \(a=0.094\), \(C=1\), \(b=-0.0012 \) for S3 (SAX J1808.4-3658), (iv) \(a=0.095\), \(C=1\), \(b=-0.0014 \) for S4 (SMC X-1), (v) \(a=0.102\), \(C=1\), \(b=-0.0012 \) for S5 (LMC X-4), (vi) \(a=0.09\), \(C=1\), \(b=-0.0098 \) for S6 (EXO 1785-248), (vii) \(a=0.165\), \(C=1\), \(b=-0.0025 \) for S7 (RX J1856-37), (viii) \(a=0.107\), \(C=1\), \(b=-0.0011\), for S8 (Cen X-3), (ix) \(a=0.095\), \(C=0.85\), \(b=-0.00077\) for S9 (PSR J1903+327), (x) \(a=0.096\), \(C=0.85\), \(b=-0.00106\) for S10 (4U 1608-52), (xi) \(a=0.099\), \(C=0.85\), \(b=-0.00072\) for S11 (Vela X-1) and (xii) \(a=0.099\), \(C=0.9\), \(b=-0.0012 \) for S12 (4U 1820-30)

Full size image
Fig. 2
figure 2

Variation of metric potentials \(e^{\nu }\) (top left) and \(e^{\lambda }\) (top right) and anisotropy (\(\Delta = p_{t} - p_{r}\), bottom) with respect to fractional radius (\(r/R\)). For plotting this figure, we have employed the same values of the constants mentioned in Fig. 1

Full size image
Fig. 3
figure 3

Variation of (\({P_{r}} / {D} \) left) and (\({P_{t}} / {D} \) right) with respect to fractional radius (\(r/R\)). For plotting this figure, we have employed the same values of the constants mentioned in Fig. 1

Full size image
Fig. 4
figure 4

Variation radial velocity of sound \(V_{r}^{2}\) (top left), transverse velocity of sound \(V_{t}^{2}\) (top right), \(V_{r}^{2} - V_{t}^{2}\) (bottom left) and \(V_{t}^{2} - V_{r}^{2}\) (bottom right) with respect to fractional radius (\(r/R\)). For plotting this figure, we have employed the same values of the constant mentioned in Fig. 1

Full size image

The velocity sound can be obtained as

$$ V_{i}^{2} = \frac{d p_{i}}{d\rho } $$
(28)

From Fig. 4, it is clear that the radial velocity of sound is greater than the transverse velocity of sound through inside the model which conform that our model is stable.

5.2 Tolman-Oppenheimer-Volkoff (TOV) equations

In this section, we examine equilibrium stage of the stellar model under the gravitational force, hydrostatics force and anisotropic force which can be described by generalized TOV (Tolman 1939; Oppenheimer and Volkoff 1939) as

$$ - \frac{M_{G} ( \rho + p_{r} )}{r^{2}} e^{\frac{\lambda -\nu }{2}} - \frac{d p_{r}}{dr} + \frac{2}{r} ( p_{t} - p_{r} ) =0 $$
(29)

where \(M_{{G}}\) is the effective gravitational mass given by:

$$ M_{G} = \frac{1}{2} r^{2} \nu ' e^{{ ( \nu -\lambda )} / {2}} $$
(30)

Plugging the value of \(M_{G}\) in Eq. (29), we get

$$ - \frac{\nu '}{r} ( \rho + p_{r} ) - \frac{d p_{r}}{dr} + \frac{2}{r} ( p_{t} - p_{r} ) =0 $$
(31)

The above equation can be expressed into three different components gravitational force \(( F_{g} )\), hydrostatic force \(( F_{h} ) \) and anisotropic force \(( F_{a} ) \) which are defined as:

$$\begin{aligned}& F_{g} = - \frac{\nu '}{r} ( \rho + p_{r} ) \end{aligned}$$
(32)
$$\begin{aligned}& F_{h} =- \frac{d p_{r}}{dr} \end{aligned}$$
(33)
$$\begin{aligned}& F_{a} = \frac{2}{r} ( p_{t} - p_{r} ) \end{aligned}$$
(34)

Figure 5 shows the behavior of the generalized TOV equations. We observe from this figure that the gravitational force \(( F_{g} ) \) is dominating in nature and counterbalanced by the joint action of hydrostatic force \(( F_{h} ) \) and anisotropic force \(( F_{a} )\) which gives that the system attains a static equilibrium.

5.3 Energy conditions

The anisotropic fluid sphere should satisfy the following three energy conditions, (i) null energy condition (NEC), (ii) weak energy condition (WEC) and (iii) strong energy condition (SEC). For satisfying the above energy conditions the following inequalities (Maurya et al. 2016b) must hold simultaneously inside the fluid sphere

  • Null energy condition (NEC): \(\rho \geq 0\)

  • Weak energy condition (WECr): \(\rho - p_{r} \geq 0\)

  • Weak energy condition (WECt): \(\rho - p_{t} \geq 0\)

  • Strong energy condition (SEC): \(\rho - p_{r} -2 p_{t} \geq 0\)

Using these inequalities we can easily justify the nature of energy conditions for the specific stellar configuration as shown in Fig. 6 that are satisfied for our proposed model.

5.4 Adiabatic index and redshift

For stability of an anisotropic fluid sphere the adiabatic index \(\gamma \) should be grater than 4/3 which was proposed by (Heintzmann and Hillebrandt 1975). The relativistic adiabatic index \(\gamma \) is given

$$ \gamma _{i} = \frac{\rho + p_{i}}{p_{i}} \frac{d p_{i}}{d\rho } $$
(35)

Figure 7 shows that \(\gamma >4/3\) everywhere within the proposed model.

The gravitational redshift of the stellar configurations given by

$$ z= e^{\frac{-\nu }{2}} -1 $$
(36)

which should be non-negative inside the stellar interior. The profile of gravitational redshift is plotted in Fig. 7 (bottom), which monotonically decreasing in nature and non-negative.

Fig. 5
figure 5figure 5

Variations of gravitational, hydrostatic and anisotropic forces acting on the system with respect to fractional radius (\(r/R\)). For plotting this figure the numerical values of constants are as follows: (i) \(a=0.086\), \(C=1\), \(b=-0.0013 \) for Her X-1 (1st row left), (ii) \(a=0.095\), \(C=1\), \(b=-0.00104\) for 4U 1538-52 (1st row right), (iii) \(a=0.094\), \(C=1\), \(b=-0.0012 \) for SAX J1808.4-3658 (2nd row left), (iv) \(a=0.095\), \(C=1\), \(b=-0.0014 \) for SMC X-1 (2nd row right), (v) \(a=0.102\), \(C=1\), \(b=-0.0012 \) for LMC X-4 (3rd row left), (vi) \(a=0.09\), \(C=1\), \(b=-0.0098 \) for EXO 1785-248 (3rd row right), (vii) \(a=0.165\), \(C=1\), \(b=-0.0025 \) for RX J1856-37 (4rh row left), (viii) \(a=0.107\), \(C=1\), \(b=-0.0011\), for Cen X-3 (4rh row right), (ix) \(a=0.095\), \(C=0.85\), \(b=-0.00077\) for PSR J1903+327 (5th row left), (x) \(a=0.096\), \(C=0.85\), \(b=-0.00106\) for 4U 1608-52 (5th row right), (xi) \(a=0.099\), \(C=0.85\), \(b=-0.00072\) for Vela X-1 (6th row left) and (xii) \(a=0.099\), \(C=0.9\), \(b=-0.0012 \) for 4U 1820-30 (6th row right)

Full size image
Fig. 6
figure 6

Variation of energy conditions with respect to fractional radius (\(r/R\)). For plotting this figure, we have employed the same values of the constant mentioned in Fig. 1

Full size image
Fig. 7
figure 7

Variation of adiabatic constants (\(\gamma _{i}\)) and redshift with respect to fractional radius (\(r/R\)). For plotting this figure, we have employed the same values of the constant mentioned in Fig. 1

Full size image
Table 1 Numerical values of parameters for compact star candidates
Full size table
Table 2 Energy density and central pressure for different compact star candidates for the above parameter value of Table 1
Full size table

6 Conclusion

In this model we have obtained a new anisotropic compact star model in class one space-time. Here we have introduced a new type of \(g_{rr}\) metric potential which is regular and monotonic increasing from center of the star see Fig. 2 (left). From Eq. (13), we observe that \(e^{\nu } = ( A+ \frac{Ba}{2b} \ln ( \frac{e^{C} -1}{e ^{C} +1} ) )^{2}\) is singularity free and positive at origin (see Fig. 2(right)) and the functions \(\frac{P_{r}}{D}\) and \(\frac{P_{t}}{D}\) are monotonically decreasing (see Fig. 3). The central and surface densities have the order of \(10^{15}~\mbox{gm}/\mbox{cm}^{3}\) and \(10^{14}~\mbox{gm}/\mbox{cm}^{3} \) respectively which is given in Table 2. This implies that our model is realistic astrophysical compact star model and it is compatible with following relativistic stars PSR J1614-2230, 4U 1608-52, SAX J1808.4-3658, LMC X-4, RX J1856-37, Vela X-1, 4U 1820-30, EXO 1785-248, PSR J1903+327, 4U 1538-52, SMC X-1, Her X-1 and Cen X-3. In this work radial pressure \(p_{r} = \frac{P_{r} c^{4}}{8\pi G R^{2}}~\mbox{dyne}/\mbox{cm}^{2}\), tangential pressure \(p_{t} = \frac{P_{t} c^{4}}{8 \pi G R^{2}}~\mbox{dyne}/\mbox{cm}^{2}\) and density \(\rho = \frac{D c^{2}}{8\pi G R ^{2}}~\mbox{gm}/\mbox{cm}^{3} \). The present model following features hold

  1. 1.

    The energy density, radial and transverse pressure of the stars are positive, finite and monotonically decreasing everywhere inside the star (Fig. 1). Also the radial pressure is vanishes at surface of the star and central pressure has the order of \(10^{35}~\mbox{dyne}/\mbox{cm}^{2}\).

  2. 2.

    The radial and transverse velocity of sound in our model satisfies the causality condition i.e. \(V_{r}^{2}, V_{t}^{2} <1 \). Also we see that radial velocity of sound is greater than the transverse velocity of sound see in Fig. 4.

  3. 3.

    We consider the generalized TOV equation for describing the equilibrium condition subject to gravitational (\(F_{g}\)), hydrostatic (\(F_{h}\)) and anisotropic forces (\(F_{a}\)), respectively and we observe from Fig. 5 that gravitational force is balanced by the joint action of hydrostatic and electric forces to attain the required stability of the model. However, the effect of electric force is less than the hydrostatic force.

  4. 4.

    The energy conditions i.e. null energy condition (NEC), weak energy condition (WEC), and strong energy condition (SEC) are satisfying for our anisotropic models (see Fig. 6).

  5. 5.

    The value of adiabatic index \(\gamma _{r}\) and \(\gamma _{t} \) for our model are greater than 4/3 at all interior point inside the star Fig. 7 which reconfirms the stability of our model.

  6. 6.

    We observe from Fig. 7 that the redshift is monotonically decreasing outward. However, it is maximum at the center and minimum at the boundary of the compact star. According to Böhmer and Harko (2006) the redshift must satisfy the condition \(Z\leq 5\). From Fig. 7, it is clear that the redshift of our models are in good agreement.

  7. 7.

    We compare our proposed compact star model with the observed data of different realistic objects. For this purpose we have calculated the physical parameters \(a,b,C,R\), \(M( M_{\Theta } )\) and \({M} / {R}\) (see Table 1).

7 Two generating function of anisotropic solution for embedding class one solution

The algorithm for generating all possible static spherically symmetric anisotropic fluid solutions of the Einstein field equations in terms of two generating functions has been already proposed Herrera et al. (2008) as:

$$ e^{\lambda } = \frac{\Phi ^{2} ( r ) e^{\int [ \frac{4+2 r^{2} \Phi ^{2} ( r )}{r^{2} \Phi ( r )} ] dr}}{r^{6} [ -2 \int ( \frac{\Phi ( r ) ( 1+ \Pi ( r ) r^{2} ) e^{\int [ \frac{4+2 r^{2} \Phi ^{2} ( r )}{r^{2} \Phi ( r )} ] dr}}{r^{8}} ) dr +F ]} $$
(37)

where \(F\) is a constant while \(\Phi ( r )\) and \(\Pi ( r ) \) are generating functions which can be determined as

$$\begin{aligned}& \Phi ( r ) = \biggl[ \frac{\nu ' r+1}{2r} \biggr] \end{aligned}$$
(38)
$$\begin{aligned}& \Pi ( r ) =8\pi ( p_{t} - p_{r} ) =8\pi \Delta ( {r} ) \end{aligned}$$
(39)

Therefore the above two generating functions \(\Phi ( r )\) and \(\Pi ( r )\) for the present embedding class one solution for anisotropic matter distribution are given as (using Eqs. (16), (13), (38) and (39)):

$$\begin{aligned}& \Phi ( r ) = \biggl[ \frac{2arbB e^{b r^{2} +C}}{ ( e^{2 ( b r^{2} +C )} -1 ) [ 2Ab+aB \ln ( \frac{e^{2 ( b r^{2} +C )} -1}{e^{2 ( b r ^{2} +C )} -1} ) ]} + \frac{1}{r} \biggr] \end{aligned}$$
(40)
$$\begin{aligned}& 8\pi \Delta = \frac{2a e^{2 ( b r^{2} +C )} ( a ^{2} r^{2} \mathrm{csch}^{2} ( b r^{2} +C ) + 2b r^{2} \cosh ( b r^{2} +C ) )}{ ( e^{2 ( b r ^{2} +C )} -1 )^{2} ( 1+ a^{2} r^{2} \mathrm{csch}^{2} ( b r^{2} +C ) ) ( \sinh ( b r^{2} +C ) + a^{2} r^{2} \mathrm{csch}^{2} ( b r^{2} +C ) )} \\& \phantom{8\pi \Delta = \,\,}{}\times \biggl[ \frac{2a e^{2 ( b r^{2} +C )} [ A+ \frac{Ba}{2b} \ln ( \frac{e^{ ( b r^{2} +C )} -1}{e ^{ ( b r^{2} +C )} +1} ) ] - e^{2 ( b r^{2} +C )} +1}{ [ A+ \frac{Ba}{2b} \ln ( \frac{e ^{ ( b r^{2} +C )} -1}{e^{ ( b r^{2} +C )} +1} ) ]} \biggr] \end{aligned}$$
(41)

These two generating functions, Eqs. (40) and (41), can provide a general embedding class one solution for anisotropic matter distribution.