Anisotropic compact star with Tolman IV gravitational potential

Abstract

In the current paper we have investigated a well-behaved new model of anisotropic compact star in ($3+1$)-dimensional spacetime. The exterior spacetime is described by the Schwarzschild vacuum solution. The model is obtained in the background of Tolman IV $g_{rr}$ metric potential. Our model is free from central singularities and satisfies all energy conditions. The solution is compatible with observed masses and radii of a few compact stars like Her X-1, PSR J0737-3039A, PSR B1913+16, RX J1856.5-3754, Cyg X-2 and PSR J1903+0327.

1 Introduction

From time immemorial, stars have captivated man’s imagination. Stars are born in clouds of primordial dust and for millions of years they lead an active life synthesizing their store of hydrogen into heavier elements by nuclear fusion. They die even spectacular deaths, causing an enormous explosion in the form of a supernova, dispersing the valuable elements far into the universe. Enriched by these elements new stars are formed in the primordial clouds. Compact stars are basically remnants of massive luminous stars. At the time of stellar evolution an outward radiation pressure from the nuclear fusions is created in its interior and it can no longer resist the ever present gravitational force. As a result the star collapses under its own weight and undergoes the process of stellar death resulting in the formation of these dense and compact stellar remnants such as white dwarfs, neutron stars and black holes. These object have exceedingly high densities relative to normal stars. Compact objects have much smaller radii and hence, much stronger surface gravity.

White dwarfs are static stellar systems where the gravity is counter-balanced by Fermi pressure of degenerate electrons. They can support maximum mass up to 1.4 $M_{\odot }$ with radii about 5000 km, mean densities of around $10^{7}~\mbox{g}\,\mbox{cm}^{-3}$ and surface potential $\mathit{GM}/Rc^{2} \approx 10^{-4}$. On the other hand, neutron stars are supported by Fermi pressure of degenerate neutrons which can support a maximum mass of $1.4~M_{\odot }$–$3~M_{\odot }$, having density equivalent to nuclear densities ${\sim} 10^{15}~\mbox{g}\,\mbox{cm}^{-3}$ and surface potential $\mathit{GM}/Rc^{2} \approx 10^{-1}$ (Shapiro and Teukolosky 1983). It is still a challenge to describe precisely the equation of state (EoS) of such exotic phases in the interior of such stars. However under the classical theory of general relativity, the composition, nature and physical features of compact stars might be described via analytic EoSs. The recent discoveries of new fascinating observational data regarding the stellar objects Her X-1, Cyg X-2, 4U 1820-30, SAX J 1808.4-3658, 4U 1728-34, PSR 0943+10 and RX J185635-3754 have further enlightened this arena of research with more theoretical and applied issues.

In this paper we have constructed a model to discuss in detail the physical properties of a compact star from the center to the surface of the star. Here we have considered Tolman-IV Tolman (1939), Thirukkanesh and Ragel (2014) form for the gravitational potential $g_{rr}$ and have assumed the matter to be anisotropy. In case of pressure anisotropy, radial pressure ($p_{r}$) differs from tangential pressure ($p_{t}$). This brings a more physical situation, as pointed out by Ruderman (1972) that nuclear matter tends to become anisotropic in nature at very high densities ($10^{15}~\mbox{gm}/\mbox{cc}$). This may occur for various reasons like existence of solid core, in presence of type-III superfluid, rotation, magnetic field, mixture of two fluid, existence of external field, phase transition, presence of electromagnetic field etc.

In an earlier work, Ponce de Leon (1993) obtained two new exact analytical solutions to Einstein’s field equations for static fluid sphere with anisotropic pressures. In addition to that, Herrera and Santos (1997) provided an exhaustive review on the subject of anisotropic fluids. A comprehensive work on the influence of local anisotropy on the structure and evolution of compact object has been studied by Herrera and Santos (1997). Bounds on the basic physical parameters for anisotropic compact general relativistic objects was proposed by Böhmer and Harko (2006). In a very recent work Bhar et al. (2015a) provide a new class of interior solutions for anisotropic stars admitting conformal motion in higher dimensional non-commutative spacetime. Bhar et al. (2015b) also obtained a model of compact star with Tolman VII metric potential and assuming a linear equation of state between the radial pressure and matter density. Rahaman et al. (2014) obtained a new class of exact solutions for the interior in ($2 + 1$)-dimensional spacetime for the perfect fluid model both with and without cosmological constant $\varLambda$. Solutions without $\varLambda$ were found to be physically acceptable. The model of Dark energy star was proposed by Bhar and Rahaman (2015c). The author also discussed the stability analysis of the model. Tikekar superdense stars with electric fields were proposed by Komathiraj and Maharaj (2007), compact models with regular charge distributions was studied by Takisa and Maharaj (2013), radial pulsations and stability of anisotropic stars with quasi-local EoS was discussed by Horvat (2011). Singh et al. (2014) have also discussed the important of charged anisotropic Tolman IV solution in modeling compact stars. Bhar (2015d) obtained a new model of singularity-free anisotropic strange quintessence star. In most of the above mentioned articles, authors either assumed one of the metric potentials and anisotropy or EoS. However, the unique feature in this article is to assumed $g_{rr}$ metric potential and radial pressure $p_{r}$, and rest of the physical variable is determined accordingly.

The plan of the paper is as follows: Sect. 2 is devoted to Interior Spacetime and Einstein field equations. New anisotropic solution in details is obtained in Sect. 3. Following that in Sect. 4 some properties of the solution and the boundary conditions are investigated. Relativistic adiabatic index and stability analysis are done in Sect. 5 and Sect. 6 respectively. Energy conditions, compactness and surface redshift are checked in the next sections and finally some concluding remarks are given in Sect. 9.

2 Interior spacetime and Einstein field equations

To describe a static spherically symmetry spacetime in ($3+ 1$)-dimension the line element can be taken in the standard form as,

$$ ds^{2}=-e^{\nu (r)}dt^{2}+e^{\lambda (r)}dr^{2}+r^{2} \bigl(d\theta^{2}+\sin ^{2}\theta d\phi^{2}\bigr) $$

(1)

Where $\lambda$ and $\nu$ are functions of the radial coordinate ‘$r$’ only.

Let us assume that the matter within the star is anisotropic in nature. Therefore the corresponding energy-momentum tensor can be written as,

$$ T_{\nu }^{\mu }=(\rho +p_{r})u^{\mu }u_{\nu }-p_{t} g_{\nu }^{\mu }+(p _{r}-p_{t}) \eta^{\mu }\eta_{\nu } $$

(2)

with $u^{i}u_{j} =-\eta^{i}\eta_{j} = 1$ and $u^{i}\eta_{j}= 0$. Here the vector $u_{i}$ is the fluid 4-velocity and $\eta^{i}$ is the space-like vector which is orthogonal to $u^{i}$, $\rho$ is the matter density, $p_{r}$ and $p_{t}$ are respectively the radial and transverse pressure of the fluid and $p_{t}$ is in the orthogonal direction to $p_{r}$. $\Delta =p_{t}-p_{r}$ is called the anisotropic factor which measures the anisotropy and it leads to an anisotropic force which is acting inward for $\Delta <0$ and outward for $\Delta >0$.

The Einstein field equations assuming $G=1=c$ are given by

$$\begin{aligned} &e^{-\lambda } \biggl[ \frac{\lambda '}{r}-\frac{1}{r^{2}} \biggr] + \frac{1}{r ^{2}}=8\pi \rho \end{aligned}$$

(3)

$$\begin{aligned} &e^{-\lambda } \biggl[ \frac{1}{r^{2}}+\frac{\nu '}{r} \biggr] - \frac{1}{r ^{2}}=8\pi p_{r} \end{aligned}$$

(4)

$$\begin{aligned} &\frac{1}{2}e^{-\lambda } \biggl[ \frac{1}{2}\nu ^{\prime\,2}+ \nu ''- \frac{1}{2}\lambda '\nu '+\frac{1}{r}\bigl(\nu '-\lambda ' \bigr) \biggr] =8\pi p _{t} \end{aligned}$$

(5)

Where ‘prime’ denotes differentiation with respect to radial co-ordinate $r$. The mass function, $m(r)$, within the radius ‘$r$’ is given by,

$$ m(r)=4\pi \int_{0}^{r}w^{2}\rho (w)dw $$

(6)

Using (6) Einstein field Eqs. (3)–(5) becomes,

$$\begin{aligned} &e^{-\lambda }=1-\frac{2m}{r} \end{aligned}$$

(7)

$$\begin{aligned} &r(r-2m)\nu '=8\pi p_{r} r^{3}+2m \end{aligned}$$

(8)

$$\begin{aligned} &\frac{4}{r}(8\pi \Delta )=8\pi (\rho +p_{r})\nu '+2\bigl(8\pi p_{r}'\bigr) \end{aligned}$$

(9)

3 The new anisotropic solution

To solve the above set of Eqs. (7)–(9), let us take the forth metric potential $g_{rr}$ as proposed by Tolman (1939) and is given by,

$$ e^{-\lambda }=\frac{(1+ar^{2})(1-cr^{2})}{1+2ar^{2}} $$

(10)

Where ‘$a$’ and ‘$c$’ are constants.

Substituting (10) into (3) the matter density can be obtained as,

$$ 8\pi \rho =\frac{3c+a \{ 3+(2a+7c)r^{2}+6acr^{4} \} }{(1+2ar ^{2})^{2}} $$

(11)

Employing Eq. (10) into Eq. (7) the expression for mass function can be obtained as,

$$ m(r)=\frac{r^{3}(a+c+acr^{2}) }{2(1+2ar^{2})} $$

(12)

Using the expression of $m(r)$ given in Eq. (12) into Eq. (8) we obtain

$$ \nu '=\frac{r(1+2ar^{2})(8\pi p_{r})}{(1+ar^{2})(1-cr^{2})}+\frac{r(a+c+acr ^{2})}{(1+ar^{2})(1-cr^{2})} $$

(13)

Now to integrate Eq. (13) let us assume the radial pressure in the form

$$ 8\pi p_{r}=\frac{p_{0}(1-ar^{2})}{(1+2ar^{2})^{2}} $$

(14)

The expression of $p_{r}$ is reasonable due to the fact that it is monotonic decreasing function of ‘$r$’ and vanishes at $r=1/ \sqrt{a}$ which gives the radius of the star where radial pressure vanishes. Moreover, it possess a finite value of central pressure equal to $p_{0}/8\pi$ for all $p_{0}>0$.

Substituting (14) into (13) we get,

$$\begin{aligned} \nu ' = & \frac{r}{(1+ar^{2})(1-cr^{2})}\frac{p_{0}(1-ar^{2})}{1+2ar ^{2}} \\ &{} + \frac{r(a+c+acr^{2})}{(1+ar^{2})(1-cr^{2})} \end{aligned}$$

(15)

On integrating Eq. (15) we get,

$$\begin{aligned} \nu = & \frac{a-2p_{0}}{2(a+c)}\log \bigl(1+ar^{2}\bigr)+ \frac{3p_{0}}{2(2a+c)}\log \bigl(1+2ar^{2}\bigr) \\ & {}-\frac{\log (1-cr^{2})}{2(a+c)} \biggl[ (2a+c)- \frac{p_{0}(a+c)}{2a+c} \biggr] +B \end{aligned}$$

(16)

Where $B$ is the constant of integration, which will be determined later from the boundary conditions.

The anisotropic factor $\Delta =p_{t}-p_{r}$ is given by,

$$\begin{aligned} \Delta = & \frac{r^{2}}{32\pi (1+2ar^{2})^{3}}\times \biggl[-4ap_{0}\bigl(5-2ar ^{2}\bigr) \\ & {} +\frac{(C_{1}+C_{2}r^{2}+C_{3}r^{4})(D_{1}+D_{2}r^{2}+D_{3}r ^{4})}{(1+ar^{2})(1-cr^{2})} \biggr] \end{aligned}$$

(17)

Where $C_{1}$, $C_{2}$, $C_{3}$, $D_{1}$, $D_{2}$ and $D_{3}$ are constants given by,

$$\begin{aligned} &C_{1}=a+c+p_{0},\qquad C_{2}=a(2a+3c-p_{0}) \\ &C_{3}=2a^{2}c,\qquad D_{1}=3c+p_{0}+3a \\ &D_{2}=a(2a+7c-p_{0}),\qquad D_{3}=6a^{2}c \end{aligned}$$

The transverse pressure $p_{t}$ is obtained as,

$$\begin{aligned} p_{t} = & \frac{p_{0}(1-ar^{2})}{8\pi (1+2ar^{2})^{2}}+\frac{r^{2}}{32 \pi (1+2ar^{2})^{3}} \\ & {}\times\biggl[ \frac{(C_{1}+C_{2}r^{2}+C_{3}r^{4})(D_{1}+D_{2}r^{2}+D_{3}r ^{4})}{(1+ar^{2})(1-cr^{2})} \\ & {}-4ap_{0}\bigl(5-2ar^{2}\bigr) \biggr] \end{aligned}$$

(18)

4 Properties of the solution and boundary conditions

The following conditions are to be fulfilled by any solutions in order to represent a physically viable configuration and well-behaved.

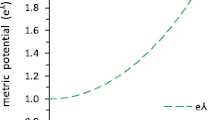
• 1. The solution should be free from physical and geometric singularities, i.e. it should yield finite and positive values of the central pressure, central density and nonzero positive value of $e^{\nu }|_{r=0}$ and $e^{\lambda }|_{r=0}=1$. The profile of the metric co-efficients are shown against $r$ in Fig. 1.

  Fig. 1

  

  The metric potential $e^{\nu }$ and $e^{\lambda }$ are plotted against $r$ inside the stellar interior

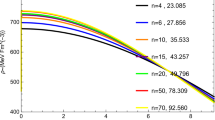
• 2. To find the behavior of the matter density ($\rho$) and radial pressure ($p_{r}$) inside the stellar interior, we have plotted the profiles of $\rho$ and $p_{r}$ in Fig. 2 and Fig. 3 respectively. The profiles show that both $\rho$ and $p_{r}$ are positive and monotonic decreasing function of $r$ inside the stellar interior and at the boundary the radial pressure vanishes. The transverse pressure $p_{t}$ is also plotted against $r$ inside the stellar interior in Fig. 4 and from the figure it is clear that $p_{t} >0$ and monotonic decreasing function of $r$.

  Fig. 2

  

  The matter density $\rho$ is plotted against $r$ inside the stellar interior

  Fig. 3

  

  The radial pressure is plotted against $r$ inside the stellar interior

  Fig. 4

  

  Transverse pressure $p_{t}$ is plotted against $r$ inside the stellar interior

• 3. Both density and pressure gradients are negative (Fig. 6), which once again verifies that both $\rho$ and $p_{r}$ are monotonic decreasing function of $r$.

• 4. For an anisotropic fluid sphere $(p_{r}+2p_{t})/\rho <1$ suggested by Bondi (1999). To check this condition for our model we have plotted $(p_{r}+2p_{t})/\rho$ vs $r$ in Fig. 7. The figure indicates that our model satisfies the condition of Bondi (1999).

• 5. The speed of sound along radial and transverse direction must obey causality condition and also has to decrease outward.

• 6. The adiabatic index $\gamma = \frac{\rho + p_{r} }{p_{r}} \frac{dp_{r} }{d\rho }$ must be greater than $4/3$ for a static configuration.

• 7. The stability factor $|v_{\mathit{st}}^{2}-v_{\mathit{sr}}^{2}|$ for a stable anisotropic configuration must lies in between 0 and 1, Herrera and Santos (1997).

• 8. The redshift of all the physically viable models needed to decreasing outward (Fig. 17).

The central pressures and the density can be written as

$$\begin{aligned} p_{r0} =& p_{t0}=\frac{p_{0}}{8\pi }>0 \end{aligned}$$

(19)

$$\begin{aligned} \rho_{0} =&\frac{3(a+c)}{8\pi }>0 \end{aligned}$$

(20)

Further the Zeldovich’s condition $p_{r0}/\rho_{0}\le 1$ is also needed to satisfy within the interior of the stellar object leading to another constraint i.e.

$$ 0< p_{0} \le 3(a+c) $$

(21)

At the boundary, the exterior solution is assumed as the Schwarzschild vacuum solution that matches exactly with the interior solution. The exterior metric is given by

$$\begin{aligned} ds^{2} = & - \biggl( 1-\frac{2M }{r} \biggr) dt^{2}+ \biggl( 1-\frac{2M }{r} \biggr) ^{-1}dr^{2} \\ &{} +r^{2}\bigl(d\theta^{2}+\sin^{2} \theta d \phi^{2}\bigr) \end{aligned}$$

(22)

At the boundary $r=r_{b}$, the two metric given in (1) and (22) are matching. Therefore we get

$$\begin{aligned} e^{\nu_{b}} =& 1-\frac{2M }{r_{b}} \end{aligned}$$

(23)

$$\begin{aligned} e^{-\lambda_{b}} =& 1-\frac{2M }{r_{b}}= \frac{(1+ar_{b}^{2})(1-cr_{b}^{2}) }{1+2ar_{b}^{2}} \end{aligned}$$

(24)

$$\begin{aligned} p_{r}(r=r_{b}) =& 0 \end{aligned}$$

(25)

On using the boundary conditions we get

$$\begin{aligned} B = & \log \biggl( 1-\frac{2M }{r_{b}} \biggr) -\frac{a-2p_{0}}{2(a+c)}~ \log \bigl(1+ar_{b}^{2}\bigr) \\ & {}-\frac{3p_{0}}{2(2a+c)}~ \log \bigl(1+2ar_{b}^{2}\bigr)+ \frac{1}{2(a+c)} \\ &{} \times\biggl[ (2a+c)-\frac{p_{0}(a+c)}{2a+c} \biggr] ~\log \bigl(1-cr_{b}^{2} \bigr) \end{aligned}$$

(26)

$$\begin{aligned} \frac{2M }{r_{b}} =& 1- \frac{(1+ar_{b}^{2})(1-cr_{b}^{2}) }{1+2ar_{b}^{2}} \end{aligned}$$

(27)

5 Stability condition

In this section we want to check the stability of our present model. First of all we want to calculate the adiabatic index ($\gamma$) which can be obtained from the given formula

$$ \gamma =\frac{\rho +p_{r}}{p_{r}}\frac{dp_{r}}{d\rho } $$

(28)

For a newtonian isotropic sphere the collapsing condition is given by $\gamma <\frac{4}{3}$ and for an anisotropic collapsing stellar configuration, it changes to (Bondi 1964)

$$\begin{aligned} \gamma < \frac{4}{3}+ \biggl[ \frac{4}{3}~\frac{p_{\mathit{ti}}-p_{\mathit{ri}} }{r|p'_{\mathit{ri}}|}+ \frac{8\pi r }{3}~\frac{\rho _{i} p_{\mathit{ri}} }{|p'_{\mathit{ri}}|} \biggr] _{\mathrm{max}} \end{aligned}$$

(29)

here $p_{\mathit{ri}}$, $p_{\mathit{ti}}$ and $\rho_{i}$ are initial values of radial pressure, transverse pressure and density respectively. For a stable anisotropic configuration, the limit on adiabatic index depends upon the types of anisotropy i.e. either $(p_{\mathit{ti}}< p_{\mathit{ri}})$ or $(p_{\mathit{ti}}>p_{\mathit{ri}})$. In our solution $\gamma$ is always greater than $4/3$ and therefore stable (Fig. 8).

Next we want to check the subliminal velocity of sound for our present model. Our proposed model of anisotropic compact star will be physically acceptable if the radial and transverse velocity of sound should be less than 1 which is known as causality conditions. Where the radial velocity $(v_{\mathit{sr}}^{2})$ and transverse velocity $(v_{\mathit{st}}^{2})$ of sound can be obtained as

$$\begin{aligned} &v_{\mathit{sr}}^{2}=\frac{dp_{r}}{d\rho } \end{aligned}$$

(30)

$$\begin{aligned} &v_{\mathit{st}}^{2}=\frac{dp_{t}}{d\rho } \end{aligned}$$

(31)

Due to the complex expressions of $v_{\mathit{sr}}^{2}$ and $v_{\mathit{st}}^{2}$ we are avoiding to write their expressions, however they are shown graphically in Figs. 9 and 10 respectively. From the figures it is clear that our model satisfies the causality conditions. Since $0< v_{\mathit{sr}}^{2}<1$, $0< v _{\mathit{st}}^{2}<1$ therefore according to Andréasson (2009) $|v_{\mathit{sr}}^{2}-v _{\mathit{st}}^{2}|<1$ which is also satisfied by our model (see Fig. 11).

6 Equilibrium condition

To check whether our model is in static equilibrium under three different forces, we consider the generalized Tolman-Oppenheimer-Volkov (TOV) equation which is represented by the equation

$$ \frac{M_{G}(\rho +p_{r})}{r^{2}}e^{\frac{\lambda -\nu }{2}}-\frac{dp _{r}}{dr}+\frac{2}{r}(p_{t}-p_{r})=0 $$

(32)

Where $M_{G} = M_{G}(r)$ is the effective gravitational mass inside the fluid sphere of radius ‘$r$’ and is defined by

$$ M_{G}(r)=\frac{1}{2}r^{2}e^{\frac{\nu -\lambda }{2}}\nu ' $$

(33)

The above expression of $M_{G}(r)$ can be derived from Tolman-Whittaker mass formula. Using the expression of Eq. (33) in (32) we obtain the modified TOV equation as,

$$\begin{aligned} &F_{g}+F_{h}+F_{a}=0 \end{aligned}$$

(34)

$$\begin{aligned} &F_{g}=-\frac{\nu^{\prime }}{2}(\rho +p_{r}) \end{aligned}$$

(35)

$$\begin{aligned} &F_{h}=-\frac{dp_{r}}{dr} \end{aligned}$$

(36)

$$\begin{aligned} &F_{a}=\frac{2}{r}(p_{t}-p_{r}) \end{aligned}$$

(37)

$F_{g}$, $F_{h}$ and $F_{a}$ are known as gravitational, hydro-statics and anisotropic forces respectively. The profile of the above three forces for our model of compact star is shown in Fig. 12, which verifies that present system is in static equilibrium under these three forces.

7 Energy conditions

In this section we want to check the energy conditions for our present model. It is well known that for an anisotropic compact star all the energy conditions namely Weak Energy Condition (WEC), Null Energy Condition (NEC) and Strong Energy Condition (SEC) are satisfied if and only if the following inequalities hold simultaneously for every points inside the stellar configuration.

$$\begin{aligned} &\text{NEC}:\quad \rho -p_{r}\geq 0 \end{aligned}$$

(38)

$$\begin{aligned} &\text{WEC}:\quad \rho -p_{r}\geq 0, \quad \rho >0 \end{aligned}$$

(39)

$$\begin{aligned} &\text{SEC}:\quad \rho -p_{r}\geq 0\quad \rho -p_{r}-2p_{t} \geq 0 \end{aligned}$$

(40)

Figure 13 verifies all the energy conditions for our present model.

8 Compactness factor and surface redshift

The compactness factor, the ratio of mass to the radius of a compact star, should satisfy $2M/r_{b} <8/9$ known as Buchdahl (1959) condition. For our present model it is obtained from the formula,

$$ u=\frac{m(r)}{r}= \frac{r^{2}(a+c+acr^{2})}{2(1+2ar^{2})} $$

(41)

The profile of $u(r)$ is shown in Fig. 15. The figure shows that $u(r)$ is a monotonic increasing function of $r$. The maximum possible ratio of mass to the radius for different compact stars are shown in Table 1. It is clear from the table that the values of compactness factor for different compact stars lies in the proposed range of Buchdahl (1959).

Table 1 Calculated masses and radii of few well-known compact star candidates

Next we will find the surface redshift function $z_{s}$ and gravitational redshift $z$ for our model of compact star and is obtained from the relationship,

$$\begin{aligned} 1+z_{s} = & (1-2u_{b})^{-\frac{1}{2}} \\ = & \sqrt{\frac{1+2ar_{b}^{2}}{1+(a-c)r_{b}^{2}-acr_{b}^{4}}}-1 \end{aligned}$$

(42)

$$\begin{aligned} z = & e^{-\nu /2}-1 \end{aligned}$$

(43)

The profile of these redshifts are shown in Figs. 16 and 17. For our present model, $z_{s}$ is monotonic increasing function of $r_{b}$ and $z$ a monotonically decreasing function of $r$. The value of surface redshift for various compact stars are shown in Table 1. It is also clear from the table that the value of surface redshift for these compact stars lies within the range $z_{s}<1$.

9 Discussion and concluding remarks

We have successfully proposed a new model of anisotropic compact star in ($3+1$)-dimensional spacetime using Tolman IV metric potential. To solve the field equations, we have assumed $g_{rr}$ metric potential and the radial pressure and rest of the physical parameter are determined from them. In the presented solution, all the physical quantities $(p_{r},p_{t}, \rho ,v_{r},v_{t},z )$ are monotonically decreasing outward (Figs. 2–4, 9, 10 and 17) and free from central singularities. Furthermore, the metric potentials, $\gamma$, $u(r)$, $m(r)$ and $z_{s}$ are increasing function with increase in radius (Figs. 1, 8, 14–16). The decreasing nature of pressure and density is again reconfirmed by Fig. 6. Here we have found an interesting result where the anisotropy is negative for $0\le r \le 3.81$ (core) and positive for $3.81< r \le 6.7$ (outer shell) (Fig. 5). At the core of the compact object, due the presence of exotic phases the equation of state (EoS) is soften. This softening of EoS reduces the value of $\gamma$ and this can be incorporated if the anisotropy is negative in (29). However, at the outer shell the nucleon superfluid domination makes the EoS stiffer thus making the value of $\gamma$ higher. This can be seen from (29) when $p_{t}>p_{r}$. Hence the present solution may leads to physically possible configuration. The trace of stress tensor to energy density ratio is less than unity and thus satisfies Bondi (1999) condition (Fig. 7). Our presented solution does satisfy the WEC, SEC and NEC (Fig. 13) as well. $|v_{\mathit{sr}}^{2}-v_{\mathit{st}}^{2}|$ is in between 0 and 1 (Fig. 11), thus satisfy condition of Andréasson (2009). The TOV equation further supports the stability of the presented models by balancing all the three forces to maintain the hydro-static equilibrium (Fig. 12).

Fig. 5

The anisotropic factor $\Delta$ is plotted against $r$ inside the stellar interior

Fig. 6

The density and pressure gradients are plotted against $r$ inside the stellar interior

Fig. 7

$\frac{p_{r}+2p_{t}}{\rho }$ is plotted against $r$ inside the stellar interior

Fig. 8

The adiabatic index $\gamma$ (red curve) is shown against $r$ inside the stellar interior and the blue line corresponds to $\gamma =\frac{4}{3}$

Fig. 9

The variation of radial velocity is shown against $r$ inside the stellar interior

Fig. 10

The variation of transverse velocity is shown against $r$ inside the stellar interior

Fig. 11

$\vert {-}v_{\mathit{st}}^{2}+v_{\mathit{sr}}^{2}\vert$ is shown against $r$ inside the stellar interior

Fig. 12

The variation of gravitational, hydro-statics and anisotropic forces are shown against $r$ inside the stellar interior

Fig. 13

Energy conditions are plotted against $r$ inside the stellar interior

Fig. 14

The mass function is shown against $r$ inside the stellar interior

Fig. 15

The compactness factor is shown against $r$ inside the stellar interior

Fig. 16

The surface redshift is shown against $r_{b}$

Fig. 17

The interior redshift $z$ is shown against $r$ inside the stellar interior

Finally we calculated the compactness factor and surface redshift of some well-known neutron star and quark star candidates. According to Freire et al. (2011), PSR J1903+0327 is a neutron star (NS) of mass $1.667\pm 0.021~M_{\odot }$. For the quark star (QS) RX J1856.5-3754, the mass and radius are bound within $0.5-1~M_{\odot }$ and 3.8–8.2 km respectively, Kohri (2003). The observed mass of PSR B1913+16 (NS) is about $1.4398\pm 0.0002~M_{\odot }$, Weisberg et al. (2010). The pulsar object PSR J0737-3039A (NS) has an observed mass of ${\le} 1.35~M_{ \odot }$ according Burgay et al. (2003). Cyg X-2 (NS) mass was determined by Casares et al. (2010) and measured to be about $1.71\pm 0.21~M_{ \odot }$. As predicted by Abubekerov et al. (2008), the X-ray pulsar Her X-1 has a mass around $0.85 \pm 0.15$, which is in agreement with our calculated mass.

Our presented models of the above mentioned compact star candidates fits very well with the observed values of masses and radii. Above all, our solution does satisfy all the energy conditions, well-behaved, obeyed causality condition, stable and free from central singularities. Hence our solution might have some astrophysical significance. However the neutral analogue (i.e. when anisotropy is zero) of the present solution doesn’t reduce to Tolman IV.