A Class of Charged Relativistic Superdense Star Models

Abstract

In this article we obtain a new class of well behaved charged solutions by using particular forms of the metric potential g ₄₄ and electric intensity, which involves a parameter K. The metric describing the superdense stars joins smoothly with the Reissner-Nordstrom metric at the pressure free boundary. This class of solutions describes well behaved charged fluid balls. The class of solutions gives range of parameter K (0.13≤K≤1.9999) for which the solution is well behaved hence, suitable for modeling of super dense star. The interior of the stars possess there energy density, pressure, pressure-density ratio and velocity of sound to be monotonically decreasing towards the pressure free interface. In view of the surface density 2×10¹⁴ gm/cm³, the maximum mass of the charged fluid balls and corresponding radius are 0.4711M _Θ and 7.0122 km. The red shift at the centre and boundary are found to be 0.1640 and 0.1100 respectively.

1 Introduction

Exact interior solutions of the Einstein-Maxwell field equations joining smoothly to the Nordstrom solution at the pressure free interface are gathering big applause due to some of the following reasons:

• Gravitational collapse of a charged fluid sphere to a point singularity may be avoided.

• Charged solutions of Einstein-Maxwell equations are useful in the study of cosmic matter.

• Charged-dust models and electromagnetic mass models are expected to provide some clue about structure of an electron.

• Several fluid spheres which do not satisfy some or all the relevant physical condition i.e. reality conditions, become relevant when they are charge.

Charged fluid model are normally of three kinds:

• The charged fluid reduces to a neutral fluid in the absence of charge.

• There is several charged fluid can not be uncharged or more correctly charge cannot vanish.

• Some charge fluid models reduces to flat space after the removal of charge. The later is said to be charged fluid with electromagnetic mass.

Many of workers have charged the well known neutral solutions to obtain the charged fluids such as Schwarzschild interior solution [2, 7], Whittaker’s interior solution by [6], charged analogue of Durgapal–Fuloria [5] solution by Gupta and Maurya [8]. Some more solutions in this context are published recently [1, 9, 10, 13–19].

In the present article our aim is to obtain a class of regular and well behaved solution. To achieve the same we consider a spherically symmetric metric with its metric potential g ₄₄=(1−Cr ²)^−1/3 and using a particular electric intensity, which involves a parameter K. The metric so obtained is joined smoothly with the Reissner-Nordstrom metric and then utilized to describe a class of super-dense star models with the surface density 2×10¹⁴ gm/cm³. The charged models so obtained are found regular and well behaved throughout the interior of the star.

2 Field Equations

Let us consider a spherically symmetric metric curvature coordinates as

$$ ds^{2} =-e^{\lambda } dr^{2} -r^{2} (d\theta ^{2} +\sin ^{2} \theta d\phi ^{2} )+e^{\nu } dt^{2}$$

(1)

where the functions λ(r) and ν(r) satisfy the Einstein-Maxwell equations

$$ -\kappa T_{j}^{i} =R_{j}^{i} -\frac{1}{2} R\delta _{j}^{i} =-\kappa \biggl[(c^{2} \rho +p)v^{i} v_{j} -p\delta _{j}^{i} +\frac{1}{4\pi }\biggl(-F^{im} F_{jm} +\frac{1}{4} \delta _{j}^{i} F_{mn} F^{mn} \biggr)\biggr]$$

(2)

with $\kappa =\frac{8\pi G}{c^{4} }$ while ρ,p,v ⁱ,F _ij denote energy density, fluid pressure, flow vector and skew-symmetric electromagnetic field tensor respectively. The resulting field equations [4] are

(3)

(4)

(5)

Let us take the transformation,

$$ e^{\nu } =B (1-Cr^{2} )^{-1/3},$$

(6)

where B and C are positive constant.

Substitution of (6) in to (3)–(5) leads to

(7)

(8)

and

$$ \frac{dY}{dx} +P(x) Y=f(x)$$

(9)

where

The solution of (9) is given by

$$ Y=FA+FI$$

(10)

where

$$F=-\int P(x) dx=\frac{x (1-x)^{7/3} }{(3-2x)^{3} } ,\qquad I=3\int \frac{[(2q^{2} C/x)-1] (3-2x)^{2} dx}{x^{2} (1- x)^{4/3} }$$

and A is arbitrary constant of integration.

3 New Class of Solutions

In order to solve the integral I for obtaining the new class of solution, we consider the electric intensity E of the form

$$ \frac{E^{2} }{C} =\frac{Cq^{2} }{x^{2} } =\frac{Kx}{2 (3-2x)^{2} }$$

(11)

where K≥0 is constant. For 0<x<2/3 and K≥0, the electric field intensity given by (10) is physically palatable since E ² remains regular and positive throughout the sphere. In addition, the electric field given by (11) vanishes at the centre of the star.

With reference of (11), (9) yields following solution

$$ Y=\left[\frac{9 Kx (1-x)^{2} }{(3-2x)^{3} } +\frac{9 (3-4x) (1-x)^{2} }{(3-2x)^{3} } +\frac{A x (1-x)^{7/3} }{(3-2x)^{3} } \right]$$

(12)

Using (12), into (7) and (8), we get the following expressions for pressure and energy density

(13)

(14)

where

$$B(x)=(162-423 x+294 x^{2} -32 x^{3} ), \qquad H(x)=(27-51 x+10 x^{2} )$$

Consequently the expressions for pressure and density gradients read as

(15)

(16)

where

$$D(x)=(27-744 x+928 x^{2} -64 x^{3} ),\qquad E(x)=(135+99x-330 x^{2} +40 x^{3} )$$

4 Conditions for Regular and Well Behaved Model

For well behaved nature of the solution implies in curvature coordinates, the following conditions should be satisfied (augmentation of Delgaty-Lake [3] and Pant et al. [16] conditions).

• (i) The solution should be free from physical and geometric singularities and non zero positive values of e ^λ and e ^ν i.e. (e ^λ) _r=0=1 and e ^v>0.

• (ii) Pressure p should be zero at boundary r=a.

• (iii) c ² ρ≥p>0 or c ² ρ≥3p>0, 0≤r≤a, where former inequality denotes weak energy condition (WEC), while the later inequality implies strong energy condition (SEC).

• (iv) (dp/dr) _r=0=0 and (d ² p/dr ²) _r=0<0 so that pressure gradient dp/dr is negative for 0<r≤a.

• (v) (dρ/dr) _r=0=0 and (d ² ρ/dr ²) _r=0<0 so that density gradient dρ/dr is negative for 0<r≤a.

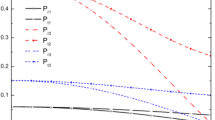
  The condition (iii) and (iv) imply that pressure and density should be maximum at the centre and monotonically decreasing towards the surface.

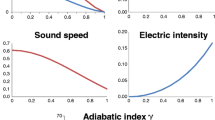
• (vi) The casualty condition (dp/c ² dρ)^1/2<1 i.e. velocity of sound should be less than that of light throughout the model. In addition to the above the velocity of sound should be decreasing towards the surface i.e. $\frac{d}{dr}(\frac{dp}{d\rho } )<0$ or $(\frac{d^{2} p}{d\rho ^{2} })>0$ for 0≤r≤a i.e. the velocity of sound is increasing with the increase of density.

• (vii) The ratio of pressure to the density (p/c ² ρ) should be monotonically decreasing with the increase of r i.e. $\frac{d}{dr}(\frac{p}{c^{2} \rho })_{r=0}=0$ and $\frac{d^{2} }{dr^{2} } (\frac{p}{c^{2} \rho })_{r=0} <0$ and $\frac{d}{dr} (\frac{p}{c^{2} \rho })$ is negative valued function for r>0.

• (viii) The central red shift Z ₀ and surface red shift Z _a should be positive and finite i.e. Z ₀=[(e ^−ν/2−1) _r=0]>0 and Z _a =[e ^λ(a)/2−1]>0 and both should be bounded.

• (ix) Electric intensity E, such that E(0)=0 is taken to be monotonically increasing i.e. (dE/dr)>0 for 0<r<a.

5 Properties of New Class of Solution

(17)

(18)

(19)

(20)

(21)

(22)

For p _r=0 and ρ _r=0 must be positive, $\frac{p_{r=0} }{c^{2}\rho _{r=0} } \le 1$ and (d ² p/dr ²) _r=0<0, (d ² ρ/dr ²) _r=0<0. Consequently we have

$$ -9K-18<A<\frac{9K}{10} +27$$

(23)

Hence velocity of sound at the centre given by

$$ \left[\frac{ dp}{ c ^{2} d\rho } \right]_{r=0} =\frac{-9K+10A-270}{45K+2A-90}$$

(24)

which should be $[\frac{ dp}{ c ^{2} d\rho }]_{r=0} <1$, for all values of K≥0 and A.

Using (13) and (14)

$$ \left[\frac{p}{c^{2} \rho } \right]=\frac{I(x)}{J(x)}$$

(25)

where

Differentiating (25) w.r.t. x

(26)

(27)

where

The expression of right hand side of (27) is negative for all values of K≥0 and A. Then pressure-density ratio $\frac{p}{c^{2} \rho }$ is maximum at the centre.

The expression for gravitational red-shift Z is given by

$$ Z=\frac{(1-x)^{1/6} }{\sqrt{B} } -1$$

(28)

The central value of gravitational red-shift to be non zero positive finite, we have

$$1>\sqrt{B} >0$$

Differentiating (28) w.r.t. x, we get,

$$ \left[\frac{d^{2} Z}{d r^{2} } \right]_{r=0} =-\frac{C}{3\sqrt{B} } <0$$

(29)

The expression of right hand side of (29) is negative, and then the gravitational red shift is the maximum at centre and monotonically decreasing towards the surface.

Differentiating (11) w.r.t. x, we get,

$$\frac{d}{dx} \left(\frac{E^{2} }{C} \right)=\frac{K}{2} \left[\frac{(3+2x)}{(3-2x)^{3} } \right]$$

$\frac{d}{dr}(\frac{E^{2} }{C})=Cr\cdot \frac{K}{2} [\frac{(3+2x)}{(3-2x)^{3} }] = +ve$ for 0<x<2/3.

Thus the electric intensity is zero at the centre and monotonically increasing towards the pressure free interface for all values of K>0.

6 Boundary Conditions

Besides the above, the charged fluid spheres is expected to join smoothly with the Reissner-Nordstrom metric at the pressure free boundary r=a

$$ ds^{2} ={-}\left(1-\frac{2M}{r} +\frac{e^{2} }{r^{2} } \right)^{-1} dr^{2} -r^{2} (d\theta ^{2} +\sin ^{2} \theta d\phi ^{2} )+\left(1-\frac{2M}{r} +\frac{e^{2} }{r^{2} } \right)dt^{2}$$

(30)

which requires the continuity of e ^λ,e ^ν and q across the boundary

(31)

(32)

(33)

(34)

The condition (34) can be utilized to compute the values of arbitrary constants A as follows:

On setting x _r=a =X=Ca ² (a being the radius of the charged sphere). Pressure at p _(r=a)=0 gives

$$ A=\left[\frac{3\cdot (18-21X+4 X^{2} )}{(3-X) \cdot (1-X)^{4/3} } \cdot \frac{(K-2)}{2} \right]$$

(35)

The expression for mass can be written as

$$m(a)=\frac{a}{2} \left[1-\frac{K X\cdot (18-39X+20X^{2} )}{2\cdot (3-2X)^{3} } -\frac{9 (3-4X) (1-X)^{2} }{(3-2X)^{3} } -\frac{A X (1-X)^{7/3} }{(3-2X)^{3} } \right]$$

such that $e^{-\lambda (a)} =1-\frac{2M}{a} +\frac{e^{2} }{a^{2} }$, where M=m(a) and $y_{(r=a)}^{2} =1-\frac{2M}{a} +\frac{e^{2} }{a^{2} }$ gives

$$B=\left[\frac{9K\cdot X(1-X)^{7/3} }{(3-2X)^{3} } +\frac{9\cdot (3-4X) (1-X)^{7/3} }{(3-2X)^{3} } +\frac{A\cdot X\cdot (1-X)^{8/3} }{(3-2X)^{3} } \right]$$

Also, if the surface density ρ _a is prescribed as 2×10¹⁴ g cm⁻³ (super dense star case) then value of constant C can be calculated for a given X(=Ca ²), using the following expression

$$\kappa c^{2} \rho _{a} =C \left[\frac{324-999 X+462 X^{2} -56 X^{3} }{(3-2X)^{4} } -\frac{K\cdot B(X)}{(3-2X)^{4} } -\frac{A\cdot (1-X)^{4/3} \cdot H(X)}{3\cdot (3-2X)^{4} } \right]$$

where

$$B(X)=(162-423 X+294 X^{2} -32 X^{3} ), \qquad H(X)=(27-51 X+10 X^{2} )$$

7 Conclusions

In this article, we have derived a class of regular and well behaved charge superdense star models using a particular electric field, which depend upon a parameter K, vanishing of which leads to the neutral case. The charged superdense star models satisfy the energy conditions c ² ρ≥3p>0, (dp/dr)<0, (dρ/dr)<0, causality condition (dp/c ² dρ)<1 and adiabatic index γ=((p+c ² ρ)/p)(dp/(c ² dρ))>1 for 0.13≤K≤1.9999. The velocity of sound and the ratio p/c ² ρ are seen monotonically decreasing towards the surface for 0.13≤K≤1.9999. The red shift is also decreasing monotonically from the centre to the pressure free interface for 0.13≤K≤1.9999. The maximum mass and the corresponding radius of the model are computed to 0.4711M _Θ and 7.0122 km respectively for K=1.9999 and Ca ²=0.2470, with the red shift Z ₀=0.1640 and Z _a =0.1100.

The proposed plan for future includes the charging of the fluid spheres and plates recently derived by two of the authors of the present paper [11, 12]. The process may provide pressure free interface which is not available in the uncharged case.

8 Tables for Numerical Values of Physical Quantities

In Tables 1–7: Z ₀ = red shift at the centre, Z _a = red shift at the surface, Solar mass M _Θ=1.475 km, G=6.673×10⁻⁸ cm³/gs², c=2.997×10¹⁰ cm/s, D=(8πG/c ²)ρa ²,

Table 1 Values of various parameters

Detailed physically behavior of the models for various K are displayed by means of graphs and tables as below, where Figs. 1–6 are given with reference of Tables 2–6.

Fig. 1

Behavior of pressure (P) versus radius

Fig. 2

Behavior of density versus radius

Fig. 3

Behavior of charge (Q) versus radius

Fig. 4

Behavior of velocity of sound versus radius

Fig. 5

Behavior of ratio of pressure and density versus radius

Fig. 6

Behavior of red shift (Z) versus radius

Table 2 K=0.2, Ca ²=0.23, Radius (a) = 6.6967 Km, Maximum mass M=0.3770M _Θ

Table 3 K=0.4, Ca ²=0.2330, Radius (a) = 6.7743 Km, Maximum mass M=0.3939M _Θ

Table 4 K=0.8, Ca ²=0.2360, Radius (a) = 6.8548 Km, Maximum mass M=0.4116M _Θ

Table 5 K=1.2, Ca ²=0.2400, Radius (a) = 6.9056 Km, Maximum mass M=0.4304M _Θ

Table 6 K=1.6, Ca ²=0.2440, Radius (a) = 6.9592 Km, Maximum mass M=0.4502M _Θ

Table 7 K=1.9999, Ca ²=0.2470, Radius (a) = 7.0122 Km, Maximum mass M=0.4711M _Θ