Charged fluid to anisotropic fluid distribution in general relativity

Abstract

A new class of well behaved anisotropic super-dense stars has been derived with the help of a given class of charged fluid distributions. The anisotropy parameter (or the electric intensity) is zero at the centre and monotonically increasing towards the pressure free interface. All the physical parameter such as energy density, radial pressure, tangential pressure and velocity of sound are monotonically decreasing towards the surface. The maximum mass measures 3.8593 solar mass and the corresponding radius is 21.2573 km for n=1 i.e. N tends to infinity.

1 Introduction

In the general theory of relativity, Einstein asserted that the governing space-time gets curved in presence of matter i.e. fluid, charge, gravitational field etc. It means for a given material distribution the corresponding space-time metric can be derived using relevant Einstein’s equations. On the other hand a curved space-time metric cannot predict a unique material distribution and the same metric can describe more than one physical situation. The preceding statement has already been supported. By the work of Tupper (1981, 1983a, 1983b) and then by Maurya and Gupta (2012a, 2012b), where they have shown that the same space-time metric can represent (i) electromagnetic field and viscous fluid (ii) perfect fluid and magnetohydrodynamic fluid (iii) perfect fluid and viscous magnetohydrodynamic fluid and (iv) anisotropic fluid and charged fluid. (Last one by Maurya-Gupta). Certainly no astronomical object has a perfect fluid distribution. Therefore it seems worthwhile to study the behaviour of the anisotropic fluid sphere in general relativity. Anisotropy in the pressure could be introduced by the existence of a solid core, by the presence of type-3A super-fluid (Kippenhahm and Weigert 1990), different kinds of phase transitions (Sokolov 1980) or by other physical phenomena. On the scale of galaxies, Binney and Tremaine (1987) have considered anisotropies in spherical galaxies, from a purely Newtonian point of view. The mixture of two gases (e.g. monatomic hydrogen or ionized hydrogen and electrons) can also formally be described as an anisotropic fluid (Letelier 1980 and Bayin 1982). Bowers and Liang (1974) have investigated the possible importance of locally anisotropic equations of state for relativistic fluid spheres by generalizing the equations of hydrostatic equilibrium to include the effects of local anisotropy. Their study shows that anisotropy may have non-negligible effects on such parameter as maximum equilibrium mass and surface red-shift. Heintzmann and Hillebrandt (1975) studied fully relativistic, anisotropic neutron star models at high densities by means of several simple assumptions and showed that for arbitrary large anisotropy there is no limiting mass for neutron stars, but that the maximum mass of a neutron star still lies beyond 3–4 M_Θ. Our aim is constructing models for relativistic anisotropic fluid spheres with physically reasonable behaviour.

In the present paper, we have studied exact solutions to Einstein’s gravitational field equations for anisotropic fluid spheres, by using a static spherically symmetric space-time that is already capable of describing a series of charged perfect fluid spheres and concluded that maximum mass of charged fluid and anisotropic fluid are very close to each other. In this process the present article also yield a new class of well behaved anisotropic fluids which are very important in the description stellar structures.

2 Field equations

Let us consider the static, spherically symmetric line element in curvature coordinates

(1)

where λ=λ(r) and ν=ν(r).

The Einstein’s field equations for charged perfect fluid distribution and anisotropic fluid distribution are given by

(2)

and

(3)

where v ⁱ is the fluid four-velocity vector for both the energy momentum tensor, and x ⁱ is unit space-like vector orthogonal to v ⁱ.

In the co-moving system we choose

(4)

From v ⁱ v _i =x ⁱ x _i =1, we obtain

(5)

The non-vanishing components of $T_{j}^{i}$ are

(6)

If the same space-time represents both the distributions then we should have

$$G_{ij} = H_{ij}. $$

Further more if the distributions have the same fluid four-velocity vector v ⁱ, then we get the following set of equations

(7)

(8)

(9)

where the prime denotes differential with respect to r. While p _r (r),p _t (r) and ρ(r) are radial pressure (in the direction of x _i ), tangential pressure (orthogonal to x _i ) and energy density respectively for the anisotropic fluid. On the other hand for $\bar{p}(r), \bar{\rho} (r)$ and $E( = \frac{q}{r^{2}})$ denote pressure, energy density and electric intensity respectively for the charged perfect fluid distribution. Also the q is given by $q(r) = 4\pi\int_{0}^{r} \sigma r^{2}e^{\lambda /2}dr = r^{2}\sqrt{ - F_{14}F^{14}} = r^{2}F^{41}e^{(\lambda + \nu )/2}$ represents the total charge contained within the sphere of radius r. Also F ₁₄ is the only non- vanishing component of the skew-symmetric electromagnetic tensor F _ij .

We are assuming p _r ≠p _t . The case in which p _r =p _t corresponds to the isotropic fluid sphere. Δ=p _t −p _r is a measure of the anisotropy and is called the anisotropy factor (Herrera and Ponce de Leon 1985). A term 2(p _t −p _r )/r appears in the conservation equations $T_{k;i}^{i} = 0$ (where a semicolon denotes the covariant derivative with respect to the metric), representing a force that is due to the anisotropic nature of the fluid. This force is directed outward when p _t >p _r and inward when p _r >p _t . The existence of a repulsive force (in the case in which p _t >p _r ) allows the construction of more compact objects when using anisotropic fluid than when using isotropic fluid (Gokhroo and Mehra 1994).

Subtracting Eq. (8) from the Eq. (9) we get

(10)

Equation (10) reveals the equivalence of the anisotropy parameter Δ=κ(p _t −p _r )=2E ².

Also the solution of Eq. (10) with the given expression of Δ may provide the anisotropic fluid distribution. Therefore if the charged distribution is already is in hand i.e. E is known, the Δ can easily be computed. The Eqs. (7)–(9) provide the expressions for energy density ρ, radial pressure p _r and tangential pressure p _t of the anisotropic fluid in terms of the energy density $\bar{\rho}$, pressure $\bar{p}$ and the electric intensity E of the charged perfect fluid. However the region of physical validity for the above physical quantities may not be same for both the fluid distributions.

For example the radial pressure p _r and pressure $\bar{p}$ can not vanish for the same radius as the electric intensity is not zero on the boundary. Also the monotonic increasing and decreasing character of various physical quantities for either fluid may not be similar in the same region. The set of values of arbitrary constants appearing in the space time given by (10) will be different for anisotropic and charged perfect fluid distributions as the former joins with the Schwarzschild exterior solution while the later joins with the Reissner–Nordstrom metric at the pressure free boundary.

Using the transformations ϕ=c ₀ r ² (c ₀ is a positive constant), e ^−λ=Y and e ^ν=y ², (7)–(10) assumes the forms

(11)

(12)

(13)

and

(14)

Now let us consider the anisotropic and charged fluid model obtained by Maurya and Gupta (2012a, 2012b) (which infact is charged analogue of Durgapal’s 1984 neutral solution) which has e ^ν=y ²=B(1−ϕ)⁻ⁿ and

(15)

On inserting y and Δ=2E ² from (15) into (14) we get

(16)

A set of new exact solution can be obtained for all those values of n for which (1+n)/(1−n) is a positive integer. The class of polynomial anisotropic solutions is derived by Maurya and Gupta (2012a, 2012b) for negative integral values of n and c ₀<0. However the present polynomial solutions are obtained for positive fractional values of n.

Let (1+n)/(1−n)=N, where N is a positive integer >1.

Then (16) gives the solution

(17)

where,

$$A_{N - k} = a_{N - k} = 0\quad \mbox{for all}\ N < k\ \mbox{and}\ i = 0\ \mbox{to}\ N - 4. $$

The above solution is the same as obtained for charged perfect fluid distribution. Therefore we have come across a space-time metric defined by the known metric potentials e ^ν(=y ²) and e ^−λ(=Y). It is interesting to see that the same time is capable of representing two physical situations viz. charged perfect fluid distribution as well as anisotropic fluid distribution. Various physical quantities for the said distributions can be furnished as below:

• (a) Charged fluid distribution: The expressions for pressure, energy density and electric intensity are already available in the article Maurya and Gupta (2012a, 2012b) subject to the defining space-time joining smoothly with the Reissiner-Nordstrom metric at the pressure free interface.

• (b) Anisotropic fluid distribution: The expressions for energy density, radial pressure and tangential pressure are given as:

(18)

(19)

and

$$ \frac{\kappa p_{t}}{c_{0}} = \frac{\Delta_{0}\phi}{[1 - \{ 2/(N + 1) \}\phi ]^{N}} + \frac{\kappa p_{r}}{c_{0}} $$

(20)

where

Consequently the expressions for pressure and density gradients read as

(21)

where

(22)

where

and

(23)

with

In order to be physically meaningful, the interior solution for static fluid spheres of Einstein’s gravitational-field equations must satisfy some more general physical requirements. The following conditions have been generally recognized to be crucial for anisotropic fluid spheres Herrera and Santos (1997).

• (i) The solution should be free from physical and geometric singularities and non zero positive values of e ^λ and e ^ν i.e. (e ^λ) _r=0=1 and e ^ν>0.

• (ii) The radial pressure p _r must be vanishing but the tangential pressure p _t may not vanish at the boundary r=a of the sphere. However the radial pressure equal to the tangential pressure at the centre of the fluid sphere.

• (iii) The density ρ and pressures p _r ,p _t should be positive inside the star.

• (iv) (dp _r /dr) _r=0=0 and (d ² p _r /dr ²) _r=0<0 so that pressure gradient dp _r /dr is negative for 0<r≤a.

• (v) (dp _t /dr) _r=0=0 and (d ² p _t /dr ²) _r=0<0 so that pressure gradient dp _t /dr is negative for 0<r≤a.

• (vi) (dρ/dr) _r=0=0 and (d ² ρ/dr ²) _r=0<0 so that density gradient dρ/dr is negative for 0<r≤a.

  The condition (iv), (v) and (vi) imply that pressure and density should be maximum at the centre and monotonically decreasing towards the surface.

• (vii) Inside the static configuration the speed of sound should be less than the speed of light, i.e.

  $$0 \le\sqrt{\frac{dp_{r}}{c^{2}d\rho}} < 1\quad \mathrm{and}\quad 0 \le\sqrt{\frac{dp_{t}}{c^{2}d\rho}} < 1 . $$

  In addition to the above the velocity of sound should be decreasing towards the surface. i.e. $\frac{d}{dr}( \frac{dp_{r}}{d\rho} ) < 0$ or $( \frac{d^{2}p_{r}}{d\rho ^{2}} ) > 0$ and $\frac{d}{dr}( \frac{dp_{t}}{d\rho} ) < 0$ or $( \frac{d^{2}p_{t}}{d\rho ^{2}} ) > 0$ for 0≤r≤a i.e. the velocity of sound is increasing with the increase of density.

• (viii) A physically reasonable energy-momentum tensor has to obey the conditions ρ≥p _r +2p _t and ρ+p _r +2p _t ≥0.

• (ix) The central red shift Z ₀ and surface red shift Z _a should be positive and finite i.e. Z ₀=[(e ^−ν/2−1) _r=0]>0 and Z _a =[e ^λ(a)/2−1]>0 and both should be bounded.

3 Properties of new class of solutions

In order to meet out the above conditions (i)–(ix), we need to supply the following data:

(24a)

(24b)

(24c)

(24d)

(24e)

(24f)

(24g)

(24h)

(24i)

In order to have (p _r ) _r=0≥0,(ρ) _r=0≥0,(d ² p _r /dr ²) _r=0<0, and (d ² ρ/dr ²) _r=0<0, we ought to satisfy the following inequalities

(25)

Further the velocity of sound at the centre reads as

(26a)

and

(26b)

which should be $0 \le[ \frac{dp_{r}}{c^{2}d\rho} ]_{r = 0} < 1$ and $0 \le[ \frac{dp_{t}}{c^{2}d\rho} ]_{r = 0} < 1$ for all values of Δ₀≥0 and A. The expression for gravitational red-shift Z is given by

(27)

For the central gravitational red-shift to be non zero positive finite, we must have

(28)

Differentiating equation (27) w.r.t. r, we get,

(29)

As the right hand side of (29) is negative we conclude that the gravitational red shift is maximum at the centre and monotonically decreasing towards the surface.

4 Boundary conditions

Besides the above, the fluid balls is expected to join smoothly with the Schwarzschild exterior solution at the pressure free boundary r=a

(30)

which requires the continuity of e ^λ and e ^ν across the boundary

(31)

(32)

and the radial pressure vanishes at the boundary i.e.

$$ p_{r}(a) = 0. $$

(33)

The condition (33) can be utilized to compute the value of the arbitrary constants A as follows:

On setting ϕ _r=a =ϕ _a =c ₀ a ² (a being the radius of the fluid balls).

The radial pressure at p _r (a)=0 gives

(34)

where

The expression for mass can be written as

(35)

such that $Y_{anis}(a) = 1 - \frac{2M}{a}$, where M=m(a) and $y^{2}(a) = 1 - \frac{2M}{a}$ gives

(36)

Also, if the surface density ρ _a is prescribed as $2 \times 10^{14}~\mathrm{g\,cm}^{ - 3}$ (super dense star case) then value of constant c ₀ can be calculated for a given ϕ _a (=c ₀ a ²), using the following expression

(37)

with

5 Physical analysis and conclusion

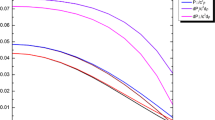
In the present article we have obtained the anisotropic super-dense star models with metric potential g ₄₄=B(1−c ₀ r ²)⁻ⁿ for positive fractional values of n such that N=(1+n)/(1−n) is a positive integer and analysed with subject to the relevant physical conditions. The maximum mass is seen increasing with the increasing values of N≥2. The maximum mass is found to be 3.8593 M_Θ at n=1 i.e. N→∞ with the corresponding radius 21.2573 km. Moreover the condition ρ−p _r −2p _t ≥0 is true for all the anisotropic star models. The radial velocity of sound $(\sqrt{dp_{r}/d\rho}\, )$ and tangential velocity of sound $(\sqrt{dp_{t}/d\rho}\, )$ are found to be monotonically decreasing towards the pressure free interface for N≥2. Red-shift for whole family of super-dense star is computed. For all the models the anisotropy parameter Δ=p _t −p _r is positive throughout the range and hence helps the outward pressure to avert the gravitational collapse of the super dense star models so obtained.

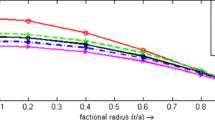
Owing to the above Fig. 1, the dash line and solid line represent the variations of masses for charged and anisotropic fluids spheres respectively for various values of N and we conclude that mass for well behaved charged stars models is always greater than the mass of anisotropic star models (subject to the conditions (i)–(ix)). The Table 1 describes the variations of mass and radius of charged and anisotropic fluid spheres corresponding to various integral values of N. Also we conclude that the masses tends to certain limit as N increases infinitely or (n=1).

Fig. 1

Behaviour of maximum mass for charged fluid and anisotropic fluid distribution versus N

Table 1 Maximum mass (M/M_Θ) and Radius (a) for different n,Δ₀ and c ₀ a ² for Charged fluid distribution and Anisotropic fluid distribution