Solutions of the Einstein’s field equations with anisotropic pressure compatible with cold star model

Abstract

In this paper we obtain a new static and spherically symmetric model of compact star whose spacetime satisfies Karmarkar’s condition (1948). The Einstein’s field equations are solved by employing a physically reasonable choice of the metric coefficient $g_{rr}$ so that the obtained solution is free from central singularities. Our model satisfies all the energy conditions as well as the causality condition. By assigning some particular values mass and radius of the compact stars PSR J0347+0432, Cen X-3 and Vela X-1 have been obtained which are very close to the observational data proposed by Antoniadis et al. (Science 340:1233232, 2013), Abubekerov et al. (Astron. Rep. 48:89, 2004) and Ash et al. (Mon. Not. R. Astron. Soc. 307:357, 1999). For the neutron star candidate PSR J0348+0432, we expect a very stiff equation of state to support its massive mass which corresponds to a large value of the adiabatic index of 6.66 at the center.

1 Introduction

In last few decades the study of compact objects has become an interesting issue to the researchers. By solving the Einstein’s Field Equations (EFEs) under different conditions one can obtain a static and spherically symmetry model of compact star. Due to highly non-linearity nature of the differential equations it is very difficult to solve the EFEs. In case of static isotropic perfect fluid model the EFEs reduce to a set of three ordinary differential equations (ODEs) with four unknowns. But recent theoretical advances show that the pressure inside a fluid sphere becomes anisotropic due to the central density $\sim10^{15}$ (Ruderman 1972) and the pressure can be decomposed into two parts: radial pressure $p_{r}$ and transverse pressure $p_{t}$. Local anisotropy in self-gravitating systems were studied by Herrera and Santos (1997). Cosenza et al. (1981) it has been suggested that superdense matter may be anisotropic, at least in some density ranges. Bowers and Liang (1974) have pointed out that anisotropy may also change the limiting values of the maximum mass of compact stars. In this generalization Herrera and Ponce de Leon (1985) studied the balance and collapse of compact spheres.

In order to solve the Einstein-Maxwell system of equations a familiar method is to assume an equation of state which represents a relationship between the pressure and the matter density. Several works are done by assuming an EOS. By assuming barotropic equation of state the models of compact star were obtained by Rahaman et al. (2014). Bhar et al. (2014, 2015) obtained the model of compact star by assuming one of the metric potential together with a linear equation of state. Malaver (2014, 2015) consider a quadratic equation of state for the matter distribution and specify particular forms for the gravitational potential and electric field intensity. By assuming the KB ansatz (Krori and Barua 1975) Bhar (2015a,b,c) obtained the model of compact stars. By assuming a special type of matter density Dev and Gleiser (2002) discussed an anisotropic star model. Rahaman et al. (2010a) have also used this density function. By using the same matter density Bhar and Rahaman (2015) proposed a new model of dark energy star consisting of five zones, namely, the solid core of constant energy density, the thin shell between core and interior, an inhomogeneous interior region with anisotropic pressures, a thin shell, and the exterior vacuum region. The model is stable under a small linear perturbation. By using Chaplygin equation of state compact star model was obtained by Rahaman et al. (2010b), Bhar (2015d). A well-behaved class of charged analogue of Durgapal solution was obtained by Mehta et al. (2013). A class of super dense stars models using charged analogues of Hajj-Boutros type relativistic fluid solutions are obtained by Pant et al. (2014).

Generalized compact spheres in electric fields was obtained by Maharaj and Komathiraj (2007). Ivanov (2002) obtained static charged perfect fluid spheres in general relativity. Böhmer and Harko (2006) obtained the upper and lower limits for the basic physical parameters (mass-radius ratio, anisotropy, redshift and total energy) for arbitrary anisotropic general relativistic matter distributions in the presence of a cosmological constant. They proved that the values of these quantities are strongly dependent on the value of the anisotropy parameter at the surface of the star. Malaver (2013a,b), Singh et al. (2015, 2016a), Singh and Pant (2015, 2016a) have used a great variety of mathematical techniques to obtain exact solutions. A different approach is also used by Gupta and Kumar (2011), Kumar et al. (2010, 2014) and Thakadiyil and Jasim (2013) to discover solutions on embedding class I.

In our present paper we obtain a new class of compact star of embedding class one. It is familiar that every $n$ dimensional Riemannian manifold $V_{n}$ is isometrically embedded into some pseudo-Euclidean space of $n(n+1)/2$ dimensions. The most important feature of this type of metric is the dependence of the metric functions $\nu$ and $\lambda$. Recently a large number of work has been done by assuming the metric potentials satisfy the condition of embedding class one. In this respect we want to mention the works of Singh and Pant (2016b,c), Singh et al. (2016b,c,f,d), Maurya et al. (2016) and Bhar et al. (2016). Inspiring these earlier work in the present paper we model a compact star of embedding class-I by assuming a new metric potential for $g_{rr}$. Our paper is organized as follows: in Sect. 2 the basic field equations have been given, in Sect. 3 field equations have been solved by taking a physically reasonable new form of the metric potential for $g_{rr}$. The conditions for well behaved solution is described in Sect. 4. The Sect. 5 is focused on matching of boundary conditions. Properties of the new solution is described in Sect. 6 and its stability analysis in given in Sect. 6.1. Finally a brief discussions are on the solution is given in Sect. 7.

2 Interior space-time and basic field equations

A static spherically symmetry $4D$ spacetime is described by the line element,

$$ ds^{2}=-e^{\nu(r)}dt^{2}+e^{\lambda(r)}dr^{2}+r^{2} \bigl(d\theta^{2}+\sin ^{2}\theta d\phi^{2}\bigr) $$

(1)

where $\lambda(r)$ and $\nu(r)$ are called the gravitational potential.

Let us assume that the matter distribution inside the stellar configuration is anisotropic in nature and correspondingly the energy-momentum tensor can be written as,

$$ T_{\nu}^{\mu}=(\rho+p_{r})u^{\mu}u_{\nu}-p_{t} g_{\nu}^{\mu}+(p _{r}-p_{t}) \eta^{\mu}\eta_{\nu} $$

(2)

with $u^{i}u_{j} =-\eta^{i}\eta_{j} = 1$ and $u^{i}\eta_{j}= 0$. The vectors $u_{i}$ and $\eta^{i}$ represent fluid 4-velocity and spacelike vector respectively and $\eta^{i}$ is orthogonal to $u^{i}$, $\rho$ is the matter density, $p_{r}$ and $p_{t}$ are respectively the radial and transverse pressure of the fluid and $p_{t}$ is in the orthogonal direction to $p_{r}$.

Assuming $G=1=c$ the Einstein field equations are given by

$$\begin{aligned} &8\pi\rho = \frac{1 - e^{-\lambda}}{r^{2}} + \frac{\lambda'e^{-\lambda}}{r} \end{aligned}$$

(3)

$$\begin{aligned} &8\pi p_{r} = \frac{\nu' e^{-\lambda}}{r} - \frac{1 - e^{-\lambda}}{r^{2}} \end{aligned}$$

(4)

$$\begin{aligned} &8\pi p_{t} = \frac{e^{-\lambda}}{4} \biggl( 2\nu'' + {\nu'}^{2} - \nu'\lambda' + \frac{2\nu'}{r}-\frac{2\lambda'}{r} \biggr) \end{aligned}$$

(5)

where $(')$ denotes differentiation with respect to radial co-ordinate $r$.

Using the Eqs. (4) and (5) we obtain the anisotropy parameter

$$\begin{aligned} \Delta =& 8\pi(p_{t}-p_{r}) \\ = & e^{-\lambda} \biggl[ \frac{\nu'' }{2}-\frac{\lambda' \nu' }{4}+ \frac{\nu^{\prime\,2} }{4}-\frac{\nu'+\lambda' }{2r}+ \frac{e^{\lambda}-1 }{r^{2}} \biggr] \end{aligned}$$

(6)

If the metric given in (1) satisfies the Karmarkar condition (Karmarkar 1948), it can represent a embedding class one spacetime i.e.

$$ R_{1414}=\frac{R_{1212}R_{3434}+R_{1224}R_{1334} }{R_{2323}} $$

(7)

with $R_{2323}\neq0$ (Pandey and Sharma 1981). This condition leads to a differential equation given by

$$ \frac{2\nu'' }{\nu'}+\nu'= \frac{\lambda' e^{\lambda}}{e^{\lambda}-1} $$

(8)

On integration we get the relationship between $\nu$ and $\lambda$ as

$$ e^{\nu}= \biggl( A+B \int\sqrt{e^{\lambda}-1}~dr \biggr) ^{2} $$

(9)

where $A$ and $B$ are constants of integration.

By using (9) we can rewrite (6) as

$$\begin{aligned} \Delta= \frac{\nu' }{4e^{\lambda}} \biggl[ \frac{2}{r}- \frac{\lambda' }{e^{\lambda}-1} \biggr] ~ \biggl[ \frac{\nu' e^{\nu }}{2rB^{2}}-1 \biggr] \end{aligned}$$

(10)

3 Generating a new anisotropic solution

To solve the above equation (9), we have assumed an entirely new type of $g_{rr}$ metric potential given by

$$ e^{\lambda}= 1+ar^{2}+br^{4} $$

(11)

where $a$ and $b$ are constants.

On integrating (9) with the help of (11) we get

$$\begin{aligned} e^{\nu} = & \biggl[ A+\frac{B (a+b r^{2})^{3/2}}{3 b} \biggr] ^{2} \end{aligned}$$

(12)

Now employing the expression of $e^{\nu}$ and $e^{\lambda}$ in (3), (4), (10) and (5), we obtain the expression for matter density and radial pressure as,

$$\begin{aligned} 8\pi\rho =& \frac{a^{2} r^{2}+a (2 b r^{4}+3)+b r^{2} (b r^{4}+5)}{(a r^{2}+b r^{4}+1)^{2}} \end{aligned}$$

(13)

$$\begin{aligned} 8\pi p_{r} =& \frac{1}{(a r^{2}+b r^{4}+1) \{B (a+b r^{2})^{3/2}+ 3 A b\}} \\ &{} \times\bigl[-a^{2} B \sqrt{a+b r^{2}} -a b \bigl\{ 2 B r\sqrt{r^{2} \bigl(a+b r^{2}\bigr)} \\ &{} +3 A \bigr\} +b \bigl\{ B \bigl(6-b r^{4}\bigr) \sqrt{a+b r^{2}}-3 A b r^{2} \bigr\} \bigr] \end{aligned}$$

(14)

and the anisotropic factor $\Delta$ and transverse pressure $p_{t}$ are obtained as,

$$\begin{aligned} \Delta =& \frac{ r\{a^{2}+2 a b r^{2}+b (b r^{4}-1) \} (a+b r^{2})^{-1/2}}{(a r^{2}+b r^{4}+1)^{2} \{ B (a+b r^{2})^{3/2}+3 A b r \}} \\ &{} \times\bigl[a^{2} B r+b \bigl\{ 3 A \sqrt{r^{2} \bigl(a+b r^{2}\bigr)}+B r \bigl(b r ^{4}-3\bigr) \bigr\} \\ &{} +2 a b B r^{3} \bigr] \end{aligned}$$

(15)

$$\begin{aligned} 8\pi p_{t} =& 8\pi p_{r}+\Delta \end{aligned}$$

(16)

Using the relationship between $e^{\lambda}$ and mass $m(r)$ i.e.

$$ e^{-\lambda}=1-\frac{2m }{r} $$

(17)

and (3) we obtain the expression for the mass function as,

$$\begin{aligned} m(r) =& \frac{r^{3}(a+br^{2})}{2(1+ar^{2}+b r^{4})} \end{aligned}$$

(18)

the compactification factor is obtained as,

$$\begin{aligned} u(r) =& \frac{2m(r) }{r} = \frac{(a+br^{2})r^{2}}{1+ar^{2}+b r^{4}} \end{aligned}$$

(19)

Now the gravitational red-shift at the stellar surface is given by

$$\begin{aligned} Z =& e^{-\nu/2}-1 = \biggl( \frac{B (a+b r^{2})^{3/2}}{3 b}+A \biggr) ^{-1}-1 \end{aligned}$$

(20)

4 Physical acceptability conditions

For well-behaved nature of the solutions for an an-isotropic fluid sphere following conditions should be satisfied:

• 1. The solution should be free from physical and geometric singularities, i.e. it should yield finite and positive values of the central pressure, central density and nonzero positive value of $e^{\nu}|_{r=0}$ and $e^{\lambda}|_{r=0}=1$.

• 2. For physically stable static configuration, the energy condition like Null Energy Condition (NEC), Weak Energy Condition (WEC), Strong Energy Condition (SEC) and Dominant Energy Condition needs to satisfy throughout the interior region i.e.

  $$\begin{aligned} &\rho\ge0;\quad \rho-p_{r} \ge0;\quad \rho-p_{t} \ge0; \\ &\rho-p_{r}-2p_{t} \ge0;\quad \rho\ge(|p_{r}|,|p_{t}|) \end{aligned}$$

• 3. The casualty condition should be obeyed i.e. velocity of sound should be less than that of light throughout the model. In addition to the above the velocity of sound should be decreasing towards the surface i.e. $\frac{d }{dr}\frac{dp_{r} }{d\rho}<0$ or $\frac{d^{2} p_{r}}{d\rho^{2}}>0$ and $\frac{d}{dr} \frac{dp_{t} }{d\rho}<0$ or $\frac{d^{2}p_{t} }{d\rho^{2}}>0$ for $0\leq r\leq r_{b}$ i.e. the velocity of sound is increasing with the increase of density and it should be decreasing outwards.

• 4. The adiabatic index, $\varGamma_{r}= \frac{\rho+p_{r} }{p_{r}}\frac{dp_{r} }{d\rho}$ for realistic matter should be $\varGamma_{r}>4/3$.

• 5. The red shift $z$ should be positive, finite and monotonically decreasing in nature with the increase in $r$.

• 6. The anisotropy factor $\Delta$ should be zero at the center and increasing towards the surface.

• 7. For a stable anisotropic compact star, $-1\leq v_{t}^{2}-v_{r}^{2} \leq0$ must be satisfied (Herrera and Santos 1997).

5 Exterior spacetime and boundary condition

Assuming the exterior spacetime is the Schwarzschild solution which has to be match smoothly with the interior solution and is given by

$$\begin{aligned} ds^{2} =& - \biggl( 1-\frac{2M}{r} \biggr) dt^{2}+\biggl( 1-\frac{2M}{r} \biggr) ^{-1}dr^{2} \\ &{} +r^{2}\bigl(d\theta^{2}+\sin^{2} \theta d\phi^{2}\bigr) \end{aligned}$$

(21)

By matching the interior solution (1) and exterior solution (21) at the boundary $r=r_{b}$ we get

$$\begin{aligned} &e^{\nu_{b}} = 1-\frac{2M }{r_{b}} = \biggl( A+\frac{B (a+b r_{b}^{2})^{3/2}}{3 b} \biggr) ^{2} \end{aligned}$$

(22)

$$\begin{aligned} &e^{-\lambda_{b}} = 1-\frac{2M }{r_{b}} = \frac{1 }{1+ar_{b}^{2}+br_{b}^{4}} \end{aligned}$$

(23)

$$\begin{aligned} &p_{r}(r_{b}) = 0 \end{aligned}$$

(24)

Using the boundary condition (22-24), we get

$$\begin{aligned} &a = \frac{1 }{r_{b}^{2}} \biggl[ \frac{1 }{1-2M/r_{b}} - br_{b}^{4}-1 \biggr] \end{aligned}$$

(25)

$$\begin{aligned} &A = \sqrt{1-\frac{2M }{r_{b}}}-\frac{B}{3b} \bigl[a+br_{b}^{2} \bigr]^{3/2} \end{aligned}$$

(26)

$$\begin{aligned} &B = \biggl[ \frac{3 b^{2} r_{b}^{2} \sqrt{1-2M/r_{b}}}{C_{1} \sqrt{a+b r_{b}^{2}}}+\frac{3 a b \sqrt{1-2M/r_{b}}}{C_{1} \sqrt{a+b r_{b}^{2}}} \biggr] \\ &\qquad {} \times \biggl[ \frac{b r_{b}^{2} (a+b r_{b}^{2})}{C_{1}}+\frac{a (a+b r_{b}^{2})}{C_{1}}-1 \biggr] ^{-1} \end{aligned}$$

(27)

where

$$\begin{aligned} &C_{1} = a^{2}+2 a b r_{b}^{2}+b^{2} r_{b}^{4}-6 b. \end{aligned}$$

(28)

6 Properties of the new solutions

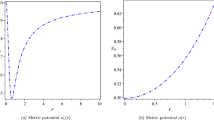
The metric potentials are plotted against $r$ in Fig. 1. From the figures we see that metric potentials are free from central singularity and

$$\begin{aligned} e^{\lambda(0)} =&1,\qquad e^{\nu(0)}= \biggl( A+\frac{Ba^{3/2}}{3b} \biggr) ^{2} \end{aligned}$$

which are constants and $(e^{\lambda})'=0$; $(e^{\nu})'=0$ at the origin $r=0$.

Fig. 1

Variation of metric potentials against $r$ by taking the same values of the constant mentioned in Table 1 for PSR J0348+0432

The central values of $p_{r}$, $p_{t}$, $\rho$ and the Zeldovich’s condition can be written as

$$\begin{aligned} 8\pi p_{r}(0) =& 8\pi p_{t}(0) \\ =& \frac{6bB\sqrt{a}-3abA-a^{5/2}B }{3bA+a^{3/2}B}>0 \end{aligned}$$

(29)

$$\begin{aligned} 8\pi\rho(0) =& 3a;\quad \forall a>0 \end{aligned}$$

(30)

$$\begin{aligned} \frac{p_{r}(0) }{\rho(0)} =& \frac{6bB\sqrt{a}-3abA-a^{5/2}B }{3a(3bA+a^{3/2}B)} \le1 \end{aligned}$$

(31)

On using (29) and (31), we get a constraint on $B/A$ given by

$$ \frac{3ab }{6b\sqrt{a} -a^{5/2}} < \frac{B }{A} \le \frac{12ab }{6b\sqrt{a}-4a^{5/2}} $$

(32)

The density and pressure gradients are given as

$$\begin{aligned} 8\pi\frac{d\rho}{dr} =& -\frac{2 r}{(a r^{2}+b r^{4}+1)^{3}} \bigl[a ^{3} r^{2}+a^{2} \bigl(3 b r^{4}+5\bigr) \\ &{} +a b r^{2} \bigl(3 b r^{4}+13\bigr) \\ &{}+b\bigl(b^{2} r^{8}+12 b r^{4}-5\bigr) \bigr] \end{aligned}$$

(33)

$$\begin{aligned} 8\pi\frac{dp_{r} }{dr} =& \frac{2(a r^{2}+b r^{4}+1)^{-2}}{\sqrt{a+b r^{2}} ~ [ B (a+b r^{2})^{3/2}+3 A b ] ^{2}} \\ &{} \times\bigl[a^{3} b B \bigl\{ B \bigl(10 b r^{4}-7\bigr) \sqrt{r^{2} \bigl(a+b r^{2}\bigr)} \\ &{}+24 A b r^{3} \bigr\} +a b^{2} f_{4}(r)+b^{3} f_{3}(r)+f_{1}(r) \\ &{} +a^{2}b^{2} f_{2}(r) \bigr] \end{aligned}$$

(34)

$$\begin{aligned} 8\pi\frac{dp_{t} }{dr} =& - \frac{(a r^{2}+b r^{4}+1)^{-3} }{(a+b r^{2})^{3/2} ~ [B (a+b r^{2})^{3/2}+3 A b]^{2}} \\ &{} \times\bigl[-2 a^{4} b B \bigl\{ B \bigl(21 b r^{4}-11\bigr) \sqrt{r^{2} \bigl(a+b r ^{2}\bigr)} \\ &{} +63 A b r^{3} \bigr\} +a^{3} b^{2} f_{6}(r)+a^{2} b^{2} f_{7}(r) \\ &{} +a b^{3} f_{9}(r)+b^{4} f_{8}(r) r^{2}+f_{5}(r) \bigr] \end{aligned}$$

(35)

provided

$$\begin{aligned} f_{1}(r) =& a^{5} B^{2} \sqrt{r^{2} \bigl(a+b r^{2}\bigr)}+a^{4} b B r \\ &{} \times\bigl\{ 5 B r \sqrt{r^{2} \bigl(a+b r^{2}\bigr)}+6 A \bigr\} \end{aligned}$$

(36)

$$\begin{aligned} f_{2}(r) =& 9 A^{2} \sqrt{r^{2} \bigl(a+b r^{2}\bigr)}+B^{2} r^{2} \bigl(10 b r ^{4}-33\bigr) \\ &{} \times\sqrt{r^{2} \bigl(a+b r^{2}\bigr)}+12 A B r \bigl(3 b r^{4}-2\bigr) \end{aligned}$$

(37)

$$\begin{aligned} f_{3}(r) =& 9 A^{2} \bigl(b r^{4}-1\bigr) \sqrt{r^{2} \bigl(a+b r^{2}\bigr)}+B^{2} r ^{2} \\ &{} \times\bigl(b^{2} r^{8}-19 b r^{4} -6\bigr) \sqrt{r^{2} \bigl(a+b r^{2}\bigr)} \\ &{} +3 A B r \bigl(2 b^{2} r^{8}-11 b r^{4}+3\bigr) \end{aligned}$$

(38)

$$\begin{aligned} f_{4}(r) =& 18 A^{2} b r^{2} \sqrt{r^{2} \bigl(a+b r^{2}\bigr)}+B^{2} \bigl(5 b ^{2} r^{8}-45 b r^{4}-6\bigr) \\ &{} \times\sqrt{r^{2} \bigl(a+b r^{2}\bigr)}+3 A b B r^{3} \bigl(8 b r^{4}-19\bigr) \end{aligned}$$

(39)

$$\begin{aligned} f_{5}(r) =& -4 a^{6} B^{2} \sqrt{r^{2} \bigl(a+b r^{2}\bigr)}-2 a^{5} b B r \\ &{} \times\bigl\{ 11 B r \sqrt{r^{2} (a+b r^{2})}+12 A \bigr\} \end{aligned}$$

(40)

$$\begin{aligned} f_{6}(r) =& -36 A^{2} \sqrt{r^{2} \bigl(a+b r^{2}\bigr)}+2 B^{2} r^{2} \bigl(65-14 b r^{4}\bigr) \\ &{} \times\sqrt{r^{2} \bigl(a+b r^{2}\bigr)}+3 A B r \bigl(26-93 b r^{4}\bigr) \end{aligned}$$

(41)

$$\begin{aligned} f_{7}(r) =& -144 A^{2} b r^{2} \sqrt{r^{2} \bigl(a+b r^{2}\bigr)}+2 B^{2} \bigl(4 b^{2} r^{8} \\ &{} +141 b r^{4} +3\bigr)\sqrt{r^{2} \bigl(a+b r^{2}\bigr)}+3 A b B r^{3} \\ &{} \times\bigl(93-107 b r^{4}\bigr) \end{aligned}$$

(42)

$$\begin{aligned} f_{8}(r) =& -36 A^{2} \bigl(3 b r^{4}-1\bigr) \sqrt{r^{2} \bigl(a+b r^{2}\bigr)} \\ &{} +2 B^{2} r^{2} \bigl(3 b^{2} r^{8} +44 b r^{4}+9\bigr) \sqrt{r^{2} \bigl(a+b r ^{2} \bigr)} \\ &{} -3 A B r \bigl(15 b^{2} r^{8}-56 b r^{4}+9 \bigr) \end{aligned}$$

(43)

$$\begin{aligned} f_{9}(r) =& -36 A^{2} \bigl(6 b r^{4}-1\bigr) \sqrt{r^{2} \bigl(a+b r^{2}\bigr)} \\ & {}+2 B^{2} r^{2} \bigl(9 b^{2} r^{8}+131 b r^{4}+12\bigr) \sqrt{r^{2} \bigl(a+b r ^{2}\bigr)} \\ & {}-9 A B r \bigl(21 b^{2} r^{8}-41 b r^{4}+4 \bigr) \end{aligned}$$

(44)

The profile of the matter density, radial and transverse pressure are plotted in Fig. 2 and Fig. 3 respectively which shows that $\rho$, $p_{r}$ and $p_{t}$ all are positive and monotonic decreasing function of $r$ inside the stellar interior and $p_{r}$ vanishes at the boundary of the star. The monotonic decreasing condition is reverified by Fig. 6. Both $p_{r}/\rho$ and $p_{t}/ \rho$ are monotonic decreasing function of $r$ and lies in the range $0< p_{r}/\rho,~p_{t}/\rho<1$ (Fig. 4) proves that the underlying fluid distribution is non-exotic in nature. The anisotropic factor $\Delta$ is plotted against $r$ in Fig. 5 which shows that $\Delta>0$ inside the stellar configuration and therefore the anisotropic force is repulsive in nature which is necessary to construct the compact object (Gokhroo and Mehra 1994). Figure 8 shows that all the energy conditions are satisfied by our present model. The mass function is plotted against $r$ in Fig. 14. The profile of mass function is monotonic increasing function of $r$ and positive inside the stellar configuration. The compactness factor and gravitational redshift are plotted in Fig. 13 and Fig. 10 respectively. It is noted that the compactification factor does not cross the Buchdahl limit $2m/r<8/9$ (Buchdahl 1939). The gravitational redshift is plotted in Fig. 10, which has maximum value at the center and it decreases radially outwards. The surface redshift, compactification factor has been obtained for different compact stars in Table 1. The values of the surface redshift lies in the range $z_{s}\leq1$. The adiabatic index $\varGamma_{r}$ (Fig. 11) is monotonic increasing outwards and $\varGamma_{r}>4/3$ everywhere inside the fluid sphere and hence the model is stable. The ratio of $(p_{r}+2p_{t})/\rho$ plotted in Fig. 9 is monotonic decreasing function of $r$ and less than 1. The profile of the radial and transverse velocity of sound is shown in Fig. 7 and the figure shows that $0< v_{r}^{2},v_{t}^{2}<1$ so causality condition holds and $|v_{r}^{2}-v_{t}^{2}|<1$ (Fig. 12), implies Andréasson (2009) condition is also satisfied.

Fig. 2

Variation of density against $r$ by taking the same values of the constant mentioned in Table 1 for PSR J0348+0432

Fig. 3

Variation of pressure against $r$ by taking the same values of the constant mentioned in Table 1 for PSR J0348+0432

Fig. 4

Variation of pressure to density ratio against $r$ by taking the same values of the constant mentioned in Table 1 for PSR J0348+0432

Fig. 5

Variation of anisotropy against $r$ by taking the same values of the constant mentioned in Table 1 for PSR J0348+0432

Table 1 Masses, radii and all the constant parameters representing well-behaved solutions that corresponds to well-known compact stars

6.1 Stability under three different forces

To check the equilibrium condition we use the generalized Tolman-Oppenheimer-Volkoff (TOV) equation described by,

$$\begin{aligned} -\frac{M_{g}(\rho+p_{r}) }{r^{2}}~e^{(\lambda-\nu)/2}- \frac{dp_{r} }{dr}+\frac{2(p_{t}-p_{r}) }{r}=0 \end{aligned}$$

(45)

where, $M_{g}(r)$ is the gravitational mass given by,

$$\begin{aligned} M_{g}(r) =& \frac{1}{2}~r^{2} \nu' e^{(\nu-\lambda)/2} \end{aligned}$$

(46)

The above equation (45) can be written in terms of balanced force equation due to anisotropy ($F_{a}$), gravity ($F_{g}$) and hydrostatic ($F_{h}$) i.e.

$$ F_{g}+F_{h}+F_{a}=0 $$

(47)

Here

$$\begin{aligned} F_{g} = & -\frac{M_{g}(\rho+p_{r}) }{r^{2}}e^{(\lambda-\nu)/2} \end{aligned}$$

(48)

$$\begin{aligned} F_{h} =& -\frac{dp_{r} }{dr} \end{aligned}$$

(49)

$$\begin{aligned} F_{a} =& \frac{2(p_{t}-p_{r}) }{r} \end{aligned}$$

(50)

The nature of three forces is represented by Fig. 15 which verifies that $F_{g}$ is counterbalanced by the combine effects of $F_{h}$ and $F_{a}$ to keep the system in equilibrium.

7 Results and conclusions

It has been observed that the physical parameters ($e^{-\lambda}$, $\rho~p_{r}$, $p_{t}$, $p_{r}/\rho$, $p_{t}/\rho$, $z$, $(p_{r}+2p_{t})/\rho$, $v _{r}^{2}$, $v_{t}^{2}$) are positive at the center and within the limit of realistic equation of state and monotonically decreasing outward (Figs. 1–4, 7, 9 and 10). However, $e^{\nu}$, anisotropy, mass, compactness parameter and $\varGamma_{r}$ are increasing outward which is necessary for a physically viable configuration (Figs. 1, 5, 11, 13, 14).

Furthermore, our presented solution satisfies all the energy condition which is needed by a physically possible configuration. The Strong Energy Condition (SEC), Weak Energy Condition (WEC), Null Energy Condition (NEC) and Dominant Energy Condition (DEC) is shown in Fig. 8. The stability factor $v_{t}^{2}-v_{r}^{2}$ must lies in between −1 and 0 for stable and 0 to 1 for unstable configuration. Therefore the presented solution satisfies stability condition (Fig. 12).

The decreasing nature of pressures and density is further justified by their negativity of their gradients, Fig. 6. The solution represents a static and stale configuration as the force acting on the fluid sphere is counter-balancing each other. For an anisotropic stellar fluid in equilibrium the gravitational force, the hydro-static pressure and the anisotropic force are acting through TOV-equation and they are counter-balancing to each other, Fig. 15. All the graph was plotted for PSR J0348+0432 by assuming $2.01M_{\odot}$, $13~\mbox{km}$ and $b = 0.000003$, the rest of the constant parameters are determined from boundary conditions and found to be $A=0.507144$, $B=0.0213879$ and $a=0.00214188$.

Fig. 6

Variation of pressure and density gradients against $r$ by taking the same values of the constant mentioned in Table 1 for PSR J0348+0432

Fig. 7

Variation of sound speed square against $r$ by taking the same values of the constant mentioned in Table 1 for PSR J0348+0432

Fig. 8

Variation of energy conditions against $r$ by taking the same values of the constant mentioned in Table 1 for PSR J0348+0432

Fig. 9

Variation of $(p_{r}+2p_{t})/\rho$ against $r$ by taking the same values of the constant mentioned in Table 1 for PSR J0348+0432

Fig. 10

Variation of red-shift against $r$ by taking the same values of the constant mentioned in Table 1 for PSR J0348+0432

Fig. 11

Variation of adiabatic index against $r$ by taking the same values of the constant mentioned in Table 1 for PSR J0348+0432

Fig. 12

Variation of stability factor against $r$ by taking the same values of the constant mentioned in Table 1 for PSR J0348+0432

Fig. 13

Variation of compactness parameter against $r$ by taking the same values of the constant mentioned in Table 1 for PSR J0348+0432

Fig. 14

Variation of mass function is plotted against $r$ by taking the same values of the constant mentioned in Fig. 1

Fig. 15

Counter-balancing of gravitational, hydrostatic and anisotropic forces acting on PSR J0348+0432 via TOV-equation for the values of the constant mentioned in Fig. 1

Using this solution, we have presented some models of well-known compact stars and compare there observed masses and radii with our calculated values in Table 1. The masses and radii provided in Table 1 matches with the observational values within acceptable statistical error (Antoniadis et al. 2013; Abubekerov et al. 2004; Ash et al. 1999). Indeed our presented models are in good agreement with the experimentally observed values. Hence the presented solution might have astrophysical significance in the future. As a special case of this solution for $a = 2\sqrt{b}$, it reduces to Singh et al. (2016c).