Charged anisotropic Buchdahl solution as an embedding class I spacetime

Abstract

We present a new solution of embedding class I describing the interior of a spherically symmetric charged anisotropic stellar configuration. The exact analytic solution has been explored by considering Buchdahl type metric potential $g_{rr}$. Using this analytic solution, we have discussed various physical aspects of a compact star. The solution is free from central singularities. The solution also satisfies WEC, SEC, NEC and DEC. The compactness parameter $2M/r_{b}$ as obtained from the solution satisfies the Buchdahl-Andreasson condition. Finally we have compared the calculated masses and radii of well-known compact star candidates like RX J1856.5-3754, XTE J1739-285, PSR B0943+10 and SAX J1808.4-3658 with their observational values.

1 Introduction

After the discovery of radio pulsars and X-ray sources, the importance of studying compact stars like neutron stars (NS) and quark stars (QS) become essential. However, the internal composition and nature of interactions are completely uncertain for compact stars. If somehow the equation of state (EOS) is well known, one can easily investigate the Tolman-Oppenheimer-Volkoff (TOV) equation to determine the complete physical features of the star. Nevertheless their EoSs can be explored via simple exact solutions. To make the exact solutions physically feasible, one needs to impose some physical restrictions as discussed in Sect. 2.

Most excitingly, on introducing electric charge one may arises a new degree of freedom i.e. “anisotropy” ($p_{t}-p_{r}$). Today the study of anisotropic bounded configurations has received widespread attention (Gron 1986; Ponce de Leon 1987; Roy 1996). There have been numerous studies to generate anisotropy by introducing solid core composed of type-IIIA superfluid (Kippenhahn and Weigert 1990) or phase transitions from normal states of pions to superconducting states (Sokolov 1980; Sawyer 1972) or due to relativistic interactions at very high density (Ruderman 1972). Most of the discovered compact star candidates has a unique signature each for the presence of magnetic moment. Therefore Weber (1999) pointed out the presence of anisotropy in immense magnetic field. Even the transport coefficients may become anisotropy and may lead to pressure anisotropy (Yakovlev 1991, 1993).

Dev and Gleiser (2002) and Gleiser and Dev (2004) have shown that the presence of anisotropic pressures in charged matter enhances the stability of the configuration under radial adiabatic perturbations as compared to isotropic matter. Herrera and Santos (1997) also discuss anisotropic stellar configuration. There have been several recent investigations of bounded fluid configuration using exact solutions (Singh and Pant 2015a,b). Some solutions on embedding class I are also presented in Gupta and Kumar (2011), Maurya et al. (2015a,b,c,d).

Eddington (1924) had discussed about an idea that the four dimensional spcetime can be considered embedded in higher-dimensional flat space. Randall and Sundram (1999), Anchordoqui and Bergila (2000) had also discussed in more details. Any manifold $V_{n}$ can always be embedded in $m=n(n+1)/2$-dimensional Pseudo-Euclidean space $E_{m}$. The minimum extra dimension $p$ of the Pseudo-Euclidean space to embedded $V_{n}$ in $E_{m}$, is called the class of the manifold $V_{n}$ and must be less than or equal to the number $(m-n)$ i.e., $n(n-1)/2$. The embedding class $p$ of relativistic spacetime $V_{4}$ is found to be VI. In particular, the class of spherical symmetric spacetime is II and plane symmetric spacetime is III.

Even the famous cosmological solution known as Friedman-Robertson-Lemaitre (1933) is of class I. Indeed, the first exact solution, the Schwarzschild’s exterior is of class II and Schwarzschild’s interior solution of constant interior density is of class I. Moreover, the famous and most realistic exterior solution that described a spinning black hole, the Kerr metric is of class V (Kuzeev 1980).

As we know that the general theory of relativity deals only with four dimensional spacetime, however embedding class solution may provide new characteristics to gravitational field, as well to physics.

Rayski (1976) linked the internal symmetries of elementary particle physics with the group of motions on embedded flat spacetime. Pavšič and Tapia (2001) have discussed the applications of embedding to general relativity, extrinsic gravity, strings and new brane world.

Many authors have discussed embedding class I solution and used it in modeling compact stars, Gupta and Kumar (2011), Maurya et al. (2015a, 2015b, 2015c, 2015d).

2 Conditions for well behaved solutions

For well-behaved nature of the solution for an anisotropic fluid sphere the following conditions should be satisfied:

• 1. The solution should be free from physical and geometric singularities, i.e. it should yield finite and positive values of the central pressure, central density and nonzero positive value of $e^{\nu }|_{r=0}$ and $e^{\lambda }|_{r=0}=1$.

• 2. The causality condition should be obeyed i.e. velocity of sound should be less than that of light throughout the interior. In addition to the above the velocity of sound should be decreasing towards the surface i.e. ${d \over dr} {dp_{r} \over d\rho }<0$ or ${d^{2} p_{r}\over d\rho ^{2}}>0$ and ${d\over dr} {dp_{t} \over d\rho }<0$ or ${d^{2}p_{t} \over d\rho ^{2}}>0$ for $0\leq r\leq r_{b}$ i.e. the velocity of sound is increasing with the increase of density and it should be decreasing outwards.

• 3. The adiabatic index, $\gamma = {\rho +p_{r} \over p_{r}} {dp_{r} \over d\rho }$ for realistic matter should be $\gamma > 4/3$.

• 4. The red-shift $z$ should be positive, finite and monotonically decreasing in nature with the increase of the radial coordinate.

• 5. The anisotropy factor $\Delta$ should be zero at the center.

• 6. For a stable anisotropic compact star, $0 < |v_{t}^{2}-v_{r}^{2}| \leq 1$ must be satisfied, Herrera and Santos (1997).

3 The Einstein-Maxwell field equations

The interior of the super-dense star is assumed to be described by the line element

$$ ds^{2} = e^{\nu (r)}dt^{2} - e^{\lambda (r)}dr^{2} - r^{2}\bigl(d\theta ^{2} + \sin^{2}{\theta }d \phi^{2}\bigr) $$

(1)

For our model the energy-momentum tensor for the stellar fluid is

$$ T_{ab} = \operatorname{diag} \bigl( \rho +E^{2}, -p_{r}+E^{2}, -p_{t}-E^{2}, -p _{t}-E^{2} \bigr) $$

(2)

where $\rho$, $p_{r}$, $p_{t}$ and $E^{2}=q^{2}/r^{4}$ are the energy density, radial pressure, tangential pressure and electric field respectively.

The Einstein field equations for the line element (1) are

$$\begin{aligned} &8\pi \rho =\frac{ ( 1 - e^{-\lambda } ) }{r^{2}} + \frac{ \lambda'\,e^{-\lambda }}{r}-E^{2} \end{aligned}$$

(3)

$$\begin{aligned} &8\pi p_{r} = \frac{\nu '\, e^{-\lambda }}{r} - \frac{ ( 1 - e^{- \lambda } ) }{r^{2}}+E^{2} \end{aligned}$$

(4)

$$\begin{aligned} &8\pi p_{t} = \frac{e^{-\lambda }}{4} \biggl( 2\nu '' + {\nu '}^{2} - \nu '\lambda ' + \frac{2\nu '}{r}-\frac{2\lambda '}{r} \biggr) -E^{2} \end{aligned}$$

(5)

$$\begin{aligned} &\sigma (r) = {e^{-\lambda /2} \over 4\pi r^{2}} \bigl(r^{2}E \bigr)' \end{aligned}$$

(6)

where primes represent differentiation with respect to the radial coordinate $r$ and $\sigma (r)$ is the proper charge density. In generating the above field equations we have utilized geometrized units where the coupling constant and the speed of light are taken to be unity. Using (4) and (5) we get

$$\begin{aligned} \Delta =& 8\pi (p_{t}-p_{r}) \\ =& e^{-\lambda } \biggl[ {\nu '' \over 2}-{\lambda ' \nu ' \over 4}+ {\nu ^{\prime\,2} \over 4}-{\nu '+\lambda ' \over 2r}+ {e^{\lambda }-1 \over r^{2}} \biggr] -2E^{2} \end{aligned}$$

(7)

If the metric given in (1) satisfies the Karmarkar (1948) condition, it can represent an embedding class I spacetime i.e.

$$ R_{1414}={R_{1212}R_{3434}+R_{1224}R_{1334} \over R_{2323}} $$

(8)

with $R_{2323}\neq 0$ (Pandey and Sharma 1981). This condition leads to a differential equation given by

$$ {2\nu '' \over \nu '}+\nu '= {\lambda '\, e^{\lambda }\over e^{\lambda }-1} $$

(9)

On integration we get the relationship between $\nu$ and $\lambda$ as

$$ e^{\nu }= \biggl( A+B \int \sqrt{e^{\lambda }-1} dr \biggr) ^{2} $$

(10)

where $A$ and $B$ are constants of integration.

By using (10) we can rewrite (7) as

$$\begin{aligned} \Delta = {\nu ' \over 4e^{\lambda }} \biggl[ {2\over r}- {\lambda ' \over e^{\lambda }-1} \biggr] \biggl[ {\nu ' e^{\nu }\over 2rB^{2}}-1 \biggr] -2E ^{2} \end{aligned}$$

(11)

Here $\Delta =8\pi (p_{t}-p_{r})$ is the measure of anisotropy.

4 A new class of well-behaved embedding class-I solution

To solve the above equation (10), we have assumed $g_{rr}$ metric potential of Buchdahl (1959) given by

$$ e^{\lambda }={2(1+ar^{2}) \over 2-ar^{2}} $$

(12)

where $a$ is constant having a dimension of length⁻².

Using the metric potential (12) in (10), we get

$$\begin{aligned} e^{\nu }= \biggl[ A-{\sqrt{3}B \over \sqrt{a}\sqrt{2-ar^{2}}} \biggr] ^{2} \end{aligned}$$

(13)

Using (12) and (13), we can rewrite the expression of density, $p_{r}$, $\Delta$, $p_{t}$ and $\sigma (r)$ as

$$\begin{aligned} &8\pi \rho = \frac{a^{2} (3 r^{2}-2 k r^{6} )+a (9-4 k r ^{4})-2 k r^{2}}{2(a r^{2}+1)^{2}} \end{aligned}$$

(14)

$$\begin{aligned} & \begin{aligned}[b] 8\pi p_{r} & = { \Bigl[a r (\sqrt{3} B r \sqrt{\frac{a r^{2}}{2-a r^{2}}}+A )-2 \sqrt{3} B \sqrt{\frac{a r^{2}}{2-a r^{2}}}\,\Bigr]^{-1} \over 2 (a r^{2}+1 ) \sqrt{\frac{a r^{2}}{2-a r^{2}}} } \\ &\quad {} \times ar \biggl[a \biggl\{ A \sqrt{\frac{a r^{2}}{2-a r^{2}}} \bigl(2 k r ^{4}-3 \bigr)+\sqrt{3} B r\bigl(5-2 k r^{4}\bigr) \biggr\} \\ & \quad {} +2 k r^{2} \biggl(A \sqrt{\frac{a r^{2}}{2-a r^{2}}}-\sqrt{3} B r \biggr) \biggr] \end{aligned} \end{aligned}$$

(15)

$$\begin{aligned} \Delta &= {r^{2} (a r^{2}+1)^{-2} \over 4 \sqrt{3} B \sqrt{\frac{a r^{2}}{2-a r^{2}}}-2a r \Bigl\{ \sqrt{3} B r \sqrt{\frac{a r^{2}}{2-a r^{2}}}+A \Bigr\} } \\ &\quad {}\times \biggl[a^{3} r \biggl\{ 4 \sqrt{3} B r\bigl(k r^{4}-1\bigr) \sqrt{\frac{a r ^{2}}{2-a r^{2}}} + A\bigl(4 k r^{4}-3\bigr) \biggr\} \\ &\quad {} +4 a k r \biggl\{ A-3 \sqrt{3} B r \sqrt{\frac{a r^{2}}{2-a r^{2}}} \biggr\} \\ &\quad {} +8 a^{2} \biggl\{ \sqrt{3} B \sqrt{\frac{a r^{2}}{2-a r^{2}}}+A k r^{3} \biggr\} \\ & \quad {} -8 \sqrt{3} B k \sqrt{\frac{a r^{2}}{2-a r^{2}}} \biggr] \end{aligned}$$

(16)

$$\begin{aligned} &8\pi p_{t} = 8\pi p_{r}+\Delta \end{aligned}$$

(17)

$$\begin{aligned} &\sigma = {3\sqrt{k} \over 4\pi }\sqrt{ {2-ar^{2} \over 2(1+ar^{2})}} \end{aligned}$$

(18)

where we have assumed the charge distribution $q(r) {=} \sqrt{k}r^{3}$, where $k>0$, is the charge parameter.

Now the pressure and density gradients can be written as

$$\begin{aligned} & \begin{aligned}[b] 8\pi {d\rho \over dr} & = - \bigl(1+ar^{2}\bigr)^{-3} \bigl[r \bigl\{ a^{3} r^{2}\bigl(2 k r^{4}+3\bigr) \\ & \quad {} +3 a^{2} \bigl(2 k r^{4}+5\bigr)+6 a k r^{2}+2 k \bigr\} \bigr] \end{aligned} \end{aligned}$$

(19)

$$\begin{aligned} & \begin{aligned}[b] 8\pi {dp_{r} \over dr} & = -\frac{a r^{3}}{f_{5}(r)(a r^{2}-2) (a r ^{2}+1)^{2} \sqrt{\frac{a r^{2}}{2-a r^{2}}}} \\ &\quad {}\times \biggl[a^{4} f_{4}(r) r^{2}-a^{3} f_{2}(r)-6 a^{2} f_{3}(r) \\ & \quad {} +24 B^{2} k \sqrt{\frac{a r^{2}}{2-a r^{2}}}+4 a f_{1}(r) k \biggr] \end{aligned} \end{aligned}$$

(20)

$$\begin{aligned} & \begin{aligned}[b] 8\pi {dp_{t} \over dr} &= {ar^{3} \over 2 f_{5}(r) (ar^{2}-2)(a r^{2}+1)^{3}\sqrt{\frac{a r^{2}}{2-a r^{2}}}} \\ &\quad {}\times \biggl[a^{5} f_{9}(r) r^{5}-a^{4} f_{8}(r) r^{2}-2 a^{3} f_{10}(r) \\ &\quad {} +4 a^{2} f_{7}(r)+48 B^{2} k \sqrt{ \frac{a r^{2}}{2-a r^{2}}} \\ &\quad {} +8 a f_{6}(r) k \biggr] \end{aligned} \end{aligned}$$

(21)

where

$$\begin{aligned} & \begin{aligned}[b] f_{1}(r) & = 2AkrA^{2} \sqrt{\frac{a r^{2}}{2-a r^{2}}}+6 B^{2} r ^{2} \sqrt{ \frac{a r^{2}}{2-a r^{2}}} \\ &\quad {} -2 \sqrt{3} A B r \end{aligned} \end{aligned}$$

(22)

$$\begin{aligned} & \begin{aligned}[b] f_{2}(r) & = -6 A^{2} \sqrt{ \frac{a r^{2}}{2-a r^{2}}}+12 B^{2} r ^{2} \sqrt{\frac{a r^{2}}{2-a r^{2}}} \bigl(k r^{4}+5\bigr) \\ & \quad {} +17 \sqrt{3} A B r \end{aligned} \end{aligned}$$

(23)

$$\begin{aligned} & \begin{aligned}[b] f_{3}(r) & = -A^{2} k r^{2} \sqrt{\frac{a r^{2}}{2-a r^{2}}}+B ^{2} \sqrt{ \frac{a r^{2}}{2-a r^{2}}} \bigl(3 k r^{4}-10\bigr) \\ & \quad {} +2 \sqrt{3} A B k r^{3} \end{aligned} \end{aligned}$$

(24)

$$\begin{aligned} & \begin{aligned}[b] f_{4}(r) & = \sqrt{\frac{a r^{2}}{2-a r^{2}}} \bigl[3 B^{2} r^{2} \bigl(2 k r^{4}+5 \bigr)-A^{2}\bigl(2 k r^{4}+3\bigr) \bigr] \\ & \quad {} +\sqrt{3} A B r \bigl( 4 k r^{4}+7 \bigr) \end{aligned} \end{aligned}$$

(25)

$$\begin{aligned} & \begin{aligned}[b] f_{5}(r) & = \biggl[a r \biggl\{ \sqrt{3} B r \sqrt{\frac{a r^{2}}{2-a r^{2}}}+A \biggr\} \\ & \quad {} -2 \sqrt{3} B \sqrt{\frac{a r^{2}}{2-a r^{2}}} \biggr]^{2} \end{aligned} \end{aligned}$$

(26)

$$\begin{aligned} & \begin{aligned}[b] f_{6}(r) & = A^{2} \sqrt{ \frac{a r^{2}}{2-a r^{2}}}+12 B^{2} r ^{2} \sqrt{\frac{a r^{2}}{2-a r^{2}}} \\ &\quad {} -2 \sqrt{3} A B r \end{aligned} \end{aligned}$$

(27)

$$\begin{aligned} & \begin{aligned}[b] f_{7}(r) & = 5 A^{2} k r^{2} \sqrt{\frac{a r^{2}}{2-a r^{2}}}+3 B ^{2} \sqrt{ \frac{a r^{2}}{2-a r^{2}}} \bigl(k r^{4}-18\bigr) \\ & \quad {} -10 \sqrt{3} A B k r^{3} \end{aligned} \end{aligned}$$

(28)

$$\begin{aligned} & \begin{aligned}[b] f_{8}(r) & = \bigl[4 A^{2} \bigl(k r^{4}-3\bigr)+6 B^{2} r^{2}\bigl(2 k r^{4}+5\bigr) \bigr] \\ &\quad {}\times \sqrt{\frac{a r^{2}}{2-a r^{2}}}+\sqrt{3} A B r\bigl(23-8 k r^{4}\bigr) \end{aligned} \end{aligned}$$

(29)

$$\begin{aligned} & \begin{aligned}[b] f_{9}(r) & = 6 B^{2} r \bigl(2 k r^{4}-1\bigr) \sqrt{\frac{a r^{2}}{2-a r ^{2}}} \\ & \quad {} +\sqrt{3} A B \bigl(8 k r^{4}-1\bigr) \\ &\quad {} -4 A^{2} k r^{3} \sqrt{\frac{a r^{2}}{2-a r^{2}}} \end{aligned} \end{aligned}$$

(30)

$$\begin{aligned} & \begin{aligned}[b] f_{10}(r) & = \bigl[6 B^{2} r^{2} \bigl(5 k r^{4}-16\bigr)-6 A^{2} \bigl(k r^{4}-2\bigr) \bigr] \\ & \quad {} \times \sqrt{\frac{a r^{2}}{2-a r^{2}}}+\sqrt{3} A B r\bigl(12 k r^{4}-31\bigr) \end{aligned} \end{aligned}$$

(31)

5 Properties of the new solution

The central pressure and density at the interior is given by

$$\begin{aligned} &8\pi p_{r}(r=0) = 8\pi p_{t}(r=0) = \frac{10 \sqrt{3} a B-3 \sqrt{2} a^{3/2} A}{2 \sqrt{2a} A-4 \sqrt{3} B}>0 \end{aligned}$$

(32)

$$\begin{aligned} &\rho (r=0) = {9a \over 2}>0, \quad \forall a>0 \end{aligned}$$

(33)

To satisfy Zeldovich’s condition at the interior, $p_{r}/\rho$ at center must be $\le 1$. Therefore

$$\begin{aligned} \frac{10 \sqrt{3} a B-3 \sqrt{2} a^{3/2} A}{ 9a(\sqrt{2a} A-2 \sqrt{3} B)} \le 1 \end{aligned}$$

(34)

On using (32) and (34) we get a constraint on $B/A$ given as

$$ {\sqrt{6a}\over 10}< {B \over A} \le {\sqrt{6a} \over 7} $$

(35)

Now the velocity of sound inside the stellar interior can be determined by using

$$ v_{r}^{2}={dp_{r}/dr \over d\rho /dr}, \qquad v_{t} ^{2}={dp_{t}/dr \over d\rho /dr} $$

(36)

The relativistic adiabatic index is given by

$$ \varGamma = {\rho +p_{r} \over p_{r}} {dp_{r} \over d\rho } $$

(37)

For a static configuration at equilibrium $\varGamma$ has to be more than $4/3$.

The modified Tolman-Oppenheimer-Volkoff (TOV) equation for anisotropic fluid distribution was given by Ponce de Leon (1987) as

$$\begin{aligned} -{M_{g}(\rho +p_{r}) \over r^{2}}\, e^{(\lambda -\nu )/2}- {dp_{r} \over dr}+ {2\Delta \over r}+{\sigma q \over r^{2}}\, e^{\lambda /2}=0 \end{aligned}$$

(38)

provided

$$\begin{aligned} M_{g}(r) =& {1\over 2} r^{2} \nu'\, e^{(\nu -\lambda )/2} \end{aligned}$$

(39)

The above equation (38) can be written in terms of balanced force equation due to anisotropy ($F_{a}$), gravity ($F_{g}$), hydrostatic ($F_{h}$) and electrostatic force $F_{e}$ i.e.

$$ F_{g}+F_{h}+F_{a}+F_{e}=0 $$

(40)

Here

$$\begin{aligned} &F_{g} = -{M_{g}(\rho +p_{r}) \over r^{2}}\,e^{(\lambda -\nu )/2} \end{aligned}$$

(41)

$$\begin{aligned} &F_{h} = -{dp_{r} \over dr} \end{aligned}$$

(42)

$$\begin{aligned} &F_{a} = {2\Delta \over r} \end{aligned}$$

(43)

$$\begin{aligned} &F_{e} = {\sigma q \over r^{2}}\,e^{\lambda /2} \end{aligned}$$

(44)

The TOV equation (40) can be represented by the figure showing that the forces are counter balanced to each other (Fig. 12).

6 Matching of interior and exterior spacetime

Assuming the exterior spacetime to be the ReissnerNordstrom solution which has to match smoothly with our interior solution and is given by

$$\begin{aligned} ds^{2} =& \biggl( 1-{2M\over r}+{Q^{2}\over r^{2}} \biggr) dt^{2}- \biggl( 1- {2M\over r}+ {Q^{2}\over r^{2}} \biggr) ^{-1}dr^{2} \\ & {}-r^{2}\biggl(d\theta^{2}+\sin^{2} \theta d \phi^{2}\biggr) \end{aligned}$$

(45)

By matching the first and second fundamental forms the interior solution (1) and exterior solution (45) at the boundary $r=r_{b}$ (Darmois-Isreali condition) we get

$$\begin{aligned} & \begin{aligned}[b] e^{\nu_{b}} &= \biggl( 1- {2M \over r_{b}}+{Q^{2}\over r_{b}^{2}} \biggr) \\ & = \biggl[A-\frac{\sqrt{3} B}{\sqrt{a} \sqrt{2-a r_{b}^{2}}} \biggr]^{2} \end{aligned} \end{aligned}$$

(46)

$$\begin{aligned} &e^{-\lambda_{b}} = \biggl( 1-{2M \over r_{b}}+{Q^{2}\over r_{b}^{2}} \biggr) = {2-ar_{b}^{2} \over 2(1+ar_{b}^{2})} \end{aligned}$$

(47)

$$\begin{aligned} &p_{r}(r_{b}) = 0 \end{aligned}$$

(48)

where we set $q(r=r_{b})=Q$.

Using the boundary condition (46)–(48), we get

$$\begin{aligned} &{B \over A} = { \bigl(3a-2akr_{b}^{4}-2kr_{b}^{2} \bigr)\sqrt{{a \over 2-ar_{b}^{2}}} \over 5\sqrt{3}a-2\sqrt{3}~kr_{b}^{2}-2\sqrt{3} akr_{b}^{4}} \end{aligned}$$

(49)

$$\begin{aligned} &A = \sqrt{{2-ar_{b}^{2} \over 2(1+ar_{b}^{2})}}+\frac{ \sqrt{3} B}{\sqrt{a} \sqrt{2-a r_{b}^{2}}} \end{aligned}$$

(50)

$$\begin{aligned} &{2M \over r_{b}} = 1-{2-ar_{b}^{2} \over 2(1+ar_{b}^{2})}+kr_{b} ^{4} \end{aligned}$$

(51)

Now the gravitational red-shift at the surface and within the interior of the stellar system are given by

$$\begin{aligned} &z_{s} = e^{-\nu_{b}/2}-1=\sqrt{ {2(1+ar_{b}^{2}) \over 2-ar_{b}^{2}}}-1 \end{aligned}$$

(52)

$$\begin{aligned} &z = \biggl[A-\frac{\sqrt{3} B}{\sqrt{a} \sqrt{2-a r^{2}}} \biggr]^{-1}-1 \end{aligned}$$

(53)

The mass function of the solution can be determined using the equation given below:

$$\begin{aligned} m(r) = & {1 \over 2} \int_{0}^{r} \bigl(8\pi \rho r^{2}+E^{2} r^{2} \bigr)dr+{q^{2} \over 2r} \\ = & \frac{k r^{5}}{2}+\frac{3 a r^{3}}{4(a r^{2}+1)} \end{aligned}$$

(54)

7 Results and conclusion

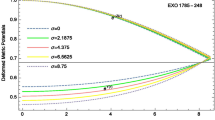
It has been observed that the physical parameters ($p_{r}$, $p_{ \perp }$, $\rho$, $p_{r}/\rho$, $p_{\perp }/\rho$, $v_{r}^{2}$, $v_{\perp } ^{2}$, $z$, $\sigma$) are positive at the center and within the limit of realistic equation of state and monotonically decreasing outward (Fig. 2, 3, 4, 8, 9, 11). However the metric potentials, $\varGamma$, $E^{2}$ and mass function are increasing outward which is necessary for a physically viable configuration (Fig. 1, 6, 13, 15). The anisotropy possesses negative value (i.e. $p_{r}>p_{t}$) for $0 \le r \le 4.26\mbox{ km}$ and increases from this point and beyond signifying that $p_{t}>p_{r}$ (Fig. 5). The decreasing nature of pressures and density are further verified by their negative values of pressure and density gradients as shown in Fig. 7.

Fig. 1

Variation of metric potential with radius

Fig. 2

Variation of density with radius

Fig. 3

Variation of pressure with radius

Fig. 4

Variation of pressure to density ratio with radius

Fig. 5

Variation of anisotropy with radius

Fig. 6

Variation of adiabatic index with radius

Fig. 7

Variation of pressure and density gradients with radius

Fig. 8

Variation of red-shift with radius

Fig. 9

Variation of proper charge density with radius

Furthermore, our solution satisfies all the energy conditions as required by a physically possible configuration. The Strong Energy Condition (SEC), Weak Energy Condition (WEC), Null Energy Condition (NEC) and Dominant Energy Condition (DEC) are shown in Fig. 14. The stability factor $|v_{\perp }^{2}-v_{r}^{2}|$ must be in between 0 and 1, which is also satisfied by our presented solution (Fig. 10). The counter-balancing of different forces acting on the fluid system is represented by TOV equation and is also graphically shown in Fig. 12. This signifies that our solution represents a stable hydro-static equilibrium.

Fig. 10

Variation of stability factor $\vert v^{2}_{\perp }-v^{2} _{r}\vert$ with radius

Fig. 11

Variation of velocity of sound with radius

Fig. 12

Variation of different forces acting on TOV-equation to maintain the hydrostatic equilibrium

Fig. 13

Variation of $E^{2}$ with radius

Fig. 14

Variation of energy conditions with radius

Fig. 15

Variation of mass function with radius

From the above analysis it is confirmed that the model is physically viable and free from singularity. Therefore, we use the solution to model some of the well known compact star candidates by optimizing their masses and radii which match with the observed values.

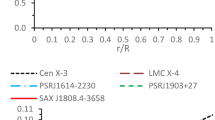
Plugging in $G$ and $c$ in the relevant equations, we have found masses and radii of some compact stars. Numerical values for all cases are shown in Table 1 for different stars. The mass and radius of SAX J1808.4-3658 matches quite well as suggested by Bhattacharyya (2001) where it was measured to be $2.27~M_{\odot }$ and 9.73 km. According to Kohri (2003) the mass and radius of RX J1856.5-3754 is expected around $0.9~M_{\odot }$ and 1.9–4.1 km. XTE J1739-217 and PSR B0943+10 are quark star candidates according to Antoniadis et al. (2013), Zhang et al. (2007). Their observed masses and radii are $1.51~M_{ \odot }$, 10.9 km and $0.02~M_{\odot }$, 2.6 km respectively. For all the presented compact star models, the compactness parameter $2M/r_{b}$ is within the Buchdahl bound Fig. 16. As we know that the Buchdahl-Andreasson limit is given by Andreasson (2008)

$$\begin{aligned} \sqrt{M} \le {\sqrt{R} \over 3}+\sqrt{{R \over 9}+ {Q^{2} \over 3R}} \end{aligned}$$

(55)

The above equation can be rearrange as given below

$$\begin{aligned} {2M\over R} \le {4\over 9} +{4\over 9} \biggl[ 1+{3Q^{2} \over R^{2}} \biggr] ^{1/2}+{2Q^{2}\over R^{2}} \end{aligned}$$

(56)

Fig. 16

Variation of compactness parameter and Buchdahl Limit with radius

Table 1 Masses and radii of few well-known compact star candidates

It is obvious that the right hand side of the above equation (56) is always greater than $8/9$. Therefore, any solution satisfies Buchdahl condition will also satisfy Buchdahl-Andreasson condition.