Singularity free charged anisotropic solutions of Einstein–Maxwell field equations in general relativity

Abstract

In this paper, we present generalization of anisotropic analogue of charged Heintzmann’s solution of the general relativistic field equations in curvature coordinates. These exact solutions are stable and well behaved in all respect for a wide range of anisotropy parameter and charge parameter. We have found that these new solutions are suitable for the modeling of super dense stars like neutron stars and quark stars because they yield a wide range of masses and radii with simple mathematical expressions. By tuning different values of the few parameters, we can model various neutron stars and quark stars which are compatible with the experimentally observed values of masses and radii. Therefore, we have synchronized our solution with the observed values of some of the compact stars XTE J1739 − 217, EXO 0748 − 676, PSR J1614 − 2230, PSR J0348 + 0432 and PSR B0943 + 10.

1 Introduction

Almost 8 decades ago, Oppenheimer and Volkoff [1] obtained the maximum mass of neutron star (NS) using general relativistic equation of hydrostatic equilibrium called TOV equation. In this model they assumed the equation of state (EOS) for free Fermi gas of neutrons at T = 0 and yield a maximum mass 0.71 $M_{\odot}$. Since then researchers are trying to explore alternative EOS which may increase the maximum mass limit of neutron star. Due to the lack of comprehensive knowledge of the internal structure of neutron star, it is still a big puzzle to find the exact EOS of such compact objects. In spite of such incomprehensive knowledge, researchers are interested to find analytic exact solutions of Einstein’s field equation by assuming certain geometry of space–time that satisfies all physical constraints. Such analytic solutions enable us to find simple algebraic expressions of the EOS and the distribution of matter in the interior of stellar objects.

Due to the highly nonlinear nature of Einstein’s field equations it is difficult to obtain new exact solutions. A good collection of static, spherically symmetric perfect fluid solutions are obtained by some authors [2, 3]. In this paper we have presented a new class of anisotropic solutions of Einstein–Maxwell’s field equations. Since the EOS of neutron star (NS) which is bound by gravity and strange quark star (SQS) bound by the strong quark–quark interaction are highly uncertain, there is a need to reconsider their EOSs. For higher densities, the presence of anisotropic nature of the fluid is highly possible because of certain reasons which we have discussed in next few sections.

Because of very intense surface magnetic field of a newly born NS or SQS, the matter inside the stars may generate pressure anisotropy [4]. Further, the pressure anisotropy may cause if the stellar core is solid or presence of type-IIIA superfluid [5]. Moreover, the possible formation of superfluid neutrons at critical temperature $T_{c} \sim 10^{10} \,{\text{K}}$ with energy gap $E_{g} \sim 1\,{\text{MeV}}$, as a consequence of BCS theory of neutrons [6]. Nowadays superfluidity explains the sudden change in the time period of pulsars called “glitches”. Inclusion of neutron superfluid is also significant to discuss because it affects the neutrinos emission rate through modified Urca process to investigate its thermal evolution [7]. The EOS containing ground state of $npe\mu$ matter associating nucleon–nucleon (NN) and NNN interaction provide a stiff EOS with $M_{max} \simeq 1.9$–2.1 $M_{\odot}$.

For higher densities (above the typical nuclear density, $\rho_{0}$), the electrons are replaced by pions ($\pi^{ - }$) and exist as free pions at $\rho { \gtrsim }1.5\rho_{0}$. This happens when the chemical potential of electron exceeds the rest mass of pion [8]. Pions undergo “Bose–Einstein Condensation” forming superconducting pions due to pion–nucleon strong attraction in the p-wave [9–12]. Due to the presence of superconducting pions at the interior of NS, the EOS get stiffer which can support more maximum mass up to 3 $M_{\odot}$ with a radius 14 km [13].

Above all these, if the density increase beyond $3\rho_{0} ,$ kaons ($K^{ - }$) begin to contribute the EOS and start condensation due to strong attraction of s-wave kaon–nucleon forming superconducting kaons causing anisotropy [14]. Further, the meson condensation can also lead to anisotropy in pressure [11]. The inclusion of kaon condensation gives soft EOS supporting a maximum mass of ${\text{NS}} \, \lesssim \, 2\,{M_{\odot}}$ [15]. The existence of $\varLambda , \varXi , \varSigma^{ - }$ hyperons and ∆ resonances are possible at the core of NS where the density goes beyond $1.2 \times 10^{15} \,{\text{g}}\,{\text{cm}}^{ - 3}$ [16]. A model NS that contain hyperons at the core, lead to a very soft EOS with $M_{max} \simeq 1.4\,{M_{\odot}}$ [17]. The latest result for NS with hyperons inside the core can support $M_{max} \, \lesssim \, 1.8$–1.9 $M_{\odot}$.

Due to the consequence of heavy ion collisions of classical pion field, there is possible to form coherent pions production [18]. A large fluctuation in the ratio of number of charge-to-neutral pions is the cause during the collisions. Further investigations suggested that such a large fluctuation in pion ratio occurs due to “Disoriented Chiral Condensation (DCC)” [19, 20]. In order to observe DCC, a large number of coherent pions must be produced. This occurs through skyrmion and anti-skyrmion formation [21]. As suggested by Wong [22], skyrmions are not single baryon, but quantum mechanical superposition of baryons and resonance states. Recently, Dong et al. [23] have discussed the astrophysical significance of skyrmion matters in modeling compact stars. They have mentioned that half-skyrmions may appear in dense baryonic matter when skyrmions are put into on crystal which strongly affects the nuclear tensor forces and influence the EOS. The matter consists of half-skyrmions has a vanishing quark condensation but non-vanishing pion decay constant and can be interpreted as hadronic dual of strong-coupled quark matter. Dong et al. also suggested the change over from skyrmion to half-skyrmion matter alter the EOS from soft to stiff at a density above nuclear density, resulting compact stars as massive as ~2.4 $M_{\odot}$.

Recent observations have suggested some X-rays pulsars e.g. Her X − 1, RX J856.5 − 3754, XTE J1739 − 285, PSR B0943 + 10 etc. cannot be explained by a neutron star model, rather a quark star model [4, 24, 25]. The possible existence of stable quark stars has been studied earlier [26, 27]. The formation of strange quark matter (SQM) inside a neutron star may take place in a slow combustion [28–30] through weak interaction via strangeness changing process. A theoretical determination has been performed by Olesen et al. [31] showing the conversion time scale may ranges from 0.1 s to a few minutes depending on the NS temperature, baryon matter EOS and Strange Quark Matter (SQM) parameters. Slow combustion front is hydrodynamically unstable leading to a supersonic detonation front with conversion time scale of ~0.1 ms [32]. Consequently, the supersonic detonation would eject the outer layer of the neutron star leaving behind a strange quark star. The conversion process to the inner engines may emit long gamma ray bursts or probably a rapidly rotating strange quark star is left behind. At higher densities ~10¹⁵ g cm⁻³, nuclear matter may be anisotropic when its interactions are relativistic [33]. Recently Farook et al. [35] discussed stability problem of a fluid sphere.

Considering the presence of some charges is also important while modeling compact stars because the gravitational collapse can be counter balanced by the electric repulsion in addition to the pressure gradient. Some authors have [34, 35] proposed models for charged perfect fluid that inhibits the growth of space–time curvature to avoid singularities. Thus it is enviable to study the implications of Einstein–Maxwell field equations with reference to the general relativistic prediction of gravitational collapse. For these purposes anisotropic and charged fluid ball models are required. Including strong electric field due to the inclusion of electric charge also cause pressure anisotropy [36].

Dev and Gleiser [37] have revealed that pressure anisotropy affects the physical properties, stability and structure of stellar matter. The stability of stellar bodies is improved for positive measure of anisotropy when compared to configurations of isotropic stellar objects. The presence of anisotropic pressures in charged matter enhances the stability of the configuration under radial adiabatic perturbations as compared to isotropic matter, [38]. Herrera and Santos [39] have also anticipated an anisotropic model can be a stable model if and only if $- 1 < v_{ \bot }^{2} - v_{r}^{2} \, \lesssim \, 0$.

Many papers have been published by several authors who obtained the parametric classes of exact solutions for perfect fluid with charge and neutral fluids [40–42].

Note, more realistic models of super-dense stars should incorporate not only charge but anisotropy too and indeed some authors have done so by using curvature coordinates [43–45]. Recently anisotropic charge solution in isotropic coordinates has been discussed by [46, 47] with all degree of suitability. Regarding the stability of neutron stars and quark stars, various models have been discussed in [48, 49]. Discussion has been made by [50–52] of collapsing stars which include emission of radiation.

In our solutions, we choose seed solution of [53] and found the solutions by assuming appropriate functional form of charge parameter and anisotropic parameter in such a way that the obtained solution is well behaved in all respects. Further, for a particular value of parameter it reduces to [54]. The external field of such ball is to be matched with Reissner–Nordström solution.

2 Conditions for well behaved solutions

Well behaved nature of the solutions for anisotropic fluid sphere should satisfy the following conditions:

• 1. The solution should be free from physical and geometric singularities, i.e. it should yield finite and positive values of the central pressure, central density and nonzero positive value of $(e^{\nu } )_{r = 0}$ and $(e^{\lambda } )_{r = 0} = 1$.

• 2. Following [55, 56], the solution should have positive value of ratio of trace of energy stress tensor to energy density $(P_{r} + 2P_{ \bot } )/ \rho c^{2}$, and less than 1(weak energy condition) and less than 1/3 (strong energy condition) throughout within the star, monotonically decreasing.

• 3. The casualty condition should be obeyed i.e. velocity of sound should be less than that of light throughout the model. In addition to the above the velocity of sound should be decreasing towards the surface i.e.$\frac{d}{dr} \frac{{dp_{r} }}{d\rho } < 0\;{\text{or}}\;\frac{{d^{2} p_{r} }}{{d\rho^{2} }} > 0$ and $\frac{d}{dr} \frac{{dp_{ \bot } }}{d\rho } < 0\;or\;\frac{{d^{2} p_{ \bot } }}{{d\rho^{2} }} > 0$ for $0 \le r \le r_{b}$ i.e. the velocity of sound is increasing with the increase of density and it should be decreasing outward.

• 4. $\frac{dp}{d\rho } \ge \frac{p}{\rho }$ should be satisfied everywhere within the ball. The adiabatic index, $\gamma = \frac{{\rho + p_{r} }}{{p_{r} }} \frac{{dp_{r} }}{d\rho }$ for realistic matter should be $\gamma \ge 1$.

• 5. The red shift $z$ should be positive, finite and monotonically decreasing in nature with the increase of $r$.

• 6. Electric field intensity $E$, such that $E_{r = 0} = 0,$ is taken to be monotonically increasing.

• 7. The anisotropy factor ∆ should be zero at the center and increasing towards the surface.

• 8. For a stable anisotropic compact star, $- 1 \, \lesssim \, v_{ \bot }^{2} - v_{r}^{2} \, \lesssim \, 0$ must be satisfied [39].

3 Einstein–Maxwell field equations of anisotropic charge fluid distribution

The interior metric of a static spherically symmetric matter distribution in curvature coordinates is given by,

$$ ds^{2} = - e^{\lambda } dr^{2} - r^{2} \left( {d\theta^{2} + { \sin }^{2} \theta d\phi^{2} } \right) + c^{2} e^{\nu } dt^{2} $$

(1)

where $\lambda$ and $\nu$ are functions of r only.

Einstein–Maxwell field equations for a non empty space–time are

$$ \begin{aligned} {\mathcal{R}}_{\rho }^{\mu } - \frac{1}{2}{\mathcal{R}} \delta_{\rho }^{\mu } &= - \frac{8\pi G}{{c^{4} }}T_{\rho }^{\mu } \\ & = - \frac{8\pi G}{{c^{4} }} \left[ {\left( {p_{ \bot } + \rho c^{2} } \right) v^{\mu } v_{\rho } - p_{ \bot } \delta_{\rho }^{\mu } + \left( {p_{r} - p_{ \bot } } \right) \chi_{\rho } \chi^{\mu } } \right. \\ & \quad \quad \left. { + \frac{1}{4\pi } \left( { - F^{\mu \sigma } F_{\rho \sigma } + \quad \frac{1}{4}\delta_{\rho }^{\mu } F_{\sigma \alpha } F^{\sigma \alpha } } \right)} \right] \\ \end{aligned} $$

(2)

where ${\mathcal{R}}_{\rho }^{\mu }$ is Ricci tensor, $T_{\rho }^{\mu }$ is energy–momentum tensor, ${\mathcal{R} }$ the scalar curvature, $F_{\rho \sigma }$ is the electromagnetic field tensor, $p_{r}$ and $p_{ \bot }$ denote radial and transverse pressure respectively, $\rho$ the density distribution, $v^{\mu }$ the four velocity and $\chi^{\mu }$ is the unit space-like vector in radial direction.

For the metric Eq. (1) the Einstein–Maxwell’s field equations of gravitation (Eq. (2))for a non-empty space–time reduces to the following set of relevant equations:

$$ \frac{8\pi G}{{c^{4} }} p_{r} = \frac{{\nu^{{\prime }} }}{r} e^{ - \lambda } - \frac{{1 - e^{ - \lambda } }}{{r^{2} }} + \frac{{q^{2} }}{{r^{4} }} $$

(3)

$$ \frac{8\pi G}{{c^{4} }} p_{ \bot } = e^{ - \lambda } \left( {\frac{{\nu^{{\prime\prime }} }}{2} - \frac{{\lambda^{{{\prime } }} \nu^{{{\prime } }} }}{4} + \frac{{\nu{{^{\prime 2} }} }}{4} + \frac{{\nu^{{{\prime } }} - \lambda^{{{\prime } }} }}{2r}} \right) - \frac{{q^{2} }}{{r^{4} }} $$

(4)

$$ \frac{8\pi G}{{c^{2} }} \rho = \frac{{\lambda^{\prime}}}{r} e^{ - \lambda } + \frac{{1 - e^{ - \lambda } }}{{r^{2} }} - \frac{{q^{2} }}{{r^{4} }} $$

(5)

where prime (′) denotes the differentiation with respect to $r$ and $q$ the charge inside the radius.

By assuming the metric potential as that of [53]

$$ e^{\nu } = B(1 + c_{1} r^{2} )^{3} $$

(6)

Eqs. (3) and (4) are reduced to

$$ \frac{8\pi G}{{c^{4} }} \left( {p_{ \bot } - p_{r} } \right) = \varDelta = e^{ - \lambda } \left( {\frac{{\nu^{{\prime \prime }} }}{2} + \frac{{\nu^{{{\prime 2}}} }}{4} - \frac{{\nu^{{\prime }} }}{2r} - \frac{1}{{r^{2} }}} \right) - \lambda^{{\prime }} e^{ - \lambda } \left( {\frac{{\nu^{{\prime }} }}{4} + \frac{1}{2r}} \right) + \frac{1}{{r^{2} }} - \frac{{2q^{2} }}{{r^{4} }} $$

(7)

Assuming $Y = e^{ - \lambda } \;{\text{and}}\;x = c_{1} r^{2}$ by using Eq. (6), Eq. (7) is reduced to

$$ \frac{dY}{dx} + \frac{1 + x}{1 + 4x}\left[ {\frac{3x}{{\left( {1 + x} \right)^{2} }} - \frac{1}{x}} \right] Y + \frac{1 + x}{1 + 4x} \left( { \frac{1}{x } - \frac{\varDelta }{{c_{1} }} - \frac{{2E^{2} }}{{c_{1} }}} \right) = 0 \quad {\text{where}}\quad E^{2} = \frac{{q^{2} }}{{r^{4} }} $$

(8)

Our task is to explore the solutions of Eq. (8) and obtain a physically meaningful matter distribution by assuming anisotropy ∆ and electric field E.

In the conservation equation, there is a non-vanishing term $2(p_{ \bot } - p_{r} )/r$, which represents a force because of the anisotropic nature of the fluid. This force will be outward when $p_{ \bot } > p_{r}$ and inward when $p_{ \bot } < p_{r}$ [56]. Because of the existence of an outward force for $p_{ \bot } > p_{r}$, it has more advantage for modeling more massive compact objects with anisotropic fluid than with isotropic fluid.

4 New class of solutions

To solve the above Eq. (8), we consider ∆ and E of the following form:

$$ \frac{\varDelta }{{c_{1} }} = \frac{\delta x}{{\left( {1 + x} \right)^{2s} }}\quad {\text{and}}\quad \frac{{E^{2} }}{{c_{1} }} = \frac{{c_{1} q^{2} }}{{x^{2} }} = \frac{kx}{{2\left( {1 + x} \right)^{2n} }} $$

(9)

where k and δ are non-zero positive constants, n and s are real numbers. The anisotropy and electric intensity are so assumed that the model is physically significant and well behaved i.e. ∆ and E remain regular and positive throughout the sphere as well as both should vanish at the center of the star and increase towards the boundary.

Substituting Eq. (9) into Eq. (8) we have,

$$ \frac{dY}{dx} + \frac{1 + x}{1 + 4x}\left[ {\frac{3x}{{\left( {1 + x} \right)^{2} }} - \frac{1}{x}} \right] Y + \frac{1 + x}{1 + 4x} \left( { \frac{1}{x } - \frac{\delta x}{{\left( {1 + x} \right)^{2s} }} - \frac{kx}{{\left( {1 + x} \right)^{2n} }}} \right) = 0 $$

(10)

which yield the following solution,

$$ Y(x) = e^{ - \lambda } = \frac{x}{{ns\left( {1 + x} \right)}}\left( {\frac{ns}{x} + \frac{ks + n\delta - ns}{2}} \right) + \frac{A x}{{\left( {x + 1} \right)\sqrt {1 + 4x} }} $$

(11)

where $A$ is an arbitrary constant.

Now the expressions for density and pressures are given by

$$ \begin{aligned} \frac{1}{{c_{1} }} \frac{8\pi G}{{c^{4} }} p_{r} & = \frac{{\left( {1 + x} \right)^{2n - 2 } \left[ {x\left\{ {7\left( {ks + n\delta } \right) - 9ns} \right\} + ks + n\delta + 9ns} \right] + knsx}}{{2ns\left( {x + 1} \right)^{2n} }} \\ & \quad + \frac{{A\left( {7 x + 1} \right)}}{{\left( {x + 1} \right)^{2} \sqrt {1 + 4x} }} \\ \end{aligned} $$

(12)

$$ \begin{aligned} \frac{1}{{c_{1} }} \frac{8\pi G}{{c^{4} }} p_{ \bot } & = \frac{{\left( {1 + x} \right)^{2n - 2 } \left[ {x\left\{ {7\left( {ks + n\delta } \right) - 9ns} \right\} + ks + n\delta + 9ns} \right] + knsx}}{{2ns\left( {x + 1} \right)^{2n} }} \\ & \quad + \frac{{A\left( {7 x + 1} \right)}}{{\left( {x + 1} \right)^{2} \sqrt {1 + 4x} }} + \frac{\delta x}{{\left( {1 + x} \right)^{2s} }} \\ \end{aligned} $$

(13)

$$ \begin{aligned} \frac{1}{{c_{1} }} \frac{8\pi G}{{c^{2} }} \rho & = \frac{{n\left( {1 + x} \right)^{2n} \left( {3 + x} \right)\left( {3s - \delta } \right) - ks\left[ {nx\left( {1 + x} \right)^{2} + \left( {1 + x} \right)^{2n} \left( {3 + x} \right)} \right]}}{{2ns\left( {1 + x} \right)^{2n + 2} }} \\ & \quad - \frac{{A\left( {9x + 3} \right)}}{{\left( {x + 1} \right)^{2} \left( {1 + 4x} \right)^{3/2} }} \\ \end{aligned} $$

(14)

5 Properties of the new solutions

The central values of the pressures and density is given by

$$ \left[ { \frac{1}{{c_{1} }} \frac{8\pi G}{{c^{4} }} p_{r} } \right]_{r = 0} = \left[ { \frac{1}{{c_{1} }} \frac{8\pi G}{{c^{4} }} p_{ \bot } } \right]_{r = 0} = \frac{ks + n\delta + 9ns}{2ns} + A > 0 $$

(15)

a non-zero positive finite value.

$$ \left[ {\frac{1}{{c_{1} }} \frac{8\pi G}{{c^{2} }} \rho } \right]_{r = 0} = \frac{9ns - 3ks - 3n\delta - 6A}{2ns} > 0,\quad {\text{a}}\,{\text{non-zero}}\,{\text{positive}}\,{\text{finite}}\,{\text{value}} $$

(16)

Since the Zeldovich’s condition $[p/\rho c^{2} ]_{r = 0} \le 1$ has to be satisfied at the center the super-dense star, we have

$$ A \le - \frac{2ks + 2n\delta }{ns + 3} $$

(17)

Differentiating Eqs. (12)–(14) with respect to x we get

$$ \begin{aligned} \frac{1}{{c_{1} }} \frac{8\pi G}{{c^{4} }} \frac{{dp_{r} }}{dx} & = \frac{{ - ks\left[ {2n^{2} x\left( {1 + x} \right)^{2} - n\left( {1 + x} \right)^{3} + \left( {1 + x} \right)^{2n} \left( {7x - 5} \right)} \right] + n\left( {1 + x} \right)^{2n} \left[ {9s\left( {x - 3} \right) + \delta \left( {5 - 7x} \right)} \right]}}{{2ns\left( {x + 1} \right)^{2n + 3} }} \\ & \quad - \frac{{3A\left( {14x^{2} + x - 1} \right)}}{{\left( {1 + x} \right)^{3} \left( {1 + 4x} \right)^{3/2} }} \\ \end{aligned} $$

(18)

$$ \begin{aligned} \frac{1}{{c_{1} }} \frac{8\pi G}{{c^{4} }} \frac{{dp_{ \bot } }}{dx} & = \frac{{ - ks\left[ {2n^{2} x\left( {1 + x} \right)^{2} - n\left( {1 + x} \right)^{3} + \left( {1 + x} \right)^{2n} \left( {7x - 5} \right)} \right] + n\left( {1 + x} \right)^{2n} \left[ {9s\left( {x - 3} \right) + \delta \left( {5 - 7x} \right)} \right]}}{{2ns\left( {x + 1} \right)^{2n + 3} }} \\ & \quad - \frac{{3A\left( {14x^{2} + x - 1} \right)}}{{\left( {1 + x} \right)^{3} \left( {1 + 4x} \right)^{3/2} }} + \frac{{\delta \left( {1 + x - 2sx} \right)}}{{\left( {1 + x} \right)^{2s + 1} }} \\ \end{aligned} $$

(19)

$$ \begin{aligned} \frac{1}{{c_{1} }} \frac{8\pi G}{{c^{2} }} \frac{d\rho }{dx} & = \frac{{ks\left[ {2n^{2} x\left( {1 + x} \right)^{2} - n\left( {1 + x} \right)^{3} + \left( {1 + x} \right)^{2n} \left( {x + 5} \right)} \right] - n\left( {1 + x} \right)^{2n} \left( {5 + x} \right)\left( {3s - \delta } \right)}}{{2ns\left( {x + 1} \right)^{2n + 3} }} \\ & \quad + \frac{{3A\left( {30x^{2} + 23x + 5} \right)}}{{\left( {1 + x} \right)^{3} \left( {1 + 4x} \right)^{5/2} }} \\ \end{aligned} $$

(20)

The second-order differentiation for pressures and density are negative

$$ \left( { \frac{1}{{c_{1} }} \frac{8\pi G}{{c^{4} }} \frac{{d^{2} p_{r} }}{{dx^{2} }}} \right)_{r = 0} < 0,\quad \left( {\frac{1}{{c_{1} }} \frac{8\pi G}{{c^{4} }} \frac{{d^{2} p_{ \bot } }}{{dx^{2} }}} \right)_{r = 0} < 0, \quad \left( {\frac{1}{{c_{1} }} \frac{8\pi G}{{c^{2} }} \frac{{d^{2} \rho }}{{dx^{2} }}} \right)_{r = 0} < 0 $$

Signifying that pressures and density are decreasing outward and maximum at the center. In the light of Eqs. (18), (19) and (20), the speed of sound can determine by

$$ v_{r}^{2} = {{\frac{{dp_{r} }}{dx}} \mathord{\left/ {\vphantom {{\frac{{dp_{r} }}{dx}} {\frac{d\rho }{dx}}}} \right. \kern-0pt} {\frac{d\rho }{dx}}} \quad {\text{and}}\quad v_{ \bot }^{2} = {{\frac{{dp_{ \bot } }}{dx}} \mathord{\left/ {\vphantom {{\frac{{dp_{ \bot } }}{dx}} {\frac{d\rho }{dx}}}} \right. \kern-0pt} {\frac{d\rho }{dx}}} $$

(21)

For a stable anisotropic model, $- 1 < v_{ \bot }^{2} - v_{r}^{2} \, \lesssim \, 0$ needs to be satisfied. Now the expression for gravitational red-shift ($z$) and adiabatic index ($\gamma$) are given by

$$ z = e^{{ - \frac{\nu }{2}}} - 1 = \frac{{\left( {1 + x} \right)^{{ - \frac{3}{2}}} }}{\sqrt B } - 1\quad {\text{and}}\quad \gamma = \frac{{\rho + p_{r} }}{{p_{r} }} \frac{dp}{d\rho } $$

(22)

Since the central value of gravitational red-shift to be non-zero positive finite, we have $0 < \sqrt B < 1$.

Differentiating Eq. (22) with respect to x we get,

$$ \left[ {\frac{dz}{dx}} \right]_{x = 0} = - \frac{1}{2\sqrt B } < 0 $$

(23)

The expression on Eq. (23) is negative, implying that the gravitation red-shift is maximum at the center and decreases outward.

$$ \left[ {\frac{d}{dx}\frac{{E^{2} }}{{c_{1} }}} \right]_{x = 0} = \frac{k}{2} > 0\quad {\text{and}}\quad \left[ {\frac{d}{dx} \frac{\varDelta }{{c_{1} }}} \right]_{x = 0} = \delta > 0 $$

(24)

Equation (24) signifies the electric field and anisotropy are minimum (i.e. zero) at the center and monotonically increasing outward.

6 Boundary conditions

The interior solutions so obtained are matched with the exterior solution of Reissner–Nordström solution given by

$$ ds^{2} = \left( {1 - \frac{2GM}{{c^{2} r}} + \frac{{e^{2} }}{{ r^{2} }} } \right)c^{2} dt^{2} - \left( {1 - \frac{2GM}{{c^{2} r}} + \frac{{e^{2} }}{{ r^{2} }} } \right)^{ - 1} dr^{2} - r^{2} ( d\theta^{2} + { \sin }^{2} \theta d\phi^{2} ) $$

(25)

where M is the mass of the fluid ball as determined by the external observer and $r \ge r_{b}$ is the radial coordinate of the exterior region. Since Eq. (25) is considered as the exterior solution, thus we shall arrive at the following conclusions by matching with Eq. (1) at the boundary $r = r_{b}$:

$$ e^{{\nu_{b} }} = \left( {1 - \frac{2GM}{{c^{2} r_{b} }} + \frac{{e^{2} }}{{ r_{b}^{2} }} } \right) = B\left( {1 + X} \right)^{3} $$

(26)

$$ q \left( {r = r_{b} } \right) = e $$

(27)

$$ e^{{ - \lambda_{b} }} = \left( {1 - \frac{2GM}{{c^{2} r_{b} }} + \frac{{e^{2} }}{{ r_{b}^{2} }} } \right) = \frac{X}{{ns\left( {1 + X} \right)}}\left( {\frac{ns}{X} + \frac{ks + n\delta - ns}{2}} \right) + \frac{A X}{{\left( {X + 1} \right)\sqrt {1 + 4X} }} $$

(28)

$$ {\text{And}}\,p_{r} (r = r_{b} ) = 0,\quad {\text{provided}}\,X = c_{1} r_{b}^{2} $$

(29)

Using Eq. (29), we can determine the constant A and obtained as

$$ A = \frac{{\sqrt {1 + 4X} \left( {1 + X} \right)^{2n - 2} \left[ {X\left\{ {9ns - 7\left( {ks + n\delta } \right)} \right\} - ks - n\delta - 9ns} \right] - kns X\sqrt {1 + 4X} }}{{ 2ns\left( {7X + 1} \right)\left( {1 + X} \right)^{2n - 2} }} $$

(30)

Equating Eqs. (26) and (28), we get obtain the expression of B

$$ B = \frac{X }{{ns\left( {1 + X} \right)^{4} }}\left( {\frac{ns}{X} + \frac{ks + n\delta - ns}{2}} \right) + \frac{A X}{{\left( {X + 1} \right)^{4} \sqrt {1 + 4X} }} $$

(31)

Finally in the view of Eqs. (26) and (6) we arrive to the expression of mass

$$ M = \frac{{r_{b} c^{2} }}{2G}\left[ {1 - B \left( {1 + X} \right)^{3} + \frac{{k X^{2} }}{{2\left( {1 + X} \right)^{2n} }}} \right] $$

(32)

Also the equation for central value of red-shift is given as

$$ z_{0} = B^{ - 1/2} - 1 $$

(33)

Our presented solutions satisfy all the energy conditions, such as Null Energy Condition (NEC), Weak Energy Condition (WEC), Strong Energy Condition (SEC) and Dominant Energy Condition throughout the interior region (Fig. 8):

$$ \begin{aligned} & \rho + p_{r} \ge 0; \rho + p_{ \bot } \ge 0;\quad \rho \ge 0;\quad \rho + p_{r} + 2p_{ \bot } \ge 0;\quad \rho \ge \left| {p_{r} } \right|, \left| {p_{ \bot } } \right|;\quad \rho + E^{2} \ge 0; \\ & \rho + p_{ \bot } + E^{2} \ge 0\quad {\text{and}}\quad \rho + p_{r} + 2p_{ \bot } + E^{2} \ge 0. \\ \end{aligned} $$

7 Results and discussions

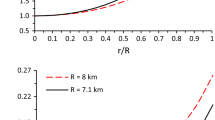
It has been observed that the physical parameters $\left( {p_{r} , p_{ \bot } ,\rho ,\frac{{p_{r} }}{{c^{2} \rho }},\frac{{p_{ \bot } }}{{c^{2} \rho }},\frac{{dp_{r} }}{{c^{2} d\rho }},\frac{{dp_{ \bot } }}{{c^{2} d\rho }},z} \right)$ are positive at the centre and within the limit of realistic equation of state and monotonically decreasing (Figs. 1, 2, 3, 4, 7). However, the anisotropic parameter, electric field and adiabatic index are minima at the center and increasing outward (Figs. 2, 5, 6). Thus, the solutions are well behaved for all values of $n, s, X$ and $\delta$ for specific values mentioned above. If we change any of the specified parameter for each case, then all other parameter should also change until the solution is well behaved. Because of these wide values of all the parameters, we can model many different types of ultra-cold compact stars like quark stars and neutron stars. From Fig. 7, it is also observed that the ratio with trace of stress tensor to energy density is also decreasing outward. For a perfect fluid it is sufficient enough to check the trend of pressure to density ratio whether the obtained solution is well behaved or not. However, for an anisotropic fluid it is also desired to check the trend of $(p_{r} + 2p_{ \bot } )/c^{2} \rho$, which should be decreasing outward. As seen from Fig. 8, we can conclude that $- 1 < v_{ \bot }^{2} - v_{r}^{2} \, \lesssim \, 0$ is satisfied for all the models, which means that our models of anisotropic compact stars are stable. Form Fig. 9, we can verify our solutions satisfying all the energy conditions.

Fig. 1

March of pressure for (1) $n = 1, \,s = 2$, (2) $n = 2,\, s = 3$ and (3) $n = - 2,\, s = 3$ with radius

Fig. 2

March of energy density $\rho c^{2}$ and $\gamma$ for (1) $n = 1,\, s = 2$, (2) $n = 2,\, s = 3$ and (3) $n = - 2, s = 3$ with radius

Fig. 3

March of pressure to energy density ratio for (1) $n = 1,\, s = 2$, (2) $n = 2, s = 3$ and (3) $n = - 2, s = 3$ with radius

Fig. 4

March of $v^{2} /c^{2}$ for (1) $n = 1, \,s = 2$, (2) $n = 2, \,s = 3$ and (3) $n = - 2, s = 3$ with radius

Fig. 5

March of anisotropy for (1) $n = 1,\, s = 2$, (2) $n = 2, \,s = 3$ and (3) $n = - 2, s = 3$ with radius

Fig. 6

March of electric field intensity for (1) $n = 1, s = 2$, (2) $n = 2, s = 3$ and (3) $n = - 2, s = 3$ with radius

Fig. 7

March of trace of stress tensor to the energy density ratio and red-shift for (1) $n = 1, s = 2$, (2) $n = 2, s = 3$ and (3) $n = - 2, s = 3$ with radius

Fig. 8

March of stability factor $v_{ \bot }^{2} - v_{r}^{2}$ with radius for the well known compact star candidates

Fig. 9

The energy conditions are plotted against $r/r_{b}$

Now we present some models of super dense quark stars and neutron stars based on the particular solutions discussed above by assuming surface density $\rho_{b} = 4.6888 \times 10^{14} \,{\text{g}}\,{\text{cm}}^{ - 3}$ for quark star and $\rho_{b} = 2.7 \times 10^{14} \,{\text{g}}\,{\text{cm}}^{ - 3}$ for neutron star. Corresponding to $n = 2, \,s = 1, \,k = 4$ and $\delta = 1$, the mass and radius for $X_{max} = 0.16$ is $2.45\,{\text{M}}_{ \odot } ,\, 14.6\,{\text{km}}$ (Neutron star) and $1.86\,{\text{M}}_{ \odot } ,\, 11.1\,{\text{km}}$ (quark star). For $n = 2, \,s = 3,\, k = 2$ and $\delta = 5$, the mass and radius correspond to $X_{max} = 0.128$ is $1.99\,M_{ \odot } ,\, 14.02\,{\text{km}}$ (Neutron star) and $1.51\,{\text{M}}_{ \odot } ,\, 10.64\,{\text{km}}$ (quark star). Similarly, for $n = - 2,\, s = 3,\,k = 2$ and $\delta = 8$, the mass and radius correspond to $X_{max} = 0.1$ is $1.83 \,{\text{M}}_{ \odot } ,\,14.39\,{\text{km}}$ (Neutron star) and $1.39\,{\text{M}}_{ \odot } ,\, 10.92\,{\text{km}}$ (quark star). The well behaved class of relativistic stellar models obtained in this work may have astrophysical significance in the study of more realistic internal structure of compact star. Therefore, we have used our solution to model certain compact objects whose radii and masses are well known, Table 1. Here EXO 0748 − 676, PSR J1614 − 2230 and PSR J0348 + 0432 are NS [57–59] candidates as well as XTE J1739 − 217 and PSR B0943 are quark star [60, 61] candidates.

Table 1 Comparison of mass and radius for well known compact star with our calculated values

Now a special case of our solution $n = 0.5,\, s = 3,\, k = 2.6,\,\delta = 5 \,{\text{and}}\,X = 0.00373$ needs to be given attention for the quark star PSR B0943 + 10 because as seen from Fig. 10, $v_{r}^{2 } \,{\text{and}}\, v_{ \bot }^{2}$ is almost constant at about 0.162 and 0.123 respectively similar to MIT Bag model of quark stars. MIT Bag model gives $v_{r}^{2 } = 0.333$ and constant thorough the star. But our obtained $v_{r}^{2 }$ is about one-half the value as given by MIT Bag Model. This decrease in radial speed of sound may be because of the anisotropic nature of the fluid. Also we know that MIT Bag Model of quark is not a physical model because it assumes that the quarks are freely moving inside the bag of hadrons without any interaction. Because of such over simplified assumption, sound speed in quark star matter using EOS from MIT Bag Model may be over estimated. From the above Table 1, we observe that our solution is useful in modeling of compact stars.

Fig. 10

March of sound speed square for PSR B0943 + 10 (0.02 $M_{\odot}$, 2.6 km) which is a quark star candidate correspond to $n = 0.5, \, s = 3,\, k = 2.6,\, \delta = 5 \,{\text{and}}\,X = 0.00373$ for our solution

8 Conclusions

From the above discussions we can conclude that the presented neutron star model of mass 2.45 $M_{\odot}$ may contain an EOS for half-skyrmion matter [23] or $\pi^{ - }$ condensation [13] leading to its mass. For neutron stars of mass 1.99 $M_{\odot}$, 1.97 $M_{\odot}$ (PSR J1614 − 2230), 2.01 $M_{\odot}$ (PSR J0348 + 0432) and 2.1 $M_{\odot}$ (EXO 0748 − 676), we expect the EOS to contain ground state of $npe\mu$ matter with NN and NNN strong interaction giving rise to their mass within the range 1.9–2.1 $M_{\odot}$. Lastly, the NS with mass 1.83 $M_{\odot}$ is expected to contain hyperons condensation inside its core.