On some stochastic comparisons of arithmetic and geometric mixture models

Abstract

Most studies on reliability analysis have been conducted in homogeneous populations. However, homogeneous populations can rarely be found in the real world. Populations with specific components, such as lifetime, are usually heterogeneous. When populations are heterogeneous, it raises the question of whether these different modeling analysis strategies might be appropriate and which one of them should be preferred. In this paper, we provide mixture models, which have usually been effective tools for modeling heterogeneity in populations. Specifically, we carry out a stochastic comparison of two arithmetic (finite) mixture models using the majorization concept in the sense of the usual stochastic order, the hazard rate order, the reversed hazard rate order and the dispersive order both for a general case and for some semiparametric families of distributions. Moreover, we obtain sufficient conditions to compare two geometric mixture models. To illustrate the theoretical findings, some relevant examples and counterexamples are presented.

1 Introduction

Most studies on reliability measures have been conducted in homogeneous case. However, in the real world, homogeneous populations can rarely be found. Populations with specific components are usually heterogeneous and consist of a finite number of homogeneous sub-populations. Ignoring the heterogeneity in populations can lead to some fundamental errors in reliability analysis. Finite (arithmetic) mixture models are usually suitable tools for considering heterogeneity in populations.

Let ${\bar{F}}(x; {\varvec{p}})$ be the survival function (SF) of arithmetic (finite) mixture with n homogeneous sub-populations with the SF’s ${\bar{F}}_{i}(x)$, $i =1,\ldots ,n$. Then

$$\begin{aligned} {\bar{F}}(x; {\varvec{p}})=\sum _{i=1}^{n} p_{i} {\bar{F}}_{i}(x), \end{aligned}$$

(1)

where ${\varvec{p}}=(p_{1}, \ldots , p_{n})$ are the mixing proportions such that $\sum _{i=1}^{n} p_{i}=1$ and $p_{i} \ge 0$, for $i \in \{1,2, \ldots , n\}$. The corresponding cumulative distribution function (CDF) and probability density function (PDF) of (1) can be expressed as

$$\begin{aligned} F(x; {\varvec{p}})=\sum _{i=1}^{n} p_{i} F_{i}(x) \end{aligned}$$

(2)

and

$$\begin{aligned} f(x; {\varvec{p}})=\sum _{i=1}^{n} p_{i} f_{i}(x), \end{aligned}$$

(3)

respectively, where $F_{i}$ and $f_{i}$ are the CDF and PDF of ${\bar{F}}_{i}$, $i=1, \ldots , n$, respectively.

In the following, we present some practical examples where the finite mixture models have been applied.

• In most industrialized populations, there are usually two groups of components: defective components with shorter lifetimes and standard components with longer lifetimes. When mixed, they will lead a heterogeneous populations (Block et al. 2003).

• In industrial populations, components are usually combined with two or more different production lines due to different work shifts, different raw materials, the quality of resources and components used in the production process, the history of operation and maintenance, random environment, human error, etc. Obviously, due to the mentioned diversity in the production line, the lifetime distribution of the components of one production line is different from other production lines and will lead to a heterogeneous population (Finkelstein 2008; Cha and Finkelstein 2013).

• In industrial populations, there is usually more than one reason for the failures that occur in a component. The failure distribution for each reason can be estimated using a density function. Thus, the overall distribution can be modeled using a finite mixture model (Davis 1952).

• In reliability theory, the distribution function or the reliability function of a coherent system consists of n independent and identically distributed components can be expressed as a linear combination of the distribution function or the reliability function of the ordered lifetime of these components, respectively. This is in fact a mixture of the ordered lifetime (Amini-Seresht and Zhang 2017).

The interested readers may refer to Titrington et al. Titterington et al. (1985) and Everitt and Hand Everitt and Hand (1981) for some more applications of finite mixture models. Further, some generalizations of finite mixture models by considering the effect of severe conditions can be found in Shojaee et al. Shojaee et al. (2021) and Shojaee et al. Shojaee et al. (2021).

   Hazra and Finkelstein Hazra and Finkelstein (2018), using the concept of majorization, have provided the sufficient conditions to compare two finite mixtures for some semi-parametric families of distributions. Nadeb and Torabi Nadeb and Torabi (2020), using the majorization concept, have provided a stochastic comparison for two finite mixtures in the sense of usual stochastic order, hazard rate order and reversed hazard rate order. Albabtain et al. Albabtain et al. (2020) by considering a parametric family of weighted distributions, have provided some stochastic comparisons for their mixtures. Some stochastic comparisons of mixture models can be found in Shaked and Shanthikumar Shaked and Shanthikumar (2007), Navarro Navarro (2008), Navarro Navarro (2016) Amini and Zhang Amini-Seresht and Zhang (2017), Navarro and Aguila Navarro and del Aguila (2017), Misra and Naqvi Misra and Naqvi (2018) and Badia and Lee Badia and Lee (2020), to name a few.

   Now, let us consider the geometric mixture of CDF’s $F_{i}$, $i=1,\ldots , n$, which can be given as follows.

$$\begin{aligned} F_{G}(x;{\varvec{p}})=\prod _{i=1}^{n}{F}^{{p}_{i}}_{i}(x), \end{aligned}$$

(4)

where $p_{i} \ge 0$, $i =1,2, \ldots , n$, are the mixing proportions such that $\sum _{i=1}^{n} p_{i}=1$. In the following, we arrive at the geometric mixture (4) from the arithmetic mixture (2) by using concept of the proportional reversed hazard model.

Assume that we have a mixed population with the mixture CDF as

$$\begin{aligned} F(x; {\varvec{p}})=\sum _{i=1}^{n} p_{i} F_{i}(x). \end{aligned}$$

Let the severe conditions acts on each subpopulation uniformly, according to the proportional reversed hazard model, so that the CDF of i-th subpopulation becomes $F_{i}^{\gamma }(x)$, $i=1, \ldots , n$. Then, the CDF of a randomly selected item is

$$\begin{aligned} F_{s}(x; {\varvec{p}})=\sum _{i=1}^{n} p_{i} F_{i}^{\gamma }(x). \end{aligned}$$

Now, assume that we shield the selected item from the severe conditions, which can be modelled as

$$\begin{aligned} F_{\textrm{shield}}(x; {\varvec{p}})=\left( \sum _{i=1}^{n} p_{i} F_{i}^{\gamma }(x)\right) ^{\frac{1}{\gamma }}. \end{aligned}$$

Now let $\gamma \rightarrow 0$, then we have

$$\begin{aligned} \lim _{\gamma \rightarrow 0}F_{\textrm{shield}}(x; {\varvec{p}})=\lim _{\gamma \rightarrow 0}\left( \sum _{i=1}^{n} p_{i} F_{i}^{\gamma }(x)\right) ^{\frac{1}{\gamma }}=\prod _{i=1}^{n} {F}^{{p}_{i}}_{i}(x)=F_{G}(x;{\varvec{p}}). \end{aligned}$$

So, we arrive at the geometric mixture (4) which has the meaningful interpretation (see also Asadi et al. 2019). Also, some reliability interpretations of the geometric mixture (in term of parallel systems) are as follows.

• $F_{G}(x;{\varvec{p}})=\prod _{i=1}^{n}{F}^{{p}_{i}}_{i}(x)$ can be considered as a generalized proportional reversed hazards (GPRH) model (Navarro 2016).

• Let $p_{i}=\frac{1}{n}$, $i=1, \ldots , n$, then we get $F_{G}^{n}(x;{\varvec{p}})=\prod _{i=1}^{n}{F}_{i}(x)$, which is the CDF of a n-components parallel system, where the i-th component has CDF ${F}_{i}(x)$.

• It is easy to see that $F_{G}(x;{\varvec{p}})=\prod _{i=1}^{n}{F}^{{p}_{i}}_{i}(x)$ is the CDF of a parallel system that consists of n independent components, where the CDF of the i-th component follows from the PRH model with the baseline CDF ${F}_{i}(x)$ and the PRH parameter $p_{i}$, $i = 1, \ldots , n$.

• The geometric mixture can be represented as $F_{G}(x;{\varvec{p}})=Q(F_{1}, \ldots , F_{n})$, where Q is a generalized distorted distribution with the distortion function $Q(u_{1}, \ldots , u_{n})=\prod _{i=1}^{n}{u}^{{p}_{i}}_{i}$ (Navarro and del Aguila 2017).

   In this paper, motivated by Nadeb and Torabi Nadeb and Torabi (2020), we compare two finite (arithmetic) mixture models in the sense of hazard rate order, the reversed hazard rate order and the dispersive order when the vector of parameters and the vector of proportions of the first mixture majorizes the second one. In fact, we extend the results of Hazra and Finkelstein Hazra and Finkelstein (2018) and Nadeb and Torabi Nadeb and Torabi (2020) both for general case and for some semiparametric families of distributions. Further, since the geometric mixture model have the meaningful interpretations, we provide sufficient conditions to compare two geometric mixture model in the sense of usual stochastic order and the reversed hazard rate order with different baseline random variables and different mixing probabilities.

   The organization of the paper is as follows. Section 2 presents some basic concepts, definitions and lemmas that will be used in the paper. In Sect. 3, we provide sufficient conditions to compare two finite mixtures for general case and for some other semiparametric families of distributions in the sense of the usual stochastic order, the hazard rate order, the reversed hazard rate order and the dispersive order. Section 4 is devoted to stochastic comparisons of two geometric mixture models in the sense of the usual stochastic order and the reversed hazard rate order with different mixing probabilities and different baseline random variables. Finally, Sect. 5 concludes the paper.

2 Preliminaries

In this section, we present some basic definitions of stochastic orders and lemmas that will be used to our developments. Consider two random variables X and Y with PDF’s f and g, CDF’s F and G, SF’s ${\bar{F}}$ and ${\bar{G}}$, hazard rate functions $r_{X}$ and $r_{Y}$, reversed hazard rate functions ${\tilde{r}}_{X}$ and ${\tilde{r}}_{Y}$, quantile functions $F^{-1}$ and $G^{-1}$, respectively. The following definitions are useful in our derivations.

Definition 2.1

The distribution F is said to be increasing (decreasing) failure rate (IFR (DFR)) if its failure rate $r_X(x)$ is non-decreasing (non-increasing) in x.

Definition 2.2

The random variable X is said to be smaller than Y in the:

• Usual stochastic order (denoted by $F\le _{st} G$) if ${\bar{F}}(x)\le {\bar{G}}(x)$ for all x or equivalently $E[\phi (X)] \le E[\phi (Y)]$ for all increasing functions $\phi$ for which the expectations exist.

• Hazard rate order (denoted by $F\le _{hr}G$) if ${\bar{G}}(x)/{\bar{F}}(x)$ is increasing in x, for all x or equivalently $r_X(x)\ge r_Y(x)$, for all x.

• Reversed hazard rate order (denoted by $F\le _{rh}G$) if G(x)/F(x) is increasing in x, for all x or equivalently ${\tilde{r}}_X(x)\le {\tilde{r}}_Y(x)$, for all x.

• Dispersive order (denoted by $F\le _{disp}G$) if ${G}^{-1}(u)-{F}^{-1}(u)$ is increasing in $u \in (0,1)$.

• Likelihood ratio order (denoted by $F\le _{lr}G$) if g(x)/f(x) is increasing in x, for all x.

Definition 2.3

(Marshall et al. 2011). Let $x_{(1)} \le \cdots \le x_{(n)}$ and $y_{(1)} \le \cdots \le y_{(n)}$ be increasing arrangements of ${\varvec{x}}=(x_{1},\ldots ,x_{n})$ and ${\varvec{y}}=(y_{1},\ldots ,y_{n})$, respectively.

• (i) If $\sum _{j=1}^{i}x_{(j)} \le \sum _{j=1}^{i}y_{(j)}$ for $i=1,\ldots ,n-1$, and $\sum _{j=1}^{n}x_{(j)}= \sum _{j=1}^{n}y_{(j)}$, then ${\varvec{x}}$ is said to majorize ${\varvec{y}}$ and denoted by ${\varvec{x}} {\mathop {\succeq }\limits ^{m}}{\varvec{y}}$.

• (ii) If $\sum _{j=1}^{i}x_{(j)} \le \sum _{j=1}^{i}y_{(j)}$ for $i=1,\ldots ,n$, then ${\varvec{x}}$ is said to weakly supermajorize ${\varvec{y}}$, and denoted by ${\varvec{x}} {\mathop {\succeq }\limits ^{w}}{\varvec{y}}$.

• (iii) If $\sum _{j=i}^{n}x_{(j)} \ge \sum _{j=i}^{n}y_{(j)}$ for $i=1,\ldots ,n$, then ${\varvec{x}}$ is said to weakly submajorize ${\varvec{y}}$, denoted by ${\varvec{x}} {\succeq }_{w}{\varvec{y}}$.

   It is clear that the majorization order implies both weak submajorization and supermajorization orders. A function that preserves the ordering of majorization is called the Schur-convex function (Marshall et al. 2011).

Definition 2.4

(Marshall et al. 2011). A real-valued function $\phi$ defined on a set ${\mathbb {A}} \subseteq {\mathbb {R}}^{n}$ is said to be Schur-convex (Schur-concave) on ${\mathbb {A}}$ if ${\varvec{x}} {\mathop {\succeq }\limits ^{m}}{\varvec{y}}$ implies $\phi ({\varvec{x}}) \ge (\le ) \phi ({\varvec{y}})$ for any ${\varvec{x}}, {\varvec{y}} \in {\mathbb {A}}$.

Characterizations of Schur-convex (Schur-concave) functions is given in the following lemma.

Lemma 2.5

(Marshall et al. 2011). Let $I \subseteq {\mathbb {R}}$ be an open interval and let $\phi : I^{n} \rightarrow {\mathbb {R}}$ be a real-valued, continuously differentiable function. Then, $\phi$ is Schur-convex (Schur-concave) on $I^{n}$ if and only if

• (i) $\phi$ is symmetric on $I^{n}$, and

• (ii) for all $i \ne j$ and all ${\varvec{x}} \in I^{n}$,

  $$\begin{aligned} (x_{i}-x_{j}) \left( \frac{\partial \phi }{\partial x_{i}}({\varvec{x}})-\frac{\partial \phi }{\partial x_{j}}({\varvec{x}})\right) \ge 0\,(\le 0), \end{aligned}$$

  where $\frac{\partial \phi }{\partial x_{i}}$ is the partial derivative of $\phi$ with respect to its i-th argument.

The next lemma provides some conditions under which the weak supermajorization and the weak submajorization orders are preserved.

Lemma 2.6

(Marshall et al. 2011). Consider the real-valued function $\phi$, defined on a set ${\mathbb {A}} \subseteq {\mathbb {R}}^{n}$. Then,

• (i) ${\varvec{x}}{\succeq }_{w}{\varvec{y}}$ implies $\phi ({\varvec{x}})\ge \phi ({\varvec{y}})$ if and only if $\phi$ is increasing and Schur-convex on ${\mathbb {A}}$;

• (ii) ${\varvec{x}} {\mathop {\succeq }\limits ^{w}}{\varvec{y}}$ implies $\phi ({\varvec{x}})\ge \phi ({\varvec{y}})$ if and only if $\phi$ is decreasing and Schur-convex on ${\mathbb {A}}$.

Before we start to obtain the main result, let

$$\begin{aligned} {\mathcal {S}}_{n}=\{ ({\varvec{x}}, {\varvec{y}}): x_{i}, y_{i} \ge 0 \ \ \ \ (x_{i}-x_{j}) (y_{i}-y_{j}) \le 0, \ \ \ i,j=1,\ldots ,n\}. \end{aligned}$$

Lemma 2.7

(Bartoszewicz 1987) For two non-negative random variables X and Y with CDF’s F and G, respectively, if X or Y have decreasing failure rate and $F \ge _{hr} G$, then $F \ge _{disp} G$.

3 Stochastic comparisons of arithmetic mixtures using majorization concept

In this section, we compare two arithmetic mixtures in the sense of usual stochastic order, hazard rate order, reversed hazard rate order and dispersive order, specifically when the vector of parameters and the vector of proportions of the first mixture majorizes the second one.

3.1 Usual stochastic order

Mirhossaini and Dolati Mirhossaini and Dolati (2008) and Shaw and Buckley Shaw and Buckley (2009) have introduced Transmuted-G (TG) model, which is a flexible model. We say that ${\bar{F}}(x ; \alpha )$ belongs to TG model, if its survival function can be expressed as the form ${\bar{F}}(x ; \alpha )={\bar{F}}(x)(1-\alpha F(x))$, where $\alpha \in [-1,1]$ and F(x) and ${\bar{F}}(x)$ are the baseline CDF and the baseline SF, respectively.

Theorem 3.1

Let

$$\begin{aligned} {\bar{F}}(x; {\varvec{p}}, \varvec{\alpha })=\sum _{i=1}^{n} p_{i} {\bar{F}} (x; \alpha _{i}) \end{aligned}$$

and

$$\begin{aligned} {\bar{F}}(x; {\varvec{q}}, \varvec{\beta })=\sum _{i=1}^{n} q_{i} {\bar{F}} (x; \beta _{i}) \end{aligned}$$

be SF’s of two n-component arithmetic mixtures with $({\varvec{p}}, \varvec{\alpha }) \in {\mathcal {S}}_{2}$ and $({\varvec{q}}, \varvec{\beta }) \in {\mathcal {S}}_{2}$, respectively, in which the baseline SF belong to the TG model, i.e. ${\bar{F}}(x ; \alpha )={\bar{F}}(x)(1-\alpha F(x))$, for all x. If ${\varvec{p}}{\mathop {\ge }\limits ^{m}} {\varvec{q}}$, $\varvec{\alpha } {\mathop {\ge }\limits ^{w}} ({\mathop {\le }\limits ^{w}}) \varvec{\beta }$, then

$$\begin{aligned} {F}(x; {\varvec{p}}, \varvec{\alpha }) \ge _{st} {F}(x; {\varvec{q}}, \varvec{\beta }). \end{aligned}$$

Proof

It is clear that ${\bar{F}}(x ; \alpha )={\bar{F}}(x)(1-\alpha F(x))$ is decreasing (increasing) and convex (concave) in $0<\alpha \le 1 (-1\le \alpha <0)$. Thus, the proof follows from Theorem 3.3 of Nadeb and Torabi (2020). $\square$

Remark 3.2

Nadeb and Torabi have provided the necessary and sufficient conditions for likelihood ratio ordering between two arithmetic mixtures whenever the sub-populations belong to the TG model, which are different from the condition given in Theorem 3.1.

Theorem 3.3

Let

$$\begin{aligned} {\bar{F}}(x; {\varvec{p}}, \varvec{\alpha })=\sum _{i=1}^{n} p_{i} {\bar{F}} (x; \alpha _{i})\end{aligned}$$

and

$$\begin{aligned} {\bar{F}}(x; {\varvec{q}}, \varvec{\beta })=\sum _{i=1}^{n} q_{i} {\bar{F}} (x; \beta _{i})\end{aligned}$$

be SF’s of two n-component arithmetic mixtures with $({\varvec{p}}, \varvec{\alpha }) \in {\mathcal {S}}_{2}$ and $({\varvec{q}}, \varvec{\beta }) \in {\mathcal {S}}_{2}$, respectively, in which the baseline SF belong to the additive hazard model, i.e. ${\bar{F}}(x ; \alpha )={\bar{F}}(x)e^{-\alpha x}$, for all x. If ${\varvec{p}}{\mathop {\ge }\limits ^{m}} {\varvec{q}}$, $\varvec{\alpha } {\mathop {\ge }\limits ^{w}} \varvec{\beta }$, then

$$\begin{aligned} {F}(x; {\varvec{p}}, \varvec{\alpha }) \ge _{st} {F}(x; {\varvec{q}}, \varvec{\beta }). \end{aligned}$$

Proof

It is clear that ${\bar{F}}(x ; \alpha )={\bar{F}}(x)e^{-\alpha x}$ is decreasing and convex in $\alpha >0$. Thus, the proof follows from Theorem 3.3 of Nadeb and Torabi (2020). $\square$

3.2 Hazard rate order

In the following theorem, we provide sufficient conditions to compare two arithmetic mixtures, ${\bar{F}}(x; {\varvec{p}}, \varvec{\alpha })$ and ${\bar{F}}(x; {\varvec{q}}, \varvec{\beta })$, in the sense of hazard rate order.

Theorem 3.4

Let

$$\begin{aligned} {\bar{F}}(x; {\varvec{p}}, \varvec{\alpha })=\sum _{i=1}^{2} p_{i} {\bar{F}} (x; \alpha _{i})\end{aligned}$$

and

$$\begin{aligned} {\bar{F}}(x; {\varvec{q}}, \varvec{\beta })=\sum _{i=1}^{2} q_{i} {\bar{F}} (x; \beta _{i})\end{aligned}$$

be SF’s of two 2-component arithmetic mixtures with $({\varvec{p}}, \varvec{\alpha }) \in {\mathcal {S}}_{2}$ and $({\varvec{q}}, \varvec{\beta }) \in {\mathcal {S}}_{2}$, respectively. Let $r(x;\alpha )$ be increasing and concave in $\alpha >0$ for all x. If ${\varvec{p}}{\mathop {\ge }\limits ^{m}} {\varvec{q}}$, $\varvec{\alpha } {\mathop {\ge }\limits ^{m}} \varvec{\beta }$, then

$$\begin{aligned} {F}(x; {\varvec{p}}, \varvec{\alpha }) \ge _{hr} {F}(x; {\varvec{q}}, \varvec{\beta }). \end{aligned}$$

Proof

Denote by $r(x; {\varvec{p}}, \varvec{\alpha })$ and $r(x; {\varvec{q}}, \varvec{\beta })$ the hazard functions of ${\bar{F}}(x; {\varvec{p}}, \varvec{\alpha })$ and ${\bar{F}}(x; {\varvec{q}}, \varvec{\beta })$, respectively. To proof the theorem, first we show that $r(x; {\varvec{p}}, \varvec{\alpha }) \le r(x; {\varvec{p}}, \varvec{\beta })$. The proof of the first part follows from the proof of Theorem 6.3 of Shojaee et al. (2021b) because the arithmetic mixture is a special case of the generalized finite $\alpha$-mixture. In the second part, we will show $r(x; {\varvec{p}}, \varvec{\beta }) \le r(x; {\varvec{q}}, \varvec{\beta })$. Without loss of generality, suppose that $p_{1} \ge p_{2} >0$ and $q_{1} \ge q_{2} >0$, and then $({\varvec{p}}, \varvec{\alpha }) \in {\mathcal {S}}_{2}$ and $({\varvec{q}}, \varvec{\beta }) \in {\mathcal {S}}_{2}$, yields $0<\alpha _{1} \le \alpha _{2}$ and $0<\beta _{1} \le \beta _{2}$. Then

$$\begin{aligned} r(x; {\varvec{p}}, \varvec{\beta })=\frac{\sum _{i=1}^{2} p_{i} r(x; \beta _{i}) {\bar{F}}(x; \beta _{i})}{\sum _{i=1}^{2}p_{i} {\bar{F}}(x; \beta _{i})}=\frac{\Psi _{1}(x; {\varvec{p}}, \varvec{\beta })}{\Psi _{2}(x; {\varvec{p}}, \varvec{\beta })}.\end{aligned}$$

Thus,

$$\begin{aligned} \frac{\partial r(x; {\varvec{p}}, \varvec{\beta })}{\partial p_{1}} -\frac{\partial r(x; {\varvec{p}}, \varvec{\beta })}{\partial p_{2}}&=\dfrac{\frac{\partial \Psi _{1}(x; {\varvec{p}}, \varvec{\beta })}{\partial p_{1}}\Psi _{2}(x; {\varvec{p}}, \varvec{\beta })-\frac{\partial \Psi _{2}(x; {\varvec{p}}, \varvec{\beta })}{\partial p_{1}}\Psi _{1}(x; {\varvec{p}}, \varvec{\beta })}{\Psi _{2}^{2}(x; {\varvec{p}}, \varvec{\beta })}\\&-\dfrac{\frac{\partial \Psi _{1}(x; {\varvec{p}}, \varvec{\beta })}{\partial p_{2}}\Psi _{2}(x; {\varvec{p}}, \varvec{\beta })-\frac{\partial \Psi _{2}(x; {\varvec{p}}, \varvec{\beta })}{\partial p_{2}}\Psi _{1}(x; {\varvec{p}}, \varvec{\beta })}{\Psi _{2}^{2}(x; {\varvec{p}}, \varvec{\beta })}. \end{aligned}$$

After some algebra calculations, we get

$$\begin{aligned} \frac{\partial r(x; {\varvec{p}}, \varvec{\beta })}{\partial p_{1}} -\frac{\partial r(x; {\varvec{p}}, \varvec{\beta })}{\partial p_{2}}{\mathop {=}\limits ^{sgn}} {\bar{F}}(x;\beta _{1}){\bar{F}}(x;\beta _{2}) \big (r(x;\beta _{1})-r(x;\beta _{2})\big ) \le 0, \end{aligned}$$

because from assumption $r(x;\beta )$ is increasing in $\beta$ and $\beta _{1} \le \beta _{2}$. Consequently,

$$\begin{aligned} (p_{1}-p_{2})\bigg (\frac{\partial r(x; {\varvec{p}}, \varvec{\beta })}{\partial p_{1}} -\frac{\partial r(x; {\varvec{p}}, \varvec{\beta })}{\partial p_{2}}\bigg ) \le 0. \end{aligned}$$

Therefore, according to Lemma 2.5, $r(x; {\varvec{p}}, \varvec{\beta })$ is is Schur-concave. Now, using condition ${\varvec{p}}{\mathop {\ge }\limits ^{m}} {\varvec{q}}$, we have: $r(x; {\varvec{p}}, \varvec{\beta }) \le r(x; {\varvec{q}}, \varvec{\beta })$. Thus, in general, $r(x; {\varvec{p}}, \varvec{\alpha }) \le r(x; {\varvec{q}}, \varvec{\beta })$ and proof is completed. $\square$

Remark 3.5

Theorem 3.4 extends the results of Theorems 4.1, 4.2 and 4.3 of Nadeb and Torabi (2020) which are concerned the hazard rate order between two arithmetic mixtures in terms of ${\varvec{p}}$, $\varvec{\alpha }$ and $({\varvec{p}}, \varvec{\alpha })$, respectively, whenever the sub-populations belong to the proportional hazard rate model.

The following theorem provides the sufficient conditions to compare two arithmetic mixtures in the sense of the hazard rate order when the sub-population belong to the additive hazard model.

Theorem 3.6

Let ${\bar{F}}(x;\alpha )$ belong to the additive hazard model, ${\bar{F}}(x;\alpha )={\bar{F}}(x) e^{-\alpha x}$ for all x, where ${\bar{F}}(x)$ is the baseline SF. Then, for ${\varvec{p}}{\mathop {\ge }\limits ^{m}} {\varvec{q}}$, $\varvec{\alpha } {\mathop {\ge }\limits ^{m}} \varvec{\beta }$, $({\varvec{p}}, \varvec{\alpha }) \in {\mathcal {S}}_{2}$ and $({\varvec{q}}, \varvec{\beta }) \in {\mathcal {S}}_{2}$, we have

$$\begin{aligned} {F}(x; {\varvec{p}}, \varvec{\alpha }) \ge _{hr} {F}(x; {\varvec{q}}, \varvec{\beta }).\end{aligned}$$

Proof

In this case, $r(x; \alpha )=r(x)+\alpha$, where r(x) is the baseline hazard rate. It is easy to see that $r(x; \alpha )$ is increasing and concave in $\alpha >0$. Thus the proof follows from Theorem 3.4. $\square$

Theorem 3.7

Let ${\bar{F}}(x;\alpha )$ belong to the accelerated lifetime (scale) model, ${\bar{F}}(x;\alpha )={\bar{F}}(\alpha x)$ for all x, where ${\bar{F}}(x)$ is the baseline SF. Also, let xr(x) is increasing and concave for all x. Then, for ${\varvec{p}}{\mathop {\ge }\limits ^{m}} {\varvec{q}}$, $\varvec{\alpha } {\mathop {\ge }\limits ^{m}} \varvec{\beta }$, $({\varvec{p}}, \varvec{\alpha }) \in {\mathcal {S}}_{2}$ and $({\varvec{q}}, \varvec{\beta }) \in {\mathcal {S}}_{2}$, we have

$$\begin{aligned} {F}(x; {\varvec{p}}, \varvec{\alpha }) \ge _{hr} {F}(x; {\varvec{q}}, \varvec{\beta }).\end{aligned}$$

Proof

In this case, $r(x; \alpha )=\alpha r(\alpha x)$ and the result follows from Theorem 3.4. $\square$

To illustrate the validity of Theorem 3.4, consider the following numerical example.

Example 3.8

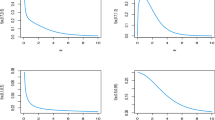
Consider the standard Exponential distribution with SF ${\bar{F}}(x; \alpha )=\exp (-\alpha x)$, $x \in [0, \infty )$. Obviously, ${\bar{F}}(x; \alpha )$ is decreasing in $\alpha$ for all x. On the other hand, $r(x; \alpha )=\alpha$ is increasing and concave in $\alpha$. Set $(p_{1}, p_{2})=(0.7, 0.3)$, $(q_{1}, q_{2})=(0.6, 0.4)$, $(\alpha _{1}, \alpha _{2})=(0.5, 0.8)$, $(\beta _{1}, \beta _{2})=(0.6, 0.7)$. Ii is easy to see that ${\varvec{p}}{\mathop {\ge }\limits ^{m}} {\varvec{q}}$, $\varvec{\alpha } {\mathop {\ge }\limits ^{m}} \varvec{\beta }$, $({\varvec{p}}, \varvec{\alpha }) \in {\mathcal {S}}_{2}$ and $({\varvec{q}}, \varvec{\beta }) \in {\mathcal {S}}_{2}$. Thus, all conditions of Theorem 3.4 are satisfied. Figure 1a depicts the plots of $r(x; {\varvec{p}}, \varvec{\alpha })$ and $r(x; {\varvec{q}}, \varvec{\beta })$.

The following counterexample shows that conditions $({\varvec{p}}, \varvec{\alpha }) \in {\mathcal {S}}_{2}$ and $({\varvec{q}}, \varvec{\beta }) \in {\mathcal {S}}_{2}$ in Theorem 3.4 can not be dropped.

Counterexample 3.9

Consider Example 3.8 and set $(p_{1}, p_{2})=(0.7, 0.3)$, $(q_{1}, q_{2})=(0.7, 0.3)$, $(\alpha _{1}, \alpha _{2})=(0.9, 0.6)$, $(\beta _{1}, \beta _{2})=(0.8, 0.7)$. Ii is easy to see that ${\varvec{p}}{\mathop {\ge }\limits ^{m}} {\varvec{q}}$, $\varvec{\alpha } {\mathop {\ge }\limits ^{m}} \varvec{\beta }$, but $({\varvec{p}}, \varvec{\alpha }) \notin {\mathcal {S}}_{2}$ and $({\varvec{q}}, \varvec{\beta }) \notin {\mathcal {S}}_{2}$. Figure 1b depicts the plot of $d(x)=r(x; {\varvec{p}}, \varvec{\alpha })-r(x; {\varvec{q}}, \varvec{\beta })$.

Fig. 1

a $r(x; {\varvec{p}}, \varvec{\alpha })$ (solid) and $r(x; {\varvec{q}}, \varvec{\beta })$ (dash dot) in Example 3.8. b $d(x)=r(x; {\varvec{p}}, \varvec{\alpha })-r(x; {\varvec{q}}, \varvec{\beta })$ in Counterexample 3.9

3.3 Dispersive order

The following theorem provides sufficient conditions to compare two arithmetic mixtures, ${\bar{F}}(x; {\varvec{p}}, \varvec{\alpha })$ and ${\bar{F}}(x; {\varvec{q}}, \varvec{\beta })$, in the sense of dispersive order, when ${\bar{F}} (x; \alpha )$ have decreasing failure rate (DFR).

Theorem 3.10

Let

$$\begin{aligned} {\bar{F}}(x; {\varvec{p}}, \varvec{\alpha })=\sum _{i=1}^{2} p_{i} {\bar{F}} (x; \alpha _{i}) \end{aligned}$$

and

$$\begin{aligned} {\bar{F}}(x; {\varvec{q}}, \varvec{\beta })=\sum _{i=1}^{2} q_{i} {\bar{F}} (x; \beta _{i}) \end{aligned}$$

be SF’s of two 2-component arithmetic mixtures with $({\varvec{p}}, \varvec{\alpha }) \in {\mathcal {S}}_{2}$ and $({\varvec{q}}, \varvec{\beta }) \in {\mathcal {S}}_{2}$, respectively. Let $r(x;\alpha )$ be increasing and concave in $\alpha >0$ for all x. Also, suppose that the baseline SF, ${\bar{F}} (x; \alpha )$, be a DFR distribution. If ${\varvec{p}}{\mathop {\ge }\limits ^{m}} {\varvec{q}}$, $\varvec{\alpha } {\mathop {\ge }\limits ^{m}} \varvec{\beta }$, then

$$\begin{aligned} {F}(x; {\varvec{p}}, \varvec{\alpha }) \ge _{disp} {F}(x; {\varvec{q}}, \varvec{\beta }). \end{aligned}$$

Proof

As we know, if each ${\bar{F}} (x; \alpha _{i})$ is DFR, then ${\bar{F}}(x; {\varvec{p}}, \varvec{\alpha })$ is DFR (Barlow and Proschan, 1975). On the other hand, from Theorem 3.4, ${F}(x; {\varvec{p}}, \varvec{\alpha }) \ge _{hr} {F}(x; {\varvec{q}}, \varvec{\beta })$. Consequently, ${F}(x; {\varvec{p}}, \varvec{\alpha }) \ge _{disp} {F}(x; {\varvec{q}}, \varvec{\beta })$ follows from Lemma 2.7 and proof is completed. $\square$

Remark 3.11

Theorem 3.10 extends the results of Theorems 4.4 of Nadeb and Torabi (2020) in general case.

Theorem 3.12

Let ${\bar{F}}(x;\alpha )$ belong to the additive hazard model, ${\bar{F}}(x;\alpha )={\bar{F}}(x) e^{-\alpha x}$ for all x, where ${\bar{F}}(x)$ is the baseline SF. Also, suppose that ${\bar{F}}(x)$ be a DFR distribution. Then, for ${\varvec{p}}{\mathop {\ge }\limits ^{m}} {\varvec{q}}$, $\varvec{\alpha } {\mathop {\ge }\limits ^{m}} \varvec{\beta }$, $({\varvec{p}}, \varvec{\alpha }) \in {\mathcal {S}}_{2}$ and $({\varvec{q}}, \varvec{\beta }) \in {\mathcal {S}}_{2}$, we have

$$\begin{aligned} {F}(x; {\varvec{p}}, \varvec{\alpha }) \ge _{disp} {F}(x; {\varvec{q}}, \varvec{\beta }). \end{aligned}$$

Proof

The proof follows from Theorem 3.6 and Lemma 2.7. $\square$

Theorem 3.13

Let ${\bar{F}}(x;\alpha )$ belong to the accelerated lifetime (scale) model, ${\bar{F}}(x;\alpha )={\bar{F}}(\alpha x)$ for all x, where ${\bar{F}}(x)$ is the baseline SF. Also, let xr(x) is increasing and concave for all x. Further, suppose that ${\bar{F}}(x;\alpha )$ be a DFR distribution. Then, for ${\varvec{p}}{\mathop {\ge }\limits ^{m}} {\varvec{q}}$, $\varvec{\alpha } {\mathop {\ge }\limits ^{m}} \varvec{\beta }$, $({\varvec{p}}, \varvec{\alpha }) \in {\mathcal {S}}_{2}$ and $({\varvec{q}}, \varvec{\beta }) \in {\mathcal {S}}_{2}$, we have

$$\begin{aligned} {F}(x; {\varvec{p}}, \varvec{\alpha }) \ge _{disp} {F}(x; {\varvec{q}}, \varvec{\beta }). \end{aligned}$$

Proof

The proof follows from Theorem 3.7 and Lemma 2.7. $\square$

3.4 Reversed hazard rate order

This subsection is concerned the reversed hazard rate order of arithmetic mixtures.

Theorem 3.14

Let

$$\begin{aligned} {F}(x; {\varvec{p}}, \varvec{\alpha })=\sum _{i=1}^{2} p_{i} {F} (x; \alpha _{i}) \end{aligned}$$

and

$$\begin{aligned} {F}(x; {\varvec{q}}, \varvec{\beta })=\sum _{i=1}^{2} q_{i} {F} (x; \beta _{i}) \end{aligned}$$

be SF’s of two 2-component arithmetic mixtures with $({\varvec{p}}, \varvec{\alpha }) \in {\mathcal {S}}_{2}$ and $({\varvec{q}}, \varvec{\beta }) \in {\mathcal {S}}_{2}$, respectively. Let ${\tilde{r}}(x;\alpha )$ be increasing and concave in $\alpha >0$ for all x. If ${\varvec{p}}{\mathop {\ge }\limits ^{m}} {\varvec{q}}$, $\varvec{\alpha } {\mathop {\ge }\limits ^{m}} \varvec{\beta }$, then

$$\begin{aligned} {F}(x; {\varvec{p}}, \varvec{\alpha }) \le _{rh} {F}(x; {\varvec{q}}, \varvec{\beta }). \end{aligned}$$

Proof

The proof is similar to the proof of Theorem 3.4 and therefore for the sake of brevity omitted here. $\square$

   At the end of this section, the following counterexample demonstrates that the result of Theorem 3.4 (3.14) cannot be extended to the likelihood ratio order.

Counterexample 3.15

Consider Example 3.8. Set $(p_{1}, p_{2})=(0.53, 0.47)$, $(q_{1}, q_{2})=(0.53, 0.47)$, $(\alpha _{1}, \alpha _{2})=(0.5, 0.8)$, $(\beta _{1}, \beta _{2})=(0.6, 0.7)$. Ii is easy to see that ${\varvec{p}}{\mathop {\ge }\limits ^{m}} {\varvec{q}}$, $\varvec{\alpha } {\mathop {\ge }\limits ^{m}} \varvec{\beta }$, $({\varvec{p}}, \varvec{\alpha }) \in {\mathcal {S}}_{2}$ and $({\varvec{q}}, \varvec{\beta }) \in {\mathcal {S}}_{2}$. Thus, all conditions of Theorem 3.4 are satisfied. In this case the ratio of the densities is as follows:

$$\begin{aligned} g(x)=\frac{0.265 \exp (-0.5 x)+0.376 \exp (-0.8 x) }{0.318 \exp (-0.6 x)+0.329 \exp (-0.7 x)}. \end{aligned}$$

Figure 2 depicts the plot of $g(x)=\frac{f(x; {\varvec{p}}, \varvec{\alpha })}{f(x; {\varvec{q}}, \varvec{\beta })}$. One can see that, from Fig. 2, g(x) is not monotone function in x, which indicates that the likelihood ratio ordering does not hold between $F(x; {\varvec{p}}, \varvec{\alpha })$ and $F(x; {\varvec{q}}, \varvec{\beta })$.

Fig. 2

g(x) in Counterexample 3.15 for $x \in [0,4]$

4 Stochastic comparisons of geometric mixtures

In this section, we consider the geometric mixture model (4) and provide some stochastic comparisons in the sense of the usual stochastic order and the reversed hazard rate order. If we denote by ${\tilde{r}}_{F_G}(x; {\varvec{p}})$ the reversed hazard rate of geometric mixture model (4), we have

$$\begin{aligned} {\tilde{r}}_{F_G}(x; {\varvec{p}})=\sum _{i=1}^{n} p_{i}{\tilde{r}}_{i}(x), \end{aligned}$$

where ${\tilde{r}}_{i}(x)$, $i=1, \ldots , n$, is the reversed hazard rate corresponding to i-th subpopulation. This, in turn, implies that the time behavior of the reversed hazard rate of $F_{G}(x;{\varvec{p}})$ depends of time the behavior the reversed hazard rate ${\tilde{r}}_{i}(x)$, $i=1, \ldots , n$. For example, if ${\tilde{r}}_{i}(x)$, $i=1, \ldots , n$, are increasing (decreasing) reversed hazard rate so is the reversed hazard rate of $F_{G}(x;{\varvec{p}})$. Also, if we denote by ${\tilde{r}}_{\min }(x)=\min \{ {\tilde{r}}_{1}(x), \ldots , {\tilde{r}}_{n}(x)\}$ and ${\tilde{r}}_{\max }(x)=\max \{ {\tilde{r}}_{1}(x), \ldots , {\tilde{r}}_{n}(x)\}$, then we have

$$\begin{aligned} {\tilde{r}}_{\min }(x) \le {\tilde{r}}_{F_G}(x; {\varvec{p}}) \le {\tilde{r}}_{\max }(x). \end{aligned}$$

In the next theorem, we extend a result of Navarro and Aguila (2017) on arithmetic mixture to the geometric mixture model.

Theorem 4.1

Let $F_{G}(x;{\varvec{p}})$ and $F_{G}(x;{\varvec{q}})$ be two n-component finite geometric mixture models with mixing probabilities ${{\varvec{p}}=(p_{1}, \ldots , p_{n})}$ and ${{\varvec{q}}=(q_{1}, \ldots , q_{n})}$, respectively. Assume that

$$\begin{aligned} F_{1} \ge _{st} F_{2} \ge _{st} \cdots \ge _{st}F_{n}. \end{aligned}$$

Then,

$$\begin{aligned} F_{G}(x;{\varvec{p}})\le _{st} F_{G}(x;{\varvec{q}}) \end{aligned}$$

if and only if ${\varvec{p}} \ge _{st}{\varvec{q}}$ (i.e. $\sum _{i=1}^{k}q_{i}\ge \sum _{i=1}^{k}p_{i}$ for all $k \in \lbrace 1,2, \ldots ,n-1\rbrace$).

Proof

To proof the “if ” part of the theorem, note that by assumption $F_{1} \ge _{st} F_{2} \ge _{st} \cdots \ge _{st}F_{n}$, we have: $F_{1} \le F_{2} \le \cdots \le F_{n}$. Thus, $F_{i}$ is increasing in $i=1, 2, \ldots , n$, and hence $\phi (i)=\log F_{i}$ is increasing in $i=1, 2, \ldots , n$. Now, by assumption ${\varvec{p}} \ge _{st}{\varvec{q}}$ we have:

$$\begin{aligned} \sum _{i=1}^{n} p_{i}\log F_{i} \ge \sum _{i=1}^{n} q_{i}\log F_{i}. \end{aligned}$$

Hence,

$$\begin{aligned} F_{G}(x;{\varvec{p}})=\exp \bigg (\sum _{i=1}^{n} p_{i}\log F_{i}\bigg ) \ge \exp \bigg (\sum _{i=1}^{n} q_{i}\log F_{i} \bigg )=F_{G}(x;{\varvec{q}}). \end{aligned}$$

This means that $F_{G}(x;{\varvec{p}})\le _{st} F_{G}(x;{\varvec{q}})$.

To prove the “only if ” part of the theorem, note that from $F_{G}(x;{\varvec{p}})\le _{st} F_{G}(x;{\varvec{q}})$, we get

$$\begin{aligned} {F}_{1}^{p_{1}} \cdots {F}_{k}^{p_{k}} \cdots {F}_{n}^{1-\sum _{i=1}^{n-1}p_{i}}\ge {F}_{1}^{q_{1}} \cdots {F}_{k}^{q_{k}} \cdots {F}_{n}^{1-\sum _{i=1}^{n-1}q_{i}}. \end{aligned}$$

This is equivalent to

$$\begin{aligned} 1 \le \left( \frac{{F}_{2}}{{F}_{1}} \right) ^{p_{2}-q_{2}} \cdots \left( \frac{{F}_{k}}{{F}_{1}} \right) ^{p_{k}-q_{k}} \cdots \left( \frac{{F}_{n}}{{F}_{1}} \right) ^{p_{n}-q_{n}}. \end{aligned}$$

From the assumption $F_{1} \ge _{st} F_{2} \ge _{st} \cdots \ge _{st}F_{n}$ with choosing ${F}_{1}={F}_{2}= \cdots ={F}_{k}$ and ${F}_{k+1}= \cdots ={F}_{n-1}={F}_{n}=1$, we have

$$\begin{aligned} 1\le ({{F}_{1}})^{(\sum _{i=k+11}^{n}q_{i}-\sum _{i=k+1}^{n}p_{i})}. \end{aligned}$$

Hence, $\sum _{i=k+1}^{n}p_{i}\ge \sum _{i=k+1}^{n}q_{i}$, i.e., ${\varvec{p}} \ge _{st} {\varvec{q}}$ and the proof is completed.

$\square$

In the following theorem, we extend the “if” part of Theorem 4.1.

Theorem 4.2

Let $F_{G}(x;{\varvec{p}})$ and $G_{G}(x;{\varvec{q}})$ be two n-component finite geometric mixture models with mixing probabilities ${{\varvec{p}}=(p_{1}, \ldots , p_{n})}$ and ${{\varvec{q}}=(q_{1}, \ldots , q_{n})}$, respectively. Assume that

• (i) $F_{1}\ge _{st}F_{2}\ge _{st} \cdots {\ge _{st}} F_{n}$,

• (ii) ${\varvec{p}}\ge _{st}{\varvec{q}}$ (i.e. $\sum _{i=1}^{k}q_{i}\ge \sum _{i=1}^{k}p_{i}$ for all $k \in \lbrace 1,2,\ldots ,n-1\rbrace$),

• (iii) $F_{i} \le _{st} G_{i}$ for all ${i \in \{1,\ldots , n\}}$.

Then, we have:

$$\begin{aligned} F_{G}(x;{\varvec{p}})\le _{st} G_{G}(x;{\varvec{q}}). \end{aligned}$$

Proof

To proof the theorem, first, we prove that $F_{G}(x;{\varvec{q}})\le _{st} G_{G}(x;{\varvec{q}})$. From $F_{i} \le _{st} G_{i}$ for $i=1,\ldots ,n$, we have ${F}_{i}(x) \ge {G}_{i}(x)$ for any x, $i=1,\ldots ,n$. Hence,

$$\begin{aligned} \prod _{i=1}^{n}{F}^{{q}_{i}}_{i} \ge \prod _{i=1}^{n}{G}^{{q}_{i}}_{i}. \end{aligned}$$

Thus,

$$\begin{aligned} F_{G}(x;{\varvec{q}})\le _{st} G_{G}(x;{\varvec{q}}). \end{aligned}$$

(5)

From conditions (i), (ii) and Theorem 4.1 we have: $F_{G}(x;{\varvec{p}})\le _{st} F_{G}(x;{\varvec{q}})$. By relation (5), $F_{G}(x;{\varvec{q}})\le _{st} G_{G}(x;{\varvec{q}})$. Thus, $F_{G}(x;{\varvec{p}})\le _{st} G_{G}(x;{\varvec{q}})$. This complete the proof. $\square$

The following example is an application of Theorem 4.2.

Example 4.3

Suppose that in the first population the mixing probabilities are ${\varvec{p}}=(p_{1}, p_{2}, p_{3})=(\frac{1}{3}, \frac{1}{3}, \frac{1}{3})$, and each component has an exponential distribution with SF ${\bar{F}}_{i}(t)=e^{-\lambda _{i} t}$, for $t \in [0,+\infty )$, where $(\lambda _{1}, \lambda _{2}, \lambda _{3})=(0.3, 0.6, 0.9)$, while in the second population there exist unequal mixing probabilities ${\varvec{q}}=(q_{1}, q_{2}, q_{3})=(0.45, 0.45, 0.1)$, and each component has an exponential distribution with SF ${\bar{G}}_{i}(t)=e^{-\gamma _{i} t}$, for $t \in [0,+\infty )$, where $(\gamma _{1}, \gamma _{2}, \gamma _{3})=(0.2, 0.5, 0.8)$. It is easy to see that all condition of Theorem 4.2 are satisfied.

The following theorem extends a result of Amini and Zhang (2017) on arithmetic mixture to the geometric mixture model.

Theorem 4.4

Let $F_{G}(x;{\varvec{p}})$ and $G_{G}(x;{\varvec{q}})$ be two n-component finite geometric mixture models with mixing probabilities ${{\varvec{p}}=(p_{1},\ldots , p_{n})}$ and ${{\varvec{q}}=(q_{1},\ldots , q_{n})}$, respectively. Assume that

• (i) $F_{1}\ge _{rh}F_{2}\ge _{rh} \cdots {\ge _{rh}} F_{n}$,

• (ii) ${\varvec{p}}\ge _{st}{\varvec{q}}$ (i.e. $\sum _{i=1}^{k}q_{i}\ge \sum _{i=1}^{k}p_{i}$ for all $k \in \lbrace 1,2,\ldots ,n-1\rbrace$),

• (iii) $F_{i} \le _{rh} G_{i}$ for all ${i \in \{1,\ldots ,n\}}$.

Then, we have:

$$\begin{aligned} F_{G}(x;{\varvec{p}})\le _{rh} G_{G}(x;{\varvec{q}}). \end{aligned}$$

Proof

First we prove that $F_{G}(x;{\varvec{p}})\le _{rh} F_{G}(x;{\varvec{q}})$. In order to prove this it is enough to show that ${\tilde{r}}_{F_G}(x; {\varvec{p}}) - {\tilde{r}}_{F_G}(x; {\varvec{q}}) \ge 0$, where ${\tilde{r}}_{F_G}(x; {\varvec{p}})$ and ${\tilde{r}}_{F_G}(x; {\varvec{q}})$ are the reversed hazard rates corresponding to $F_{G}(x;{\varvec{p}})$ and $F_{G}(x;{\varvec{q}})$, respectively. From assumption $F_{1}\ge _{rh}F_{2}\ge _{rh} \cdots {\ge _{rh}} F_{n}$, we have ${\tilde{r}}_{1}(x) \ge {\tilde{r}}_{2}(x) \ge \cdots \ge {\tilde{r}}_{n}(x)$. On the other hand, we can rewritten ${\tilde{r}}_{F_G}(x; {\varvec{p}}) - {\tilde{r}}_{F_G}(x; {\varvec{q}})=\sum _{i=1}^{n} {\tilde{r}}_{i}(x) (p_{i}-q_{i})$ as follows:

$$\begin{aligned} \sum _{i=1}^{n} {\tilde{r}}_{i}(x) (p_{i}-q_{i})&=\big ({\tilde{r}}_{n}(x)-{\tilde{r}}_{n-1}(x)\big )\big (p_{n}-q_{n}\big )\\&\quad + \big ({\tilde{r}}_{n-1}(x)-{\tilde{r}}_{n-2}(x)\big )\Big (\sum _{i=n-1}^{n}(p_{i}-q_{i})\Big )\\&\quad + \big ({\tilde{r}}_{n-2}(x)-{\tilde{r}}_{n-3}(x)\big )\Big (\sum _{i=n-2}^{n}(p_{i}-q_{i})\Big )+ \cdots \\&\quad + \big ({\tilde{r}}_{2}(x)-{\tilde{r}}_{1}(x)\big )\Big (\sum _{i=2}^{n}(p_{i}-q_{i})\Big )\\&\quad +{\tilde{r}}_{1}(x)\Big (\sum _{i=1}^{n}(p_{i}-q_{i})\Big ). \end{aligned}$$

(it is clear that the coefficients of ${\tilde{r}}_{i}$’s are equal on both sides of the equation) Thus $\sum _{i=1}^{n} {\tilde{r}}_{i}(x) (p_{i}-q_{i}) \le 0$ because $\big ({\tilde{r}}_{i}(x)-{\tilde{r}}_{j}(x)\big ) \le 0$ for all $i \ge j$, $i,j=1,2,\ldots ,n$ and also from assumption, $\sum _{i=k}^{n} p_{i} \ge \sum _{i=k}^{n} q_{i}$ for all $k \in \{1, 2,\ldots , n-1\}$. Thus,

$$\begin{aligned} F_{G}(x;{\varvec{p}})\le _{rh} F_{G}(x;{\varvec{q}}). \end{aligned}$$

(6)

Now, we prove that $F_{G}(x;{\varvec{p}})\le _{rh} G_{G}(x;{\varvec{p}})$. We must to show that ${\tilde{r}}_{F_{G}}(x;{\varvec{p}}) \le {\tilde{r}}_{G_{G}}(x;{\varvec{p}})$ or, equivalently, ${\tilde{r}}_{F_{G}}(x;{\varvec{p}}) - {\tilde{r}}_{G_{G}}(x;{\varvec{p}}) \le 0$, where ${\tilde{r}}_{G_{G}}(x;{\varvec{p}})$ is the reversed hazard rate of $G_{G}(x;{\varvec{p}})$. Obviously,

$$\begin{aligned} {\tilde{r}}_{F_{G}}(x;{\varvec{p}}) - {\tilde{r}}_{G_{G}}(x;{\varvec{p}})=\sum _{i=1}^{n} p_{i}\big ({\tilde{r}}_{F_i}(x)-{\tilde{r}}_{G_i}(x)\big ), \end{aligned}$$

where ${\tilde{r}}_{F_i}(x)$ and ${\tilde{r}}_{G_i}(x)$, $i=1, \ldots , n$ are the reversed hazard rates of $F_{i}$ and $G_{i}$, $i=1, \ldots , n$, respectively. From assumption $F_i\le _{rh} G_i$, we have: ${\tilde{r}}_{F_i}(x)-{\tilde{r}}_{G_i}(x)\le 0$ and thus,

$$\begin{aligned} F_{G}(x;{\varvec{p}})\le _{rh} G_{G}(x;{\varvec{p}}). \end{aligned}$$

(7)

From (6), $F_{G}(x;{\varvec{p}})\le _{rh} F_{G}(x;{\varvec{q}})$. On the other hand, from (7), it can be derived that $F_{G}(x;{\varvec{q}})\le _{rh} G_{G}(x;{\varvec{q}})$. Hence, we obtain that $F_{G}(x;{\varvec{p}})\le _{rh} G_{G}(x;{\varvec{q}})$. This complete the proof. $\square$

Remark 4.5

All the results of Sect. 4 for the geometric mixture model $F_{G}(x;{\varvec{p}})$ in (4) were based on assumption $\sum _{i=1}^{n}p_i=1$. This model, as mentioned before, is a special case of generalized proportional reversed hazards model in which $p_{i}$’s can be any arbitrary positive real numbers. It should be noted that all the results related to the geometric mixture model are remain valid for the generalized proportional reversed hazard model.

To end this section, we can give the following lower bound for the arithmetic mixture by using the weighted arithmetic mean-geometric mean inequality (Li et al., 2018):

$$\begin{aligned} F_{G}(x;{\varvec{p}})= \prod _{i=1}^{n}{F}^{{p}_{i}}_{i}(x) \le \sum _{i=1}^{n} p_{i} F_{i}(x)= F(x; {\varvec{p}}). \end{aligned}$$

5 Conclusions

In this paper, we have considered the mixture models as suitable tools for considering heterogeneity in populations. Our interest stems from the fact that populations with specific components, such as the lifetime, are usually heterogeneous. We have proposed the arithmetic (finite) mixture models by using the effect of severe conditions (in the terms of proportional reversed hazard rate model). We have arrived at the geometric mixture models. Furthermore, we have provided some examples interpreting the use of the arithmetic and the geometric mixture models. We have obtained the sufficient conditions, using the concept of majorization, to compare two arithmetic mixture models in the sense of the usual stochastic order, the hazard rate order, the reversed hazard rate order and the dispersive order. In fact, we have extended the results given in the literature to a general case and some other semiparametric families of distributions. To help better understand the assumptions and limitations, we have employed the some numerical examples and counterexamples. We have provided the sufficient conditions for stochastic comparisons of two geometric mixture models in the sense of the usual stochastic order and the reversed hazard rate order with different mixing probabilities and different baseline random variables. Finally, the obtained results can straightforwardly be used on reliability analysis when populations are heterogeneous.