Stochastic comparisons of distorted distributions, coherent systems and mixtures with ordered components

Abstract

A distribution function F is a generalized distorted distribution of the distribution functions $F_1,\ldots ,F_n$ if $F=Q(F_1,\ldots ,F_n)$ for an increasing continuous distortion function Q such that $Q(0,\ldots ,0)=0$ and $Q(1,\ldots ,1)=1$. In this paper, necessary and sufficient conditions for the stochastic (ST) and the hazard rate (HR) orderings of generalized distorted distributions are provided when the distributions $F_1,\ldots ,F_n$ are ordered. These results are used to obtain distribution-free ordering properties for coherent systems with heterogeneous components. In particular, we determine all the ST and HR orderings for coherent systems with 1–3 independent components. We also compare systems with dependent components. The results on distorted distributions are also used to get comparisons of finite mixtures.

1 Introduction

The stochastic comparison of coherent systems is a relevant problem in the reliability theory. Several results have been provided for systems with independent and identically distributed (IID) components. Sufficient conditions for the stochastic (ST), hazard rate (HR) and likelihood ratio (LR) orderings were given in Kochar et al. (1999). These conditions are based on the mixture representation for the system distribution obtained from the system signature, see, e.g., Samaniego (2007). They are distribution-free, that is, they do not depend on the common distribution of the components. Similar sufficient conditions were given in Navarro et al. (2008) to obtain comparisons between systems with different numbers of components comparing all the coherent systems with 1–4 IID components. Recently, necessary and sufficient conditions for comparison of systems with IID components were provided in Navarro (2016). They were used to get all the orderings between systems with 1–4 IID components. Sufficient conditions for the mean residual life order were stated in Navarro and Gomis (2016) for systems with IID components. The results for the IID case were extended to coherent systems with exchangeable (dependent) components in Navarro et al. (2008). In Navarro and Rubio (2011) it was proved that these conditions are necessary and sufficient conditions for the orderings of coherent systems with exchangeable components. Further results can be seen in Navarro and Rychlik (2010).

However, in practice, in many situations the components cannot be assumed to be identically distributed (ID). In the literature, there are few results on distribution-free comparisons of coherent systems with heterogeneous (non ID) components. Balakrishnan and Torrado (2016) provided comparison results for parallel systems with independent components. Some sufficient conditions for the stochastic order of coherent systems were obtained in Navarro and Rubio (2012). They were used to get ST ordering properties for systems with 1–3 independent components. Recent results on residual lifetimes and inactivity times of systems can be seen in Zhang and Balakrishnan (2016), Goli and Asadi (2017) and Samadi et al. (2017).

The distribution of a coherent system with heterogeneous (possibly dependent) components can be represented as a generalized distorted distribution of the component distributions, that is, it can be written as

$$\begin{aligned} F(t)=Q(F_1(t),\ldots ,F_n(t)) \end{aligned}$$

where $F_1,\ldots ,F_n$ represent the component distribution functions and the distortion (or aggregation) function $Q:[0,1]^n\rightarrow [0,1]$ is an increasing continuous function such that $Q(0,\ldots ,0)=0$ and $Q(1,\ldots ,1)=1$. The generalized distorted distributions were defined in Navarro et al. (2014) extending the well known concept of distorted distributions obtained when $n=1$. Ordering properties for distorted and generalized distorted distributions were given in Navarro et al. (2013, 2014, 2015, 2016) and Navarro and Rychlik (2010). These results were used to provide ordering properties for systems with homogeneous and heterogeneous components in Navarro (2016), Navarro et al. (2016) and Samaniego and Navarro (2016).

In this paper, we obtain necessary and sufficient conditions for the stochastic, hazard rate and reversed hazard rate orderings of generalized distorted distributions when the baseline distribution functions $F_1,\ldots ,F_n$ are ordered (Sect. 2). These results improve the results for the ST order given in Navarro and Rubio (2012). These conditions are used (Sect. 3) jointly with the results given in Navarro et al. (2016) to get all the orderings properties for coherent systems with 1–3 independent components. We consider both the case of arbitrary components and the case of ordered components. The conditions obtained here can also be applied to compare coherent systems with heterogeneous dependent components. The conditions for generalized distorted distributions are also applied (Sect. 4) to provide distribution-free ordering properties for finite mixtures when the baseline members of the mixture are ordered.

Throughout the paper, we say that a function $h:{\mathbb {R}}^n\rightarrow {\mathbb {R}}$ is increasing (decreasing) if $h(x_1,\ldots ,x_n)\le (\ge ) h(y_1,\ldots ,y_n)$ for all $x_i\le y_i$, $i=1,\ldots ,n$. Analogously, if g, h are two functions $g,h:S\rightarrow {\mathbb {R}}$, then $g\le h$ means that $g(x_1,\ldots ,x_n)\le h(x_1,\ldots ,x_n)$ for all $(x_1,\ldots ,x_n)\in S$. We shall use the notation $D_i h$ for the partial derivative of function h with respect to its $i\hbox {th}$ variable. To simplify the notation, the product $\prod _{i=1}^n x_i$ is represented as $x_1\ldots x_n$.

Next we give the definitions of the stochastic orderings studied in this paper. Their basic properties and some applications can be seen in Barlow and Proschan (1975), Shaked and Shanthikumar (2007) and Belzunce et al. (2016). Let X and Y be two non-negative random variables with distribution functions $F_X$ and $F_Y$ and reliability functions $\overline{F}_X=1-F_X$ and $\overline{F}_Y=1-F_Y$. Then:

(i) We say that X is less than Y in the (usual) stochastic (ST) order (shortly written as $X\le _{ST}Y$ or as $F_X\le _{ST} F_Y$) if $\overline{F}_X\le \overline{F}_Y.$

(ii) We say that X is less than Y in the hazard rate (HR) order (shortly written as $X\le _{HR}Y$ or as $F_X\le _{HR} F_Y$) if $\overline{F}_Y/\overline{F}_X$ is increasing.

(iii) We say that X is less than Y in the reversed hazard rate (RHR) order (shortly written as $X\le _{RHR}Y$ or as $F_X\le _{RHR} F_Y$) if $F_Y/F_X$ is increasing.

In the ratios considered in (ii) and (iii), we take $a/b=+\infty$ for $a>0$ and $b=0$. They are not considered when $a=b=0$.

If X and Y have finite means and $X\le _{ST}Y$ holds, then $E(X)\le E(Y)$. The meaning of the HR ordering is deduced from the following equivalence: $X\le _{HR}Y$ if and only if

$$\begin{aligned} (X-t|X>t)\le _{ST} (Y-t|Y>t) \end{aligned}$$

for all $t\ge 0$ such that these conditional distributions are defined, that is, their residual lifetimes are ST ordered for any age $t\ge 0$. The HR order implies the ST order. Analogously, the meaning of the RHR order is obtained from the following equivalence: $X\le _{RHR}Y$ if and only if

$$\begin{aligned} (t-X|X\le t)\ge _{ST} (t-Y|Y\le t) \end{aligned}$$

for all $t\ge 0$ such that these conditional distributions are defined, that is, the inactivity times are ST ordered for any age $t\ge 0$. The RHR ordering implies the ST order. The relationships between these stochastic orders are the following:

2 Comparisons of generalized distorted distributions

First we give the formal definition of generalized distorted distributions given in Navarro et al. (2014).

Definition 1

We say that a distribution function F is a generalized distorted distribution (GDD) of the distribution functions $F_1,\ldots ,F_n$ if

$$\begin{aligned} F(t)=Q(F_1(t),\ldots ,F_n(t)) \end{aligned}$$

(1)

for all t, where the distortion (or aggregation) function $Q:[0,1]^n\rightarrow [0,1]$ is an increasing continuous function such that $Q(0,\ldots ,0)=0$ and $Q(1,\ldots ,1)=1$.

Note that the conditions on Q are enough to assure that the right hand side of (1) defines a proper distribution function for all distribution functions $F_1,\ldots ,F_n$. Also note that representation (1) is similar to a copula representation but that here F is a univariate distribution function while copulas are used to obtain multivariate distributions. If $n=1$ then F is called a distorted distribution. The distorted distributions were introduced in the Risk Theory to represent uncertainty, see Hürlimann (2004) and the references therein. They can also be used to represent coherent systems with identically distributed (ID) components, see Navarro et al. (2013). The generalized distorted distributions were introduced in Navarro et al. (2014, 2016) and they can be used to represent the distributions of coherent systems with non-ID (NID) components. They can also be used to represent finite mixtures and other statistical distributions.

If representation (1) holds, then the respective reliability functions $\overline{F}=1-F$, $\overline{F}_1=1-F_1,\ldots ,\overline{F}_n=1-F_n$ satisfy

$$\begin{aligned} \overline{F}(t)=\overline{Q}(\overline{F}_1(t),\ldots ,\overline{F}_n(t)) \end{aligned}$$

(2)

for all t, where $\overline{Q}$ is called the dual distortion function (see Hürlimann 2004) and can be written as

$$\begin{aligned} \overline{Q}(u_1,\ldots ,u_n)=1-Q(1-u_1,\ldots ,1-u_n) \end{aligned}$$

for $u_1,\ldots ,u_n\in [0,1]$. The function $\overline{Q}$ satisfies the same properties as Q, that is, it is an increasing continuous function in $[0,1]^n$ such that $\overline{Q}(0,\ldots ,0)=0$ and $\overline{Q}(1,\ldots ,1)=1$. Representations (1) and (2) are equivalent but sometimes it is better to use (2) instead of (1) (or vice versa).

The first ordering results for generalized distorted distributions are given in the following proposition extracted from Navarro et al. (2016).

Proposition 1

Let $F_{Q_1}=Q_1(F_1,\ldots ,F_n)$ and $F_{Q_2}=Q_2(F_1,\ldots ,F_n)$ be two GDD based on $F_1,\ldots ,F_n$. Then:

(i) $F_{Q_1}\le _{ST}F_{Q_2}$ for all $F_1,\ldots ,F_n$ if and only if $\overline{Q}_1\le \overline{Q}_2$ in $[0,1]^n$.

(ii) $F_{Q_1}\le _{HR}F_{Q_2}$ for all $F_1,\ldots ,F_n$ if and only if $\overline{Q}_2/\overline{Q}_1$ is decreasing in $[0,1]^n$.

(iii) $F_{Q_1}\le _{RHR}F_{Q_2}$ for all $F_1,\ldots ,F_n$ if and only if $Q_2/Q_1$ is increasing in $[0,1]^n$.

The preceding proposition will be used in the next section to compare coherent systems with arbitrary components. In some situations it could be of interest to assume that the components are ordered. In this case we will need the following new results for generalized distorted distributions. The result for the ST order can be stated as follows.

Proposition 2

Let $F_{Q_1}=Q_1(F_1,\ldots ,F_n)$ and $F_{Q_2}=Q_2(F_1,\ldots ,F_n)$ be two GDD based on $F_1,\ldots ,F_n$. Then $F_{Q_1}\le _{ST}F_{Q_2}$ for all $F_1,\ldots ,F_n$ such that

$$\begin{aligned} F_1\ge _{ST} \ldots \ge _{ST} F_n \end{aligned}$$

holds if and only if $\overline{Q}_1\le \overline{Q}_2$ in $D=\{(u_1,\ldots ,u_n)\in [0,1]^n: u_1\ge \cdots \ge u_n\}$.

The proof is immediate. A similar result can be obtained by using the distortion functions $Q_1$ and $Q_2$.

Analogously, we have the following result for the HR order of generalized distorted distributions with HR ordered baseline distributions. This is the main theoretical result of the paper.

Proposition 3

Let $F_{Q_1}=Q_1(F_1,\ldots ,F_n)$ and $F_{Q_2}=Q_2(F_1,\ldots ,F_n)$ be two GDD based on $F_1,\ldots ,F_n$. Then $F_{Q_1}\le _{HR}F_{Q_2}$ for all $F_1,\ldots ,F_n$ such that

$$\begin{aligned} F_1\ge _{HR} \cdots \ge _{HR} F_n \end{aligned}$$

(3)

holds if and only if the function

$$\begin{aligned} H(v_1,\ldots ,v_n)=\frac{\overline{Q}_2(v_1,v_1v_2,\ldots ,v_1\ldots v_n)}{\overline{Q}_1(v_1,v_1v_2,\ldots ,v_1\ldots v_n)} \end{aligned}$$

(4)

is decreasing in $[0,1]^n$.

Proof

First, we note that if (3) holds, then the function $\overline{F}_{i+1}(t)/\overline{F}_{i}(t)$ is decreasing in t and so $\overline{F}_{i+1}(t)/\overline{F}_{i}(t)\in [0,1]$ for all t and $i=1,\ldots ,n-1$. Hence the ratio $\overline{F}_{Q_2}/\overline{F}_{Q_1}$ can be written as

$$\begin{aligned} \frac{\overline{F}_{Q_2}(t)}{\overline{F}_{Q_1}(t)} =H\left( \overline{F}_1(t),\frac{\overline{F}_{2}(t)}{\overline{F}_{1}(t)},\ldots , \frac{\overline{F}_{n}(t)}{\overline{F}_{n-1}(t)}\right) \end{aligned}$$

(5)

for the function H defined by (4).

To prove that it is a sufficient condition for the hazard rate ordering note that $\overline{F}_1$ is always decreasing and if $\overline{F}_{i+1}/\overline{F}_{i}$ is decreasing and H is decreasing, then, from the preceding representation (5), the ratio $\overline{F}_{Q_2}/\overline{F}_{Q_1}$ is increasing and $F_{Q_1}\le _{HR}F_{Q_2}$ holds.

Let us prove now that it is a necessary condition. Clearly, it is enough to study the monotonicity of H over $(0,1)^n$. Fix $\varvec{u}\le \varvec{v}$ with $\varvec{u}=(u_1,\ldots ,u_n)$ and $\varvec{v}=(v_1,\ldots ,v_n)$. We want to show that $H(\varvec{u})\ge H(\varvec{v})$. Let us consider the following reliability functions

$$\begin{aligned} \overline{F}_i(t)= \left\{ \begin{array}{l@{\quad }l} 1, &{} t<1\\ v_1\ldots v_i, &{} 1\le t<2\\ u_1\ldots u_i, &{} 2\le t <3\\ 0, &{} t \ge 3 \end{array} \right. \end{aligned}$$

for $i = 1,\ldots ,n$. It is easy to see that $F_1\ge _{HR} \cdots \ge _{HR} F_n$. Furthermore, $F_{Q_1}\le _{HR}F_{Q_2}$ implies

$$\begin{aligned} \frac{\overline{F}_{Q_2}(1)}{\overline{F}_{Q_1}(1)}\le \frac{\overline{F}_{Q_2}(2)}{\overline{F}_{Q_1}(2)} \end{aligned}$$

which, from (5), is equivalent to $H(\varvec{u})\ge H(\varvec{v})$. $\square$

Example 1 shows how the preceding propositions can be applied to compare coherent systems with ordered components. To this purpose we just need to study the monotonicity of the function H defined in (4) in the set $(0,1)^n$. This proposition is also used to obtain the results given in Table 3 and, in Sect. 4, to compare finite mixtures. A similar proposition for the RHR ordering is stated in the following proposition. The proof is analogous to that of the preceding proposition.

Proposition 4

Let $F_{Q_1}=Q_1(F_1,\ldots ,F_n)$ and $F_{Q_2}=Q_2(F_1,\ldots ,F_n)$ be two GDD based on $F_1,\ldots ,F_n$. Then $F_{Q_1}\le _{RHR}F_{Q_2}$ for all $F_1,\ldots ,F_n$ such that

$$\begin{aligned} F_1\le _{RHR} \cdots \le _{RHR} F_n \end{aligned}$$

(6)

holds if and only if the function

$$\begin{aligned} \frac{Q_2(v_1,v_1v_2,\ldots ,v_1\ldots v_n)}{Q_1(v_1,v_1v_2,\ldots ,v_1\ldots v_n)} \end{aligned}$$

(7)

is increasing in $[0,1]^n$.

3 Comparisons of coherent systems

First we note that, if T is the lifetime of a coherent system with component lifetimes $X_1,\ldots ,X_n$ having distribution functions $F_1,\ldots ,F_n$, then the system distribution $F_T$ can be written (see, e.g., Navarro et al. 2014, 2016) as

$$\begin{aligned} F_T(t)=Q(F_1(t),\ldots ,F_n(t)) \end{aligned}$$

(8)

for all t, that is, it is a generalized distortion distribution of the component distribution functions, where the distortion function Q only depends on the structure of the system and on the copula of the random vector $(X_1,\ldots ,X_n)$.

The respective reliability functions $\overline{F}_T=1-F_T$, $\overline{F}_1=1-F_1,\ldots ,\overline{F}_n=1-F_n$ satisfy

$$\begin{aligned} \overline{F}_T(t)=\overline{Q}(\overline{F}_1(t),\ldots ,\overline{F}_n(t)) \end{aligned}$$

(9)

for all t, where $\overline{Q}$ is the dual distortion function associated to Q. If the components are independent, then the function $\overline{Q}$ is a strictly increasing multinomial in $[0,1]^n$ called reliability function of the structure (see Barlow and Proschan 1975, p. 21). The $\overline{Q}$ functions for all the systems with 1–3 independent components are given in Table 1.

Table 1 Dual distortions functions of coherent systems with 1–3 INID components

Table 2 Relationships for the ST order between the coherent systems with independent components given in Table 1

Then we can use the results included in the preceding section to provide necessary and sufficient conditions for the ST, HR and RHR ordering properties of coherent systems. In our opinion, it is more interesting to study comparison results when the components are ordered since, under this assumption, we have different systems depending on how we place the different components. These results could also be used to study where the best components should be placed at the system structure to obtain a more reliable system. Some comparison results in this direction were also given in Navarro and Rubio (2012) for the ST order under the condition

$$\begin{aligned} X_1\ge _{ST}\cdots \ge _{ST}X_n. \end{aligned}$$

(10)

These results were obtained by using a sufficient condition based on the graph signature of the system. We can provide better results now by using the necessary and sufficient conditions for the ST order given in Proposition 2. By applying this proposition to systems with 1–3 independent components satisfying (10), we have the properties given in Table 2. These ordering results coincide with that obtained in Navarro and Rubio (2012). Note that now we know that these are all the distribution-free ST orderings for these systems. Also note that the results are different from that obtained without condition (10) (given also in Table 2). Moreover, the comparison results provided here can also be applied to systems with dependent components.

In our knowledge, in the literature there are no distribution-free comparison results for HR orderings of general coherent system with heterogeneous components. Some results for parallel systems were given in Balakrishnan and Torrado (2016). In this case we are going to assume the following condition for the component lifetimes

$$\begin{aligned} X_1\ge _{HR}\cdots \ge _{HR}X_n. \end{aligned}$$

(11)

To get necessary and sufficient conditions for the HR order under (11) we shall use Proposition 3. Let us see a simple example on how this proposition can be applied.

Example 1

Let us consider a parallel system with two independent components with reliability functions $\overline{F}_1,\overline{F}_2$. Then $T=X_{2:2}=\max (X_1,X_2)$ and the system reliability is

$$\begin{aligned} \overline{F}_T(t) =\overline{F}_1(t)+\overline{F}_2(t)-\overline{F}_1(t)\overline{F}_2(t)=\overline{Q}(\overline{F}_1(t),\overline{F}_2(t)), \end{aligned}$$

where $\overline{Q}(u_1,u_2)=u_1+u_2-u_1u_2$. Hence, as

$$\begin{aligned} \frac{\overline{Q}(u_1,u_2)}{u_1}=\frac{u_1+u_2-u_1u_2}{u_1}=1+u_2(-1+1/u_1) \end{aligned}$$

is decreasing in $u_1$ and increasing in $u_2$ in the set $(0,1)^2$, by Proposition 1, (ii), we have that T and $X_1$ are not HR ordered (for all $F_1,F_2$). In a similar way, it can be proved that T and $X_2$ are not HR ordered (for all $F_1,F_2$). Note that this is a quite unexpected property (the parallel system should be better than its components). However, as

$$\begin{aligned} \frac{\overline{Q}(u_1,u_2)}{u_1u_2}=\frac{u_1+u_2-u_1u_2}{u_1u_2}=\frac{1}{u_2}+\frac{1}{u_1}-1 \end{aligned}$$

is decreasing, by Proposition 1, (ii), we obtain $X_{1:2}\le _{HR}X_{2:2}$ for all $F_1,F_2$, that is, the series system is HR-worse than the parallel system when the components are independent (a well known property). Surprisingly, this property is not necessarily true for dependent components, see Navarro and Shaked (2006). Of course, we always have $X_{1:2}\le _{ST}X_{i}\le _{ST}X_{2:2}$ for $i=1,2$.

Now we add the condition

$$\begin{aligned} X_1\ge _{HR}X_2, \end{aligned}$$

(12)

that is, the first component is HR better than the second one. Under this condition, if we want to compare T with $X_2$ (the worst component) by using Proposition 3, we obtain the function

$$\begin{aligned} H(v_1,v_2)=\frac{\overline{Q}(v_1,v_1v_2)}{v_1v_2}=\frac{v_1+v_1v_2-v^2_1v_2}{v_1v_2}=1-v_1+\frac{1}{v_2}. \end{aligned}$$

As H is a decreasing function in $(0,1]^2$, we have $X_2\le _{HR}T$ for all $F_1,F_2$ satisfying (12).

However, if we want to compare T with $X_1$ (the best component) by using Proposition 3, we get

$$\begin{aligned} H(v_1,v_2)=\frac{v_1+v_1v_2-v^2_1v_2}{v_1}=1+v_2(1-v_1). \end{aligned}$$

As H is a decreasing function of $v_1$ and an increasing function of $v_2$ in $[0,1]^2$, we have that $X_1$ and T are not HR ordered for all $F_1,F_2$ satisfying (12).

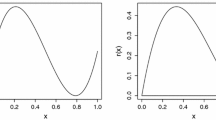
For example, when $X_i\sim Exp(\mu _i)$ with means $\mu _i=1/i$ for $i=1,2$, the respective hazard rate functions are 1 and 2. So (12) holds and hence $X_2\le _{HR}X_{2:2}$ holds. In Fig. 1, we plot the respective hazard rate functions and we see that this property holds. However, there we see that, in this case, $X_1\le _{HR}X_{2:2}$ does not hold. Actually, in this example, the residual lifetime of $X_1$ at time t will be ST better than that of $X_{2:2}$ for $t\in (t_0,\infty )$ for a $t_0\in (0,1)$ (see Fig. 1).

Fig. 1

Hazard rate functions of $X_1,X_2$ and $X_{1:2}$ (constant values 1, 2, 3) and $X_{2:2}$ when $X_i\sim Exp(\mu _i)$, with $\mu _i=1/i$ for $i=1,2$. Note that $X_{1:2}\le _{HR}X_2\le _{HR}X_{2:2}$ holds but that $X_1\le _{HR}X_{2:2}$ does not hold

Proceeding as in the preceding example we can obtain all the HR orderings for systems with independent components. In the case of coherent systems with arbitrary independent components, by using Proposition 1, we have the orderings given in Tables 2 and 3 for all the coherent systems with 1–3 components given in Table 1. As the proposition contains necessary and sufficient conditions, now we know that these are all the (distribution-free) orderings for these systems. Thus, for example, by Table 2, we know that $T_{10}=X_1$ and $T_{17}=\max (X_1,X_2)$ are ST ordered, i.e., $T_{10}\le _{ST}T_{17}$ for any $F_1,F_2$. However, by Table 3, they are not HR ordered, that is, there exist distribution functions $F_1,F_2$ such that $T_{10}\le _{HR}T_{17}$ does not hold (as we have seen in the preceding example).

The similar results for the RHR order can be obtained from Table 3 by using the following proposition for dual systems. The definition of the dual system can be seen in Barlow and Proschan (1975, p. 5). It is stated there that the minimal path (cut) sets of the dual system are the minimal cut (path) sets of the parent system. Thus we have the following lemma.

Lemma 1

Let C and K be the distributional and survival copula of the component lifetimes $(X_1,\ldots ,X_n)$ of a system. If $C=K$, then the distortion function $Q_D$ for the dual system is equal to the dual distortion function $\overline{Q}$ of the parent system and the dual distortion function $\overline{Q}_D$ for the dual system is equal to the distortion function Q of the parent system.

Proof

From Barlow and Proschan (1975, p. 12), we know that the system lifetime can be written as

$$\begin{aligned} T=\max _{i=1,\ldots ,r}\min _{j\in P_i} X_j =\min _{i=1,\ldots ,s}\max _{j\in C_i} X_j \end{aligned}$$

where $P_1,\ldots ,P_r$ are the minimal path sets and $C_1,\ldots ,C_s$ are the minimal cut sets of T. Then, by using the inclusion-exclusion formula, we have that the distortion functions in (8) and (9) can be written as

$$\begin{aligned} Q(u_1,\ldots ,u_n)=\sum _{\emptyset \ne I\subseteq \{1,\ldots ,s\}} (-1)^{|I|+1}C(\varvec{u}^{\cup _{i\in I} C_i}) \end{aligned}$$

and

$$\begin{aligned} \overline{Q}(u_1,\ldots ,u_n) =\sum _{\emptyset \ne I\subseteq \{1,\ldots ,r\}} (-1)^{|I|+1} K(\varvec{u}^{\cup _{i\in I} P_i}), \end{aligned}$$

where |I| is the cardinality of the set I and $\varvec{u}^{P}=(u_1^P,\ldots , u_n^P)$ with $u_i^P=u_i$ whenever $i\in P$ or $u_i^P=1$ whenever $i\notin P$.

Table 3 Relationships for the HR order between the coherent systems with independent components given in Table 1

Hence, if $C=K$, as the minimal path sets of the dual system are $C_1,\ldots ,C_s$, we get $\overline{Q}_D=Q$. Analogously, as the minimal cut sets of the dual system are $P_1,\ldots ,P_r$, we have $Q_D=\overline{Q}$. $\square$

We must note here that the property $C=K$ is not common. Of course, it holds for the product copula (independent components) and, for example, for the Farlie-Gumbel-Morgenstern copula

$$\begin{aligned} C(u,v)=uv(1+\theta (1-u)(1-v)), \end{aligned}$$

where $\theta \in [-1,1]$. Radially symmetric copulas satisfy this property, see Durante and Sempi (2016, pp. 32–33). However, it does not hold for other common copulas. We refer the readers interested in this property to this book and to Nelsen (2006, pp. 36–38). As an immediate consequence of Proposition 1 and Lemma 1, we have the following property.

Proposition 5

Let $T_1$ and $T_2$ be the lifetimes of two coherent systems based on the component lifetimes $(X_1,\ldots ,X_n)$. Let $T_1^D$ and $T_2^D$ be the lifetimes of the respective dual systems. If the distributional copula of $(X_1,\ldots ,X_n)$ is equal to its survival copula, then

$$\begin{aligned} T_1\le _{RHR}T_2 \text { if, and only if, } T_1^D\ge _{HR}T_2^D. \end{aligned}$$

If the components are independent, then the distributional and survival copulas are equal to the product copula. Hence, the RHR orderings for the coherent systems with 1–3 components can be obtained from Table 3 and the preceding proposition. For example, by this table we know that $T_1\le _{HR} T_i$ for $i=2,\ldots ,18$. As $T_{18}$ is the lifetime of the dual system of $T_1$, then $T_{18}\ge _{RHR} T_i$ holds for $i=2,\ldots ,18$.

Fig. 2

Hazard rate ordering relationships between the coherent systems with 1–3 independent components given in Table 1 when (11) holds

The comparison results given in Tables 2 and 3 for arbitrary independent components are quite expectable results. Now, by using Proposition 3 and proceeding as in the preceding example, we obtain all the HR orderings for all the coherent systems with 1–3 independent components under the condition

$$\begin{aligned} X_1\ge _{HR}X_2 \ge _{HR}X_3. \end{aligned}$$

(13)

The ordering results are given in Table 3 and are summarized in Fig. 2. The respective results for the RHR order can be obtained in a similar way by using Proposition 4. We want to note that a lot of calculations are needed to get the results given in Table 3. Thus, for any pair of systems, we computed the associated function H and we determined if it is decreasing in $v_1,v_2$ and $v_3$ in $[0,1]^3$. In case of a positive answer, then the HR ordering holds under (13). In case of a negative answer, then we know that the HR ordering does not hold for all $F_1,F_2,F_3$ satisfying (13). To show how these calculations can be done, we include the following example.

Example 2

Let us consider the coherent systems numbers 7 and 14 in Table 1 with lifetimes $T_7=\min (X_1,\max (X_2,X_3))$ and $T_{14}=\max (X_1,\min (X_2,X_3))$. We assume that the component lifetimes $X_1,X_2,X_3$ are independent. Then the reliability function of $T_7$ is

$$\begin{aligned} \Pr (T_7>t)&=\Pr (\max (\min (X_1,X_2),\min (X_1,X_3))>t)\\&=\Pr (\{\min (X_1,X_2)>t\}\cup \{\min (X_1,X_3)>t\})\\&=\Pr (\min (X_1,X_2)>t)+\Pr (\min (X_1,X_3)>t)\\&\quad \,-\Pr (\min (X_1,X_2,X_3)>t)\\&=\overline{F}_1(t)\overline{F}_2(t)+\overline{F}_1(t)\overline{F}_3(t)-\overline{F}_1(t)\overline{F}_2(t)\overline{F}_3(t)\\&=\overline{Q}_7(\overline{F}_1(t),\overline{F}_2(t),\overline{F}_3(t)), \end{aligned}$$

where $\overline{F}_1,\overline{F}_2,\overline{F}_3$ are the component reliability functions and

$$\begin{aligned} \overline{Q}_7(u_1,u_2,u_3)=u_1 u_2+u_1 u_3- u_1 u_2 u_3. \end{aligned}$$

Thus we obtain the distortion function given in line 7 of Table 1. The distortion function of $T_{14}$, given by

$$\begin{aligned} \overline{Q}_{14}(u_1,u_2,u_3)=u_1+u_2 u_3- u_1 u_2 u_3 \end{aligned}$$

(see line 14 of Table 1) can be deduced in a similar way. As

$$\begin{aligned} \overline{Q}_{14}(u_1,u_2,u_3)-\overline{Q}_7(u_1,u_2,u_3)&=u_1+u_2 u_3-u_1 u_2-u_1 u_3\\&\ge u_1(1+u_2 u_3- u_2- u_3)\\&=u_1(1- u_2)(1- u_3)\ge 0 \end{aligned}$$

for all $u_1,u_2,u_3\in [0,1]$, by Proposition 1, we have $T_7\le _{ST}T_{14}$ for all $F_1, F_2,F_3$. So in line 7, column 14 of Table 2 we put a 2.

To compare these systems in the HR order we compute

$$\begin{aligned} \frac{\overline{Q}_{14}(u_1,u_2,u_3)}{\overline{Q}_7(u_1,u_2,u_3)}&=\frac{u_1+u_2 u_3-u_1u_2u_3}{u_1 u_2+u_1 u_3-u_1u_2u_3}\\&=\frac{1+u_2 u_3/u_1-u_2u_3}{u_2+u_3-u_2u_3}. \end{aligned}$$

Clearly, this ratio is decreasing in $u_1$ in the set $(0,1]^3$. However, for $u_3=1$, we get

$$\begin{aligned} \frac{\overline{Q}_{14}(u_1,u_2,1)}{\overline{Q}_7(u_1,u_2,1)}&=1-u_2+u_2/u_1 \end{aligned}$$

which is strictly increasing in $u_2$ for all $u_1\in (0,1)$. Hence, by Proposition 1, $T_7\le _{HR}T_{14}$ does not hold for all $F_1, F_2,F_3$.

Next we want to study if $T_7\le _{HR}T_{14}$ holds under condition (13). To this purpose we write the ratio of the dual distortion functions as

$$\begin{aligned} \frac{\overline{Q}_{14}(u_1,u_2,u_3)}{\overline{Q}_7(u_1,u_2,u_3)}&=\frac{1+u_1 (u_2/u_1)^2 (u_3/u_2)-u^2_1 (u_2/u_1)^2 (u_3/u_2)}{u_1 (u_2/u_1)+ u_1 (u_2/u_1)(u_3/u_2)-u^2_1 (u_2/u_1)^2 (u_3/u_2)}\\&=H(u_1,u_2/u_1,u_3/u_2) \end{aligned}$$

where

$$\begin{aligned} H(v_1,v_2,v_3)=\frac{1+v_1 v_2^2 v_3-v^2_1 v_2^2 v_3}{v_1 v_2+ v_1 v_2v_3-v^2_1 v_2^2 v_3} \end{aligned}$$

is the function considered in Proposition 3. Then we need to study if H is a decreasing function (in $v_1,v_2,v_3$) in the set $[0,1]^3$. For the partial derivative $D_3 H$ of H with respect of $v_3$ we obtain

$$\begin{aligned} D_3 H(v_1,v_2,v_3)&=_{sign} v_1 v_2^2 (1-v_1)-1+v_1v_2\\&\le v_1v_2^2(1-v_1)-1+v_1\\&=-(1-v_1) (1-v_1v_2^2)\le 0 \end{aligned}$$

for all $v_1,v_2,v_3\in (0,1)$. Therefore H decreases in $v_3$ in the set $[0,1]^3$. Analogously, straightforward calculations prove that H also decreases in $v_1$ and $v_2$ in the set $[0,1]^3$. Hence, by Proposition 3, $T_7\le _{HR}T_{14}$ holds for all $F_1, F_2,F_3$ such that (13) holds. So in line 7, column 14 of Table 3 we put a 1. Moreover, as by Table 3 we do not have any other system lifetime $T_j$ such that $T_7\le _{HR}T_{j}\le _{HR}T_{14}$ holds under condition (13), systems 7 and 14 are connected in Fig. 2. Moreover, as the dual system of $T_7$ is $T_{14}$ (and vice versa), by Proposition 4, we have $T_7\le _{RHR}T_{14}$ under condition (13). If we want to study the ordering $T_7\le _{RHR}T_{14}$ under condition (6), by Proposition 4, it holds if the function in (7), given by

$$\begin{aligned} G(v_1,v_2,v_3)=\frac{Q_{14}(v_1,v_1v_2,v_1v_2v_3)}{Q_{7}(v_1,v_1v_2,v_1v_2v_3)}, \end{aligned}$$

is increasing in $v_1,v_2,v_3$. As the dual of system 7 is system 14, we have $Q_{14}=\overline{Q}_{7}$ and $Q_{7}=\overline{Q}_{14}$. Hence

$$\begin{aligned} G(v_1,v_2,v_3)=\frac{\overline{Q}_{7}(v_1,v_1v_2,v_1v_2v_3)}{\overline{Q}_{14}(v_1,v_1v_2,v_1v_2v_3)}=\frac{1}{H(v_1,v_2,v_3)}, \end{aligned}$$

where H is the function obtained in Proposition 3 for the ordering $T_7\le _{HR}T_{14}$. We have proved that H is decreasing and so, G is increasing and $T_7\le _{RHR}T_{14}$ holds for all $F_1,F_2,F_3$ satisfying (13).

We conclude this section with an example which shows that the results given in Sect. 2 can also be used to compare coherent systems with dependent components.

Example 3

Let us consider the series and parallel systems with lifetime $T_1=X_{1:2}=\min (X_1, X_2)$ and $T_2=X_{2:2}=\max (X_1, X_2)$ with two dependent components having the following Clayton-Oakes (CO) survival copula

$$\begin{aligned} K(u_1,u_2)=\left( u_1^{1-\theta }+u_2^{1-\theta }-1\right) ^{1/(1-\theta )} \end{aligned}$$

for $\theta >1$. Then, the system reliability functions are

$$\begin{aligned} \overline{F}_{T_1}(t)=\overline{Q}_1(\overline{F}_1(t),\overline{F}_2(t)) \end{aligned}$$

and

$$\begin{aligned} \overline{F}_{T_2}(t)=\overline{Q}_2(\overline{F}_1(t),\overline{F}_2(t)) \end{aligned}$$

where $\overline{F}_1, \overline{F}_2$ are the component reliability functions,

$$\begin{aligned} \overline{Q}_1(u_1,u_2)=K(u_1,u_2)=\left( u_1^{1-\theta }+u_2^{1-\theta }-1\right) ^{1/(1-\theta )} \end{aligned}$$

and

$$\begin{aligned} \overline{Q}_2(u_1,u_2)= & {} K(u_1,1)+K(1,u_2)-K(u_1,u_2)\\ {}= & {} u_1+u_2-\left( u_1^{1-\theta }+u_2^{1-\theta }-1\right) ^{1/(1-\theta )}. \end{aligned}$$

These systems are always ordered in the ST order, that is, $X_{1:2}\le _{ST} X_{2:2}$ for all $F_1, F_2$ and any survival copula K. To compare these systems in the HR order under a CO survival copula when $\theta =2$, we compute

$$\begin{aligned}&\overline{Q}_1(u_1,u_2)=K(u_1,u_2)=\frac{u_1 u_2}{u_1+u_2-u_1 u_2},\\&\overline{Q}_2(u_1,u_2)=u_1+u_2-\frac{u_1 u_2}{u_1+u_2-u_1 u_2} \end{aligned}$$

and

$$\begin{aligned} \frac{\overline{Q}_2(u_1,u_2)}{\overline{Q}_1(u_1,u_2)}= & {} \frac{u_1+u_2-u_1 u_2}{u_2}+ \frac{u_1+u_2-u_1 u_2}{u_1}-1 \\= & {} \frac{u_1}{u_2}+\frac{u_2}{u_1}-u_1-u_2+1. \end{aligned}$$

It is easy to see that this ratio is not decreasing in $u_1$ and $u_2$ in $[0,1]^2$ (e.g., when $u_2=0.1$). Hence, surprisingly, we have that $X_{1:2}$ and $X_{2:2}$ are not HR ordered for all $F_1, F_2$.

Next, we can compare these systems under condition (12). To this purpose we compute the function in (4) obtaining

$$\begin{aligned} H(v_1,v_2)=\frac{\overline{Q}_2(v_1,v_1v_2)}{\overline{Q}_1(v_1,v_1v_2)}=1+\frac{1}{v_2}+v_2-v_1-v_1v_2. \end{aligned}$$

The partial derivatives $D_iH$ of H with respect of $v_i$, $i=1,2$, satisfy

$$\begin{aligned} D_1H(v_1,v_2)=-1-v_2< 0 \end{aligned}$$

and

$$\begin{aligned} D_2H(v_1,v_2)=1-\frac{1}{v_2^2}-v_1 \le 0 \end{aligned}$$

in $[0,1]^2$, that is, H is a decreasing function in $[0,1]^2$. Hence, by Proposition 3, $X_{1:2} \le _{HR} X_{2:2}$ holds for all $F_1, F_2$ under condition (12) and a CO survival copula with $\theta =2$. A similar study can be done for other values of the dependence parameter $\theta$.

4 Comparisons of finite mixtures

The results on generalized distorted distributions can also be applied to compare finite mixtures defined as follows.

Definition 2

We say that $F_{{\mathbf {p}}}$ is a mixture of the distribution functions $F_1,\ldots ,F_n$ with the non-negative weights in the vector ${\mathbf {p}}=(p_1,\ldots ,p_n)$ satisfying $p_1+\cdots +p_n=1$ if

$$\begin{aligned} F_{{\mathbf {p}}}=p_1F_1+\cdots +p_nF_n. \end{aligned}$$

(14)

Clearly, the assumptions on the weights imply that the right hand side of the preceding expression determines a proper distribution function for any distribution functions $F_1,\ldots ,F_n$. The respective reliability functions will satisfy

$$\begin{aligned} \overline{F}_{{\mathbf {p}}}=p_1\overline{F}_1+\cdots +p_n\overline{F}_n. \end{aligned}$$

They can be represented as $F_{{\mathbf {p}}}=Q_{{\mathbf {p}}}(F_1,\ldots ,F_n)$ and $\overline{F}_{{\mathbf {p}}}=\overline{Q}_{{\mathbf {p}}}(\overline{F}_1,\ldots ,\overline{F}_n)$ with

$$\begin{aligned} Q_{{\mathbf {p}}}(u_1,\ldots ,u_n)=\overline{Q}_{{\mathbf {p}}}(u_1,\ldots ,u_n)=p_1u_1+\cdots +p_n u_n. \end{aligned}$$

Hence they are generalized distorted distributions. Therefore, we can use the results given in Sect. 2 to obtain distribution-free comparison results for finite mixtures. In this sense, we shall assume that

$$\begin{aligned} F_1\ge _{ST}\cdots \ge _{ST}F_n \end{aligned}$$

(15)

or

$$\begin{aligned} F_1\ge _{HR}\cdots \ge _{HR}F_n \end{aligned}$$

(16)

hold. Then, by using Proposition 2, we get the following result.

Proposition 6

If $F_{{\mathbf {p}}}$ and $F_{\mathbf {q}}$ are two finite mixtures based on $F_1,\ldots ,F_n$, then

$$\begin{aligned} F_{{\mathbf {p}}}\le _{ST}F_{\mathbf {q}} \end{aligned}$$

holds for all $F_1,\ldots ,F_n$ satisfying (15) if and only if ${\mathbf {p}}\ge _{ST}\mathbf {q}$ (i.e. $p_1+\cdots +p_k\le q_1+\cdots +q_k$ for all $k\in \{1,\ldots ,n-1\}$).

Proof

The ‘if’ part is obtained from Theorem 1.A.6 in Shaked and Shanthikumar (2007, p. 7).

By using Proposition 2, we have that $F_{{\mathbf {p}}}\le _{ST}F_{\mathbf {q}}$ holds for all $F_1,\ldots ,F_n$ satisfying (15) if and only if

$$\begin{aligned} (q_1-p_1)u_1+\cdots +(q_n-p_n)u_n\ge 0 \end{aligned}$$

in $D=\{(u_1,\ldots ,u_n)\in [0,1]^n: u_1\ge \cdots \ge u_n\}$. Then, for $k\in \{1,\ldots ,n-1\}$, taking $u_1=\cdots =u_k=1$ and $u_{k+1}=\cdots =u_n=0$, we get

$$\begin{aligned} (q_1-p_1)+\cdots +(q_k-p_k)\ge 0. \end{aligned}$$

Hence $q_1+\cdots +q_k\ge p_1+\cdots +p_k$ for all $k\in \{1,\ldots ,n-1\}$ and so ${\mathbf {p}}\ge _{ST}\mathbf {q}$ holds. $\square$

From the preceding proposition, in the case $n=2$, we have the trivial condition $q_1\ge p_1$ and in the case $n=3$, we obtain $q_1\ge p_1$ and $q_3\le p_3$.

Analogously, by using Proposition 3, we obtain the following result.

Proposition 7

If $F_{{\mathbf {p}}}$ and $F_{\mathbf {q}}$ are two finite mixtures based on $F_1,\ldots ,F_n$, then

$$\begin{aligned} F_{{\mathbf {p}}}\le _{HR}F_{\mathbf {q}} \end{aligned}$$

holds for all $F_1,\ldots ,F_n$ satisfying (16) if and only if

$$\begin{aligned} H(v_2,\ldots ,v_n)=\frac{q_1+q_2v_2+\cdots +q_nv_2\ldots v_n}{p_1+p_2v_2+\cdots +p_nv_2\ldots v_n} \end{aligned}$$

(17)

is decreasing in $[0,1]^{n-1}$.

Proof

First note that in this case the ratio of the respective reliability functions can be written as

$$\begin{aligned} \frac{\overline{F}_{\mathbf {q}}(t)}{\overline{F}_{{\mathbf {p}}}(t)} =H\left( \frac{\overline{F}_{2}(t)}{\overline{F}_{1}(t)},\ldots , \frac{\overline{F}_{n}(t)}{\overline{F}_{n-1}(t)}\right) \end{aligned}$$

for all t, where H is given by (17). Notice that H does not depend on $v_1$. Then, by Proposition 3, we have that

$$\begin{aligned} F_{{\mathbf {p}}}\le _{HR}F_{\mathbf {q}} \end{aligned}$$

holds for all $F_1,\ldots ,F_n$ satisfying (16) if and only if $H(v_2,\ldots ,v_n)$ is decreasing in $[0,1]^{n-1}$. $\square$

In the case $n=2$, we have the condition $q_1\ge p_1$. This is also a well known result (see, e.g., Navarro et al. 2009). In the case $n=3$, we obtain the following new result for the HR order.

Corollary 1

If $F_{{\mathbf {p}}}$ and $F_{\mathbf {q}}$ are two finite mixtures based on $F_1,F_2,F_3$, then

$$\begin{aligned} F_{{\mathbf {p}}}\le _{HR}F_{\mathbf {q}} \end{aligned}$$

holds for all $F_1,F_2,F_3$ satisfying (16) if and only if the following conditions hold:

(i) $q_3\le p_3$ and

(ii) $p_1q_2\le q_1 p_2$.

Proof

If $n=3$ then the function H defined in the preceding proposition can be written as

$$\begin{aligned} H(v_2,v_3)=\frac{q_1+q_2v_2+q_3 v_2v_3}{p_1+p_2v_2+p_3v_2v_3}. \end{aligned}$$

Then it is decreasing in $v_2$ in the set $[0,1]^2$ if and only if

$$\begin{aligned} (q_2+q_3v_3)p_1-(p_2+p_3v_3)q_1\le 0 \end{aligned}$$

for all $v_3\in [0,1]$. This property is equivalent to

$$\begin{aligned} (p_1q_3-q_1p_3)v_3\le q_1p_2-p_1q_2 \end{aligned}$$

for all $v_3\in [0,1]$. This property holds if and only if it holds for $v_3=0$ and $v_3=1$. If $v_3=1$, then we have

$$\begin{aligned} (1-q_1)p_1\le (1-p_1)q_1 \end{aligned}$$

which is equivalent to $p_1 \le q_1$. If $v_3=0$, then we have

$$\begin{aligned} 0\le q_1p_2-p_1q_2 \end{aligned}$$

which is equivalent to (ii).

Analogously, H is decreasing in $v_3$ in the set $[0,1]^2$ if and only if

$$\begin{aligned} (p_1+p_2v_2)q_3-(q_1+q_2v_2)p_3\le 0 \end{aligned}$$

for all $v_2\in [0,1]$. This property is equivalent to

$$\begin{aligned} (p_2q_3-q_2p_3)v_2\le q_1p_3-p_1q_3 \end{aligned}$$

for all $v_2\in [0,1]$. This property holds if and only if it holds for $v_2=0$ and $v_2=1$. If $v_2=0$, then we have

$$\begin{aligned} 0\le q_1p_3-p_1q_3 \end{aligned}$$

which is equivalent to $p_1q_3\le q_1 p_3$. If $v_2=1$, then we have

$$\begin{aligned} p_2q_3-q_2p_3\le q_1p_3-p_1q_3, \end{aligned}$$

that is,

$$\begin{aligned} (1-p_3)q_3\le (1-q_3)p_3, \end{aligned}$$

which is equivalent to (i).

Finally, if (ii) holds, then

$$\begin{aligned} p_1q_2+p_1q_1\le q_1 p_2+p_1q_1 \end{aligned}$$

and, as (i) implies $p_1+p_2\le q_1+q_2$, then

$$\begin{aligned} p_1(q_1+q_2) \le q_1 (p_1+p_2) \le q_1 (q_1+q_2) \end{aligned}$$

and so $p_1\le q_1$ and $p_1q_3\le q_1 p_3$ hold. $\square$

The respective results for the RHR order can be obtained in a similar way by Proposition 4. Note that conditions (i) and $p_1\le q_1$ in the preceding corollary are the necessary and sufficient conditions to have the ST ordering under (15) when $n=3$. To get the HR ordering under (16), we need to replace $p_1\le q_1$ by condition (ii).

Remark 1

Note that the ‘if’ parts of Propositions 6 and 7 can be applied to ‘negative’ mixtures, that is, to distribution functions that can be written as in (14) but with some negative weights. Negative mixtures appear in different statistical procedures, including order statistics and coherent system representations, see Navarro (2016) and the references therein. The term generalized mixture is used to manage both cases (positive and negative mixtures) together. Note that negative mixtures cannot be represented as generalized distorted distributions (since the corresponding $Q_{{\mathbf {p}}}$ is decreasing in the variables with negative weights). However, the ST and HR orderings hold for negative mixtures when the conditions in Propositions 6 and 7, respectively, are satisfied. The proofs are similar to that of Propositions 2 and 3. Note that, in this case, the condition ${\mathbf {p}}\ge _{ST}\mathbf {q}$ in Proposition 6 should be written as: $q_1+\cdots +q_k\le p_1+\cdots +p_k$ for all $k\in \{1,\ldots ,n-1\}$ (since the vectors ${\mathbf {p}}$ and $\mathbf {q}$ cannot be seen as probability mass vectors).

The following examples show how to apply the preceding theoretical results to some finite mixtures.

Example 4

Let us consider the mixtures with weights ${\mathbf {p}}=(1/3,1/3,1/3)$ and $\mathbf {q}=(1/2,1/4,1/4)$. Then a straightforward calculation shows that the conditions (i) and (ii) in the preceding corollary hold. Then we have

$$\begin{aligned} F_{{\mathbf {p}}}\le _{HR}F_{\mathbf {q}} \end{aligned}$$

for all $F_1,F_2,F_3$ satisfying (16). As (i) and $p_1\le q_1$ hold, we also have

$$\begin{aligned} F_{{\mathbf {p}}}\le _{ST}F_{\mathbf {q}} \end{aligned}$$

for all $F_1,F_2,F_3$ satisfying (15).

Example 5

Let us consider the finite mixtures with weights ${\mathbf {p}}=(p_1,p_2,p_3)$ and $\mathbf {q}=(q_1,q_2,q_3)$ and let us assume that $p_1=q_1>0$. In this case, condition (ii) in Corollary 1 is equivalent to $q_2\le p_2$. Therefore, by using that $q_1+q_2+q_3=1=p_1+p_2+p_3$, implies $q_2+q_3=p_2+p_3$, properties (i) and (ii) hold if and only if $p_i=q_i$ for $i=1,2,3$. Hence

$$\begin{aligned} F_{{\mathbf {p}}}\le _{HR}F_{\mathbf {q}} \end{aligned}$$

holds for all $F_1,F_2,F_3$ satisfying (16) if and only if $F_{{\mathbf {p}}}=F_{\mathbf {q}}$. For example, the mixtures with weights ${\mathbf {p}}=(1/3,1/3,1/3)$ and $\mathbf {q}=(1/3,1/2,1/6)$ are not HR ordered for all $F_1,F_2,F_3$ satisfying (16). This is a quite unexpected property since in $\mathbf {q}$ we give a greater weight to the second component which is HR-better than the third one. However,

$$\begin{aligned} F_{{\mathbf {p}}}\le _{ST}F_{\mathbf {q}} \end{aligned}$$

holds for all $F_1,F_2,F_3$ satisfying (15) since (i) and $p_1=q_1$ hold for these values. In general, if $p_1=q_1$, then $F_{{\mathbf {p}}}\le _{ST}F_{\mathbf {q}}$ holds for all $F_1,F_2,F_3$ satisfying (15) if and only if $q_3\le p_3$.

Example 6

Let us consider the finite mixtures with weights ${\mathbf {p}}=(p_1,p_2,p_3)$ and $\mathbf {q}=(q_1,q_2,q_3)$. Let us assume that $p_1=0<q_1$. Then, condition (ii) in Corollary 1 holds. Therefore

$$\begin{aligned} F_{{\mathbf {p}}}\le _{HR}F_{\mathbf {q}} \end{aligned}$$

holds for all $F_1,F_2,F_3$ satisfying (16) if and only if (i) $q_3\le p_3$ is satisfied. In particular, it holds if $q_3= 0$. For example, the mixtures with weights ${\mathbf {p}}=(0,1/2,1/2)$ and $\mathbf {q}=(q_1,q_2,q_3)$ are HR ordered under (16) if and only if $q_3\le 1/2$.

5 Conclusions

Necessary and sufficient conditions have been obtained for distribution-free stochastic (ST) and hazard rate (HR) comparisons of generalized distorted distributions with ordered components. The examples provided here prove that these theoretical results are useful in practice to get stochastic comparisons of coherent systems and finite mixtures. In particular, all the ST and HR ordering relationships between all the coherent systems with 1–3 independent components have been determined. The procedures used here improve preceding results and can also be used to compare systems with more components and/or with dependent components.

The results obtained here can also be applied to compare any other distributions which can be represented as generalized distorted distributions. For example, if two reliability functions satisfy the generalized proportional hazard rate (GPHR) model used to define the conditionally dependent frailty models (see, e.g., Fernández-Ponce et al. 2016) and can be written as

$$\begin{aligned} \overline{F}_{\varvec{\alpha }}(t)=\overline{F}_1^{\alpha _1}(t)\ldots \overline{F}_n^{\alpha _n}(t) \end{aligned}$$

and

$$\begin{aligned} \overline{F}_{\varvec{\beta }}(t)=\overline{F}_1^{\beta _1}(t)\ldots \overline{F}_n^{\beta _n}(t) \end{aligned}$$

for some parameters $\alpha _1,\ldots ,\alpha _n,\beta _1,\ldots ,\beta _n>0$, then, from Proposition 3, $\overline{F}_{\mathbf {\alpha }}\le _{HR}\overline{F}_{\mathbf {\beta }}$ holds for all $F_1,\ldots ,F_n$ satisfying (3) if and only if $\alpha _i+\cdots +\alpha _n\ge \beta _i+\cdots +\beta _n$ for $i=1,\ldots ,n$.