On Some Properties of $\alpha$-Mixtures

Abstract

The $\alpha$-mixtures is a new, flexible family of distributions that includes many mixture models as special cases. This paper is mainly focused on relevant stochastic comparisons and ageing properties of $\alpha$-mixtures of survival functions. In particular, we prove that ageing properties of $\alpha$-mixtures for additive and multiplicative hazards models depend on the properties of the baseline failure rate functions and the corresponding conditional moments of mixing distributions. Partial orderings of the finite $\alpha$-mixtures in the sense of the usual stochastic order and the hazard rate order are discussed. Finally, we extend some results on the shape of the mixture failure rate obtained in the literature for usual mixtures to the case of $\alpha$-mixtures.

1 Introduction

1.1 Motivation and related literature

Mixture models are useful statistical tools for analyzing heterogeneous populations in different areas of research such as reliability, risk, survival analysis, etc. Heterogeneity in practice can arise in various ways. For instance, the manufactured items are often heterogeneous and the corresponding reliability characteristics in a population of items, therefore, are variable from one subpopulation to another. This occurs due to many different reasons such as quality of resources and components used in the production process, operation and maintenance history, random environment, human errors, etc. Neglecting existing heterogeneity can result in substantial errors when describing reliability and performance characteristics of engineering systems. Another important source of heterogeneity in data analysis can be described as follows. Let T be a nonnegative random variable with the cumulative distribution function (CDF) F(t), $t\ge 0$. In reliability and survival analysis, this function is usually estimated based on the failure times available from the experiments that are carried out. On the other hand, some additional information is often available that is useful for the more precise estimation procedure. Examples of additional information can be external conditions of operation, observations of internal parameters and prior opinions of experts on parameters values, etc.

Let a random variable $\Lambda$ be an external covariate (that can be also interpreted as frailty in our context) taking values in $[0,\infty )$ with the CDF, $\Pi (\lambda )$. Moreover, assume that $F(t|\lambda )$, $\bar{F}(t|\lambda )$, $f(t|\lambda )$ and $r(t|\lambda )$ are, respectively, the CDF, the survival function (SF), the PDF and the failure rate of the random variable T conditioned on $\Lambda =\lambda$. Obviously, F(t) and $F(t|\lambda )$, are related as follows.

$$\begin{aligned} F(t)=\int _{0}^{\infty } F(t|\lambda )d\Pi (\lambda ). \end{aligned}$$

(1)

This is known in the literature as the mixture CDF (that is also often called the arithmetic mixture). Many authors have investigated various properties of mixture models. For some basic ageing properties of mixture models, we refer to Barlow and Proschan (1981), Block and Savits (1976) and Savits (1985). Block et al. (1993) and Block and Joe (1997) have studied the tail behavior of failure rates of mixtures. Lynch (1999) showed that the necessary and sufficient condition for a mixture to have an increasing failure rate is that the mixing distribution should have an increasing failure rate. Block et al. (2003) have studied the closure properties of mixture models under different ageing concepts. Badia et al. (2002) have considered the additive and multiplicative failure rate mixing models and discussed the relevant ageing properties of these models. Cha and Badia (2016) have investigated an information-based burn-in procedure for repairable systems.

Mixtures for the multivariate proportional hazard model have been studied by Badia and Lee (2020). Finkelstein and Esaulova (2001) have considered additive and multiplicative models. Finkelstein and Esaulova (2006) have discussed the problem of mixture failure rate ordering (in the sense of the likelihood ratio order) for the ordered mixing distributions. Navarro and Hernandez (2004) have developed some techniques to determine the shape of the failure rate and of the mean residual life function. Navarro (2008) have studied ordering properties, monotonicity and the limiting behaviour of the Glaser’s function for mixtures. Ordering properties, monotonicity and the limiting behavior of finite mixtures based on the mean residual life function were investigated by Navarro and Hernandez (2008). Shaked and Spizzichino (2001) have studied monotonicity and the limiting behaviour of the failure rate for a mixed distribution. Navarro et al. (2009) have considered the generalized mixtures and have obtained some properties for the corresponding mixture failure rate. Navarro (2016) studied the hazard rate and likelihood ratio orders in generalized mixtures and provided some applications. Badia and Cha (2017) have extended the bending properties of the mixture failure rates (see Section 5) to the cases of the reversed failure rate, the mean residual lifetime and the mean inactivity time. Hazra and Finkelstein (2018) have considered two finite mixtures and have obtained stochastic comparisons for the semiparametric families such as proportional hazards, accelerated lifetimes and proportional reversed hazards. Amini-Seresht and Zhang (2017) have obtained stochastic comparisons for two classical finite mixture models in the sense of the hazard rate, the reversed hazard rate, the likelihood ratio, the mean residual lifetime and the mean inactivity time orders with different baseline random variables and different mixing proportions. Navarro and del Aguila (2017) have obtained necessary and sufficient conditions for stochastic comparisons of the finite mixtures. For a comprehensive reference on failure modeling of mixture models in reliability and risk, we refer to Finkelstein (2008).

1.2 The $\alpha$-mixture model

Recently, Asadi et al. (2019) have introduced a flexible mixture model indexed by parameter $\alpha \in {R}$ that was called the $\alpha$-mixture model. For the continuous mixing random variable $\Lambda$, the $\alpha$-mixture for the SF is defined as follows.

$$\begin{aligned} \bar{F}(t,\alpha )=\left\{ \begin{array}{ll} \left( \int _{0}^{\infty } \bar{F}^{\alpha }(t|\lambda ) \pi (\lambda ) d\lambda \right) ^{\frac{1}{\alpha }}, &{} {\alpha \ne 0}, \\ \bar{F}_{gm}(t), &{} \alpha =0, \end{array} \right. \end{aligned}$$

(2)

where $\bar{F}_{gm}(t)=\lim _{\alpha \rightarrow 0}\bar{F}(t,\alpha )$ and $\pi (\lambda )$ is the PDF of the random variable $\Lambda$.

In the discrete case, the finite $\alpha$-mixture for n sub-populations with SFs $\bar{F}_{i}$, $i=1,2,...,n$, is defined as

$$\begin{aligned} \bar{F}(t,\alpha )=\left\{ \begin{array}{ll} \left[ \sum _{i=1}^{n} p_{i}{\bar{F}_{i}}^{\alpha }(t) \right] ^{1/\alpha }, &{} {\alpha \ne 0}, \\ \bar{F}_{gm}(t), &{} \alpha =0, \end{array} \right. \end{aligned}$$

(3)

$\bar{F}_{gm}(t)=\lim _{\alpha \rightarrow 0}\bar{F}(t,\alpha )$ and $p_{i}$ is the mixing proportion such that $p_{i}\ge 0$, for $i \in \left\{ 1, 2, . . . , n\right\}$ and $\sum _{i=1}^{n} p_{i}=1.$ Clearly, in models (2) and (3), $\alpha =1$ yields the well-known in the literature arithmetic (ordinary) mixture of survival functions. Moreover, for $\alpha =-1$ we arrive at the corresponding harmonic mixture, whereas the case when $\alpha \rightarrow 0$, as shown by Asadi et al. (2019), defines the geometric mixture, which is the mixture of the corresponding failure rates. In particular, for the finite mixture (3), the SF and the failure rate of the geometric mixture, denoted by $\bar{F}_{gm}(t)$ and $r_{gm}(t)$, respectively, can be written as:

$$\begin{aligned} \bar{F}_{gm}(t)=\prod _{i=1}^{n}\bar{F}_{i}^{p_{i}}(t), \end{aligned}$$

and

$$\begin{aligned} r_{gm}(t)=\sum _{i=1}^{n}p_{i} r_{i}(t), \end{aligned}$$

where $r_{i}(t)$, $i=1,...,n$, is the failure rate that corresponds to the i-th sub-population. For the continuous case, we have:

$$\begin{aligned} \bar{F}_{gm}(t)=\exp \left( \int _{0}^{\infty } \log (\bar{F}(t | \lambda )) \pi (\lambda )d\lambda \right) , \end{aligned}$$

and

$$\begin{aligned} r_{gm}(t)=\int _{0}^{\infty } r(t|\lambda ) \pi (\lambda ) d\lambda . \end{aligned}$$

Thus we see that the $\alpha$-mixture model is a meaningful generalization of conventional mixture models.

Asadi et al. (2019) have discussed several stochastic and aging properties of the $\alpha$-mixture model. In the current study, on the one hand, we discuss in detail some important specific models of mixing, whereas, on the other hand, further generalizations and new results for the basic model are presented.

In the following, we first provide some examples interpreting the use of the $\alpha$-mixture family.

• (i) Asadi et al. (2019) compared the reliability function of two m-component series systems, which are constructed based on the following two different policies: First, a component is randomly selected from a set of n components in which the probability of selecting the ith component is $p_{i}$, $i=1, 2, \dots , n$. Then the selected component is used to construct an m-component series system of same type. In this case the reliability function of constructed m-component series system is:

  $$\begin{aligned} \mathcal {\bar{F}}_{1}(t)=\sum _{i=1}^{n} p_{i} \bar{F}^{m}_{i}(t)=\bar{F}^{m}(t,m), \end{aligned}$$

  where $\bar{F}(t,m)$, is the SF of the finite $\alpha$-mixture with $\alpha =m$, and $\bar{F}_{i}(t)$, $i=1, \dots , n$, is the SF of the i-th component. This model can be considered as “mixing at the system level”. In the second policy, first we mixed n components and assume that the proportion of i-th component in mixed population is $p_{i}$, $i=1, \dots , n$ and drawn all of m components randomly from the mixed population to construct a series system. Let the SF of the i-th component is $\bar{F}_{i}(t)$, $i=1, \dots , n$, then the reliability function of constructed m-component series system is:

  $$\begin{aligned} \mathcal {\bar{F}}_{2}(t)=\left( \sum _{i=1}^{n} p_{i} \bar{F}_{i}(t)\right) ^{m}=\bar{F}^{m}(t,1) , \end{aligned}$$

  where $\bar{F}(t,1)$, is the SF of the finite $\alpha$-mixture with $\alpha =1$. This model can be considered as “mixing at the component level ”. By monotone decreasing property of $\alpha$-mixture, we have $\mathcal {\bar{F}}_{2} \le _{st} \mathcal {\bar{F}}_{1}$. That means, the constructed series system with homogeneous components are more reliable than the constructed series system with heterogeneous components.

• (ii) Cha (2011) and Hazra et al. (2017) have considered some variants of the model described in part (i), that can be expressed as in terms of finite $\alpha$-mixtures. Let we have a mixed population of n components such that the proportion of the i-th component in the population is $p_{i}$, $i=1, \dots ,n$. According to cited authors, to build an m-component series system, first one component is randomly selected from n components and then $l_{1}$ components are extracted from the selected component; then another component is randomly selected from the n components and $l_{2}$ components are extracted of the newly selected component; and so on. The process continues until the m components of the series system are completed after d steps. Thus, the SF of constructed m-components series system is:

  $$\begin{aligned} \mathcal {\bar{F}}_{3}(t)=\prod _{j=1}^{d} \left( \sum _{i=1}^{n} p_{i} \bar{F}^{l_{j}}_{i}(t)\right) =\prod _{j=1}^{d} \bar{F}^{l_{j}}(t,l_{j}), \end{aligned}$$

  where $\sum _{j=1}^{d} l_{j}=m$, for $1\le d \le m$. In this model $\bar{F}(t,l_{j})$ is the SF of the finite $\alpha$-mixture with $\alpha =l_{j}$, $j=1, \dots , d$.

Another interpretation of the $\alpha$-mixture can be given as follows. Assume that a single component (from a homogeneous population) is operating in a laboratory (mild) conditions and its the lifetime is described by the failure rate r(t) and the survival function $\bar{F}(t)$. Let the severe conditions in the field act according to the multiplicative-additive hazard model in such a way that the failure rate of an item becomes $r_{s}(t)=\alpha r(t)+\beta$, where $\alpha >1$ and $\beta \ge 0$. Assume that this item is shielded from the severe conditions to arrive at the laboratory conditions, which obviously can be modelled as

$$\begin{aligned} r(t)=\frac{r_{s}(t)-\beta }{\alpha }, \end{aligned}$$

with the ’original’ survival function $\bar{F}(t)$. Assume now that we have a mixed population with the mixture survival function

$$\begin{aligned} \bar{F}_{m}(t)=\sum _{i=1}^{n} p_{i}{\bar{F}_{i}}(t). \end{aligned}$$

Denote the failure rates for sub-populations by $r_{i}(t)$, $i=1,2,...,n$. Then the mixture failure rate (the failure rate of a randomly selected from the population item) is

$$\begin{aligned} r_{m}(t)=\sum _{i=1}^{n}p_{i}(t)r_{i}(t), \end{aligned}$$

where

$$\begin{aligned} p_{i}(t)=\frac{p_i\bar{F}_{i}(t)}{\sum _{j=1}^{n}p_j\bar{F}_{j}(t)},\quad i=1,...,n, \end{aligned}$$

see, for example, Navarro and Hernandez (2004) and Finkelstein (2008). If the severe condition acts on each sub-population uniformly, then this failure rate will change to

$$\begin{aligned} r_{s}^{\alpha ,\beta }(t)=&\sum _{i=1}^{n}p_{i}^{\alpha ,\beta }(t)(\alpha r_{i}(t)+\beta )\\ =&\alpha \sum _{i=1}^{n}p_{i}^{\alpha ,\beta }(t) r_{i}(t)+\beta , \end{aligned}$$

where

$$\begin{aligned} p^{\alpha ,\beta }_{i}(t)=&\frac{p_ie^{-\beta t}\bar{F}_{i}^{\alpha }(t)}{\sum _{i=1}^{n}p_ie^{-\beta t}\bar{F}_{i}^{\alpha }(t)}\\ =&\frac{p_i\bar{F}_{i}^{\alpha }(t)}{\sum _{i=1}^{n}p_i\bar{F}_{i}^{\alpha }(t)}\equiv p^{\alpha }_{i}(t). \end{aligned}$$

Similar to the homogeneous case, let us shield the selected item from the severe conditions, thus putting it back to laboratory conditions. This can be modelled as

$$\begin{aligned} \frac{r_{s}^{\alpha ,\beta }(t)-\beta }{\alpha }= & {} \sum _{i=1}^{n}p_{i}^{\alpha }(t) r_{i}(t). \end{aligned}$$

(4)

The right hand side of (4) is, in fact, the failure rate that corresponds to (3) (see Asadi et al. (2019)). Thus, the $\alpha$-mixture had naturally emerged in this practical setting. Another important observation that can be drawn from this example is that heterogeneity destroys the natural property for items from homogeneous populations, i.e., when one goes from the laboratory conditions to severe condition (by multiplicative-additive transformation of the corresponding failure rate) and then back again, the failure rate of an item does not change. This can be considered as some paradox, although its explanation is quite clear from our discussion. It is worth noting also that the location parameter of the transformation, $\beta$ does not have any effect on the failure rate and only the scale parameter, $\alpha$ is relevant. It should be also emphasized that the above discussion with obvious alterations can be applied to the case of an environment which is milder than the laboratory environment, i.e., when $0<\alpha \le 1$.

1.3 Organization of the paper

The rest of the paper is organized as follows. In Section 2, we obtain some expressions for the conditional mean of the mixing distribution and investigate its relation to the failure rate of the conditional random variable T conditioned on $\Lambda$. Section 3, is devoted to the study of some ageing properties of $\alpha$-mixtures of survival functions. In Section 4, we discuss the partial orderings of finite $\alpha$-mixtures in the sense of usual stochastic order and the hazard rate order. Finally, in Section 5, we obtain results on ’down and up bending properties’ of the failure rate in $\alpha$-mixtures, which extends some results reported in the literature for the ordinary (arithmetic) mixture models.

2 Some ageing properties of $\alpha$-mixtures

Consider the parametric $\alpha$-mixture model (2). The corresponding PDF is

$$\begin{aligned} f(t,\alpha )= \left( \int _{0}^{\infty } f(t |\lambda )\bar{F}^{\alpha -1}(t|\lambda ) \pi (\lambda ) d\lambda \ \right) \left( \int _{0}^{\infty } \bar{F}^{\alpha }(t|\lambda ) \pi (\lambda ) d\lambda \right) ^{\frac{1}{\alpha }-1}. \end{aligned}$$

(5)

Let $\alpha \ne 0$. In this case, the failure rate for the $\alpha$-mixture family can be given as follows:

$$\begin{aligned}&r(t,\alpha )=\frac{f(t,\alpha )}{\bar{F}(t,\alpha )}=\frac{\int _{0}^{\infty } f(t |\lambda ) \bar{F}^{\alpha -1}(t |\lambda ) \pi (\lambda ) d\lambda }{\int _{0}^{\infty } \bar{F}^{\alpha }(t |\lambda ) \pi (\lambda ) d\lambda } \end{aligned}$$

(6)

$$\begin{aligned}&=\int _{0}^{\infty }r(t | \lambda )\pi _{\alpha }(\lambda | t)d\lambda , \end{aligned}$$

(7)

where

$$\begin{aligned} \pi _{\alpha }(\lambda | t)=\frac{\bar{F}^{\alpha }(t |\lambda )\pi (\lambda )}{\int _{0}^{\infty } \bar{F}^{\alpha }(t | \lambda )\pi (\lambda )d\lambda }. \end{aligned}$$

(8)

Note that, in the case of $\alpha >0$, $\pi _{\alpha }(\lambda | t)$ can be considered as the conditional PDF of $\Lambda | T_{\alpha } \ge t$, where $T_{\alpha }$ is described by the SF $\bar{F}^{\alpha }(t | \lambda )$ for $\alpha > 0$. For $\alpha \le 0$, for each $t>0$, $\pi _{\alpha }(\lambda | t)$ can be considered as the weighted density corresponding to $\pi (\lambda )$, with the weight function $\bar{F}^{\alpha }(t | \lambda )$.    Denote by $E_{\alpha }(\Lambda |t)$ the conditional expectation of $\Lambda$, that is,

$$\begin{aligned} E_{\alpha }(\Lambda |t)=\int _{0}^{\infty } \lambda \pi _{\alpha }(\lambda |t)d\lambda . \end{aligned}$$

The derivative of $E_{\alpha }(\Lambda |t)$ with respect to t is

$$\begin{aligned} \phi _{\alpha }(t)= \frac{\partial }{\partial t} E_{\alpha }(\Lambda |t)= \int _{0}^{\infty } \lambda \frac{\partial }{\partial t}\pi _{\alpha }(\lambda |t)d\lambda , \end{aligned}$$

where

$$\begin{aligned} \frac{\partial }{\partial t}\pi _{\alpha }(\lambda |t)= & {} \alpha \left( r(t,\alpha )\frac{\pi (\lambda )\bar{F}^{\alpha }(t|\lambda )}{\int _{0}^{\infty } \pi (\lambda )\bar{F}^{\alpha }(t|\lambda )} -\frac{\pi (\lambda )f(t|\lambda )\bar{F}^{\alpha -1}(t|\lambda )}{\int _{0}^{\infty } \pi (\lambda )\bar{F}^{\alpha }(t|\lambda )}\right) \nonumber \\= & {} \alpha \pi _{\alpha }(\lambda |t)\left[ r(t,\alpha )-r(t|\lambda )\right] . \end{aligned}$$

(9)

Therefore,

$$\begin{aligned} \phi _{\alpha }(t)= & {} \alpha \left( r(t,\alpha )E_{\alpha }(\Lambda |t)-E_{\alpha }(\Lambda r(t|\Lambda ))\right) \nonumber \\= & {} -\alpha Cov_{\alpha }(\Lambda , r(t|\Lambda )). \end{aligned}$$

(10)

Thus, if $r(t|\lambda )$ is increasing in $\lambda$ and $\alpha >0 \ (\alpha <0)$, then $E_{\alpha }(\Lambda |t)$ is decreasing (increasing) in t. If $r(t|\lambda )$ is decreasing in $\lambda$ and $\alpha >0 \ (\alpha <0)$, then $E_{\alpha }(\Lambda |t)$ is increasing (decreasing) in t. It should be noted also that when $\alpha =0$, we have $\phi _{\alpha }(t)=0$ and, therefore, $E_{\alpha }(\Lambda |t)$ does not depend on t.

Consider the following examples.

Example 2.1

Let $F(t|\lambda )$ be the Weibull distribution with parameters $(\lambda ,\beta )$. In this case, $r(t|\lambda )=\lambda \beta (\lambda t)^{\beta -1}$, which is increasing in $\lambda$. Let $\Lambda$ be described by the truncated exponential distribution with parameter $\vartheta$ in the interval [0, 5]. Then

$$\begin{aligned} E_{\alpha }(\Lambda |t)=\int _{0}^{5} \lambda \frac{\vartheta e^{-\vartheta \lambda } e^{-\alpha (\lambda t)^{\beta }}}{\int _{0}^{5}\vartheta e^{-\vartheta \lambda } e^{-\alpha (\lambda t)^{\beta }}d \lambda } d \lambda . \end{aligned}$$

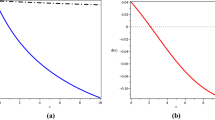
Since $r(t|\lambda )$ is increasing in $\lambda$, $E_{\alpha }(\Lambda |t)$ is a decreasing (increasing) function of t for $\alpha >0 \ (\alpha <0)$. Figure 1 depicts the plots of $E_{\alpha }(\Lambda |t)$ for different values of $\alpha$ and $\vartheta =1$ and $\beta =1.5$.

Fig. 1

The plots of $E_{\alpha }(\Lambda |t)$ in Example 2.1: For $\alpha <0$ (left) and $\alpha >0$ (right) for parameter values $\vartheta =1$ and $\beta =1.5$

Fig. 2

The plots of $E_{\alpha }(\Lambda |t)$ in Example 2.2 for $\alpha <0$ (left) and $\alpha >0$ (right) for parameter values $\vartheta =3$ and $\theta =2$

Example 2.2

Let the baseline distribution F(t) be exponential with parameter $\theta$ and assume that the population’s heterogeneity is modelled by $r(t|\lambda )=\frac{\theta }{\lambda }$, with $\Lambda$ described by the truncated exponential distribution with parameter $\vartheta$ in the interval $[5,\infty )$. In this case, we have

$$\begin{aligned} E_{\alpha }(\Lambda |t)=\int _{5}^{\infty } \lambda \frac{\vartheta e^{-\vartheta \lambda } e^{-\alpha \frac{\theta }{\lambda } t}}{\int _{5}^{\infty }\vartheta e^{-\vartheta \lambda } e^{-\alpha \frac{\theta }{\lambda } t}d \lambda } d \lambda . \end{aligned}$$

Since $r(t|\lambda )$ decreasing in $\lambda$, $E_{\alpha }(\Lambda |t)$ is an increasing (decreasing) function of t for $\alpha >0 \ (\alpha <0)$. Figure 2 shows the plots of $E_{\alpha }(\Lambda |t)$ for different values of $\alpha$ and $\vartheta =3$ and $\theta =2$.

3 Additive and multiplicative models

Two special important cases of $r(t|\lambda )$ in (7) are the additive and the multiplicative hazard models. In this section, we will discuss these two models. The results of this section are the extensions of the results of Finkelstein and Esaulova (2001). We will formulate the conditions for the preservation of the IFR (DFR) closure property for this specific models. It will be shown that the conditional PDF (8) plays an important role in determining the shape of $r(t,\alpha )$.

3.1 Additive model

In the additive hazard model, we have $r(t|\lambda )=r(t)+\lambda$, where r(t) is the baseline failure rate. Hence, the failure rate $r(t,\alpha )$ in this case is

$$\begin{aligned} r(t,\alpha )=\int _{0}^{\infty } r(t|\lambda )\pi (\lambda |t)d\lambda = r(t) +E_{\alpha }(\Lambda |t) \end{aligned}$$

(11)

and $\phi _{\alpha }(t)$ in (10) becomes

$$\begin{aligned} \phi _{\alpha }(t)=-\alpha Var_{\alpha }(\Lambda |t). \end{aligned}$$

(12)

The following lemma can be formulated as a consequence of this result .

Lemma 3.1

The conditional expectation of $\Lambda$ in the additive model is a decreasing (increasing) function of $t \in [0,\infty )$ for $\alpha >0 \ (\alpha <0)$.

The following theorem explores the behavior of ${r(t,\alpha )}$ in the additive model.

Theorem 3.2

Let r(t) be an increasing (decreasing) convex (concave) function in $[0,\infty )$ in the additive model. Assume that $Var_{\alpha }(\Lambda |t)$ is decreasing in $t \in [0,\infty )$ and

$$\begin{aligned} \alpha Var_{\alpha }(\Lambda |0)>(<)r^{\prime }(0). \end{aligned}$$

(13)

Then, $r(t,\alpha )$ decreases (increases) in [0, c) and increases (decreases) in $[c,\infty )$ for $\alpha >0 \ (\alpha <0)$, where c can be uniquely determined by $\alpha Var(\Lambda | t)= r^{\prime }(t)$ .

Proof

from (11) and (12), we have

$$\begin{aligned} r^{\prime }(t,\alpha )=r^{\prime }(t)+\frac{\partial }{\partial t} E_{\alpha }(\Lambda |t)=r^{\prime }(t)-\alpha Var_{\alpha }(\Lambda |t). \end{aligned}$$

Since $\alpha Var_{\alpha }(\Lambda |0)>(<) r^{\prime }(0)$, we have $r^{\prime }(0,\alpha )< (>)0$. Again, since r(t) is increasing (decreasing) and convex (concave), we have $(r^{\prime }(t))^{\prime }>(<)0$ and $r^{\prime }(t)$ is increasing (decreasing) in t. On the other hand, when $Var_{\alpha }(\Lambda |t)$ is decreasing in t, then $\alpha Var_{\alpha }(\Lambda |t)$ is decreasing (increasing). Thus, there exists $c>0$ such that $r^{\prime }(t)>(<)\alpha Var_{\alpha }(\Lambda |t)$. This implies for all $t>c,$ $r^{\prime }(t,\alpha )>(<)0$ and for all $t<c$, $r^{\prime }(t,\alpha )<(>)0$. Consequently, $r(t,\alpha )$ is decreasing (increasing) in [0, c) and is increasing (decreasing) in $[c,\infty )$ and c can be obtained from equation $\alpha Var_{\alpha }(\Lambda |t)= r^{\prime }(t)$. This completes the proof. $\square$

Corollary 3.3

If other assumptions of Theorem 3.2 are met, whereas instead of inequality (13), the following inequality holds

$$\begin{aligned} \alpha Var_{\alpha }(\Lambda |0)\le (\ge ) r^{\prime }(0), \end{aligned}$$

then, $r(t,\alpha )$ is increasing (decreasing) in $[0,\infty )$. This means that the IFR (DFR)-closure property holds under this assumption for the $\alpha$-mixture when $\alpha >0 \ (\alpha <0)$.

3.2 Multiplicative model

In the multiplicative hazard model, we have $r(t|\lambda )=\lambda r(t)$. Hence,

$$\begin{aligned} r(t,\alpha )=\int _{0}^{\infty } r(t|\lambda )\pi (\lambda |t)d\lambda = r(t)E_{\alpha }(\Lambda |t) \end{aligned}$$

(14)

and

$$\begin{aligned} \phi _{\alpha }(t)=-\alpha r(t)Var_{\alpha }(\Lambda |t). \end{aligned}$$

(15)

Thus,

$$\begin{aligned} r^{\prime }(t,\alpha )=r^{\prime }(t) E_{\alpha }[\Lambda |t]+ r(t) \frac{\partial }{\partial t} E_{\alpha }(\Lambda |t). \end{aligned}$$

(16)

From (16), the $\alpha$-mixture will be IFR (DFR) if and only if for all $t \in (0,\infty )$

$$\begin{aligned} \frac{r^{\prime }(t)}{r(t)} \ge (\le ) - \frac{\frac{\partial }{\partial t} E_{\alpha }(\Lambda |t)}{E_{\alpha }[\Lambda |t]}. \end{aligned}$$

(17)

Similar to Lemma 3.1, we have the following result for the multiplicative model.

Corollary 3.4

From the identity (10), we conclude that the conditional expectation of $\Lambda$ in the multiplicative model is a decreasing (increasing) function of $t \in (0,\infty )$ for $\alpha >0 \ (\alpha <0)$. Also, by (15), the inequality in (17) can be rewritten as

$$\begin{aligned} \frac{r^{\prime }(t)}{r^2(t)} \ge (\le ) \frac{\alpha Var_{\alpha }(\Lambda |t)}{E_{\alpha }[\Lambda |t]}. \end{aligned}$$

(18)

Thus, the IFR (DFR) (DFR (IFR)) properties of the $\alpha$-mixture model depend on the behavior of the baseline failure rate function r(t) and the first and the second conditional moments of $\Lambda$.

4 Stochastic comparisons of $\alpha$-mixtures

The goal of this section is to investigate partial orderings of finite $\alpha$-mixtures in the sense of the usual stochastic order and the hazard rate order. But first, we recall the definitions of the usual stochastic and the hazard rate orders and then obtain some basic comparisons for the continuous $\alpha$-mixtures

• The random variable X (with the CDF F) is said to be smaller than Y (with the CDF G) in the usual stochastic order (denoted by $X\le _{st}Y$ or $F\le _{st} G$) if $\bar{F}(x)\le \bar{G}(x)$ for all x, where $\bar{F}(x)$ and $\bar{G}(x)$ denote the survival functions of X and Y, respectively.

• The random variable X is said to be smaller than Y in the hazard rate order (denoted by $X\le _{hr}Y$ or $F\le _{hr}G$) if    $\bar{G}(x)/\bar{F}(x)$ is increasing in x, for all x. When F and G are absolutely continuous, $F\le _{hr}G$ if and only if $r_X(x)\ge r_Y(x)$, for all x, where $r_X(x)$ and $r_Y(x)$ denote the failure rates corresponding to F and G, respectively.

The following theorems provide generalizations of Theorems 1.A.6 and 1.B.14 of Shaked and Shanthikumar (2007) obtained for ordinary mixtures.

Theorem 4.1

Consider a family of SFs $\left\{ \bar{F}(t | \lambda ), \lambda \in {[0, \infty )} \right\}$. Suppose that $\Lambda _{1}$ and $\Lambda _{2}$ are two random variables with distribution functions $\Pi _{1}$ and $\Pi _{2}$, respectively, with supports in $[0,\infty )$. Assume that the SF of $T_{i}$, $i=1,2$, is given by

$$\begin{aligned} \bar{F}_{i}(t,\alpha )= \left( \int _{0}^{\infty } \bar{F}^{\alpha }(t | \lambda ) d\Pi _{i}(\lambda ) \right) ^{\frac{1}{\alpha }}. \end{aligned}$$

If $T|\lambda \le _{st} T|\lambda ^{\prime }$ whenever $\lambda \le \lambda ^{\prime }$ and if $\Lambda _{1} \le _{st} \Lambda _{2}$, then $T_{1} \le _{st} T_{2}.$

Proof

We consider three different cases for $\alpha$.

• Assume first, that $\alpha >0$. By assumption $T|\lambda \le _{st} T|\lambda ^{\prime }$, we have: $\bar{F}(t | \lambda )$ is increasing in $\lambda$ and hence, $\bar{F}^{\alpha }(t | \lambda )$ is increasing in $\lambda$ for all t since $\alpha >0$. Thus, assumption $\Lambda _{1} \le _{st} \Lambda _{2}$ implies that

  $$\begin{aligned} \int _{0}^{\infty } \bar{F}^{\alpha }(t | \lambda )d\Pi _{1}(\lambda )\le \int _{0}^{\infty } \bar{F}^{\alpha }(t | \lambda )d\Pi _{2}(\lambda ). \end{aligned}$$

  Raising both sides of the inequality to the power $\frac{1}{\alpha }$ results in $T_{1} \le _{st} T_{2}$.

• Assume now that $\alpha \rightarrow 0$. In this case,

  $$\begin{aligned} {\bar{F}_{gm,i}}(t)= \exp \left( \int _{0}^{\infty } \log (\bar{F}(t | \lambda )) d\Pi _{i}(\lambda ) \right) . \end{aligned}$$

  Again, as $T|\lambda \le _{st} T|\lambda ^{\prime }$, $\bar{F}(t |\lambda )$ is increasing in $\lambda$ for all t, and hence $\log (\bar{F}(t | \lambda ))$ is increasing in $\lambda$ for all t. Thus by $\Lambda _{1} \le _{st} \Lambda _{2}$, we have

  $$\begin{aligned} \int _{0}^{\infty } \log (\bar{F}(t | \lambda ))d\Pi _{1}(\lambda )\le \int _{0}^{\infty } \log (\bar{F}(t | \lambda ))d\Pi _{2}(\lambda ). \end{aligned}$$

  Hence,

  $$\begin{aligned} {\bar{F}_{gm,1}}(t)= \exp \left( \int _{0}^{\infty } \log (\bar{F}(t | \lambda )) d\Pi _{1}(\lambda ) \right) \le \exp \left( \int _{0}^{\infty } \log (\bar{F}(t | \lambda )) d\Pi _{2}(\lambda ) \right) = {\bar{F}_{gm,2}}(t). \end{aligned}$$

  This means that $T_{1} \le _{st} T_{2}$ and the proof is completed.

• When $\alpha <0$, assumption $T|\lambda \le _{st} T|\lambda ^{\prime }$ and the property that $\bar{F}(t | \lambda )$ is increasing, in $\lambda$ for all t imply that $\bar{F}^{\alpha }(t | \lambda )$ is decreasing in $\lambda$ for all t. Thus, by assumption $\Lambda _{1} \le _{st} \Lambda _{2}$, we get

  $$\begin{aligned} \int _{0}^{\infty } \bar{F}^{\alpha }(t | \lambda )d\Pi _{1}(\lambda )\ge \int _{0}^{\infty } \bar{F}^{\alpha }(t | \lambda )d\Pi _{2}(\lambda ). \end{aligned}$$

  Raising both sides of the inequality to the power $\frac{1}{\alpha }$, gives the result since $\alpha <0$. Hence, for all values of $\alpha$, assumptions of the theorem give $T_{1} \le _{st} T_{2}$ . $\square$

We need also the following definition and the theorem from Joag-dev et al. (1995).

Definition 4.2

Joag-dev et al. (1995). A pair of measurable real functions $(g_{1}, g_{2})$, is said to satisfy positivity of the second order determinant ($DP_{2}$) condition if

• (i) $g_{1}$ is nonnegative while $g_{2}$ may take negative values.

• (ii) for every $x_{1}\le x_{2}$,

  $$\begin{aligned} g_{1}(x_{1})g_{2}(x_{2})\ge g_{1}(x_{2})g_{2}(x_{1}). \end{aligned}$$

Theorem 4.3

Joag-dev et al. (1995). Let $(g_{1}, g_{2})$ be a pair of functions satisfying the $DP_{2}$ property and the SFs $\bar{F}(t,\lambda )$ be $TP_{2}$ in $(\lambda , t)$. Suppose that for $i = 1, 2$, $\int g_{i}(t)dF_{\lambda }(t)$ exists and is finite. Further, suppose that $g_{l}(t)$ is increasing in t. Then for $i= 1, 2$, $h_{i}(t)=\int g_{i}(t)dF_{\lambda }(t)$ is $DP_{2}$, or equivalently,

$$\begin{aligned} \int g_{1}(t)dF_{1}(t)\int g_{2}(t)dF_{2}(t)\ge \int g_{1}(t)dF_{2}(t)\int g_{2}(t)dF_{1}(t). \end{aligned}$$

The following theorem extends Theorem 1.B.14 of Shaked and Shanthikumar (2007) to the $\alpha$-mixture family.

Theorem 4.4

Let assumptions of Theorem 4.1 be met. If $T|\lambda \le _{hr} T|\lambda ^{\prime },$ whenever $\lambda \le \lambda ^{\prime }$ and if $\Lambda _{1} \le _{hr} \Lambda _{2}$, then $T_{1} \le _{hr} T_{2}.$

Proof

• Let $\alpha >0$. By assumption $T|\lambda \le _{hr} T|\lambda ^{\prime }$, the function $\bar{F}(t |\lambda )$ and hence, $\bar{F}^{\alpha }(t | \lambda )$ are $TP_{2}$ as functions of $\lambda \in [0,\infty )$ and $t \in R$. By $\Lambda _{1} \le _{hr} \Lambda _{2}$, $\bar{\Pi }_{i}(\lambda )$, as a function of $\lambda \in [0,\infty )$ and $i \in \lbrace 1,2\rbrace$, is $TP_{2}$. Also, $\bar{F}(t | \lambda )$ is increasing in $\lambda$ (because $X \le _{hr} Y \Longrightarrow X \le _{st} Y$) and so is $\bar{F}^{\alpha }(t | \lambda )$. Therefore, by Theorem 4.3

  $$\begin{aligned} \int _{0}^{\infty } \bar{F}^{\alpha }(t | \lambda )d\Pi _{1}(\lambda )\int _{0}^{\infty } \bar{F}^{\alpha }(t^{\prime } | \lambda )d\Pi _{2}(\lambda )\ge \int _{0}^{\infty } \bar{F}^{\alpha }(t | \lambda )d\Pi _{2}(\lambda )\int _{0}^{\infty } \bar{F}^{\alpha }(t^{\prime } | \lambda )d\Pi _{1}(\lambda ). \end{aligned}$$

  If both sides are raised into power $\frac{1}{\alpha }$, we get

  $$\begin{aligned} \bar{F}_{1}(t,\alpha )\bar{F}_{2}(t^{\prime },\alpha )\ge \bar{F}_{2}(t,\alpha )\bar{F}_{1}(t^{\prime },\alpha ). \end{aligned}$$

  Thus, $\bar{F}_{i}(t,\alpha )$ is $TP_{2}\in \lbrace 1,2\rbrace$ and $t \in R$.

• The case $\alpha \longrightarrow 0$ is similar to the case $\alpha >0$.

• Assume that $\alpha <0$. In this case, the initial inequality is reversed and since $\alpha < 0$ it follows that:

  $$\begin{aligned} \bar{F}_{1}(t,\alpha )\bar{F}_{2}(t^{\prime },\alpha )\ge \bar{F}_{2}(t,\alpha )\bar{F}_{1}(t^{\prime },\alpha ). \end{aligned}$$

  Consequently, $\bar{F}_{i}(t,\alpha )$ is $TP_{2}\in \lbrace 1,2\rbrace$ and $t \in R$ and hence, $T_{1} \le _{hr} T_{2}.$ This completes the proof. $\square$

4.1 Stochastic comparisons of finite $\alpha$-mixtures

The finite $\alpha$-mixture of SFs, $\bar{F}_{i}$ with PDF’s $f_i$, for $i=1,2,..,n$, is defined by relationship (3). When $\alpha =1$, we get the arithmetic mixture of $\bar{F}_i$’s. When $\alpha \rightarrow 0$, we obtain the geometric means of $\bar{F}_i$’s.

$$\begin{aligned} \bar{F}_{gm}(t)=\prod _{i=1}^{n}\bar{F}^{p_{i}}_{i}(t), \end{aligned}$$

which can be considered as a generalized proportional hazards model. Note that, when $p_{i}=\frac{1}{n}$, we get $\bar{F}_{gm}^{n}(t)=\prod _{i=1}^{n}\bar{F}_{i}(t)$, which is the reliability function of a series system that consists of n independent components, where the $i-th$ component has reliability $\bar{F}_{i}(t)$. If $\alpha =-1$, we get the harmonic means of $\bar{F}_i$’s. In this case, the reliability function can be written as

$$\begin{aligned} \bar{F}_{hm}(t)=\frac{1}{\sum _{i=1}^{n}\frac{p_{i}}{\bar{F}_{i}(t)}}. \end{aligned}$$

The corresponding PDF of (3) is as follows:

$$\begin{aligned} f(t,\alpha )=\left[ \sum _{i=1}^{n} p_{i}f_{i}(t){\bar{F}_{i}}^{\alpha -1}(t) \right] \left[ \sum _{i=1}^{n} p_{i}{\bar{F}_{i}}^{\alpha }(t) \right] ^{\frac{1}{\alpha }-1}. \end{aligned}$$

(19)

Denote by $r(t,\alpha )$ and $r_{i}(t)$ the failure rate of the finite $\alpha$-mixture and the failure rate of the $i-th$ component. Then

$$\begin{aligned} r(t,\alpha )=\frac{f(t,\alpha )}{\bar{F}(t,\alpha )}=\sum _{i=1}^{n} r_{i}(t) p^{\alpha }_{i}(t), \end{aligned}$$

(20)

where

$$\begin{aligned} p^{\alpha }_{i}(t)=\frac{p_{i} \bar{F}_{i}^{\alpha }(t)}{\sum _{i=1}^{n} p_{i} \bar{F}_{i}^{\alpha }(t)}. \end{aligned}$$

The following theorem extends a result of Navarro and del Aguila (2017) on arithmetic mixture of survival functions to the $\alpha$-mixture family

Theorem 4.5

Let $F_{p}(t,\alpha )$ and $F_{q}(t,\alpha )$ be two n-component finite $\alpha$-mixture models with mixing probabilities $\mathbf{p =(p_{1},..., p_{n})}$ and $\mathbf{q =(q_{1},..., q_{n})}$, respectively. Assume that

$$\begin{aligned} F_{1} \ge _{st} F_{2} \ge _{st}... \ge _{st}F_{n}. \end{aligned}$$

Then,

$F_{p}(t,\alpha )\le _{st} F_{q}(t,\alpha )$

if and only if $\mathbf{p } \ge _{st}\mathbf{q }$ (i.e. $\sum _{i=1}^{k}q_{i}\ge \sum _{i=1}^{k}p_{i}$ for all $k \in \lbrace 1,2,...,n-1\rbrace$).

Proof

The “if ” part of the theorem follows from Theorem 4.1 . We will prove now the “only if ” part of this theorem. First, assume that $\alpha >0$. From $F_{p}(t,\alpha )\le _{st} F_{q}(t,\alpha )$, we have

$$\begin{aligned} \left[ \sum _{i=1}^{n} p_{i}{\bar{F}_{i}}^{\alpha }\right] ^{\frac{1}{\alpha }}\le \left[ \sum _{i=1}^{n} q_{i}{\bar{F}_{i}}^{\alpha }\right] ^{\frac{1}{\alpha }}. \end{aligned}$$

Since $\alpha >0$,

$$\begin{aligned} \left[ \sum _{i=1}^{n} p_{i}{\bar{F}_{i}}^{\alpha }\right] \le \left[ \sum _{i=1}^{n} q_{i}{\bar{F}_{i}}^{\alpha }\right] . \end{aligned}$$

From the assumption that $F_{1} \ge _{st} F_{2} \ge _{st}... \ge _{st}F_{n}$ with the choice $\bar{F}_{1}=\bar{F}_{2}=...=\bar{F}_{k}=1$ and $\bar{F}_{k+1}=...=\bar{F}_{n}=0$, we have $\sum _{i=1}^{k} p_{i}\le \sum _{i=1}^{k} q_{i}$. That is, ${{{\varvec{p}}}} \ge _{st} {{{\varvec{q}}}}$.

If $\alpha \rightarrow 0$, from $F_{gm,p}\le _{st} F_{gm,q}$ we have

$$\begin{aligned} \bar{F}_{1}^{p_{1}}...\bar{F}_{k}^{p_{k}}...\bar{F}_{n}^{1-\sum _{i=1}^{n-1}p_{i}}\le \bar{F}_{1}^{q_{1}}...\bar{F}_{k}^{q_{k}}...\bar{F}_{n}^{1-\sum _{i=1}^{n-1}q_{i}}. \end{aligned}$$

This is equivalent to

$$\begin{aligned} 1 \le (\frac{\bar{F}_{1}}{\bar{F}_{n}})^{q_{1}-p_{1}}...(\frac{\bar{F}_{k}}{\bar{F}_{n}})^{q_{k}-p_{k}}... (\frac{\bar{F}_{n-1}}{\bar{F}_{n}})^{q_{n-1}-p_{n-1}}. \end{aligned}$$

From the assumption $F_{1} \ge _{st} F_{2} \ge _{st}... \ge _{st}F_{n}$ with choosing $\bar{F}_{1}=\bar{F}_{2}=...=\bar{F}_{k}=1$ and $\bar{F}_{k+1}=...=\bar{F}_{n-1}=\bar{F}_{n}$, we have

$$\begin{aligned} 1\le ({\bar{F}_{n}})^{(\sum _{i=1}^{k}p_{i}-\sum _{i=1}^{k}q_{i})}. \end{aligned}$$

This, in turn, implies that $\sum _{i=1}^{k}q_{i}\ge \sum _{i=1}^{k}p_{i}$, i.e., ${{{\varvec{p}}}} \ge _{st} {{{\varvec{q}}}}$.

Assume that $\alpha <0$. From $F_{p}(t,\alpha )\le _{st} F_{q}(t,\alpha )$. we have

$$\begin{aligned} \left[ \sum _{i=1}^{n} p_{i}{\bar{F}_{i}}^{\alpha }\right] ^{\frac{1}{\alpha }}\le \left[ \sum _{i=1}^{n} q_{i}{\bar{F}_{i}}^{\alpha }\right] ^{\frac{1}{\alpha }}. \end{aligned}$$

Since $\alpha <0$, we have

$$\begin{aligned} \left[ \sum _{i=1}^{n} q_{i}{\bar{F}_{i}}^{\alpha }\right] \le \left[ \sum _{i=1}^{n} p_{i}{\bar{F}_{i}}^{\alpha }\right] . \end{aligned}$$

From the assumption $F_{1} \ge _{st} F_{2} \ge _{st}... \ge _{st}F_{n}$ with the choice $\bar{F}_{1}=\bar{F}_{2}=...=\bar{F}_{k}=1$ and $\bar{F}_{k+1}=...=\bar{F}_{n}=\bar{F}_{n}$, we have

$$\begin{aligned} \left[ \sum _{i=1}^{k}q_{i}+{\bar{F}_{n}}^{\alpha } \sum _{i=k+1}^{n}q_{i} \right] \le \left[ \sum _{i=1}^{k}p_{i}+{\bar{F}_{n}}^{\alpha } \sum _{i=k+1}^{n}p_{i}\right] \end{aligned}$$

or

$$\begin{aligned} \left[ \sum _{i=1}^{k}q_{i}+{\bar{F}_{n}}^{\alpha }(1- \sum _{i=1}^{k}q_{i}) \right] \le \left[ \sum _{i=1}^{k}p_{i}+{\bar{F}_{n}}^{\alpha } (1-\sum _{i=1}^{k}p_{i})\right] . \end{aligned}$$

Thus,

$$\begin{aligned} \left[ \sum _{i=1}^{k}q_{i}(1-{\bar{F}_{n}}^{\alpha }) \right] \le \left[ \sum _{i=1}^{k}p_{i}(1-{\bar{F}_{n}}^{\alpha }) \right] . \end{aligned}$$

As $\alpha <0$ and $0 \le \bar{F}_{n}\le 1$, then $(1-{\bar{F}_{n}}^{\alpha })\le 0$. Hence, $\sum _{i=1}^{k}q_{i}\ge \sum _{i=1}^{k}p_{i}$, i.e., ${{{\varvec{p}}}} \ge _{st}{{{\varvec{q}}}}$ completing the proof. $\square$

The following theorem gives an extension to the “if” part of Theorem 4.5.

Theorem 4.6

Let $F_{p}(t,\alpha )$ and $G_{q}(t,\alpha )$ be two n-component finite $\alpha$-mixture models with mixing probabilities $\mathbf{p =(p_{1},..., p_{n})}$ and $\mathbf{q =(q_{1},..., q_{n})}$, respectively. Assume that

• (i) $F_{1}\ge _{st}F_{2}\ge _{st}...{\ge _{st}} F_{n}$,

• (ii) $\mathbf{p }\ge _{st}\mathbf{q }$ (i.e. $p_{1}+...+p_{k}\le q_{1}+...+q_{k}$ for all $k \in \lbrace 1,2,...,n-1\rbrace$),

• (iii) $F_{i} \le _{st} G_{i}$ for all ${i \in \{1,...,n\}}$.

Then, we have:

$$\begin{aligned} F_{p}(t,\alpha )\le _{st} G_{q}(t,\alpha ). \end{aligned}$$

Proof

First, we prove that $F_{{q}}(t,\alpha )\le _{st} G_{{q}}(t,\alpha )$. Let $\alpha >0$. From $F_{i} \le _{st} G_{i}$ for $i=1,...,n$, we have $\bar{F}_{i}(t) \le \bar{G}_{i}(t)$ for any t, $i=1,...,n$. Since $\alpha >0$, $\bar{F}^{\alpha }_{i} \le \bar{G}^{\alpha }_{i}$ for $i=1,...,n$. Thus,

$$\begin{aligned} \sum _{i=1}^{n} {q}_{i}\bar{F}^{\alpha }_{i} \le \sum _{i=1}^{n} {q}_{i}\bar{G}^{\alpha }_{i}. \end{aligned}$$

Consequently,

$$\begin{aligned} \left[ \sum _{i=1}^{n} {q}_{i}\bar{F}^{\alpha }_{i}\right] ^{\frac{1}{\alpha }} \le \left[ \sum _{i=1}^{n} {q}_{i}\bar{G}^{\alpha }_{i} \right] ^{\frac{1}{\alpha }}. \end{aligned}$$

This means $F_{{q}}(t,\alpha )\le _{st} G_{{q}}(t,\alpha )$ for $\alpha >0$.

Let $\alpha <0$. The assumption $F_{i} \le _{st} G_{i}$ implies that $\bar{F}^{\alpha }_{i} \ge \bar{G}^{\alpha }_{i}$ for $i=1,...,n$. Thus,

$$\begin{aligned} \sum _{i=1}^{n} {q}_{i}\bar{G}^{\alpha }_{i} \le \sum _{i=1}^{n} {q}_{i}\bar{F}^{\alpha }_{i}. \end{aligned}$$

and since $\alpha <0$, we have

$$\begin{aligned} \left[ \sum _{i=1}^{n} {q}_{i}\bar{F}^{\alpha }_{i}\right] ^{\frac{1}{\alpha }} \le \left[ \sum _{i=1}^{n} {q}_{i}\bar{G}^{\alpha }_{i} \right] ^{\frac{1}{\alpha }}. \end{aligned}$$

This means $F_{{q}}(t,\alpha )\le _{st} G_{{q}}(t,\alpha )$ for $\alpha <0$.

If $\alpha \rightarrow 0$, $\bar{F}_{gm,{q}}=\prod _{i=1}^{n}\bar{F}^{{q}_{i}}_{i}$ and $\bar{G}_{gm,{q}}=\prod _{i=1}^{n}\bar{G}^{{q}_{i}}_{i}$ and from assumption $\bar{F}_{i}(t) \le \bar{G}_{i}(t)$ for $i=1,...,n$, we have

$$\begin{aligned} \prod _{i=1}^{n}\bar{F}^{{q}_{i}}_{i} \le \prod _{i=1}^{n}\bar{G}^{{q}_{i}}_{i}. \end{aligned}$$

Thus, $F_{gm,{q}}(t)\le _{st} G_{gm,{q}}(t)$ and for all values of $\alpha$, we obtain

$$\begin{aligned} F_{{q}}(t,\alpha )\le _{st} G_{{q}}(t,\alpha ). \end{aligned}$$

(21)

From conditions (i), (ii) and Theorem 4.5 we have: $F_{p}(t,\alpha )\le _{st} F_{q}(t,\alpha )$. By relation (21), $F_{q}(t,\alpha )\le _{st} G_{q}(t,\alpha )$. Thus, $F_{p}(t,\alpha )\le _{st} G_{q}(t,\alpha )$ and hence, the proof is complete. $\square$

4.2 The hazard rate order of $\alpha$-mixture

The following theorem is an extension of Proposition 7 of Navarro and del Aguila (2017).

Theorem 4.7

Let $F_{p}(t,\alpha )$ and $F_{q}(t,\alpha )$ be two n-component finite $\alpha$-mixture models with mixed proportions $\mathbf{p =(p_{1}, . . . , p_{n})}$ and $\mathbf{q =(q_{1}, . . . , q_{n})}$, respectively. Assume that

$$\begin{aligned} F_{1} \ge _{hr} ... \ge _{hr}F_{n}. \end{aligned}$$

Then,

$$\begin{aligned} F_{p}(t,\alpha )\le _{hr} F_{q}(t,\alpha ) \end{aligned}$$

if and only if

$$\begin{aligned} H(v_{2},v_{3},...,v_{n})=\left[ \frac{q_{1}+q_{2}v_{2}^{\alpha }+q_{3}(v_{2}v_{3})^{\alpha }+...+q_{n}(v_{2}...v_{n})^{\alpha }}{p_{1}+p_{2}v_{2}^{\alpha }+p_{3}(v_{2}v_{3})^{\alpha }+...+p_{n}(v_{2}...v_{n})^{\alpha }}\right] ^{\frac{1}{\alpha }} \end{aligned}$$

is decreasing in $[0,1]^{n-1}$.¹

Proof

The case of $\alpha \rightarrow 0$ follows from Navarro and del Aguila (2017). In what follows, we assume that $\alpha \not =0$. The assumption $F_{1} \ge _{hr} ... \ge _{hr}F_{n}$ implies that the function $\frac{\bar{F}_{i+1}(t)}{\bar{F}_{i}(t)}\in [0,1]$ is decreasing in t, $i = 1,..., n - 1$. The ratio of the respective reliability functions can be written as

$$\begin{aligned} \frac{\bar{F}_{q}(t,\alpha )}{\bar{F}_{p}(t,\alpha )}=\left[ \frac{q_{1}+q_{2}v_{2}^{\alpha }+q_{3}(v_{2}v_{3})^{\alpha }+...+q_{n}(v_{2}...v_{n})^{\alpha }}{p_{1}+p_{2}v_{2}^{\alpha }+p_{3}(v_{2}v_{3})^{\alpha }+...+p_{n}(v_{2}...v_{n})^{\alpha }}\right] ^{\frac{1}{\alpha }}= H(v_{2},v_{3},...,v_{n}) \end{aligned}$$

for all t, where $v_{i+1}=\frac{\bar{F}_{i+1}(t)}{\bar{F}_{i}(t)},\;\; i=1,...,n-1$.

To prove the ’if’ part, note that, for $\alpha \not =0$, as $\frac{\bar{F}_{i+1}(t)}{\bar{F}_{i}(t)}$ is decreasing, H is also decreasing. Hence, $F_{p}(t,\alpha )\le _{hr} F_{q}(t,\alpha )$. This completes the ‘if’ part of the theorem.

To prove the ‘only if’ part, we need to show that under the conditions of the theorem, if $F_{p}(t,\alpha )\le _{hr} F_{q}(t,\alpha )$, H is decreasing over $(0, 1)^{n-1}$. For fixed ${u}\le {v}$² with ${u}=(u_{2},...,u_{n})$ and ${v}=(v_{2},...,v_{n})$, we have to show that $H({u})\ge H({v})$. Consider the following reliability functions from Navarro and del Aguila (2017)

$$\begin{aligned} \bar{F}_{i}(t)=\left\{ \begin{array}{ll} 1, &{} t<1 \\ v_{2}...v_{i}, &{} 1<t<2\\ u_{2}...u_{i}, &{} 2<t<3\\ 0, &{} t\ge 3 \end{array} \right. \end{aligned}$$

for $i=1,...,n$. It is easy to see that $F_{1} \ge _{hr} ... \ge _{hr}F_{n}$. On the other hand, $F_{p}(t,\alpha )\le _{hr} F_{q}(t,\alpha )$ implies

$$\begin{aligned} \frac{\bar{F}_{q}(1,\alpha )}{\bar{F}_{p}(1,\alpha )} \le \frac{\bar{F}_{q}(2,\alpha )}{\bar{F}_{p}(2,\alpha )}, \end{aligned}$$

which is equivalent to $H({u})\ge H({v})$ for $\alpha \ne 0$.

This completes the proof. $\square$

Theorem 4.8

Let $F_{p}(t,\alpha )$ and $G_{q}(t,\alpha )$ be two n-component finite $\alpha$-mixture models with mixed proportions $\mathbf{p} =(p_{1}, . . . , p_{n})$ and $\mathbf{q} =(q_{1}, . . . , q_{n})$, respectively. Suppose that

• (i) $G_{1} \ge _{hr} ... \ge _{hr}G_{n}$ and $F_{1} \ge _{hr} ... \ge _{hr}F_{n}$;

• (ii) $\frac{\bar{F}_{i}(t)}{\bar{G}_{i}(t)}$ is increasing (decreasing) in $i \in \lbrace 1,2,...,n\rbrace$;

• (iii) $F_{i} \le _{hr} G_{i}$ for all $i \in \lbrace 1,2,...,n\rbrace$;

• (iv) $p_{i}q_{j} \le p_{j}q_{i}$ for all $1\le i \le j \le n$.

Then, $F_{p}(t,\alpha )\le _{hr} G_{q}(t,\alpha )$ for $\alpha >0 \ (\alpha <0)$.

Proof

First, we prove that, for $\alpha \not = 0$, $F_{p}(t,\alpha )\le _{hr} F_{q}(t,\alpha )$. In order to prove this, we have to show that $\frac{\bar{F}_{q}(t,\alpha )}{\bar{F}_{p}(t,\alpha )}$ is increasing in t. That is, we should show that

$$\begin{aligned} R(t)\equiv [A(t)]^{1/\alpha }, \end{aligned}$$

is increasing in t, where

$$\begin{aligned} A(t)=\left[ \frac{\sum _{i=1}^{{n}} q_{i}{\bar{F}_{i}}^{\alpha }(t)}{\sum _{i=1}^{{n}} p_{i}{\bar{F}_{i}}^{\alpha }(t)}\right] . \end{aligned}$$

Differentiating R(t) with respect to t, gives

$$\begin{aligned} R^{\prime }(t)=\frac{1}{\alpha } A^{\prime }(t) [A(t)]^{\frac{1}{\alpha }-1}, \end{aligned}$$

where

$$\begin{aligned} A^{\prime }(t){\mathop {=}\limits ^{sign}}&\alpha \left\{ -\sum _{i=1}^{{n}} q_{i} f_{i}(t){\bar{F}_{i}}^{\alpha -1}(t) \sum _{j=1}^{{n}} p_{j}{\bar{F}_{j}}^{\alpha }(t)+\sum _{i=1}^{{n}} p_{i} f_{i}(t){\bar{F}_{i}}^{\alpha -1}(t) \sum _{j=1}^{{n}} q_{j}{\bar{F}_{j}}^{\alpha }(t) \right\} \\ =&\alpha \left\{ \sum _{i=1}^{{n}} \sum _{j=1}^{{n}} (p_{i}q_{j}-p_{j}q_{i})f_{i}(t){\bar{F}_{i}}^{\alpha -1}(t){\bar{F}_{j}}^{\alpha }(t)\right\} \\ =&\alpha \left\{ \sum _{i=1}^{{n}-1} \sum _{j=i+1}^{{n}} (p_{i}q_{j}-p_{j}q_{i})\left( f_{i}(t){\bar{F}_{i}}^{\alpha -1}(t){\bar{F}_{j}}^{\alpha }(t)-f_{j}(t){\bar{F}_{j}}^{\alpha -1}(t){\bar{F}_{i}}^{\alpha }(t)\right) \right\} \\ =&\alpha \left\{ \sum _{i=1}^{{n}-1} \sum _{j=i+1}^{{n}} (p_{i}q_{j}-p_{j}q_{i})\left( r_{i}(t)-r_{j}(t)\right) {\bar{F}_{i}}^{\alpha }(t) {\bar{F}_{j}}^{\alpha }(t)\right\} . \end{aligned}$$

Consequently,

$$\begin{aligned} R^{\prime }(t){\mathop {=}\limits ^{sign}}&\left\{ \sum _{i=1}^{{n}-1} \sum _{j=i+1}^{{n}} (p_{i}q_{j}-p_{j}q_{i})\left( r_{i}(t)-r_{j}(t)\right) {\bar{F}_{i}}^{\alpha }(t) {\bar{F}_{j}}^{\alpha }(t)\right\} . \end{aligned}$$

As $F_{i} \ge _{hr} F_{j}$ for $i \le j$ from condition (i), we have $r_{i}(t)-r_{j}(t)\le 0$ for $i \le j$. From condition (iv), $p_{i}q_{j}- p_{j}q_{i} \le 0$. Hence , $R^{\prime }(t)\ge 0$ which, in turn, implies that for $\alpha \not = 0$

$$\begin{aligned} F_{p}(t,\alpha )\le _{hr} F_{q}(t,\alpha ). \end{aligned}$$

(22)

Now, let us prove that $F_{p}(t,\alpha )\le _{hr}G_{p}(t,\alpha )$ for $\alpha >0$.

From (20), the expressions for the failure rate functions that correspond to $F_{p}(t,\alpha )$ and $G_{p}(t,\alpha )$ can be written as

$$\begin{aligned} r_{F}(t,\alpha )=\sum _{i=1}^{n} r_{F_{i}}(t) p_{i}(t) \end{aligned}$$

and

$$\begin{aligned} r_{G}(t,\alpha )=\sum _{i=1}^{n} r_{G_{i}}(t) q_{i}(t) \end{aligned}$$

respectively, where $q_{i}(t)=\frac{p_{i} \bar{G}_{i}^{\alpha }(t)}{\sum _{i=1}^{n} p_{i} \bar{G}_{i}^{\alpha }(t)}$ for $i=1,...,n$. To prove $F_{p}(t,\alpha )\le _{hr} G_{p}(t,\alpha )$ for $\alpha >0$, we need to show that $\psi (t)=r_{F}(t,\alpha )-r_{G}(t,\alpha )$ is non-negative for all $t\ge 0$. Note that,

$$\begin{aligned} \psi (t)=&\sum _{i=1}^{n} r_{F_{i}}(t) p_{i}(t)-\sum _{i=1}^{n} r_{G_{i}}(t) q_{i}(t)\\ \ge&\sum _{i=1}^{n} r_{G_{i}}(t) p_{i}(t)-\sum _{i=1}^{n} r_{G_{i}}(t) q_{i}(t)\equiv \xi (t), \end{aligned}$$

where the inequality follows from condition (iii). Thus, it suffices to show that $\xi (t)$ is non-negative for all $t\ge 0$. Consider two non-negative discrete random variables W and V on a sample space $\lbrace 1, . . . , n\rbrace$ with probability mass functions $q_{i}(t)$ and $p_{i}(t)$,$i = 1, . . . , n$, respectively. Thus $\xi (t)$ can be written as

$$\begin{aligned} \xi (t)=E[\phi (V)]-E[\phi (W)], \end{aligned}$$

(23)

where $\phi (i)=r_{G_{i}}(.)$, $i=1,...,{n}$. To prove that (23) is non-negative, it is sufficient to show that $\phi (i)$ is increasing in i and ${W} \le _{st} {V}$. Based on condition (i), we have $r_{G_{1}}(t)\le ...\le r_{G_{n}}(t)$ for all $t\ge 0$. Thus, $\phi (i)$ is increasing in i. On the other hand, one can see that

$$\begin{aligned} \frac{p_{i}(t)}{q_{i}(t)} \varpropto (\frac{\bar{F}_{i}(t)}{\bar{G}_{i}(t)})^{\alpha }\;\;i \in \lbrace 1,...,n\rbrace . \end{aligned}$$

Hence, condition (ii) implies that $\frac{p_{i}(t)}{q_{i}(t)}$ is increasing in $i \in \lbrace 1,...,n\rbrace$, which means that ${W} \le _{lr}{V}$, which in turn implies ${W} \le _{st}{V}$. Thus, $\xi (t)$ is non-negative and for $\alpha >0$,

$$\begin{aligned} F_{p}(t,\alpha )\le _{hr}G_{p}(t,\alpha ). \end{aligned}$$

(24)

Under assumptions of the theorem, from (22) and (24), we conclude that for $\alpha >0$, $F_{q}(t,\alpha )\le _{hr} G_{q}(t,\alpha )$.

The case $\alpha <0$ can be considered in a similar way. This completes the proof. $\square$

Remark 4.1

When $\alpha =1$, a result similar to Theorem 4.8 (with slightly different conditions) is obtained by Amini-Seresht and Zhang (2017).

In Theorem 4.8, we assumed that $\alpha \not =0$. In the following theorem, we prove a result for $\alpha \rightarrow 0$, under conditions different from those given in Theorem 4.8.

Theorem 4.9

Let $F_{gm,p}(t)$ and $G_{gm,q}(t)$ be two n-component finite $\alpha$-mixture models when $\alpha \rightarrow 0$ with mixing proportions $\mathbf{p =(p_{1}, . . . , p_{n})}$ and $\mathbf{q =(q_{1}, . . . , q_{n})}$, respectively. Assume that

• (i) $F_{1} \ge _{hr} ... \ge _{hr}F_{n}$;

• (ii) $\mathbf{p }\ge _{st}\mathbf{q }$ (i.e. $p_{1}+...+p_{k}\le q_{1}+...+q_{k}$ for all $k \in \lbrace 1,2,...,n-1\rbrace$);

• (iii) $F_i \le _{hr} G_i$ for all ${ i \in \{ 1,2,...,n\}}$.

Then,

$$\begin{aligned} F_{gm,p}(t)\le _{hr} G_{gm,q}(t) . \end{aligned}$$

Proof

First we prove that $F_{gm,p}(t)\le _{hr} G_{gm,p}(t)$. Denote by $r_{F,p}(t)$ and $r_{G,p}(t)$ the failure rates of $F_{gm,p}(t)$ and $G_{gm,p}(t)$, respectively. Thus,

$$\begin{aligned} r_{F,p}(t)=\sum _{i=1}^{n} p_{i}r_{F_i}(t) \end{aligned}$$

and

$$\begin{aligned} r_{G,p}(t)=\sum _{i=1}^{n} p_{i}r_{G_i}(t). \end{aligned}$$

We must to show that $r_{F,p}(t) \ge r_{G,p}(t)$ or, equivalently, $r_{F,p}(t) - r_{G,p}(t) \ge 0$. Obviously,

$$\begin{aligned} r_{F,p}(t) - r_{G,p}(t)=\sum _{i=1}^{n} p_{i}(r_{F_i}(t)-r_{G_i}(t)). \end{aligned}$$

From $F_i\le _{hr} G_i$, we have: $r_{F_i}(t)-r_{G_i}(t)\ge 0$ and thus,

$$\begin{aligned} F_{gm,p}(t)\le _{hr} G_{gm,p}(t). \end{aligned}$$

(25)

Under assumptions $F_{1} \ge _{hr} ... \ge _{hr}F_{n}$ and $\sum _{i=k}^{n}q_{i}\le \sum _{i=k}^{n}p_{i}$ for all ${ k \in \lbrace 1,2,...,n-1\rbrace }$, it follows from results of Section 5 in Navarro and del Aguila (2017), that $F_{gm,p}(t)\le _{hr} F_{gm,q}(t)$. On the other hand , from (25), it can be derived that $F_{gm,q}(t)\le _{hr} G_{gm,q}(t)$. Hence, we obtain that $F_{gm,p}(t)\le _{hr} G_{gm,q}(t)$. $\square$

Remark 4.2

It was assumed while defining the geometric mixture model $\bar{F}_{gm}(t)$ in (3) that $\sum _{i=1}^{n}p_i=1$. This is a special case of the generalized proportional hazards model defined in Navarro and del Aguila (2017) for the case when $p_i$’s are arbitrary positive real numbers. It can be easily shown that our results obtained throughout the paper for the geometric model, remain valid for this case as well.

5 Bending properties of $\alpha$-mixtures

In this section, we provide some generalizations of results on “bending properties” for ’ordinary’ mixture failure rates (see Finkelstein and Esaulova (2006) and Badia and Cha (2017)). These properties are about comparing the general $\alpha$-mixture failure rate $r(t,\alpha )$ with its specific case when $\alpha =0$, which is the geometric mixture failure rate that was defined in the Introduction. The latter is just the mixture of sub-populations failure rates via the unconditional mixing distribution. See the discussion on importance of these comparisons for heterogeneous populations modelling in Finkelstein (2008).

First, we need the following definitions:

Definition 5.1

The weak bending down (up) property holds for the failure rate function $r(t,\alpha )$ if

$$\begin{aligned} r(t,\alpha )\le (\ge ) r_{gm}(t), \quad \forall t> 0. \end{aligned}$$

In addition to this inequality, if

$$\begin{aligned} r_{gm}(t)-r(t,\alpha ) \uparrow (\downarrow ) \ in\ t>0, \end{aligned}$$

(26)

holds, then the strong bending down (up) property holds for the failure rate $r(t,\alpha )$.

In Definition 5.1, if we replace the condition (26) by “$\frac{r(t,\alpha )}{r_{gm}(t)}$ is decreasing (increasing) in t”  then we say that the modified strong bending down (up) property holds for the failure rate $r(t,\alpha )$.

We need also the following lemma ( Cuadras (2002)):

Lemma 5.2

Let $\Lambda$ be a random variable and f(x), g(x) be real functions.

• (a) If both f(x) and g(x) are increasing; or if both f(x) and g(x) are decreasing, then $E[f(\Lambda ) g(\Lambda )]\ge E[f(\Lambda )]E[g(\Lambda )]$.

• (b) If f(x) is increasing and g(x) is decreasing, then $E[f(\Lambda ) g(\Lambda )]\le E[f(\Lambda )]E[g(\Lambda )]$.

The following theorem shows the weak bending down (up) property for $\alpha >0 \ (\alpha <0)$.

Theorem 5.3

Let T be the $\alpha$-mixture of the family of random variables $\lbrace T|\lambda : \lambda \in [0,\infty ) \rbrace$ with the mixing random variable $\Lambda$. If $T|\lambda \uparrow$ $[\downarrow ]$ in $\lambda$ in hr stochastic order, then $r(t,\alpha )\le (\ge )\ r_{gm}(t)$ for $\alpha >0 \ (\alpha <0)$.

Proof

The proof for the case of finite $\alpha$-mixture can be found in Asadi et al. (2019). The proof for general mixtures is similar. $\square$

Let us consider the following example.

Example 5.1

Let $T|\lambda$ have Pareto distribution with hazard rate, $r(t | \lambda )=\frac{\lambda }{\beta +t}$, where $\lambda >0$ and $\beta >0$ are the shape and the location parameters, respectively. Obviously, for fixed $\beta$, $r(t | \lambda )$ is an increasing function of $\lambda$ and hence $T|\lambda \downarrow$ in hr stochastic order. Thus, for any mixing distribution with support in $[0, \infty )$, the bending down (up) property holds in the weak sense for the hazard rate for $\alpha >0 \ (\alpha <0)$. Let $\Lambda$ have an exponential distribution with density $\pi (\lambda )=\theta e^{-\theta \lambda }$, $\lambda >0$, $\theta >0$. Thus

$$\begin{aligned} r_{gm}(t)=\int _{0}^{\infty } \frac{\lambda }{\beta +t} \ \theta e^{-\theta \lambda } \ d \lambda =\frac{1}{\theta (\beta +t)}, \end{aligned}$$

and

$$\begin{aligned} r(t,\alpha )=\int _{0}^{\infty } \frac{\lambda }{\beta +t} \dfrac{(\frac{\beta }{\beta +t})^{\lambda \alpha } \theta e^{-\theta \lambda }}{\int _{0}^{\infty } (\frac{\beta }{\beta +t})^{\lambda \alpha } \theta e^{-\theta \lambda } d \lambda } d \lambda =\frac{1}{(\beta +t)(\theta -\alpha \ln (\frac{\beta }{\beta +t}))}. \end{aligned}$$

Figure 3 shows the plots of $r_{gm}(t)$ and $r(t, \alpha )$ for different values of $\alpha$, $\alpha =1, 1.5, -1, -1.5$, for $\beta =1$ and $\theta =5$. (Note that in the case of $\alpha <0$ we must have $\theta >\alpha \ln (\frac{\beta }{\beta +t})$).

Fig. 3

The plot of $r_{gm}(t)$ and $r(t, \alpha )$ for different values of $\alpha$, for parameter values $\beta =1$ and $\theta =5$, in Example 5.1

The following theorem establishes conditions for a strong bending property to hold. It will be proved under the following regularity conditions. We assume that:

• (i) the support of the random variable $T|\lambda$ does not depend on $\Lambda$;

• (ii) partial derivatives exist.

• (iii) interchanging derivatives and integrals are allowed.

Theorem 5.4

Let T be the $\alpha$-mixture for the family of random variables $\lbrace T|\lambda : \lambda \in [0,\infty ) \rbrace$ with the mixing random variable $\Lambda$. Assume that $\frac{\partial }{\partial t} r(t | \lambda )$ is decreasing [increasing] in $\lambda$ and $T|\lambda \uparrow$ $[\downarrow ]$ in $\lambda$ in the usual stochastic order. Then the strong bending down (up) property holds for $\alpha > 0\ (\alpha <0)$. That is, the weak bending down (up) property holds for $\alpha > 0 \ (\alpha <0)$ and

$$\begin{aligned} r_{gm}(t)-r(t,\alpha )= E[r(t | \Lambda )]-\frac{E[r(t | \Lambda ) \bar{F}^{\alpha }(t | \Lambda )]}{E[\bar{F}^{\alpha }(t | \Lambda )]} \end{aligned}$$

is an increasing (decreasing) function of t for $\alpha > 0\ (\alpha <0)$.

Proof

Let $A(t)=r_{gm}(t)-r(t,\alpha )$. We show that $A^{\prime }(t)$ is non negative (non positive) for $\alpha > 0\ (\alpha <0)$. After some algebra, we have

$$\begin{aligned} A^{\prime }(t)=&E[\frac{\partial }{\partial t} r(t | \Lambda )]-\frac{E\big [\frac{\partial }{\partial t} r(t | \Lambda )\bar{F}^{\alpha }(t | \Lambda )\big ]}{E[\bar{F}^{\alpha }(t | \Lambda )]}\\&-\frac{\alpha \lbrace E[f(t | \Lambda )\bar{F}^{\alpha -1}(t | \Lambda )r(t | \Lambda )]E[\bar{F}^{\alpha }(t | \Lambda )]- E^{2}[f(t | \Lambda )\bar{F}^{\alpha -1}(t | \Lambda )] \rbrace }{E^{2}[\bar{F}^{\alpha }(t | \Lambda )]}. \end{aligned}$$

Let $h(t|\Lambda )=f(t | \Lambda ) \bar{F}^{\frac{\alpha }{2}-1}(t | \Lambda )$ and $g(t|\Lambda )=\bar{F}^{\frac{\alpha }{2}}(t | \Lambda )$. Then, the Cauchy-Schwartz inequality implies that

$$\begin{aligned} E^{2}[f(t | \Lambda )\bar{F}^{\alpha -1}(t | \Lambda )]&=E^2(h(t|\Lambda )g(t|\Lambda ))\\&\le E(h^2(t|\Lambda ))E(g^2(t|\Lambda ))\\&=E[f(t | \Lambda )\bar{F}^{\alpha -1}(t | \Lambda )r(t| \Lambda )]E[\bar{F}^{\alpha }(t | \Lambda )]. \end{aligned}$$

Hence

$$\begin{aligned} A^{\prime }(t)\ge (\le )\ E[\frac{\partial }{\partial t} r(t | \Lambda )]-\frac{E[\frac{\partial }{\partial t} r(t | \Lambda )\bar{F}^{\alpha }(t | \Lambda )]}{E[\bar{F}^{\alpha }(t | \Lambda )]}. \end{aligned}$$

From lemma 5.2 (b) for $\alpha >0$ (lemma 5.2 (a) for $\alpha <0$) with functions $f(\lambda )=\frac{\partial }{\partial t} r(t | \lambda )$ and $g(\lambda )=\bar{F}^{\alpha }(t | \lambda )$, which are monotone in the different (same) directions for $\alpha >0$ ($\alpha <0$), under the assumptions, we have

$$\begin{aligned} \frac{E[\frac{\partial }{\partial t} r(t | \Lambda )\bar{F}^{\alpha }(t | \Lambda )]}{E[\bar{F}^{\alpha }(t | \Lambda )]} \le (\ge )\frac{E[\frac{\partial }{\partial t} r(t | \Lambda )]E[\bar{F}^{\alpha }(t | \Lambda )]}{E[\bar{F}^{\alpha }(t | \Lambda )]}=E[\frac{\partial }{\partial t} r(t | \Lambda )]. \end{aligned}$$

Hence, A(t) is $\uparrow$ ($\downarrow$) in t.

The weak bending down (up) property follows by monotonicity of A and the fact that

$$\begin{aligned} r(0,\alpha )=\frac{E[ r(0 | \Lambda )\bar{F}^{\alpha }(0 | \Lambda )]}{E[\bar{F}^{\alpha }(0 | \Lambda )]}=E[ r(0 | \Lambda )]=r_{gm}(0) . \end{aligned}$$

$\square$

Consider the following example as an illustration of the strong bending property for hazard rate for $\alpha$-mixtures.

Example 5.2

Let $T | \lambda$ have an exponential distribution with hazard rate, $r(t | \lambda )=\lambda$. Thus all conditions of Theorem 5.4 are met. Now, assume that $\lambda \sim G(\theta ,1)$, where $G(\theta ,1)$ is Gamma distribution with parameters $\theta$ and 1. Then,

$$\begin{aligned} r_{gm}(t)=\int _{0}^{+\infty } \lambda \ \frac{\lambda ^{\theta -1} e^{-\lambda }}{\Gamma (\theta ) } d \lambda =\theta , \end{aligned}$$

and

$$\begin{aligned} r(t,\alpha )=\int _{0}^{+\infty } \lambda \ \dfrac{(e^{-\lambda t})^{\alpha } \lambda ^{\theta -1} e^{-\lambda }}{\int _{0}^{+\infty }(e^{-\lambda t})^{\alpha }\lambda ^{\theta -1} e^{-\lambda } \ d \lambda } \ d \lambda =\frac{\theta }{(1+\alpha t)}. \end{aligned}$$

Thus,

$$\begin{aligned} A(t)=r_{gm}(t)-r(t,\alpha )=\theta \ (\frac{\alpha t}{1+\alpha t}), \end{aligned}$$

which is an increasing (decreasing) function of t for $\alpha >0 \ (\alpha <0)$. Thus the strong bending down (up) property holds for $\alpha > 0\ (\alpha <0)$.

The next theorem provides a result on the modified strong bending property of $\alpha$-mixtures.

Theorem 5.5

Let T be the $\alpha$-mixture of the family of random variables $\lbrace T|\lambda : \lambda \in [0,\infty ) \rbrace$ with the mixing random variable $\Lambda$. Assume that $\frac{\partial }{\partial t} r(t | \lambda )$ is decreasing [increasing] in $\lambda$, $\bar{F}(t | \lambda )$ is increasing [decreasing] in $\lambda$ and $T|\lambda$ is DFR for all $\lambda$. Then T satisfies the modified strong bending down (up) property for $\alpha > 0$ ($\alpha < 0$). That is,

$$\begin{aligned} \frac{r(t,\alpha )}{r_{gm}(t)} \end{aligned}$$

is the decreasing (increasing) function of t for $\alpha > 0$ ($\alpha < 0$).

Proof

The proof follows using the same arguments as in part (a) of Theorem 3 of Badia and Cha (2017). $\square$

Theorem 5.6

Let r(t) be the baseline failure rate and let the family of random variables, $\left\{ T|\lambda : \lambda > 0\right\}$, satisfy the proportional hazards model, $r(t | \lambda ) = \lambda r(t)$. Then the $\alpha$-mixture for this family possesses the modified strong bending down (up) property for $\alpha >0 \ (\alpha <0)$.

Proof

Using (7) and considering representation $\bar{F}(t|\lambda )=\exp (-\int _{0}^{t} r(u|\lambda )du)$, the $\alpha$-mixture failure rate can be written as

$$\begin{aligned} r(t,\alpha )&=\frac{E[r(t | \Lambda ) \bar{F}^{\alpha }(t | \Lambda )]}{E[\bar{F}^{\alpha }(t | \Lambda )]}\nonumber \\&=r(t)\frac{E\left[ \Lambda \; \mathrm {exp}\left\{ -\alpha \Lambda \int _{0}^{t} r(u)du \right\} \right] }{E\left[ \mathrm {exp}\left\{ -\alpha \Lambda \int _{0}^{t} r(u)du \right\} \right] } \nonumber \\&=r(t)r_{\mathrm {exp}}\left( \alpha \int _{0}^{t} r(u)du\right) , \end{aligned}$$

(27)

where, the second equality follows from the assumption $r(t | \lambda ) = \lambda r(t)$, and in the last equality $r_{\mathrm {exp}}(t)$ is the failure rate of the $\alpha$-mixture of a family of random variables $\left\{ T|\lambda : \lambda > 0\right\}$, in which $T|\lambda$ is exponential with mean $\frac{1}{\lambda }$. The exponential distribution is DFR (IFR) and the DFR (IFR) property is preserved under $\alpha$-mixture for $\alpha >0 \ (\alpha <0)$ (see, Asadi et al. (2019)). Therefore, $r_{\mathrm {exp}}(t)$ for any mixing random variable $\lambda$ is a decreasing (increasing) function in t . According to (27), we have

$$\begin{aligned} \frac{r(t,\alpha )}{r_{gm}(t)}=\frac{1}{E[\Lambda ]}r_{\mathrm {exp}}\left( \alpha \int _{0}^{t} r(u)du\right) \end{aligned}$$

and the result follows since $r_{\mathrm {exp}}(t)$ is decreasing (increasing) in t for $\alpha >0$ ($\alpha <0$). $\square$

6 Conclusions

The $\alpha$-mixture model, as a parametric model, provides the unified tool to study various heterogeneous populations that were described in the literature by ordinary mixtures, geometric mixtures and harmonic mixtures of survival functions.

In this paper, we have studied stochastic comparisons and ageing properties of $\alpha$-mixtures of survival functions. In particular, we have investigated the $\alpha$-mixture under particular cases of additive and multiplicative hazards models. It was proved that the aging characteristics of $\alpha$-mixture model directly depend on the properties of the baseline failure rate functions and the corresponding conditional moments of mixing distributions. Stochastic comparisons of finite $\alpha$-mixtures in the sense of the usual stochastic order and the hazard rate order were also discussed.

We have extended the results available in the literature on “bending properties” for mixture failure rates. More specifically, we compared the the failure rate of the $\alpha$-mixture, as a function of parameter $\alpha$, with its specific case when $\alpha =0$. This latter case corresponds to the geometric mixture failure rate, which is just the mixture of sub-populations failure rates via the unconditional mixing distribution.