1 Introduction

One of the most common problems we face in the real world, especially in the survival analysis and the theory of reliability, is the existence of heterogeneity in populations. For example, the lifetime of production components in an industrial factory may differ due to different raw materials, different work shifts, etc, leading to a heterogeneous population (Finkelstein 2008). Therefore, to avoid possible errors in the relevant analysis, suitable tools such as mixture models are needed.

   Various aspects of mixture models have been investigated by many authors. For example, some closure and ageing properties of mixture models can be found in Barlow and Proschan (1981); Savits (1985); Lynch (1999); Block and Savits (1976); Badia et al. (2002) and Block et al. (2003), respectively.

   In demography and survival analysis, Vaupel et al. (1979) first used the frailty models (also, see Aalen (1992, 2005)). Finkelstein (2005), using the concept of population heterogeneity, explained the deceleration in mortality rates.

   Finkelstein (2002) studied the relationship between the mean waiting time and the reversed hazard rate (RH). Specifically, he proved that the RH ordering implies the mean waiting time ordering. Gupta and Wu (2001) introduced the proportional reversed hazard rate (PRH) model, and studied some properties of its structure. Gupta and Gupta (2007) investigated the monotonicity of the RH for the PRH model. They, also, provided the Fisher information as well as the statistical inference for the model. Li and Li (2008) considered a mixture with the PRH model as the baseline model and investigated the properties of the model. In particular, they proved that the mixture random variable and the mixing random variable are positively likelihood dependent, and provided a lower bound for the cumulative distribution function (CDF) of the mixture.

   Li et al. (2010), motivated by Finkelstein (2005) and Finkelstein and Esaulova (2006), discussed the bending property for the mixture RH using the properties of the conditional random variable. Also, they investigated preservation of decreasing RH in the mixture model, and provided a lower bound for the cumulative distribution of the mixture. The bending property of the mixture hazard rate for the RH has been extended by Badia and Cha (2017).

   Navarro (2016) considered generalized mixture models (mixtures with negative weights) and provided some conditions for comparing two generalized mixtures in the sense of likelihood ratio (LR) order and the RH order with different mixing weights (see, also, Navarro and del Aguila 2017). Stochastic comparisons of two finite mixtures in the sense of the RH and the LR orders with different mixing proportions and different baseline distributions were provided by Amini-Seresht and Zhang (2017). Panja et al. (2022), compared two finite mixtures where the corresponding baseline distributions follow from proportional reversed hazards, proportional hazards, and proportional odds in the sense of usual stochastic order and the hazard rate order. Stochastic comparisons of general proportional mean past lifetime frailty model were studied by Hooti et al. (2022).

   Recently, Asadi et al. (2019) suggested \(\alpha\)-mixtures of survival functions (SFs) and Shojaee et al. (2021) provided some stochastic comparisons and some new reliability interpretations for \(\alpha\)-mixtures of SFs based on the multiplicative-additive hazard rate transform. For some generalizations of finite mixtures of SFs, we refer to Shojaee et al. (2022). \(\alpha\)-mixtures of cumulative distribution functions (CDFs) proposed by Asadi et al. (2019), considered in this paper, were not studied so far. Moreover, no results exist on the ageing properties, stochastic comparisons, conditional characteristics, etc., of \(\alpha\)-mixtures of CDFs in the literature. On the other hand, some meaningful interpretations exist for \(\alpha\)-mixtures of cumulative distribution functions (CDFs) (see Sect. 2). Therefore, in this paper, we consider \(\alpha\)-mixtures of CDFs, and study some properties of this family.

   The organization of the paper is as follows. Section 2 introduces \(\alpha\)-mixtures of cumulative distribution functions (CDFs), and provide some reliability interpretations of the model. Section 3 studies some properties of the reversed hazard rate (RH) of \(\alpha\)-mixtures of CDFs. Section 4 discusses on conditional characteristics, and provides some results on the bending down (up) property of the RH for \(\alpha\)-mixtures based on the conditional characteristics. Section 5 provides some conditions for comparing finite \(\alpha\)-mixtures, with different mixing probabilities and different baseline distributions, in the sense of the RH order and usual stochastic order. Finally, Sect. 6 concludes the paper.

1.1 Notations and Definitions

Consider two random variables X and Y with the CDF’s F and G, the SF’s \({\bar{F}}\) and \({\bar{G}}\), the probability density functions (PDF’s) f and g, the RH functions \({\tilde{r}}_X(x)\) and \({\tilde{r}}_Y(x)\), respectively.

Definition 1.1

We say that the random variable X or its distribution F is a decreasing (increasing) RH (DRH (IRH)) if its reversed failure rate \({\tilde{r}}_X(x)\) is nonincreasing (nondecreasing) in x.

Definition 1.2

The random variable X is said to be smaller than the random variable Y in the sense of

  • The usual stochastic order if \({\bar{F}}(x)\le {\bar{G}}(x)\) for all x, and denoted by \(X\le _{st}Y\) or \(F\le _{st} G\).

  • The RH order if G(x)/F(x) is increasing in x, for all x, or \({\tilde{r}}_X(x)\le {\tilde{r}}_Y(x)\) for all x, and denoted by \(X\le _{rh}Y\) or \(F\le _{rh}G\).

  • The LR order if g(x)/f(x) is increasing in x for all x in the support of X and Y, and denoted by \(X\le _{lr}Y\) or \(F\le _{lr} G\).

Also, the following lemma from Cuadras (2002) to get the main results is needed.

Lemma 1.3

Let \(\Gamma\) to be a random variable and f(x), g(x) be real functions.

  1. (a)

    If both f(x) and g(x) be increasing (decreasing), then

    $$\begin{aligned} E[f(\Gamma ) g(\Gamma )]\ge E[f(\Gamma )]E[g(\Gamma )].\end{aligned}$$
  2. (b)

    If g(x) be decreasing and f(x) be increasing, then

    $$\begin{aligned}E[f(\Gamma ) g(\Gamma )]\le E[f(\Gamma )]E[g(\Gamma )].\end{aligned}$$

2 The \(\alpha\)-Mixture Model

2.1 Infinite \(\alpha\)-Mixture

Let the random variable X has the \(\alpha\)-mixture distribution. We denote CDF, PDF, and RH of X by \({F}_{\alpha }(x)\), \(f_{\alpha }(x)\) and \({\tilde{r}}_{\alpha }(x)\), respectively. Also, suppose that the mixing random variable \(\Gamma\) (as a covariate) has PDF and CDF, \(\pi (\gamma )\) and \(\Pi (\gamma )\), respectively. Further, suppose that \({F}(x|\gamma )\), \(f(x|\gamma )\) and \({\tilde{r}}(x|\gamma )\) refer to the CDF, PDF and RH of the random variable \(X|\gamma\), respectively. Consider the \(\alpha\)-mixture model as below (Asadi et al. 2019):

$$\begin{aligned} {F}_{\alpha }(x)=\left\{ \begin{array}{ll} \left( \displaystyle\int _{0}^{\infty } {F}^{\alpha }(x|\gamma ) \pi (\gamma ) d\gamma \right) ^{\frac{1}{\alpha }}, &{} {\alpha \ne 0}, \\ {F}_{gm}(x), &{} \alpha =0, \end{array} \right. \end{aligned}$$
(1)

where \({F}_{gm}(x)=\lim _{\alpha \rightarrow 0}{F}_{\alpha }(x)\).

The corresponding PDF of the semi parametric \(\alpha\)-mixture model (1) is as follows:

$$\begin{aligned} f_{\alpha }(x)= \left( \int _{0}^{\infty } f(x |\gamma ){F}^{\alpha -1}(x|\gamma ) \pi (\gamma ) d\gamma \ \right) \left( \int _{0}^{\infty } {F}^{\alpha }(x|\gamma ) \pi (\gamma ) d\gamma \right) ^{\frac{1}{\alpha }-1}. \end{aligned}$$
(2)

   Using (1) and (2), the RH of the model for \(\alpha \ne 0\) is obtained as follows:

$$\begin{aligned} {\tilde{r}}_{\alpha }(x)=\frac{f_{\alpha }(x)}{{F}_{\alpha }(x)}=\frac{\int _{0}^{\infty } f(x |\gamma ) {F}^{\alpha -1}(x |\gamma ) \pi (\gamma ) d\gamma }{\int _{0}^{\infty } {F}^{\alpha }(x |\gamma ) \pi (\gamma ) d\gamma } \end{aligned}$$
(3)
$$\begin{aligned} =\int _{0}^{\infty }{\tilde{r}}(x | \gamma )\pi _{\alpha }(\gamma | x)d\gamma , \end{aligned}$$
(4)

where

$$\begin{aligned} \pi _{\alpha }(\gamma | x)=\frac{{F}^{\alpha }(x |\gamma )\pi (\gamma )}{\int _{0}^{\infty } {F}^{\alpha }(x |\gamma )\pi (\gamma )d\gamma }, \end{aligned}$$
(5)

is the conditional PDF of \(\Gamma | X_{\alpha } \le x\), where \(X_{\alpha }\) has the CDF \({F}^{\alpha }(x | \gamma )\) for \(\alpha > 0\).

In the case \(\alpha \rightarrow 0\), we obtain

$$\begin{aligned} {F}_{gm}(x)=\lim _{\alpha \rightarrow 0} {F}_{\alpha }(x)=\exp \bigg (\int _{0}^{\infty } \log {F}(x|\gamma )\pi (\gamma )d\gamma \bigg ), \end{aligned}$$

with the RH

$$\begin{aligned} {\tilde{r}}_{gm}(x)=\int _{0}^{\infty } {\tilde{r}}(x | \gamma )\pi (\gamma )d\gamma . \end{aligned}$$
(6)

2.2 Finite \(\alpha\)-Mixture Model

The finite \(\alpha\)-mixture of n sub-populations with distribution functions \({F}_{i}\), \(i=1,2,...,n\), is defined as

$$\begin{aligned} {F}_{\alpha }(x)=\left\{ \begin{array}{ll} \left[ \sum _{i=1}^{n} p_{i}{{F}_{i}}^{\alpha }(x) \right] ^{1/\alpha }, &{} {\alpha \ne 0}, \\ {F}_{gm}(x), &{} \alpha =0, \end{array} \right. \end{aligned}$$
(7)

where \({F}_{gm}(x)=\lim _{\alpha \rightarrow 0}{F}_{\alpha }(x)\) and \(p_{i}\ge 0\) is the mixing proportion.

The corresponding PDF of (7) is as follows:

$$\begin{aligned} f_{\alpha }(x)=\left[ \sum _{i=1}^{n} p_{i}f_{i}(x){{F}_{i}}^{\alpha -1}(x) \right] \left[ \sum _{i=1}^{n} p_{i}{{F}_{i}}^{\alpha }(x) \right] ^{\frac{1}{\alpha }-1}. \end{aligned}$$
(8)

If \({\tilde{r}}_{i}(x)\) and \({\tilde{r}}_{\alpha }(x)\) be the RH of the i-th subpopulation and the finite \(\alpha\)-mixture RH, respectively, then

$$\begin{aligned} {\tilde{r}}_{\alpha }(x)=\frac{f_{\alpha }(x)}{{F}_{\alpha }(x)}=\sum _{i=1}^{n} {\tilde{r}}_{i}(x) p_{i}(x), \end{aligned}$$
(9)

where

$$\begin{aligned} p_{i}(x)=\frac{p_{i} {F}_{i}^{\alpha }(x)}{\sum _{j=1}^{n} p_{j} {F}_{j}^{\alpha }(x)}.\end{aligned}$$

The CDF and the RH for the case \(\alpha \rightarrow 0\) in model (7) denoted by \({F}_{gm}(x)\) and \({\tilde{r}}_{gm}(x)\), respectively, and are as follows:

$$\begin{aligned} {F}_{gm}(x)=\prod _{i=1}^{n}{F}_{i}^{p_{i}}(x), \end{aligned}$$
(10)

and

$$\begin{aligned} {\tilde{r}}_{gm}(x)=\sum _{i=1}^{n}p_{i} {\tilde{r}}_{i}(x). \end{aligned}$$

Clearly, the \(\alpha\)-mixture model (7) includes the following models as a special case:

  • For \(\alpha =1\), we have the usual arithmetic mixture distribution.

  • For \(\alpha \rightarrow 0\), we arrive at the CDF of the mixture RH model (10).

  • For \(\alpha =-1\), we have the harmonic mixture (mean) of the baseline CDFs:

    $$\begin{aligned} {F}_{hm}(x)=\bigg (\sum _{i=1}^{n}\frac{p_{i}}{F_{i}(x)} \bigg )^{-1}, \ \ \ x>0.\end{aligned}$$

  • For \(\alpha =\frac{1}{m}\) and \(n=2\), the \(\alpha\)-mixture is the following binomial expansion mixture:

    $$\begin{aligned} {F}_{\frac{1}{m}}(x)=\sum _{k=0}^{m}B_{k,m} p^{m-k} (1-p)^{k}{F_{1}(x)}^{1-\frac{k}{m}} {F_{2}(x)}^{\frac{k}{m}}, \end{aligned}$$

    where \(B_{k,m}\) is the binomial coefficient (Asadi et al. 2019). In particular, for \(\alpha =\frac{1}{2}\), we have:

    $$\begin{aligned} {F}_{\frac{1}{2}}(x)=p^{2}F_{1}(x)+(1-p^{2}F_{2}(x)+2p(1-p)\big ( F_{1}(x)F_{2}(x)\big )^{\frac{1}{2}}, \end{aligned}$$
    (11)

    which is a weighted mean of \(F_{1}(x)\), \(F_{2}(x)\) and \(\big ( F_{1}(x)F_{2}(x)\big )^{\frac{1}{2}}\). Thus, it is similar to the Heronian mean of the two CDFs. The Heronian mean is defined by equal weights given to the three terms in (11) (Bullen 2003).

Also, for example, for the infinite \(\alpha\)-mixture of SFs, if we let the baseline distribution be an Exponential distribution and consider the Gamma mixing random variable, we arrive at the generalized Pareto distribution (Asadi et al. 2019), which is a Pareto distribution with decreasing hazard rate for \(\alpha >0\), Exponential distribution with constant hazard rate for \(\alpha \rightarrow 0\), and rescaled Beta distribution with increasing hazard rate for \(\alpha <0\), respectively.

2.3 Reliability Interpretations (in the Term of Parallel System)

For different values of \(\alpha\), the reliability interpretations of the \(\alpha\)-mixture is itemized as follows.

  • The case \(\alpha >0\). Motivated by Shojaee et al. (2021), we can give the following interpretation for the \(\alpha\)-mixture model. Suppose that the proportion and the CDF of the i-th component (subpopulation) in a mixed population in laboratory conditions are \(p_{i}\) and \({F}_{i}(x)\), \(i=1,\dots ,n\), respectively. Let the hard condition based on the PRH model acts on each component uniformly. Therefore, the i-th component CDF will be \({F}_{i}^{\alpha }(x)\), where \(\alpha >0\). Then, the CDF of a randomly selected component in the hard conditions is

    $$\begin{aligned} {F}_{h}(x,\alpha )=\sum _{i=1}^{n} p_{i}{F}_{i}^{\alpha }(x). \end{aligned}$$

    Now, if we shield the component from the hard conditions to keep it on the laboratory condition, then, the CDF of the selected component in the laboratory conditions will equal to

    $$\begin{aligned} {F}_{\alpha }(x)=\bigg (\sum _{i=1}^{n} p_{i}{F}_{i}^{\alpha }(x)\bigg )^{\frac{1}{\alpha }}, \end{aligned}$$

    where \({F}_{\alpha }(x)\) is the CDF of the \(\alpha\)-mixture model.

  • The case that \(\alpha\) is a positive integer. Two different methods for constructing an m-component parallel system from n different types of components has been proposed by Cha (2011).

    1. 1.

      Mixing at the system level. In this method, a component is chosen randomly from n different types of components, and the system is built from the selected component. Thus, the m-component parallel system has the following CDF:

      $$\begin{aligned} \mathcal {{F}}_{1}^{m}(x)=\sum _{i=1}^{n} p_{i} {F}^{m}_{i}(x),\end{aligned}$$

      where \(\mathcal {{F}}_{1}(x)\) denote the CDF of the \(\alpha\)-mixture model with \(\alpha =m\).

    2. 2.

      Mixing at the component level. In this method, the components of the parallel system are selected one by one from the mixed population of components. Thus, the m-component parallel system has the following CDF:

      $$\begin{aligned} \mathcal {{F}}_{2}^{m}(x)=\left( \sum _{i=1}^{n} p_{i} {F}_{i}(x)\right) ^{m},\end{aligned}$$

      where \(\mathcal {{F}}_{1}(x)\) denote the CDF of the finite \(\alpha\)-mixture with \(\alpha =1\).

    The monotone decreasing property of \(\alpha\)-mixtures (Asadi et al. 2019) yields \(\mathcal {{F}}_{2} \ge _{st} \mathcal {{F}}_{1}\). This means to construct a m-component parallel system, it is better we have ‘mixing at the component level’rather than ‘mixing at the system level’. Hazra et al. (2017) have generalized these two models as follows.

    1. 3.

      The components are grouped as d groups and the first \(l_{1}\) components are randomly selected from one of the sub-populations; then we draw \(l_{2}\) components similarly and continue in the same way until m components are selected after d steps. The CDF of the constructed parallel system is:

      $$\begin{aligned} \mathcal {{F}}_{3}(x)=\prod _{j=1}^{d} \left( \sum _{i=1}^{n} p_{i} {F}^{l_{j}}_{i}(x)\right) =\prod _{j=1}^{d} {F}^{l_{j}}_{l_{j}}(x), \end{aligned}$$

      where \(\sum _{j=1}^{d} l_{j}=m\), for \(1\le d \le m\) and \({F}_{l_{j}}(x)\) is the CDF of the finite \(\alpha\)-mixture with \(\alpha =l_{j}\).

  • The finite \(\alpha\)-mixture can be considered as \(F_{\alpha }(x)= Q(F_1, \dots , F_n)\), where Q is a generalized distorted distribution in which the distortion function is: \(Q(u_1, \dots , u_n)=\big ( \sum _{i=1}^{n}p_{i}u_{i}^{\alpha }\big )^{1/\alpha }\) (Navarro and del Aguila 2017).

  • As it was already mentioned in Asadi et al. (2019), \(\alpha\)-mixtures as a unified model combine two popular models: mixture models and proportional reversed hazard (PRH) models. They are actually PRH models with baseline models that are mixtures of PRH models with different baselines and a common PRH parameter \(\alpha\).

  • The case \(\alpha \rightarrow 0\). \(F_{gm}(x)=\prod _{i=1}^{n} F_{i}^{p_{i}}\) can be considered as a generalized proportional reversed hazard rate (GPRH) model (Navarro 2016). Also, it is easy to see that \({F}_{gm}(x)\) is the CDF of a n-components parallel system, where the CDF of the i-th component is the PRH model with the PRH parameter \(p_{i}\) and the baseline CDF \({F}_{i}(x)\), \(i=1, \dots , n\). For more applications of \({F}_{gm}(x)\), we refer to Shojaee and Babanezhad (2023).

3 Properties of the the \(\alpha\)-Mixture Reversed Hazard Rate

   Let us consider a 2-component finite \(\alpha\)-mixture with CDF’s \({F}_{1}(x)\) and \({F}_{2}(x)\) and RH’s \({\tilde{r}}_{1}(x)\) and \({\tilde{r}}_{2}(x)\), respectively. In this case

$$\begin{aligned} {\tilde{r}}_{\alpha }(x)&= \left[ {\tilde{r}}_{1}(x) \frac{ p{{F}_{1}}^{\alpha }(x)}{ p{{F}_{1}}^{\alpha }(x)+ (1-p){{F}_{2}}^{\alpha }(x)}+ {\tilde{r}}_{2}(x) \frac{ (1-p){{F}_{2}}^{\alpha }(x)}{ p{{F}_{1}}^{\alpha }(x)+ (1-p){{F}_{2}}^{\alpha }(x)}\right] \nonumber \\&=\left[ {\tilde{r}}_{1}(x) p_{\alpha }(x) +{\tilde{r}}_{2}(x) (1-p_{\alpha }(x))\right] , \end{aligned}$$
(12)

where the time varying probability is

$$\begin{aligned} p_{\alpha }(x)=\frac{ p{{F}_{1}}^{\alpha }(x)}{ p{{F}_{1}}^{\alpha }(x)+ (1-p){{F}_{2}}^{\alpha }(x)},\end{aligned}$$

Based on the time varying probability, we can show that:

$$\begin{aligned} \min \{{\tilde{r}}_{1}(x), {\tilde{r}}_{2}(x)\} \le {\tilde{r}}_{\alpha }(x) \le \max \{{\tilde{r}}_{1}(x), {\tilde{r}}_{2}(x)\}.\end{aligned}$$

In particular, if \(F_{1} \le _{rh} F_{2}\), then

$$\begin{aligned} {\tilde{r}}_{1}(x) \le {\tilde{r}}_{\alpha }(x) \le {\tilde{r}}_{2}(x).\end{aligned}$$

Now, we can give the following result (without proof).

Theorem 3.1

Let the components of a finite \(\alpha\)-mixture be ordered based on the RH ordering. That means, there exist a \({\tilde{r}}_{\min }(x)=\min \{ {\tilde{r}}_{1}(x), \dots , {\tilde{r}}_{n}(x)\}\) whose RH dominated by the RH’s of all other components, and there exist a \({\tilde{r}}_{\max }(x)=\max \{ {\tilde{r}}_{1}(x), \dots , {\tilde{r}}_{n}(x)\}\) whose RH dominates the RH’s of all other components. Then

$$\begin{aligned} F_{\min } \le _{rh} F_{\alpha } \le _{rh} F_{\max },\end{aligned}$$

where \(F_{\min }\) and \(F_{\max }\) are the CDF’s of \({\tilde{r}}_{\min }(x)\) and \({\tilde{r}}_{\max }(x)\), respectively.

The following theorem states that the RH of \(\alpha\)-mixture increases in \(\alpha\).

Theorem 3.2

Suppose that the baseline RH’s of the components (\({\tilde{r}}_{i}(x), i=1, \dots , n\)) of a finite \(\alpha\)-mixture are ordered either decreasingly or increasingly, then the \(\alpha\)-mixture RH is increasing in \(\alpha \in (-\infty , +\infty )\).

Proof

The proof of the theorem is similar (with a slight difference) to the proof of Theorem 3.3 of Asadi et al. (2019) and it is omitted here. \(\square\)

Corollary 3.3

Let the baseline RHs of the components (\({\tilde{r}}_{i}(x), i=1, \dots , n\)) of a finite \(\alpha\)-mixture are ordered either decreasingly or increasingly, then

$$\begin{aligned} F_{hm}(x) \le _{rh} F_{gm}(x) \le _{rh} F_{am}(x).\end{aligned}$$

Also, the closure property of the 2-component finite \(\alpha\)-mixture can be studied directly. One can derivative from (12) with respect to x as follows:

$$\begin{aligned} {\tilde{r}}^{\prime }_{\alpha }(x)&= {\tilde{r}}^{\prime }_{1}(x) p_{\alpha }(x)+ p^{\prime }_{\alpha }(x) {\tilde{r}}_{1}(x)+ {\tilde{r}}^{\prime }_{2}(x) (1-p_{\alpha }(x))-p^{\prime }_{\alpha }(x) {\tilde{r}}_{2}(x)\\&= {\tilde{r}}^{\prime }_{1}(x) p_{\alpha }(x)+ {\tilde{r}}^{\prime }_{2}(x) (1-p_{\alpha }(x))+p^{\prime }_{\alpha }(x)({\tilde{r}}_{1}(x)- {\tilde{r}}_{2}(x)) \\&= {\tilde{r}}^{\prime }_{1}(x) p_{\alpha }(x)+ {\tilde{r}}^{\prime }_{2}(x) (1-p_{\alpha }(x))-\alpha p_{\alpha }(x)(1-p_{\alpha }(x))({\tilde{r}}_{1}(x)- {\tilde{r}}_{2}(x))^{2}. \end{aligned}$$

Hence, as \({\tilde{r}}^{\prime }_{i}(x) \le 0\), \(i=1,2\), \({\tilde{r}}_{\alpha }^{\prime }(x) \le 0\) for \(\alpha > 0\). That means the finite \(\alpha\)-mixture has DRH for \(\alpha > 0\), if it’s components have DRH. Similarly, the finite \(\alpha\)-mixture has IRH for \(\alpha < 0\), if it’s components have IRH (as \({\tilde{r}}^{\prime }_{i}(x) \ge 0\) for \(i=1,2\), then \({\tilde{r}}^{\prime }_{\alpha }(x) \ge 0\) for \(\alpha < 0\)).

4 Some Results Based on Conditional Characteristics

In this section, we present some results based on conditional characteristics. We also discuss the bending properties of the RH based on the properties of the conditional random variable. We extend the bending properties of the RH for ordinary mixtures to \(\alpha\)-mixtures. These properties are about comparing the RH of the \(\alpha\)-mixture with its specific case when \(\alpha =0\), see Badia and Cha (2017) for example.

The following theorem states that the conditional PDF, \(\pi _{\alpha }(\gamma | x)\), can be ordered in the LR ordering.

Theorem 4.1

  1. (a)

    Assume that the baseline RH, \({\tilde{r}}(x|\gamma )\), is increasing (decreasing) in \(\gamma\) for all \(x\ge 0\). Then the conditional PDF, \(\pi _{\alpha }(\gamma | x)\),is increasing (decreasing) in \(x\ge 0\) in the LR ordering for \(\alpha > 0\).

  2. (b)

    Suppose that the baseline RH, \({\tilde{r}}(x|\gamma )\), be increasing (decreasing) in \(\gamma\) for all \(x\ge 0\). Then the conditional PDF, \(\pi _{\alpha }(\gamma | x)\), is decreasing (increasing) in \(x\ge 0\) in the LR ordering for \(\alpha < 0\).

Proof

We give proof only for part (a) because the proof for part (b) is completely similar. By considering the representation \(F(x|\gamma )=\exp \big (-\int _{x}^{+\infty } {\tilde{r}}(u|\gamma )du\big )\), and using relation (5) for all \(x_2 \ge x_1 \ge 0\), we get

$$\begin{aligned} \frac{\pi _{\alpha }(\gamma | x_{2})}{\pi _{\alpha }(\gamma |x_{1})}&= \frac{F^{\alpha }(x_{2}|\gamma ) \pi (\gamma )}{\int _{0}^{+\infty } F^{\alpha } (x_{2}| \gamma ) \pi (\gamma ) d \gamma } \times \frac{ \int _{0}^{+\infty } F^{\alpha }(x_{1} | \gamma ) \pi (\gamma ) d \gamma }{ F^{\alpha }(x_{1}| \gamma ) \pi (\gamma ) }\\&=\frac{\exp \big ( - \alpha \int _{x_{2}}^{+\infty } {\tilde{r}}(u | \gamma ) du\big )}{\exp \big ( - \alpha \int _{x_{1}}^{+\infty } {\tilde{r}}(u | \gamma ) du\big )} \times \frac{\int _{0}^{+\infty } F^{\alpha }(x_{1} | \gamma ) \pi (\gamma ) d \gamma }{\int _{0}^{+\infty } F^{\alpha }(x_{2} | \gamma ) \pi (\gamma ) d \gamma }\\&=\exp \big ( \alpha \int _{x_{1}}^{x_{2}} {\tilde{r}}(u | \gamma ) du\big ) \times \frac{\int _{0}^{+\infty } F^{\alpha }(x_{1}| \gamma ) \pi (\gamma ) d \gamma }{\int _{0}^{+\infty } F^{\alpha }(x_{2}| \gamma ) \pi (\gamma ) d\gamma } . \end{aligned}$$

From assumption \({\tilde{r}}(x|\gamma )\) is increasing (decreasing) in \(\gamma\) for all \(x\ge 0\), the first part of last equality is increasing (decreasing) in \(\gamma\) for all \(x_2 \ge x_1 \ge 0\). \(\square\)

The result of Theorem 4.1 states that the family of conditional mixing random variables is increasing (decreasing) in the sense of likelihood ratio for \(\alpha >0\) (\(\alpha <0\)). It means that with the increase of time, the value of the density of the conditional mixing random variable will decrease.

The next corollary is obtained directly from Theorem 4.1.

Corollary 4.2

  1. (a)

    if \({\tilde{r}}(x|\gamma )\) be increasing (decreasing) in \(\gamma\) for all \(x\ge 0\), then, the conditional CDF, \(\Pi _{\alpha }(\gamma | x)\), is decreasing (increasing) in x for any \(\gamma \ge 0\) for \(\alpha > 0\).

  2. (b)

    if \({\tilde{r}}(x|\gamma )\) be increasing (decreasing) in \(\gamma\) for all \(x\ge 0\), then, the conditional CDF, \(\Pi _{\alpha }(\gamma | x)\), is increasing (decreasing) in x for any \(\gamma \ge 0\) for \(\alpha <0\).

Proof

The result follows from Theorem 4.1, because the LR order implies usual stochastic order. \(\square\)

Corollary 4.3

  1. (a)

    Suppose that the baseline RH belongs to the PRH model, \({\tilde{r}}(x|\gamma )=\gamma {\tilde{r}}(x)\). Then, the conditional PDF, \(\pi _{\alpha }(\gamma | x)\), is increasing (decreasing) in \(x\ge 0\) in the LR ordering for \(\alpha > 0\) (\(\alpha <0\)).

  2. (b)

    Let the baseline RH belongs to the PRH model, \({\tilde{r}}(x|\gamma )=\gamma {\tilde{r}}(x)\). Then, the conditional CDF, \(\Pi _{\alpha }(\gamma | x)\), is decreasing (increasing) in x for any \(\gamma \ge 0\) for \(\alpha >0\) (\(\alpha <0\)).

Corollary 4.4

  1. (a)

    Suppose that the baseline RH belongs to the additive reversed hazard rate (ARH), \({\tilde{r}}(x|\gamma )={\tilde{r}}(x)+\gamma\). Then the conditional PDF, \(\pi _{\alpha }(\gamma | x)\), is increasing (decreasing) in \(x\ge 0\) in the LR ordering for \(\alpha > 0\) (\(\alpha <0\)).

  2. (b)

    Let the baseline RH belongs to the ARH model, \({\tilde{r}}(x|\gamma )={\tilde{r}}(x)+\gamma\). Then, the conditional CDF, \(\Pi _{\alpha }(\gamma | x)\), is decreasing (increasing) in x for any \(\gamma \ge 0\) for \(\alpha >0\) (\(\alpha <0\)).

Before we start the discussion of the bending property of the model for the RH, we need the following definition.

Definition 4.5

The weak bending down (up) property of the RH function, \({\tilde{r}}_{\alpha }(x)\), holds if

$$\begin{aligned} {\tilde{r}}_{\alpha }(x)\le (\ge ) {\tilde{r}}_{gm}(x), \quad \forall x> 0. \end{aligned}$$

In addition to this inequality, if we have

$$\begin{aligned} {\tilde{r}}_{gm}(x)-{\tilde{r}}_{\alpha }(x) \uparrow (\downarrow ) \ in\ x>0, \end{aligned}$$
(13)

then the strong bending down (up) property of the RH \({\tilde{r}}_{\alpha }(x)\) holds.

Theorem 4.6

Suppose that the baseline RH, \({\tilde{r}}(x|\gamma )\) is monotone in \(\gamma\) for all \(x \ge 0\). Then, the weak bending down (up) property for the \(\alpha\)-mixture RH function holds. That means \({\tilde{r}}_{\alpha }(x) \le (\ge ) {\tilde{r}}_{gm}(x)\) for all \(x \ge 0\) for \(\alpha >0\) (\(\alpha <0\)).

Proof

We give proof only for \(\alpha >0\), because the proof for \(\alpha <0\) is similar. Let \({\tilde{r}}(x|\gamma )\) is increasing (decreasing) in \(\gamma\), thus \(F(x|\gamma )\) is decreasing (increasing) in \(\gamma\). Since \(\alpha >0\), \(F^{\alpha }(x|\gamma )\) is decreasing (increasing) in \(\gamma\). On the other hand, from (4) we can rewritten the reversed hazard rate of \(\alpha\)-mixture as follows:

$$\begin{aligned} {\tilde{r}}_{\alpha }(x)=\frac{E[{\tilde{r}}(x|\gamma ) F^{\alpha }(x|\gamma )]}{E[F^{\alpha }(x|\gamma )]}. \end{aligned}$$
(14)

Thus, the result follows from Lemma 1.3 (b) with choosing \(f(\gamma )={\tilde{r}}(x|\gamma )\) and \(g(\gamma )=F^{\alpha }(x|\gamma )\). \(\square\)

The following two corollaries are obtained directly form Theorem 4.6.

Corollary 4.7

Suppose that the baseline RH belongs to the PRH model, \({\tilde{r}}(x|\gamma )=\gamma {\tilde{r}}(x)\). Then, the weak bending down (up) property for the \(\alpha\)-mixture RH function holds. That means \({\tilde{r}}_{\alpha }(x) \le (\ge ) {\tilde{r}}_{gm}(x)\) for all \(x \ge 0\) for \(\alpha >0\) (\(\alpha <0\)).

Corollary 4.8

Suppose that the baseline RH belongs to the ARH model, \({\tilde{r}}(x|\gamma )={\tilde{r}}(x)+\gamma\). Then, the weak bending down (up) property for the \(\alpha\)-mixture RH function holds. That means \({\tilde{r}}_{\alpha }(x) \le (\ge ) {\tilde{r}}_{gm}(x)\) for all \(x \ge 0\) for \(\alpha >0\) (\(\alpha <0\)).

Remark 4.9

From Theorem 4.6, one can extract the following lower (upper) bound for \(\alpha\)-mixture. For \(\alpha >0\) (\(\alpha <0\))

$$\begin{aligned}F_{\alpha }(x)\ge (\le ) \exp \big ( - \int _{x}^{\infty } {\tilde{r}}_{gm}(t) dt\big ).\end{aligned}$$

The following theorem concerns the strong bending property of the RH of \(\alpha\)-mixtures.

Theorem 4.10

Let the baseline RH, \({\tilde{r}}(x|\gamma )\), is increasing in \(\gamma\) for all \(x \ge 0\) and \(\frac{\partial }{\partial \gamma } {\tilde{r}}(x|\gamma )\) is decreasing in x for all \(\gamma \ge 0\). Then, the strong bending down (up) property for \(\alpha\)-mixture RH holds. That means \({\tilde{r}}_{gm}(x)-{\tilde{r}}_{\alpha }(x)\) is decreasing (increasing) in \(x \ge 0\) for \(\alpha > 0\) (\(\alpha < 0\)).

Proof

We give proof only for \(\alpha >0\) because the proof for \(\alpha <0\) is similar. By integrating by part, it is easy to see that

$$\begin{aligned} \Delta {\tilde{r}}(x)={\tilde{r}}_{gm}(x)-{\tilde{r}}_{\alpha }(x)&=\int _{0}^{\infty }{\tilde{r}}(x|\gamma ) \left[ \pi (\gamma )- \pi _{\alpha }(\gamma |x)\right] d \gamma \\&=\int _{0}^{\infty } - \frac{\partial }{\partial \gamma }{\tilde{r}}(x|\gamma ) \left[ \Pi (\gamma )- \Pi _{\alpha }(\gamma | x)\right] d \gamma \ge 0 ,\ \ \ \forall x \ge 0 \end{aligned}$$

From Theorem 4.6, we have \({\tilde{r}}_{gm}(x)\ge {\tilde{r}}_{\alpha }(x)\), and by Corollary 4.2 (a) \(\Pi (\gamma )- \Pi _{\alpha }(\gamma | x) \le 0\) and from assumption \(\frac{\partial }{\partial \gamma }{\tilde{r}}(x| \gamma )\) is decreasing in x, thus \(\Delta {\tilde{r}}(x)\) is decreasing in x for \(\alpha >0\). This completes the proof. \(\square\)

Corollary 4.11

Suppose that the baseline RH belongs to the PRH model, \({\tilde{r}}(x|\gamma )=\gamma {\tilde{r}}(x)\). In addition, suppose that \({\tilde{r}}(x)\) is decreasing in x. Then, the strong bending down (up) property for \(\alpha\)-mixture RH holds. That means \({\tilde{r}}_{gm}(x)-{\tilde{r}}_{\alpha }(x)\) is decreasing (increasing) in \(x \ge 0\) for \(\alpha > 0\) (\(\alpha < 0\)).

Corollary 4.12

Suppose that the baseline RH belongs to the ARH, \({\tilde{r}}(x|\gamma )={\tilde{r}}(x)+\gamma\). Further, assume that \({\tilde{r}}(x)\) is decreasing in x. Then, the strong bending down (up) property for \(\alpha\)-mixture RH holds. That means \({\tilde{r}}_{gm}(x)-{\tilde{r}}_{\alpha }(x)\) is decreasing (increasing) in \(x \ge 0\) for \(\alpha > 0\) (\(\alpha < 0\)).

The following example is considered as an application of Theorem 4.6 and Theorem 4.10 together with Remark 4.9.

Example 4.13

Assume that the random variable \(X|\gamma\) has the following CDF:

$$\begin{aligned} F(x|\gamma )=\frac{x^{2}+2x\gamma }{1+2\gamma }, \ \ \ 0\le x \le 1, \ \ \gamma >0. \end{aligned}$$

The corresponding PDF of \(X|\gamma\) can be obtained as:

$$\begin{aligned} f(x|\gamma )=\frac{2}{1+2\gamma } (x+\gamma ). \end{aligned}$$

Hence, the RH of \(X|\gamma\) is

$$\begin{aligned} {\tilde{r}}(x|\gamma )=\frac{2}{x^{2}+2\gamma x} (x+\gamma ).\end{aligned}$$

Clearly, \({\tilde{r}}(x|\gamma )\) is a decreasing function of \(\gamma\), because

$$\begin{aligned} \frac{\partial }{\partial \gamma }{\tilde{r}}(x|\gamma )&=\frac{2 \big (x^{2}+2\gamma x \big )-4x\big (x+\gamma \big )}{\big (x^{2}+2\gamma x \big )^{2}} \\&=-\frac{2x^{2}}{\big (x^{2}+2\gamma x \big )^{2}} \le 0. \end{aligned}$$

Thus, based on Theorem 4.6, for any mixing random variable \(\Gamma\) with support in \(\gamma \in [0, \infty )\), the weak bending down (up) property holds for the \(\alpha\)-mixture RH for \(\alpha >0\) (\(\alpha <0\)). Assume that the mixing random variable \(\Gamma\) be uniform (0, 1). Therefore, we have

$$\begin{aligned} {\tilde{r}}_{gm}(x)=\int _{0}^{1} \frac{2}{x^{2}+2\gamma x} (x+\gamma )\ d\gamma , \end{aligned}$$

and

$$\begin{aligned} {\tilde{r}}_{\alpha }(x)=\int _{0}^{1} \frac{2 (x+\gamma )}{x^{2}+2\gamma x} \dfrac{\big (\frac{x^{2}+2\gamma x}{1_2\gamma }\big )^{\alpha }}{\int _{0}^{1} \big (\frac{x^{2}+2\gamma x}{1_2\gamma }\big )^{\alpha } \ d\gamma }\ d\gamma . \end{aligned}$$

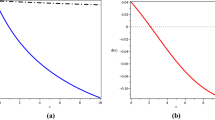
Fig. 1 shows the plot of \({\tilde{r}}_{gm}(x)\) and \({\tilde{r}}_{\alpha }(x)\) for different values of \(\alpha\). As can be seen from Fig. 1 a (b), the weak bending down (up) property holds for the \(\alpha\)-mixture RH for \(\alpha >0\) (\(\alpha <0\)).

The conditions of Theorem 4.10, also, are established. Figure 2 a (b) shows the strong bending down (up) property for the \(\alpha\)-mixture RH for \(\alpha >0\) (\(\alpha <0\)). That means \({\tilde{r}}_{gm}(x)-{\tilde{r}}_{\alpha }(x)\) is decreasing (increasing) function of x for \(\alpha >0\) (\(\alpha <0\)). Finally, from Remark 4.9, a lower bound for the CDF of the \(\alpha\)-mixture is shown in Fig. 3.

Fig. 1
figure 1

The plots of \({\tilde{r}}_{\alpha }(x)\) and \({\tilde{r}}_{gm}(x)\) in Example 4.13: For \(\alpha >0\) (left) and \(\alpha <0\) (right)

Full size image
Fig. 2
figure 2

The plots of \({\tilde{r}}_{gm}(x)-{\tilde{r}}_{\alpha }(x)\) in Example 4.13: For \(\alpha >0\) (left) and \(\alpha <0\) (right)

Full size image
Fig. 3
figure 3

Lower bound for the CDF of the \(\alpha\)-mixture in Example 4.13

Full size image

   At the end of this section, we present some conditions for comparing two \(\alpha\)-mixtures in the RH ordering and the usual stochastic ordering. The following theorems generalize Theorems 1.A.6 and 1.B.52 of Shaked and Shanthikumar (2007) to the \(\alpha\)-mixture models.

The following theorem states that if the baseline distribution and the mixing random variable are ordered in the sense of the usual stochastic order, then the corresponding \(\alpha\)-mixtures are also ordered in the sense of the usual stochastic order.

Theorem 4.14

Assume that \(\left\{ {F}(x | \gamma ), \gamma \in {[0, \infty )} \right\}\) be a family of CDF’s. Consider two random variables \(\Gamma _{1}\) and \(\Gamma _{2}\), with supports in \([0,\infty )\), with distribution functions \(\Pi _{1}\) and \(\Pi _{2}\), respectively. Let the CDF of \(X_{i}\), \(i=1,2\), is given by

$$\begin{aligned} {F}_{\alpha ,i}(x)= \left( \int _{0}^{\infty } {F}^{\alpha }(x| \gamma ) d\Pi _{i}(\gamma ) \right) ^{\frac{1}{\alpha }}. \end{aligned}$$

If \(X|\gamma \le _{st} X|\gamma ^{\prime }\) whenever \(\gamma \le \gamma ^{\prime }\) and if \(\Gamma _{1} \le _{st} \Gamma _{2}\), then \(X_{1} \le _{st} X_{2}.\)

Proof

To proof the theorem, we must consider the following different cases for \(\alpha\).

  • Let \(\alpha >0\). From assumption \(X|\gamma \le _{st} X|\gamma ^{\prime }\), \({F}(x | \gamma )\) is decreasing in \(\gamma\). Hence, since \(\alpha >0\), \({F}^{\alpha }(x | \gamma )\) is decreasing in \(\gamma\). Now, from assumption \(\Gamma _{1} \le _{st} \Gamma _{2}\) one can see that

    $$\begin{aligned} \int _{0}^{\infty } {F}^{\alpha }(x | \gamma )d\Pi _{1}(\gamma )\ge \int _{0}^{\infty } {F}^{\alpha }(x | \gamma )d\Pi _{2}(\gamma ). \end{aligned}$$

    Now, by raising both sides of the inequality to the power \(\frac{1}{\alpha }\), we have \({F}_{\alpha ,1}(x) \ge {F}_{\alpha ,2}(x)\). This means that \(X_{1} \le _{st} X_{2}\).

  • Now, suppose that \(\alpha \rightarrow 0\). We have,

    $$\begin{aligned} {{F}_{gm,i}}(x)= \exp \left( \int _{0}^{\infty } \log ({F}(x | \gamma )) d\Pi _{i}(\gamma ) \right) . \end{aligned}$$

    Again, since \(X|\gamma \le _{st} X|\gamma ^{\prime }\), \({F}(x |\gamma )\) is decreasing in \(\gamma\), then \(\log ({F}(x | \gamma ))\) is decreasing in \(\gamma\). Thus, by assumption \(\Gamma _{1} \le _{st} \Gamma _{2}\), we have

    $$\begin{aligned} \int _{0}^{\infty } \log ({F}(x| \gamma ))d\Pi _{1}(\gamma )\ge \int _{0}^{\infty } \log ({F}(x | \gamma ))d\Pi _{2}(\gamma ). \end{aligned}$$

    Consequently, \(X_{1} \le _{st} X_{2}\) follows from

    $$\begin{aligned} {{F}_{gm,1}}(x)= \exp \left( \int _{0}^{\infty } \log ({F}(x | \gamma )) d\Pi _{1}(\gamma ) \right) \ge \exp \left( \int _{0}^{\infty } \log ({F}(x| \gamma )) d\Pi _{2}(\gamma ) \right) = {{F}_{gm,2}}(x). \end{aligned}$$

  • Finally, let \(\alpha <0\). By assumption \(X|\gamma \le _{st} X|\gamma ^{\prime }\), \({F}(x | \gamma )\) is decreasing in \(\gamma\), and since \(\alpha <0\), \({F}^{\alpha }(x | \gamma )\) is increasing in \(\gamma\). Now, assumption \(\Gamma _{1} \le _{st} \Gamma _{2}\), yields

    $$\begin{aligned} \int _{0}^{\infty } {F}^{\alpha }(x | \gamma )d\Pi _{1}(\gamma )\le \int _{0}^{\infty } {F}^{\alpha }(x | \gamma )d\Pi _{2}(\gamma ). \end{aligned}$$

    Since \(\alpha <0\), by raising both sides of the inequality to the power \(\frac{1}{\alpha }\), we arrive at the result. Hence, \(X_{1} \le _{st} X_{2}\) holds for all values of \(\alpha\), and proof is completed.

\(\square\)

Theorem 4.15

Assume that \(\left\{ {F}(x | \gamma ), \gamma \in {[0, \infty )} \right\}\) be a family of CDFs. Consider two random variables \(\Gamma _{1}\) and \(\Gamma _{2}\), with supports in \([0,\infty )\), with distribution functions \(\Pi _{1}\) and \(\Pi _{2}\), respectively. Let the CDF of \(X_{i}\), \(i=1,2\), is given by

$$\begin{aligned} {F}_{\alpha ,i}(x)= \left( \int _{0}^{\infty } {F}^{\alpha }(x| \gamma ) d\Pi _{i}(\gamma ) \right) ^{\frac{1}{\alpha }}. \end{aligned}$$

If \(X|\gamma \le _{rh} X|\gamma ^{\prime }\) whenever \(\gamma \le \gamma ^{\prime }\) and if \(\Gamma _{1} \le _{rh} \Gamma _{2}\), then \(X_{1} \le _{rh} X_{2}.\)

Proof

The proof of the theorem, we refer to the proof of Theorem 4.4 of Shojaee et al. (2021).

The above theorem states that if the baseline distribution and the mixing random variable are ordered in the sense of the RH order, then the corresponding \(\alpha\)-mixtures are also ordered in the sense of the RH order. \(\square\)

5 Ordering Results for Finite \(\alpha\)-Mixtures

This section is compared two finite \(\alpha\)-mixtures in the some popular cases.

5.1 Usual Stochastic Order

The next theorem compares two finite \(\alpha\)-mixture with same baseline distribution functions and different mixing probabilities in the sense of usual stochastic order which is extension of some result of Navarro and del Aguila (2017) to the case of \(\alpha\)-mixture.

Theorem 5.1

Let \(F_{\alpha }(x,{\varvec{p}})\) and \(F_{\alpha }(x,{\varvec{q}})\) be two finite \(\alpha\)-mixtures with mixing probabilities \({{\varvec{p}}=(p_{1},..., p_{n})}\) and \({{\varvec{q}}=(q_{1},..., q_{n})}\), respectively. Suppose that

$$\begin{aligned}F_{1} \ge _{st} F_{2} \ge _{st}... \ge _{st}F_{n}.\end{aligned}$$

Then,

$$\begin{aligned}F_{\alpha }(x,{\varvec{p}}) \le _{st} F_{\alpha }(x,{\varvec{q}})\end{aligned}$$

if and only if \({\varvec{p}} \ge _{st}{\varvec{q}}\).

Proof

We will give proof only for the “only if” part of the theorem because the “if” part of the theorem follows from Theorem 4.14. To proof the theorem, three different cases for \(\alpha\) is considered.

  • Let \(\alpha >0\). From \(F_{\alpha }(x,{\varvec{p}}) \le _{st} F_{\alpha }(x,{\varvec{q}})\), we get

    $$\begin{aligned} \left[ \sum _{i=1}^{n} p_{i}{{F}_{i}}^{\alpha }\right] ^{\frac{1}{\alpha }}\ge \left[ \sum _{i=1}^{n} q_{i}{{F}_{i}}^{\alpha }\right] ^{\frac{1}{\alpha }}, \end{aligned}$$

    and for \(\alpha >0\), we have

    $$\begin{aligned} \left[ \sum _{i=1}^{n} p_{i}{{F}_{i}}^{\alpha }\right] \ge \left[ \sum _{i=1}^{n} q_{i}{{F}_{i}}^{\alpha }\right] . \end{aligned}$$

    The assumption \(F_{1} \ge _{st} F_{2} \ge _{st}... \ge _{st}F_{n}\) yields \(F_{1} \le F_{2} \le ... \le F_{n}\). Now, by choosing \({F}_{1}={F}_{2}=...={F}_{k}=0\) and \({F}_{k+1}=...={F}_{n}=1\), we have \(\sum _{i=k+1}^{n} p_{i}\ge \sum _{i=k+1}^{n} q_{i}\) or \(\sum _{i=1}^{k} p_{i}\le \sum _{i=1}^{k} q_{i}\). This means that, \({\varvec{p}} \ge _{st}{\varvec{q}}\).

  • The proof for the case \(\alpha \rightarrow 0\) is given in Theorem 4.1 of Shojaee and Babanezhad (2023).

  • Suppose now that \(\alpha <0\). From \(F_{\alpha }(x,{\varvec{p}}) \le _{st} F_{\alpha }(x,{\varvec{q}})\), it is easy to see that

    $$\begin{aligned} \left[ \sum _{i=1}^{n} p_{i}{{F}_{i}}^{\alpha }\right] ^{\frac{1}{\alpha }}\ge \left[ \sum _{i=1}^{n} q_{i}{{F}_{i}}^{\alpha }\right] ^{\frac{1}{\alpha }}, \end{aligned}$$

    and hence since \(\alpha <0\), we get

    $$\begin{aligned} \left[ \sum _{i=1}^{n} q_{i}{{F}_{i}}^{\alpha }\right] \ge \left[ \sum _{i=1}^{n} p_{i}{{F}_{i}}^{\alpha }\right] . \end{aligned}$$

    By assumption \(F_{1} \ge _{st} F_{2} \ge _{st}... \ge _{st}F_{n}\) with choosing \({F}_{1}={F}_{2}=...={F}_{k}={F}_{k}\) and \({F}_{k+1}=...={F}_{n}=1\), we have

    $$\begin{aligned} \left[ \sum _{i=1}^{k}q_{i}{F}_{k}^{\alpha }+ \sum _{i=k+1}^{n}q_{i} \right] \ge \left[ \sum _{i=1}^{k}p_{i}{F}_{k}^{\alpha }+ \sum _{i=k+1}^{n}p_{i}\right] \end{aligned}$$

    Then,

    $$\begin{aligned} \left[ \sum _{i=1}^{k}q_{i}({F}_{k}^{\alpha }-1) \right] \ge \left[ \sum _{i=1}^{k}p_{i}({F}_{k}^{\alpha }-1) \right] . \end{aligned}$$

    Now, since \(\alpha <0\) and \(0 \le {F}_{k}\le 1\), then \(({\bar{F}}_{k}^{\alpha }-1)\ge 0\). Consequently, \(\sum _{i=1}^{k}q_{i}\ge \sum _{i=1}^{k}p_{i}\), that means, \({\varvec{p}} \ge _{st}{\varvec{q}}\).

\(\square\)

The following theorem compares two finite \(\alpha\)-mixtures with different baseline CDF’s and different mixing probabilities in the sense of usual stochastic order.

Theorem 5.2

Let \(F_{\alpha }(x,{\varvec{p}})\) and \(F_{\alpha }(x,{\varvec{q}})\) be two finite \(\alpha\)-mixtures with mixing probabilities \({{\varvec{p}}=(p_{1},..., p_{n})}\) and \({{\varvec{q}}=(q_{1},..., q_{n})}\), respectively. Suppose that

  1. (i)

    \(F_{1}\ge _{st}F_{2}\ge _{st}...{\ge _{st}} F_{n}\),

  2. (ii)

    \({\varvec{p}}\ge _{st}{\varvec{q}}\),

  3. (iii)

    \(F_{i} \le _{st} G_{i}\) for all \({i \in \{1,...,n\}}\).

Then, we get:

$$\begin{aligned} F_{\alpha }(x,{\varvec{p}}) \le _{st} G_{\alpha }(x,{\varvec{q}}).\end{aligned}$$

Proof

We will prove the theorem for three different cases of \(\alpha\). To proof the theorem, first, we will prove that \(F_{\alpha }(x,{\varvec{p}}) \le _{st} G_{\alpha }(x,{\varvec{p}})\).

  • Suppose that \(\alpha >0\). By assumption \(F_{i} \le _{st} G_{i}\) for \(i=1,...,n\), we get \({F}_{i}(x) \ge {G}_{i}(x)\) for any x, and hence, \({F}^{\alpha }_{i} \ge {G}^{\alpha }_{i}\) for \(i=1,...,n\). Thus,

    $$\begin{aligned}\sum _{i=1}^{n} {p}_{i}{F}^{\alpha }_{i} \ge \sum _{i=1}^{n} {p}_{i}{G}^{\alpha }_{i}. \end{aligned}$$

    By raising the both side of inequality to power \(\frac{1}{\alpha }\), we obtain

    $$\begin{aligned}\left[ \sum _{i=1}^{n} {p}_{i}{F}^{\alpha }_{i}\right] ^{\frac{1}{\alpha }} \ge \left[ \sum _{i=1}^{n} {p}_{i}{G}^{\alpha }_{i} \right] ^{\frac{1}{\alpha }}. \end{aligned}$$

    This means that, for \(\alpha >0\), \(F_{\alpha }(x,{\varvec{p}}) \le _{st} G_{\alpha }(x,{\varvec{p}})\).

  • Assume now that \(\alpha <0\). The assumption \(F_{i} \le _{st} G_{i}\) yields \({F}^{\alpha }_{i} \le {G}^{\alpha }_{i}\), \(i=1,...,n\). Thus,

    $$\begin{aligned}\sum _{i=1}^{n} {p}_{i}{F}^{\alpha }_{i} \le \sum _{i=1}^{n} {p}_{i}{G}^{\alpha }_{i}, \end{aligned}$$

    and then, we have

    $$\begin{aligned}\left[ \sum _{i=1}^{n} {p}_{i}{F}^{\alpha }_{i}\right] ^{\frac{1}{\alpha }} \ge \left[ \sum _{i=1}^{n} {p}_{i}{G}^{\alpha }_{i} \right] ^{\frac{1}{\alpha }}. \end{aligned}$$

    This means that, for \(\alpha <0\), \(F_{\alpha }(x,{\varvec{p}}) \le _{st} G_{\alpha }(x,{\varvec{p}})\).

  • The proof for the case \(\alpha \rightarrow 0\) is given in Theorem 4.2 of Shojaee and Babanezhad (2023). Thus, \(F_{gm}(x, {\varvec{p}})\le _{st} G_{gm}(x, {\varvec{p}})\).

Consequently, for all values of \(\alpha\), we have

$$\begin{aligned} F_{\alpha }(x,{\varvec{p}}) \le _{st} G_{\alpha }(x,{\varvec{p}}). \end{aligned}$$
(15)

Theorem 5.1 together with conditions (i) and (ii) yields: \(F_{\alpha }(x,{\varvec{p}}) \le _{st} F_{\alpha }(x,{\varvec{q}})\). From relation (15), we get \(F_{\alpha }(x,{\varvec{q}}) \le _{st} G_{\alpha }(x,{\varvec{q}})\), and hence \(F_{\alpha }(x,{\varvec{p}}) \le _{st} G_{\alpha }(x,{\varvec{q}})\). This is completing the proof. \(\square\)

The following example as an application of Theorem 5.2 compares two parallel systems.

Example 5.3

Suppose that a system designer needs a highly reliable parallel system to build a device. He knows the first population is a mixture of three 4-components parallel systems with equal mixing probabilities \({\varvec{p}}=(p_{1}, p_{2}, p_{3})=(\frac{1}{3}, \frac{1}{3}, \frac{1}{3})\), in such a way that the components of each parallel system have an exponential distribution with CDF \({F}_{i}(x)=1-e^{-\gamma _{i} x}\), for \(x \in [0,+\infty )\), where \((\gamma _{1}, \gamma _{2}, \gamma _{3})=(0.3, 0.6, 0.9)\), while the second population is a mixture of three 4-components parallel systems with unequal mixing probabilities \({\varvec{q}}=(q_{1}, q_{2}, q_{3})=(0.45, 0.45, 0.1)\), in such a way that the components of each parallel system have an exponential distribution with CDF \({G}_{i}(x)=1-e^{-\lambda _{i} x}\), for \(x \in [0,+\infty )\), where \((\lambda _{1}, \lambda _{2}, \lambda _{3})=(0.2, 0.5, 0.8)\). Denote by \({F}_{4}(x,{\varvec{p}})\) and \({G}_{4}(x,{\varvec{q}})\), the CDF of 3-component finite \(\alpha\)-mixture with mixing probabilities \({\varvec{p}}=(p_{1}, p_{2}, p_{3})\) and \({\varvec{q}}=(q_{1}, q_{2}, q_{3})\), respectively. The CDF of randomly selection of the parallel systems from the first and the second population are \({F}^{4}_{4}(x,{\varvec{p}})\) and \({G}^{4}_{4}(x,{\varvec{q}})\), respectively. It is easy to see that all condition of Theorem 5.2 are satisfied. Thus, \(F_{4}(x,{\varvec{p}})\le _{st} G_{4}(x,{\varvec{q}})\). Consequently, \({\bar{F}}^{4}_{4}(x,{\varvec{p}})\le {\bar{G}}^{4}_{4}(x,{\varvec{q}})\) for all \(x \in [0,+\infty )\). Therefore, it is better for the system designer to choose his parallel system from the second population.

5.2 The RH Order

The following theorem compares two finite \(\alpha\)-mixture models with same baseline distribution functions and different mixing probabilities in the sense of RH order, which extends Proposition 2.5 of Navarro (2016) on ordinary mixture to the \(\alpha\)-mixture of CDF’s.

Theorem 5.4

Let \(F_{\alpha }(x,{\varvec{p}})\) and \(F_{\alpha }(x,{\varvec{q}})\) be two finite \(\alpha\)-mixtures with mixing probabilities \({{\varvec{p}}=(p_{1},..., p_{n})}\) and \({{\varvec{q}}=(q_{1},..., q_{n})}\), respectively. Suppose that

$$\begin{aligned}F_{1} \ge _{rh} F_{2} \ge _{rh}... \ge _{rh}F_{n}.\end{aligned}$$

Then for \(\alpha \not = 0\),

$$\begin{aligned}F_{\alpha }(x,{\varvec{p}}) \le _{rh} F_{\alpha }(x,{\varvec{q}})\end{aligned}$$

if \(p_{i}q_{j} \le p_{j}q_{i}\) for all \(1\le i \le j \le n\).

Proof

We will show that \(\frac{F_{\alpha }(x,{\varvec{q}})}{F_{\alpha }(x,{\varvec{p}})}\) is increasing in x. We have to show that H(x) is increasing in x, where

$$\begin{aligned} H(x) =\frac{F_{\alpha }(x,{\varvec{q}})}{F_{\alpha }(x,{\varvec{p}})}\equiv [B(x)]^{1/\alpha }, \end{aligned}$$

where

$$\begin{aligned} B(x)=\left[ \frac{\sum _{i=1}^{{n}} q_{i}{{F}_{i}}^{\alpha }(x)}{\sum _{i=1}^{{n}} p_{i}{{F}_{i}}^{\alpha }(x)}\right] . \end{aligned}$$

By differentiating H(x) with respect to x, we have

$$\begin{aligned} H^{\prime }(x)=\frac{1}{\alpha } B^{\prime }(x) [B(x)]^{\frac{1}{\alpha }-1}, \end{aligned}$$

where

$$\begin{aligned} B^{\prime }(x){\mathop {=}\limits ^{sign}}&\alpha \left\{ \sum _{i=1}^{{n}} q_{i} f_{i}(x){{F}_{i}}^{\alpha -1}(x) \sum _{j=1}^{{n}} p_{j}{{F}_{j}}^{\alpha }(x)-\sum _{i=1}^{{n}} p_{i} f_{i}(x){{F}_{i}}^{\alpha -1}(x) \sum _{j=1}^{{n}} q_{j}{{F}_{j}}^{\alpha }(x) \right\} \\ =&\alpha \left\{ \sum _{i=1}^{{n}} \sum _{j=1}^{{n}} (p_{j}q_{i}-p_{i}q_{j})f_{i}(x){{F}_{i}}^{\alpha -1}(x){{F}_{j}}^{\alpha }(x)\right\} \\ \end{aligned}$$

Thus, after some algebra calculations, we get

$$\begin{aligned} H^{\prime }(x){\mathop {=}\limits ^{sign}}&\left\{ \sum _{i=1}^{{n}-1} \sum _{j=i+1}^{{n}} (p_{j}q_{i}-p_{i}q_{j})\left( {\tilde{r}}_{i}(x)-{\tilde{r}}_{j}(x)\right) {{F}_{i}}^{\alpha }(x) {{F}_{j}}^{\alpha }(x)\right\} . \end{aligned}$$

where \({\tilde{r}}_{i}(x)\) is the RH of \(F_{i}(x)\), \(i=1,\dots , n\). From condition \(F_{i} \ge _{rh} F_{j}\) for \(i \le j\), we have \({\tilde{r}}_{i}(x)-{\tilde{r}}_{j}(x)\ge 0\) for \(i \le j\). By assumption \(p_{i}q_{j}\le p_{j}q_{i}\), we get \(p_{j}q_{i}- p_{i}q_{j} \ge 0\). Hence, \(H^{\prime }(x)\ge 0\), and \(F_{\alpha }(x,{\varvec{p}}) \le _{rh} F_{\alpha }(x,{\varvec{q}})\) for \(\alpha \not = 0\). \(\square\)

The following theorem compares two finite \(\alpha\)-mixtures with different baseline distribution functions and different mixing probabilities in the sense of RH order.

Theorem 5.5

Let \(F_{\alpha }(x,{\varvec{p}})\) and \(F_{\alpha }(x,{\varvec{q}})\) be two finite \(\alpha\)-mixtures with mixing probabilities \({{\varvec{p}}=(p_{1},..., p_{n})}\) and \({{\varvec{q}}=(q_{1},..., q_{n})}\), respectively. Let

  1. (i)

    \(G_{1} \ge _{rh}... \ge _{rh}G_{n}\) or \(F_{1} \ge _{rh}... \ge _{rh}F_{n}\);

  2. (ii)

    \(\frac{{G}_{i}(x)}{{F}_{i}(x)}\) is decreasing (increasing) in \(i \in \lbrace 1,2,...,n\rbrace\);

  3. (iii)

    \(F_{i} \le _{rh} G_{i}\), \(i=1,2,\dots ,n\);

  4. (iv)

    \(p_{i}q_{j} \le p_{j}q_{i}\) for all \(1\le i \le j \le n\).

Then for \(\alpha >0 \ (\alpha <0)\),

$$\begin{aligned} F_{\alpha }(x,{\varvec{p}})\le _{rh} G_{\alpha }(x,{\varvec{q}}).\end{aligned}$$

Proof

We give proof only for \(\alpha >0\). The proof for \(\alpha <0\) can be considered in a similar way. Without loss of generality, it was assumed that \(G_{1} \ge _{rh}... \ge _{rh}G_{n}\). From (9), the RH of \(F_{\alpha }(x,{\varvec{p}})\) can be written as

$$\begin{aligned} {\tilde{r}}_{\alpha , F}(x)=\sum _{i=1}^{n} {\tilde{r}}_{F_{i}}(x) p_{i}(x), \end{aligned}$$

where \({\tilde{r}}_{F_{i}}(x)\) is the RH of \(F_{i}(x)\), \(i=1,\dots , n\), and \(p_{i}(x)=\frac{p_{i} {F}_{i}^{\alpha }(x)}{\sum _{j=1}^{n} p_{j} {F}_{j}^{\alpha }(x)}\), \(i=1,\dots , n\). Similarly, the RH of \(G_{\alpha }(x,{\varvec{q}})\) is

$$\begin{aligned} {\tilde{r}}_{\alpha , G}(x)=\sum _{i=1}^{n} {\tilde{r}}_{G_{i}}(x) q_{i}(x) \end{aligned}$$

where \({\tilde{r}}_{G_{i}}(x)\) is the RH of \(G_{i}(x)\), \(i=1,\dots , n\), and \(q_{i}(x)=\frac{q_{i} {G}_{i}^{\alpha }(x)}{\sum _{j=1}^{n} q_{j} {G}_{j}^{\alpha }(x)}\), \(i=1,...,n\). To proof the theorem, we must to show that \(\phi (x)={\tilde{r}}_{\alpha , G}(x)-{\tilde{r}}_{\alpha ,F}(x)\) is non-negative for all \(x\ge 0\). Note that, from condition (iii) the following inequality holds

$$\begin{aligned} \phi (x)=&\sum _{i=1}^{n} {\tilde{r}}_{G_{i}}(x) q_{i}(x)-\sum _{i=1}^{n} {\tilde{r}}_{F_{i}}(x) p_{i}(x)\\ \ge&\sum _{i=1}^{n} {\tilde{r}}_{F_{i}}(x) q_{i}(x)-\sum _{i=1}^{n} {\tilde{r}}_{F_{i}}(x) p_{i}(x)\equiv \xi (x). \end{aligned}$$

Thus, we must to to show that \(\xi (x)\) is non-negative for all \(x\ge 0\). On the other hand, \(\xi (x)\) can be rewritten as

$$\begin{aligned} \xi (x)=E[\psi (W)]-E[\psi (V)], \end{aligned}$$
(16)

where W and V are discrete random variables with PDF’s \(q_{i}(x)\) and \(p_{i}(x)\),\(i = 1,..., n\), respectively, and \(\psi (i)={\tilde{r}}_{F_{i}}(.)\), \(i=1,...,{n}\). To show that (16) is non-negative, it is enough to show that \({W} \le _{st} {V}\) and \(\psi (i)\) is decreasing in i. From condition (i), we can see that \(r_{F_{1}}(x)\ge ...\ge r_{F_{n}}(x)\) for all \(x\ge 0\). Therefore, \(\psi (i)\) is decreasing in i. Also, we have

$$\begin{aligned} \frac{q_{i}(x)}{p_{i}(x)} \varpropto (\frac{{G}_{i}(x)}{{F}_{i}(x)})^{\alpha };\ \ i \in \lbrace 1,...,n\rbrace . \end{aligned}$$

Thus, from condition (ii), we can see that \(\frac{p_{i}(x)}{q_{i}(x)}\) is decreasing in \(i \in \lbrace 1,...,n\rbrace\). That means: \({W} \le _{lr}{V}\). Hence, \({W} \le _{st}{V}\). Thus, \(\xi (x)\) is non-negative and for \(\alpha >0\),

$$\begin{aligned} F_{\alpha }(x,{\varvec{p}})\le _{rh} G_{\alpha }(x,{\varvec{p}}). \end{aligned}$$
(17)

From Theorem 5.4, we have: \(G_{\alpha }(x,{\varvec{p}})\le _{rh} G_{\alpha }(x,{\varvec{q}})\), and hence by relation (17), we conclude that \(F_{\alpha }(x,{\varvec{p}})\le _{rh} G_{\alpha }(x,{\varvec{q}})\) for \(\alpha >0\). The case \(F1\ge _{rh} \dots \ge _{rh}F_{n}\), can be prove in similar way. \(\square\)

Remark 5.6

Theorem 5.5 extends a result of Amini-Seresht and Zhang (2017) in ordinary mixture (\(\alpha =1\)) to the \(\alpha\)-mixture family.

Remark 5.7

In Theorem 5.5, it was assumed that \(\alpha \not =0\). A similar result for the geometric mixture model \({F}_{gm}(x)\) in (7) have been obtained by Shojaee and Babanezhad (2023), under different conditions from Theorem 5.5.

6 Conclusions

\(\alpha\)-mixtures of cumulative distribution functions (CDFs) are useful tools for modeling heterogeneity in real-life populations by incorporating the effect of hard conditions (in terms of the proportional reversed hazard (PRH) model).

   In this paper, we investigated the reversed hazard rate (RH) of \(\alpha\)-mixtures. In particular, we showed that if the components of a finite \(\alpha\)-mixture have decreasing or increasing baseline RHs, then \(\alpha\)-mixtures have increasing RHs in \(\alpha\) for all \(\alpha \in (-\infty , +\infty )\). We stated that \(\pi _{\alpha }(\gamma | x)\) is the conditional probability density function (PDF) and can be ordered by the likelihood ratio (LR) ordering. Specifically, we proved that if the baseline RHs are increasing (decreasing) in \(\gamma\) for all \(x \ge 0\), then \(\pi _{\alpha }(\gamma | x)\) increases (decreases) in \(x \ge 0\) according to the LR order for \(\alpha >0\). We also proved a similar result for \(\alpha <0\). We obtained some results on the bending properties of the RH for \(\alpha\)-mixtures.

   Finally, we provided sufficient conditions for comparing finite \(\alpha\)-mixtures with different mixing probabilities and different baseline distributions according to the RH order and the usual stochastic order.