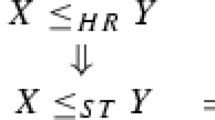Stochastic comparisons of generalized mixtures and coherent systems

Abstract

A distribution function $F$ is a generalized mixture of the distribution functions $F_1,\ldots ,F_k$ if $F=w_1 F_1+\ldots +w_k F_k$, where $w_1,\ldots ,w_k$ are some real numbers (weights) which should satisfy $w_1+\ldots +w_k=1$. If all the weights are positive, then we have a classical finite mixture. If some weights are negative, then we have a negative mixture. Negative mixtures appear in different applied probability models (order statistics, estimators, coherent systems, etc.). The conditions to obtain stochastic comparisons of classical (positive) mixtures are well known in the literature. However, for negative mixtures, there are only results for the usual stochastic order. In this paper, conditions for hazard rate and likelihood ratio comparisons of generalized mixtures are obtained. These theoretical results are applied in this paper to study distribution-free comparisons of coherent systems using their representations as generalized mixtures. They can also be applied to other probability models in which the generalized mixtures appear.

1 Introduction

A distribution function $F$ is a generalized mixture of the distribution functions $F_1,\ldots ,F_k$ if $F=\sum _{i=1}^k w_iF_i$, where $w_1,\ldots ,w_k$ are some real numbers (weights). Obviously, the weights satisfy $\sum _{i=1}^k w_i=1$. If all the weights are positive, then we have a classical finite mixture (called here positive mixture). However, for some distribution functions, some weights (not all of them) can be negative. If some weights are negative, then we have a negative mixture. It is well known that positive mixtures are used to describe populations formed by the mixture of different subpopulations. However, the meaning of negative mixtures is not so clear. Generalized mixtures can be used to manage both cases together. They can be traced back to Everitt and Hand (1981), Wu and Lee (1998) and Wu (2001). Recent results can be seen in Franco et al. (2014) and in the references therein. They were used to define families of distributions in Baggs and Nagaraja (1996) where the generalized mixtures of exponential distributions were called generalized hyperexponential distributions. The negative mixtures also appear (without a specific name) in other probability models such as order statistics, see David and Nagaraja (2003, pp. 46 and 99); marginal distributions of multivariate models, see Kotz et al. (2000, p. 356); distributions of the maximum likelihood estimators of exponential parameters under step-stress models, see Balakrishnan and Xie (2007a, (2007b), Balakrishnan et al. (2009) or distributions of progressively censored order statistics, see Kamps and Cramer (2001), Balakrishnan and Cramer (2008) and Balakrishnan and Cramer (2014, p. 36). Finally, the generalized mixtures are also useful to represent the distributions of coherent systems. The basic concepts in the theory of reliability and some applications can be seen in the classic book by Barlow and Proschan (1975). The distributions of coherent systems can be represented both as positive mixtures (see Samaniego 1985, 2007; Kochar et al. 1999) and as negative mixtures (see Block et al. 2003; Navarro et al. 2007, 2009; Navarro and Rubio 2010, and Sect. 3).

The stochastic orders play a relevant role in different applied probability fields (see Shaked and Shanthikumar 2007). The most relevant orders are the (usual) stochastic order, the hazard rate order and the likelihood ratio order. The conditions to obtain comparisons based on these orders of classical (positive) mixtures are well known in the literature and can be seen in Theorems 1.A.6, 1.B.14 and 1.C.17 of Shaked and Shanthikumar (2007), respectively. The conditions for the reversed hazard rate order were given in Theorem 1.B.52 of Shaked and Shanthikumar (2007). These results were used to obtain ordering properties of coherent systems in Kochar et al. (1999), Navarro et al. (2008b) and Navarro and Rubio (2011) using the representation of their distributions as positive mixtures of order statistics’ distributions when the component lifetimes are independent and identically distributed (IID) or exchangeable. Other comparison results were obtained recently in Navarro et al. (2015) and Samaniego and Navarro (2016). However, for negative mixtures, in the literature, there are only (in our knowledge) comparison results for the stochastic order given in Theorem 3.2 of Navarro et al. (2008a) and Proposition 2.4 of Navarro and Rubio (2012) (see next section). There is also a result for the hazard rate order given in Navarro et al. (2009), but only for the case $k=2$.

In this paper, conditions for hazard rate, reversed hazard rate and likelihood ratio comparisons of generalized mixtures are given (Sect. 2). To illustrate these theoretical results, they are applied to obtain distribution-free comparisons of coherent systems using their representations as negative mixtures. These comparisons include the cases of systems with independent and identically distributed components (Sect. 3), with independent non-identically distributed components (Sect. 4) and with dependent components (Sect. 5). Some conclusions are given in Sect. 6.

Throughout the paper, we say that a function $g:{\mathbb {R}} \rightarrow {\mathbb {R}}$ is increasing (decreasing) if $g(x)\le g(y)$ ($\ge$) for all $x\le y$. The stochastic orders mentioned above can be defined as follows. Their basic properties and applications can be seen in Shaked and Shanthikumar (2007).

Let $X$ and $Y$ be two random variables with absolutely continuous distribution functions $F_X$ and $F_Y$, reliability functions $\overline{F}_X=1-F_X$ and $\overline{F}_Y=1-F_Y$ and probability density functions $f_X=F_X'$ and $f_Y=F_Y'$. Then:

• $X$ is said to be less than $Y$ in the (usual) stochastic order (denoted by $X\le _\mathrm{ST}Y$ or $F_X\le _\mathrm{ST}F_Y$) if $\overline{F}_X\le \overline{F}_Y$,

• $X$ is said to be less than $Y$ in the hazard rate order (denoted by $X\le _\mathrm{HR}Y$ or $F_X\le _\mathrm{HR}F_Y$) if $\overline{F}_Y/\overline{F}_X$ is increasing,

• $X$ is said to be less than $Y$ in the reversed hazard rate order (denoted by $X\le _\mathrm{RHR}Y$ or $F_X\le _\mathrm{RHR}F_Y$) if $F_Y/F_X$ is increasing,

• $X$ is said to be less than $Y$ in the likelihood ratio order (denoted by $X\le _\mathrm{LR}Y$ or $F_X\le _\mathrm{LR}F_Y$) if $f_Y/f_X$ is increasing in the union of their support.

The relationships between these orders are the following. The reverse implications do not hold.

$$\begin{aligned} \begin{array}{ccc} X \le _\mathrm{LR} Y &{} \Rightarrow &{} X \le _\mathrm{HR} Y \\ \Downarrow &{} {} &{} \Downarrow \\ X \le _\mathrm{RHR} Y &{} \Rightarrow &{} X \le _\mathrm{ST} Y. \end{array} \end{aligned}$$

If $X$ and $Y$ are absolutely continuous, then $X\le _\mathrm{HR}Y$ holds if and only if $h_X\ge h_Y$, where $h_X=f_X/\overline{F}_X$ and $h_Y=f_Y/\overline{F}_Y$ are the respective hazard rate functions. Analogously, $X\le _\mathrm{RHR}Y$ holds if and only if $\overline{h}_X\le \overline{h}_Y$, where $\overline{h}_X=f_X/F_X$ and $\overline{h}_Y=f_Y/F_Y$ are the respective reversed hazard rate functions. The proofs can be seen in Shaked and Shanthikumar (2007). Finally, if the probability density functions are differentiable, then $X\le _\mathrm{LR}Y$ holds if and only if $\eta _X\ge \eta _Y$, where $\eta _X=-f'_X/f_X$ and $\eta _Y=-f'_Y/f_Y$ are the respective eta (Glaser) functions (see Glaser 1980).

2 Main results for generalized mixtures

First of all, we give the formal definition of generalized mixtures.

Definition 2.1

Let $F,F_1,\ldots ,F_k$ be distribution functions. Then, we say that $F$ is a generalized mixture of $F_1,\ldots ,F_k$ with weights $w_1,\ldots ,w_k\in {\mathbb {R}}$ if

$$\begin{aligned} F(t)=w_1F_1(t)+ \cdots +w_k F_k(t) \end{aligned}$$

(2.1)

for all $t$. We say that $F$ is a positive mixture when $w_1,\ldots ,w_k\ge 0$. We say that $F$ is a negative mixture when there exists at least an index $i\in \{1,\ldots ,k\}$ such that $w_i<0$.

As an immediate consequence of the preceding definition, we obtain

$$\begin{aligned} w_1+\cdots +w_k=1. \end{aligned}$$

Note that, in (2.1), we assume that $F$ is a proper distribution function since the right-hand side of (2.1) does not need to define a proper distribution function (see, e.g., Franco et al. 2014). Of course, it will define a proper distribution function for all $F_1,\ldots ,F_n$ when $w_i\ge 0$ for $i=1,\ldots ,k$ and $w_1+\cdots +w_k=1$ (classical or positive mixtures). Finally, note that similar representations hold both for the respective reliability functions and probability density functions. For example, if (2.1) holds and $\overline{F}$, $\overline{F}_1,\ldots ,\overline{F}_k$ are the respective reliability functions, then

$$\begin{aligned} \overline{F}(t)=w_1\overline{F}_1(t)+ \cdots +w_k \overline{F}_k (t). \end{aligned}$$

(2.2)

As we have already mentioned in the introduction, ordering properties of classical (positive) mixtures can be seen in Shaked and Shanthikumar (2007). For generalized mixtures, in the literature there are only results for the ST and HR orders. The results for the ST order obtained in Theorem 3.2 of Navarro et al. (2008a) can be stated as follows.

Proposition 2.1

Let $F_p$ and $F_q$ be two generalized mixtures satisfying (2.1) with weights $p_1,\ldots ,p_k$ and $q_1,\ldots ,q_k$, respectively. Let us assume that

$$\begin{aligned} F_1 \ge _\mathrm{ST} \cdots \ge _\mathrm{ST} F_k. \end{aligned}$$

(2.3)

If $\sum _{i=j}^k p_i \ge \sum _{i=j}^k q_i$ for $j=2,\ldots ,k$, then $F_p \le _\mathrm{ST} F_q$.

When all the weights are nonnegative, the preceding result coincides with the result for classical finite mixtures obtained from Theorem 1.A.6 of Shaked and Shanthikumar (2007). Another result for the ST order was obtained in Proposition 2.4 of Navarro and Rubio (2012) without assumption (2.3).

A similar result was obtained in Navarro et al. (2009) for the HR ordering of generalized mixtures with $k=2$. It can be stated as follows.

Proposition 2.2

Let $F_p$ and $F_q$ be two generalized mixtures satisfying (2.1) with $k=2$ and weights $p_1,p_2$ and $q_1,q_2$, respectively. Let us assume that

$$\begin{aligned} F_1 \ge _\mathrm{HR} F_2. \end{aligned}$$

(2.4)

If $p_1 \le q_1$, then $F_p \le _\mathrm{HR} F_q$.

Now, we can give the first main result of the paper in which the preceding result is extended to generalized mixtures with $k>2$.

Proposition 2.3

Let $F_p$ and $F_q$ be two generalized mixtures satisfying (2.1) with weights $p_1,\ldots ,p_k$ and $q_1,\ldots ,q_k$, respectively. Let us assume that

$$\begin{aligned} F_1 \ge _\mathrm{HR} \cdots \ge _\mathrm{HR} F_k. \end{aligned}$$

(2.5)

If $p_iq_j \le p_jq_i$ for all $1\le i\le j\le k$, then $F_p \le _\mathrm{HR} F_q$.

Proof

From the definition, $F_p \le _\mathrm{HR} F_q$ holds if $\overline{F}_q/\overline{F}_p$ is increasing, that is, if

$$\begin{aligned} R(t)=\frac{q_1\overline{F}_1(t)+ \cdots +q_k \overline{F}_k (t)}{p_1\overline{F}_1(t)+ \cdots +p_k \overline{F}_k (t)} \end{aligned}$$

is increasing in $t$. By differentiating, we have

$$\begin{aligned} R'(t)&=_\mathrm{sign}-\sum _{i=1}^k q_i f_i(t) \sum _{j=1}^k p_j \overline{F}_j(t) +\sum _{i=1}^k p_i f_i(t) \sum _{j=1}^k q_j \overline{F}_j(t)\\&=\sum _{i=1}^k \sum _{j=1}^k (p_iq_j-p_jq_i) f_i(t) \overline{F}_j(t)\\&=\sum _{i=1}^{k-1} \sum _{j=i+1}^k (p_iq_j-p_jq_i) \left( f_i(t) \overline{F}_j(t)-f_j(t) \overline{F}_i(t)\right) \\&=\sum _{i=1}^{k-1} \sum _{j=i+1}^k (p_iq_j-p_jq_i) (h_i(t)-h_j(t))\overline{F}_i(t)\overline{F}_j(t), \end{aligned}$$

where $h_i=f_i/\overline{F}_i$ is the hazard rate function of $F_i$ for $i=1,\ldots ,k$. As $F_i \ge _\mathrm{HR} F_j$ for $i\le j$, we have $h_i\le h_j$ for $i\le j$. Hence, $h_i(t)-h_j(t)\le 0$ for $i\le j$. Finally, as $p_iq_j \le p_jq_i$, then $p_iq_j-p_jq_i\le 0$ and hence $R'(t)\ge 0$ and $F_p \le _\mathrm{HR} F_q$ holds. $\square$

In particular, if $k = 2$, then the condition stated in the preceding proposition ($p_iq_j \le p_jq_i$, $i\le j$) reduces to $p_1q_2 \le p_2q_1.$ As $p_1+p_2=1$ and $q_1+q_2=1$, this condition is equivalent to

$$\begin{aligned} p_1(1-q_1) \le (1-p_1)q_1 \end{aligned}$$

or to $p_1\le q_1$. So, Proposition 2.3 reduces to Proposition 2.2 when $k=2$. However, in the case of positive mixtures, the condition given in the preceding proposition does not coincide with the condition obtained from Theorem 1.B.14 in Shaked and Shanthikumar (2007) (the condition given here is stronger).

Next, we give the second main result of the paper with the condition for the LR ordering of generalized mixtures.

Proposition 2.4

Let $F_p$ and $F_q$ be two generalized mixtures satisfying (2.1) with weights $p_1,\ldots ,p_k$ and $q_1,\ldots ,q_k$, respectively. Let us assume that

$$\begin{aligned} F_1 \ge _\mathrm{LR} \cdots \ge _\mathrm{LR} F_k. \end{aligned}$$

(2.6)

If $p_iq_j \le p_jq_i$ for all $1\le i\le j\le k$, then $F_p \le _\mathrm{LR} F_q$.

Proof

From the definition, $F_p \le _\mathrm{LR} F_q$ holds if $f_q/f_p$ is increasing, that is, if

$$\begin{aligned} r(t)=\frac{q_1f_1(t)+ \cdots +q_k f_k (t)}{p_1f_1(t)+ \cdots +p_k f_k (t)} \end{aligned}$$

is increasing in $t$. By differentiating, we have

$$\begin{aligned} r'(t)&=_\mathrm{sign}\sum _{i=1}^k q_i f'_i(t) \sum _{j=1}^k p_j f_j(t) -\sum _{i=1}^k p_i f'_i(t) \sum _{j=1}^k q_j f_j(t)\\&=-\sum _{i=1}^k \sum _{j=1}^k (p_iq_j-p_jq_i) f'_i(t) f_j(t)\\&=-\sum _{i=1}^{k-1} \sum _{j=i+1}^k (p_iq_j-p_jq_i) (f'_i(t) f_j(t)-f'_j(t)f_i(t)) \\&=\sum _{i=1}^{k-1} \sum _{j=i+1}^k (p_iq_j-p_jq_i) (\eta _i(t)-\eta _j(t))f_i(t)f_j(t), \end{aligned}$$

where $\eta _i=-f_i/f_i$ is the eta function of $F_i$ for $i=1,\ldots ,k$. As $F_i \ge _\mathrm{LR} F_j$ for $i\le j$, we have $\eta _i\le \eta _j$ for $i\le j$. Hence, $\eta _i(t)-\eta _j(t)\le 0$ for $i\le j$. Finally, as $p_iq_j \le p_jq_i$, then $p_iq_j-p_jq_i\le 0$ and hence $r'(t)\ge 0$ and $F_p \le _\mathrm{LR} F_q$ holds. $\square$

In the case of positive mixtures, the condition stated in the preceding proposition ($p_iq_j \le p_jq_i$ for all $1\le i\le j\le k$) is equivalent to the condition obtained from Theorem 1.C.17 of Shaked and Shanthikumar (2007). In the case $k=2$, this condition is equivalent to $p_1\le q_1$ (as we have seen above).

A similar result can be obtained for the RHR order.

Proposition 2.5

Let $F_p$ and $F_q$ be two generalized mixtures satisfying (2.1) with weights $p_1,\ldots ,p_k$ and $q_1,\ldots ,q_k$, respectively. Let us assume that

$$\begin{aligned} F_1 \ge _\mathrm{RHR} \cdots \ge _\mathrm{RHR} F_k. \end{aligned}$$

(2.7)

If $p_iq_j \le p_jq_i$ for all $1\le i\le j\le k$, then $F_p \le _\mathrm{RHR} F_q$.

Proof

From the definition, $F_p \le _\mathrm{RHR} F_q$ holds if $F_q/F_p$ is increasing, that is, if

$$\begin{aligned} g(t)=\frac{q_1F_1(t)+ \cdots +q_k F_k (t)}{p_1F_1(t)+ \cdots +p_k F_k (t)} \end{aligned}$$

is increasing in $t$. By differentiating, we have

$$\begin{aligned} g'(t)&=_\mathrm{sign}\sum _{i=1}^k q_i f_i(t) \sum _{j=1}^k p_j F_j(t) -\sum _{i=1}^k p_i f_i(t) \sum _{j=1}^k q_j F_j(t)\\&=\sum _{i=1}^k \sum _{j=1}^k (p_jq_i-p_iq_j) f_i(t) F_j(t)\\&=\sum _{i=1}^{k-1} \sum _{j=i+1}^k (p_jq_i-p_iq_j) (f_i(t) F_j(t)-f_j(t)F_i(t)) \\&=\sum _{i=1}^{k-1} \sum _{j=i+1}^k (p_jq_i-p_iq_j) \left( \,\overline{h}_i(t)-\overline{h}_j(t)\right) F_i(t)F_j(t), \end{aligned}$$

where $\overline{h}_i=f_i/F_i$ is the RHR function of $F_i$ for $i=1,\ldots ,k$. As $F_i \ge _\mathrm{RHR} F_j$ for $i\le j$, we have $\overline{h}_i\ge \overline{h}_j$ for $i\le j$. Hence $\overline{h}_i(t)-\overline{h}_j(t)\ge 0$ for $i\le j$. Finally, as $p_iq_j \le p_jq_i$, then $p_iq_j-p_jq_i\ge 0$ and hence $g'(t)\ge 0$ and $F_p \le _\mathrm{RHR} F_q$ holds. $\square$

The preceding results can be improved when the distributions $F_1,\ldots ,F_k$ satisfy the Proportional Hazard Rate (PHR) model, that is, when $\overline{F}_i=\overline{G}^{\alpha _i}$ for $i=1,\ldots ,k$, where $\alpha _1,\ldots ,\alpha _k>0$ and $\overline{G}$ is a reliability function. The distribution-free results for this case can be stated as follows.

Proposition 2.6

Let $F_p$ and $F_q$ be two generalized mixtures satisfying (2.1) with weights $p_1,\ldots ,p_k$ and $q_1,\ldots ,q_k$, respectively. Let us assume that $F_1,\ldots ,F_k$ satisfy the PHR model with $\overline{F}_i=\overline{G}^{\alpha _i}$ and $\alpha _i>0$ for $i=1,\ldots ,k$. Then, the following conditions are equivalent:

• (i) $F_p \le _\mathrm{HR} F_q$ holds for all reliability functions $\overline{G}$.

• (ii) The weights satisfy

  $$\begin{aligned} \sum _{i=1}^{k-1} \sum _{j=i+1}^k (p_iq_j-p_jq_i) (\alpha _i-\alpha _j)x^{\alpha _i+\alpha _j-2} \ge 0 \quad {{for\,\,all}} \quad x\in (0,1). \end{aligned}$$

  (2.8)

Proof

From the definition, $F_p \le _\mathrm{HR} F_q$ holds if and only if $R(t)=\overline{F}_{q}(t)/\overline{F}_{p}(t)$ is increasing in $t$. Then, proceeding as in the proof of Proposition 2.3, we have

$$\begin{aligned} R'(t)&=_\mathrm{sign}\sum _{i=1}^{k-1} \sum _{j=i+1}^k (p_iq_j-p_jq_i) (h_{i}(t)-h_{j}(t))\overline{F}_i(t)\overline{F}_j(t), \end{aligned}$$

where $h_{i}=f_{i}/\overline{F}_{i}$ is the hazard rate function of $F_{i}$ for $i=1,\ldots ,k$. Under the PHR model assumption, we obtain $h_i(t)=\alpha _i h_G(t)$ for $i=1,\ldots ,k$ where $h_G=-\overline{G}'/\overline{G}$ is the hazard rate associated to $G=1-\overline{G}$. Therefore,

$$\begin{aligned} R'(t)&=_\mathrm{sign}\sum _{i=1}^{k-1} \sum _{j=i+1}^k (p_iq_j-p_jq_i) (\alpha _i-\alpha _j)\overline{G}^{\alpha _i+\alpha _j}(t) \end{aligned}$$

and so $T_1 \le _\mathrm{HR} T_2$ holds for all $\overline{G}$ if and only if (2.8) holds. $\square$

Proposition 2.7

Let $F_p$ and $F_q$ be two generalized mixtures satisfying (2.1) with weights $p_1,\ldots ,p_k$ and $q_1,\ldots ,q_k$, respectively. Let us assume that $F_1,\ldots ,F_k$ satisfy the PHR model with $\overline{F}_i=\overline{G}^{\alpha _i}$ and $\alpha _i>0$ for $i=1,\ldots ,k$. Then, the following conditions are equivalent:

• (i) $F_p \le _\mathrm{LR} F_q$ holds for all reliability functions $\overline{G}$.

• (ii) The weights satisfy

  $$\begin{aligned} \sum _{i=1}^{k-1} \sum _{j=i+1}^k (p_iq_j-p_jq_i) \alpha _i\alpha _j(\alpha _i-\alpha _j)x^{\alpha _i+\alpha _j-2} \ge 0 \quad {{ for\,\,all }} \quad x\in (0,1). \end{aligned}$$

  (2.9)

Proof

From the definition, $F_p \le _\mathrm{LR} F_q$ holds if and only if $r(t)=f_{q}(t)/f_{p}(t)$ is increasing in $t$. Then, proceeding as in the proof of Proposition 2.4, we have

$$\begin{aligned} r'(t)&=_\mathrm{sign}\sum _{i=1}^{k-1} \sum _{j=i+1}^k (p_iq_j-p_jq_i) (\eta _{i}(t)-\eta _{j}(t))f_i(t)f_j(t), \end{aligned}$$

where $\eta _{i}=-f'_{i}/f_{i}$ is the eta function of $F_{i}$ for $i=1,\ldots ,k$. Under the PHR model assumption, we obtain $f_i(t)=\alpha _i g(t) \overline{G}^{\alpha _i-1}(t)$ and

$$\begin{aligned} \eta _{i}(t)=\frac{\alpha _i(\alpha _i-1)g^2(t)\overline{G}^{\alpha _i-2}(t)-\alpha _ig'(t)\overline{G}^{\alpha _i-1}(t)}{\alpha _i g(t)\overline{G}^{\alpha _i-1}(t)}=\eta _G(t)+(\alpha _i-1)h_G(t), \end{aligned}$$

where $G=1-\overline{G}$, $g=G'$, $\eta _G=-g'/g$ and $h_G=g/\overline{G}$. Therefore,

$$\begin{aligned} r'(t)&=_\mathrm{sign}\sum _{i=1}^{k-1} \sum _{j=i+1}^k (p_iq_j-p_jq_i) \alpha _i\alpha _j(\alpha _i-\alpha _j)\overline{G}^{\alpha _i+\alpha _j-2}(t) \end{aligned}$$

and so $T_1 \le _\mathrm{LR} T_2$ holds for all $\overline{G}$ if and only if (2.9) holds. $\square$

The analogous result for the stochastic order can be stated as follows. The proof is easy.

Proposition 2.8

Let $F_p$ and $F_q$ be two generalized mixtures satisfying (2.1) with weights $p_1,\ldots ,p_k$ and $q_1,\ldots ,q_k$, respectively. Let us assume that $F_1,\ldots ,F_k$ satisfy the PHR model with $\overline{F}_i=\overline{G}^{\alpha _i}$ and $\alpha _i>0$ for $i=1,\ldots ,k$. Then, the following conditions are equivalent:

• (i) $F_p \le _\mathrm{ST} F_q$ holds for all reliability functions $\overline{G}$.

• (ii) The weights satisfy

  $$\begin{aligned} \sum _{i=1}^{k} (q_j-p_j)x^{\alpha _i} \ge 0 \quad {{ for\,\,all }} \quad x\in (0,1). \end{aligned}$$

  (2.10)

The preceding results can also be improved when the distributions $F_1,\ldots ,F_k$ satisfy the Proportional Reversed Hazard Rate (PRHR) model, that is, when $F_i=G^{\alpha _i}$ for $i=1,\ldots ,k$, where $\alpha _1,\ldots ,\alpha _k>0$ and $G$ is a distribution function. The results can be stated as follows. The proofs are similar to that of Propositions 2.6, 2.7 and 2.8.

Proposition 2.9

Let $F_p$ and $F_q$ be two generalized mixtures satisfying (2.1) with weights $p_1,\ldots ,p_k$ and $q_1,\ldots ,q_k$, respectively. Let us assume that $F_1,\ldots ,F_k$ satisfy the PRHR model with $F_i=G^{\alpha _i}$ and $\alpha _i>0$ for $i=1,\ldots ,k$. Then:

• (i) $F_p \le _\mathrm{ST} F_q$ holds for all distribution functions $G$ if, and only if,

  $$\begin{aligned} \sum _{i=1}^{k} (p_i-q_i)x^{\alpha _i}\ge 0 \quad \text { for all }\quad x\in (0,1). \end{aligned}$$

  (2.11)

• (ii) $F_p \le _\mathrm{RHR} F_q$ holds for all distribution functions $G$ if, and only if,

  $$\begin{aligned} \sum _{i=1}^{k-1} \sum _{j=i+1}^k (p_jq_i-p_iq_j) (\alpha _i-\alpha _j)x^{\alpha _i+\alpha _j-2}\ge 0 \quad \text { for all } \quad x\in (0,1). \end{aligned}$$

  (2.12)

• (iii) $F_p \le _\mathrm{LR} F_q$ holds for all distribution functions $G$ if, and only if,

  $$\begin{aligned} \sum _{i=1}^{k-1} \sum _{j=i+1}^k (p_jq_i-p_iq_j) \alpha _i\alpha _j(\alpha _i-\alpha _j)x^{\alpha _i+\alpha _j-2}\ge 0 \quad \text { for all } \quad x\in (0,1). \end{aligned}$$

  (2.13)

3 Comparisons of coherent systems with IID components

Let us use the theoretical results obtained above to compare coherent systems under different assumptions. We start with the more simple case of coherent systems with $n$ components having independent and identically distributed (IID) lifetimes $X_1,\ldots ,X_n$. In this case, it is well known (see, e.g., Navarro et al. 2007) that the reliability function $\overline{F}_T$ of a coherent system with lifetime $T$ can be written as

$$\begin{aligned} \overline{F}_T(t)=a_1\overline{F}_{1:1}(t)+\cdots +a_n\overline{F}_{1:n}(t) \end{aligned}$$

(3.1)

for all $t$, where $a_1,\ldots ,a_n$ are some coefficients (real numbers which can be negative) and $\overline{F}_{1:i}(t)=\Pr (X_{1:i}>t)$ is the reliability function of the series system obtained with the first $i$ components whose lifetime is $X_{1:i}=\min (X_1,\ldots ,X_i)$ for $i=1,\ldots ,n$. The vector $\mathbf {a}=(a_1,\ldots ,a_n)$ with the coefficients in representation (3.1) was called in Navarro et al. (2007) the minimal signature of the system. Obviously, the representation in (3.1) is a generalized mixture. Note that, if we want to compare $T$ with another system with $m>n$ components, then we can just add zeros to representation (3.1) obtaining the minimal signature $\mathbf {a}^{(m)}$ of order $m$ given by the $m$-dimensional vector $\mathbf {a}^{(m)}=(a_1,\ldots ,a_n,0,\ldots ,0)$. The same representation (3.1) holds for mixed systems which are mixtures of coherent systems (see, e.g., Navarro et al. 2008b).

Under the IID assumption, it is well known that $\overline{F}_{1:i}(t)=\overline{F}^i(t)$, where $\overline{F}$ is the common components’ reliability function. Hence, the PHR model holds for representation (3.1) with $\alpha _i=i$ for $i=1,\ldots ,n$. Thus, from the results given in the preceding section, we can obtain the following proposition. The proof is easy.

Proposition 3.1

Let $T_1$ and $T_2$ be the lifetimes of two coherent (or mixed) systems with minimal signatures of order $n$, $(p_1,\ldots ,p_n)$ and $(q_1,\ldots ,q_n)$. Assume that both systems are based on IID components having a common absolutely continuous distribution $F$. Then:

• (i) $T_1 \le _\mathrm{ST} T_2$ holds for all $F$ if and only if

  $$\begin{aligned} \sum _{i=1}^{n} (q_i-p_i)x^{i} \ge 0 \quad \text { for all } \quad x\in (0,1). \end{aligned}$$

  (3.2)

• (ii) $T_1 \le _\mathrm{HR} T_2$ holds for all $F$ if and only if

  $$\begin{aligned} \sum _{i=1}^{n-1} \sum _{j=i+1}^n (j-i)(p_jq_i-p_iq_j)x^{i+j-2} \ge 0 \quad \text { for all } \quad x\in (0,1). \end{aligned}$$

  (3.3)

• (iii) $T_1 \le _\mathrm{LR} T_2$ holds for all $F$ if and only if

  $$\begin{aligned} \sum _{i=1}^{n-1} \sum _{j=i+1}^n ij(j-i)(p_jq_i-p_iq_j)x^{i+j-2} \ge 0 \quad \text { for all } \quad x\in (0,1). \end{aligned}$$

  (3.4)

Note that, in the case of IID components, the conditions stated in the preceding proposition are distribution-free necessary and sufficient conditions for the respective orders, while the conditions given in Kochar et al. (1999) and Navarro et al. (2008b) are just sufficient conditions. However, these last conditions are necessary and sufficient conditions for the respective orders in the case of exchangeable components (see Navarro and Rubio 2011). Therefore, we can use the preceding proposition to try to improve the ordering results obtained in these references for the IID case as can be seen in the following example. The results for the exchangeable case given in Navarro and Rubio (2011) cannot be improved.

Example 3.1

Let us consider the coherent systems with lifetimes $T_1=\min (X_1,$ $\max (X_2,X_3,X_4))$ and $T_2=\max (X_1, \min (X_2,X_3,X_4))$ by assuming that they have components with IID lifetimes $X_1,X_2,X_3,X_4$ having a common absolutely continuous distribution function $F$. The respective minimal signatures are $\mathbf {p}=(0,3,-3,1)$ and $\mathbf {q}=(1,0,1,-1)$ (see, e.g., lines 13 and 24 in Table 1 of Navarro and Rubio 2011). These two systems cannot be HR ordered using the conditions given in Kochar et al. (1999) as can be seen in Figure 2 of Navarro and Rubio (2011). However, we can use the preceding proposition to know if they are HR or LR ordered for all $F$. Thus, we compute the polynomial in (3.4) obtaining

$$\begin{aligned} v(x)=6x-18x^{2}-6x^{3}+48x^{4}-24x^{5}. \end{aligned}$$

The roots are $0$, $1/2$ (double), $(1+\sqrt{5})/2\cong 1.618034$ and $(1-\sqrt{5})/2\cong -0.618034$. Hence, as $v(1)=6$, we can prove that $v(x)\ge 0$ for all $x\in (0,1)$. Therefore, we have $T_1\le _\mathrm{LR}T_2$ for all $F$. Then, we can improve the results given in Figure 3 of Navarro and Rubio (2011). As a consequence, they are also HR ordered and we can improve the results given in Figure 2 of Navarro and Rubio (2011).

In a similar way, if we want to compare the system $T_1$ above with the single component $X_1$, whose minimal signature of order $4$ is of course $\mathbf {q}=(1,0,0,0)$, then we compute the polynomial in (3.4) obtaining

$$\begin{aligned} v(x)=6x-18x^{2}+12x^{3}. \end{aligned}$$

The roots are $0,1/2,1$ and hence $v(x)$ takes positive and negative values in $(0,1)$ (see Fig. 1, left). Therefore, we conclude that $T_1$ and $X_1$ are not LR ordered for all $F$ (they cannot be LR ordered using other procedures). Analogously, to study if they are HR ordered, we compute the polynomial in (3.3) obtaining

$$\begin{aligned} r(x)=3x-6x^{2}+3x^{3}. \end{aligned}$$

The roots are $0$ and $1$ (double) and hence $r(x)\ge 0$ for all $x\in (0,1)$ (see Fig. 1, right). Therefore, $T_1\le _\mathrm{HR}X_1$ for all $F$. This coincides with the result given in Figure 2 of Navarro and Rubio (2011).

Fig. 1

Plot of the polynomials in conditions (3.4) (left) and (3.3) (right) for the comparison of the system $T_1$ given in Example 3.1 and a single component $X_1$. As the left plot takes positive and negative values in $(0,1)$, then they are not LR ordered for all $F$. As the right plot is nonnegative in $(0,1)$, then $T_1\le _\mathrm{HR}X_1$ for all $F$

Proceeding as in the preceding example, we have obtained all the HR and LR ordering relationships between all the coherent systems with four or less IID components. They are given in Figs. 2 and 3. The black arrows indicate orderings that were obtained using signatures of order 4 in Navarro et al. (2008b). The bold (thick line) arrows indicate new orderings obtained in the present paper that cannot be obtained from signatures of order $4$. Now, we know that the orderings given in these figures are all the distribution-free ordering relationships in the IID case and that systems not connected are not ordered in the IID case (for all $F$). Notice that, it may happen that some systems be ordered for some specific distribution functions (e.g., for a degenerate distribution $F$, all the systems are equal in law and so they are LR ordered). The ordering properties obtained from Proposition 3.1(i), for the ST order are exactly the same as that obtained in Figure 1 of Navarro et al. (2008b) using signatures of order $4$. Now, we know that there are no more ST orderings between these systems in the IID case (for all $F$).

Fig. 2

Hazard rate orderings for all the coherent systems with 1–4 IID components

Fig. 3

Likelihood ratio orderings for all the coherent systems with 1–4 IID components

To obtain the analogous results for the RHR order we need to use that, under the assumption of IID component lifetimes, it is well known (see, e.g., Navarro et al. 2007) that the distribution function $F_T$ of a coherent system with lifetime $T$ can be written as

$$\begin{aligned} F_T(t)=b_1F_{1:1}(t)+\cdots +b_n F_{n:n}(t) \end{aligned}$$

(3.5)

for all $t$, where $b_1,\ldots ,b_n$ are some coefficients (which can be negative) and $F_{i:i}(t)=\Pr (X_{i:i}\le t)$ is the distribution function of the parallel system obtained with the first $i$ components whose lifetime is $X_{i:i}=\max (X_1,\ldots ,X_i)$ for $i=1,\ldots ,n$. The vector $\mathbf {b}=(b_1,\ldots ,b_n)$ with the coefficients in representation (3.5) was called in Navarro et al. (2007) the maximal signature of the system. Obviously, the representation in (3.5) is a generalized mixture. Again, notice that if we want to compare $T$ with another system with $m>n$ components, then we can just add zeros to representation (3.5) obtaining the maximal signature $\mathbf {b}^{(m)}$ of order $m$ given by the $m$-dimensional vector $\mathbf {b}^{(m)}=(b_1,\ldots ,b_n,0,\ldots ,0)$. The same representation (3.5) holds for mixed systems which are mixtures of coherent systems. To compute maximal signatures, we can use that the maximal signature of a coherent system coincides (see Navarro et al. 2007) with the minimal signature of its dual system (i.e., the system obtained by changing $\min$ by $\max$ and vice versa in the expression for the system’s lifetime). Thus, for example, as the systems considered in Example 3.1 are dual systems, then their respective maximal signatures are $(1,0,1,-1)$ and $(0,3,-3,1)$.

Under the IID assumption, it is well known that $F_{i:i}(t)=F^i(t)$, where $F$ is the common components’ distribution function. Hence, the PRHR model holds for representation (3.5) with $\alpha _i=i$ for $i=1,\ldots ,n$. Thus, from the results given in the preceding section, we can obtain the following proposition.

Proposition 3.2

Let $T_1$ and $T_2$ be the lifetimes of two coherent (or mixed) systems with maximal signatures of order $n$, $(p_1,\ldots ,p_n)$ and $(q_1,\ldots ,q_n)$. Assume that both systems are based on IID components having a common absolutely continuous distribution $F$. Then:

• (i) $T_1 \le _\mathrm{ST} T_2$ holds for all $F$ if, and only if,

  $$\begin{aligned} \sum _{i=1}^{n} (p_i-q_i)x^{i}\ge 0 \quad \text { for all } \quad x\in (0,1). \end{aligned}$$

  (3.6)

• (ii) $T_1 \le _\mathrm{RHR} T_2$ holds for all $F$ if and only if,

  $$\begin{aligned} \sum _{i=1}^{n-1} \sum _{j=i+1}^n (j-i)(p_iq_j-p_jq_i) x^{i+j-2}\ge 0\quad \text { for all } \quad x\in (0,1). \end{aligned}$$

  (3.7)

• (iii) $T_1 \le _\mathrm{LR} T_2$ holds for all $F$ if, and only if,

  $$\begin{aligned} \sum _{i=1}^{n-1} \sum _{j=i+1}^n ij(j-i)(p_iq_j-p_jq_i) x^{i+j-2}\ge 0 \quad \text { for all } \quad x\in (0,1). \end{aligned}$$

  (3.8)

As an immediate consequence, we obtain that two coherent systems with lifetimes $T_1$ and $T_2$ satisfy $T_1\le _\mathrm{RHR}T_2$ if and only if $T_2^D\le _\mathrm{HR}T^D_1$, where $T^D_1$ and $T^D_2$ are the lifetimes of their dual systems (a well-known fact).

The final example shows that this technique can also be used to compare more complex (real) systems with many components whenever we are able to obtain their representations as negative mixtures of series or parallel systems.

Example 3.2

Let us consider two consecutive linear $k$-out-of-$n$:$F$ systems. These systems have $n$ linearly ordered components and they fail when (at least) $k$ consecutive components fail. They are used in practice to model oil/water pipeline (and other similar) transportation systems. Let us assume that, in a specific path, we have two options. In the first one, the transportation system can be built using $n=8$ components and the system fails when $k=4$ consecutive components fails. In the second one, it can be built using $n=10$ components and the system fails when $k=6$ consecutive components fails. Which system is the best option? We assume that the component lifetimes in both systems are IID with a common absolutely continuous distribution $F$. We denote the respective system lifetimes by $T_1$ and $T_2$. It is well known (see, e.g., expression (2.2) in Navarro and Eryilmaz 2007) that the distribution function $F_{k|n:F}$ of a consecutive linear $k$-out-of-$n$:$F$ system with IID components and $k\ge n/2$ can be written as the following negative mixture

$$\begin{aligned} F_{k|n:F}(t)=(n-k+1) F_{k:k}(t)-(n-k)F_{k+1:k+1}(t). \end{aligned}$$

Therefore, the distributions of the two systems considered above can be written as

$$\begin{aligned} F_{T_1}(t)=5F_{4:4}(t)-4F_{5:5}(t) \end{aligned}$$

and

$$\begin{aligned} F_{T_2}(t)=5F_{6:6}(t)-4F_{7:7}(t). \end{aligned}$$

In this case, we can study if they are LR ordered by computing the polynomial in (3.8) which gives

$$\begin{aligned} \overline{v}(x)=1200x^8-2280x^9+1120x^{10}. \end{aligned}$$

This polynomial is nonnegative in $(0,1)$ (the only root is $x=0$) and so $T_1\le _\mathrm{LR}T_2$ holds for all $F$.

4 Comparisons of coherent systems with independent components

If $T$ is the lifetime of a coherent system with components having independent lifetimes $X_1,\ldots ,X_n$, then from (1) in Agrawal and Barlow (1984) (see also (3.1) in Block et al. 2003), its reliability function can be written as

$$\begin{aligned} \overline{F}_T(t)= \sum _{i=1}^r \overline{F}_{P_i}(t)-\sum _{i=1}^{r-1} \sum _{j=i+1}^r \overline{F}_{P_i\cup P_j}(t)+\cdots +(-1)^{r+1} \overline{F}_{P_1\cup \cdots \cup P_r}(t), \end{aligned}$$

(4.1)

where $\overline{F}_{P}(t)=\Pr (X_P>t)$ is the reliability function of the series system with components in $P$ with lifetime $X_P=\min _{j\in P}X_j$ for $P\subseteq \{1,\ldots ,n\}$ and where $P_1,\ldots ,P_r$ are the minimal path sets of the system (see page 9 in Barlow and Proschan 1975). A path set is a set of indexes $P\subseteq \{1,\ldots ,n\}$ such that if all the components in $P$ work, then the system works. A path set $P$ is a minimal path set if it does not contain other path sets. Obviously, representation (4.1) is a generalized mixture.

If the components are independent, then

$$\begin{aligned} \overline{F}_{P}(t)=\Pr (X_P>t)=\Pr (\min _{j\in P}X_j>t)=\prod _{j\in P}\overline{F}_j(t), \end{aligned}$$

(4.2)

where $\overline{F}_j(t)=\Pr (X_j>t)$ is the reliability function of component $j$, for $j=1,\ldots ,n$. Unfortunately, this condition is not enough to assure that the distributions used in representation (4.1) are ordered (see, e.g., Navarro and Rubio 2012). Hence, we need some additional assumptions. Thus, we can assume that the components satisfy the PHR model, that is, $\overline{F}_j=\overline{G}^{\beta _j}$ for $j=1,\ldots ,n$, where $\overline{G}$ is a baseline reliability function and $\beta _j>0$ for $j=1,\ldots ,n$. Hence, the distributions in representation (4.1) also satisfy the PHR model and the reliability function of the system can be written as

$$\begin{aligned} \overline{F}_T(t)= \sum _{i=1}^k p_i \overline{G}_i(t), \end{aligned}$$

(4.3)

where $\overline{G}_i(t)=\overline{G}^{\alpha _i}(t)$ for $j=1,\ldots ,n$, for appropriate coefficients $\alpha _1,\ldots ,\alpha _k>0$. The same holds for non-coherent systems (see Borgonovo 2010). Hence, Propositions 2.6 and 2.7 can be applied jointly with representation (4.3) to obtain comparison results for coherent systems. As in the preceding section, we note that in representation (4.3) we can add zeros when it is needed to assure that both systems have a generalized mixture representation based on the same baseline distributions. Let us see an example.

Example 4.1

Let us consider the coherent system with lifetime $T=\min (X_1,$ $\max (X_2,X_3))$, where we assume that $X_1,X_2,X_3$ are independent with absolutely continuous distributions $F_1,F_2,F_3$. We want to compare this system with a 2-out-of-3 system (i.e., a system which works if at least two of its three components work). Its lifetime coincides with the second-order statistic $X_{2:3}$ from $X_1,X_2,X_3$. As $T\le X_{2:3}$, then from Theorem 1.A.1 in Shaked and Shanthikumar (2007), we have $T\le _\mathrm{ST}X_{2:3}$ for any $F_1,F_2,F_3$. So, we want to study if this ordering holds for the HR order and/or the LR order. The minimal path sets of $T$ are $\{1,2\}$ and $\{1,3\}$. Therefore, from (4.1) and (4.2), its reliability function can be written as

$$\begin{aligned} \overline{F}_{T}(t)=\overline{F}_1(t)\overline{F}_2(t)+\overline{F}_1(t)\overline{F}_3(t)-\overline{F}_1(t)\overline{F}_2(t)\overline{F}_3(t). \end{aligned}$$

Analogously, the minimal path sets of $X_{2:3}$ are $\{1,2\},\{1,3\}$ and $\{2,3\}$ (all the subsets of $\{1,2,3\}$ with cardinality 2). Therefore, from (4.1) and (4.2), its reliability function can be written as

$$\begin{aligned} \overline{F}_{2:3}(t)=\overline{F}_1(t)\overline{F}_2(t)+\overline{F}_1(t)\overline{F}_3(t) +\overline{F}_2(t)\overline{F}_3(t)-2\overline{F}_1(t)\overline{F}_2(t)\overline{F}_3(t). \end{aligned}$$

Now, we can assume that the components satisfy the PHR model, that is, $\overline{F}_j=\overline{G}^{\beta _j}$ for $j=1,2,3$, where $\overline{G}$ is a baseline reliability function and $\beta _j>0$ for $j=1,2,3$. Hence, the systems’ reliability functions can be represented as in (4.3) with $\alpha _1=\beta _1+\beta _2$, $\alpha _2=\beta _1+\beta _3$, $\alpha _3=\beta _2+\beta _3$, and $\alpha _4=\beta _1+\beta _2+\beta _3$, with the following coefficients: $p_1=1$, $p_2=1$, $p_3=0$ and $p_4=-1$ (for $T$) and $q_1=1$, $q_2=1$, $q_3=1$ and $p_4=-2$ (for $X_{2:3}$). Then, from Proposition 2.6, $T\le _\mathrm{HR}X_{2:3}$ holds for all $\overline{G}$ if and only if the weights satisfy (2.8). A straightforward calculation shows that this condition is equivalent to

$$\begin{aligned} r(x)=\beta _3x^{\beta _2}(x^{\beta _1}-1)+\beta _2x^{\beta _3}(x^{\beta _1}-1) +\beta _1(x^{\beta _2}+x^{\beta _3}-x^{\beta _2+\beta _3})\ge 0 \end{aligned}$$

for all $x\in (0,1)$.

For example, if $\beta _i=i$ for $i=1,2,3$, then

$$\begin{aligned} r(x)=x^2(-2+2x+2x^2-x^3). \end{aligned}$$

This function takes positive and negative values for $x\in (0,1)$ with a root at $x_0\cong 0.68889$. Hence, these systems are not HR ordered for all $\overline{G}$. Their hazard rate functions for the case $\overline{G}(t)=\exp (-t)$, $t\ge 0$ (exponential baseline distribution), can be seen in Fig. 4 (left). In this case, they are not HR ordered. However, if $\beta _1=3$, $\beta _2=2$ and $\beta _3=1$, then

$$\begin{aligned} r(x)=x(1+2x-3x^2+2x^3+x^4). \end{aligned}$$

This function is nonnegative for all $x\in (0,1)$. Hence, $T\le _\mathrm{HR}X_{2:3}$ holds for any $\overline{G}$. Their hazard rate functions for the case $\overline{G}(t)=\exp (-t)$, $t\ge 0$ (exponential baseline distribution), can be seen in Fig. 4 (right). In this case, we can study if they are also LR ordered using the condition in (2.9) which is equivalent to

$$\begin{aligned} v(x)=30x^{6}+12x^{5}+30x^{9}+48x^{8}-54x^{7}\ge 0 \end{aligned}$$

for all $x\in (0,1)$. By plotting this function we see that it is nonnegative in $(0,1)$ and hence we have $T\le _\mathrm{LR}X_{2:3}$ for any $\overline{G}$ when $\beta _1=3$, $\beta _2=2$ and $\beta _3=1$.

Fig. 4

Plots of the hazard rate functions for the systems in Example 4.1 when $\beta _1=1, \beta _2=2$ and $\beta _3=3$ (left) $\beta _1=3,\beta _2=2$ and $\beta _3=1$ (right)

5 Comparisons of general coherent systems

Let $T$ be the lifetime of a coherent system with possibly dependent components having lifetimes $X_1,\ldots ,X_n$ with a joint reliability function

$$\begin{aligned} {\overline{\mathbf{F}}}(x_1,\ldots ,x_n)=\Pr (X_1>x_1,\ldots ,X_n>x_n). \end{aligned}$$

Then, the reliability function of $T$ can be written as in (4.1) (see (3.4) in Navarro et al. 2008a), where, in this case, $\overline{F}_{P}(t)=\Pr (X_P>t)$ can be computed as

$$\begin{aligned} \overline{F}_{P}(t)={\overline{\mathbf{F}}}\left( t^P_1,\ldots ,t^P_n\right) \end{aligned}$$

where $t^P_i=t$ if $i\in P$ and $t^P_i=0$ if $i\notin P$. Obviously, again (4.1) is a generalized mixture representation.

If the joint distribution of $(X_1,\ldots ,X_n)$ is exchangeable (i.e., ${\overline{\mathbf{F}}}$ is permutation invariant), then representation (4.1) can be simplified to (3.1), where

$$\begin{aligned} \overline{F}_{1:i}(t)={\overline{\mathbf{F}}}(\underbrace{t,\ldots ,t}_{i-\mathrm{times}},\underbrace{0,\ldots ,0}_{(n-i)-\mathrm{times}}). \end{aligned}$$

Hence, if

$$\begin{aligned} \overline{F}_{1:1}\ge _\mathrm{HR} \cdots \ge _\mathrm{HR} \overline{F}_{1:n} \end{aligned}$$

(5.1)

holds, then condition (2.5) in Proposition 2.3 holds. Therefore, this proposition and representation (3.1) can be used to compare two coherent systems in the HR ordering. Analogously, if

$$\begin{aligned} \overline{F}_{1:1}\ge _\mathrm{LR} \cdots \ge _\mathrm{LR} \overline{F}_{1:n} \end{aligned}$$

(5.2)

holds then condition (2.7) in Proposition 2.4 holds. Hence, this proposition and representation (3.1) can be used to compare two coherent systems in the LR ordering. Let us see an example. However, (5.1) and (5.2) are not necessarily true as can be seen in Navarro and Shaked (2006) and Navarro (2008), respectively. So, we need to assume them to obtain ordering properties.

Example 5.1

Let us consider again the coherent systems studied in Example 4.1. We assume that they have components with lifetimes $X_1,X_2,X_3$ having a common exchangeable distribution. The minimal signature of $T=\min (X_1, \max (X_2,X_3))$ is $\mathbf {p}=(0,2,-1)$ (see, e.g., line 5, in Table 1 of Navarro and Rubio 2011) and that of $X_{2:3}$ is $\mathbf {q}=(0,3,-2)$ (see, e.g., line 6, in Table 1 of Navarro and Rubio 2011). To study if the condition in Proposition 2.4 holds, we compute the following table:

$p_iq_j$	$q_1=0$	$q_2=3$	$q_3=-2$
$p_1=0$	0	0	0
$p_2=3$	0	6	$-4$
$p_3=-2$	0	$-3$	2

Thus, we see that $p_iq_j \le p_jq_i$ for all $1\le i\le j\le k$ and hence, from Proposition 2.4, we have $T\le _\mathrm{LR}X_{2:3}$ for any exchangeable distribution such that (5.2) holds. Analogously, from Proposition 2.3, we have $T\le _\mathrm{HR}X_{2:3}$ for any exchangeable distribution such that (5.1) holds. These ordering properties were already obtained in Figures 2 and 3 of Navarro et al. (2008b) using signatures and assuming that the order statistics are HR or LR ordered (respectively). We must note that the conditions in Propositions 2.3 and 2.4 are not necessary conditions for the HR and LR orderings. Thus, sometimes, we can obtain better HR or LR ordering results using the procedures given in Navarro et al. (2008b) and Navarro and Rubio (2011) for the exchangeable case under the assumption that the order statistics are HR or LR ordered.

The general representation obtained from (4.1) can also be used to obtain ordering properties whenever the baseline distributions in this generalized mixture representation are HR (or LR) ordered. Let us see an example.

Example 5.2

Let us consider again the coherent system studied in Example 4.1 with lifetime $T=\min (X_1, \max (X_2,X_3))$. We want to compare it with the series system with lifetime $X_{1:3}=\min (X_1,X_2,X_3)$. The representation obtained from (4.1) for the reliability of $T$ is

$$\begin{aligned} \overline{F}_T(t)=\overline{F}_{\{1,2\}}(t)+\overline{F}_{\{1,3\}}(t)-\overline{F}_{1:3}(t). \end{aligned}$$

This is a generalized mixture representation with baseline reliability functions $\overline{F}_{\{1,2\}}$, $\overline{F}_{\{1,3\}}$ and $\overline{F}_{1:3}$ and coefficients $q_1=1$, $q_2=1$, and $q_3=-1$. Obviously, the reliability function of the series system $X_{1:3}$ is obtained with the coefficients $p_1=p_2=0$ and $p_3=1$. To see if the condition in Proposition 2.4 holds, we compute the following table:

$p_iq_j$	$q_1=1$	$q_2=1$	$q_3=-1$
$p_1=0$	0	0	0
$p_2=0$	0	0	0
$p_3=1$	1	1	$-$1

As the condition holds, we obtain $X_{1:3}\le _\mathrm{LR}T$ for any joint distribution such that $F_{\{1,2\}}\ge _\mathrm{LR}F_{\{1,3\}}\ge _\mathrm{LR}F_{1:3}$ holds. Obviously, a similar property is obtained if $F_{\{1,3\}}\ge _\mathrm{LR}F_{\{1,2\}}\ge _\mathrm{LR}F_{1:3}$ holds. Analogously, from Proposition 2.3, we obtain $X_{1:3}\le _\mathrm{HR}T$ for any joint distribution such that $F_{\{1,2\}}\ge _\mathrm{HR}F_{\{1,3\}}\ge _\mathrm{HR}F_{1:3}$ holds.

The two examples above show that it is important to have HR and LR ordering properties of series systems. These properties were studied in Navarro and Shaked (2006) and Navarro (2008), respectively. The HR ordering properties are related with monotonicity properties of the hazard gradient of ${\overline{\mathbf{F}}}$ (see Theorem 2.1 in Navarro and Shaked 2006). Thus, for example, $F_{\{1,3\}}\ge _\mathrm{HR}F_{1:3}$ holds if and only if ${\overline{\mathbf{F}}}(t,0,t)/{\overline{\mathbf{F}}}(t,t,t)$ is increasing. Proceeding as in Proposition 2.3, it is easy to see that this property holds when $h_i(t,0,t)\le h_i(t,t,t)$ for $i=1,3$, where $\mathbf {h}=(h_1,h_2,h_3)$ is the hazard gradient of ${\overline{\mathbf{F}}}$ and

$$\begin{aligned} h_i(x_1,x_2,x_3)=-\frac{D_i{\overline{\mathbf{F}}}(x_1,x_2,x_3)}{{\overline{\mathbf{F}}}(x_1,x_2,x_3)}, \quad i=1,2,3. \end{aligned}$$

6 Conclusions

In this paper, conditions for stochastic comparisons of generalized mixtures are obtained. Specific conditions are obtained for mixtures under the proportional hazard rate and the proportional reversed hazard rate models. These theoretical results are applied to obtain new distribution-free conditions to get comparisons of coherent systems under different assumptions. The comparisons obtained improve the results obtained using classical (positive) mixtures. The results on generalized mixtures can be used to compare other statistical concepts which can also be represented as generalized mixtures.