An importance learning method for non-probabilistic reliability analysis and optimization

Abstract

With the time-consuming computations incurred by nested double-loop strategy and multiple performance functions, the enhancement of computational efficiency for the non-probabilistic reliability estimation and optimization is a challenging problem in the assessment of structural safety. In this study, a novel importance learning method (ILM) is proposed on the basis of active learning technique using Kriging metamodel, which builds the Kriging model accurately and efficiently by considering the influence of the most concerned point. To further accelerate the convergence rate of non-probabilistic reliability analysis, a new stopping criterion is constructed to ensure accuracy of the Kriging model. For solving the non-probabilistic reliability-based design optimization (NRBDO) problems with multiple non-probabilistic constraints, a new active learning function is further developed based upon the ILM for dealing with this problem efficiently. The proposed ILM is verified by two non-probabilistic reliability estimation examples and three NRBDO examples. Comparing with the existing active learning methods, the optimal results calculated by the proposed ILM show high performance in terms of efficiency and accuracy.

1 Introduction

Structural design optimization plays a prominent role in practical engineering analysis, which aims to provide an optimal design within specified objective functions and constraints. However, the uncertainties stemming from its environment and incomplete knowledge about the examined system are unavoidable, and how to account for them is of great importance for optimization design (Li and Azarm 2008; Moon et al. 2018; Wang and Wang 2012). This can promote the development of non-deterministic structural optimization method, in which probabilistic approach and non-probabilistic approach are two representative methods (Huang et al. 2016b; Keshtegar and Lee 2016; Lee et al. 2013; Youn et al. 2005). The former is dedicated to performing the optimization design for uncertain structures, whose input random parameters can be described as the precise probabilistic distribution (Azarm and Mourelatos 2006; Du and Chen 2004; Rashki et al. 2014; Youn and Wang 2008). The latter focuses on handling the optimization design with uncertain-but-bounded variables (Jiang et al. 2007; Qiu et al. 2009). Unfortunately, it is commonly difficult to acquire enough experimental data in the complex engineering problems for constructing the probabilistic model, and thus non-probabilistic approach becomes a promising way to qualify the safety level of structures with inherent uncertain factors (Bae et al. 2018; Karuna and Manohar 2017; Moens and Vandepitte 2006). Until now, a variety of non-probabilistic models were proposed, which can be generally divided into two types, interval model (Elishakoff and Elettro 2014; Liu et al. 2016; Muscolino et al. 2016) and convex model (Ganzerli and Pantelides 2000; Jiang et al. 2014).

Currently, the research interests in the non-probabilistic theory can be traced to Ben-Haim and Elishakoff’s pioneering research (Ben-Haim 1994; Ben-Haim 1995; Ben-Haim and Elishakoff 1995), in which an effective tool for assessing structural safety level with limited sample information was developed. Qiu and Elishakoff (1998) introduced the interval analysis to carry out non-probabilistic reliability-based design optimization (NRBDO) successfully for a 6-bar plane truss. Majumder and Rao (2009) established a multi-objective optimization method for minimizing structural weight and energy required of aircraft wing structures with interval parameters. Moens and Vandepitte (2006) gave an exhaustive overview for non-deterministic method and pointed out that the non-probabilistic approach appears to be less sensitive to the effect of subjective data by comparing with the probabilistic approach. Additionally, the definition of non-probabilistic reliability index was also established, which is more conservative in comparison to the probabilistic model (Guo et al. 2013; Jiang et al. 2017; Kang and Luo 2010).

For complex engineering problems, the computations of the performance functions are always time-consuming; the pursuit of high efficiency for computing the non-probabilistic reliability indices is vital in real-life engineering problems. Until now, various advanced methods for non-probabilistic reliability analysis have been well introduced to improve the computational efficiency. Based on worst-case-scenario technique, Lombardi and Haftka (1998) utilized the inverse optimization technique to enhance the efficiency of optimization with load uncertainties. Kang et al. (2011) introduced a concerned performance approach to alleviate the unbearable computational burden, which was further extended to solve a topology optimization problem (Kang and Zhang 2016). Luo et al. (2011) established a sequential approximate programming method for solving the hybrid model involving the probabilistic and non-probabilistic uncertain parameters simultaneously. Moreover, Meng et al. (2015) developed a chaos control method to estimate the concerned point of ellipsoid convex model, and the computational efficiency was improved significantly for buckling analysis of stiffened shells. Hao et al. (2017) investigated the Wolfe-Powell criterion to select a suitable chaos control factor in chaos control method. Based upon a super parametric convex model, Meng and Zhou (2018) also created a new target performance approach to efficiently evaluate the non-probabilistic reliability of structures.

Recently, some approximate mathematical models, i.e., metamodels, are popular as surrogates for improving the efficiency of non-probabilistic reliability calculation through substituting into the actual performance functions. Jiang et al. (2008) presented a sequential computation method for handing the interval parameters, in which the Latin hypercube sampling (LHS) and response surface method (RSM) are combined together to evaluate the intervals of constraints. Based on the moving least square method with function data, Youn and Choi (2004) integrated the RSM to accelerate the convergence rate of performance function. Wang and Chen (2017) suggested an adaptive extreme RSM for solving time-variant reliability analysis problems. Bai et al. (2014) combined RSM with convex model to perform the correlation analysis technique. Zhang et al. (2017) employed RSM-based time-dependent reliability estimation technique, which can decrease the number of function calls to estimate the reliability of stochastic dynamic structures. Marelli and Sudret (2018) created an active learning method for polynomial chaos expansions based on bootstrap resampling.

Compared with RSM surrogate model, the Kriging model not only can give predicted values for any input variables but also can estimate the local variance owing to its stochastic process property (Hawchar et al. 2018; Huang et al. 2016a). Based on this variance, the Kriging model can carry out the design of experiments (DoE) in an active learning manner, which can be considered as a major advantage of Kriging. The efficient global optimization and sequential Kriging-based optimization are considered as two distinguished representatives (Bichon et al. 2012; Huang et al. 2006; Jones et al. 1998). Inspired from the efficient global optimization and the contour assessment method of Ranjan et al. (2008), Bichon et al. (2012) developed a fully active learning method to implement the probabilistic reliability analysis, and then it was further extended to solve the system reliability problems with multiple failure modes (Bichon et al. 2011). Khodaparast et al. (2011) applied the Kriging for interval model updating, which was able to predict the regions of input and output uncertain parameters. Wang and Wang (2013) suggested a maximum confidence enhancement method, in which an ordinary Kriging model was employed to speed up the calculation process. Hu and Du (2015) applied the Kriging model to compute the reliability index of the time-variant problems. Lee and Jung (2008) constructed a constraint boundary sampling (CBS) criterion to sequentially add new points in the vicinity of the limit state function (LSF). Echard et al. (2011) suggested an active learning reliability method combining the Kriging model and Monte Carlo simulation, in which a new learning function U is created to efficiently predict the sign of performance functions (Echard et al. 2013). Moustapha et al. (2016) established a two stage procedure to enhance the local and global accuracies of function U. Chen et al. (2014) presented a local adaptive sampling strategy, which can generate new sample points around the design point to construct the Kriging model. Moreover, Yang et al. (2015) developed an expected risk function (ERF) by using expected improvement function to approximate the sign of performance functions, and then the failure probability can be easily calculated (Yang et al. 2014). Also, Li et al. (2006) utilized the Kriging variance for dealing with the multi-objective problems. All these active learning methods devoted to improving the computational efficiency of failure probability in probabilistic domain, but rare works can be found to solve the NRBDO problem. Besides, the existing active learning methods only consider the predicted value and variance, which means the samples on the LSF have the same opportunity to be selected. However, the most concerned point (MCP), i.e., the most important point on the LSF, is ignored during the learning process. Therefore, it requires a large amount of samples to approximate the entire LSF accurately. If the new samples are generated only in the local region around the MCP, the convergence rate can be significantly improved.

The purpose of this paper is to investigate the performance of the active learning methods in the non-probabilistic reliability estimation and NRBDO problems, and an importance learning method (ILM) is further developed to enhance the efficiency. By considering the influence of MCP during DOE, the task of predicted the entire LSF is degraded into the simple prediction of MCP. A Kriging model is first constructed with a rather small set of sample points and then is progressively rebuilt using the proposed importance learning function (ILF). In each iterative step, only the local region at the neighborhood of the MCP is approximated accurately. Then, the new sample points are adaptively added into DOE. Furthermore, a novel active learning function based on the ILF is established to solve the NRBDO problems with multiple LSFs. The outline of this paper is presented as follows: Sect. 2 reviews the basic theory of the non-probabilistic reliability estimation. Section 3 introduces fundamental of the Kriging model and several popular active learning functions. Then, the proposed method is described in detail in Sect. 4. Section 5 uses two non-probabilistic reliability estimation examples and two NRBDO examples to verify the accuracy and efficiency of the proposed method. In Sect. 5, some concluding remarks are drawn.

2 Review of non-probabilistic reliability analysis

2.1 Convex model

A n-dimensional interval model is one widely utilized non-probabilistic model, which can be described as a rectangle, as shown in Fig. 1a (Kang et al. 2011). The interval model is formulated as follows,

$$ E=\left\{\mathbf{x}|{x}_1^2\le {\varepsilon}_1^2,\dots, {x}_{\mathrm{i}}^2\le {\varepsilon}_{\mathrm{i}}^2,\dots, {x}_{\mathrm{n}}^2\le {\varepsilon}_{\mathrm{n}}^2\right\} $$

(1)

where n is the number of uncertain-but-bounded variables x. ε_i is the radius of interval, which can be determined by its upper bound ${x}_{\mathrm{i}}^{\mathrm{L}}$ and lower bound ${x}_{\mathrm{i}}^{\mathrm{U}}$. The value of ε_i can be computed by ${\varepsilon}_{\mathrm{i}}=\frac{x_{\mathrm{i}}^{\mathrm{U}}-{x}_{\mathrm{i}}^{\mathrm{L}}}{2}$.

Fig. 1

Two types non-probabilistic parameter models: a Interval model {‖q_i‖ ≤ 1, i = 1, 2, 3}. b Ellipsoid model {‖q₁, q₂, q₃‖ ≤ 1}

A n-dimensional ellipsoid model is another popular non-probabilistic to handle the uncertain-but-bounded parameters, as shown in Fig. 1b (Jiang et al. 2013). The ellipsoid model is described as follows,

$$ E=\left\{\mathbf{x}|{\left(\frac{\mathbf{x}-{\mathbf{x}}^{\mathrm{C}}}{{\mathbf{x}}^{\mathrm{C}}}\right)}^{\mathrm{T}}\mathbf{W}\left(\frac{\mathbf{x}-{\mathbf{x}}^C}{{\mathbf{x}}^C}\right)\le {\varepsilon}^2\right\} $$

(2)

where x^C is a vector of the nominal values. The uncertain parameter vector contains n variables {x₁, x₂, …, x_n}. W is a characteristic matrix of the ellipsoid model, which is a real symmetric positive definite matrix. ε is the radius of the ellipsoid model, which is similar to the interval model. The diagonal elements of W contain the information of the reference variation coefficients of uncertain variables, while non-diagonal elements represent the correlation relationship between different variables. In general, the matrix W and the number ε can be determined according to the instrument measurements, where the minimum volume method can be used to compute their values (Jiang et al. 2011; Kang and Zhang 2016). Especially, when the uncertain variables are independent, all the non-diagonal elements of W become 0. The radius of ith nominal value x_i can be obtained by the following transformation: ${x}_{\mathrm{i}}^{\mathrm{r}}=\frac{x_{\mathrm{i}}^{\mathrm{C}}}{\sqrt{W_{\mathrm{i}\mathrm{i}}}}$, where W_ii is ith diagonal element of W.

There are various uncertain sources in practical engineering, and the ellipsoid model is another promising convex model. To implement the non-probabilistic reliability analysis conveniently, the uncertain-but-bounded vector x can be transformed into a dimensionless uncertain vector δ that can be expressed as,

$$ \mathbf{x}=\left(1+\boldsymbol{\updelta} \right)\cdot {\mathbf{x}}^{\mathrm{C}} $$

(3)

When eigenvalue decomposition is implemented for the characteristic matrix W, an eigenvector Q and eigenvalue matrix Λ can be obtained accordingly. Then, the uncertain variables vector x can be easily converted into the normalized uncertain variables vector q using the following formula,

$$ \mathbf{q}=\left(1/\varepsilon \right){\boldsymbol{\Lambda}}^{1/2}{\mathbf{Q}}^{\mathrm{T}}\boldsymbol{\updelta} \kern0.2em $$

(4)

Through the above normalized transformation, the ellipsoid model in (2) can be rewritten as,

$$ E=\left\{{\mathbf{q}}^{\mathrm{T}}\mathbf{q}\le 1\right\} $$

(5)

Thus, the ellipsoid is converted into spheres with unit radius in q-space. Similarly, the normalized uncertain variables vector q can be reversely transformed as uncertain-but-bounded variables vector x through the conversion formula, i.e., x = (1 + ε(Λ^1/2Q^T)⁻¹q) ⋅ x^C.

2.2 Non-probabilistic reliability index

In the structural engineering, the safety level is determined by the non-probabilistic reliability index, which is defined as the max-min distance from the origin to corresponding LSF (G(q) = 0) in q-space. As mentioned in Sect. 2.1, the uncertain-but-bounded variables x are converted into the normalized uncertain variables q, and then the corresponding LSF g(x) is transformed as G(q). The LSF divides the uncertain domain into two parts, i.e., safety domain G(q) ≥ 0 and failure domain G(q) < 0. In the study of Kang et al. (2011), the non-probabilistic reliability index of interval model and ellipsoid model can be obtained by,

$$ \eta =\operatorname{sgn}\left(G(0)\right)\underset{\mathbf{q}:G\left(\mathbf{q}\right)=0}{\min}\left(\max \left(|{q}_1|,...,|{q}_{\mathrm{i}}|,...,|{q}_{\mathrm{n}}|\right)\right) $$

(6)

$$ \eta =\operatorname{sgn}\left(G(0)\right)\underset{\mathbf{q}:\mathrm{G}\left(\mathbf{q}\right)=0}{\min}\left({\mathbf{q}}^{\mathrm{T}}\mathbf{q}\right) $$

(7)

where non-probabilistic reliability index η is called as non-probabilistic reliability index, the optimal solution q^∗ of (7) is defined as the MCP. sgn(⋅) represents the signum function. If G(0) > 0, sgn(G(0)) = 1, else if G(0) < 0, sgn(G(0)) =  − 1 and if G(0) = 0, sgn(G(0)) = 0. When η = 1, it means the unit ellipsoid or interval set is tangent to the limit state surface, and then the critical state is reached. When η > 1, all combinations of uncertain variables are located in the safety domain, meaning the structure is reliable. When 0 ≤ η < 1, some failure events may occur, and the structure is unsafe.

2.3 Non-probabilistic reliability-based design optimization

In NRBDO, the reliability index is selected as the constraint condition. Without loss of generality, the mathematical formulas of NRBDO are typically expressed as,

$$ {\displaystyle \begin{array}{l}\mathrm{find}\kern1.5em \mathbf{d},{\mathbf{x}}^{\mathrm{C}}\\ {}\underset{\mathbf{d}}{\min}\kern1.5em C\left(\mathbf{d},{\mathbf{x}}^{\mathrm{C}}\right)\\ {}\mathrm{s}.\mathrm{t}.\kern2.1em {\eta}_{\mathrm{j}}\left(\mathbf{d},\mathbf{x},\mathbf{p}\right)\ge {\underset{\_}{\eta}}_{\mathrm{j}},\kern1em j=1,2,\dots, m\\ {}\kern3.299999em {\mathbf{d}}^{\left(\mathrm{L}\right)}\le \mathbf{d}\le {\mathbf{d}}^{\left(\mathrm{U}\right)},{\mathbf{x}}^{\mathrm{C}\left(\mathrm{L}\right)}\le {\mathbf{x}}^{\mathrm{C}}\le {\mathbf{x}}^{\mathrm{C}\left(\mathrm{U}\right)}\end{array}} $$

(8)

where d and x represent the deterministic and uncertain design variables, and p is a vector of the uncertain parameters. x^C is the nominal values of x and can be considered as the design variables vector. d^(L) and x^C(L) are the low bounds of d and x^C, while d^(U) and x^C(U) are the corresponding upper bounds. η_j denotes the jth non-probabilistic reliability index, which is estimated by (7). Evidently, the solution of the NRBDO problems consists of double loops, i.e., the inner loop seeks the non-probabilistic reliability constraint at the current design point, while the outer loop updates the design variables based on the results of inner loop. Herein, the sequential quadratic programming technique can be applied to solve the NRBDO problems.

3 Active learning method for Kriging model

3.1 Basic of the Kriging model

For the sake of convenience, the uncertain parameters y are denoted as the input parameters of Kriging. In the Kriging model, the real responses Y = [g(x₁), g(x₂), …, g(x_k)]^T for the kth sample point can be replaced by the approximate response g(x), and it is consisted by a regression part f^T(x)β and a Gaussian process z(x),

$$ g\left(\mathbf{x}\right)={\mathbf{f}}^{\mathrm{T}}\left(\mathbf{x}\right)\boldsymbol{\upbeta} +z\left(\mathbf{x}\right) $$

(9)

where f(x) = [f₁(x), f₂(x), …, f_m(x)]^T is the vector of basis functions. β = [β₁, β₂, …, β_m]^T is the vector of regression coefficients. z(x) is stationary Gaussian process with means zero, and the covariance function for any two sample points x_i and x_j are defined as follows,

$$ \operatorname{cov}\left(z\left({\mathbf{x}}_{\mathrm{i}}\right),z\left({\mathbf{x}}_{\mathrm{j}}\right)\right)={\sigma}_{\mathrm{z}}^2R\left({\mathbf{x}}_{\mathrm{i}},{\mathbf{x}}_{\mathrm{j}}\right) $$

(10)

where R(x_i, x_j) is the correlation function that can be assumed following Gaussian distribution. By using the generalized least square regression, the regression coefficients and the process variance can be assessed by,

$$ \boldsymbol{\upbeta} ={\left({\mathbf{F}}^{\mathrm{T}}{\mathbf{R}}^{-1}\mathbf{F}\right)}^{-1}{\mathbf{F}}^{\mathrm{T}}{\mathbf{R}}^{-1}\mathbf{Y} $$

(11)

$$ {\widehat{\sigma}}_{\mathrm{z}}^2=\frac{1}{k}{\left(\mathbf{Y}-\mathbf{F}\boldsymbol{\upbeta } \right)}^{\mathrm{T}}{\mathbf{R}}^{-1}\left(\mathbf{Y}-\mathbf{F}\boldsymbol{\upbeta } \right) $$

(12)

where F is a matrix with F_ij = f_j(x_i),   i = 1, 2, …, k,  j = 1, 2, …, m.

Once the Kriging model is built successfully, a best linear unbiased predictor and Kriging variance for any unknown point x₀ can be evaluated using the following formulas,

$$ \widehat{g}\left({\mathbf{x}}_0\right)={\mathbf{f}}^{\mathrm{T}}\left({\mathbf{x}}_0\right)\boldsymbol{\upbeta} +{\mathbf{r}}_0^{\mathrm{T}}{\mathbf{R}}^{-1}\left(\mathbf{Y}-\mathbf{F}\boldsymbol{\upbeta } \right) $$

(13)

$$ {\widehat{\sigma}}_{\widehat{g}}^2\left({\mathbf{x}}_0\right)={\widehat{\sigma}}^2\left(1+{\mathbf{u}}^{\mathrm{T}}{\left({\mathbf{F}}^{\mathrm{T}}{\mathbf{R}}^{-1}\mathbf{F}\right)}^{-1}\mathbf{u}-{\mathbf{r}}_0^{\mathrm{T}}{\mathbf{R}}^{-1}{\mathbf{r}}_0\right) $$

(14)

where r₀ = [R(x₀, x₁), R(x₀, x₂), …, R(x₀, x_k)]^T and u = F^TR⁻¹r₀ − f(x₀).

The Kriging Toolbox DACE (Lophaven et al. 2002) is used to build the Kriging model in this study, which can provide the important predicted values ${\widehat{\sigma}}_{\widehat{g}}^2\left({\mathbf{x}}_0\right)$ for $\widehat{g}\left({\mathbf{x}}_0\right)$. Benefiting from the advantage of the Kriging variance, the active learning technique is widely developed to alleviate the heavy computational burden in probabilistic domain.

3.2 Expected feasibility function

In reliability analysis, the prediction of the LSF is crucial. An expected feasibility function (EFF) can be applied to give an indication for the actual values of the performance functions, which is expected to satisfy the equality constraints g(x) = a in efficient reliability analysis method (Bichon et al. 2008). The EFF makes a trade-off between exploiting the random space with good results and exploring the random space with higher variance of the Kriging model for the LSF. It can be formulated as follows,

$$ {\displaystyle \begin{array}{l}\mathrm{EFF}\left(\widehat{g}\left(\mathbf{x}\right)\right)=\left(\widehat{g}\left(\mathbf{x}\right)-a\right)\left[2\Phi \left(\frac{a-\widehat{g}\left(\mathbf{x}\right)}{{\widehat{\sigma}}_{\widehat{g}}\left(\mathbf{x}\right)}\right)-\Phi \left(\frac{\left(a-\overline{z}\right)-\widehat{g}\left(\mathbf{x}\right)}{{\widehat{\sigma}}_{\widehat{g}}\left(\mathbf{x}\right)}\right)-\Phi \left(\frac{\left(a+\overline{z}\right)-\widehat{g}\left(\mathbf{x}\right)}{{\widehat{\sigma}}_{\widehat{g}}\left(\mathbf{x}\right)}\right)\right]\\ {}\kern6.399996em -{\widehat{\sigma}}_{\widehat{g}}\left(\mathbf{x}\right)\left[2\phi \left(\frac{a-\widehat{g}\left(\mathbf{x}\right)}{{\widehat{\sigma}}_{\widehat{g}}\left(\mathbf{x}\right)}\right)-\phi \left(\frac{\left(a-\overline{z}\right)-\widehat{g}\left(\mathbf{x}\right)}{{\widehat{\sigma}}_{\widehat{g}}\left(\mathbf{x}\right)}\right)-\phi \left(\frac{\left(a+\overline{z}\right)-\widehat{g}\left(\mathbf{x}\right)}{{\widehat{\sigma}}_{\widehat{g}}\left(\mathbf{x}\right)}\right)\right]\\ {}\kern6.099997em +\left[\Phi \left(\frac{\left(a+\overline{z}\right)-\widehat{g}\left(\mathbf{x}\right)}{{\widehat{\sigma}}_{\widehat{g}}\left(\mathbf{x}\right)}\right)-\Phi \left(\frac{\left(a-\overline{z}\right)-\widehat{g}\left(\mathbf{x}\right)}{{\widehat{\sigma}}_{\widehat{g}}\left(\mathbf{x}\right)}\right)\right]\end{array}} $$

(15)

where Φ(⋅) and ϕ(⋅) are the cumulative distribution function and probability density function, respectively. $\overline{z}$ is proportional to the standard deviation, and the value of $\overline{z}$ is set as $2{\widehat{\sigma}}_{\widehat{g}}^2\left(\mathbf{x}\right)$, which refers to the relevant literature (Echard et al. 2011). Similar to the expected improvement function, the points that the expected performance function value is close to the threshold and points with a large predicted uncertainty ${\widehat{\sigma}}_{\widehat{g}}^2\left(\mathbf{x}\right)$ should be sequentially selected as new points. In the case of non-probabilistic reliability estimation, the threshold value of a is 0, which aims to predict the LSF.

3.3 Expected risk function

Yang et al. (2014) suggested an ERF to improve the predicted accuracy of the LSF by picking out the wrongly predicted point with the largest risk. Then, the efficiency of reliability estimation is improved, and the formulation of ERF is expressed as follows,

$$ \mathrm{ERF}\left(\widehat{g}\left(\mathbf{x}\right)\right)=-\operatorname{sgn}\left(\widehat{g}\left(\mathbf{x}\right)\right)\widehat{g}\left(\mathbf{x}\right)\varPhi \left(-\operatorname{sgn}\left(\widehat{g}\left(\mathbf{x}\right)\right)\frac{\widehat{g}\left(\mathbf{x}\right)}{{\widehat{\sigma}}_{\widehat{g}}\left(\mathbf{x}\right)}\right)+{\widehat{\sigma}}_{\widehat{g}}\left(\mathbf{x}\right)\phi \left(\frac{\widehat{g}\left(\mathbf{x}\right)}{{\widehat{\sigma}}_{\widehat{g}}\left(\mathbf{x}\right)}\right) $$

(16)

where ERF(·) can give the risk degree of the sign of the constraint for any point. Thus, this point is expected to be wrongly predicted by the Kriging model. The larger value of the ERF is, the higher risk of this point will be wrongly predicted. Based on the active learning method, the LSF can be predicted accurately; therefore, the computational cost of reliability analysis will be reduced significantly.

3.4 Learning function U of AK-MCS

Echard et al. (2011) constructed a learning function U to judge which point has the largest probability to be wrongly predicted. The definition is as

$$ U=\frac{\mid \widehat{g}\left(\mathbf{x}\right)\mid }{{\widehat{\sigma}}_{\widehat{g}}\left(\mathbf{x}\right)} $$

(17)

This function U gives more opportunities in the vicinity of predicted LSF rather than those with high Kriging variance ${\widehat{\sigma}}_{\widehat{g}}\left(\mathbf{x}\right)$. The failure probability using function U is assessed slower than that using EFF, and this function converges toward the actual failure probability more quickly for solving probabilistic problems.

3.5 Constraint boundary sampling

The CBS uses the normal probability density function to perform reliability analysis with multiple probabilistic constraints, i.e., g_i(x), i = 1, 2, …, m, in which m is the number of performance functions. The values of the learning function will become large when the sample points are located near the LSF or corresponding predicted values with a large error. The formulation is given as,

$$ \mathrm{CBS}\left(\widehat{g}\left(\mathbf{x}\right)\right)=\Big\{{\displaystyle \begin{array}{l}D\sum \limits_{\mathrm{i}=1}^{\mathrm{m}}\phi \left(\frac{{\widehat{g}}_i\left(\mathbf{x}\right)}{{\widehat{\sigma}}_{{\widehat{g}}_i}\left(\mathbf{x}\right)}\right)\kern2em \mathrm{if}\kern0.24em {\widehat{g}}_{\mathrm{i}}\left(\mathbf{x}\right)\ge 0,\kern1em \forall i\\ {}0\kern7.75em \mathrm{otherwise}\end{array}} $$

(18)

where D denotes the minimum distance from the existing sample points, which is used to make the samples consecutively located on the LSF. In the CBS, when the predicted points are located in the infeasible region, the value of sampling criterion becomes 0. For this reason, the computational efficiency can be further improved by ignoring sample points to construct the LSF in the infeasible region. Meanwhile, the minimum distance D is maximized to ensure the sample uniformly distribution. Although these active learning methods are successfully utilized for assessing the failure probability, the accuracy and efficiency in the non-probabilistic domain remain unknown.

4 The proposed method

4.1 Importance learning method

As above-mentioned, the Kriging model can speed up the reliability estimation and optimization process by replacing the actual performance function, in which the DoE of Kriging model is the key. A series of active learning techniques were developed to predict the LSF, such as the CBS, EFF, and ERF. However, these methods ignore the importance degree of different points on LSF. According to the definition in (7), once the MCP near the LSF is obtained, we can directly compute the non-probabilistic reliability index other than predicting the entire LSF. Therefore, it is more rational to consider the importance degree of the points for an active learning function. As plotted in Fig. 2, when the value of non-probabilistic reliability index of the point q₁ is smaller than that of the q₂, it means the point q₁ is closer to the MCP and more important than the point q₂. Following this concept, the prediction of the LSF is converted to search the MCP, and thus only a small number of samples are required to find this point. This new active learning function is called the ILF, and the formulation is defined as,

$$ \mathrm{ILF}\left(\widehat{g}\left(\mathbf{x}\right)\right)=\frac{1}{\eta \left(\mathbf{x}\right)}\phi \left(\frac{\widehat{g}\left(\mathbf{x}\right)}{\widehat{\sigma}\left(\mathbf{x}\right)}\right) $$

(19)

where η(x) is the value of non-probabilistic reliability index at the current point, and it can be computed by,

$$ \eta \left(\mathbf{x}\right)=\operatorname{sgn}\left(g\left({\mathbf{x}}^{\mathrm{C}}\right)\right)\left(\max \left(\sqrt{F{\left({\mathbf{x}}_1\right)}^{\mathrm{T}}F\left({\mathbf{x}}_1\right)},\sqrt{F{\left({\mathbf{x}}_2\right)}^{\mathrm{T}}F\left({\mathbf{x}}_2\right)},...,\sqrt{F{\left({\mathbf{x}}_{\mathrm{k}}\right)}^{\mathrm{T}}F\left({\mathbf{x}}_{\mathrm{k}}\right)}\right)\right) $$

(20)

where F(·) denotes the transformation from the uncertain-but-bounded variables x into normalized uncertain variables q, which is computed by the mentioned methods in Sect. 2.1. The proposed ILF considers three different factors, i.e., the predicted value of performance function, Kriging variance and importance degree. The term $\phi \left(\frac{\widehat{g}\left(\mathbf{x}\right)}{\widehat{\sigma}\left(\mathbf{x}\right)}\right)$ is employed to ensure the new points generating near the LSF with large Kriging variance, while the non-probabilistic reliability index η(x) contains the information of the importance degree. Evidently, the smaller value of η(x) is, the more important of the point becomes (Fig. 2). By considering the importance degree, the new samples generated using the proposed ILF move toward the MCP gradually, which results in the improving both the computational efficiency and accuracy of reliability analysis. To fully exploit the potential of ILF, we add one point each time into the DOE, so it may require a large number of iterations for high dimensional problems. However, it should be emphasized that the calculation of predicted performance function by Kriging is very cheap, and thus ILF is very efficient, especially for complex engineering systems.

Fig. 2

The iterative process of the proposed ILM

It is well-known that a terminated criterion needs to provide for metamodeling-based reliability analysis technique. Herein, a new relative error is proposed as the terminated criterion to guarantee the accuracy of the Kriging model, in which the information of the predicted performance functions and non-probabilistic reliability index are used. Assume a new sample point x^′ is obtained in the kth iterative step using the proposed ILF, the proposed termination criterion can be defined as follows,

$$ {\displaystyle \begin{array}{l}{\delta}_{\mathrm{max}}=\max \left\{{\delta}_1,{\delta}_2\right\}\\ {}{\delta}_1=\frac{\mid \widehat{g}\left({\mathbf{x}}^{\prime}\right)-g\left({\mathbf{x}}^{\prime}\right)\mid }{\max \left\{g\left({\mathbf{x}}_1\right),\dots, g\left({\mathbf{x}}_{\mathrm{n}}\right)\right\}-\min \left\{g\left({\mathbf{x}}_1\right),\dots, g\left({\mathbf{x}}_{\mathrm{n}}\right)\right\}}\times 100\%\\ {}{\delta}_2=\mid \frac{\eta^{\mathrm{k}}-{\eta}^{\mathrm{k}-1}}{\eta^{\mathrm{k}}}\mid \times 100\%\end{array}} $$

(21)

where $\widehat{g}\left(\cdot \right)$ and g(⋅) denote the Kriging performance function and actual performance function, respectively. The point set {x₁, x₂, …, x_n} represents the existing training sample points in the design domain. And δ₁ represents the maximum value of relative error between the predicted values and actual performance function values, while δ₂ represents the relative error of the non-probabilistic reliability index between the previous and current iterative steps. Thus, the proposed non-probabilistic reliability estimation method is considered as convergent when the relative error is less than a small enough value Δ, where Δ is set as 10⁻⁵ in the procedure.

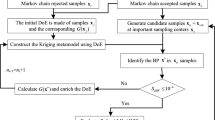
A flowchart of the proposed method is given in Fig. 4a. Firstly, the initial DOE is generated uniformly according to the dimension and computational cost, then a Kriging model is built using the initial DOE. Secondly, a new point x^k is generated using the proposed ILF in (19), in which the particle swarm optimization algorithm is used (Birge 2003). Besides, the actual value of performance function is calculated at this point. Thirdly, the DOE is updated by adding a new point into the training sample points set. Finally, a new Kriging model is reconstructed based on all training samples and relative errors are calculated based on the newly-established Kriging model. This process is carried out until the terminated criterion is satisfied.

4.2 NRBDO based on the proposed ILM

NRBDO always need to deal with the multiple non-probabilistic reliability index constraints simultaneously, which means the MCPs of all constraints should be calculated. To this end, the proposed ILM is extended to solve the NRBDO problems with multiple performance functions and constraints. A two-dimensional example with three non-probabilistic reliability constraints is shown in Fig. 3. When the constraint functions g₁(x) and g₂(x) are active (Fig. 3a), the ILF values of performance functions g₁(x) and g₂(x) are larger than that of performance function g₃(x); this is due to η₃(x) > η₁(x) and η₃(x) > η₂(x). Similarly, when the constraint functions g₁(x) and g₃(x) are active (Fig. 3b), the ILF values of performance functions g₁(x) and g₃(x) are larger than that of performance function g₂(x). Hence, we maximize the ILF values of all constraints to obtain the MCPs, i.e., the minimum non-probabilistic reliability index value from LSFs to the current optimum point. Note that the points located in the infeasible region are useless for solving NRBDO problems. The proposed ILF for NRBDO problems can be redefined as,

$$ \mathrm{ILF}\left(\widehat{g}\left(\mathbf{x}\right)\right)=\Big\{{\displaystyle \begin{array}{l}\max \left\{\frac{1}{\eta_1\left(\mathbf{x}\right)}\phi \left(\frac{{\widehat{g}}_1\left(\mathbf{x}\right)}{{\widehat{\sigma}}_{{\widehat{g}}_1}\left(\mathbf{x}\right)}\right),\frac{1}{\eta_2\left(\mathbf{x}\right)}\phi \left(\frac{{\widehat{g}}_2\left(\mathbf{x}\right)}{{\widehat{\sigma}}_{{\widehat{g}}_2}\left(\mathbf{x}\right)}\right),\dots, \frac{1}{\eta_{\mathrm{m}}\left(\mathbf{x}\right)}\phi \left(\frac{{\widehat{g}}_{\mathrm{m}}\left(\mathbf{x}\right)}{{\widehat{\sigma}}_{{\widehat{g}}_m}\left(\mathbf{x}\right)}\right)\right\}\kern1.24em \mathrm{if}\kern0.24em {\widehat{g}}_{\mathrm{i}}\left(\mathbf{x}\right)\ge -{\varepsilon}_{\mathrm{g}},\kern1em \forall i\\ {}0\kern29.12001em \mathrm{otherwise}\end{array}} $$

(22)

Fig. 3

A sketch of the ILM for NRBDO problem

According to (19), the computational cost can be greatly decreased. For NRBDO model with multiple non-probabilistic reliability constraints, the proposed ILM only focuses on the active constraints; on the contrary, the inactive constraints are ignored during the optimization process. Therefore, we only need to validate the accuracy of the active constraints. As mentioned above, the proposed ILM first adds the sample point located near the active LSF, which means that the accuracy of the active constraints is always higher than that of the inactive constraints. Similar with ILM in reliability assessment, we also update one point each time. It should be noted that the active checking condition ${\widehat{g}}_{\mathrm{i}}\left(\mathbf{x}\right)\ge -{\varepsilon}_{\mathrm{g}}$ is established based on Kriging performance functions. ε_g is a small value to improve the robustness for highly nonlinear problems, and it is set to be 10⁻³ in this study. It should be noted that the active checking condition may produce some errors during the initial iterative process. However, as the increase of iterations, the error is gradually decreased until it is vanished.

During each iterative step of the NRBDO, enough samples should be generated to guarantee the accuracy of MCP and movement of design variables. Therefore, the terminated criterion for NRBDO problems is necessary by considering the reliability system with multiple constraints.

$$ {\displaystyle \begin{array}{l}{\delta}_{\mathrm{min}}=\min \left\{{\delta}_{11},...,{\delta}_{1j}...,{\delta}_{1m}\right\}\\ {}{\delta}_{1j}=\max \left\{\frac{\mid {\widehat{g}}_{\mathrm{j}}\left({\mathbf{x}}^{\prime}\right)-{g}_{\mathrm{j}}\left({\mathbf{x}}^{\prime}\right)\mid }{\max \left\{{g}_{\mathrm{j}}\left({\mathbf{x}}_1\right),\dots, {g}_{\mathrm{j}}\left({\mathbf{x}}_{\mathrm{n}}\right)\right\}-\min \left\{{g}_{\mathrm{j}}\left({\mathbf{x}}_1\right),\dots, {g}_{\mathrm{j}}\left({\mathbf{x}}_{\mathrm{n}}\right)\right\}}\times 100\%\right\}\end{array}} $$

(23)

where ${\widehat{g}}_{\mathrm{j}}\left(\cdot \right)$ and g_j(⋅) are the values of jth Kriging model and actual performance function, respectively.

4.3 Procedures and flowcharts

A flowchart of the proposed ILM for NRBDO problems is given in Fig. 4b, and the procedures are generalized as follows,

• (a) Initialize the sample set s⁰, the design variables d⁽⁰⁾, and x^C(0) for NRBDO problems.

• (b) Build a Kriging model based on the initial sample set. Then, the NRBDO approach is carried out based on the Kriging model.

• (c) Select new sample points using the proposed ILF and add these points to the initial sample set s^k. Then, a new Kriging model is rebuilt for the objective functions and constraints based on the new sample points and corresponding responses.

• (d) Based on the new Kriging model in step (3), the NRBDO approach is performed to update the design variables.

• (e) Calculate the relative error according to (23)

• (f) If the convergence condition is satisfied, then stop the iteration. Otherwise, set k = k + 1, back to step (3) to update the Kriging model.

Fig. 4

a Non-probabilistic reliability analysis using the ILF. b The ILF for NRBDO

5 Numerical examples

In this section, five numerical examples are applied to verify the efficiency and accuracy of the proposed ILM by comparing with LHS method and other four popular active learning methods from probabilistic domain (i.e., EFF, ERF, function U, and CBS). The results calculated using the analytical (Anal.) method are considered as a benchmark solution, in which the actual LSFs and objective functions are used. Meanwhile, the Kriging-based learning methods are compared with the analytical method to validate their effectiveness. For NRBDO problems, the relative errors of calculated results between the analytical method and Kriging-based methods are calculated by $\frac{\left\Vert \mathbf{d}-{\mathbf{d}}^{\ast}\right\Vert }{\left\Vert {\mathbf{d}}^{\ast}\right\Vert}\times 100\%$, where d^∗ denotes the values of design variables computed using the analytical method at the optimum point. In addition, the non-probabilistic reliability analysis and NRBDO approach are performed based on the advanced nominal value method (Meng et al. 2018) to further test the accuracy of the proposed method. The finite difference method is used to calculate the sensitivities of objective and performance functions during the NRBDO process.

5.1 Mathematical example 1

The first example is a two-dimensional nonlinear function, which is modified from the reference (Bichon et al. 2008).

$$ g\left(\mathbf{x}\right)={x}_1^3+{x}_2^3-18 $$

(24)

where both of two uncertain variables x₁ and x₂ are assumed to lie within the range of [5, 15].

The results computed using the analytical method are shown in Fig. 5, in which the nominal values of x₁ and x₂ are set as (10.0, 10.0). The location is denoted as black “_*.” The black curve denotes the actual LSF, and the red curve denotes the Kriging model-based LSF. The red “×” denote the locations of sample points during the Kriging model-based non-probabilistic reliability analysis. To compare the accuracy of different active learning methods in a fair way, nine initial sample points are generated by the grid sampling with three-level full factorial design to construct the initial Kriging model. The relative errors ∣η − η^∗ ∣ / ∣ η^∗ ∣  × 100% between different methods are used to compare the accuracy, where η and η^∗ denote the actual and Kriging non-probabilistic reliability indices, respectively. Besides, the number of sample size and CPU time are also given to demonstrate the efficiency. The unit of the CPU time is second.

Fig. 5

Non-probabilistic reliability analysis of different methods for example 1. a LHS, b EFF, c ERF, d function U, e CBS, f ILM

The results computed using the analytical method are listed in Table 1. The actual non-probabilistic reliability index is 1.5840. The LHS method with 60 sample points is shown in Fig. 5a, and dotted square denotes the geometric figure of non-probabilistic model. Since the samples are evenly distributed in the entire uncertain space, the relative error between the LHS method and the analytical method is quite small. Since the calculation of performance function is very cheap, a small amount of CPU time is required.

Table 1 The optimal results for example 1

The reliability analysis results computed using the EFF, ERF, function U, and CBS methods are illustrated in Fig. 5b–e, respectively. Comparing with LHS, EFF generates most of sample points near the LSF despite of few samples locating at the top right corner. Thus, the number of samples of EFF is far less than that of LHS, while the accuracy is also accordingly increased. ERF is slightly better than EFF; this may be because EFF requires considering an additional parameter $\overline{z}$. Function U in AK-MCS generates the samples near the LSF with the large value of Kriging variance, so the LSF is predicted accurately. CBS considers the minimum distance between the existing samples, so the samples more evenly than that generated by function U. It is also very efficient and accurate. But all these active learning methods approximate the LSF in entire design space, it needs a large number of sample points. The sampling process of the proposed ILM is illustrated in Fig. 5f, which indicates that the sample points move toward the CPF gradually. Besides, the CPU time are also given in Table 1; the CPU time of these active learning methods is higher than that of LHS, because it needs constantly solving optimization problem. However, since the prediction by Kriging model is efficient, the sampling process is also very fast. The CPU time of these active learning methods has a same trend with the sample numbers of these methods, and the proposed ILM is the most effective method. For complex engineering problem, the DoE of Kriging-based method occupies most of CPU time, so the proposed method has a great potential for reducing the CPU time for complex engineering systems.

The compared results of all methods are shown in Table 1. “Sample size” represents the number of function calls for different Kriging model-based non-probabilistic reliability analysis methods. The efficiency of the active learning methods, i.e., EFF, ERF, function U, and CBS, is much improved compared with the LHS method. In terms of the computational accuracy, the relative error between the proposed ILM and analytical method is 0 as shown in Table 1, which is more accurate than other methods provided in this study. In addition, the sample size of the proposed method is only 16, which is the least among all the methods; in other words, the number of function calls is nearly 1/2 of that of ERF and function U. It also needs to point out that the proposed ILM only generates the sample points on the LSF in the vicinity of the MCP, which is an obvious improvement by comparing with the provided reference methods.

5.2 Mathematical example 2

The second example is a highly nonlinear mathematical example, which is modified from reference (Bichon et al. 2008). The performance function is given as follows,

$$ g\left(\mathbf{x}\right)=\frac{\left({x}_1^2+4\right)\left({x}_2-1\right)}{20}-\sin \frac{5{x}_1}{2}-2 $$

(25)

where the nominal values of uncertain variables x₁ and x₂ are 1.5 and 2.5, and the radii of x₁ and x₂ are assumed as 1. Thus, the mathematical expression of the ellipsoid model is formulated as ${\left(\frac{\mathbf{x}-{\mathbf{x}}^{\mathrm{C}}}{{\mathbf{x}}^{\mathrm{C}}}\right)}^{\mathrm{T}}\left[\begin{array}{l}2.25\kern1em 0\\ {}0\kern2em 6.25\end{array}\right]\left(\frac{\mathbf{x}-{\mathbf{x}}^{\mathrm{C}}}{{\mathbf{x}}^{\mathrm{C}}}\right)\le 1$.

The performance function is highly nonlinear, as shown in Fig. 6. The coordinate of the MCP computed using the analytical method is (1.9406, 3.5924). Nine initial sample points are also generated by the grid sampling with 3-level full factorial design to construct the initial Kriging model for the EFF, ERF, function U, CBS, and ILM. The reliability analysis results of the LHS method are shown in Fig. 6b, there are totally 120 sample points evenly generated in the entire uncertain space. However, many sample points are located far from the MCP, which results in the approximate LSF is inaccurate. The results computed using the EFF, ERF, and CBS methods are illustrated in Fig. 6c–e, respectively. It is observed that most of sample points generated using three active learning methods are located near the LSF; thus, both the efficiency and accuracy are improved remarkably. Among these three active learning methods, EFF shows the most accuracy, but it also needs more sample points.

Fig. 6

Non-probabilistic reliability analysis of different methods for example 2. a LHS, b EFF, c ERF, d function U, e CBS, f ILM

The compared results of all methods are shown in Table 2. Unlike the EFF, ERF, and CBS methods, most of sample points generated using the proposed ILM are located in the local region around the MCP, and thus, the LSF near the neighborhood of the MCP can provide enough accuracy. As shown in Fig. 6, the ILM is more accurate than the LHS, EFF, ERF, function U, and CBS methods, while the computational cost of the ILM is greatly reduced by considering the influence of non-probabilistic reliability index during the active learning process. Also, the CPU time of the proposed method is significantly reduced compared to other active learning methods.

Table 2 The optimal results for example 2

5.3 NRBDO mathematical example

There are three performance functions and two uncertain variables in this NRBDO example (Meng et al. 2016). The design variables are selected as the nominal values, and the reference variation coefficients of nominal values are assumed as 10%. The NRBDO model is defined as follows,

$$ {\displaystyle \begin{array}{l}\mathrm{find}\kern2.7em \mathbf{d}={\left[{x}_1^{\mathrm{C}},{x}_2^{\mathrm{C}}\right]}^{\mathrm{T}}\\ {}\min \kern2.799999em {x}_1^{\mathrm{C}}+{x}_2^{\mathrm{C}}\\ {}\mathrm{s}.\mathrm{t}.\kern3.399999em {\eta}_{\mathrm{i}}\left[{g}_{\mathrm{i}}\left(\mathbf{x}\right)\ge 0\right]\ge {\underset{\_}{\eta}}_i,\kern1.8em i=1,\kern0.3em 2,\kern0.3em 3,\\ {}\kern4.499998em 0\le {x}_1^{\mathrm{C}}\le 10,\kern1.5em 0\le {x}_2^{\mathrm{C}}\le 10,\\ {}\kern0.1em \mathrm{where}\kern1.6em {g}_1(x)=\frac{x_1^2{x}_2}{20}-1,\\ {}\kern4.399998em {g}_2(x)=\frac{{\left({x}_1+{x}_2-5\right)}^2}{30}+\frac{{\left({x}_1-{x}_2-12\right)}^2}{120}-1,\\ {}\kern4.399998em {g}_3(x)=\frac{80}{\left({x}_1^2+8{x}_2+5\right)}-1,\\ {}\kern4.399998em {\underset{\_}{\eta}}_1={\underset{\_}{\eta}}_2={\underset{\_}{\eta}}_3=1,\\ {}\kern4.299998em {\mathbf{d}}^{(0)}={\left[5.0,5.0\right]}^{\mathrm{T}}\end{array}} $$

(26)

The compared optimization results and NRBDO solutions of different methods for example 3 are listed in Table 3 and Fig. 7. To compare the optimal results of different methods, the non-probabilistic reliability index at the optimum is tested by ANVM. The optimal results are identical to those in reference (Meng et al. 2016). The initial sample sizes of different Kriging model-based NRBDO approaches are equal to nine, which is also generated using grid sampling with three-level full factorial design.

Table 3 The optimal results for example 3

Fig. 7

NRBDO solutions of different methods for example 2. a LHS, b EFF, c ERF, d function U, e CBS, f ILM

From Table 3 and Fig. 7, it can be observed that the samples generated by the LHS method are evenly distributed in the design space, which requires a large number of sample points to find the optimum. As shown in Fig. 7b, c, the EFF and ERF methods generate new sample points near the LSF, so they are more efficient than the LHS method. For function U, the samples located on the LSF g₃ are more than those located on the LSFs g₁ and g₂, so it is less accurate than EFF and ERF. But the number of samples of function U is less than that of EFF and ERF. For CBS, the samples are evenly distributed on LSF in the feasible region, whose efficiency is further improved to a certain extent than function U. Compared with the EFF, ERF, and CBS methods, the proposed ILM only adds the sample points on the LSFs at the neighborhood of the MCP, while the inactive constraint g₃ is ignored owing to the large value of non-probabilistic reliability constraint. Therefore, it is a more efficient and accurate approach than other prevalent active learning methods for solving the NRBDO problems in terms of the number of function calls and CPU time.

5.4 A speed reducer

A speed reducer contains seven uncertain variables and 11 non-probabilistic reliability constraints, as shown in Fig. 8. The objective functions are the structural weight, while physical quantities, involving bending stress, contact stress, longitudinal displacement, stress of the shaft, and geometry constraints, are deemed as the constraints. All uncertain parameters are considered as the uncertain-but-bounded variables, and the reference coefficients of variation of nominal values are assumed as 1%. The deterministic optimum solution is selected as the initial design and the NBRDO model is formulated as follows,

$$ {\displaystyle \begin{array}{l}\mathrm{find}\kern0.7em \mathbf{d}={\left[{x}_1^{\mathrm{C}},{x}_2^{\mathrm{C}},{x}_3^{\mathrm{C}},{x}_4^{\mathrm{C}},{x}_5^{\mathrm{C}},{x}_6^{\mathrm{C}},{x}_7^{\mathrm{C}}\right]}^{\mathrm{T}}\\ {}\min \kern0.9000001em f\left(\mathbf{d}\right)=0.7854{x}_1^{\mathrm{C}}{\left({x}_2^{\mathrm{C}}\right)}^2\left(3.3333{\left({x}_3^{\mathrm{C}}\right)}^2+14.9334{x}_3^{\mathrm{C}}-43.0934\right)-1.508{x}_1^{\mathrm{C}}\\ {}\kern5.619999em \left({\left({x}_6^{\mathrm{C}}\right)}^2+{\left({x}_7^{\mathrm{C}}\right)}^2\right)+7.477\left({\left({x}_6^{\mathrm{C}}\right)}^3+{\left({x}_7^{\mathrm{C}}\right)}^3\right)+0.7854\left({x}_4^{\mathrm{C}}{\left({x}_6^{\mathrm{C}}\right)}^2+{x}_5^{\mathrm{C}}{\left({x}_7^{\mathrm{C}}\right)}^2\right)\\ {}\mathrm{s}.\mathrm{t}.\kern1.1em {\eta}_{\mathrm{i}}\left[{g}_{\mathrm{i}}\left(\mathbf{x}\right)\ge 0\right]\ge {\underset{\_}{\eta}}_i,\kern0.5em i=1,2,\dots, 11,\\ {}\kern2.1em {g}_1\left(\mathbf{x}\right)=\frac{27}{x_1{x}_2^2{x}_3}-1,\kern1.2em {g}_2\left(\mathbf{x}\right)=\frac{397.5}{x_1{x}_2^2{x}_3^2}-1,\\ {}\kern2.1em {g}_3\left(\mathbf{x}\right)=\frac{1.93{x}_4^3}{x_2{x}_3{x}_6^4}-1,\kern1.2em {g}_4\left(\mathbf{x}\right)=\frac{1.93{x}_5^3}{x_2{x}_3{x}_7^4}-1,\\ {}\kern2em {g}_5\left(\mathbf{x}\right)=\frac{\sqrt{{\left(745{x}_4/\left({x}_2{x}_3\right)\right)}^2+16.9\times {10}^6}}{0.1{x}_6^3}-1100,\\ {}\kern2em {g}_6\left(\mathbf{x}\right)=\frac{\sqrt{{\left(745{x}_5/\left({x}_2{x}_3\right)\right)}^2+157.5\times {10}^6}}{0.1{x}_7^3}-850,\\ {}\kern1.14em {g}_7\left(\mathbf{x}\right)={x}_2{x}_3-40,\kern0.8000001em {g}_8\left(\mathbf{x}\right)=5-\frac{x_1}{x_2},\\ {}\kern2.1em {g}_9\left(\mathbf{x}\right)=\frac{x_1}{x_2}-12,\kern0.9000001em {g}_{10}\left(\mathbf{x}\right)=\frac{1.5{x}_6+1.9}{x_4}-1,\\ {}\kern2.1em {g}_{11}\left(\mathbf{x}\right)=\frac{1.1{x}_7+1.9}{x_5}-1,\\ {}\kern2.1em {\underset{\_}{\eta}}_1={\underset{\_}{\eta}}_2=\dots ={\underset{\_}{\eta}}_{11}=1.0,\\ {}\kern2.1em 2.6\le {x}_1^{\mathrm{C}}\le 3.6,\kern0.37em 0.7\le {x}_2^{\mathrm{C}}\le 0.8,\kern0.5em 17\le {x}_3^{\mathrm{C}}\le 28,\\ {}\kern2.2em 7.3\le {x}_4^{\mathrm{C}}\le 8.3,7.3\le {x}_5^{\mathrm{C}}\le 8.3,\\ {}\kern2.1em 2.9\le {x}_6^{\mathrm{C}}\le 3.9,\kern0.37em 5.0\le {x}_7^{\mathrm{C}}\le 5.5,\\ {}\kern2.1em {\mathbf{d}}^0={\left[3.5,0.7,17.0,7.3,7.72,3.35,5.29\right]}^{\mathrm{T}}\end{array}} $$

(27)

Fig. 8

A speed reducer

The compared results for the speed reducer are listed in Table 4, while the non-probabilistic reliability index at the optimum is validated by the ANVM, as shown in Table 5. The abbreviation “inact.” denotes this non-probabilistic reliability constraint is inactive in Table 5. The numbers of initial sample point for the EFF, ERF, function U, CBS, and ILM are 36, which is sampled by the LHS method. It can be seen that the efficiency of the LHS method is low. EFF, function U, and ERF are more efficient than the LHS. However, the minimum non-probabilistic reliability index calculated using the EFF, function U, and ERF methods are 0.9948, 0.8810, and 0.9924, respectively. The CBS method is more efficient than the LHS, ERF, function U, and EFF methods, and the corresponding minimum non-probabilistic reliability index at the optimum is 0.9938. The minimum non-probabilistic reliability index of the proposed ILM is 1.0000, and thus, it is obviously more accurate than other active learning functions. In addition, the number of sample size is less than other comparative methods. Also, the CPU time of the proposed method is less than that of other active learning methods. Therefore, it can be concluded that the proposed ILM shows a high performance in terms of accuracy and efficiency.

Table 4 The optimal results for speed reducer

Table 5 Non-probabilistic reliability index of speed reducer at the optimum

5.5 A welded beam

As shown in Fig. 9, the weight of weld beam is minimized, while the non-probabilistic reliability constraints are related to shear stress, bending stress, buckling and displacement (Meng et al. 2016). There are four uncertain-but-bounded variables, and their nominal values are selected as design variables. The reference coefficients of variation of nominal values are selected as 5%. The deterministic optimum results are selected as the initial design, and the NBRDO model is formulated as follows,

$$ {\displaystyle \begin{array}{l}\mathrm{find}\kern1em \mathbf{d}={\left[{x}_1^{\mathrm{C}},{x}_2^{\mathrm{C}},{x}_3^{\mathrm{C}},{x}_4^{\mathrm{C}}\right]}^{\mathrm{T}}\\ {}\min \kern1.12em f\left(\mathbf{d},\mathbf{z}\right)={c}_1{\left({x}_1^{\mathrm{C}}\right)}^2{x}_2^{\mathrm{C}}+{c}_2{x}_3^{\mathrm{C}}{x}_4^{\mathrm{C}}\left({z}_2+{x}_2^{\mathrm{C}}\right)\\ {}\mathrm{s}.\mathrm{t}.\kern1.52em {\eta}_{\mathrm{i}}\left[{g}_{\mathrm{i}}\left(\mathbf{x},\mathbf{z}\right)\ge 0\right]\ge {\underset{\_}{\eta}}_i,i=1,\dots, 5,\\ {}\mathrm{where}\kern0.24em {g}_1\left(\mathbf{x},\mathbf{z}\right)=\tau \left(\mathbf{x},\mathbf{z}\right)/{z}_6-1,{g}_2\left(\mathbf{x},\mathbf{z}\right)=\sigma \left(\mathbf{x},\mathbf{z}\right)/{z}_7-1,\\ {}\kern2.9em {g}_3\left(\mathbf{x},\mathbf{z}\right)={x}_1/{x}_4-1,{g}_4\left(\mathbf{x},\mathbf{z}\right)=\delta \left(\mathbf{x},\mathbf{z}\right)/{z}_5-1,\\ {}\kern2.9em {g}_5\left(\mathbf{x},\mathbf{z}\right)=1-{P}_{\mathrm{c}}\left(\mathbf{x},\mathbf{z}\right)/{z}_1,\\ {}\kern2.9em \tau \left(\mathbf{x},\mathbf{z}\right)={\left[t{\left(\mathbf{x},\mathbf{z}\right)}^2+\frac{2t\left(\mathbf{x},\mathbf{z}\right) tt\left(\mathbf{x},\mathbf{z}\right){x}_2}{2R\left(\mathbf{x}\right)}+ tt{\left(\mathbf{x},\mathbf{z}\right)}^2\right]}^{1/2},\\ {}\kern2.9em t\left(\mathbf{x},\mathbf{z}\right)=\frac{z_1}{\sqrt{2}{x}_1{x}_2}, tt\left(\mathbf{x},\mathbf{z}\right)=\frac{M\left(\mathbf{x},\mathbf{z}\right)R\left(\mathbf{x}\right)}{J\left(\mathbf{x}\right)},\\ {}\kern2.9em \sigma \left(\mathbf{x},\mathbf{z}\right)=\frac{6{z}_1{z}_2}{x_3^2{x}_4},\delta \left(\mathbf{x},\mathbf{z}\right)=\frac{4{z}_1{z}_2^3}{z_3{x}_3^3{x}_4},\\ {}\kern2.9em M\left(\mathbf{x},\mathbf{z}\right)={z}_1\left({z}_2+\frac{x_2}{2}\right),R\left(\mathbf{x}\right)=\left(\frac{\sqrt{x_2^2+{\left({x}_1+{x}_3\right)}^2}}{2}\right),\\ {}\kern2.9em J\left(\mathbf{x}\right)=\sqrt{2}{x}_1{x}_2\left[{x}_2^2/12+{\left({x}_1+{x}_3\right)}^2/4\right],\\ {}\kern2.9em {P}_{\mathrm{c}}\left(\mathbf{x},\mathbf{z}\right)=\frac{4.013{x}_3{x}_4^3\sqrt{z_3{z}_4}}{6{z}_2^2}\left(1-\frac{x_3}{4{z}_2}\sqrt{\frac{z_3}{z_4}}\right),\\ {}\kern1.78em {\underset{\_}{\eta}}_1={\underset{\_}{\eta}}_2=\dots ={\underset{\_}{\eta}}_5=1.0,\\ {}\kern2.9em 3.175\le {x}_1^{\mathrm{C}}\le 50.8,\kern0.62em 0\le {x}_2^{\mathrm{C}}\le 254,\\ {}\kern2.9em 0\le {x}_3^{\mathrm{C}}\le 254,\kern0.62em 0\le {x}_4^{\mathrm{C}}\le 50.8,\\ {}\kern2.8em {\mathbf{d}}^{(0)}={\left[6.208,157.82,210.62,6.208\right]}^{\mathrm{T}}\end{array}} $$

(28)

Fig. 9

A welded beam

The compared results for the welded beam design are shown in Table 6. The non-probabilistic reliability index at the optimum is listed in Table 7, which is validated by the ANVM. The numbers of initial sample points for the EFF, ERF, function U, CBS, and ILM are 24, which are sampled by the LHS method.

Table 6 The optimal results for welded beam

Table 7 Non-probabilistic reliability index of welded beam at the optimum

For the LHS method, 360 samples are generated in the entire design space, and the optimum converges to (10.1555, 175.8606, 112.7095, and 12.3325). It is obviously found that the accuracy of the NRBDO results computed by the LHS method is poor. The EFF method improves the accuracy of Kriging model to a certain extent through adding the sample points near the LSF; however, the minimum non-probabilistic reliability index at the optimum is far less than 1. Thus, the optimal results computed by EFF have the risk of failure. Other three active learning methods, including ERF, function U, and CBS methods, exhibit similar behavior for this highly nonlinear problem. The approximate difficulty of the proposed ILM is significantly decreased because of only approximating the MCP in the local region, and thus, the accuracy is significantly improved. Also, the number of function calls and CPU time are about half of any other comparative methods.

6 Conclusions

This study investigates the active learning methods for the non-probabilistic reliability analysis and optimization and develops an ILM for improving the computational efficiency and accuracy. Considering the importance degree of non-probabilistic reliability index during the active learning process, an ILF is proposed to accurately predict the MCP in the vicinity of LSF. Then, the proposed ILM is further extended to solve the NRBDO problems with multiple performance functions accurately and efficiently by constructing the system ILF. In addition, in order to ensure the accuracy, two new stopping criterions are proposed to distinguish the convergence condition of the non-probabilistic reliability analysis and optimization, which is also an innovation point of the proposed algorithm.

The efficiency and accuracy of the proposed ILM are validated through two non-probabilistic reliability analysis examples and three NRBDO examples. The compared results with one typical sampling method (LHS) and four popular active learning methods (EFF, ERF, function U, and CBS) indicated that the proposed ILM is more efficient and accurate. The results validated by the advanced nominal value method are almost identical to the results computed by the actual performance functions, which verifies that the proposed ILM is more accurate than other comparative methods. In the future, the application of the ILM for large-scale engineering systems will be reinforced.