A local adaptive sampling method for reliability-based design optimization using Kriging model

Abstract

Reliability-based design optimization (RBDO) in practical applications is hindered by its huge computational cost during structure reliability evaluating process. Kriging-model-based RBDO is an effective method to overcome this difficulty. However, the accuracy of Kriging model depends directly on how to select the sample points. In this paper, the local adaptive sampling (LAS) is proposed to enhance the efficiency of constructing Kriging models for RBDO problems. In LAS, after initialization, new samples for probabilistic constraints are mainly selected within the local region around the current design point from each optimization iteration, and in the local sampling region, sample points are first considered to be located on the limit state constraint boundaries. The size of the LAS region is adaptively defined according to the nonlinearity of the performance functions. The computation capability of the proposed method is demonstrated using three mathematical RBDO problems and a honeycomb crash-worthiness design application. The comparison results show that the proposed method is very efficient.

1 Introduction

Reliability-based design optimization has received extensive attention in the past few decades. Unlike deterministic optimization, RBDO considers uncertainties of design variables stemming from various sources. A typical RBDO problem is formulated as follows:

$$\begin{array}{lll} && {} {find:{\boldsymbol{d}},{\boldsymbol{\mu}}_{\boldsymbol{X}}} \notag\\ && {} \text{min:}f\left({{\boldsymbol{d}},{\boldsymbol{\mu}}_{\boldsymbol{X}}}\right) \notag\\ && {} {s.t.:Prob\left({g_{i} ({{\boldsymbol{d}},{\boldsymbol{X}}})\ge 0}\right)\ge R_{i} ,\;i=1,\cdots ,N} \notag\\ && {} {{\boldsymbol{d}}^{Lower}\le {\boldsymbol{d}}\le {\boldsymbol{d}}^{Upper},{\boldsymbol{\mu}}_{\boldsymbol{X}}^{Lower}\le {\boldsymbol{\mu}}_{\mathbf{X}} \le {\boldsymbol{\mu}}_{\boldsymbol{X}}^{Upper}} \end{array} $$

(1)

where, f(d, μ _X ) is the objective function, Prob (g _i (d, μ _X ) ≥ 0) is the feasible probability of satisfying the ith constraint; g _i (d, X) denotes the performance function of the ith probabilistic constraint; d is the vector of the deterministic design variables; X is the vector of random design variables; μ _X denotes the mean vector of X; N is the number of probabilistic constraints; R _i denotes the target feasible probability for the ith probabilistic constraint.

The probabilistic constraints in (1) are usually implicit functions which need to be evaluated through reliability analysis, such as Monte Carlo simulation (MCS) (see e.g., Lee et al. 2008, 2011a, b; Kuczera et al. 2010; Valdebenito and Schuëller 2011) or analytical reliability methods. MCS is achieved through realizing random variables and determining whether a particular event occurs for the simulation instance (Li et al. 2010). The ratio of the number of failures to the total number of sampling is regarded as the probability of failure. MCS is computationally expensive, especially when the probability of failure is low. Analytical reliability methods include the first order reliability analysis method (FORM) (Dersjö and Olsson 2011) and second order reliability analysis method (SORM) (Kiureghian and Stefano 1991). The reliability index approach (RIA) (see e.g., Enevoldsen and Sørensen 1994; Reddy et al. 1994; Gasser and Schuëller 1997; Grandhi and Wang 1998; Nikolaidis and Burdisso 1988; Tu and Choi 1999; Lin et al. 2011), performance measure approach (PMA) (Youn et al. 2005a) and dimension reduction method (DRM) (Lee et al. 2008, 2012) are commonly used due to their higher efficiency compared to simulation methods. Also, many other reliability methods have been developed to perform reliability analysis efficiently, including the advanced mean value method (AMV) (Wu et al. 1990), the hybrid mean value (HMV) (Youn et al. 2005b) and the arc search method (Du et al. 2004).

The integration strategies of the reliability analysis and optimization procedures in RBDO have great influence on the accuracy and efficiency of the results (Valdebenito and Schuëller 2010; Aoues and Chateauneuf 2010). Double-loop method has two nested loops which makes it inefficient; Single-loop method (see e.g., Chen et al. 1997; Kirjner-Neto et al. 1998; Kharmanda et al. 2002; Agarwal et al. 2007; Liang et al. 2008; Shan and Wang 2008) has only one loop through replacing the reliability analysis by its Karush–Kuhn–Tucker (KKT) optimality conditions; Decoupled-loop method (see e.g., Royset et al. 2001; Wu et al. 2001; Du and Chen 2004; Cheng et al. 2006; Zou and Mahadevan 2006; Ching and Hsu 2008; Yi et al. 2008; Cho and Lee 2011; Chen et al. 2013a, b) performs the optimization and reliability analysis sequentially, so it has a good balance between the accuracy and efficiency in solving RBDO problems.

To improve the efficiency of RBDO, metamodels are applied in RBDO to substitute the true constraint function evaluations. Choi et al. (2001), Youn and Choi (2004), and Lee and Song (2011) used moving least square method for RBDO. Kim and Choi (2008) proposed an RSM with prediction interval estimation. Zhao et al. (2009) used the RSM and sequential sampling for probabilistic design. Basudhar and Missoum (2008) proposed the adaptive explicit decision functions for probabilistic design and optimization using support vector machines (SVM). Mourelatos (2005) adopted symmetric optimal Latin hypercube sampling and Kriging model for design optimization under uncertainty. Pretorius et al. (2004) used Kriging model as both local and global approximation for continuous casting design optimization. Ju and Lee (2008) proposed an RBDO method using the moment method and Kriging model. Lee and Jung (2008) applied a constraint boundary sampling method and Kriging model for RBDO. Zhuang and Pan (2012) proposed a new sequential sampling method for design under uncertainty. Huang and Chan (2010) proposed a modified efficient global optimization algorithm for RBDO. Zhao et al. (2011) proposed dynamic Kriging for design optimization. Lee et al. (2012) proposed an enhanced dimension reduction method with variable sampling points for RBDO.

Kriging models are fitted from the space-filling sampling, such as Latin Hypercube sampling (LHS), which locates evenly sample points within the whole design domain if design and analysis of computer experiments are concerned. However, in the optimization and reliability analysis processes, the limit state constraint boundaries are more critical than the other regions. The constraint boundary sampling method proposed by Lee and Jung (2008) is more efficient, because it approximates the limit state constraint boundaries over the design region. However, in the RBDO computing process, only the local region in the vicinity of the current design point is required to be more accurate than the others. Therefore, it will be more rational to improve the accuracy of the Kriging model on the limit state constraint boundaries which are in the relatively small region around the current design point, rather than making the whole limit state boundaries within the design region being accurate.

In this paper, the LAS method will be proposed to improve the efficiency and accuracy of RBDO using Kriging model. In LAS, the Kriging models will be gradually constructed based on all the existing samples: after initialization, new samples will be added within the critical LAS region to make the sampling more effective for RBDO problems. The size of LAS region will be adaptively defined according to the nonlinearity of the constraint function in the vicinity of the current design point. The constraint boundary sampling criterion and mean squared error criterion are adaptively used to locate sample points for the probabilistic constraints in RBDO. The simulation reliability method, Monte Carlo simulation (MCS), will be selected to perform reliability analysis in this paper.

This paper is organized as follows: the commonly used simulation method MCS and Kriging model will be reviewed in Section 2; the proposed LAS will be explained in Section 3; Section 4 then uses illustrative examples to demonstrate the application of LAS with four comparison experiments conducted; in Section 5, the conclusion will be drawn.

2 Commonly used method in RBDO and Kriging model

2.1 Reliability analysis method MCS

As above mentioned, MCS is achieved through realizing random variables and determining whether a particular event occurs for the simulation instance (Li et al. 2010). The ratio of the number of failures to the total number of sampling is regarded as the probability of failure. When the probability of failure is low, MCS will be computationally expensive. However, when combining with Kriging model, the computational cost of MCS could be ignored, and the sensitivity information $\frac {\partial P_{j} \left ( {{\boldsymbol {\mu }}_{\boldsymbol {X}}^{k}} \right )}{{\boldsymbol {\mu }}_{\boldsymbol {X}}}$ for the probability of failure $P_{j} \left ( {{\boldsymbol {\mu }}_{\boldsymbol {X}}^{k}} \right )$ can also be obtained as follows.

$$\begin{array}{@{}rcl@{}} \frac{\partial P_{j}\left(\boldsymbol{\mu}^{k}_{\boldsymbol{X}}\right)}{\partial\boldsymbol{\mu}_{\boldsymbol{X}}} &=&\frac{\partial}{\partial\boldsymbol{\mu}}\int_{g_{j}(\boldsymbol{X})\leq0}f_{\boldsymbol{X}}(\boldsymbol{X})d\boldsymbol{X}\notag\\ &=&\int_{g_{j}(X)\leq0}\frac{\partial f_{\boldsymbol{X}}(\boldsymbol{X})}{\partial\boldsymbol{\mu}_{\boldsymbol{X}}}d{\boldsymbol{X}}\\ &=&\int_{g_{j}(X)\leq0}\frac{\left(\frac{\partial f_{\boldsymbol{X}}(\boldsymbol{X})}{\partial\boldsymbol{\mu}_{\boldsymbol{X}}}\right)}{f_{\boldsymbol{X}} (\boldsymbol{X})}f_{\boldsymbol{X}}(\boldsymbol{X})d{\boldsymbol{X}}\notag\\ &=&\frac{1}{N}\sum\nolimits_{i=1}^{N}\frac{I_{F}\left(X^{i}\right)}{f_{\boldsymbol{X}}\left(X^{i}\right)} \frac{\partial f_{\boldsymbol{X}}\left(X^{i}\right)}{\partial\boldsymbol{\mu}_{\boldsymbol{X}}}\notag \end{array} $$

(2)

where X are the random design variables, f _X (X) represents the joint probability density function of X, N is the number of test points in MCS.

The test points X ⁱ, i = 1,⋯, N in (2) are the same as that used for estimating the probability of failure $P_{j} \left ({\boldsymbol {\mu }_{\boldsymbol {X}}^{k}}\right )$. In other words, the estimation of $\frac {\partial P_{j}\left ({\boldsymbol {\mu }_{\boldsymbol {X}}^{k}}\right )}{{\boldsymbol {\mu }}_{\boldsymbol {X}}}$ does not require additional MCS runs, and it can be obtained while calculating the probability of failure $P_{j} \left ({\boldsymbol {\mu }_{\boldsymbol {X}}^{k}}\right )$. Details about the (2) are in references (Lu et al. 2009; Song et al. 2009).

2.2 Kriging model

Kriging model (also called Gaussian process model) was proposed by a South African geostatistician (Sacks et al. 1989). In Kriging model, the response at a certain sample point not only depends on the design parameters but is also affected by the points in its neighborhood. The spatial correlation between design points is considered (Sacks et al. 1989; Lophaven et al. 2002).

The notations for constructing Kriging models of the constraint function g(x) are used in the description. The corresponding Kriging approximations are denoted as $\widehat {g}( {\boldsymbol {x}} )$. Kriging is based on the assumption that the response function $\widehat {g}( {\boldsymbol {x}} )$ is composed of a regression model $f(\boldsymbol {x})^{T} \boldsymbol {\beta }$ and stochastic process Z(x) as follows (Picheny et al. 2010; Huang and Chan 2010; Kim et al. 2009a):

$$ \widehat{g}( {\boldsymbol{x}} )=f(\boldsymbol{x})^{T}{{\boldsymbol{\beta}}}+Z({\boldsymbol{x}}) $$

(3)

where f(x) is the trend function which consists of a vector of regression functions; β is the trend coefficient vector; Z(x) is assumed to have a zero mean and a spatial covariance function between Z(x) and Z(w) as follows:

$$ Cov\left[ {Z( {\boldsymbol{x}} ),Z( {\boldsymbol{w}} )} \right]={{\boldsymbol{\sigma}} }_{Z}^{2} {\boldsymbol{R}}\left( {{{\boldsymbol{\theta}} },{\boldsymbol{x}},{\boldsymbol{w}}} \right) $$

(4)

where ${{\boldsymbol {\sigma }} }_{Z}^{2}$ is the process variance and R is the correlation function defined by its set of parameters θ (Echard et al. 2011; Kim et al. 2009b).

Several models exist to define the correlation function, but the squared-exponential function (also called anisotropic Gaussian model) is commonly used (Bichon et al. 2008; Rasmussen and Williams 2006; Sacks et al. 1989), and is selected here for R:

$$ {\boldsymbol{R}}\left( {{{\boldsymbol{\theta}}},{\boldsymbol{x}},{\boldsymbol{w}}}\right)=\prod\nolimits_{i=1}^{n} {exp\left[ {-\theta_{i} \left( {x_{i} -w_{i}}\right)^{2}} \right]} $$

(5)

where x _i and w _i are the ith coordinates of the points x and w, n is the number of coordinates in the points x and w, and θ _i is a scalar which gives the multiplicative inverse of the correlation length in the ith direction. An anisotropic correlation function is preferred here, as in reliability studies the random variables are often of different natures (Echard et al. 2011).

The mean square error (MSE) of Kriging prediction exactly at the training point is equal to zero. However, at the testing points which are away from these training points, the MSEs increase highly.

3 Local adaptive sampling

As mentioned above, in the design optimization and reliability analysis processes, the local region in the vicinity of the current design point should be fitted accurately, and the limit state constraint boundaries within the local region are more critical than the non-boundary domain. So in this paper, after initial sampling, the proposed LAS method will add new samples along the limit state constraint boundaries within the local region around the current design point, this will make the Kriging models for the probabilistic constraint functions more precise within the critical design region, and the sampling process will be more effective.

Section 3.1 will first discuss the size of the LAS region, then the LAS criterions will be introduced in Section 3.2. and the procedures and flowchart of the proposed LAS method will be introduced in Section 3.3.

3.1 Size of the LAS region

In the reliability analysis process, the β-sphere region whose radius is equal to the target reliability index || u || = β ^t is very important. So the LAS region should be larger than the β-sphere region. Zhao et al. (2009) proposed a local support for reliability analysis, which is defined as a super-sphere whose radius is cβ ^t, where c is the scaling factor which is chosen as 1.2 ∼ 1.5.

The Kriging prediction error in the boundary of the local window is usually very large, especially for highly nonlinear functions. So, in this paper, to ensure the accuracy of the Kriging model within β ^t-sphere, the local window should be enlarged for highly nonlinear functions due to the Kriging prediction boundary effect.

This paper adaptively chooses the scaling factor according to the nonlinearity of the performance functions.

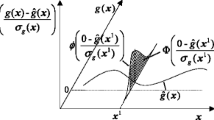
For linear and moderate nonlinear performance functions as in Fig. 1a, it is easy to improve the accuracy of the Kriging model within a small local sampling region. However, for highly nonlinear performance functions in Fig. 1b, to ensure the accuracy of Krging models within the β ^t-sphere, a larger local sampling region should be selected due to the Kriging prediction boundary effect.

Fig. 1

a Linear performance function. b Non-linear performance function

If the gradient values of a performance function are constant as in Fig. 1a, it means the performance function is linear; otherwise, if the gradient values of a constraint function vary widely as in Fig. 1b, then the constraint function is highly nonlinear. In other words, the variance ${{\boldsymbol {\sigma }} }_{i}^{2}$ of the gradient values can reveal the nonlinearity of the ith constraint function. The nonlinearity coefficient nc of a performance function is defined as follows:

$$ nc=\frac{2}{\pi} \arctan \left( {\max \left\| {{{\boldsymbol{\sigma}} }_{i}^{2}} \right\|} \right),\;i=1,\cdots ,N $$

(6)

where ${{\boldsymbol {\sigma }} }_{i}^{2} =\text {variance}\left ( {\nabla \widehat {g}_i ( {{\boldsymbol {x}}^{1}} ),\cdots ,\nabla \widehat {g}_{i} \left ( {{\boldsymbol {x}}^{M}} \right )} \right ),\;\left \| {{{\boldsymbol {\sigma }} }_{i}^{2}}\right \|=\sqrt {{{\boldsymbol {\sigma }} }_{i}^{2} \cdot \left ( {{{\boldsymbol {\sigma }} }_{i}^{2}} \right )^{T}} ,\;\nabla \widehat {g}_{i} \left ( {\boldsymbol {x}}\right )$ is the gradient value predicted by Kriging model for the ith performance function, $\left (\boldsymbol {x}^{1},~\cdots , \boldsymbol {x}^{M}\right )$ are the M testing points evenly located within the β-sphere region. N is the number of performance functions.

The length of the variance $\left \| {{{\boldsymbol {\sigma }} }_{i}^{2}} \right \|$ in (6) is converted from $\left \| {{{\boldsymbol {\sigma }} }_{i}^{2}} \right \|\in \left . \left [{0,+\infty }\right . \right )$ to nc ∈ [0, 1), and the radius of the LAS region is defined as follows:

$$ R=1.2\beta^{t} + 0.3 nc \beta^t=( {1.2+0.3nc} )\beta^t $$

(7)

where β ^t is the maximum target reliability index among the N probabilistic constraints $\beta ^t=\max \left ({\beta _{i}^{t}}\right ),\quad i=1,\cdots ,N.$

Equation (7) shows that the LAS region is larger than the β-sphere region. For linear constraint function, nc is equal to 0, then the radius in (7) is 1.2β ^t. For highly nonlinear performance function, nc is close to 1, and the radius in (7) is equal to (1.2 + 0.3)β ^t = 1.5β ^t. So the size of the LAS region is adaptively defined according to the nonlinearity of the performance functions, and the range of the LAS region 1.2β ^t ∼ 1.5β ^t is identical with that from Zhao et al. (2009).

3.2 LAS criterion

For simplicity, we use the vector x to replace the design variables (d, μ _X ) from RBDO, then the constraint functions in (1) become g _i (x), = 1,⋯, N. The proposed LAS is used to construct Kriging models for these constraint functions. In each design iteration, the LAS method will add new samples to the existing sample sets to reconstruct the Kriging models, and these new samples are selected from a local region around the current design point. Within the local region, new samples will first be selected along the limit state constraint boundaries which are more critical in RBDO than the others. However, if this region does not contain any limit state constraint boundary, the mean square error of the Kriging prediction will be used to select sample points within this region.

3.2.1 Constraint boundary sampling (CBS) criterion

The CBS criterion was proposed by Lee and Jung (2008). When there is sufficient sample data to construct the Kriging model, the prediction of g(x) approaches the normal distribution with mean $\widehat {g}( {\boldsymbol {x}} )$ and standard deviation $\sqrt {MSE( {\boldsymbol {x}} )}$, where $\sqrt {MSE\left ( {\boldsymbol {x}} \right )}$ is the mean square error (MSE) of the Kriging prediction $\widehat {g}( {\boldsymbol {x}})$.

If the failure region is defined as g(x) < 0, then the probability of the Kriging prediction satisfying the constraint g(x) ≥ 0 is as follows:

$$ p( {\boldsymbol{x}} )=1-\Phi \left( {\frac{0-\widehat{g}\left( {\boldsymbol{x}} \right)}{~\sqrt {MSE( {\boldsymbol{x}} )}} } \right)=\Phi \left( {\frac{\widehat{g}\left({\boldsymbol{x}} \right)}{\text{}\sqrt {MSE( {\boldsymbol{x}})}} } \right) $$

(8)

Then the probability density function $\phi \left ( {\widehat {g}\left ( {\boldsymbol {x}} \right )} \left / {\sqrt {MSE( { \boldsymbol {x}} )}} \right .\right )$ can be used to measure the closeness of the Kriging prediction $\widehat {g}( {\boldsymbol {x}} )$ to the limit state constraint g(x) = 0. The CBS criterion is defined as follows:

$$ CBS=\left\{ {{\begin{array}{cc} {\sum\nolimits_{i=1}^{N} {\phi \left( {\frac{\widehat{g}_{i} \left( {\boldsymbol{x}} \right)}{\text{}\sqrt {MSE_{i} ( { \boldsymbol{x}} )}} }\right)\cdot D,}} & {\text{if}\,\widehat{g}_{i} \left( {\boldsymbol{x}} \right)\ge 0,\,\forall i} \hfill \\ 0 & \text{otherwise} \end{array}}}\right. $$

(9)

where D is the minimal distance from the current sample point x to the existing sample points.

3.2.2 MSE criterion

If the LAS region does not contain any constraint boundary, then we use the MSE multiplied by D from (9) as the sampling criterion:

$$ C_{MSE} =\sum\nolimits_{i=1}^{N} {\sqrt {MSE_{i} ( {\boldsymbol{x}} )}\cdot D} $$

(10)

A large value of C _MSE means the Kriging prediction might have a large error at this point, so we need to add this point to the training points set.

In order to determine appropriate number of sample points, it is necessary to define termination criterion. In this paper, we use the relative prediction error of the Kriging model at the new sample point x′ as follows:

$$ Error=\max\left\{\frac{\left|{\widehat{g}_{i}}(\boldsymbol{x}^{\prime})-g_{i}(\mathrm{x}^{\prime})\right|} {Range(g_{i}(\boldsymbol{x}))}\right\},\quad i=1,\cdots,N $$

(11)

where Range(g _i (x)) = max(g _i (x)) − min(g _i (x)), x ∈ (x ¹,⋯, x ^m), g _i (x′) is the ith true constraint function value at the new sample point, $\widehat {g}_{i} ({\boldsymbol {x}^{\prime }})$ is the Kriging prediction value, m is the number of existing sample points, and Range(g _i (x)) denotes the difference between the maximum and minimum values of the ith true constraint function among the existing sample points.

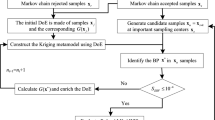
Flowchart of the LAS process is shown in Fig. 2. After initialization and definition of the LAS region, the CBS criterion is first used to select a new sample point within the local region along the limit state constraint boundaries. If no boundary sample point is found using the CBS criterion, then the MSE criterion will be applied to select sample point where the prediction error is large. And then responses of the constraint functions at the new sample point are evaluated, and the Kriging models are reconstructed based on all the existing samples. This process will be conducted until the termination criterion is satisfied.

Fig. 2

LAS sampling process

As seen in Fig. 3, there are two constraints, the region within the dotted-line is the LAS region, d ^k is the design point from the kth design iteration, and β ^t is the target reliability index. The LAS region around d ^k is completely located within the feasible domain, when CBS is first used to select sample point along limit state constraints, no boundary sample point could be found, then the MSE criterion is applied in this region to add new samples to the existing sample sets. d ^k+1 is the design point from the (k + 1)th design iteration, d* denotes the optimal RBDO design. Constraint boundaries pass through the LAS regions around d ^{k+ 1} and d*, so the CBS could find sample points efficiently in these regions along the limit state constraint boundaries, and the MSE criterion will not be used.

Fig. 3

Local adaptive sampling

3.3 Procedures and flowchart of the LAS method

The flowchart of the LAS method is in Fig. 4, and the procedures are as follows:

• 1. Initialize the sample set s ⁰ for probabilistic constraints using Latin hypercube sampling method, and initialize the design variables $\left ({{\boldsymbol {d}}^{0}, {\boldsymbol {\mu }}_{\boldsymbol {X}}^{0}}\right )$.

• 2. Evaluate the responses of the constraint functions in RBDO at the initial sample points s ⁰, then construct the Kriging models for the constraint functions based on the initial sample points and the corresponding responses.

• 3. In the kth iteration, before starting the LAS process, this paper first defines the size of the LAS region according to the nonlinearity of the constraint functions in the vicinity of the current design point $\left ( {{ \boldsymbol {d}}^{k},{\boldsymbol {\mu }}_{\boldsymbol {X}}^{k}} \right )$.

• 4. Within the LAS region defined in step (3), add new samples to the existing sample set s ^k using the proposed LAS criterions. Evaluate the responses of the probabilistic constraints at the sample point, then reconstruct the Kriging models for the probabilistic constraints based on all the existing sample points and the corresponding responses.

• 5. With the reconstructed Kriging models in step (4), conduct optimization using the MCS method to solve the RBDO problem.

• 6. If converged, then end, otherwise, k = k + 1, go to step (3).

Fig. 4

Flowchart of the LAS method

4 Application

In order to verify the accuracy and efficiency of the proposed LAS method, four examples are tested and compared to analytical method (Anal.) which calls the true probabilistic functions, Kriging-model-based RBDO methods using Latin Hypercube sampling (LHS), constraint boundary sampling (CBS) and the sequential sampling method (SS) (Zhao et al. 2009). In all methods, Monte Carlo simulation (MCS) is used to perform reliability analysis. The design results will be assessed through the relative error ${\left \| \boldsymbol {d}^{\ast }-\boldsymbol {d}_{A}^{\ast }\right \|}/ {\left \|{\boldsymbol {d}_{A}^{\ast }}\right \|}$, where ${\boldsymbol {d}}_{A}^{\ast }$ is the design from analytical method which directly calls the true performance functions or computer simulations. Also, the design results are assessed through Monte Carlo simulation (MCS) with a million sampling size.

4.1 Example 1

This example (Lee and Jung 2008) has two random design variables and two probabilistic constraints. All random variables are statistically independent and have normal distributions as follows:

$$ \begin{array}{lll} {find:{\boldsymbol{d}}=\left[ {d_{1} ,d_{2}}\right]^{\mathrm{T}}} \\ {\min:f( {\boldsymbol{d}} )=\left( {d_1-3.7}\right)^2+\left({d_{2} -4} \right)^{2}} \\ {s.t.:\text{prob}\left[{g_{i} ( {\boldsymbol{X}} )<0}\right]\le \Phi\left( {-\beta_{i}^{t}} \right),i={1},{2}} \\ {g_{1} ( {\boldsymbol{X}} )=-X_{1} \sin \left({4X_{1}}\right)-1.1X_{2}\sin \left({2X_{2}}\right)} \\ {g_{2} ( {\boldsymbol{X}} )=X_{1} +X_{2} -3} \\ {0.0\le d_{1} \le 3.7,\quad 0.0\le d_{2} \le 4.0} \\ {X_{i} \sim N\left( {d_{i} ,0.10^{2}} \right),\;i=1,2} \\ {\beta_{1}^{t} =\beta_{2}^{t} =2.0,\;{\boldsymbol{d}}^{(0)}=\left[{2.50,2.50} \right]^{\text{T}}} \end{array}$$

(12)

The target function decreases up and to the right in the design domain. The first constraint g ₁(X) = 0 is highly nonlinear, as seen in Fig. 5a. The shaded area is the feasible region. The optimal RBDO design point “+” is located at (2.8421, 3.2320). The circle around the optimal design point d ^opt is the β ^t-circle.

Fig. 5

True limit state functions and sampling process of LHS for example 1

Latin hypercube sampling with 45 sample points is shown in Fig. 5b. The solid-line curves are the limit state constraints predicted by the Kriging models, and the dotted-line curves are the true constraints. “×” denote locations of the sample points. It can be seen that the sample points are evenly located within the whole design domain when using LHS, even in the infeasible region in the left bottom of the design space. However, the first constraint is inaccurate in the region around the optimal design point d ^opt.

The constraint boundary sampling adopts grid sampling with nine points, 3-level full factorial design, as initial sampling. Forty-five points are used to approximate the two constraints. As seen in Fig. 6a, most of the sample points are located along the limit state constraints, and the two limit state constraints are precisely approximated in the whole design domain. However, there are only three sample points in the region around the optimal design point d ^opt. So most of the sample points are not fully exploited in improving the accuracy of results.

Fig. 6

Sampling processes of CBS and SS for example 1

The SS method builds several separate local Kriging models as shown in Fig. 6b. In each design iteration, the SS method chooses a local window, and the Kriging models are constructed only using the samples within the current local window. It can be seen that the local windows gradually approach to the optimal design point. Although a lot of samples are selected, but only the samples which locate within the current local window are used to build the Kriging models. Therefore, these samples are not fully exploited.

The LAS also uses grid sampling with nine points as initial sampling. Twenty-two sample points are adopted to approximate the two constraints. we can see from Fig. 7, although the first constraint reveals inaccuracy in the region away from the optimal design point, the accuracy of the optimal design point can still be ensured, because the LAS selects sample points on the limit state constraint boundaries in the vicinity of the current design point, and during the optimization process, all the existing samples are used to construct the Kriging models, so the Kriging models are gradually becoming precise while the new samples are added.

Fig. 7

Sampling processes of LAS for example 1

The comparison results for the example 1 are shown in Table 1. ‘Anal.’ is the analytical method which directly calls the true functions. For the Kriging-model-based RBDO methods, CBS is more accurate than LHS, the SS is more efficient than CBS, the LAS uses the smallest number of samples and it is also the most accurate Kriging-model-based RBDO method.

Table 1 Summary of the optimization results for example 1

The iteration histories of the SS method and LAS method are shown in Tables 2 and 3. “Obj”. denotes the objective function value, “Radius” is the scaling factor c for the size of the local LAS region cβ ^t, “New samples” denotes the new samples added in each design iteration. It can be seen that both of the SS and LAS methods use five iterations, but the LAS method is more accurate.

Table 2 Iteration history of the SS method for example 1

Table 3 Iteration history of the LAS method for example 1

4.2 Example 2

This is a non-linear mathematical problem (see e.g., Zhao et al. 2009; Lee et al. 2011a, b). There are two random design variables X ₁, X ₂ and three probabilistic constraints g ₁, g ₂, g ₃. No deterministic design variable or random parameter exists. All random variables are statistically independent and have normal distributions.

$$ \begin{array}{l} {find:{\boldsymbol{d}}=\left[{d_{1},d_{2}}\right]^{\mathrm{T}}} \\ {\min:f({\boldsymbol{d}})=10-d_1+d_{2}} \\ {s.t.:\text{prob}\left[{g_{i}({\boldsymbol{X}})\le 0}\right]\le {\Phi}\left({-\beta_{i}^{t}}\right),i={1},{2}} \\ {g_{1} ({\boldsymbol{X}})={X_{1}^{2} X_{2}}/{20-1}} \\ {g_{2} ({\boldsymbol{X}})=1-\left({0.9063X_{1} +0.4226X_2-6} \right)^{2}} \\ {\quad \quad \quad \quad -( {0.9063X_{1} +0.4226X_{2} -6} )^3+0.6}\\ \quad \quad \quad \quad \times \left( {0.9063X_{1} +0.4226X_{2} -6}\right)^{4}\\ \quad \quad \quad \quad +( {-0.4226X_{1} +0.9063X_{2}})\\ {g_{3} ( {\boldsymbol{X}} )={80}/ {\left( {X_{1}^{2} +8X_{2} +5} \right)-1}} \\ {0.0\le d_{i} \le 10.0,\quad \quad X_{i} \sim N\left( {d_{i} ,0.50^{2}} \right),\;i=1,2} \\ {\beta_{1}^{t} =\beta_{2}^{t} =\beta_{3}^{t} =2.0,\quad {\boldsymbol{d}}^{\left( 0 \right)}=[ {5.00,5.00} ]^{\mathrm{T}}} \end{array} $$

(13)

The target function decreases down and to the right in design space. The second constraint is highly nonlinear, as seen in Fig. 8a. The optimal design point d ^opt for RBDO is located at (4.6868,2.0513). The shaded area is the feasible region. The circle around the optimal design is the β ^t-circle.

Fig. 8

True limit state functions and sampling process of LHS for example 2

Latin hypercube sampling is shown in Fig. 8b. The solid-line curves are the limit state constraints predicted by Kriging models, and the dotted-line curves are the true constraints. 50 points are evenly located within the whole design space. However, many sample points are located out of the feasible region, and the limit state constraints 2 and 3 are not accurate.

As seen in Fig. 9a, with nine grid points as initialization, the CBS applies 43 points to approximate the three constraints. Most of these samples are located on the boundaries of the limit state constraints within the feasible region. The boundaries of the feasible region are well approximated. However, very few sample points are located in the region around the optimal design points, which means many sample points are not well explored in improving the accuracy of the results.

Fig. 9

Sampling processes of CBS and SS for example 2

The SS method is shown in Fig. 9b. It can be seen that the local windows move to the optimal design gradually, and many samples are selected in the vicinity of the optimal design point. However, most of these samples are not located on the limit state functions, and the SS method only uses the samples within the current local window to construct Kriging models, therefore, the Kriging model for constraint g ₂(X) is not accurate.

LAS uses nine grid samples as initial sampling, and total 31 sample points are used to approximate the three constraints. As seen in Fig. 10, the local sampling region moves to the optimal design point gradually, and when the local region contains limit state constraints, most of these sample points will be located on the limit state constraint boundaries. So the boundaries of constraint 1 and 2 around the optimal design point are well fitted, and they will ensure the accuracy of the optimal design.

Fig. 10

Sampling processes of the LAS for example 2

The comparison results for the example 2 are shown in Table 4. The CBS is more accurate and efficient than the LHS. The SS method is more efficient than CBS. The number of samples for LAS is equal to 31, which means that LAS is the most efficient. The relative error from LAS is 0.04 %, and the MCS results are very close to the target value 2.0, so the proposed LAS method is also very accurate.

Table 4 Summary of the optimization results for the example 2

The iteration histories of the SS method and LAS method are shown in Tables 5 and 6. It can be seen that both of the SS and LAS methods use four iterations, but the LAS method is more accurate.

Table 5 Iteration history of the SS method for example 2

Table 6 Iteration history of the LAS method for example 2

4.3 A speed reducer

A speed reducer shown in Fig. 11 is used to rotate the engine and propeller with efficient velocity in light plane (Cho and Lee 2011). This problem has seven random variables and 11 probabilistic constraints. The objective function is to minimize the weight and probabilistic constraints are related to physical quantities such as bending stress, contact stress, longitudinal displacement, stress of the shaft, and geometry constraints. The random design variables are gear width (X ₁), gear module (X ₂), the number of pinion teeth (X ₃), distance between bearings (X ₄, X ₅), and diameter of each shaft (X ₆, X ₇).

Fig. 11

A speed reducer

All random variables are statistically independent and have normal distributions. The description of the RBDO model of the speed reducer is as follows:

$$ \begin{array}{l} {find\!:{\boldsymbol{d}}=\left[ {d_1 ,d_2 ,d_3 ,d_4 ,d_5 ,d_6 ,d_7}\right]^{\mathrm{T}}} \\[6pt] \min\!:\!f( {\boldsymbol{d}} )=0.7854d_1 d_2^2 \left(3.3333d_3^2 + 14.9334d_3\right.\\[6pt]\left. {\kern8pc} - 43.0934 \right)-1.5080d_1 \left( {d_6^2 +d_7^2}\right) \\[6pt] {\quad \quad \quad \quad \quad \quad +7.4770\left( {d_6^3 +d_7^3}\right)\!+\!0.7854\left( {d_4 d_6^2 +d_5 d_7^2} \right)} \\[6pt] {s.t.\!:\mathrm{prob}[ {g_i ( {\boldsymbol{X}} )>0} ]\le{\Phi} \left( {-\beta_i^t} \right),\;i=1,\cdots ,11} \\[6pt] {g_1 ( {\boldsymbol{X}} )={27} / {X_1 X_2^2 X_3-1},\quad g_2 ( {\boldsymbol{X}} )\!=\!{397.5}/ {X_1 X_2^2 X_3^2 \!-\!1}} \\[6pt] {g_3 ( {\boldsymbol{X}} ) {\kern-3pt} = {\kern-3pt}{1.93X_4^3} {\kern-.5pt}/{\kern-.5pt} {X_2 X_3 X_6^4 {\kern-3pt} - {\kern-3pt} 1},\,\, g_4 ( {\boldsymbol{X}} ){\kern-3pt}={\kern-3pt} {1.93X_5^3}/ {X_2 X_3 X_7^4 {\kern-3pt} - {\kern-3pt} 1}} \\[6pt] {g_5 ( {\boldsymbol{X}} )=\left(\sqrt{\left( {{745X_{4}} / {({X_{2} X_{3}} )}} \right)^{2}+16.9\times10^{6}}\right)}\\[6pt]{\kern5.8pc} / \left(0.1X_{6}^{3}\right)-1100\\[6pt] {g_6 ( {\boldsymbol{X}} )=\left(\sqrt{\left( {{745X_{5}} / {( {X_{2} X_{3}})}}\right)^{2}+157.5\times 10^{6}}\right)}\\[6pt]{\kern5.8pc} {/\left(0.1X_{7}^{3}\right)-850} \\[6pt] {g_7 ( {\boldsymbol{X}} )\!=\!X_2 X_3 \!-\! 40,\quad \quad \quad g_8 ( {\boldsymbol{X}} )\!=\!{5-X_1} / {X_2} } \\[6pt] {g_9 ( {\boldsymbol{X}} )\!=\!{X_1} / {X_2} -12,\quad \quad \;g_{10} ( {\boldsymbol{X}} )\!=\!{( {1.5X_6 \!+\! 1.9} )}/ {X_4 \!-\! 1}} \\[6pt] {g_{11} ( {\boldsymbol{X}} )={( {1.1X_7 +1.9} )}/ {X_5 -1}} \\[6pt] {2.6\le d_1 \le 3.6,\quad 0.7\le d_2 \le 0.8,\quad 17\le d_3 \le 28} \\[6pt] {7.3\le d_4 \le 8.3,\quad 7.3\le d_5 \le 8.3,\quad 2.9\le d_6 \le 3.9} \\[6pt] {5.0\le d_7 \le 5.5,\quad X_j \sim N( {d_j ,0.005^2} ),\quad j=1,\cdots ,7} \\[6pt] {\beta_1^t =\cdots =\beta_{11}^t =3.0} \\[6pt] {{\boldsymbol{d}}^{( 0 )}=\left[{3.2,\;0.75,\;23,\;8.0,\;8.0,\;3.6,\;5.0} \right]^{\mathrm{T}}} \end{array} $$

(14)

The comparison results for the speed reducer are shown in Tables 7 and 8. The initial sampling sizes for CBS, SS and LAS are all 36 using LHS. From Table 7, it can be seen that the CBS is more accurate and efficient than the LHS, but the SS method is not accurate. The number of samples in LAS is equal to 46, so it is very efficient. The design results from the LAS method are almost identical with that from the analytical method, which conforms that the proposed LAS is also very accurate.

Table 7 Summary of the optimization results for example 3

Table 8 Summary of the MCS results for example 3

The iteration histories of the SS and LAS methods are shown in Tables 9, 10, 11 and 12. Both of the two methods have two design iterations. However, the SS method uses only the samples within the local window to construct the Kriging models, so in the second design iteration, the SS needs 36 new samples to build the Kriging models. But the LAS applies all the existing samples to build the Kriging models, so in the second iteration of the LAS method, only 10 new samples are selected. It can be seen that the LAS is more efficient and accurate.

Table 9 Iteration history of the SS method for example 3

Table 10 Iteration MCS results of the SS method for example 3

Table 11 Iteration history of the LAS method for example 3

Table 12 Iteration MCS results of the LAS method for example 3

4.4 Honeycomb crashworthiness design

As shown in Fig. 12, this example (Sun et al. 2010) is about the Honeycomb cellular materials or structures that have been an important research topic recently for its outstanding potential in energy absorption, thermal isolation and dynamic and acoustic damper. This study deals with the predominantly axial (H-direction) crushing of aluminum honeycombs, as it provides the best mechanical performance and has been most often utilized in practice.

Fig. 12

Nomenclature of the hexagonal honeycomb

The dimension of each cell is described as follows: w is the cell size defined by the distance of opposite sides in the cell, d the side length of honeycomb cell, D the width of honeycomb cell, t the thickness of single foil. The foil material used in the experiment is an aluminum alloy, whose constitutive behavior is assumed to be elastoplastic with von-Mises isotropic plastic hardening, given by

$$ \sigma =\sigma_{0} +\sigma_{t} \varepsilon $$

(15)

The objective is to maximize the specific energy absorption (SEA) defined in the crash energy absorbed by unit weight of the honeycomb as

$$ \text{SEA}=\frac{\mathrm{Total\;absorbed\;energy}}{\mathrm{Total\;structural\;weight}} $$

(16)

The deceleration peak α _max during crashing is the probabilistic constraint. It is known that the variations of factors t and σ ₀ appears more sensitive to SEA and α _max. Therefore, these two parameters are selected as the design variables to optimize the honeycomb structure for the crashworthiness criteria.

Axial impact test was conducted on honeycomb structures as in Fig. 13 to validate the computational modeling. Figure 14 shows the deformation with its buckling and folding pattern for element size = 1 mm at different time steps.

Fig. 13

Axial impact test

Fig. 14

Experimental and numerical deformation pattern at different time steps

The optimization problem is defined as below:

$$ {\begin{array}{l} {find:\mu_{t} ,\mu_{\sigma_{0}} } \\ {\text{max}:SEA({\mu_{t} ,\mu_{\sigma_{0}} } )} \\ {s.t.:\text{prob}\left[ {\alpha_{\max} \le \alpha_{\text{const}}} \right]\ge {\Phi} ( {\beta^{t}} )} \\ {t\sim N\left( {\mu_{t} ,0.004^{2}} \right),\;\sigma_{0} \sim N\left( {\mu_{\sigma_{0}} ,0.006^{2}} \right)} \\ {0.05\le \mu_{t} \le 0.20,\;0.15\le \mu_{\sigma_{0}} \le 0.40,} \\ {\beta^t=3.0,\;\left( {\mu_{t}^{\left( 0 \right)} ,\;\mu_{\sigma_{0}}^{( 0 )}} \right)=[ {0.10,0.30.} ]^{\mathrm{T}}} \end{array}} $$

(17)

Where (t, σ ₀) is the random design variable vector, α _const is the upper limit of the peak acceleration, which is set as 30 g herein.

The comparison results for the Honeycomb crashworthiness design are shown in Table 13. CBS is more efficient than the LHS, and the SS method is more accurate and effective than CBS. In LAS, the number of samples is only 15, so it is very efficient. The optimal design from the LAS method is almost identical with that in analytical method; and the relative error is 0.003 %, therefore the LAS is also very accurate.

Table 13 Summary of the optimization results for example 4

The iteration histories of the SS and LAS methods are shown in Tables 14 and 15, from which it can be seen that LAS has the same number of the iterations, but it is more accurate than the SS method.

Table 14 Iteration history of the SS method for example 4

Table 15 Iteration history of the LAS method for example 4

5 Conclusion

The LAS method is proposed to improve the efficiency and accuracy of Kriging-model-based RBDO. It selects new samples from the local region which is around the current design point in each optimization iteration, and within the local region, sample points are first considered to be located on the limit state constraint boundaries. The size of the LAS region is adaptively defined according to the nonlinearity of the performance functions.

Several examples are tested in order to verify the accuracy and efficiency of the proposed method. Through the examples it is seen that the proposed LAS method is very efficient. The MCS results for LAS are almost identical with the target values, which verifies that the proposed LAS is very accurate. Also, the LAS uses the smallest number of samples, which shows that the computational cost can be reduced significantly.

There are still many work can be done to improve the accuracy of RBDO problems. For example, when samples are close to the limit state boundaries, it is better to use the support vector regression (SVR) method to the fit the implicit models; and the active constraints strategy will also improve the efficiency of the RBDO problem. In the future work, we will study these issues to make the LAS method more applicable to RBDO problems.