1 Introduction

There are many uncertainties existing in practical engineering problems, such as structure sizes, material characteristics and boundary conditions. Traditional reliability analysis and design methods adopt the probability model to deal with these uncertain variables, which include the first order reliability method (FORM) (Hasofer and Lind 1974; Rackwitz and Fiessler 1978; Madsen et al. 2006; Wu et al. 1990), second order reliability method (SORM) (Breitung 1984), reliability-based design optimization (RBDO) (Enevoldsen and Sørensen 1994; Kuschel and Rackwitz 1997; Wu and Wang 1998; Li et al. 2001), etc. Traditional probability method generally needs a large number of samples to establish the random distributions of uncertain variables, while in practical problems some variables are often difficult to get enough samples since the cost and test condition are limited. Thus some assumptions have to be made for the distribution functions when using the probability method to deal with some practical engineering problems. However, the existing research (Ben-Haim and Elishakoff 1990) has indicated that a tiny deviation of the probability distribution might cause a large reliability calculation error, and it will be more obvious when the failure probability of a problem is very small (Ben-Haim 1994; Elishakoff 1995). For example (Ben-Haim 1994), through the reliability analysis for a cylindrical tube under uncertain pressure load, it could be found that a 5.3 % deviation of the pressure’s distribution parameters caused a ten times reliability calculation error. In order to solve the above problem, in recent years two kinds of probability-interval mixed uncertain models were established to deal with the parametric uncertainty with limited information. In the first kind of hybrid model, all the uncertain parameters are divided into two types: variables with sufficient samples and variables lacking samples. The former can be treated as random variables and given precise probability distribution functions; while the latter can only be given intervals since lacking sufficient information. So far some work (Penmetsa and Grandhi 2002; Guo and Lu 2002; Cheng et al. 2005; Du 2007; Luo et al. 2008; Wang and Qiu 2010; Fang et al. 2014; Alibrandi and Koh 2015; Guo and Du 2009) has been carried out for this uncertain model. (Penmetsa and Grandhi 2002) developed a probability-interval hybrid reliability assessment method based on an approximate model. (Guo and Lu 2002) gave a reliable probability measure method for structures based on the probability and non-probability models. (Cheng et al. 2005) put forward a structural robustness design method based on the hybrid model when probabilistic and non-probabilistic uncertainties existed simultaneously. (Du 2007) presented two kinds of probability-interval hybrid reliability models, and the corresponding efficient decoupling algorithms were established to deal with the nested optimization process. (Luo et al. 2008) used a quantified measure for the non-probabilistic reliability based on the multi-ellipsoid convex model. (Wang and Qiu 2010) evaluated the reliability of the probability and interval mixed uncertain structural system and established the mathematical model of reliability analysis. (Alibrandi and Koh 2015) presented a novel procedure based on FORM; and the probability-interval hybrid reliability problem was decoupled to several reliability problems in which the limit state functions were defined only in terms of the random variables. In the second kind of probability and interval hybrid model, the uncertain variables are all treated as random variables, while some crucial distribution parameters can only be given variation intervals since the lack of samples. This model was first introduced to structural analysis by (Elishakoff and Colombi 1993, 1994), and the worst response of a random vibration structure was investigated. (Zhu and Elishakoff 1996) studied a periodic finite-span beam subjected to the stochastic acoustic pressure with bounded parameters, and formulated the transverse displacement and the bending moment responses of the structure. (Qiu et al. 2008) introduced an interval approach to conventional reliability theory to obtain the system failure probability interval. (Jiang et al. 2011, 2012) proposed several efficient hybrid reliability analysis methods by combining probability and non-probability models. (Zhang et al. 2013) constructed a probability model for uncertainty structures on the basis of limited information and proposed a quasi-Monte Carlo simulation methodology to compute the bounds of structural failure probability.

All the above mentioned researches were mainly concentrated on reliability assessment of the probability-interval hybrid models, in which the upper and lower bounds of reliability degree or the failure probability were evaluated for the structure with mixed uncertainties. Nevertheless, there are few researches on structural reliability optimization design for the probability-interval mixed uncertain problem. The RBDO can take full consideration of the influence of parametric uncertainty on constraints, thus it can ensure that the obtained optimal solution meets the reliability request. It plays an important role in safety design of engineering structures and products. RBDO has presently become an important research area in the field of structural reliability. A series of effective methods of RBDO has been developed, which include the single-loop decoupling method (Du and Chen 2004; Liang et al. 2004; Cheng et al. 2006; Shan and Wang 2008; Chen et al. 2013) and the response-surface-based method (Youn and Choi 2004; Kim 2008; Shan and Wang 2009; Zhuang and Pan 2012; Li et al. 2013), etc. Traditional RBDO methods are generally based on the probability model which requires a large number of samples to establish precise probability distribution functions of the uncertain parameters. Thus by introducing the probability-interval mixed uncertainty modeling technique into the RBDO problem, it seems hopeful and promising to significantly reduce the dependence of the traditional RBDO on samples and hence greatly expand the practicability of RBDO method in many complex engineering problems. However, there are so far few researches on the probability-interval hybrid reliability-based design optimization (HRBDO). (Du and Sudjianto 2003; Du 2012) used the biggest failure probability to measure the structural reliability under mixed uncertainties, and a corresponding single-layer decoupling algorithm was proposed. (Kang and Luo 2010) presented a RBDO approach with a probability and convex set hybrid model. These works are all based on the first kind of hybrid model, and on the best knowledge of the authors there are still no relevant studies related to the second kind of hybrid model.

Based on the second kind of probability-interval hybrid model, the paper thus aims to develop a new RBDO model and corresponding efficient solution algorithm such that provide an effective reliability design tool for many complex engineering problems. The remainder of this paper is organized as follows. General concept of the RBDO problem with precise distribution parameters is introduced in Section 1. Section 2 formulates the hybrid RBDO model as well as the solution algorithm. Section 3 presents three numerical examples to demonstrate the validity of the proposed method. Concluding remarks are drawn in section 4.

2 Traditional RBDO with precise probability distributions

There generally exists an amount of uncertainty in practical engineering problems such as loads, material parameters, geometrical sizes, etc. The result of a traditional deterministic optimization may be unsafe if we do not take the uncertainty into account. RBDO can fully take into account the impact of the uncertain parameters on the constraints in the optimization process, and whereby enables the optimization results to meet the requirements of reliability. A conventional RBDO problem with precise distributions can generally be formulated as follows (Du and Chen 2004):

$$ \begin{array}{l}\underset{\mathbf{d},{\boldsymbol{\upmu}}_{\mathbf{X}}}{ \min}\kern0.5em f\left(\mathbf{d},{\boldsymbol{\upmu}}_{\mathbf{X}},{\boldsymbol{\upmu}}_{\mathbf{P}}\right)\\ {}\mathrm{s}.\mathrm{t}.\kern1em Prob\left({g}_j\left(\mathbf{d},\mathbf{Z}\right)\ge 0\right)\ge {R}_j^{\mathrm{t}},\kern1.5em j=1,2,\dots, {n}_g\\ {}\kern3.5em \mathbf{Z}=\left[\mathbf{X},\mathbf{P}\right],\kern0.5em {\mathbf{d}}^l\le \mathbf{d}\le {\mathbf{d}}^u,{\boldsymbol{\upmu}}_{\mathbf{X}}^l\le {\boldsymbol{\upmu}}_{\mathbf{X}}\le {\boldsymbol{\upmu}}_{\mathbf{X}}^u\kern3.5em \end{array} $$
(1)

where f and g j are objective function and the j -th constraint, respectively; n g is the number of constraints; d denotes the n d -dimensional deterministic design vector; X denotes the n X -dimensional random design vector. P denotes the n P -dimensional random parameter vector; μ X and μ P denote the mean vectors of X and P, respectively. Z denotes the n Z -dimensional random vector consisted of X and P, and its mean vector is μ Z ; The superscripts l, u denote the range of the variable values. In practical engineering problems, f and g j are generally nonlinear implicit functions. The former is correlated with d, μ X and μ P , and the latter is correlated with d, X and P. Prob denotes the probability of the constraint satisfaction, which is also called the reliability degree; R t j is the target reliability degree of the j -th constraint.

Assuming that X and P are independent to each other, for an arbitrary d and μ X , the reliability degree of the j -th constraint can be stated as:

$$ Prob\left({g}_j\left(\mathbf{Z}\right)\ge 0\right)={\displaystyle {\int}_{g_j\ge 0}{h}_{\mathbf{Z}}\left(\mathbf{Z}\right)}d\mathbf{Z} $$
(2)

where h Z (Z) represents the joint probability density function of Z.

At present, FORM (Hasofer and Lind 1974; Rackwitz and Fiessler 1978; Madsen et al. 2006; Wu et al. 1990) is the most common method to conduct the reliability analysis of the constraint. Its basic idea is to transform the constraint function from the original space (Z space) to the standard normal space (U space), and then establish the linear approximation of the constraint function at the most probable failure point (MPP) for efficiently calculating the reliability. The transformation of the random variables from the Z space to the U space can be formulated as (Madsen et al. 2006):

$$ \begin{array}{ll}\varPhi \left({U}_i\right)={F}_{Z_i}\left({Z}_i\right),\hfill & i=1,2,\dots, {n}_Z\hfill \\ {}{U}_i={\varPhi}^{-1}\left({F}_{Z_i}\left({Z}_i\right)\right),\hfill & {Z}_i={F}_{Z_i}^{-1}\left(\varPhi \left({U}_i\right)\right)\hfill \end{array} $$
(3)

where \( {F}_{Z_i} \) and \( {F}_{Z_i}^{-1} \) denote the cumulative distribution function and its inverse function of Z i , respectively. Φ and Φ − 1 are the standard normal cumulative distribution function and its inverse function, respectively. U denotes the vector of Z in the standard normal space. Then, the probability constraints in Eq. (1) can be rewritten as:

$$ \begin{array}{l} Prob\left({g}_j\left(\mathbf{d},\mathbf{Z}\right)\ge 0\right)={\displaystyle {\int}_{G_j\ge 0}{h}_{\mathbf{U}}\left(\mathbf{U}\right)d\mathbf{U}\ge {R}_j^t}\hfill \\ {}{R}_j^t=\varPhi \left(\hbox{-} {\beta}_j^t\right),\kern2.5em j=1,2,\dots, {n}_g\hfill \end{array} $$
(4)

where G j is the constraint function of g j in the U space; h U is the joint probability density function of the standard normal vector U; β t j denotes the target reliability index of the j -th constraint.

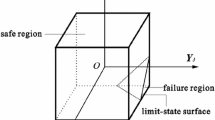
Reliability index approach (RIA) (Hasofer and Lind 1974; Rackwitz and Fiessler 1978) is usually adopted to deal with Eq. (4) among the existing FORMs. In RIA, the reliability index of the jth constrain, β j , denotes the minimum distance between the limit-state surface and the original point in the U space, which can be calculated by:

$$ \begin{array}{l}{\beta}_j=\underset{\mathbf{U}}{ \min}\kern0.5em \left\Vert \mathbf{U}\right\Vert \\ {}\mathrm{s}.\mathrm{t}.\kern0.5em {G}_j\left(\mathbf{U}\right)=0\end{array} $$
(5)

Its optimal solution U MPP, j and reliability index β * j can be obtained using some well established algorithms such as the HL-RF iterations (Hasofer and Lind 1974; Rackwitz and Fiessler 1978) or the improved HL-RF iterations (iHL-RF) (Madsen et al. 2006). If β j  ≥ β t j is true, it means that the constraint satisfies the reliability requirement.

Based on the above analysis, RBDO uses probabilistic constraints to establish a direct link between the uncertain variables and the design point, and the constraint reliability under uncertainty should be evaluated for each involved design point. Thus, a two-layer nested optimization will be involved when solving the RBDO problem. In the outer layer, the optimization of design variables requires calling the reliability analysis in the inner layer repeatedly, which generally leads to a very low computational efficiency. So far, a series of decoupling strategies have been proposed to solve the above mentioned nested optimization, such as the sequence optimization method and reliability analysis (SORA) (Du and Chen 2004), the single-loop method (Liang et al. 2004), the sequential approximate programming method (Cheng et al. 2006), etc. The fundamental principle of these methods is to separate the reliability analysis from the design optimization, and whereby construct a sequence of efficient iterations.

3 The hybrid RBDO method with interval distribution parameters

In practical RBDO problems, we often encounter a situation that some important distribution parameters (such as the mean value, standard deviation, etc.) of the random variables can only be given variation intervals rather than deterministic values since lacking sufficient experimental data. As thus, the interval distribution parameters are included in the random variables Z in Eq. (1). In this paper, we use an n Y -dimensional interval vector \( \mathbf{Y}=\left({Y}_1,{Y}_2,\dots, {Y}_{n_Y}\right) \) to represent all the interval distribution parameters existing in the random vector Z:

$$ {Y}_i\in \left[{Y}_i^{\mathrm{L}},{Y}_i^{\mathrm{U}}\right],\kern0.5em i=1,2,\dots, {n}_Y $$
(6)

where Y L i and Y U i are the lower and upper bounds of the j -th interval distribution parameter respectively. Thus the constraint function of g j can be rewritten as g j (d, Z, Y). For convenience of analysis, we assume that each random variable Z i contains a single interval variable Y i at most in its distribution function.

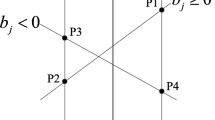
The reliability of the constraint then can be represented as Prob(g j (d, Z, Y) ≥ 0). As shown in Fig. 1, the limit-state surface defined in g j (d, Z, Y) = 0 will divide the Z space into a feasible domain and a failure domain. For each specific Y′ within the intervals the g j (d, Z, Y′) = 0 will be a limit-state surface, and hence after synthesizing all the possible cases of Y′, g j (d, Z, Y) = 0 actually is no longer a surface but a strip composed of two boundary surfaces \( \underset{\mathbf{Y}}{ \max }{g}_j\left(\mathbf{d},\mathbf{Z},\mathbf{Y}\right)=0 \) and \( \underset{\mathbf{Y}}{ \min }{g}_j\left(\mathbf{d},\mathbf{Z},\mathbf{Y}\right)=0 \). Then, the reliability of the constraint also has a lower bound Pr L j and an upper bound Pr U j (Du 2007; Jiang et al. 2011):

$$ P{r}_j^{\mathrm{U}}= Prob\left(\underset{\mathbf{Y}}{ \max }{g}_j\left(\mathbf{d},\mathbf{Z},\mathbf{Y}\right)\ge 0\right) $$
(7)
$$ P{r}_j^{\mathrm{L}}= Prob\left(\underset{\mathbf{Y}}{ \min }{g}_j\left(\mathbf{d},\mathbf{Z},\mathbf{Y}\right)\ge 0\right) $$
(8)
Fig. 1
figure 1

Limit-state strip caused by the interval variables

Full size image

For a practical RBDO problem, the maximal failure probability is generally what we most care about. Thus in order to ensure a safety design, this paper selects the minimal reliability (or the maximal failure probability) to measure the reliability of each constraint, and whereby creates a hybrid RBDO model as follows:

$$ \begin{array}{l}\underset{\mathbf{d},{\boldsymbol{\upmu}}_{\mathbf{X}}}{ \min}\kern0.5em f\left(\mathbf{d},{\boldsymbol{\upmu}}_{\mathbf{X}},{\boldsymbol{\upmu}}_{\mathbf{P}}\right)\\ {}s.t.\kern1em P{r}_j^{\mathrm{L}}= Prob\left(\underset{\mathbf{Y}}{ \min }{g}_j\left(\mathbf{d},\mathbf{Z},\mathbf{Y}\right)\ge 0\right)\ge {R}_j^{\mathrm{t}},\kern1.5em j=1,2,\dots, {n}_g\\ {}\kern3.5em \mathbf{Z}=\left[\mathbf{X},\mathbf{P}\right],\kern0.5em {\mathbf{d}}^l\le \mathbf{d}\le {\mathbf{d}}^u,\kern0.5em {\boldsymbol{\upmu}}_{\mathbf{X}}^l\le {\boldsymbol{\upmu}}_{\mathbf{X}}\le {\boldsymbol{\upmu}}_{\mathbf{X}}^u,\\ {}\kern3.5em {Y}_i\in \left[{Y}_i^{\mathrm{L}},{Y}_i^{\mathrm{U}}\right],i=1,2,\dots, {n}_Y\end{array} $$
(9)

3.1 Hybrid reliability analysis of the constraints

For a design point [d, μ X ], the reliability of g j can be expressed as:

$$ Prob\left(\underset{\mathbf{Y}}{ \min }{g}_j\left(\mathbf{d},\mathbf{Z},\mathbf{Y}\right)\ge 0\right)\ge {R}_j^{\mathrm{t}} $$
(10)

When the reliability analysis is based on RIA, the following optimization problem needs to solve (Jiang et al. 2011):

$$ \begin{array}{l}\kern2em {\beta}_j=\underset{\mathbf{U}}{ \min}\kern0.5em \left\Vert \mathbf{U}\right\Vert \\ {}\mathrm{s}.\mathrm{t}.\kern0.5em \underset{\mathbf{Y}}{ \min }{G}_j\left(\mathbf{U},\mathbf{Y}\right)=0\\ {}\kern2.5em {Y}_i\in \left[{Y}_i^{\mathrm{L}},{Y}_i^{\mathrm{U}}\right],i=1,2,\dots, {n}_Y\end{array} $$
(11)

Obviously, Eq. (11) is a two-layer nested optimization problem. The inner-layer optimization is the interval analysis:

$$ \begin{array}{l}{G}_j\left(\mathbf{U},{\mathbf{Y}}_j^{*}\right)=\underset{\mathbf{Y}}{ \min }{G}_j\left(\mathbf{U},\mathbf{Y}\right)\\ {}\mathrm{s}.\mathrm{t}.\kern1em {Y}_i\in \left[{Y}_i^{\mathrm{L}},{Y}_i^{\mathrm{U}}\right],i=1,2,\dots, {n}_Y\kern0.5em \end{array} $$
(12)

And the outer-layer optimization is the reliability analysis:

$$ \begin{array}{l}{\beta}_j=\underset{\mathbf{U}}{ \min}\left\Vert \mathbf{U}\right\Vert \\ {}\mathrm{s}.\mathrm{t}.\kern0.75em {G}_j\left(\mathbf{U},{\mathbf{Y}}_j^{*}\right)=0\end{array} $$
(13)

According to the authors’ recent work (Jiang et al. 2011), for the hybrid reliability problem formulated in Eq. (11), the maximal failure probability appears on a certain boundary combination of the interval vector when the distribution function of a random variable contains only one interval parameter. Taking n Y  = 2 as an example, there are a total of four boundary combinations, Y 1 = (Y L1 , Y L2 ), Y 2 = (Y L1 , Y U2 ), Y 3 = (Y U1 , Y L2 ) and Y 4 = (Y U1 , Y U2 ), and the maximal failure probability Y * j must be one of these four cases. For a more general case, the boundary combinations of interval variables Y i , i = 1, 2, …, n Y have \( {2}^{n_Y} \) cases. In theory, the reliability analysis can be carried out for all the cases:

$$ \left.\begin{array}{l}{\beta}_j=\underset{\mathbf{U}}{ \min}\kern0.5em \left\Vert \mathbf{U}\right\Vert \\ {}\mathrm{s}.\mathrm{t}.\kern0.5em {G}_j\left(\mathbf{U},{\mathbf{Y}}_i\right)=0\end{array}\right\}i=1,2,\dots, {2}^{n_Y} $$
(14)

Each Y i has a corresponding reliability index β j ; the minimum β * j and the corresponding Y * j represent the worst reliability situation of the constraint. Then, the Eq. (10) can be changed to:

$$ Prob\left({g}_j\left(\mathbf{d},\mathbf{Z},{\mathbf{Y}}_j^{*}\right)\ge 0\right)\ge {R}_j^{\mathrm{t}} $$
(15)

Though the above approach can be used to deal with the nested optimization in Eq. (11), will still need to solve many times of multi-variable optimization problems in Eq. (14) and hence require much computational cost. In order to further improve computational efficiency, an approximation method is given here to solve Eq. (14) more efficiently. For a particular boundary case Y i of the interval parameters, the reliability index β j of g j denotes the minimum distance between the limit-state surface G j (U, Y i ) = 0 and the original point U 0 as shown in Fig. 2. According to the fundamental principles of RIA (Madsen et al. 2006), Eq. (14) can be expressed as:

$$ {G}_j\left(-{\beta}_j\frac{\nabla {G}_j\left({\mathbf{U}}_{\mathrm{MPP},\kern0.5em j},{\mathbf{Y}}_i\right)}{\left\Vert \nabla {G}_j\left({\mathbf{U}}_{\mathrm{MPP},\kern0.5em j},{\mathbf{Y}}_i\right)\right\Vert },{\mathbf{Y}}_i\right)=0,\kern0.5em i=1,2,\dots, {2}^{n_Y} $$
(16)

where ∇G j (U MPP, j , Y i ) represents the gradient vector of the constraint function with respect to the random variables. For a constraint that does not yet meet the requirement of reliability, the distance between U MPP, j and the mean value point U 0 is relatively close. Thus the contour of the constraint function G j (U, Y i ) = G j (U 0, Y i ) generally has a very similar shape as G j (U, Y i ) = 0. Therefore in Eq. (16) we can use the gradient vector ∇G j (U 0 , Y i ) substitute the actual gradient vector ∇G j (U MPP, j , Y i ), and whereby an approximate MPP Ũ MPP, j and corresponding reliability index \( {\tilde{\beta}}_j \) can be obtained by solving the following equation:

$$ {G}_j\left(-{\tilde{\beta}}_j\frac{\nabla {G}_j\left({\mathbf{U}}_{\mathbf{0}},{\mathbf{Y}}_i\right)}{\left\Vert \nabla {G}_j\left({\mathbf{U}}_{\mathbf{0}},{\mathbf{Y}}_i\right)\right\Vert },{\mathbf{Y}}_i\right)=0,\kern1em i=1,2,\dots, {2}^{n_Y} $$
(17)
Fig. 2
figure 2

The calculation of MPP

Full size image
Fig. 3
figure 3

Shifting vector of the uncertain constraint

Full size image

For a certain Y i , the above equation is a root-finding problem of the nonlinear equation with only one unknown variable \( {\tilde{\beta}}_j \), which can be efficiently solved by the well-known Newton iteration method (Burden and Faires 1985):

$$ {\left({\tilde{\beta}}_j\right)}_{k+1}={\left({\tilde{\beta}}_j\right)}_k+\frac{\left\Vert \nabla {G}_j\left({\mathbf{U}}_{\mathbf{0}},{\mathbf{Y}}_i\right)\right\Vert }{\nabla {G}_j\left({\mathbf{U}}_{\mathbf{0}},{\mathbf{Y}}_i\right)}\frac{G_j\left(-{\left({\tilde{\beta}}_j\right)}_k\frac{\nabla {G}_j\left({\mathbf{U}}_{\mathbf{0}},{\mathbf{Y}}_i\right)}{\left\Vert \nabla {G}_j\left({\mathbf{U}}_{\mathbf{0}},{\mathbf{Y}}_i\right)\right\Vert}\right)}{G_j^{\prime}\left(-{\left({\tilde{\beta}}_j\right)}_k\frac{\nabla {G}_j\left({\mathbf{U}}_{\mathbf{0}},{\mathbf{Y}}_i\right)}{\left\Vert \nabla {G}_j\left({\mathbf{U}}_{\mathbf{0}},{\mathbf{Y}}_i\right)\right\Vert}\right)} $$
(18)

where k represents the iteration step. Generally, the solution of the above root-finding problem is much more efficient than the multi-variable optimization in Eq. (14).

3.2 The decoupling strategy

Through the above method, the computational cost of the inner-layer hybrid reliability analysis can be significantly reduced, while on the whole the nested optimization problem of the hybrid RBDO still exists. To further enhance the calculation efficiency of the optimization process, the strategy of incremental shifting vector (ISV) is introduced here to establish a more efficient algorithm for the hybrid RBDO. The ISV technique is a new decoupling algorithm for RBDO which is proposed by the authors recently (Huang et al. 2016). Just like the existing decoupling algorithms (Du and Chen 2004; Liang et al. 2004), the basic idea of ISV is also to convert the nested optimization into a sequential iterative process of the design optimization and the reliability analysis. During the stage of design optimization, the original uncertain constraints are transformed to deterministic constrains, and a new design point is obtained by solving this deterministic optimization problem. In the reliability analysis stage, a reliability assessment is implemented on the new design point, based on which the deterministic design optimization can be also created for the next iteration. The design optimization and the reliability analysis are alternately executed until convergence.

As shown in Fig. 3, the core of ISV is to transform the probabilistic constraint in Eq. (15) into a deterministic constraint, through constructing a shifting vector. For convenience of illustration, we assume that the constraint g j contains only Z = [X, P] but no d. Firstly, the random vector is replaced by the mean vector μ Z , namely its uncertainty is not considered; the Z space is then divided into two domains by the constraint boundary g j (μ Z ) = 0, the feasible domain g j (μ Z ) ≥ 0 and the failure domain g j (μ Z ) < 0. Then, the consideration of uncertainty will result in the decrease of the feasible domain, and its probabilistic constraint boundary Prob{g j (Z, Y * j ) ≥ 0} = R t j will be located inside the feasible domain g j (μ Z ) ≥ 0. In the ISV technique, the approximate equivalent boundary of the probabilistic constraint is obtained through moving g j (μ Z ) = 0 to g j (μ Z  − S j ) = 0 by a vector S j . In the hybrid RBDO algorithm of this study, the shifting vector S (k) j of the k -th iteration step is calculated by combining an increment of shifting vector Δ S (k) j and the shifting vector in the previous iteration step:

$$ {\mathbf{S}}_j^{(k)}={\mathbf{S}}_j^{\left(k-1\right)}+\varDelta {\mathbf{S}}_j^{(k)} $$
(19)

Apparently, the movement of the constraint boundary is incremental since the shifting vector is just an adjustment for the previous iteration.

Figure 4 is used to illustrate the calculation of the shifting vector increment. For the convenience of description, the entire analysis process is executed in the U space, and S (k) U,j denotes the k-th shifting vector in U space. The curve G j (U − S (k − 1) U,j , Y * (k) j ) = 0 is the equivalent constraint boundary of the previous iteration, and the left side of this curve is assumed to be feasible domain where the current design is located. It is worth mentioning that the corresponding constraint G j in the U space is also related to k since the updating of the mean vector μ (k) Z in original space. Taking parametric randomness into account, the random space of the design point is a circle centered at the original point, and the radius of the circle is the target reliability index β t j . When the constraint boundary G j (U − S (k − 1) U,j , Y * (k) j ) = 0 passes through this circle, it means that the current design does not meet the reliability requirement since the actual reliability index β * (k) j of the current design is less than the target reliability index β t j , and their difference is denoted as Δβ (k) j  = β t j  − β * (k) j . To further improve the reliability, a small adjustment is required by moving the constraint boundary towards the direction of the feasible domain. The equivalent constraint boundary then should be moved Δβ (k) j towards the gradient direction of the MPP of the last iteration step. The shifting vector increment thus can be constructed through:

$$ \varDelta {\mathbf{S}}_{\mathbf{U},j}^{(k)}=\left({\beta}_j^{\mathrm{t}}-{\beta}_j^{*(k)}\right)\left(-\frac{\nabla {G}_j\left({\mathbf{U}}_{\mathrm{MPP},\kern0.5em j}^{(k)},{\mathbf{Y}}_j^{*(k)}\right)}{\left\Vert \nabla {G}_j\left({\mathbf{U}}_{\mathrm{MPP},\kern0.5em j}^{(k)},{\mathbf{Y}}_j^{*(k)}\right)\right\Vert}\right) $$
(20)
Fig. 4
figure 4

The calculation of the shifting vector increment

Full size image

As mentioned before, the gradient direction of U 0 and U (k)MPP, j are generally close to each other. For the purpose of decreasing the calculation amount, we use the gradient vector of G j at U 0 to approximately substitute the gradient vector at U (k)MPP, j , and hence Eq. (20) can be changed to:

$$ \varDelta {\mathbf{S}}_{\mathbf{U},j}^{(k)}=\left({\beta}_j^{\mathrm{t}}-{\beta}_j^{*(k)}\right)\left(-\frac{\nabla {G}_j\left({\mathbf{U}}_{\mathbf{0}},{\mathbf{Y}}_j^{*(k)}\right)}{\left\Vert \nabla {G}_j\left({\mathbf{U}}_{\mathbf{0}},{\mathbf{Y}}_j^{*(k)}\right)\right\Vert}\right) $$
(21)

where β * (k) j and Y * (k) j are obtained through the hybrid reliability analysis. Transforming Δ S (k) U,j to the original space by Eq. (3), the required increment Δ S (k) j of the shifting vector can be obtained.

In the k -th iteration step, after calculating the shifting vector increments for all the constraints, the shifting vector S (k) j can be set. Then, the uncertain constraints in Eq. (9) can be transformed to the deterministic constraints, and whereby a deterministic design optimization can be formulated:

$$ \begin{array}{l}\underset{\mathbf{d},{\boldsymbol{\upmu}}_{\mathbf{X}}}{ \min}\kern0.5em f\left(\mathbf{d},{\boldsymbol{\upmu}}_{\mathbf{X}},{\boldsymbol{\upmu}}_{\mathbf{P}}\right)\\ {}\mathrm{s}.\mathrm{t}.\kern1em {g}_j\left(\mathbf{d},{\boldsymbol{\upmu}}_{\mathbf{Z}}-{\mathbf{S}}_j^{(k)}\right)\ge 0,\kern1em j=1,2,\dots, {n}_g\\ {}\kern3.5em {\boldsymbol{\upmu}}_{\mathbf{Z}}=\left[{\boldsymbol{\upmu}}_{\mathbf{X}},{\boldsymbol{\upmu}}_{\mathbf{P}}\right],{\mathbf{d}}^l\le \mathbf{d}\le {\mathbf{d}}^u,{\boldsymbol{\upmu}}_{\mathbf{X}}^l\le {\boldsymbol{\upmu}}_{\mathbf{X}}\le {\boldsymbol{\upmu}}_{\mathbf{X}}^u\kern0.5em \end{array} $$
(22)

The constraint hybrid reliability analysis and the deterministic design optimization then can be carried out alternately until convergence.

As can be observed, after using the ISV technique to solve the hybrid RBDO problem, the shifting vector is updated based on its historical information. Therefore the adjustment of the equivalent constraint boundary is incremental. This strategy ensures that the equivalent constraint boundary will not be changed drastically between two consecutive iteration steps and the numerical oscillation during the iteration process could be well avoided.

3.3 The computational procedure

As shown in Fig. 5, the flowchart of the proposed hybrid RBDO algorithm can be summarized in the following steps:

Fig. 5
figure 5

Flowchart of the proposed method

Full size image

  • Step 1: Solve the following deterministic optimization problem to obtain an initial point [d (0), μ (0) X ] and set S (0) j  = 0:

    $$ \begin{array}{l}\underset{\mathbf{d},{\boldsymbol{\upmu}}_{\mathbf{X}}}{ \min}\kern0.5em f\left(\mathbf{d},{\boldsymbol{\upmu}}_{\mathbf{X}},{\boldsymbol{\upmu}}_{\mathbf{P}}\right)\\ {}\mathrm{s}.\mathrm{t}.\kern1em {g}_j\left(\mathbf{d},{\boldsymbol{\upmu}}_{\mathbf{Z}}\right)\ge 0\kern0.5em ,j=1,2,\dots, {n}_g\\ {}\kern3.5em {\boldsymbol{\upmu}}_{\mathbf{Z}}=\left[{\boldsymbol{\upmu}}_{\mathbf{X}},{\boldsymbol{\upmu}}_{\mathbf{P}}\right],{\mathbf{d}}^l\le \mathbf{d}\le {\mathbf{d}}^u,{\boldsymbol{\upmu}}_{\mathbf{X}}^l\le {\boldsymbol{\upmu}}_{\mathbf{X}}\le {\boldsymbol{\upmu}}_{\mathbf{X}}^u\end{array} $$
    (23)

  • Step 2: Carry out the hybrid reliability analysis of the constraints and set k := k + 1. Based on the optimal solution obtained in the last iteration, Eq. (17) is adopted to execute the hybrid reliability analyses for the constraints. Then, the interval vector boundary combination Y * (k) j and the corresponding reliability index β * (k) j are obtained.

  • Step 3: Calculate the shifting vector. The reliability is judged for all the constraints. If β * (k) j  ≥ β t j , Δ S (k) j is set to be 0; otherwise, Δ S (k) j can be calculated through Eq. (21), and a new shifting vector is calculated by S (k) j  = S (k − 1) j  + Δ S (k) j .

  • Step 4: Set up and solve the design optimization problem in Eq. (22) to obtain an optimal solution [d (k), μ (k) X ] of the current iteration step.

  • Step 5: Repeat 2–4 until all the increments of shifting vectors are equal to zero and simultaneously the following condition is satisfied:

    $$ \left|\frac{f\left({\mathbf{d}}^{(k)},{\boldsymbol{\upmu}}_{\mathbf{X}}^{(k)},{\boldsymbol{\upmu}}_{\mathbf{P}}\right)-f\left({\mathbf{d}}^{\left(k-1\right)},{\boldsymbol{\upmu}}_{\mathbf{X}}^{\left(k-1\right)},{\boldsymbol{\upmu}}_{\mathbf{P}}\right)}{f\left({\mathbf{d}}^{(k)},{\boldsymbol{\upmu}}_{\mathbf{X}}^{(k)},{\boldsymbol{\upmu}}_{\mathbf{P}}\right)}\right|\le \varepsilon $$
    (24)

    where ε is a given error limit.

  • Step 6: Output the optimal solution [d*, μ * X ] = [d (k), μ (k) X ].

4 Numerical examples and discussions

4.1 A cantilever beam

A cantilever beam modified from literature (Liang et al. 2004) is considered, as shown in Fig. 6. The beam with a length L = 100 in is subjected to a vertical load F 1 and a lateral load F 2. The width w and thickness t of the beam’s cross-section serve as the design variables and the goal is to minimize the cross-sectional area. Two failure modes are considered, namely the stress at the fixed end of the beam should be less than an allowable yield stress Γ 0 and the displacement of the free end of the beam should be less than an allowable displacement D 0 = 2.5 in. The structure sizes w and t, the loads F 1 and F 2, the allowable yield stress Γ 0, and the Young’s modulus E are all random variables as shown in Table 1, and it can be found that some parameters of these variables’ probability distributions are only given intervals. A hybrid RBDO problem is then created as:

$$ \begin{array}{l}\underset{{\boldsymbol{\upmu}}_{\mathbf{X}}}{ \min}\kern0.5em f\left({\boldsymbol{\upmu}}_{\mathbf{X}}\right)={\mu}_w\cdot {\mu}_t\\ {}\mathrm{s}.\mathrm{t}.\kern1em P{r}_j^{\mathrm{L}}= Prob\left\{{g}_j\left(\mathbf{X},\mathbf{P},\mathbf{Y}\right)\ge 0\right\}\ge \varPhi \left(\hbox{-} {\beta}_j^{\mathrm{t}}\right),\kern1em {\beta}_{{}_j}^{\mathrm{t}}=3.0,j=1,\kern0.5em 2\\ {}\kern3.5em {g}_1\left(\mathbf{X},\mathbf{P},\mathbf{Y}\right)\kern0.5em ={\varGamma}_0-\left(\frac{600}{w{t}^2}{F}_1+\frac{600}{w^2t}{F}_2\right)\\ {}\kern3.5em {g}_2\left(\mathbf{X},\mathbf{P},\mathbf{Y}\right)\kern0.5em ={D}_0-\frac{4{L}^3}{Ewt}\sqrt{{\left(\frac{F_1}{t^2}\right)}^2+{\left(\frac{F_2}{w^2}\right)}^2}\\ {}\kern4em \mathbf{X}=\left(w,t\right),\kern0.5em \mathbf{P}=\left({F}_1,{F}_2,{\varGamma}_0,E\right),\kern0.5em \mathbf{Y}=\left({\sigma}_w,{\sigma}_t,{\mu}_{F_1},{\mu}_{F_2},{\sigma}_{\varGamma_0},\kern0.5em {\sigma}_E\right)\\ {}\kern4em 0\ \mathrm{in}<{\mu}_w<5.0\kern0.5em \mathrm{in},\kern1em ,\kern1em 0\ \mathrm{in}<{\mu}_t<5.0\kern0.5em \mathrm{in},\kern1em \end{array} $$
(25)
Fig. 6
figure 6

A cantilever beam (Liang et al. 2004)

Full size image
Table 1 Random variables and distributions of the cantilever beam
Full size table

To investigate the properties of our hybrid RBDO method better, we construct two approaches under our ISV computational framework. The only difference of these two approaches is that the first approach uses the approximate reliability analysis in Eq. (17) at each iteration step while the second one uses the conventional reliability analysis in Eq. (14), and they are called HRBDO_I and HRBDO_II, respectively. Furthermore, to verify the accuracy of the proposed method, a double-loop method called HRBDO_III is used to obtain the reference solutions. The basic principle of HRBDO_III is that the outer layer uses the genetic algorithm (Roger 2000) to conduct the design optimization, while the inner layer carries out the precise hybrid reliability analysis (Jiang et al. 2011). What’s more, to illustrate the necessity to consider the mixed uncertainty, SORA (Du and Chen 2004) is also adopted for the conventional RBDO analysis in which the interval uncertainties of the distribution parameters are neglected and they are replaced directly by their midpoints. All design optimization problems during iteration processes are solved by the sequential quadratic programming (Roger 2000). A start point for the four methods is set to μ start X  = (2.047mm, 3.746mm), and the optimization results and iteration processes are shown in Table 2 and Fig. 7. Firstly, it can be found that HRBDO_I and HRBDO_II both converge to the stable solutions only after a small number of iterations, which are very close to the reference solution from HRBDO_III, while their efficiency is far superior to that of HRBDO_III. Secondly, by comparing HRBDO_I with HRBDO_II, it shows that the introduction of the approximate reliability analysis does not cause an obvious error for the overall analysis, while significantly improves the efficiency of the optimization process. The number of the constraint functional evaluations of HRBDO_I is 2084, and it is about only one-fifth that of HRBDO_II which is 10384. Finally, through comparing the solutions from HRBDO_I and SORA, an obvious difference can be found. If we conduct the hybrid reliability analysis (Jiang et al. 2011) to the solution of SORA considering the interval distribution parameters, two reliability index intervals for the constraints, [2.5, 3.1] and [2.7, 3.3], can be obtained. As can be observed, the minimal reliability indexes, β *1  = 2.5 and β *2  = 2.7, will obviously violate the target reliability indexes β t1  = β t2  = 3.0. It further indicates that an unsafe design might be achieved in practical RBDO problems if we simply use a deterministic value to deal with the interval distribution parameter.

Table 2 Optimization results of the cantilever beam
Full size table
Fig. 7
figure 7

The iteration process for the cantilever beam problem

Full size image

4.2 A vehicle crashworthiness problem

Crashworthiness design is playing an important role in current product development of vehicles. Its final design exerts great effects not only on the overall performance of an automobile but also the passengers’ life safety. Vehicle crashworthiness can be divided into a variety of forms, such as low-speed offset collision and high-speed frontal collision and so on. In order to meet the requirements of vehicle’s performance such as crashworthiness and lightweight, the structural optimization design is generally required. As shown in Fig. 8, a vehicle crashworthiness problem modified based on the literature (Jiang and Deng 2014) is investigated in this paper, in which its high-speed and low-speed crashworthiness will be both considered. The design variables X 1 − X 5 are the thicknesses of the frontal bumper, the inner plate of crash box, the outer plate of crash box, the inner plate of frontal longitudinal and the outer plate of frontal longitudinal, respectively. The total mass M of the five parts is used as the objective function. Two vehicle crashworthiness cases serve as the constraints, which are the 15 km/h low-speed offset collision and the 56 km/h high-speed frontal collision. In the former case, the vehicle body should be protected because passengers are generally safe enough. In other words, the fee of the damage repair should be reduced by decreasing the deformation of the front longitudinal as much as possible. Hence, the total energy absorption E of the inner and outer plates of the front longitudinal should be less than a given value E 0. In the high velocity impact case, the safety of passengers is mainly concerned about. Thus, the mean integration acceleration of the left backseat, ā, the intrusions of the two upper and lower mark points located in the engine, I H and I L, are required to be less than the given values ā 0, I H0 , I L0 , respectively. The target reliability indexes of the four constraints are set to β t j  = 2.0, j = 1, 2, 3, 4. The random variables and their probability distributions are shown in Table 3, in which some distribution parameters are only given intervals since lacking information. A hybrid RBDO problem thus can be created in the following form:

$$ \begin{array}{l}\underset{{\boldsymbol{\upmu}}_{\mathbf{X}}}{ \min}\kern0.5em M\left({\boldsymbol{\upmu}}_{\mathbf{X}}\right)=2.088{\mu}_{X_1} + 0.404{\mu}_{X_2}+0.22{\mu}_{X_3}+1.2{\mu}_{X_4}+0.887{\mu}_{X_5}\\ {}\mathrm{s}.\mathrm{t}.\kern1em P{r}_j^{\mathrm{L}}= Prob\left({g}_j\left(\mathbf{X},\mathbf{Y}\right)\ge 0\right)\ge \varPhi \left(-{\beta}_j^{\mathrm{t}}\right),\kern1em {\beta}_{{}_j}^{\mathrm{t}}=2.0,\kern0.5em j=1,\kern0.5em 2,\kern0.5em 3,\kern0.5em 4\\ {}\kern3.5em {g}_1\kern0.5em ={E}_0-E\left(\mathbf{X},\mathbf{Y}\right),\kern0.5em {g}_2\kern0.5em ={\overline{a}}_0-\overline{a}\left(\mathbf{X},\mathbf{Y}\right),\kern0.5em \\ {}\kern3.5em {g}_3\kern0.5em ={I}_0^{\mathrm{H}}-{I}^{\mathrm{H}}\left(\mathbf{X},\mathbf{Y}\right),\kern0.5em {g}_4\kern0.5em ={I}_0^{\mathrm{L}}-{I}^{\mathrm{L}}\left(\mathbf{X},\mathbf{Y}\right)\kern0.5em \\ {}\kern3.5em \mathbf{Y}={\boldsymbol{\upsigma}}_{\mathbf{X}},{\overline{a}}_0=40\kern0.5em \mathrm{g},\kern0.5em {E}^0=300\kern0.5em \mathrm{J},\kern0.5em {I}_0^{\mathrm{H}}=350\kern0.5em \mathrm{mm},\kern0.5em {I}_0^{\mathrm{L}}=200\kern0.5em \mathrm{mm}\kern3.5em \\ {}\kern3.5em 2.0\mathrm{mm}\le {\mu}_{X_1}\le 3.0\mathrm{mm},\kern0.5em 1.0\mathrm{mm}\le {\mu}_{X_2}\le 3.0\mathrm{mm},\ 1.0\mathrm{mm}\le {\mu}_{X_3}\le 2.5\mathrm{mm},\ \\ {}\kern3.5em 1.5\mathrm{mm}\le {\mu}_{X_4}\le 3.0\mathrm{mm},\kern0.75em 1.0\mathrm{mm}\le {\mu}_{X_5}\le 3.0\mathrm{mm}\end{array} $$
(26)
Fig. 8
figure 8

A vehicle crashworthiness problem considering both the low-speed and high-speed properties

Full size image
Table 3 Random variables and distributions in the vehicle crashworthiness problem
Full size table
Table 4 Response surface models of the four constraint functions in the vehicle crashworthiness problem
Full size table

Two finite element models (FEMs) are created to analyze the low-speed and high-speed collision cases. As shown in Fig. 9, each FEM has 755 components, 998220 nodes and 977742 elements. To promote the subsequent optimization efficiency, four second-order polynomial response surface models are created for the constraints based on 65 samples, as shown in Table 4, and they will be used to replace the time-consuming FEMs. To test their accuracy, six points are randomly selected in the design space and the results of the response surfaces and the FEMs are compared at these points, as shown in Table 5. It can be found that the created response surface models have acceptable accuracy as their relative errors from the FEMs are relatively small. The start point of the optimization is set as μ start X  = (2.40mm, 2.40mm, 2.40mm, 2.40mm, 2.40mm). At this start point, the actual reliability index vector of the constraints is β start = (0.0, 6.7, 0.0, 6.0), which Obviously violates the target reliability requirements. After carrying out the hybrid RBDO analysis using HRBDO_I, a stable solution is obtained after only 4 iteration steps, as shown in Fig. 10. To demonstrate the accuracy of the proposed method, a reference solution is also obtained by using HRBDO_III. The results of the two methods are listed in Table 6. It can be found that the thicknesses of the five parts are optimized and all reliabilities of the safety and crashworthiness constraints at the optimum are satisfied. What’s more, the total mass of these parts is decreased from 11.52 to 10.57 kg. Also, the results show that the present method has a fine accuracy since it outputs a very close result to the reference solution.

Fig. 9
figure 9

FEMs for the vehicle crashworthiness problem

Full size image
Table 5 Accuracy test of the response surface models in the vehicle crashworthiness problem
Full size table
Fig. 10
figure 10

The iteration process for the vehicle crashworthiness problem

Full size image
Table 6 Optimization results for the vehicle crashworthiness problem
Full size table

4.3 A structural design problem of tablet computer

Currently, electronic devices usually have a high integrated density and large power dissipation. It is necessary for its structural design to consider various aspects of design requirements (Hirohata et al. 2006; Hadim and Suwa 2008), such as appearance, portability, and environmental adaptation, etc. Tablet computer is a typical consumer electronic device, and the appearance design is usually given high-priority, for instance, the minimal size of the product is required. And other design requirements, such as a high-temperature environment, accidental fall and operating safety, should be considered during the structural design of tablet computers. Thus, an excellent structural design can ensure the tablet computer to work reliably or not to be damaged in various extreme conditions, such as high temperature, alternating temperature, and free fall and so on. This subsection considers the hybrid RBDO problem of a 7-inches tablet computer, as illustrated in Fig. 11. The tablet computer mainly consists of the following parts: the touch screen, the display, the battery, the mainboard, the inner bracket, the front shell and the back shell. The minimization of the tablet’s thickness is served as the design objective. Four work conditions are involved and they are high-temperature, room-temperature, and alternating temperature and free fall, respectively. Case 1: under the high-temperature (45 °C), and the temperature T CH of the chip on the main board is not allowed to be higher than the given temperature T CH0  = 65 °C. Case 2: to ensure daily-using comfortably, the shell surface temperature T SH should be less than T SH0  = 40 °C with a full load under the room temperature (25 °C) for an hour continuously. Case 3: during the alternative temperature [0 °C, 40 °C], the electronic components may be failure because of the thermal stress caused by the difference of thermal expansion coefficients of various materials. In order to make sure the operating safety, the thermal stress Γ BA of the battery is required to be less than the given value Γ BA0  = 24Mpa. Case 4: during the collision of the 0.5 m-height free fall, the maximal stress Γ TS of the touch screen is not allowed to be more than the material breaking strength Γ TS0  = 100Mpa. The design variables of the hybrid RBDO problem are: the thickness of the front shell, the display, the inner bracket, the back shell; the parameters are Young’s modulus and the thermal expansion coefficient of the viewing screen, Young’s modulus and the thermal expansion coefficient of the battery, the power dissipation of the mainboard and the display. All above four design variables and six parameters are random variables, and the details of distributions are given in Table 7. It indicates that some distributions parameters can only be given by intervals, while others can be given by the accurate values. The target reliability indexes of constraints are set to β t j  = 2.0, j = 1, 2, 3, 4. This practical hybrid RBDO model is written as:

$$ \begin{array}{l}\underset{{\boldsymbol{\upmu}}_{\mathbf{X}}}{ \min}\kern0.5em f\left({\boldsymbol{\upmu}}_{\mathbf{X}}\right)={\mu}_{X_1}+{\mu}_{X_2}+{\mu}_{X_3}+{\mu}_{X_4}\\ {}\mathrm{s}.\mathrm{t}.\kern1em P{r}_j^{\mathrm{L}}= Prob\left({g}_j\left(\mathbf{X},\mathbf{P},\mathbf{Y}\right)\ge 0\right)\ge \varPhi \left(-{\beta}_j^{\mathrm{t}}\right),\kern0.5em {\beta}_j^{\mathrm{t}}=2.0,\kern0.5em j=1,\kern0.5em 2,\kern0.5em 3,4\\ {}\kern2.5em {g}_1\kern0.5em ={T}_0^{\mathrm{CH}}-{T}^{\mathrm{CH}}\left(\mathbf{X},\mathbf{P},\mathbf{Y}\right),\kern0.5em {g}_2\kern0.5em ={T}_0^{\mathrm{SH}}-{T}^{\mathrm{SH}}\left(\mathbf{X},\mathbf{P},\mathbf{Y}\right),\kern0.5em \\ {}\kern2.5em {g}_3\kern0.5em ={\varGamma}_0^{\mathrm{BA}}-{\varGamma}^{\mathrm{BA}}\left(\mathbf{X},\mathbf{P},\mathbf{Y}\right),{g}_4\kern0.5em ={\varGamma}_0^{\mathrm{TS}}-{\varGamma}^{\mathrm{TS}}\left(\mathbf{X},\mathbf{P},\mathbf{Y}\right),\\ {}\kern2.5em \mathbf{Y}=\left({\sigma}_{P_1},{\sigma}_{P_2},{\sigma}_{P_3},{\sigma}_{P_4}\right),\kern1em \\ {}\kern2.5em 4.00\mathrm{mm}\le {\mu}_{X_1}\le 6.00\mathrm{mm},\kern0.5em 0.50\mathrm{mm}\le {\mu}_{X_2}\le 2.00\mathrm{mm},\\ {}\kern2.5em 0.50\mathrm{mm}\le {\mu}_{X_3}\le 2.00\mathrm{mm},\kern0.5em 0.50\mathrm{mm}\le {\mu}_{X_4}\le 2.00\mathrm{mm}\end{array} $$
(27)
Fig. 11
figure 11

A 7-inch tablet computer

Full size image
Table 7 Random variables and distributions in the tablet structural design problem
Full size table

Four FEMs are established corresponding to the above four cases as shown in Fig. 12. The information of the FEMs is listed in Table 8. To achieve parameterization and improve efficiency, the second-order polynomial response surfaces are created based on 65 samples correspondingly, as formulated in Table 9. As before, six points are randomly selected and the results at these points from the FEMs and response surfaces are compared, and the accuracy test is listed in Table 10. We select μ start X  = (6.00mm, 1.20mm, 1.20mm, 1.00mm) as a start point. At this start point, the actual reliability index vector of the constraints is β start = (0.0, 2.9, 0.0, 6.8), which Obviously violates the target reliability requirements. That is to say, the high-temperature performance and the daily-using safety cannot be guaranteed. This may not only lead to the tablet-operating failure, but also the damage to users’ personal safety. After conducting the hybrid RBDO analysis, the solution from HRBDO_I and the reference solution via HRBDO_III are listed in Table 11. Figure 13 shows the iteration process which indicates that the proposed method can converge rapidly after only 3 iterations. And It can be seen that there is only a tiny difference between our HRBDO_I solutions and the reference solutions. The structural thickness of optimized tablet is f(μ * X ) = 6.39mm, which is a 32.0 % reduction in compared with that of the start point. And the reliability indexes β* = (2.0, 2.0, 2.2, 7.2) at the solutions μ * X  = (4.00mm, 0.52mm, 1.37mm, 0.50mm) can meet the target reliability requirement. This is meaningful because the final design is reliable and more aligned with consumers’ expectations about the appearance and portability for the tablet.

Fig. 12
figure 12

FEMs for the tablet structural design problem

Full size image
Table 8 FEMs information of the tablet structural design problem
Full size table
Table 9 Response surfaces for the four constraint functions of the tablet structural design problem
Full size table
Table 10 Accuracy test of the response surface models in the tablet structural design problem
Full size table
Table 11 Optimization results for the tablet structural design problem
Full size table
Fig. 13
figure 13

The iteration process for the tablet structural design problem

Full size image

5 Conclusion

In practical RBDO problems, random variables are generally used to deal with the uncertain parameters, while in many cases some distribution parameters of the random variables can only be given intervals since lacking sufficient samples. In this paper, we created a hybrid RBDO model for a class of problems with interval distribution parameters, and also proposed an efficient solution algorithm for this model, which provided a potential tool for reliability design of many complex structures. This paper has the following two innovations. Firstly, an approximate probability-interval hybrid reliability analysis method was given, which could avoid the multi-variable optimization in the inner-layer reliability analysis and hence reduce the computational cost greatly. Secondly, an ISV strategy was employed to deal with the nested optimization of hybrid RBDO, which could convert the nested optimization into an efficient sequential iterative process of the design optimization and the hybrid reliability analysis. The numerical example analyses show that the proposed hybrid RBDO method is not only efficient but also robust. Also, it seems promising to extend this method to deal with some other important problems in this field in the future, such as multidisciplinary reliability design optimization, multi-objective reliability design optimization, etc.