An active learning Kriging-assisted method for reliability-based design optimization under distributional probability-box model

Abstract

Due to lack of sufficient data and information in engineering practice, it is often difficult to obtain precise probability distributions of some uncertain variables and parameters in reliability-based design optimization (RBDO). In this paper, distributional probability-box (p-box) model is employed to quantify these uncertain variables and parameters. To reduce the computational cost in RBDO associated with expensive and time-consuming constraints, an active learning Kriging-assisted method is proposed. In this method, the sequential optimization and reliability assessment (SORA) method is extended for RBDO under distributional p-box model. Kriging metamodels are constructed to make the replacement of actual constraints. To remove unnecessary computational expense on constructing Kriging metamodels, a screening criterion is built and employed for the judgment of active constraints in RBDO. Then, an active learning function is defined to find out update samples, which are adopted for sequentially refining Kriging metamodel of each active constraint by focusing on its limit-state surface (LSS) around the most probable target point (MPTP) at the solution of SORA. Several examples, including a welded beam problem and a piezoelectric energy harvester design, are provided to test the accuracy and efficiency of the proposed active learning Kriging-assisted method.

1 Introduction

Uncertainties often exist in practical engineering problems, which may stem from changing operating and environmental conditions, manufacturing tolerances, insufficient information, and so on. Constraint feasibility at the optimal solution of deterministic design optimization cannot be guaranteed when fluctuations of uncertain variables and parameters exist. To this end, reliability-based design optimization (RBDO) is developed, in which failure probabilities of constraints are evaluated (Tu et al. 1999; Youn et al. 2003; Lee et al. 2012; Li et al. 2015a). Uncertainties are often classified into random and epistemic uncertainties. Generally, random uncertainties are quantified by classical probability theory, which requires sufficient data and knowledge to establish precise probability distributions. In some engineering problems, however, there is not enough information to build precise probability distributions of some uncertainties, which are often taken as epistemic uncertainties. There are some available tools to describe the epistemic uncertainties, such as possibility theory (Mourelatos and Zhou 2008), fuzzy theory (Li et al. 2015b; Wang et al. 2018), interval model (Wang and Qiu 2010; Yang et al. 2015a; Zhang et al. 2018b, 2019b), convex model (Meng and Zhou 2018; Meng et al. 2020), evidence theory (Zhang et al. 2015, 2018a; Yang et al. 2019), and probability-box (p-box) model (Ferson 1996; Ferson and Ginzburg 1996; Ferson and Hajagos 2004; Jiang et al. 2011). Among these tools, p-box model provides a simple framework to quantify epistemic uncertainties by imprecise probability distributions with a pair of lower and upper cumulative distribution functions (CDFs) (Schöbi and Sudret 2017). P-box model permits the existence of uncertain variables without exceedingly precise assumptions on the definition of distribution parameters in reliability analysis (Beer et al. 2013), and has attracted much attention in the description of epistemic uncertainties. The p-box model can be classified into distributional p-box model and distribution-free p-box model (Schöbi and Sudret 2017). The RBDO under distributional p-box model is focused on in this work.

In RBDO, it is significant to handle two essentials, including reliability analysis and integration strategies of reliability analysis and optimization procedure (Chen et al. 2014). For reliability analysis under distributional p-box model, Zhang et al. (2010) develop an interval Monte Carlo simulation (IMCS) to calculate the interval of failure probability. In IMCS, Monte Carlo simulation (MCS) is applied to generate random samples in the standard normal space, and then the maximum and minimum values of each constraint function are calculated at each sample in terms of the distribution parameter intervals in distributional p-box model. Due to lots of constraint evaluations required by IMCS, its applications are restricted in the cases with time-consuming computer simulations, such as finite element analysis. To enhance the efficiency of IMCS, variation-reduction sampling methods are introduced in reliability analysis, such as line sampling (Koutsourelakis et al. 2004; de Angelis et al. 2015) and subset simulation (Au and Beck 2001; Alvarez et al. 2018). Compared with IMCS, variation-reduction sampling methods need fewer simulated samples and the evaluation number of true constraints is reduced. Alternatively, to estimate the failure probability interval in reliability analysis under distributional p-box model, Jiang et al. (2011) propose two analytical methods based on reliability index approach (RIA) and performance measurement approach (PMA), respectively.

To further cut down the evaluation number of the actual constraints in reliability analysis, metamodel-assisted methods have attracted great attention, where the actual constraints are replaced by metamodels. Many types of metamodels have been applied in reliability analysis, such as polynomial response surface (Guan and Melchers 2001; Wang and Wang 2012; Shayanfar et al. 2017; Zhang et al. 2017), neural networks (Pedroni et al. 2010; Xiao et al. 2018), support vector machine (Basudhar and Missoum 2010; Song et al. 2013; Zhang et al. 2019d), M5Tree (Keshtegar and Kisi 2017, 2018), and Kriging (Xiao et al. 2019a, b, 2020; Zhang et al. 2019a). Unlike other metamodels, Kriging metamodel not only predicts the response of a constraint function, but also provides the local prediction variance (Wang and Wang 2013; Zhang et al. 2020a, b). Based on Kriging, Yang et al. (2015b) propose a combination method of an expected risk function and IMCS for reliability analysis under distributional p-box model. Schöbi and Sudret (2017) develop a method with multi-level Kriging metamodels to perform reliability analysis in consideration of two types of p-box models. For hybrid reliability analysis under random and distributional p-box variables, it is determined that the bounding limit-state surfaces (LSSs) in the standard normal space are the crucial regions for estimation of failure probability bounds and an update strategy is developed to refine the Kriging metamodel of the performance function by focusing on these crucial regions (Zhang et al. 2019c).

In RBDO, the integration strategies of optimization procedure and reliability analysis have a significant influence on solving efficiency. The nested strategy in the double-loop method respectively performs reliability analysis and optimization procedure in inner and outer loop, which shows a low solving efficiency (Keshtegar et al. 2020). Compared with the nested strategy, decoupled strategies in the single-loop method (Liang et al. 2007) and sequential optimization and reliability assessment (SORA; Du and Chen 2004) are more efficient. In RBDO under distributional p-box model, Huang et al. (2017) develop a decoupled strategy by an incremental shifting vector technique to convert the nested RBDO into a sequential iterative process of deterministic design optimization and reliability analysis.

In cases with time-consuming constraints, the application of metamodels in RBDO has been also investigated. Lee and Jung (2008) develop a constraint boundary sampling (CBS) strategy to construct the Kriging metamodels by focusing on refining the approximated LSSs of constraints around the feasible region of deterministic design optimization. Then, the double-loop method with PMA is applied to perform RBDO based on Kriging metamodels, where each constraint is replaced by a Kriging metamodel. To cut down the computational cost on the construction of Kriging metamodels in RBDO, some local metamodeling strategies have been developed, such as important boundary sampling strategy (Chen et al. 2015), local approximation method using the most probable point (Li et al. 2016), and adaptive directional boundary sampling strategy (Meng et al. 2018). Among these methods, CBS can be extended to RBDO under distributional p-box model. However, some unnecessary computational cost may be caused by CBS because some local regions of the LSSs are far from the RBDO solution and do not need to be perfectly approximated by metamodels. For the other local approximation methods, it is difficult to apply them to RBDO under distributional p-box model because their Kriging metamodels are constructed based on the local characteristics of RBDO under probability model.

In this paper, an active learning Kriging-assisted method is proposed for RBDO under distributional p-box model. As a decoupled strategy, SORA has higher execution efficiency than the double-loop method, even though the true constraints are substituted by metamodels. Thus, in this work, SORA is extended to RBDO under distributional probability-box model. To alleviate the computational burden of SORA in the cases with time-consuming constraints, Kriging metamodel is established for each constraint based on initial training samples. It is noted that maybe not all constraints are active during RBDO. To avoid unnecessary computational cost on the construction of Kriging metamodels, a screening criterion is presented to judge the active constraints. Generally, it is difficult to integrate IMCS with SORA. And when SORA is used for RBDO, the crucial approximated region for reliability analysis is the LSSs around the most probable target points (MPTPs) of active constraints at the solution of SORA. Thus, to refine Kriging metamodels in SORA, some existing update strategies (Yang et al. 2015b; Schöbi and Sudret 2017; Zhang et al. 2019c) cannot be directly used. Then, in this work, an active learning function is defined and employed to obtain update samples of the Kriging metamodels in SORA. These update samples will be sequentially added into the set of initial training samples and used to refine the Kriging metamodel of each active constraint by concentrating on its LSS around the MPTP at the solution of SORA. The framework of the proposed method is that (1) initial Kriging metamodels are built; (2) SORA is extended and performed to find the MPTPs at the solution of SORA; (3) active constraints are screened out based on the prediction uncertainties; (4) Kriging metamodels of active constraints are updated based on MPTPs and prediction uncertainties; (2) and (4) are repeated until the solution of SORA no longer changes. Four examples, including a welded beam problem and a piezoelectric energy harvester design, are tested to validate the performance of the proposed method. The results show that the proposed method is accurate and efficient for RBDO under distributional p-box model. The evaluations of actual constraints can be greatly decreased by the proposed method.

2 SORA for RBDO under distributional p-box model

In this section, the RBDO under distributional p-box model is described mathematically, and the extended application of SORA in solving RBDO under distributional p-box model is given.

2.1 RBDO under distributional p-box model

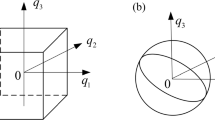
In this work, distributional p-box model is used to describe epistemic uncertainties, where undetermined distribution parameters are described by intervals. The description of the p-box variable and parameter is presented in Fig. 1. In Fig. 1a, a p-box parameter P with an interval distribution mean is presented. To take an example, the distribution standard deviation of P is 1, and the interval of the distribution mean of P is [0, 2]. The nominal value μ_p of P is set to the midpoint of the interval, i.e., μ_p = 1. In Fig. 1b, a p-box variable X with an interval distribution standard deviation is presented, where the interval of the distribution standard deviation of X is [1, 2]. The nominal value μ_x of X is set to the distribution mean of X, which is a design variable in RBDO. To take an example, μ_x is equal to 0 in Fig. 1b.

Fig. 1

Description of the p-box variable and parameter

Let Z denote the vector of p-box variables and parameters with interval distribution parameters. The vector of the interval distribution parameters is represented by Y. And let y denote the realization of Y. Due to the existence of interval distribution parameters, the CDF of the z_i is also an interval. Its upper and lower bounds are denoted by ${\overline{F}}_{z_i}$ and ${\underline{F}}_{z_i}$, respectively. In addition, it is difficult to directly perform reliability analysis in the space of Z. Generally, reliability analysis under p-box model can be performed by means of ${\overline{F}}_{z_i}$ and ${\underline{F}}_{z_i}$. When a point w = [w₁, …, w_q] in the standard normal space is transformed into the space of Z by using $\left[{\underline{z}}_i,\kern0.5em {\overline{z}}_i\right]=\left[{\overline{F}}_{z_i}^{-1}\left(\Phi \left({w}_i\right)\right),\kern0.5em {\underline{F}}_{z_i}^{-1}\left(\Phi \left({w}_i\right)\right)\right]$, an interval $\left[\underline {\mathbf{z}},\overline{\mathbf{z}}\right]$ can be obtained, where q is the total number of p-box variables and parameters, and Φ is the standard normal CDF. Thus, w in the standard normal space corresponds to an interval $\left[\underline {\mathbf{z}},\overline{\mathbf{z}}\right]$ in Z space. Then, the response G(w, Y) of a constraint in the standard normal space at w is not a deterministic value but an interval $\left[\underline{G}\left(\mathbf{w},\mathbf{Y}\right),\kern0.5em \overline{G}\left(\mathbf{w},\mathbf{Y}\right)\right]$, where

$$ \underline{G}\left(\mathbf{w},\mathbf{Y}\right)=\underset{\mathbf{z}\in \left[\underline {\mathbf{z}},\overline{\mathbf{z}}\right]}{\min }g\left(\mathbf{z}\right),\kern0.5em \overline{G}\left(\mathbf{w},\mathbf{Y}\right)=\underset{\mathbf{z}\in \left[\underline {\mathbf{z}},\overline{\mathbf{z}}\right]}{\max }g\left(\mathbf{z}\right) $$

(1)

Because the CDFs of Z change with y, and the transformation between w and z is realized based on the CDFs, (1) can be rewritten as

$$ \underline{G}\left(\mathbf{w},\mathbf{Y}\right)=\underset{\mathbf{y}}{\min }g\left(\mathbf{z}\left(\mathbf{y}\right)\right),\kern0.5em \overline{G}\left(\mathbf{w},\mathbf{Y}\right)=\underset{\mathbf{y}}{\max }g\left(\mathbf{z}\left(\mathbf{y}\right)\right) $$

(2)

Hence, in the standard normal space, the LSS of the constraint is not a single hypersurface but a band enclosed by the lower bounding LSS $\underline{S}$ and the upper bounding LSS $\overline{S}$ as shown in Fig. 2, where $\underline{S}$ and $\overline{S}$ are expressed as

$$ \underline{S}:\kern1em \underline{G}\left(\mathbf{w},\mathbf{Y}\right)=0,\kern1em \overline{S}:\kern1em \overline{G}\left(\mathbf{w},\mathbf{Y}\right)=0 $$

(3)

Fig. 2

Bounding LSSs in the standard normal space

Under the distributional p-box model, the reliability degree of a constraint is an interval value (Jiang et al. 2011). Its lower and upper bounds can be respectively calculated by

$$ {R}^l=P\left(\underline{G}\left(\mathbf{W},\mathbf{Y}\right)>0\right)=P\left(\left\{\underset{\mathbf{y}}{\min }g\left(\mathbf{Z}\left(\mathbf{y}\right)\right)\right\}>0\right) $$

(4)

$$ {R}^u=P\left(\overline{G}\left(\mathbf{W},\mathbf{Y}\right)>0\right)=P\left(\left\{\underset{\mathbf{y}}{\max }g\left(\mathbf{Z}\left(\mathbf{y}\right)\right)\right\}>0\right) $$

(5)

where W is the vector of random parameters with the standard normal distribution, and w is considered the realization of W.

Generally, the upper bound of the failure probability is considered in RBDO. Therefore, the lower bound of the reliability degree is adopted in this work to ensure a safety design. Then, a RBDO problem under distributional p-box model can be typically formulated as

$$ {\displaystyle \begin{array}{l}\mathrm{find}:\kern0.33em d,{\mu}_x\\ {}\min \kern0.76em :f\left(d,{\mu}_x,{\mu}_p\right)\\ {}s.t.\kern0.86em :P\left(\left\{\underset{y}{\min }{g}_j\left(d,Z(y)\right)\right\}>0\right)\ge {R}_j^t,\kern1.32em j=1,2,\dots, {n}_g\\ {}\kern2.64em Z=\left[X,P\right],\kern0.33em {d}^l\le d\le {d}^u,\kern0.33em {\mu}_x^l\le {\mu}_x\le {\mu}_x^u\kern0.33em \\ {}\kern2.64em y=\left[{y}_1,{y}_2,\dots, {y}_{n_y}\right],\kern0.33em {y}_i\in \left[{y}_i^l,{y}_i^u\right],\kern0.33em i=1,2,\dots, {n}_y\end{array}} $$

(6)

where f is the objective function. The vector of the p-box variables is denoted by X. The vector of the p-box parameters is represented by P. The vectors μ_x and μ_p represent the nominal values of X and P, respectively. In this work, for a p-box variable X, its distribution mean is considered its nominal value μ_x. For a p-box parameter P, when its distribution mean is a deterministic value, this value is considered the nominal value μ_p. When its distribution mean is an interval value, the midpoint of the interval is considered the nominal value μ_p. The vector d denotes the deterministic variables. The vectors d^l and d^u are the lower and upper bounds of optimization domain of d. The vectors ${\boldsymbol{\upmu}}_{\mathbf{x}}^l$ and ${\boldsymbol{\upmu}}_{\mathbf{x}}^u$ denote the lower and upper bounds of optimization domain of μ_x, respectively. The target reliability degree of the jth constraint is denoted by ${R}_j^t$. In this work, the fixed bounds of interval distribution parameters are considered. In (6), for a p-box parameter, the fixed interval bounds can be considered for both its distribution mean and standard deviation. For a p-box variable, the fixed interval bounds can be considered for its distribution standard deviation. In this work, the bounds of the distribution mean of the p-box variable are not considered. When the distribution mean of a p-box variable is set to an interval value, the bounds of this interval are constantly changing during RBDO, which is complex and will be researched in our future work.

2.2 RBDO under distributional p-box model by SORA

SORA is proposed by Du and Chen (2004) for RBDO only with random uncertainty, which can efficiently decouple RBDO into a sequential cycle of deterministic optimization and reliability analysis. In this work, SORA is extended to handle RBDO under distributional p-box model. Specifically, the deterministic optimization problem in the (k + 1)th cycle is formulated as

$$ {\displaystyle \begin{array}{l}\mathrm{find}:\kern0.33em d,{\mu}_x\\ {}\min :\kern0.33em f\left(d,{\mu}_x,{\mu}_p\right)\\ {}s.t.\kern1.08em {g}_j\left(d,{\mu}_z+{s}_j^{\left(k+1\right)}\right)>0,{s}_j^{\left(k+1\right)}={z}_{MPTP,j}^{(k)}-{\mu}_z^{(k)},j=1,2,\dots, {n}_g\\ {}{\mu}_z=\left[{\mu}_x,{\mu}_p\right],\kern0.58em {d}^l\le d\le {d}^u,\kern0.66em {\mu}_x^l\le {\mu}_x\le {\mu}_x^u\end{array}} $$

(7)

where ${\boldsymbol{\upmu}}_{\mathbf{z}}^{(k)}$is the design point in the kth cycle, and ${\mathbf{z}}_{MPTP,j}^{(k)}$ is the MPTP of the jth constraint in the kth cycle. The offset vector of the jth constraint at the (k + 1)th cycle is denoted by ${\mathbf{s}}_j^{\left(k+1\right)}$. The number of constraints is n_g. ${\mathbf{z}}_{MPTP,j}^{(k)}$ is obtained by PMA in the kth cycle. μ_z will be determined in the (k + 1)th cycle.

In PMA, a constraint reliability is analyzed based on the minimum response ${G}_j^{\mathrm{min}}$, which is calculated by

$$ {\displaystyle \begin{array}{l}\mathrm{find}:\kern0.5em \mathbf{w},\mathbf{y}\\ {}\min :{G}_j\left(\mathbf{w},\mathbf{y}\right)\\ {}s.t.\kern1em \left\Vert \mathbf{w}\right\Vert ={\beta}_j^t\\ {}\kern3em \mathbf{y}=\left[{y}_1,{y}_2,\dots, {y}_{n_y}\right],\kern0.5em {y}_i\in \left[{y}_i^l,{y}_i^u\right],\kern0.5em i=1,2,\dots, {n}_y\end{array}} $$

(8)

where w is the vector of variables with the standard normal distribution and transformed by w = T(z), and G_j(w) = g_j(z). T is the Rosenblatt transformation function. The optimal value of (8) is denoted by ${G}_j^{\mathrm{min}}$. If ${G}_j^{\mathrm{min}}$ is not less than 0, the jth constraint will satisfy the target reliability degree $\Phi \left({\beta}_j^t\right)$, where ${\beta}_j^t$ is the target reliability index of the jth constraint. It can be seen that (8) is a two-layer nested optimization problem (Jiang et al. 2011). The outer-layer optimization is employed to perform reliability analysis as follows

$$ {\displaystyle \begin{array}{l}\mathrm{find}:\kern0.5em \mathbf{w}\\ {}\min :{G}_j\left(\mathbf{w},\mathbf{y}\right)\\ {}s.t.\kern1em \left\Vert \mathbf{w}\right\Vert ={\beta}_j^t\end{array}} $$

(9)

The inner-layer optimization is modeled in (10), which is applied to realize interval analysis and obtain y.

$$ {\displaystyle \begin{array}{l}\mathrm{find}:\kern0.5em \mathbf{y}\\ {}\min :{G}_j\left(\mathbf{w},\mathbf{y}\right)\\ {}s.t.\kern1em \mathbf{y}=\left[{y}_1,{y}_2,\dots, {y}_{n_y}\right],\kern0.5em {y}_i\in \left[{y}_i^l,{y}_i^u\right],\kern0.5em i=1,2,\dots, {n}_y\end{array}} $$

(10)

The optimization in (10) can be realized by $\underset{\mathbf{z}\in \left[\underline {\mathbf{z}},\overline{\mathbf{z}}\right]}{\min }{g}_j\left(\mathbf{z}\right)$ based on (1). The optimal solution of PMA based on (9) and (10) is the MPTP of the jth constraint, i.e., w_{MPTP, j}. In the original design space, the MPTP is represented by z_{MPTP, j}. For the inner-layer optimization in (10), its solution is determined by the transformation function T and the constraint function. Only when both T and the constraint function are monotonous with regard to the interval distribution parameters, the solution of (10) will be the bounds of the interval distribution parameters. Generally, it is difficult to judge the monotony of the constraint function, especially when it is a black-box one. Thus, it is unsuitable that the RBDO under distributional p-box model is considered the RBDO under random variables by simplifying the interval distributional parameters to their bounds.

For a RBDO problem under distributional p-box model, its solution obtained by the SORA method is illustrated in Fig. 3. In this figure, ${\boldsymbol{\upmu}}_{\mathbf{x}}^{\ast }$ denotes the obtained solution of SORA. X₁ and X₂ are p-box variables, whose distribution standard deviations are interval values. For a simple illustration, different β^t-circles correspond to different distribution standard deviations of the p-box variables.

Fig. 3

RBDO under distributional p-box model by SORA

3 An active learning Kriging-assisted method for RBDO under distributional p-box model

In practical engineering problems, the evaluation of constraints may be time-consuming. To decrease the evaluation number of the true constraints in RBDO under distributional p-box model, the Kriging metamodel is introduced to approximate each constraint in this work. It is noted that maybe not all constraints are active in RBDO. Considering prediction uncertainties of Kriging metamodel, a screening criterion is established and used for the judgment of active constraints. Then, an active learning function is defined to obtain update samples for refining Kriging metamodels by focusing on the LSSs around the MPTPs of active constraints at the solution of SORA. Finally, based on SORA, the active learning Kriging-assisted method is proposed for RBDO under distributional p-box model.

3.1 Screening criterion for active constraints

As shown in Fig. 3, g₃ is an inactive constraint while g₁ and g₂ are active constraints. The LSS of g₃ is far from the solution of SORA. It can be observed that inactive constraints do not affect the solution of SORA. The update of Kriging metamodels should concentrate on the approximation accuracy of the active constraints. Thus, it is necessary to screen out the active constraints.

At the solution of SORA, the MPTPs of active constraints are located on the LSSs while the MPTPs of inactive constraints are not on the LSSs. As presented in Fig. 3, x_{MPTP, 1} and x_{MPTP, 2} are located on the LSSs of g₁ and g₂, while x_{MPTP, 3} is far from the LSS of g₃. Thus, the screening criterion for active constraints can be established based on the MPTPs at the solution of SORA. Specifically, if g_j(d^∗, z_{MPTP, j}) > 0, g_j is inactive, while g_j is active if g_j(d^∗, z_{MPTP, j}) = 0. The vector d^∗ represents deterministic variables in the solution of SORA.

For the Kriging metamodel, its prediction $\mathcal{G}$ at an untried point obeys a normal distribution with the mean $\hat{g}$ and variance ${\sigma}_{\hat{g}}^2$, i.e., $\mathcal{G}\sim N\left(\hat{g},{\sigma}_{\hat{g}}^2\right)$. When a constraint g(d, z) is replaced by the Kriging metamodel, the probability of correctly predicting the sign of $\hat{g}\left(\mathbf{d},\mathbf{z}\right)$ is equal to Φ(U(d, z)), where U is a learning function formulated as (11) (Echard et al. 2011). Because Φ(2) > 97.7%, if $\hat{g}\left(\mathbf{d},\mathbf{z}\right)>0$ and U(d, z) > 2, the probability of $\mathcal{G}\left(\mathbf{d},\mathbf{z}\right)>0$ will be larger than 97.7%.

$$ U\left(\mathbf{d},\mathbf{z}\right)=\frac{\left|\hat{g}\left(\mathbf{d},\mathbf{z}\right)\right|}{\sqrt{\sigma_{\hat{g}}^2\left(\mathbf{d},\mathbf{z}\right)}} $$

(11)

Thus, in this paper, for the approximated constraints by Kriging metamodels, the screening criterion is established by considering the prediction uncertainties of the Kriging metamodels. Specifically, if ${\hat{g}}_j\left({\mathbf{d}}^{\ast },{\mathbf{z}}_{MPTP,j}\right)>0$ and U(d^∗, z_{MPTP, j}) > 2, ${\hat{g}}_j$is inactive, while ${\hat{g}}_j$is active if U(d^∗, z_{MPTP, j}) ≤ 2.

3.2 An active learning function for Kriging update

During RBDO by SORA, the MPTPs are employed to judge the reliability degree of constraints in reliability analysis. Additionally, in the deterministic optimization, the MPTPs are used to calculate the offset vectors. Thus, the approximation accuracy of the MPTPs is crucial in RBDO when the constraints are replaced by Kriging metamodels. As shown in Fig. 3, at the solution of SORA obtained by SORA, the MPTP of each active constraint is the intersection point between the LSS of the constraint and the β^t-circle. To obtain a high approximation accuracy of the MPTP of each active constraint, the location information of the above intersection point can be utilized when selecting update samples for Kriging metamodel refinement. Meanwhile, the update samples that are too close to existing training samples cannot provide sufficiently new information for Kriging metamodel refinement. Thus, the shortest distance between a new update sample and the existing training samples is considered in the selection of update samples. Based on the two above considerations, an active learning function for Kriging update in RBDO under distributional p-box model is defined as (12).

$$ {F}_p\left({\mathbf{d}}^{\ast },\mathbf{z}\right)=\frac{U\left({\mathbf{d}}^{\ast },\mathbf{z}\right)E\left(\mathbf{z}\right)}{D\left(\mathbf{z}\right)} $$

(12)

where F_p denotes the active learning function. d^∗ is the vector of deterministic variables at the solution of SORA. The point with the minimum value of F_p is selected as an update sample. From (11), it can be found that U is directly dependent on the prediction value and variance of the Kriging metamodel. The closer $\hat{g}$ is to 0 and the larger the prediction variance of the Kriging metamodel is, the smaller U is. Thus, in (9), U is applied to make the update sample located around the LSS of a constraint. In addition, E is employed to enhance the chance of points located around the β^t-circle being selected, which is formulated as (13).

$$ E\left(\mathbf{z}\right)={e}^{{\left(\left\Vert T\left(\mathbf{z}\right)\right\Vert -{\beta}_j^t\right)}^2} $$

(13)

In (13), T is a transformation operation, such as Nataf transformation and Rosenblatt transformation, which is used to transform z into the standard normal space. In T, the mean and standard deviation of each p-box variable and parameter are taken from the corresponding ones at the solution of SORA. In (12), D(z) is the shortest distance between the update sample and existing training samples in terms of p-box variables and parameters, which is used to avoid the update samples around the existing training samples which are chosen. D(z) is evaluated by

$$ D\left(\mathbf{z}\right)=\frac{\left\Vert \mathbf{z}-{\mathbf{z}}_{\mathrm{min}}\right\Vert }{\left\Vert {\mathbf{z}}^u-{\mathbf{z}}^l\right\Vert } $$

(14)

where z_min is the existing training sample with the shortest distance from z. The vectors z^u and z^l are the upper and lower bounds of z, respectively. For the purpose of adequately covering the uncertain space of P during the establishment of Kriging metamodels, five-sigma rule is adopted to define the initial sampling space of P in this work based on the experience in Bichon et al. (2008), i.e., $\left[{\boldsymbol{\upmu}}_{\mathbf{p}}^l-5{\boldsymbol{\upsigma}}_{\mathbf{p}}^u,{\boldsymbol{\upmu}}_{\mathbf{p}}^u+5{\boldsymbol{\upsigma}}_{\mathbf{p}}^u\right]$, which is also considered the bounds of uncertain space of P. ${\boldsymbol{\upmu}}_{\mathbf{p}}^l$ and ${\boldsymbol{\upmu}}_{\mathbf{p}}^u$ are the lower and upper bounds of the distribution mean vector of p-box parameters, respectively, and ${\boldsymbol{\upsigma}}_{\mathbf{p}}^u$ is the upper bound of the distribution standard deviation vector of p-box parameters. Then, the vector z^u and z^l are set to $\left[{\boldsymbol{\upmu}}_{\mathbf{x}}^u,{\boldsymbol{\upmu}}_{\mathbf{p}}^u+5{\boldsymbol{\upsigma}}_{\mathbf{p}}^u\right]$ and $\left[{\boldsymbol{\upmu}}_{\mathbf{x}}^l,{\boldsymbol{\upmu}}_{\mathbf{p}}^l-5{\boldsymbol{\upsigma}}_{\mathbf{p}}^u\right]$, respectively.

3.3 Generation of candidate update samples

To obtain the candidate update samples for each active constraint g_j, a hypersphere is defined in the standard normal space and its radius is set to ${\beta}_j^t$. The spherical coordination is shown in (15), where u_m is the mth p-box variable or parameter in z.

$$ \left\{\begin{array}{l}{u}_1=\rho \cos {\alpha}_1\\ {}{u}_2=\rho \sin {\alpha}_1\cos {\alpha}_2\\ {}\vdots \\ {}{u}_{m-1}=\rho \sin {\alpha}_1\sin {\alpha}_2\sin {\alpha}_3\cdots \sin {\alpha}_{m-2}\cos {\alpha}_{m-1}\\ {}{u}_m=\rho \sin {\alpha}_1\sin {\alpha}_2\sin {\alpha}_3\cdots \sin {\alpha}_{m-2}\sin {\alpha}_{m-1}\end{array}\right. $$

(15)

Then, the hypersphere can be represented as

$$ {\boldsymbol{\Delta}}_j=\left\{\left(\rho, {\alpha}_i\right)|\rho \in \left[0,{\beta}_j^t\right],\kern0.5em {\alpha}_i\in \left[0,2\pi \right];i=1,2,\dots, m\hbox{-} 1\right\} $$

(16)

In each region Δ_j, N_c candidate samples are randomly generated based on (ρ, α_i) and then transformed into the original design space by the inverse transformation operation T⁻¹, where the mean is z_{MPTP, j} and the standard deviations of p-box variables and parameters are those at the solution of SORA. Then, the samples located outside $\left[{\boldsymbol{\upmu}}_{\mathbf{x}}^l,{\boldsymbol{\upmu}}_{\mathbf{x}}^u\right]$ in (7) will be deleted. Among the remaining candidate points in the original design space, the point with the minimum F_p is selected as an update sample.

3.4 Procedure of the proposed method

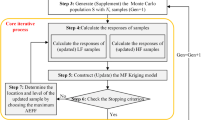
In this section, based on SORA, the active learning Kriging-assisted method is proposed for RBDO under distributional p-box model. The flowchart of the proposed method is presented in Fig. 4. The procedure of the proposed method is described as follows.

Fig. 4

Flowchart of the proposed method

Step 1: Establish the initial Kriging metamodel for each constraint. For deterministic and p-box variables, their design space is taken as the sampling region. For p-box parameters, their sampling region is set to $\left[{\boldsymbol{\upmu}}_{\mathbf{p}}^l-5{\boldsymbol{\upsigma}}_{\mathbf{p}}^u,{\boldsymbol{\upmu}}_{\mathbf{p}}^u+5{\boldsymbol{\upsigma}}_{\mathbf{p}}^u\right]$. Initial training samples are generated in these sampling regions, and the corresponding responses of constraints are evaluated. Generally, the number of initial training samples can be determined according to the dimension of the problem and the involved computational cost (Li et al. 2016). Then, initial Kriging metamodels of constraints are established.

Step 2: Perform RBDO under distributional p-box model by SORA. The iteration information iter is set to 1. Based on the built Kriging metamodels of constraints, SORA is performed and the solution of SORA is denoted by ${\left({\mathbf{d}}^{\ast },{\boldsymbol{\upmu}}_{\mathbf{x}}^{\ast}\right)}_{iter}$.

Step 3: Screen out active constraints. Based on the screening criterion in the “Screening criterion for active constraints” section, active constraints are screened out. Let n_a denote the number of active constraints g_k (k = 1, 2,…, n_a).

Step 4: Generate candidate points for each active constraint. At the solution of SORA, N_c candidate samples are generated around the MPTP of each active constraint as described in the “Generation of candidate update samples” section.

Step 5: Select update samples for each active constraint. For each active constraint, based on its candidate points, an update sample (d^∗, z)_new is selected based on the active learning function in the “An active learning function for Kriging update” section.

Step 6: Update the Kriging metamodel of each active constraint. For each active constraint g_k, if iter = 1, its response is calculated at the new update sample. The relative prediction error ε_k of the Kriging metamodel at the new update sample is estimated by (17) (Chen et al. 2014). Then, the Kriging metamodel is updated.

$$ {\varepsilon}_k=\frac{\left|{g}_k{\left({\mathbf{d}}^{\ast },\mathbf{z}\right)}_{\mathrm{new}}-{\hat{g}}_k{\left({\mathbf{d}}^{\ast },\mathbf{z}\right)}_{\mathrm{new}}\right|}{R\left({g}_k\right)} $$

(17)

where R(g_k) = max(g_k) − min(g_k). max(g_k) and min(g_k) are the maximum and minimum values of the active constraint g_k at the existing training samples, respectively.

When iter > 1, for each active constraint, if ε_k ≤ 10⁻⁶ which is evaluated in the last update, the region in the vicinity of the MPTP of the active constraint is well approximated, and the corresponding Kriging metamodel will not be updated. Otherwise, the response of the active constraint at the new update sample is calculated, and ε_k is recalculated at the new update sample. Then, the corresponding Kriging is updated.

Step 7: Implement SORA for RBDO under distributional p-box model. The iteration information iter is set to iter + 1. Based on the Kriging metamodels of constraints, SORA is performed and the solution of SORA is denoted by ${\left({\mathbf{d}}^{\ast },{\boldsymbol{\upmu}}_{\mathbf{x}}^{\ast}\right)}_{iter}$.

Step 8: Judge the convergence condition of the proposed method. If the convergence condition in (18) is satisfied, the procedure will go to Step 9; otherwise, go back to Step 3.

$$ \frac{\left\Vert {\left({\mathbf{d}}^{\ast },{\boldsymbol{\upmu}}_{\mathbf{x}}^{\ast}\right)}_{iter}-\Big({\mathbf{d}}^{\ast },{\boldsymbol{\upmu}}_{\mathbf{x}}^{\ast}\Big){}_{iter-1}\right\Vert }{\left\Vert {\left({\mathbf{d}}^{\ast },{\boldsymbol{\upmu}}_{\mathbf{x}}^{\ast}\right)}_{iter}\right\Vert +{10}^{-16}}\le {10}^{-3} $$

(18)

Step 9: Output the RBDO solution under distributional p-box model.

4 Test examples

In this section, four examples including a welded beam problem and a piezoelectric energy harvester design are tested to validate the performance of the proposed method. In this study, it is assumed that the responses of all constraints are obtained by running a simulator (i.e., a computer code) at an input. Thus, the responses of all constraints at the new update sample can be obtained simultaneously and used to update all constraints.

4.1 Mathematical example 1

This example is modified from a popular two-dimensional nonlinear mathematical problem (Youn and Choi 2004), which is convenient to clearly present the metamodel update process in the proposed method. This problem includes three constraints with two p-box variables. Its RBDO model is formulated as

$$ {\displaystyle \begin{array}{l}\mathrm{find}\kern0.33em {\mu}_x=\left[{\mu}_1,{\mu}_2\right]\\ {}\min \kern0.33em f\left({\mu}_x\right)={\mu}_2-{\mu}_1\\ {}s.t.\kern0.33em P\left(\left\{\underset{y}{\min }{g}_j\left(x(y)\right)\right\}>0\right)\ge {R}_j^t,\kern0.58em j=1,2,3\\ {}{g}_1(x)=\frac{x_1^2{x}_2}{20}-1\\ {}{g}_2(x)=\frac{{\left({x}_1+{x}_2-5\right)}^2}{30}+\frac{{\left({x}_1-{x}_2-12\right)}^2}{120}-1\\ {}{g}_3(x)=\frac{80}{\left({x}_1^2+8{x}_2+5\right)}-1\\ {}x=\left[{x}_1,{x}_2\right],\kern0.33em {x}_i\sim N\left({\mu}_i,{y}_i^2\right),0\le {\mu}_i\le 10,{y}_i\in \left[\mathrm{0.3,0.4}\right],\kern0.58em i=1\ \mathrm{and}\ 2\\ {}{\mu}_x^{(0)}=\left[5,5\right]\end{array}} $$

(19)

where x₁ and x₂ are p-box variables. The target reliability degrees ${R}_j^t$ (j = 1, 2, 3) are set to $\Phi \left({\beta}_j^t\right)$, where ${\beta}_j^t$ is the target reliability index of constraints and ${\beta}_j^t=3$ in this example.

In this example, the proposed method is compared with SORA, the double-loop method, Latin hypercube sampling (LHS) with Kriging, and CBS with Kriging. For LHS with Kriging, LHS is applied to generate 40 training points and then Kriging metamodels of constraints are built based on the training points. Based on built Kriging metamodels, SORA is performed without Kriging update. The training points and RBDO solution obtained from LHS with Kriging are presented in Fig. 5. It can be seen that constraint g₂ is not well approximated around its MPTP at the RBDO solution.

Fig. 5

Training samples, the LSSs of true and approximated constraints in LHS with Kriging

In CBS and the proposed method, the initial Kriging metamodels of three constraints are established based on 9 training samples, which are generated by 3-level full factorial design as shown in Figs. 6 and 7. Figure 6 shows all update samples obtained by CBS. It can be seen that the majority of these update samples are scattered on the LSSs around the feasible region of deterministic design optimization. In CBS, SORA is performed to obtain the RBDO solution based on updated Kriging metamodels. For the proposed method, the LSSs of the true and approximated constraints are also provided in Fig. 8. It can be seen that the LSSs of three true constraints cannot be well approximated by initial Kriging metamodels. Based on the screening criterion for active constraints in the “Screening criterion for active constraints” section, it can be judged that constraints g₂ and g₃ are active while g₁ is inactive. By using the proposed active learning Kriging-assisted method, 12 update samples are sequentially searched out and used in the update of Kriging metamodels, which are shown in Fig. 8. It can be observed that the majority of update samples are located around the active constraints g₂ and g₃, and the LSSs of g₂ and g₃ around the MPTPs are well approximated at the RBDO solution of the proposed method. Thus, it is demonstrated that the proposed method can well screen out the active constraints and achieve the accurate approximation of the LSSs around the MPTPs of active constraints at the RBDO solution.

Fig. 6

Update samples, the LSSs of true and approximated constraints in CBS with Kriging

Fig. 7

Initial training samples, and the LSSs of true and approximated constraints when iter = 1 for the proposed method

Fig. 8

Update samples, the LSSs of true and approximated constraints in the proposed method

Comparative results are listed in Table 1. From Table 1, it can be seen that SORA, the double-loop method, CBS with Kriging, and the proposed method have very similar RBDO solutions. The reliability analysis method in Jiang et al. (2011) is implemented to evaluate the reliability indexes of three constraints at the RBDO solution, which are provided in Table 1. Except LHS with Kriging, the minimum reliability indexes in the other methods satisfy the target value. For the double-loop method and SORA, the number of calls to constraints is associated with the evaluation of constraint responses and the calculation of constraint gradients. In terms of the sample size in evaluations of the true constraints, the proposed method only requires 21 samples to obtain the final Kriging metamodels of constraints, which are much fewer than the other methods. The proposed method shows the highest efficiency. Thus, it is demonstrated that the proposed method is very accurate and efficient for RBDO under distributional p-box model.

Table 1 Comparative results in mathematical example 1

4.2 Mathematical example 2

This problem is modified from Kang and Luo (2010), which involves two constraints, two uncertain variables with interval distributional parameters, and two uncertain parameters with interval distributional parameters. This example is used to validate the performance of the proposed method in the case with both p-box variables and p-box parameters. The RBDO model of this example is formulated as follows.

$$ {\displaystyle \begin{array}{l}\mathrm{find}:\kern0.33em {\mu}_x={\left[{\mu}_1,{\mu}_2\right]}^{\mathrm{T}}\\ {}\min :f\left({\mu}_x\right)={\left({\mu}_1+3\right)}^2+{\left({\mu}_2+3\right)}^2\\ {}s.t.\kern0.86em :\kern0.33em P\left(\left\{\underset{y}{\min }{g}_j\left(z(y)\right)\right\}>0\right)\ge {R}_j^t,z=\left[x,p\right],\kern0.33em j=1\ \mathrm{and}\ 2\\ {}\kern2.41em {g}_1\left(z(y)\right)={x}_1\left({x}_2+{p}_1\right)-{p}_2\\ {}{g}_2\left(z(y)\right)={\left({x}_2+{p}_1\right)}^2{p}_2-{x}_1\\ {}\kern2.31em {x}_1\sim N\left({\mu}_1,{y}_1^2\right),{x}_2\sim N\left({\mu}_2,{y}_2^2\right),{p}_1\sim N\left({y}_3,{0.01}^2\right),{p}_2\sim N\left({y}_4,{0.1}^2\right)\\ {}\kern2.41em 0\le {\mu}_1\le 10,\kern0.33em 1\le {\mu}_2\le 10,{y}_1\in \left[\mathrm{0.1,0.11}\right],{y}_2\in \left[\mathrm{0.1,0.11}\right],{y}_3\in \left[\mathrm{0.2,0.22}\right],{y}_4\in \left[\mathrm{2,2.2}\right]\end{array}} $$

(20)

where x₁ and x₂ are p-box variables, and p₁ and p₂ are p-box parameters. In this example, the target reliability degree ${R}_j^t$ (j = 1 and 2) is set to Φ(3).

In CBS and the proposed method, initial Kriging metamodels are built based on 20 initial training samples, which are uniformly generated by LHS. For LHS with Kriging, LHS is applied to generate 100 training points and then Kriging metamodels of constraints are built based on the training points. The optimization results of the double-loop method, SORA, LHS with Kriging, CBS with Kriging, and the proposed method are listed in Table 2. It can be noticed that the optimized objective value and RBDO solution obtained by the proposed method are very close to those of the double-loop method and SORA. The minimum reliability indexes in all the five methods satisfy the target value. However, the RBDO solutions of LHS with Kriging and CBS with Kriging are conservative. The proposed method only needs 37 samples to build the final Kriging metamodels of constraints, which are the fewest among the five methods. Therefore, the proposed method shows high accuracy and efficiency for RBDO under distributional p-box model.

Table 2 Comparative results in mathematical example 2

4.3 A welded beam

This example associates with a welded beam as shown in Fig. 9, which includes 5 constraints and 4 p-box variables. The RBDO problem of this example is formulated as follows.

$$ {\displaystyle \begin{array}{l}\mathrm{find}:\kern0.33em {\mu}_x={\left[{\mu}_1,{\mu}_2,{\mu}_3,{\mu}_4\right]}^{\mathrm{T}}\\ {}\min \kern0.33em :f\left({\mu}_x\right)={c}_1{\mu}_1^2{\mu}_2+{c}_2{\mu}_3{\mu}_4\left({m}_2+{\mu}_2\right)\\ {}s.t.\kern0.58em :P\left(\left\{\underset{y}{\min }{g}_j\left(x(y)\right)\right\}>0\right)\ge {R}_j^t,\kern0.33em j=1,2,\dots, 5\\ {}{g}_1\left(x(y)\right)=1-\frac{\tau \left(x(y)\right)}{m_6},{g}_2\left(x(y)\right)=1-\frac{\sigma \left(x(y)\right)}{m_7},{g}_3\left(x(y)\right)=1-\frac{x_1}{x_4}\\ {}{g}_4\left(x(y)\right)=1-\frac{\delta \left(x(y)\right)}{m_5},{g}_5=\frac{P_c\left(x(y)\right)}{m_1}-1\\ {}\tau \left(x(y)\right)={\left(t{\left(x(y)\right)}^2+\frac{2t\left(x(y)\right) tt\left(x(y)\right){x}_2}{2R\left(x(y)\right)}+ tt{\left(x(y)\right)}^2\right)}^{0.5}\\ {}t\left(x(y)\right)=\frac{m_1}{\sqrt{2}{x}_1{x}_2}, tt\left(x(y)\right)=\frac{M\left(x(y)\right)R\left(x(y)\right)}{J\left(x(y)\right)},M\left(x(y)\right)={m}_1\left({m}_2+\frac{x_2}{2}\right)\\ {}R\left(x(y)\right)=\frac{\sqrt{x_2^2+{\left({x}_1+{x}_3\right)}^2}}{2},J\left(x(y)\right)=\sqrt{2}{x}_1{x}_2\left(\frac{x_2^2}{12}+\frac{{\left({x}_1+{x}_3\right)}^2}{4}\right)\\ {}\sigma \left(x(y)\right)=\frac{6{m}_1{m}_2}{x_3^2{x}_4},\delta \left(x(y)\right)=\frac{4{m}_1{m}_2^3}{m_3{x}_3^3{x}_4},{P}_c\left(x(y)\right)=\frac{4.013{x}_3{x}_4^3\sqrt{m_3{m}_4}}{6{m}_2^2}\left(1-\frac{x_3}{4{m}_2}\sqrt{\frac{m_3}{m_4}}\right)\\ {}{m}_1=2.6688\times {10}^4\left(\mathrm{N}\right),{m}_2=3.556\times {10}^2\left(\mathrm{mm}\right),{m}_3=2.0685\times {10}^5\left(\mathrm{MPa}\right)\\ {}{m}_4=8.274\times {10}^4\left(\mathrm{MPa}\right),{m}_5=6.35\left(\mathrm{mm}\right),{m}_6=9.377\times {10}^1\left(\mathrm{MPa}\right)\\ {}{m}_7=2.0685\times {10}^2\left(\mathrm{MPa}\right),{c}_1=6.74135\times {10}^{-5}\left(\$/{\mathrm{mm}}^3\right),{c}_2=2.93585\times {10}^{-6}\left(\$/{\mathrm{mm}}^3\right)\\ {}3.175\le {\mu}_1\le \mathrm{50.8,0}\le {\mu}_2\le \mathrm{254,0}\le {\mu}_3\le \mathrm{254,0}\le {\mu}_4\le 254,{x}_i\sim N\left({\mu}_i,{y}_i^2\right),\kern0.33em i=1,2,3,4\\ {}{y}_1\in \left[\mathrm{0.15,0.20}\right],{y}_2\in \left[\mathrm{0.15,0.20}\right],{y}_3\in \left[\mathrm{0.01,0.015}\right],{y}_4\in \left[\mathrm{0.01,0.015}\right]\\ {}{\beta}_j^t=3,\kern0.33em j=1,2,\dots, 5,\kern0.58em {\mu}_x^{(0)}={\left[\mathrm{6.208,157.82,210.62,6.208}\right]}^{\mathrm{T}}\end{array}} $$

(21)

where x_i (i = 1, 2, 3, and 4) are p-box variables. In this example, the target reliability degrees ${R}_j^t$ (j = 1, 2, …, 5) are set to Φ(3).

Fig. 9

A welded beam structure

In this example, initial Kriging metamodels in the proposed method and CBS are built based on 20 initial training samples. These initial samples are generated by LHS, and uniformly scatter in the design space. For LHS with Kriging, LHS is applied to generate 300 training points and then Kriging metamodels of constraints are built based on the training points. The comparative results of the double-loop method, SORA, LHS with Kriging, CBS with Kriging, and the proposed method are listed in Table 3. It can be seen that the RBDO solution of the proposed method is very close to those of SORA and the double-loop method. The minimum reliability indexes of the constraints at each RBDO solution obtained by the double-loop method, SORA, and the proposed method satisfy the target value, while those of LHS with Kriging and CBS with Kriging violate the target value. In the double-loop method, an inner optimization procedure in (8) is nested in an outer loop. The nested framework results in that the double-loop method is inefficient and a large number of constrain evaluations are required. The proposed method only requires 97 samples to build the final Kriging metamodels of constraints, which are the fewest among the five methods. Thus, the proposed method shows the highest efficiency for RBDO under distributional p-box model.

Table 3 Comparative results in the welded beam example

4.4 Application to a piezoelectric energy harvester

The RBDO of a piezoelectric energy harvester (Seong et al. 2017) is considered in this example. As shown in Fig. 10, the piezoelectric energy harvester includes a shim laminated by piezoelectric materials and a tip mass. The materials of shim and tip mass are blue steel and tungsten/nickel alloy, respectively. Mechanical strain is transferred into voltage or current under the piezoelectric effect. Thirty-one modes are considered in this problem, in which higher longitudinal strain is allowed as small input forces are applied to the energy harvester. Voltage is yielded along the thickness direction with longitudinal stress/strain. The piezoelectric energy harvester can be modeled by a transformer circuit. According to the Kirchhoff’s voltage law, the circuit can be described by the coupled differential equations that characterize the transformation from mechanical stress/strain to voltage. The conversion process can be simulated by Matlab Simulink. In Fig. 10, the piezoelectric material length is l_e = 2.50 × 10⁻² m. The width of the harvester is w = 2.60 × 10⁻² m. The thickness of the piezoelectric patch is t_c = 2.54 × 10⁻⁴ m. The thickness of the center shim is t_sh = 2.60 × 10⁻⁴ m. The load resistance is R = 7.35 × 10⁺⁵Ω. The piezoelectric strain coefficient is equal to − 153.9 × 10⁻¹² m/V. The Young’s modulus of PZT-5A and the shim are equal to 66 × 10⁹ Pa and 200 × 10⁹ Pa, respectively. The details of this piezoelectric energy harvester can be found in Seong et al. (2017). In this example, the length of shim l_b, the length of tip mass l_m, and the height of tip mass h_m are distributional p-box variables. The RBDO problem of this example is expressed as

$$ {\displaystyle \begin{array}{l}\mathrm{find}:\kern0.33em {\mu}_x={\left[{\mu}_1,{\mu}_2,{\mu}_3\right]}^{\mathrm{T}}\\ {}\min :f=\left({\mu}_1+{\mu}_2\right){\mu}_3w\\ {}s.t.\kern0.86em :\kern0.33em P\left(\left\{\underset{y}{\min }g\left({l}_b\left({y}_1\right),{l}_m\left({y}_2\right),{h}_m\left({y}_3\right)\right)\right\}>0\right)\ge {R}^t\\ {}\kern2.61em g\left({l}_b\left({y}_1\right),{l}_m\left({y}_2\right),{h}_m\left({y}_3\right)\right)={P}_w\left({l}_b\left({y}_1\right),{l}_m\left({y}_2\right),{h}_m\left({y}_3\right)\right)-4\times {10}^{-4}\mathrm{m}\mathrm{W}\ \\ {}\kern2.74em {l}_b\sim N\left({\mu}_1,{y}_1^2\right),{l}_m\sim N\left({\mu}_2,{y}_2^2\right),{h}_m\sim N\left({\mu}_3,{y}_3^2\right)\\ {}\kern2.64em y=\left[{y}_1,{y}_2,{y}_3\right],{y}_1\in \left[1.8\times {10}^{-3}\mathrm{m},2.00\times {10}^{-3}\mathrm{m}\right],{y}_2\in \left[2.25\times {10}^{-4}\mathrm{m},2.55\times {10}^{-4}\mathrm{m}\right]\\ {}\kern2.64em {y}_3\in \left[1.19\times {10}^{-4}\mathrm{m},1.33\times {10}^{-4}\mathrm{m}\right],w=0.026\mathrm{m}\\ {}\kern2.64em 0.08\mathrm{m}\le {\mu}_1\le 0.1\mathrm{m},0.012\mathrm{m}\le {\mu}_2\le 0.015\mathrm{m},0.008\mathrm{m}\le {\mu}_3\le 0.01\mathrm{m}\end{array}} $$

(22)

where P_w denotes the harvester output power in frequency 16 Hz and the target reliability degree R^t is set to Φ(2).

Fig. 10

A piezoelectric energy harvester

In the proposed method and CBS with Kriging, initial Kriging metamodels are established based on 60 initial training samples. In the proposed method, 22 updated samples are sequentially found out to refine the Kriging metamodels. The comparative results of SORA, CBS with Kriging, and the proposed method are provided in Table 4. It can be seen that the RBDO solution of the proposed method is the same as that of SORA. And the reliability index of the constraint at each RBDO solution of SORA and the proposed method satisfies the target value, while that of CBS with Kriging violates the target value. In terms of the efficiency, 82 samples are required by the proposed method, which are fewer than those required by SORA and CBS with Kriging. Thus, the proposed method presents very high efficiency in RBDO under distributional p-box model.

Table 4 Comparative results in the piezoelectric energy harvester example

5 Comparison and discussion

In the proposed method, performing SORA and updating Kriging metamodels are repeated until the solution of SORA no longer changes. At the initial iterations, if the initial Kriging metamodels have poor accuracy in approximations of true constraints, the solutions obtained by SORA may be far away the final RBDO solution as shown in Figs. 7 and 8. As shown in Fig. 8, the final RBDO solution is obtained after update samples are sequentially added into the DoE. From Tables 1, 2, 3, and 4, it can be seen that the proposed method can obtain very similar RBDO solutions compared with the SORA with true constraints. Thus, even though the initial Kriging metamodels show poor approximations of true constraint functions, the sequential update of Kriging metamodels in the proposed method will gradually improve the solutions obtained by SORA. In each iteration of the proposed method, the update samples are searched out around the current MPTP obtained by SORA. Thus, in each iteration, the Kriging metamodel update in the proposed method is a local manner, which can be taken as exploitation. However, in terms of the whole RBDO procedure, the Kriging metamodels in the proposed method is sequentially updated to explore the final RBDO solution. Because the implementation of SORA is based on the gradient information of objective and constraint functions, the proposed method is a local optimization method. Though it can well exploit the local regions around the solutions obtained by SORA, the proposed method has the limitation in the exploration of the global RBDO solution.

In CBS, Kriging metamodels of true constraints are sequentially updated with focusing on the LSSs around the feasible region of deterministic design optimization, as shown in Fig. 6. After the construction of Kriging metamodels is completed, SORA is performed to obtain the RBDO solution. It can be seen that the construction of Kriging metamodels in CBS is independent on the implementation of RBDO, and the local information of the RBDO solution is not used during the construction of Kriging metamodels. Simultaneously, Kriging metamodels in CBS are refined at all LSSs around the feasible region of deterministic design optimization. Thus, the Kriging metamodel update in CBS can be viewed as a global manner, which shows that CBS has good exploration ability.

Comparatively, the refined region of Kriging metamodel in CBS is larger than that in the proposed method, as shown in Figs. 6 and 8. Therefore, generally, CBS requires more update samples than the proposed method, as shown in Tables 1, 2, 3, and 4. Because no exploitation procedure exists in CBS, it is difficult to keep high approximation accuracy of the local region around the solution obtained by SORA. However, the proposed method can well refine the Kriging metamodels in the local region around the solution of SORA. From the experimental results in Tables 2, 3, and 4, it can be observed that the proposed method can provide more accurate RBDO solutions than CBS.

6 Conclusions and future work

In this paper, an active learning Kriging-assisted method is proposed to handle RBDO under distributional p-box model. In the proposed method, SORA is extended to decouple the optimization procedure and reliability analysis in the RBDO problem under distributional p-box model. To cut down the computational cost in RBDO associated with time-consuming constraints, Kriging metamodels are built to replace the actual constraints. Furthermore, to avoid unnecessary computational cost on Kriging metamodel establishment in RBDO, a screening criterion is presented to judge active constraints. Then, an active learning function is defined to gain update samples, which are employed to refine the Kriging metamodel of each active constraint by focusing on its LSS around the MPTP at the solution of SORA. To validate its accuracy and efficiency, the proposed method is compared with SORA, the double-loop method, and CBS by the test of four examples, including a welded beam problem and a piezoelectric energy harvester example. Comparative results indicate that the proposed method by refining the approximation of the LSSs around the MPTPs of active constraints at the solution of SORA is more efficient for RBDO under distributional p-box model, compared with CBS by refining the approximation of LSSs of constraints around the feasible region of deterministic design optimization.

In this work, RBDO only with epistemic uncertainties is considered, where epistemic uncertainties are quantified by the distributional p-box model. We will extend the proposed method to RBDO under hybrid random and epistemic uncertainties in the future. Because the implementation of SORA is based on the gradient information of objective and constraint functions, the proposed method is a local optimization method. Though it can well exploit the local regions around the solutions obtained by SORA, the proposed method has the limitation in the exploration of the global RBDO solution. One possible way to balance the exploitation and exploration capabilities of metamodel-assisted methods for obtaining a global RBDO solution is that evolution algorithm is combined with the proposed method, which can be investigated in the future.