1 Introduction

Many phenomena in nature are often demonstrated by nonlinear evolution equations (NEEs), such as plasma physics, electromagnetic theory, solid-state physics, chemical kinetics, fluid dynamics, and mathematical biology. Suppose we want to understand better the physical mechanism of the natural phenomenon described by NEEs. In that case, we must look for solitary wave (SW) solutions to the NEEs, so techniques for extracting SW solutions to the governing equations must be developed. Examining SW solutions to solve NEEs has become one of the most important concerns of scientists in various sciences. In recent decades, there have been many powerful techniques for obtaining SW solutions for NEEs. For example, the new extended direct algebraic technique (Vahidi et al. 2021), the generalized exponential rational function technique (Ismael et al. 2021), the Adomian decomposition technique (Sunthrayuth et al. 2021), the singular manifold technique (Saleh et al. 2021), the generalized (G'/G)-expansion technique (Li and Han 2020), the sine–cosine technique (Abdelrahman et al. 2020), the simplified Hirota’s technique (Ismael et al. 2021), the homogeneous balance technique (Fan 2000), the variational iteration approach (He 1999), the modified Sardar Sub-equation technique (Saliou et al. 2021), the Jacobi elliptic function technique (Kudryashov 1919), the simplest equation technique (Kudryashov 2005) and exp-function technique (Navickas et al. 2010), etc. (Kumar et al. 2017; Kumar et al. 2021; Khatri et al. 2019, 2020; Fatema et al. 2022; Ekramul and Ali Akbar 2021; Chu et al. 2021; Yiasir Arafat et al. 2023; Fatema et al. 2022; Arafat et al. 2022; Odabaşı 2021; Jafari et al. 2012).

In this work, by means of the new Kudryashov approach, we will get some SW solutions of the following CD and the pKP equations given in Yusufoglu and Bekir (2007) and Kumar et al. (2021):

$$v_{xt} - 4v_{x} v_{xx} - 2v_{y} v_{xx} + v_{xxxy} = 0,$$
(1)

and

$$v_{xt} + \frac{3}{2}v_{x} v_{xx} + \frac{1}{4}v_{xxx} + \frac{3}{4}v_{yy} = 0,$$
(2)

respectively. Equation (1) was to describe the (2 + 1)-dimensional interaction of a Riemann wave propagating along the y-axis with a long wave along the x-axis, first developed by Degasperis and Calogero (1976). Equation (2) can be used to describe the dynamics of small, small but limited two-dimensional waves in various fields of research, which is the generalized (2 + 1)-dimensional equation of Korteweg-de Vries (KdV) (Gao and Zhang 2020). In addition, these equations arises in number of scientific models including astrophysics, fluid mechanics, chemical kinematics, solid-state physics, plasma physics, chemical chemistry and optical fiber (Jumarie 2006; Jafari and Tajadodi 2010; Biswas and Ranasinghe 2010; Ghorbani and Saberi-Nadjafi 2007).

2 The new Kudryashov approach

The purpose of this section is to explain the use of the new Kudryashov approach (Mirhosseini-Alizamini et al. 2021) to solve nonlinear evolution equations. Suppose a nonlinear EE for \(v(x,y,t)\), in the form

$$F(v,v_{t} ,v_{x} ,v_{y} ,v_{xt} ,v_{xx} \ldots ) = 0.$$
(3)

The transformation

$$v(x,y,t) = V(\varsigma ),\quad \varsigma = x + y - \lambda t,$$
(4)

reduces (3) to the ODE

$$G(V,V^{\prime},V^{\prime\prime},V^{\prime\prime\prime}, \ldots ) = 0,$$
(5)

where \(\lambda\) is constant. Assume that in terms of \(\aleph (\varsigma )\) the solution to ODE (5) is as follows:

$$V(\varsigma ) = \sum\limits_{\iota = 1}^{\kappa } {\beta_{\iota } \aleph^{\iota } (\varsigma )} ,\quad \beta_{\kappa } \ne 0,$$
(6)

where \(\aleph (\varsigma )\) satisfies the first-order ODE in the form

$$\left( {\aleph^{\prime}(\varsigma )} \right)^{2} = \left( {\sigma (\ln \Xi )\aleph (\varsigma )} \right)^{2} \left( {1 - 4ab\aleph^{2} (\varsigma )} \right)\;,\quad \Xi > 0,\quad {\text{and}}\quad \Xi \ne 1,$$
(7)

where \(\beta_{\iota } (0 \le \iota \le \kappa ),a,b\) and \(\sigma\) are constants. The solutions of Eq. (7) is

$$\aleph (\varsigma ) = \frac{1}{{a\Xi^{\sigma \varsigma } + b\Xi^{ - \sigma \varsigma } }}.$$
(8)

Substitute Eq. (6) into Eq. (5). Consequently, we get a polynomial of this substitution. In this polynomial, we gather all terms of the same powers and equate them to zero.

This leads to a system of algebraic equations that can be solved by Maple software and gives us unknown parameters \(\beta_{0} ,\beta_{1} , \ldots ,\beta_{\kappa }\)\(\lambda\); as a result, we get the SW solutions of Eqs. (1) and (2).

3 The CD equation

To find the SW solutions of Eq. (1), transformations (4) are written as ODE as follows:

$$- \lambda V^{\prime\prime} - 4V^{\prime}V^{\prime\prime} - 2V^{\prime}V^{\prime\prime} + V^{\prime\prime\prime\prime} = 0.$$
(9)

Integrating (9) once, we obtain

$$- \lambda V^{\prime} - 3(V^{\prime})^{2} + V^{\prime\prime\prime} = 0.$$
(10)

If we catch the transformation \(\wp = V^{\prime}\), then (11) can be written as follows:

$$- \lambda \wp - 3\wp^{2} + \wp^{\prime\prime} = 0.$$
(11)

Balancing the terms \(\wp^{2}\) and \(\wp^{\prime\prime}\), we get \(2\kappa = \kappa + 2 \Rightarrow \kappa = 2.\) By substituting \(\kappa = 2\) into (6), we get

$$\wp (\varsigma ) = \beta_{0} + \beta_{1} \aleph (\varsigma ) + \beta_{2} \aleph^{2} (\varsigma ).$$
(12)

A set of algebraic equations for \({\mkern 1mu} \beta_{0} ,\beta_{1} ,\beta_{2}\) and \({\mkern 1mu} a,b,\sigma ,\lambda\) is obtained by replacing (12) in Eq. (11). These systems are found as

$$\begin{aligned} & \aleph^{0} :\; - \lambda {\mkern 1mu} \beta_{0} - 3{\mkern 1mu} \beta_{0}^{2} = 0, \hfill \\ & \aleph^{1} :\; - \lambda {\mkern 1mu} \beta_{1} - 6{\mkern 1mu} \beta_{0} \beta_{1} + \sigma^{2} \beta_{1} \ln^{2} \left( \Xi \right) = 0, \hfill \\ & \aleph^{2} :\; - \lambda {\mkern 1mu} \beta_{2} - 6{\mkern 1mu} \beta_{0} \beta_{2} - 3{\mkern 1mu} \beta_{1}^{2} + 4{\mkern 1mu} \sigma^{2} \beta_{2} \ln^{2} \left( \Xi \right) = 0, \hfill \\ & \aleph^{3} :\; - 6{\mkern 1mu} \beta_{1} \beta_{2} - 8{\mkern 1mu} \sigma^{2} \beta_{1} ab\ln^{2} \left( \Xi \right) = 0, \hfill \\ & \aleph^{4} :\; - 3{\mkern 1mu} \beta_{2}^{2} - 24{\mkern 1mu} \sigma^{2} \beta_{2} ab\ln^{2} \left( \Xi \right) = 0. \hfill \\ \end{aligned}$$
(13)

In solving the above algebraic system using Maple, the following sets are obtained.

Set I.

$$\beta_{0} = 0{\mkern 1mu} ,\quad \beta_{1} = 0{\mkern 1mu} ,\quad \beta_{2} = - 8{\mkern 1mu} \sigma^{2} ab\ln^{2} \left( \Xi \right),\quad \lambda = 4{\mkern 1mu} \sigma^{2} \ln^{2} \left( \Xi \right).$$
(14)

Set II.

$$\begin{aligned} & \beta_{0} = \frac{4}{3}\sigma^{2} \ln^{2} \left( \Xi \right){\mkern 1mu} ,\quad \beta_{1} = 0{\mkern 1mu} ,\\ & \beta_{2} = - 8\sigma^{2} ab\ln^{2} \left( \Xi \right),\quad \lambda = - 4{\mkern 1mu} \sigma^{2} \ln^{2} \left( \Xi \right). \end{aligned}$$
(15)

From Eqs. (12) and (14), we get the following SW solutions:

$$\wp_{1} (\varsigma ) = - 2{\mkern 1mu} ab\left( {\frac{2\sigma \ln \left( \Xi \right)}{{a\Xi^{\sigma \varsigma } + b\Xi^{ - \sigma \varsigma } }}} \right)^{2} .$$
(16)

Integrating Eq. (16) once, we will obtain

$$V_{1} (\varsigma ) = \frac{{4b{\mkern 1mu} \sigma {\mkern 1mu} \ln \left( \Xi \right)}}{{a{\mkern 1mu} \Xi^{{2{\kern 1pt} \sigma {\kern 1pt} \varsigma }} + b}},$$
(17)

or

$$v_{1} (x,y,t) = {\mkern 1mu} \frac{{4b\sigma {\mkern 1mu} \ln \left( \Xi \right)}}{{a{\mkern 1mu} \Xi^{{2{\kern 1pt} \sigma {\kern 1pt} \left( {x + y - 4{\kern 1pt} \sigma^{2} \ln^{2} \left( \Xi \right)t} \right)}} + b}}.$$
(18)

From Eqs. (12) and (15), we get the following SW solutions:

$$\wp_{2} (\varsigma ) = \frac{4}{3}\sigma^{2} \ln^{2} \left( \Xi \right) - 2{\mkern 1mu} ab\left( {\frac{2\sigma \ln \left( \Xi \right)}{{a\Xi^{\sigma \varsigma } + b\Xi^{ - \sigma \varsigma } }}} \right)^{2} .$$
(19)

Integrating Eq. (19) once, we will obtain

$$V_{2} (\varsigma ) = \frac{4}{3}\sigma^{2} \varsigma \ln^{2} \left( \Xi \right) - \frac{{4b{\mkern 1mu} \sigma {\mkern 1mu} \ln \left( \Xi \right)}}{{a{\mkern 1mu} \Xi^{{2{\kern 1pt} \sigma {\kern 1pt} \varsigma }} + b}},$$
(20)

or

$$\begin{aligned} v_{2} (x,y,t) &= \frac{4}{3}\sigma^{2} \left( {x + y + 4{\kern 1pt} \sigma^{2} \ln^{2} \left( \Xi \right)t} \right)\ln^{2} \left( \Xi \right) \\&\quad+ \frac{{4b{\mkern 1mu} \sigma {\mkern 1mu} \ln \left( \Xi \right){\mkern 1mu} }}{{a{\mkern 1mu} \Xi^{{2{\kern 1pt} \sigma \left( {x + y + 4{\kern 1pt} \sigma^{2} \ln^{2} \left( \Xi \right)t} \right)}} + b}}. \end{aligned}$$
(21)

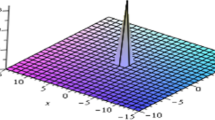
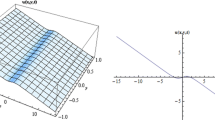
Kink-shaped soliton of Eq. (1) for \(\sigma = 2,a = 0.2,b = 0.5,y = 0.5,\Xi = 2.6,\) within the interval \(- 5 \le x\,,\,t \le 5\), the top left figure shows the 3D plot, the top right figure shows contour plot, the bottom left figure shows the 2D plot and the bottom right figure shows polar coordinates for \(t = 0,0.3,0.6\) (Fig. 1).

Fig. 1
figure 1

I 3D plot, II Contour plot, III 2D plot and IV polar coordinates of Eq. (18) when \(\sigma = 2, a = 0.2, b = 0.5,\) and \(y = 0.5,\) with \(\Xi = 2.6\)

Full size image

4 The pKP equation

To find the SW solutions of Eq. (2), transformations (4) are written as ODE as follows:

$$\left( {\frac{3}{4} - \lambda } \right)V^{\prime\prime} + \frac{3}{2}V^{\prime}V^{\prime\prime} + \frac{1}{4}V^{\prime\prime\prime\prime} = 0.$$
(22)

Integrating (22) once, we obtain

$$\left( {\frac{3}{4} - \lambda } \right)V^{\prime} + \frac{3}{2}\left( {V^{\prime}} \right)^{2} + \frac{1}{4}V^{\prime\prime\prime} = 0.$$
(23)

If we catch the transformation \(\wp = V^{\prime}\), then (23) can be written as follows:

$$\left( {\frac{3}{4} - \lambda } \right)\wp + \frac{3}{2}\wp^{2} + \frac{1}{4}\wp^{\prime\prime} = 0.$$
(24)

Balancing the terms \(\wp^{2}\) and \(\wp^{\prime\prime}\), we get \(2\kappa = \kappa + 2 \Rightarrow \kappa = 2.\) By substituting \(\kappa = 2\) into (6), we get

$$\wp (\varsigma ) = \beta_{0} + \beta_{1} \aleph (\varsigma ) + \beta_{2} \aleph^{2} (\varsigma ).$$
(25)

A set of algebraic equations for \({\mkern 1mu} \beta_{0} ,\beta_{1} ,\beta_{2}\) and \({\mkern 1mu} a,b,\sigma ,\lambda\) is obtained by replacing (25) in Eq. (24). These systems are found as

$$\begin{gathered} \aleph^{0} :\;\frac{3}{4}{\mkern 1mu} \beta_{0} - \lambda {\mkern 1mu} \beta_{0} + \frac{3}{4}\beta_{0}^{2} = 0, \hfill \\ \aleph^{1} :\frac{3}{4}\beta_{1} - \lambda {\mkern 1mu} \beta_{1} + \frac{3}{2}{\mkern 1mu} \beta_{0} \beta_{1} + \frac{1}{4}{\mkern 1mu} \sigma^{2} \beta_{1} \ln^{2} \left( \Xi \right) = 0, \hfill \\ \aleph^{2} :\;\frac{3}{4}\beta_{2} - \lambda {\mkern 1mu} \beta_{2} + \frac{3}{2}{\mkern 1mu} \beta_{0} \beta_{2} + \frac{3}{4}{\mkern 1mu} \beta_{1}^{2} + \sigma^{2} \beta_{2} \ln^{2} \left( \Xi \right) = 0, \hfill \\ \aleph^{3} :\frac{3}{2}{\mkern 1mu} \beta_{1} \beta_{2} - 2{\mkern 1mu} \sigma^{2} \beta_{1} ab\ln^{2} \left( \Xi \right) = 0, \hfill \\ \aleph^{4} :\;\frac{3}{4}{\mkern 1mu} \beta_{2}^{2} - 6{\mkern 1mu} \sigma^{2} \beta_{2} ab\ln^{2} \left( \Xi \right) = 0. \hfill \\ \end{gathered}$$
(26)

In solving the above algebraic system using Maple, the following sets are obtained.

Set I.

$$\beta_{0} = 0{\mkern 1mu} ,\quad \beta_{1} = 0{\mkern 1mu} ,\quad \beta_{2} = 8{\mkern 1mu} \sigma^{2} ab\ln^{2} \left( \Xi \right),\quad \lambda = \frac{3}{4} + {\mkern 1mu} \sigma^{2} \ln^{2} \left( \Xi \right).$$
(27)

Set II.

$$\begin{aligned} & \beta_{0} = - \frac{4}{3}\sigma^{2} \ln^{2} \left( \Xi \right){\mkern 1mu} ,\quad \beta_{1} = 0{\mkern 1mu} ,\quad \beta_{2} = 8\sigma^{2} ab\ln^{2} \left( \Xi \right),\\ & \lambda = \frac{3}{4} - {\mkern 1mu} \sigma^{2} \ln^{2} \left( \Xi \right).\end{aligned}$$
(28)

From Eqs. (25) and (27), we get the following SW solutions:

$$\wp_{1} (\varsigma ) = 2{\mkern 1mu} ab\left( {\frac{2\sigma \ln \left( \Xi \right)}{{a\Xi^{\sigma \varsigma } + b\Xi^{ - \sigma \varsigma } }}} \right)^{2} .$$
(29)

Integrating Eq. (29) once, we will obtain

$$V_{1} (\varsigma ) = - \frac{{4b\sigma {\mkern 1mu} \ln \left( \Xi \right)}}{{a{\mkern 1mu} \Xi^{{2{\kern 1pt} \sigma {\kern 1pt} \varsigma }} + b}},$$
(30)

or

$$v_{1} (x,y,t) = {\mkern 1mu} - \frac{{4b\sigma {\mkern 1mu} \ln \left( \Xi \right)}}{{a{\mkern 1mu} \Xi^{{2{\kern 1pt} \sigma {\kern 1pt} \left( {x + y - \left( {\frac{3}{4} + \sigma^{2} \ln^{2} \left( \Xi \right)} \right)t} \right)}} + b}}.$$
(31)

From Eqs. (25) and (28), we get the following SW solutions:

$$\wp_{2} (\varsigma ) = - \frac{4}{3}\sigma^{2} \ln^{2} \left( \Xi \right) + 2{\mkern 1mu} ab\left( {\frac{2\sigma \ln \left( \Xi \right)}{{a\Xi^{\sigma \varsigma } + b\Xi^{ - \sigma \varsigma } }}} \right)^{2} .$$
(32)

Integrating Eq. (32) once, we will obtain

$$V_{2} (\varsigma ) = - \frac{4}{3}\sigma^{2} \varsigma \ln^{2} \left( \Xi \right) - \frac{{4b{\mkern 1mu} \sigma {\mkern 1mu} \ln \left( \Xi \right)}}{{a{\mkern 1mu} \Xi^{{2{\kern 1pt} \sigma {\kern 1pt} \varsigma }} + b}},$$
(33)

or

$$\begin{gathered} v_{2} (x,y,t) = - \frac{4}{3}\sigma^{2} \left( {x + y - \left( {\frac{3}{4} - {\mkern 1mu} \sigma^{2} \ln^{2} \left( \Xi \right)} \right)t} \right)\ln^{2} \left( \Xi \right) \hfill \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad - \frac{{4b{\mkern 1mu} \sigma {\mkern 1mu} \ln \left( \Xi \right){\mkern 1mu} }}{{a{\mkern 1mu} \Xi^{{2{\kern 1pt} \sigma \left( {x + y - \left( {\frac{3}{4} - {\mkern 1mu} \sigma^{2} \ln^{2} \left( \Xi \right)} \right)t} \right)}} + b}}. \hfill \\ \end{gathered}$$
(34)

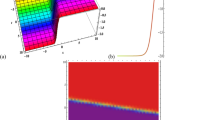
Singular Kink soliton of Eq. (2) for \(\sigma = 2,a = 0.5,b = 0.75,y = 1,\Xi = e,\) within the interval \(- 5 \le x\,,\,t \le 5\), the top left figure shows the 3D plot, the top right figure shows contour plot, the bottom left figure shows the 2D plot and the bottom right figure shows polar coordinates for \(t = 0,0.3,0.6\) (Fig. 2).

Fig. 2
figure 2

I 3D plot, II contour plot, III 2D plot and IV polar coordinates of Eq. (34) when \(\sigma = 2,a = 0.5,b = 0.75,\) and \(y = 1,\) with \(\Xi = e\)

Full size image

5 Conclusions

In this paper, we obtain the new SW solutions of the CD and pKP equations using the new Kudryashov approach and with the help of symbolic calculations. It is worthwhile to mention that this approach is effective and reliable in solving NLEEs. The applied approach will be used in further works to establish more entirely new SW solutions for other kinds of NLEEs.