1 Introduction

The nonlinear evolution equations (NLEEs) transpire in a wide spectrum of physical problems such as plasma physics, fluid dynamics, solid mechanics, nonlinear optics, oceanography, engineering, chemistry, biology, quantum field theory, and several others. It is requisite to extract traveling wave solutions of NLEEs to identify the mechanisms of the nonlinear physical phenomena characterized by these equations. Over the years much care has been paid by the research scholars for this purpose and evolved many powerful, reliable, and compact techniques for handling NLEEs. These are the inverse scattering transform method, auto Bäcklund transformation method, Hirota’s bilinear transformation method, the tanh-coth function method, the projective Riccati equation method, the ansatz method, the F-expansion method, the simplest equation method, the modified and extended simplest equation method, the extended sinh-Gordon equation expansion method, the auxiliary equation method, the \((G^{'}/G)\) -expansion method and it’s extended versions, the fractional transformation, the extended and modified auxiliary equation method, the trial function method, the reductive perturbation method, the extended modified rational expansion method, the modified extended mapping method, the extended sub-equation method and the exp[\(-G(\xi )\)]-function expansion method [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32] and many more. Essentially, there is no common integrated scheme that can be applied to all types of NLEEs. Generally, it is a challenging task to realize the exact solutions of NLEEs. Fan [33] developed a new sub-equation method to attain analytical exact solutions of NLEEs. Numerous authors presented the extended Fan sub-equation method by employing various sub-equations and realized plentiful new exact solutions of nonlinear equations [34,35,36].

In the contemporaneous work, we observe more prevailing traveling wave solutions to the subsequent higher-dimensional integrable (4+1)-dimensional nonlinear Fokas equation, restructures in the dimensionless form as

$$\begin{aligned}4U_{tx}-U_{xxxy}+U_{xyyy}+12U_{x}U_{y} +12U U_{xy}-6U_{zw}=0, \end{aligned}$$
(1)

which achieved in the important integrable generalizations of the Davey–Stewartson (DS) and Kadomtsev–Petviashvili (KP) Eq. [37]. The KP and DS equations principally utilized to represent the internal tides and surface waves effect in canals and 3-dimensional progression of the wavefront on the water of measurable depth, respectively [38]. The higher-dimensional nonlinear Fokas equation with the increasing number of physical variables may incorporate more facts, information, and properties concerning the natural phenomena [37]. Fokas at el. stretched their investigation to the nonlinear integrable partial differential equations in multi-dimensions [39].

Several authors investigated Eq. (1) by numerous analytic methodologies such as the Exp-function method, the parameter limit method [40], the \((G^{'}/G)\)-expansion method [41], the modified and the extended version of simplest equation method [23], the Hirota’s bilinear transformation method [5, 6], the extended F-expansion method [42]. Very recently, we reported localized soliton solutions of Eq. (1) in Ref.[43] using the Jacobian elliptic function method, the semi-inverse variational technique, the Padés type transformation, and the triangle function approach, respectively.

To our best knowledge, Eq. (1) is not studied elsewhere by means of the extended Fan sub-equation procedure, the exp[\(-G(\xi )\)]-function expansion technique, and the fractional Möbius transformation method. Therefore in this work, we find some new traveling wave solutions to Eq. (1) by utilizing the above-mentioned schemes.

The sections are arranged as follows: A brief narrative of the extended Fan sub-equation method, the exp-function expansion method, and the fractional Möbius transformation method are conferred in Sect. 2. In Sect. 3, we solve the (4+1)-dimensional Fokas equation by application of different methods, and different kinds of solutions namely hyperbolic, trigonometric, rational, Weierstrass, and Jacobian doubly periodic solutions are reported. In Sect. 4, graphical representations of some of the obtained solutions of Eq. (1) are portrayed and discussed. Section 5, allotted for conclusions.

2 Overview of the methods

2.1 Outlines of the extended Fan sub-equation approach

The key footsteps of the extended Fan sub-equation method are given as [44, 45]:

For a given nonlinear partial differential equation (PDE)

$$\begin{aligned} L(v, v_{t} , v_{x}, v_{y}, v_{tt} , v_{xx}, v_{yy},. . .)= 0, \end{aligned}$$
(2)

where L is a polynomial of v(x, y, t) and its partial derivatives in which the highest order derivatives and nonlinear terms are contained.

Step1 Change of variables \(v (x,y, t) = v (\xi )\), where \(\xi = \alpha x + \beta y + \epsilon t + \xi _0\) turn PDE (2) into a nonlinear ordinary differential equation (ODE) as

$$\begin{aligned} F(v, \epsilon v^{'}, \alpha v^{'}, \beta v^{'}, \epsilon ^2 v^{''}, \alpha ^2 v^{''}, \beta ^2 v^{''},...)=0, \end{aligned}$$
(3)

where \(\epsilon \) is identified as the wave speed of propagation and \(\alpha \), \(\beta \), \(\xi _0\) are arbitrary undetermined parameters. F is defined as a polynomial of \(v (\xi )\) and its partial derivatives with prime \((')=\frac{d}{d\xi }\).

Step 2 We adopt the solution of Eq. (3) in the following extended form

$$\begin{aligned} v(\xi )=\sum _{i=0}^{N}a_{i}\phi ^{i}+\sum _{i=1}^{N}b_{i}\phi ^{-i}, \end{aligned}$$
(4)

and \(\phi \) satisfies the following sub-equation

$$\begin{aligned} {\phi ^{'}}^2(\xi )={\sum _{j=0}^{4}c_j \phi ^{j}}, \end{aligned}$$
(5)

here \(c_j\), \(a_i\), \(b_i\) \((j=0,1,2,3,4; i=0,1,2,3,...,N)\) are constants to be reviewed later. Therefore, the necessary derivatives are given as

$$\begin{aligned} \frac{dv}{d\xi }= & {} \varepsilon \sqrt{\sum _{j=0}^{4}c_j \phi ^{j}} \frac{dv}{d\phi }, \end{aligned}$$
(6)
$$\begin{aligned} \frac{d^2v}{d\xi ^2}= & {} \frac{1}{2}\sum _{j=1}^{4} j c_j \phi ^{j-1}\frac{dv}{d\phi }+\sum _{j=0}^{4} c_j \phi ^{j}\frac{d^2v}{d\phi ^2}, \end{aligned}$$
(7)

where \(\varepsilon =\pm 1\). The first order Eq. (5) provides various types of fundamental solutions [45]. From these solutions, more new type of exact solutions of Eq. (2) can be achieved.

Step 3 Find the positive number N in Eq. (3) by balancing the highest order derivatives and the nonlinear terms.

Step 4 Replace Eq. (4) into Eq. (3) along with Eq.(5) resulting in a polynomial of \(\phi ^i(\xi )(i=0,1,2,...)\). Gathering all terms of same powers and setting them to be zero, provide a set of algebraic equations which can be resolved for unknown parameters with the help of Maple or Mathematica. Subsequently, the exact solutions to nonlinear Eq. (1) are retrieved.

2.2 Outlines of the exp[\(-G(\xi )\)] function expansion approach

Step 1 The solution of Eq. (3) can be specified as

$$\begin{aligned} v(\xi )=\sum _{i=0}^{N}a_{i}[\exp (-G(\xi ))]^{i}, \end{aligned}$$
(8)

where integer N is determined by balancing procedure from Eq. (3).

Step 2 The function \(G(\xi )\) satisfies the following differential equation:

$$\begin{aligned} \frac{d G(\xi )}{d\xi }=\exp (-G(\xi ))+s \exp (G(\xi ))+r, \end{aligned}$$
(9)

where s and r are constants.

The solutions of Eq. (9) read as

$$\begin{aligned} G(\xi )= & {} \ln \Big [-\frac{r}{2s}-\frac{\sqrt{r^2-4s}}{2s}\tanh \Big (\frac{\sqrt{r^2-4s}}{2}(\xi +\xi _0)\Big )\Big ],\,\,s\ne 0, r^2-4s>0, \end{aligned}$$
(10)
$$\begin{aligned} G(\xi )= & {} \ln \Big [-\frac{r}{2s}-\frac{\sqrt{r^2-4s}}{2s}\coth \Big (\frac{\sqrt{r^2-4s}}{2}(\xi +\xi _0)\Big )\Big ], \,\, s\ne 0, r^2-4s>0, \end{aligned}$$
(11)
$$\begin{aligned} G(\xi )= & {} \ln \Big [-\frac{r}{2s}+\frac{\sqrt{4s-r^2}}{2s}\tan \Big (\frac{\sqrt{4s-r^2}}{2}(\xi +\xi _0)\Big )\Big ], \,\,s\ne 0, r^2-4s<0, \end{aligned}$$
(12)
$$\begin{aligned} G(\xi )= & {} \ln \Big [-\frac{r}{2s}-\frac{\sqrt{4s-r^2}}{2s}\cot \Big (\frac{\sqrt{4s-r^2}}{2}(\xi +\xi _0)\Big )\Big ], \,\, s\ne 0, r^2-4s<0, \end{aligned}$$
(13)

Step 3 Replacing Eq. (8) into (3)along with Eq.(9) and comparing the same powers of \(\exp (-G(\xi ))\) to zero, we get polynomial equations which are solved for undetermined constants using Maple software.

Step 4 With the help of solutions of Eq. (9) from (10–13), the exact solutions of Eq. (1) are described.

2.3 Outlines of the fractional transformation approach

Step 1 Eq. (3) assumes the following form of solution as

$$\begin{aligned} \phi (\xi )=\frac{\tilde{a}+\tilde{b} f(\xi ,m)^l}{1+\tilde{d} f(\xi ,m)^l}, \end{aligned}$$
(14)

where l is defined as an integer, \(\tilde{a},\tilde{b}\) and \(\tilde{d}\) are undetermined real constants, and the modulus parameter \(m(0\le m\le 1)\) in a Jacobian elliptic function \(f(\xi ,m)\) defines the degree of localization.

Step 2 Using the balance principal, the positive integer l can be evaluated. In Eq. (14), the function \(f(\xi ,m)\) can be described as \(f(\xi ,m)=sn(\xi ,m)\), \(f(\xi ,m)=cn(\xi ,m)\) or \(f(\xi ,m)=dn(\xi ,m)\).

Step 3 Replace Eq. (14) into Eq. (3) and relating the coefficients of same powers of one of the selected Jacobian elliptic function \(f(\xi ,m)\) to zero results in a set of polynomial equations which further can be solved for unknown parameters and constants. Subsequently substituting the determined parameters into Eq. (14) and the forms of the function \(f(\xi ,m)\), the localized solutions of Eq. (1) can be attained.

3 Applications of the methods

3.1 Exact solutions of Eq. (1) via extended Fan sub-equation method

For the traveling wave solutions of Eq. (1), we adopt the subsequent wave transformation as

$$\begin{aligned}&U(x,y,z,w,t)=U(\xi ), \,\, \xi = \alpha x + \beta y + \chi z + \lambda w + \eta t + \xi _0, \end{aligned}$$
(15)

where \(\alpha \), \(\beta \), \(\chi \), \(\lambda \) and \(\eta \) are assumed to be nonzero constants and \(\xi _0\) is an arbitrary constant. On substituting Eq. (15) into Eq. (1), we get the following form of reduced ODE:

$$\begin{aligned}&(\alpha \beta ^3-\alpha ^3 \beta )U^{''''}+(4\alpha \eta -6\chi \lambda )U^{''} +12\alpha \beta (UU^{'})^{'}=0. \end{aligned}$$
(16)

Here \(\eta \) represent the velocity of propagation. On integrating Eq. (16) twice w.r.t. \(\xi \) and allowing integration constants to be zero, we obtain

$$\begin{aligned} (\alpha \beta ^3-\alpha ^3 \beta )U^{''}+(4\alpha \eta -6\chi \lambda )U+6\alpha \beta U^{2}=0. \end{aligned}$$
(17)

One can easily show that balancing the highest order derivative term \(U^{''}\) having exponent \(N+2\) with the leading nonlinear term \(U^2\) with exponent 2N in Eq. (17) provides \(N = 2\). Henceforth, the solution of Eq. (17) has the following form

$$\begin{aligned} U(\xi )=a_0+a_1\phi +a_2\phi ^2+b_1\phi ^{-1}+b_2\phi ^{-2}. \end{aligned}$$
(18)

On replacing \(U(\xi )\) and its derivatives along with Eq. (5) into Eq. (17) and relating all the coefficients of equal powers of \(\phi ^j\) , \(j=[-4, 4]\) to be zero, we realise a set of algebraic equations:

$$\begin{aligned}&12{ a_2}\alpha \beta ( { c_4}{\beta }^{2}-{ c_4}{\alpha }^{2}+{ a_2})=0, \end{aligned}$$
(19a)
$$\begin{aligned}&24 \Big \{ \Big ( -\frac{1}{6}{ c_4}{ a_1}-{\frac{5}{12}}{a_2} { c_3} \Big ) {\alpha }^{2}\nonumber \\&\quad + \Big ( {\frac{5}{12}}{ a_2}{ c_3}+\frac{1}{6}{ c4}{ a_1}\Big ) {\beta }^{2}+{ a_1}{ a_2} \Big \} \beta \alpha =0, \end{aligned}$$
(19b)
$$\begin{aligned}&\beta ( -3{ c_3}{ a_1}-8{ a_2}{ c_2}) { \alpha }^{3}+ ( ( 3{ c_3}{ a_1}+8{ a_2}{ c_2 } ) {\beta }^{3}\nonumber \\&\quad + (12{{ a^2_1}}+24{ a_0}{ a_2 } ) \beta +8\eta { a_2} ) \alpha -12\chi \lambda { a_2}=0, \end{aligned}$$
(19c)
$$\begin{aligned}&-2\beta ( 3{ a_2}{ c_1}+{ c_2}{ a_1} ) {\alpha }^{3}+ ( ( 2{ c_2}{ a_1}+6{ a_2}{ c_1 } ) {\beta }^{3}\nonumber \\&\quad + ( 24{ b_1}{ a_2}+24{ a_1}{ a_0} ) \beta +8{ a_1}\eta ) \alpha -12{ a_1}\lambda \chi =0, \end{aligned}$$
(19d)
$$\begin{aligned}&-\beta ( 4{ a_2}{ c_0}+4{ b_2}{ c_4}+{ b_1} { c_3}+{ a_1}{ c_1} ) {\alpha }^{3}\nonumber \\&\quad + ( ( 4{ a_2}{ c_0}+4{ b_2}{c_4}+{ b_1}{ c_3} +{ a_1}{ c_1}) {\beta }^{3}\nonumber \\&\quad + ( 24{ a_1}{ b_1}+12{{ a^2_0}}+24{ a_2}{ b_2} ) \beta +8{ a_0}\eta ) \alpha \nonumber \\&\quad -12\chi \lambda { a_0}=0, \end{aligned}$$
(19e)
$$\begin{aligned}&-2\beta ( 3{ b_2}{ c_3}+{ b_1}{ c_2} ) {\alpha }^{3}+ ( ( 2{ b_1}{ c_2}+6{ b_2}{ c_3} ) {\beta }^{3}\nonumber \\&\quad + ( 24{ b_2}{ a_1}+24{ a_0}{ b_1} ) \beta +8\eta { b_1} ) \alpha \nonumber \\&\quad -12\chi \lambda { b_1}=0, \end{aligned}$$
(19f)
$$\begin{aligned}&\beta ( -8{ b_2}{ c_2}-3{ b_1}{ c_1}) {\alpha }^{3}+ ( ( 8{ b_2}{ c_2}+3{ b_1}{ c_1} ) {\beta }^{3}\nonumber \\&\quad + ( 12{{ b_1}}^{2} +24{ a_0}{ b_2} ) \beta +8\eta { b_2} ) \alpha -12\chi \lambda { b_2}=0, \end{aligned}$$
(19g)
$$\begin{aligned}&24\beta \Big \{ \Big ( -{\frac{5}{12}}{ b_2}{ c_1}-\frac{1}{6}{ b_1}{ c_0}\Big ) {\alpha }^{2}\nonumber \\&\quad + \Big ( \frac{1}{6}{ b_1}{ c_0} +{\frac{5}{12}}{ b_2}{ c_1} \Big ) {\beta }^{2}\nonumber \\&\quad +{ b_1}{ b_2} \Big \} \alpha =0. \end{aligned}$$
(19h)

Solving the resulting set of algebraic equations (19a–19h) self consistently with the help of Maple and considering the different types of fundamental solutions of Eq. (5) [45], we obtain the subsequent cases which leads to different kinds of solutions of considered model equation.

Family 1 If \(c_0 = c_1 = c_3 = 0\). We have the following results

$$\begin{aligned} a_1= & {} b_1=b_2=0, a_0={\frac{-2\alpha \eta +3\chi \lambda }{3\alpha \beta }}, \nonumber \\ a_2= & {} c_4(\alpha ^2-\beta ^2), c_2={\frac{-2\alpha \eta +3\chi \lambda }{2\alpha \beta (\alpha ^2-\beta ^2)}}. \end{aligned}$$
(20)

Combining Eq. (20) with Eq. (18) and utilizing the solutions of sub-equation, we get, solitary wave solutions, singular periodic solutions and rational solution of Eq. (1) as:

$$\begin{aligned} U(\xi )= & {} {\frac{-2\alpha \eta +3\chi \lambda }{3\alpha \beta }}+c_4(\alpha ^2-\beta ^2)\nonumber \\&\Bigg [\sqrt{{\frac{2\alpha \eta -3\chi \lambda }{2\alpha \beta (\alpha ^2-\beta ^2)c_4}}}{{\,{\mathrm{sech}}\,}}\Bigg (\sqrt{{\frac{-2\alpha \eta +3\chi \lambda }{2\alpha \beta (\alpha ^2-\beta ^2)}}}\xi \Bigg )\Bigg ]^2,\nonumber \\&c_2>0, c_4<0. \end{aligned}$$
(21)
$$\begin{aligned} U(\xi )= & {} {\frac{-2\alpha \eta +3\chi \lambda }{3\alpha \beta }}+c_4(\alpha ^2-\beta ^2)\nonumber \\&\Bigg [\sqrt{{\frac{2\alpha \eta -3\chi \lambda }{2\alpha \beta (\alpha ^2-\beta ^2)c_4}}}\sec \Bigg (\sqrt{{\frac{2\alpha \eta -3\chi \lambda }{2\alpha \beta (\alpha ^2-\beta ^2)}}}\xi \Bigg )\Bigg ]^2,\nonumber \\&c_2<0, c_4>0. \end{aligned}$$
(22)
$$\begin{aligned} U(\xi )= & {} {\frac{-2\alpha \eta +3\chi \lambda }{3\alpha \beta }}+\frac{(\alpha ^2-\beta ^2)}{{\xi }^2},\nonumber \\&c_2=0, c_4>0. \end{aligned}$$
(23)

Family 2 If \( c_1=c_3=0\). We have the subsequent results

Set(i)

$$\begin{aligned} a_0= a_1 = a_2 = b_1 = 0, \chi =-\frac{2\beta \eta }{3\lambda }, \alpha +\beta =0. \end{aligned}$$
(24)

Substituting Eq. (24) with Eq. (18) and utilizing the solutions of Fan sub-equation we get the hyperbolic function wave solution, a trignometric solution and three Jacobi elliptic periodic wave solutions with double period.

$$\begin{aligned} U(\xi )= & {} b_2 \Bigg [\pm \sqrt{-\frac{c_2}{2c_4}} \tanh \Bigg (\sqrt{-\frac{c_2}{2}}\xi \Bigg )\Bigg ]^{-2}, \nonumber \\&c_2<0, c_4>0, c_0=\frac{c^2_2}{4c_4}. \end{aligned}$$
(25)
$$\begin{aligned}&U(\xi )=b_2 \Bigg [\pm \sqrt{\frac{c_2}{2c_4}} \tan \Bigg (\sqrt{\frac{c_2}{2}}\xi \Bigg )\Bigg ]^{-2}, \nonumber \\&c_2>0, c_4>0, c_0=\frac{c^2_2}{4c_4}. \end{aligned}$$
(26)
$$\begin{aligned}&U(\xi )=b_2 \Bigg [ \sqrt{-\frac{c_2m^2}{c_4(2m^2-1)}} cn \Bigg (\sqrt{\frac{c_2}{2m^2-1}}\xi \Bigg )\Bigg ]^{-2}, \nonumber \\&c_2>0, c_4<0, c_0=\frac{c^2_2m^2(1-m^2)}{c_4(2m^2-1)^2}. \end{aligned}$$
(27)
$$\begin{aligned}&U(\xi )=b_2 \Bigg [ \sqrt{-\frac{m^2}{c_4(2-m^2)}} dn \Bigg (\sqrt{\frac{c_2}{2-m^2}}\xi \Bigg )\Bigg ]^{-2},\nonumber \\&c_2>0, c_4<0, c_0=\frac{c^2_2(1-m^2)}{c_4(2-m^2)^2}. \end{aligned}$$
(28)
$$\begin{aligned}&U(\xi )=b_2 \Bigg [\pm \sqrt{-\frac{c_2m^2}{c_4(m^2+1)}} sn \Bigg (\sqrt{-\frac{c_2}{m^2+1}}\xi \Bigg )\Bigg ]^{-2}, \nonumber \\&c_2<0, c_4>0,c_0=\frac{c^2_2m^2}{c_4(m^2+1)^2}. \end{aligned}$$
(29)

Set(ii)

$$\begin{aligned} a_1= & {} b_1 = b_2=0, a_2=(\alpha ^2-\beta ^2)c_4,\nonumber \\ c_2= & {} \frac{(\alpha ^2-\beta ^2)^2 c_0c_4+3a^2_0}{(\alpha ^2-\beta ^2)a_0},\nonumber \\ \eta= & {} \frac{\alpha \beta (\alpha ^2-\beta ^2)^2 c_0c_4-3\alpha \beta a^2_0+3 \chi \lambda a_0}{2\alpha a_0}. \end{aligned}$$
(30)

Proceeding as before we substitute Eq. (30) in Eq. (18). As a result we obtain

$$\begin{aligned} U(\xi )=\, & {} a_0+(\alpha ^2-\beta ^2)c_4 \nonumber \\&\Bigg [\pm \sqrt{-{\frac{(\alpha ^2-\beta ^2)^2 c_0c_4+3a^2_0}{2c_4(\alpha ^2-\beta ^2)a_0}}} \nonumber \\&\tanh \Bigg (\sqrt{-{\frac{(\alpha ^2-\beta ^2)^2 c_0c_4+3a^2_0}{2(\alpha ^2-\beta ^2)a_0}}}\xi \Bigg )\Bigg ]^{2},\nonumber \\&c_2<0, c_4>0, c_0=\frac{c^2_2}{4c_4}. \end{aligned}$$
(31)
$$\begin{aligned} U(\xi )=\, & {} a_0+(\alpha ^2-\beta ^2)c_4 \nonumber \\&\Bigg [\pm \sqrt{{\frac{(\alpha ^2-\beta ^2)^2 c_0c_4+3a^2_0}{2c_4(\alpha ^2-\beta ^2)a_0}}} \nonumber \\&\tan \Bigg (\sqrt{{\frac{(\alpha ^2-\beta ^2)^2 c_0c_4+3a^2_0}{2(\alpha ^2-\beta ^2)a_0}}}\xi \Bigg )\Bigg ]^{2},\nonumber \\&c_2>0, c_4>0, c_0=\frac{c^2_2}{4c_4}. \end{aligned}$$
(32)
$$\begin{aligned} U(\xi )=\, & {} a_0+(\alpha ^2-\beta ^2)c_4 \nonumber \\&\Bigg [\sqrt{-\frac{[(\alpha ^2-\beta ^2)^2 c_0c_4+3a^2_0]m^2}{c_4(2m^2-1)(\alpha ^2-\beta ^2)a_0}} cn\nonumber \\&\Bigg (\sqrt{\frac{(\alpha ^2-\beta ^2)^2 c_0c_4+3a^2_0}{(2m^2-1)(\alpha ^2-\beta ^2)a_0}}\xi \Bigg )\Bigg ]^{2}, \nonumber \\&c_2>0, c_4<0, c_0\nonumber \\= & {} \frac{[(\alpha ^2-\beta ^2)^2 c_0c_4+3a^2_0]^2 m^2(1-m^2)}{c_4(2m^2-1)^2(\alpha ^2-\beta ^2)^2a^2_0}. \end{aligned}$$
(33)
$$\begin{aligned} U(\xi )=\, & {} a_0+(\alpha ^2-\beta ^2)c_4\nonumber \\&\Bigg [ \sqrt{-\frac{m^2}{c_4(2-m^2)}} dn \nonumber \\&\Bigg (\sqrt{\frac{(\alpha ^2-\beta ^2)^2 c_0c_4+3a^2_0}{(2-m^2)(\alpha ^2-\beta ^2)a_0}}\xi \Bigg )\Bigg ]^{-2},\nonumber \\&c_2>0, c_4<0, c_0\nonumber \\= & {} \frac{[(\alpha ^2-\beta ^2)^2 c_0c_4+3a^2_0]^2 (1-m^2)}{c_4(2-m^2)^2(\alpha ^2-\beta ^2)^2a^2_0}. \end{aligned}$$
(34)
$$\begin{aligned} U(\xi )=\, & {} a_0+(\alpha ^2-\beta ^2)c_4 \nonumber \\&\Bigg [\pm \sqrt{-\frac{[(\alpha ^2-\beta ^2)^2 c_0c_4+3a^2_0]m^2}{c_4(m^2+1)(\alpha ^2-\beta ^2)a_0}} sn\nonumber \\&\Bigg (\sqrt{-\frac{(\alpha ^2-\beta ^2)^2 c_0c_4+3a^2_0}{(m^2+1)(\alpha ^2-\beta ^2)a_0}}\xi \Bigg )\Bigg ]^{2}, \nonumber \\&c_2<0, c_4>0, c_0\nonumber \\= & {} \frac{[(\alpha ^2-\beta ^2)^2 c_0c_4+3a^2_0]^2 m^2}{c_4(m^2+1)^2(\alpha ^2-\beta ^2)^2a^2_0}. \end{aligned}$$
(35)

In the limit case when \(m\rightarrow 1\), \(cn(\xi ,1) = {{\,{\mathrm{sech}}\,}}(\xi )\), \(sn(\xi ,1) = \tanh (\xi )\) and \(dn(\xi ,1) = {{\,{\mathrm{sech}}\,}}(\xi )\) and this exhibits that some of the above obtained solitary wave solutions are obtained as the limiting case of the Jacobian elliptic doubly periodic wave solutions.

Family 3 If we select \(c_0 = c_1 = c_4 = 0\). We have the following set of results

$$\begin{aligned} a_2=\, & {} b_1=b_2=0, a_0={\frac{-2\alpha \eta +3\chi \lambda }{3\alpha \beta }}, \nonumber \\ a_1= & {} \frac{(\alpha ^2-\beta ^2)c_3}{4}, c_2={\frac{-4\alpha \eta +6\chi \lambda }{\alpha \beta (\alpha ^2-\beta ^2)}}. \end{aligned}$$
(36)

Therefore, we determined a bell-shaped solitary wave solution, a triangular form solution and a rational type solution as:

$$\begin{aligned} U(\xi )=\, & {} {\frac{-2\alpha \eta +3\chi \lambda }{3\alpha \beta }}\Bigg [1- \frac{3}{2} {{\,{\mathrm{sech}}\,}}^2 \Bigg (\sqrt{ \frac{-2\alpha \eta +3\chi \lambda }{2\alpha \beta (\alpha ^2-\beta ^2)}}\xi \Bigg )\Bigg ], c_2>0. \end{aligned}$$
(37)
$$\begin{aligned} U(\xi )=\, & {} {\frac{-2\alpha \eta +3\chi \lambda }{3\alpha \beta }}\Bigg [1- \frac{3}{2} \sec ^2 \Bigg (\sqrt{ \frac{2\alpha \eta -3\chi \lambda }{2\alpha \beta (\alpha ^2-\beta ^2)}}\xi \Bigg )\Bigg ], c_2<0. \end{aligned}$$
(38)
$$\begin{aligned}&U(\xi )={\frac{-2\alpha \eta +3\chi \lambda }{3\alpha \beta }}+\frac{(\alpha ^2-\beta ^2)}{\xi ^2} , c_2=0. \end{aligned}$$
(39)

Family 4 If we set \(c_2 = c_4 = 0\), \(c_3 > 0\) and \(c_0 \ne 0, c_1 \ne 0\). The set of algebraic equations (19a–19g) provide the following results:

Set(i)

$$\begin{aligned} a_2= & {} \,b_1=b_2=0,\nonumber \\ a_0=\, & {} {\frac{-2\alpha \eta +3\chi \lambda }{6\alpha \beta }},\nonumber \\ a_1=\, & {} \frac{(\alpha ^2-\beta ^2)c_3}{4},\nonumber \\ c_3= & {} -\frac{4}{3}{\frac{[4{\alpha }^{2}{\eta }^{2}-12\alpha \eta \chi \lambda +9{\chi }^{2}{\lambda }^{2}]}{{c_1}{\alpha }^{2}{ \beta }^{2} ( {\alpha }^{2}-{\beta }^{2} )^2 }}. \end{aligned}$$
(40)

Accordingly, we have the Weierstrass elliptic solution of Eq. (1) as:

$$\begin{aligned} U(\xi )= & {}\, {\frac{-2\alpha \eta +3\chi \lambda }{6\alpha \beta }}\nonumber \\&+\frac{(\alpha ^2-\beta ^2)c_3}{4} \wp \Bigg (\frac{\sqrt{c_3}}{2}, g_2,g_3\Bigg ), \end{aligned}$$
(41)

where \(g_2= \frac{3c^2_1\alpha ^2 \beta ^2 (\alpha ^2-\beta ^2)^2 }{4\alpha ^{2}\eta ^{2}-12\alpha \eta \chi \lambda +9\chi ^{2}\lambda ^{2}}\) and \(g_3= \frac{3c_0c_1\alpha ^{2} \beta ^{2} (\alpha ^{2}-\beta ^{2})^2 }{4\alpha ^{2}\eta ^{2}-12\alpha \eta \chi \lambda +9\chi ^{2}\lambda ^{2}}\).

Set(ii)

$$\begin{aligned} a_2=\, & {} 0, a_0={\frac{-2\alpha \eta +3\chi \lambda }{6\alpha \beta }}, a_1=\frac{(\alpha ^2-\beta ^2)c_3}{4},\nonumber \\ b_1=\, & {} {\frac{4{\alpha }^{2}{\eta }^{2}-12\alpha \eta \chi \lambda +9{\chi }^{2}{\lambda }^{2}}{12{c_3}{\alpha }^{2}{ \beta }^{2} ( {\alpha }^{2}-{\beta }^{2} ) }},\nonumber \\ b_2= & {} -\frac{(\alpha ^2-\beta ^2)c_0}{4},\nonumber \\ c_3=\, & {} \frac{4{\alpha }^{2}{\eta }^{2}-12\alpha \eta \chi \lambda +9{\chi }^{2}{\lambda }^{2}}{3c_1\alpha ^2 \beta ^2 ( \alpha ^{2}-\beta ^{2} )^2 }. \end{aligned} $$
(42)

Subsequently, we get the Weierstrass elliptic solution of Eq (1) as:

$$\begin{aligned}U(\xi )=&\,{\frac{-2\alpha \eta +3\chi \lambda }{6\alpha \beta }}+\frac{(\alpha ^2-\beta ^2)c_3}{4} \wp \Bigg (\frac{\sqrt{c_3}}{2}, g_2,g_3\Bigg )\nonumber \\& + {\frac{4{\alpha }^{2}{\eta }^{2}-12\alpha \eta \chi \lambda +9{\chi }^{2}{\lambda }^{2}}{12{c_3}{\alpha }^{2}{ \beta }^{2} ( {\alpha }^{2}-{\beta }^{2} ) }}\Bigg [\wp \Bigg (\frac{\sqrt{c_3}}{2}, g_2,g_3\Bigg )\Bigg ]^{-1}\nonumber \\& -\frac{(\alpha ^2-\beta ^2)c_0}{4}\Bigg [\wp \Bigg (\frac{\sqrt{c_3}}{2}, g_2,g_3\Bigg )\Bigg ]^{-2}, \end{aligned}$$
(43)

where \(g_2= \frac{-12c^2_1\alpha ^2 \beta ^2 (\alpha ^2-\beta ^2)^2 }{4\alpha ^{2}\eta ^{2}-12\alpha \eta \chi \lambda +9\chi ^{2}\lambda ^{2}}\) and \(g_3= -\frac{12c_0c_1\alpha ^{2} \beta ^{2} (\alpha ^{2}-\beta ^{2})^2 }{4\alpha ^{2}\eta ^{2}-12\alpha \eta \chi \lambda +9\chi ^{2}\lambda ^{2}}\).

Family 5 If \(c_0 = c_1 =c_2= 0\). We obtain the following results:

$$\begin{aligned} b_1=\, & {} b_2=0, a_0=\frac{-2\alpha \eta +3\chi \lambda }{3\alpha \beta }, a_1=\frac{(\alpha ^2-\beta ^2)c_3}{4},\nonumber \\ a_2=\, & {} {(\alpha ^2-\beta ^2)c_4}, \chi =\frac{2\alpha \eta }{3\lambda }, ~\alpha +\beta =0. \end{aligned}$$
(44)

We obtain rational type solution and exponential type solutions of (4+1)D nonlinear Fokas Eq. (1) as:

$$\begin{aligned} U(\xi )=\, & {} {\frac{-2\alpha \eta +3\chi \lambda }{3\alpha \beta }}+\frac{(\alpha ^2-\beta ^2)c^2_3}{c^2_3\xi ^2-4c_4}\nonumber \\& +\frac{16(\alpha ^2-\beta ^2)c_4c^2_3}{(c^2_3\xi ^2-4c_4)^2}, c_4\ne 0. \end{aligned}$$
(45)
$$\begin{aligned} U(\xi )=\, & {} {\frac{-2\alpha \eta +3\chi \lambda }{3\alpha \beta }}+\frac{(\alpha ^2-\beta ^2)c^2_3}{8c_4}\exp \Bigg (\frac{\eta c_3}{2 \sqrt{-c_4}}\xi \Bigg )\nonumber \\& +\frac{(\alpha ^2-\beta ^2)c^2_3}{4c_4}\exp \Bigg (\frac{\eta c_3}{ \sqrt{-c_4}}\xi \Bigg ), c_4<0. \end{aligned}$$
(46)

Family 6 If we set \( c_3=c_4=0\) and \(c_0=\frac{c^2_1}{4c_2}\). We have the following results

Set(i)

$$\begin{aligned} a_1=\, & {} a_2 = 0, a_0={\frac{-2\alpha \eta +3\chi \lambda }{3\alpha \beta }},~b_1=\frac{c_1}{2}(\alpha ^2-\beta ^2),\nonumber \\ b_2=\, & {} {\frac{{{ c^2_1}}( {\alpha }^{2}-{\beta }^{2}) ^{2}\alpha \beta }{-16\alpha \eta +24\chi \lambda }},~ c_2={\frac{-4\alpha \eta +6\chi \lambda }{\alpha \beta ( {\alpha }^{2}-{\beta }^{2} ) }}. \end{aligned}$$
(47)

Replacing Eq. (47) in Eq. (18), we get the following exponential solution

$$\begin{aligned} U(\xi )=\, & {\frac{-2\alpha \eta +3\chi \lambda }{3\alpha \beta }}\nonumber \\& +\frac{2{ c_1} ( {\alpha }^{2}-{\beta }^{2}) ( -2 \alpha \eta +3\chi \lambda )}{ - c_1{\alpha \beta }(\alpha ^2-\beta ^{2})+4{{\mathrm{e}}^{{\frac{\eta \sqrt{2}\sqrt{-2\alpha \eta +3\chi \lambda }\xi }{\sqrt{\alpha \beta }\sqrt{( \alpha ^2-\beta ^2) }}}}}( -2\alpha \eta +3\chi \lambda )}\nonumber \\& +\frac{2{ c^2_1\alpha \beta } ( {\alpha }^{2}-{\beta }^{2})^2 ( -2 \alpha \eta +3\chi \lambda )}{( - c_1{\alpha \beta }(\alpha ^2-\beta ^{2})+4{{\mathrm{e}}^{{\frac{\eta \sqrt{2}\sqrt{-2\alpha \eta +3\chi \lambda }\xi }{\sqrt{\alpha \beta }\sqrt{( \alpha ^2-\beta ^2) }}}}}( -2\alpha \eta +3\chi \lambda ))^2},\nonumber \\& c_2>0. \end{aligned}$$
(48)

Set(ii)

$$\begin{aligned} a_1=\, & {} a_2 = b_2=c_0=0, a_0={\frac{-2\alpha \eta +3\chi \lambda }{3\alpha \beta }},\nonumber \\ b_1=\, & {} \frac{c_1}{4}(\alpha ^2-\beta ^2),~ c_2={\frac{-4\alpha \eta +6\chi \lambda }{\alpha \beta ( {\alpha }^{2}-{\beta }^{2} ) }}. \end{aligned}$$
(49)

We can proceed in the similar manner as above and obtain the triangular periodic wave and hyperbolic solutions.

$$\begin{aligned}&U(\xi )={\frac{-2\alpha \eta +3\chi \lambda }{\alpha \beta }}\Bigg [\frac{1}{3}-\frac{ 1}{ \Big ( \eta \sin ( \sqrt{2}\sqrt{{\frac{-2\alpha \eta +3\chi \lambda }{\alpha \beta ( \alpha -\beta ) ( \alpha +\beta ) }}}\xi )-1 \Big ) }\Bigg ],\nonumber \\&\quad c_0=0,~~c_2<0, \end{aligned}$$
(50)
$$\begin{aligned}&U(\xi )={\frac{-2\alpha \eta +3\chi \lambda }{\alpha \beta }}\Bigg [\frac{1}{3}-\frac{ 1}{ \Big ( \eta \sinh ( {2}\sqrt{{\frac{-4\alpha \eta +6\chi \lambda }{\alpha \beta ( \alpha -\beta ) ( \alpha +\beta ) }}}\xi )-1 \Big ) }\Bigg ],\nonumber \\&\quad c_0=0,~~c_2>0. \end{aligned}$$
(51)

Family 7 If \( c_0=c_1=0\) and \(c_4>0\). We have the subsequent results

Set(i)

$$\begin{aligned} b_1=\, & {} b_2=0, ~ a_0={\frac{-2\alpha \eta +3\chi \lambda }{3\alpha \beta }},\nonumber \\ a_1=\, & {} \frac{c_3}{2}(\alpha ^2-\beta ^2),~a_2=c_4(\alpha ^2-\beta ^2),~ c_2={\frac{-4\alpha \eta +6\chi \lambda }{\alpha \beta ( {\alpha }^{2}-{\beta }^{2} ) }},\nonumber \\ c_4=\, & {} \frac{3}{8}{\frac{{{ c^2_3}} ( {\alpha }^{2}-{\beta }^{2}) \alpha \beta }{2\beta { c_2}{\alpha }^{3}-2{ c_2}{\beta }^{3}\alpha +2\alpha \eta -3\chi \lambda }}. \end{aligned}$$
(52)

Hence, a triangular wave and two solitary wave solutions are attained :

$$\begin{aligned} U(\xi )=\, & {} {\frac{-2\alpha \eta +3\chi \lambda }{3\alpha \beta }}\nonumber \\&+\frac{{ c_3} ( -2\alpha \eta +3\chi \lambda ) \sec \left( \frac{1}{2}\sqrt{-{\frac{-4\alpha \eta +6\chi \lambda }{ \alpha \beta ( {\alpha }^{2}-{\beta }^{2} ) }}}\xi \right) }{\alpha }{\beta } \nonumber \\&\left( \eta \sqrt{-{\frac{ ( -6\alpha \eta +9\chi \lambda ) {{ c^2_3}}}{2 \beta { c_2}{\alpha }^{3}-2{ c_2}{\beta }^{3}\alpha +2 \alpha \eta -3\chi \lambda }}}\right. \nonumber \\&\left. \tan \left( \frac{1}{2}\sqrt{-{\frac{-4\alpha \eta +6\chi \lambda }{\alpha \beta ( {\alpha }^{2} -{\beta }^{2} ) }}}\xi \right) +{ c_3}\right) \nonumber \\&+\frac{3}{8}\frac{{{ c^2_3}}({\alpha }^{2}-{\beta }^{2} ) ^{2}\alpha \beta \left( \sec \left( \frac{1}{2}\sqrt{-{\frac{-4\alpha \eta + 6\chi \lambda }{\alpha \beta ( {\alpha }^{2}-{\beta }^{2}) }}}\xi \right) \right) ^{2}}{\left( \frac{1}{2}\eta \sqrt{-{\frac{ ( -24\alpha \eta + 36\chi \lambda ) {{ c^2_3}}}{2\beta { c_2}{\alpha }^{3 }-2{ c_2}{\beta }^{3}\alpha +2\alpha \eta -3\chi \lambda }}} \tan \left( \frac{1}{2}\sqrt{-{\frac{-4\alpha \eta +6\chi \lambda }{ \alpha \beta ( {\alpha }^{2}-{\beta }^{2} ) }}}\xi \right) +{ c_3} \right) ^{2} ( 2\beta { c_2}{\alpha }^{3 }-2{ c_2}{\beta }^{3}\alpha +2\alpha \eta -3\chi \lambda )},~c_2<0, \end{aligned}$$
(53)
$$\begin{aligned} U(\xi )=\, & {} {\frac{-2\alpha \eta +3\chi \lambda }{3\alpha \beta }} \nonumber \\&+\frac{{ c_3} ( -2\alpha \eta +3\chi \lambda ) {{\,{\mathrm{sech}}\,}}\left( \frac{1}{2}\sqrt{{\frac{-4\alpha \eta +6\chi \lambda }{ \alpha \beta ( {\alpha }^{2}-{\beta }^{2} ) }}}\xi \right) }{\alpha }{\beta } \nonumber \\&\left( \eta \sqrt{{\frac{ ( -6\alpha \eta +9\chi \lambda ) {{ c^2_3}}}{2 \beta { c_2}{\alpha }^{3}-2{ c_2}{\beta }^{3}\alpha +2 \alpha \eta -3\chi \lambda }}}\right. \nonumber \\&\left. \tanh \left( \frac{1}{2}\sqrt{{\frac{-4\alpha \eta +6\chi \lambda }{\alpha \beta ( {\alpha }^{2} -{\beta }^{2} ) }}}\xi \right) +{ c_3}\right) \nonumber \\&+\frac{3}{8}\frac{{{ c^2_3}}( {\alpha }^{2}-{\beta }^{2} ) ^{2}\alpha \beta \left( {{\,{\mathrm{sech}}\,}}\left( \frac{1}{2}\sqrt{{\frac{-4\alpha \eta + 6\chi \lambda }{\alpha \beta ( {\alpha }^{2}-{\beta }^{2}) }}}\xi \right) \right) ^{2}}{\left( \frac{1}{2}\eta \sqrt{{\frac{ ( -24\alpha \eta + 36\chi \lambda ) {{ c^2_3}}}{2\beta { c_2}{\alpha }^{3 }-2{ c_2}{\beta }^{3}\alpha +2\alpha \eta -3\chi \lambda }}} \tanh \left( \frac{1}{2}\sqrt{{\frac{-4\alpha \eta +6\chi \lambda }{ \alpha \beta ( {\alpha }^{2}-{\beta }^{2} ) }}}\xi \right) +{ c_3} \right) ^{2} ( 2\beta { c_2}{\alpha }^{3 }-2{ c_2}{\beta }^{3}\alpha +2\alpha \eta -3\chi \lambda )},~c_2<0. \end{aligned}$$
(54)

Set(ii)

$$\begin{aligned} b_1=\, & {} b_2=0, ~ a_0={\frac{-2\alpha \eta +3\chi \lambda }{3\alpha \beta }},\nonumber \\ a_1=\, & {} \eta \sqrt{{\frac{ ( -4\alpha \eta +6\chi \lambda )( {\alpha }^{2}-{\beta }^{2}) { c_4}}{ \alpha \beta }}},~a_2=c_4(\alpha ^2-\beta ^2),\nonumber \\ c_2=\, & {} {\frac{-4\alpha \eta +6\chi \lambda }{\alpha \beta ( {\alpha }^{2}-{\beta }^{2} ) }}, c_3=2\eta \sqrt{c_2c_4},~\chi =\frac{2\alpha \eta }{3\lambda }. \end{aligned}$$
(55)

We attain the subsequent solitary wave solution of Eq. (1) as

$$\begin{aligned} {39f}(\xi )=\, & {} {\frac{-2\alpha \eta +3\chi \lambda }{\alpha \beta }}\nonumber \\&\Bigg (\frac{1}{3}+2\eta ^2+3\tanh \Bigg (\frac{1}{2}\sqrt{{\frac{6\chi \lambda -4\alpha \eta }{\alpha \beta ( {\alpha }^{2}-{\beta }^{2}) }}}\xi \Bigg )\nonumber \\&+\tanh \Bigg (\frac{1}{2}\sqrt{{\frac{6\chi \lambda -4\alpha \eta }{\alpha \beta ( {\alpha }^{2}-{\beta }^{2}) }}}\xi \Bigg )^2\Bigg ), c_2>0. \end{aligned}$$
(56)

3.2 Exact solutions of Eq. (1) via the exp[-\(G(\xi )\)]-function expansion method

Now from balancing procedure in Eq. (17), we obtain \(N = 2\) . Then, assuming solution of the Eq. (17) in the form

$$\begin{aligned} U(\xi )=a_0+a_{1}[\exp (-G(\xi ))]+a_{2}[\exp (-2G(\xi ))], \end{aligned}$$
(57)

By inserting Eq. (57)and its first and second order derivatives along with Eq. (9) into Eq. (17) and comparing the terms of equal powers in \(\exp (-G(\xi ))\) to zero in the resulting equation, we get

$$\begin{aligned}&-\beta s(2a_2 s+a_1 r)\alpha ^3+(s(2a_2 s+a_1 r)\beta ^3 +6\beta a^2_0+4a_0\eta )\alpha -6\chi \lambda a_0 = 0, \end{aligned}$$
(58)
$$\begin{aligned}&-(6a_2sr+a_1(r^2+2s))\beta \alpha ^3 +((6a_2s r+a_1(r^2+2s))\beta ^3 +12\beta a_0a_1+4\eta a_1)\alpha -6\chi \lambda a_1=0, \end{aligned}$$
(59)
$$\begin{aligned}&-4\beta ((r^2+2s)a_2+\frac{3}{4}a_1r)\alpha ^3 +(((8s+4r^2)a_2+3a_1r)\beta ^3 +(12a_0a_2+6a^2_1)\beta +4\eta a_2)\alpha -6\chi \lambda a_2=0, \end{aligned}$$
(60)
$$\begin{aligned}&(10((-\frac{1}{5}a_1-a_2r)\alpha ^2+(\frac{1}{5} a_1+a_2r)\beta ^2+\frac{6}{5}a_1a_2)) \alpha \beta = 0, \end{aligned}$$
(61)
$$\begin{aligned}&6\alpha \beta a_2(\beta ^2-\alpha ^2+a_2) = 0. \end{aligned}$$
(62)

Solving the Eqs. (58)-(62) with Maple, we obtain the results as given below:

$$\begin{aligned} a_0=\, & {} (\alpha ^2-\beta ^2)s, a_1 = (\alpha ^2 -\beta ^2)r, a_2 = \alpha ^2-\beta ^2, \nonumber \\ \eta=\, & {} \frac{\alpha ^3\beta r^2-4\beta s\alpha ^3+4\alpha \beta ^3 s-\alpha \beta ^3r^2+6\chi \lambda }{4\alpha }. \end{aligned}$$
(63)

Taking the advantage of solution of Eq. (9) from (10) to (13), the solution of Eq. (1) can be written as: The dark soliton solution is

$$\begin{aligned} U(\xi )=\, & {} (\alpha ^2-\beta ^2)\nonumber \\&\Bigg [s-\frac{2rs}{r+\sqrt{r^2-4s}~\tanh \Big (\frac{1}{2}\sqrt{r^2-4s} (\xi +\xi _0)\Big )}\nonumber \\&+\frac{4s^2}{\Big (r+\sqrt{r^2-4s}~\tanh \Big (\frac{1}{2}\sqrt{r^2-4s} (\xi +\xi _0)\Big )\Big )^2}\Bigg ], \end{aligned}$$
(64)

provided \(\alpha ^2-\beta ^2\ne 0\), \(s\ne 0\) and \(r^2-4s>0\).

The singular soliton solution is

$$\begin{aligned} U(\xi )=\, & {} (\alpha ^2-\beta ^2)\nonumber \\&\Bigg [s-\frac{2rs}{r+\sqrt{r^2-4s}~\coth \Big (\frac{1}{2} \sqrt{r^2-4s}(\xi +\xi _0)\Big )}\nonumber \\&+ \frac{4s^2}{\Big (r+\sqrt{r^2-4s}~\coth \Big (\frac{1}{2} \sqrt{r^2-4s}(\xi +\xi _0)\Big )\Big )^2}\Bigg ], \end{aligned}$$
(65)

provided \(\alpha ^2-\beta ^2\ne 0\), \(s\ne 0\) and \(r^2-4s>0\).

The singular periodic solutions are

$$\begin{aligned} U(\xi )=\, & {} (\alpha ^2-\beta ^2)\nonumber \\&\Bigg [s+\frac{2rs}{-r+\sqrt{4s-r^2}~\tan \Big (\frac{1}{2} \sqrt{4s-r^2}(\xi +\xi _0)\Big )}\nonumber \\&+ \frac{4s^2}{\Big (-r+\sqrt{4s-r^2}~\tan \Big (\frac{1}{2} \sqrt{4s-r^2}(\xi +\xi _0)\Big )\Big )^2}\Bigg ], \end{aligned}$$
(66)

provided \(\alpha ^2-\beta ^2\ne 0\), \(s\ne 0\) and \(r^2-4s<0\).

$$\begin{aligned} U(\xi )=\, & {} (\alpha ^2-\beta ^2)\nonumber \\&\Bigg [s-\frac{2rs}{-r+\sqrt{4s-r^2}~\cot \Big (\frac{1}{2}\sqrt{4s-r^2} (\xi +\xi _0)\Big )}\nonumber \\&+ \frac{4s^2}{\Big (-r+\sqrt{4s-r^2}~\cot \Big (\frac{1}{2}\sqrt{4s-r^2}(\xi +\xi _0)\Big )\Big )^2}\Bigg ], \end{aligned}$$
(67)

provided \(\alpha ^2-\beta ^2\ne 0\), \(s\ne 0\) and \(r^2-4s<0\).

3.3 Exact solutions of Eq. (1) via fractional Möbius transformation

Now we employ a fractional Möbius transformation to (4+1)D Fokas equation and systematically obtain localized pulses represented by hyperbolic sech and tanh functions, as well as singular periodic solutions. We proposed the following fractional transformation

$$\begin{aligned} U(\xi )=\frac{\tilde{p}+\tilde{q} f(\xi ,m)^l}{1+\tilde{r} f(\xi ,m)^l},\end{aligned}$$
(68)

where l is an integer, \(\tilde{p},\tilde{q}\) and \(\tilde{r}\) are defined as real constants, and the modulus parameter m varies between 0 and 1. Two families of localized solutions of Fokas equation are extracted from Eq. (68) for \(l=2\), \(f(\xi ,m)=cn(\xi ,m)\) and \(f(\xi ,m)=sn(\xi ,m)\).

Now we reveal the steady state solutions for \(f(\xi ,m)=cn(\xi ,m)\) in Eq. (68). Putting

$$\begin{aligned} U(\xi )=\frac{\tilde{p}+\tilde{q}~cn(\xi ,m)^2}{1+\tilde{r}~cn(\xi ,m)^2}, \end{aligned}$$
(69)

in Eq. (17) and setting the coefficients of equal powers of \(cn(\xi ,m)\) to zero will result the subsequent set of consistency equations:

$$\begin{aligned}&-2\tilde{r} \{ -\beta {m}^{2} ( \tilde{r}\tilde{p}-\tilde{q}) {\alpha }^{3}+ [ {m}^{2} ( \tilde{r}\tilde{p}-\tilde{q}) {\beta }^{3}\nonumber \\&\quad -3\beta {\tilde{r}}^{2}-2\eta \tilde{q}\tilde{r}] \alpha +3\chi \lambda \tilde{q}\tilde{r}\} =0, \end{aligned}$$
(70a)
$$\begin{aligned}&-2 ( 3{m}^{2}-2\tilde{r}+4\tilde{r}{m}^{2}) \beta ( \tilde{r}\tilde{p}-\tilde{q} ) {\alpha }^{3}\nonumber \\&\quad + \Big \{ 8 \Big [ \Big ( -\frac{1}{2}+{m}^{2}\Big ) \tilde{r}+\frac{3}{4}{m}^{2}\Big ] ( \tilde{r}\tilde{p}-\tilde{q}) {\beta }^{3}\nonumber \\&\quad + ( 6\tilde{q} ^{2}+12\tilde{p}\tilde{q}\tilde{r}) \beta +4\eta \tilde{r} (\tilde{r}\tilde{p}+2\tilde{q}) \Big \} \alpha-6\chi \lambda \tilde{r} ( \tilde{r}\tilde{p}+2\tilde{q}) =0, \end{aligned}$$
(70b)
$$\begin{aligned}&6 \Big ( -\frac{2}{3}+\tilde{r}{m}^{2}-\tilde{r}+\frac{4}{3}{m}^{2}\Big ) \beta ( \tilde{r}\tilde{p}-\tilde{q}) {\alpha }^{3}\nonumber \\&\quad + \Big \{ -6 \Big ( ( -1+{m}^{2}) \tilde{r} -\frac{2}{3}+\frac{4}{3}{m}^{2}\Big ) ( \tilde{r}\tilde{p}-\tilde{q}) {\beta }^{3}\nonumber \\&\quad +6\tilde{p} ( \tilde{r}\tilde{p}+2\tilde{q}) \beta +8\eta ( \frac{1}{2}\tilde{q}+\tilde{r}\tilde{p}) \Big \} \alpha \nonumber \\&\quad -12\chi \lambda \Big (\frac{1}{2}\tilde{q}+\tilde{r}\tilde{p}\Big )=0, \end{aligned}$$
(70c)
$$\begin{aligned}&\quad -2\beta ( -1+m) (m+1) ( \tilde{r}\tilde{p}-\tilde{q} ) {\alpha }^{3}\nonumber \\&\quad + \{ 2 (-1+m) (m+1) (\tilde{r}\tilde{p}-\tilde{q}) {\beta }^{3}\nonumber \\&\quad +6\beta {\tilde{p}}^{2}+4 \eta \tilde{p}\} \alpha -6\chi \lambda \tilde{p}=0. \end{aligned}$$
(70d)

Note that these coupled algebraic equations are found to be nonlinear in \(\tilde{p}, \tilde{q}\) and \(\tilde{r}\) and one can see from the Eq. (69) that \(\tilde{p}\tilde{r}=\tilde{q}\) infers only a constant solution and is not stated here. From the above constancy equations it is evident that for modulus parameter \(m = 0\), \(m = 1\), and with other values of m, we have distinct properties such as trigonometric, bright soliton-like, and periodic train wave solutions. Now, we mention some localized as well as periodic solitary wave solutions.

Family 1 We establish a general localized solitary wave solution when the modulus parameter \(m\rightarrow 1\), Jacobian elliptic function \(cn(\xi ,1)\rightarrow {{\,{\mathrm{sech}}\,}}(\xi )\). For the undetermined parameters \(\tilde{p}, \tilde{q}, \tilde{r}\) and \(\chi \), the set of Eqs. (70a)–(70d) can be solved consistently.

When \(\tilde{r}=0\), the structure profile of the soliton solution specified as

$$\begin{aligned} U(\xi )=(\alpha ^2-\beta ^2)\Big [\frac{2}{3}-{{\,{\mathrm{sech}}\,}}^2(\xi )\Big ] \end{aligned}$$
(71)

with \(\tilde{p}=\frac{2}{3}(\alpha ^2-\beta ^2)\), \(\tilde{q}=\beta ^2-\alpha ^2\) and parameter \(\chi \) satisfies the relation \(\chi =-\frac{2}{3}{\frac{\alpha ( {\alpha }^{2}\beta -\eta -{\beta }^{3}) }{\lambda }}\).

For the case \(\tilde{p}=\tilde{r}=0\), the background must vanishes and the generic profile of the soliton solution takes the localized form

$$\begin{aligned} U(\xi )=(\beta ^2-\alpha ^2){{\,{\mathrm{sech}}\,}}^2(\xi ) \end{aligned}$$
(72)

with \(\tilde{q}=\beta ^2-\alpha ^2\) and \(\chi =-\frac{2}{3}{\frac{\alpha ( {\alpha }^{2}\beta -\eta -{\beta }^{3}) }{\lambda }}\) satisfies the relation. It is worth to note that the profile of solutions well controlled by parameters \(\alpha \) and \(\beta \). When \(\alpha =\beta \), then the soliton profiles disappears.

For \(\tilde{p}=0\) and \(\tilde{r}=1\), we obtain the generic profile of the fractional soliton solution as

$$\begin{aligned} U(\xi )={\frac{ ( 5\alpha {\beta }^{3}-5\beta {\alpha }^{3}-4 \alpha \eta +6\chi \lambda ) { {{\,{\mathrm{sech}}\,}}}( \xi ) ^{2}}{3\alpha \beta ( 1+ {{\,{\mathrm{sech}}\,}}(\xi ) ^{2} ) }} \end{aligned}, $$
(73)

with \(\tilde{q}={\frac{ ( 5\alpha {\beta }^{3}-5\beta {\alpha }^{3}-4 \alpha \eta +6\chi \lambda )}{3\alpha \beta }}\) and \(\chi =-{\frac{2\alpha ( \beta {\alpha }^{2}-\eta -{ \beta }^{3}) }{3\lambda }}\). We note that the value of \(\alpha =\beta \) leads to the value of \(\chi =\frac{2\alpha \eta }{3\lambda }\) in the expression (73). On substituting the value of \(\chi \) in Eq. (73), the profile of the solution again vanishes.

Family 2 When \(m \rightarrow 0\), the function \(cn(\xi ,0)\rightarrow \cos (\xi )\). For \(m = 0\), Eq. (4) admits the singular trigonometric solution of the following type

$$\begin{aligned} U(\xi )=\frac{1}{3}(\alpha ^2-\beta ^2)\Bigg [\frac{1+2~\cos (\xi )^2}{1-\cos (\xi )^2}\Bigg ], \end{aligned}$$
(74)

with \(\tilde{p}=\frac{1}{3}(\alpha ^2-\beta ^2)\), \(\tilde{q}=\frac{2}{3}(\alpha ^2-\beta ^2)\), \(\tilde{r}=-1\) and \(\chi =-\frac{2}{3}{\frac{\alpha ( {\alpha }^{2}\beta -{\beta }^{3}- \eta ) }{\lambda }}\).

For \(\tilde{q}=0\), the singular trigonometric profile of the solution takes the form

$$\begin{aligned} U(\xi )=\frac{\alpha ^2-\beta ^2}{1-\cos (\xi )^2}, \end{aligned}$$
(75)

with \(\tilde{p}=\alpha ^2-\beta ^2\), \(\tilde{r}=-1\) and \(\chi =\frac{2}{3}{\frac{\alpha ( {\alpha }^{2}\beta -{\beta }^{3}+ \eta ) }{\lambda }}\). Noting that, the singular trigonometric solutions disappears for same value of \(\alpha \) and \(\beta \).

Family 3 For \(0< m < 1\), we have found the cnoidal type solutions. For special case \(\tilde{r}=0\), we attain the following general periodic wave solution as

$$\begin{aligned} U(\xi )= & {} (\alpha ^2-\beta ^2)\Bigg [(\frac{2}{3}{m}^{2}-\frac{1}{3}\pm \frac{1}{3}\sqrt{{m}^{4}-{m}^{2}+1}) -m^2 ~cn(\xi )^2\Bigg ], \end{aligned}$$
(76)

with \(\tilde{p}= (\frac{2}{3}{m}^{2}-\frac{1}{3}\pm \frac{1}{3}\sqrt{{m}^{4}-{m}^{2}+1}) (\alpha ^2-\beta ^2)\), \(\tilde{q}=(\beta ^2-\alpha ^2)m^2\) and \(\lambda =\frac{2}{3}{\frac{ ( -2{\alpha }^{2}\beta {m}^{2}+{\alpha }^{2} \beta +3 \tilde{p}\beta +\eta +2 {m}^{2}{\beta }^{3}-{\beta }^{3}) \alpha }{\chi }}\), representing a soliton train. The special case \(m = 1\) results the previously found localized solution (71).

Now, selecting \(f(\xi ,m)=sn(\xi ,m)\) in the fractional transformation (68) and exchanging Eq. (68) into Eq. (17) and comparing the equal powers of \(sn(\xi ,m)\) to zero, we can deduce the following set of constancy relations:

$$\begin{aligned}&2\tilde{r} [ -\beta {m}^{2} ( \tilde{r}\tilde{p}-\tilde{q}) {\alpha }^{3}\nonumber \\&\quad + \{ {m}^{2} ( \tilde{r}\tilde{p}-\tilde{q}) {\beta }^{3}+3\beta {\tilde{q}}^{2}+2\eta \tilde{q}\tilde{r}\} \alpha -3\chi \lambda \tilde{q}\tilde{r}] =0, \end{aligned}$$
(77a)
$$\begin{aligned}&4 \Big ( \tilde{r}+\frac{3}{2}{m}^{2}+\tilde{r}{m}^{2}\Big ) ( \tilde{r}\tilde{p}-\tilde{q}) \beta {\alpha }^{3}\nonumber \\&\quad + \Big [ -4 \Big \{ ( 1+{m}^{2}) \tilde{r}+\frac{3}{2}{m }^{2}\Big \} ( \tilde{r}\tilde{p}-\tilde{q}) {\beta }^{3} \nonumber \\&\quad + (6\tilde{q}^{2}+12 \tilde{p}\tilde{q}\tilde{r}) \beta +4\eta \tilde{r} ( \tilde{r}\tilde{p}+2\tilde{q}) \Big ] \alpha \nonumber \\&\quad -6\chi \lambda \tilde{r} ( \tilde{r}\tilde{p}+2\tilde{q}) =0, \end{aligned}$$
(77b)
$$\begin{aligned}&-6 \Big ( \tilde{r}+\frac{2}{3}+\frac{2}{3}{m}^{2}\Big ) ( \tilde{r}\tilde{p}-\tilde{q} ) \beta { \alpha }^{3}\nonumber \\&\quad + \Big \{ 6 \Big ( \tilde{r}+\frac{2}{3}+\frac{2}{3}{m}^{2}\Big ) ( \tilde{r}\tilde{p}-\tilde{q} ) {\beta }^{3}\nonumber \\&\quad +6 \tilde{p}( \tilde{r}\tilde{p}+2 \tilde{q}) \beta +8 \Big ( \frac{1}{2} \tilde{q}+\tilde{r}\tilde{p} \Big ) \eta \Big \} \alpha \nonumber \\&\quad -12 \Big ( \frac{1}{2} \tilde{q}+\tilde{r}\tilde{p} \Big ) \chi \lambda =0, \end{aligned}$$
(77c)
$$\begin{aligned}&\{ ( -2\tilde{r}\tilde{p}+2\tilde{q} ) \beta ^{3}+6\beta \tilde{p}^{2}+4 \eta \tilde{p} \} \alpha -6\chi \lambda \tilde{p}=0. \end{aligned}$$
(77d)

From above equations it is clearly specify that different values of m leads to distinct properties. For instance \(m = 0\) provides an explicit rational trigonometric solution and \(m = 1\) leads to a kink-type of solution.

Family 1 We establish general localized soliton solution for the choice of the Jacobian elliptic modulus parameter \(m = 1\). For \(m\rightarrow 1\), Jacobian elliptic function \(sn(\xi ,0)\rightarrow \tanh (\xi )\). The set of Eqs. (77a)–(77d) can be solved constantly for the undetermined set of parameters \(\tilde{p}, \tilde{q}, \tilde{r}\) and \(\chi \).

For \(\tilde{r}=0\), we have establish an exciting type of soliton solution as exact solution of nonlinear Fokas Eq. (1), given by

$$\begin{aligned} U(\xi )=(\beta ^2-\alpha ^2)\Big [\frac{1}{3}-\tanh ^2(\xi )\Big ] \end{aligned}, $$
(78)

with \(\tilde{p}=\frac{1}{3}(\beta ^2-\alpha ^2)\), \(\tilde{q}=\alpha ^2-\beta ^2\) and parameter \(\chi \) satisfies the relation \(\chi =\frac{2}{3}{\frac{\alpha ( {\alpha }^{2}\beta +\eta -{\beta }^{3}) }{\lambda }}\).

Family 2 We attain a physically exciting sinusoidal solution when \(m \rightarrow 0\), the function \(sn(\xi ,0)\rightarrow \sin (\xi )\). For \(m = 0\) and \(\tilde{p}=0\),the Fokas Equation admits the non-singular periodic solution of the subsequent type

$$\begin{aligned} U(\xi )=\frac{1}{3}{\frac{ ( -2 \beta {\alpha }^{3}+2{\beta }^{3}\alpha -2 \alpha \eta +3\chi \lambda ) ( -2\alpha \eta + 3\chi \lambda ) ( \sin ( \xi ) ) ^{2}}{ \beta \alpha ( -2\beta {\alpha }^{3}+2{\beta }^{3}\alpha -2 \alpha \eta +3\chi \lambda ) ( \sin ( \xi ) ) ^{2}+\beta \alpha ( 3\beta {\alpha }^{3}-3 {\beta }^{3}\alpha ) }}, \end{aligned}$$
(79)

with \(\tilde{r}=\frac{1}{3}{\frac{-2\beta {\alpha }^{3}+2{\beta }^{3}\alpha -2\alpha \eta +3\chi \lambda }{\beta \alpha ( {\alpha }^{2}-{\beta } ^{2} ) }}\), \(\tilde{q}=\frac{1}{9}{\frac{ ( -2\beta {\alpha }^{3}+2{\beta }^{3}\alpha -2 \alpha \eta +3\chi \lambda ) ( -2\alpha \eta +3\chi \lambda ) }{{\beta }^{2}{\alpha }^{2} ( { \alpha }^{2}-{\beta }^{2}) }}\), and \(\chi =\pm \frac{2}{3}{\frac{\alpha ( \beta {\alpha }^{2}-{\beta }^{3}\pm \eta ) }{\lambda }}\).

Family 3 For \(0< m < 1\), we have found snoidal type solutions. For special case \(\tilde{r}=0\) and \(0<m<1\), we get the following solution

$$\begin{aligned} U(\xi )=\tilde{p}-{\frac{3\tilde{p}^{2}{m}^{2}~sn(\xi )^2}{ ( 2+2{m}^{2} ) \tilde{p}-{\beta }^{2 }{m}^{2}}}, \end{aligned}$$
(80)

with \(\chi =\pm \frac{2}{3}{\frac{\sqrt{-( 2 \tilde{p}+2 \tilde{p}{m}^{2}-{\beta }^{2}{m}^{2} ) ( -2{\beta }^{2}\tilde{p}-2 {\beta }^{2} \tilde{p}{m}^{2}+{\beta }^{4}{m }^{2}+3\tilde{p}^{2}) } ( ( 3+3{m}^{2} ) \beta \tilde{p}^{2}+ ( -3{m}^{2}{\beta }^{3}+2\eta +2{m}^{2} \eta ) \tilde{p}-{m}^{2}\eta {\beta }^{2} ) }{ ( ( 2+2{m}^{2}) \tilde{p}-{\beta }^{2}{m}^{2} ) ^{2}\lambda }}\),

\(\tilde{q}={\frac{3\tilde{p}^{2}{m}^{2}}{ ( 2+2{m}^{2} ) \tilde{p}-{\beta }^{2 }{m}^{2}}}\) and \(\alpha =\frac{3}{2}{\frac{\chi \lambda ( ( -{\beta }^{2}+2 \tilde{p} ) {m} ^{2}+2\tilde{p} ) }{ ( -3\tilde{p}{\beta }^{3}+3\beta \tilde{p}^{2}+2 \eta \tilde{p}-\eta {\beta }^{2} ) {m}^{2}+3\beta \tilde{p}^{2}+ 2\eta \tilde{p}}}\).

4 Graphical results and discussions

In this section, we portrayed graphs of the some obtained solutions of the considered equation and discuss them here. We examine Figs. 1, 2, 3, 4 and 5 which depicts some of our solutions acquired in this paper. To this end, we select some special values of the parameters under constraint conditions of the obtained solutions.

Fig. 1
figure 1

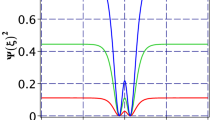
a 2D Profile of the solutions (21) by selecting parameters as \(\alpha =1.49\), \(\beta =1.50, \eta =1.0, \chi =1.0, \lambda =0.95\) and \(c_4=-1.0\) b 2D Profile of the solutions (31) by selecting parameters as \(\alpha =1.5\), \(\beta =1.8, a_0=1, c_2=2.0, c_4=1.0\) and \(c_0=-0.5\). c 2D Profile of the periodic solution (32) with parameter values as \(\alpha =1.5\), \(\beta =1.8, a_0=1, c_2=-2.0\) and \(c_0=0.5\). d 2D Profile of the periodic solution (50) with parameter values as \(\alpha =1.49\), \(\beta =1.5, \eta =1.0, \lambda =0.95, \chi =1.0\)

Full size image

In Fig. 1a, the 2D profile of the bell type solutions (21) is plotted by selecting parameters as \(\alpha =1.49\), \(\beta =1.50, \eta =1.0, \chi =1.0, \lambda =0.95\) and \(c_4=-1.0\). In Fig. 1b, the 2D profile of the bell soliton solution (31) is plotted by selecting parameters as \(\alpha =1.5\), \(\beta =1.8, a_0=1, c_2=2.0, c_4=1.0\) and \(c_0=-0.5\). This solution characterize by infinite tails. In Fig. 1c, we show the 2D profile of the periodic solution (32) with parameter values as \(\alpha =1.5\), \(\beta =1.8, a_0=1, c_2=-2.0\) and \(c_0=0.5\) within range of \(-\infty \) to \(+\infty \). In Fig. 1d, the 2D profile of the trigonometric periodic solution (50) with parameter values as \(\alpha =1.49\), \(\beta =1.5, \eta =1.0, \lambda =0.95, \chi =1.0\) is demonstrated.

Fig. 2
figure 2

a 2D Profile of the periodic solution (51) with parameter values as \(\alpha =1.49\), \(\beta =1.5, \eta =1.0, \lambda =0.95, \chi =1.0\). b 2D Profile of the periodic solution (53) with parameter values as \(\alpha =1.49\), \(\beta =1.5, \eta =1.0, \lambda =1.0, \chi =1.0, c_3=1.0\). c 2D Profile of the periodic solution (54) with parameter values as \(\alpha =1.49\), \(\beta =1.5, \eta =1.0, \lambda =1.0, \chi =1.0, c_3=1.0\). d 2D Profile of the periodic solution (56) with parameter values as \(\alpha =1.5\), \(\beta =1.0, \eta =0.5, \lambda =1.0, \chi =1.0\)

Full size image

In Fig. 2a, we plotted the 2D profile of the breather solution (51) with parameter values as \(\alpha =1.49\), \(\beta =1.5, \eta =1.0, \lambda =0.95, \chi =1.0\) and in Fig. 2b, the 2D profile of the periodic solution (53) is shown with parameter values as \(\alpha =1.49\), \(\beta =1.5, \eta =1.0, \lambda =1.0, \chi =1.0, c_3=1.0\). In Fig. 2c, the 2D profile of the periodic solution (54) exhibited with parameter values as \(\alpha =1.49\), \(\beta =1.5, \eta =1.0, \lambda =1.0, \chi =1.0, c_3=1.0\). Fig. 2d represents the 2D profile of the periodic solution (56) with parameter values as \(\alpha =1.5\), \(\beta =1.0, \eta =0.5, \lambda =1.0, \chi =1.0\).

Fig. 3
figure 3

a 2D Profile of the anti- bell soliton solution (64) with parameter values as \(\alpha =0.2\), \(\beta =0.1, r=3.0, s=1.0, \xi _0=0\). b 2D Profile of the periodic solution (66) with parameter values as \(\alpha =2\), \(\beta =1, r=3.0, s=3, \xi _0=0\)

Full size image

In Fig. 3a, the 2D profile of the dark soliton solution (64) with parameter values as \(\alpha =0.2\), \(\beta =0.1, r=3.0, s=1.0, \xi _0=0\) is portrayed. and 2D profile of the periodic solution (66) with parameter values as \(\alpha =2\), \(\beta =1, r=3.0, s=3, \xi _0=0\) is depicted in Fig. 3b.

Fig. 4
figure 4

a 2D Profile of the solutions (71) (solid line) and (72)(dotted line) for \(\alpha >\beta \) by selecting parameters as \(\alpha =1.3330\), \(\beta =1.0054\) b 2D Profile of the solutions (71) (solid line) and (72)(dotted line) for \(\beta >\alpha \) by selecting parameters as \(\alpha =1.0054\), \(\beta =1.3330\). c 2D Profile of the periodic solution (76) for \(\alpha >\beta \) with parameter values as \(\alpha =1.3330\), \(\beta =1.0054\) and \(m=0.5\) (dotted line) and for \(\beta >\alpha \) with parameter values as \(\alpha =1.0054\), \(\beta =1.3330\) and \(m=0.5\) (solid line)

Full size image

If \(\alpha >\beta \) then the Eqs.(71) and (72) represents the antibell type solitary wave solution and the 2D profiles of solutions (71) (solid line) and (72)(dotted line) plotted by selecting parameters as \(\alpha =1.3330\), \(\beta =1.0054\) in Fig. 4a. The 2D profile of the solutions (71) (solid line) and (72)(dotted line) for \(\beta >\alpha \) by selecting parameters as \(\alpha =1.0054\), \(\beta =1.3330\) are depicted in Fig 4b. The condition \(\beta >\alpha \), in the Eqs.(71) and (72) leads to the bell type solitary wave profiles as depicted in Fig. 4b. The profile of Jacobi doubly periodic solution (76) is shown in Fig. 4c for \(\alpha >\beta \) with parameter values as \(\alpha =1.3330\), \(\beta =1.0054\) and \(m=0.5\) (dotted line) and for \(\beta >\alpha \) with parameter values as \(\alpha =1.0054\), \(\beta =1.3330\) and \(m=0.5\) (solid line) and it can be observed that the phase of the periodic solution reverses for the different choices of parameters \(\alpha \) and \(\beta \).

Fig. 5
figure 5

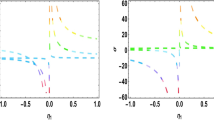
a 2D Profile of the solution (78) for \(\alpha <\beta \) with parameter values as \(\alpha =1.3221\) and \(\beta =1.5435\)(solid line) and for \(\alpha >\beta \) with parameter values as \(\alpha =1.5435\) and \(\beta =1.3221\) (dotted line). b 2D Profile of the trigonometric solutions (79) with parameter values as \(\alpha =1.3221\), \(\beta =1.5435\), \(\eta =1.0\), \(\chi =1.0\) and \(\lambda =1.0\).(c)2D Profile of the periodic solution (80) with parameter values as \(\beta =1.3330\), \(\alpha =1.0054\) for \(m=0.1\) (solid black line), \(m=0.5\) (dotted black line) and \(m=0.9\) (dotted blue line), respectively

Full size image

In Fig. 5a, we depicts the profile of solitary wave solution (78) for \(\alpha <\beta \) with parameter values as \(\alpha =1.3221\) and \(\beta =1.5435\) (solid line) and for \(\alpha >\beta \) with parameter values as \(\alpha =1.5435\) and \(\beta =1.3221\) (dotted line). In Fig 5b, the 2D profile of the trigonometric solutions (79) with parameter values as \(\alpha =1.3221\), \(\beta =1.5435\), \(\eta =1.0\), \(\chi =1.0\) and \(\lambda =1.0\) are depicted. In Fig. 5c, the 2D profile of the periodic solution (80) with parameter values as \(\beta =1.3330\), \(\alpha =1.0054\) for \(m=0.1\) (solid black line), \(m=0.5\) (dotted black line) and \(m=0.9\) (dotted blue line) are portrayed, respectively. It can be seen that for \(\alpha = \beta \), the soliton profile vanishes. The solution (80) is plotted in Fig. 5c for different values of modulus parameter \(m=0.1,0.5,0.9\) which exhibits that with change in modulus parameter the degree of energy localization of the solution changes and the profile of the solution remain periodic as long as m varies between 0 and 1.

From the above drawn figures, we can realized that these solutions take the form of the bright and dark soliton solutions, the kink soliton solutions, the breather solution, the the doubly periodic wave solutions, and the other type of singular and nonsingular soliton solutions. These figures exhibits the dynamical behavior of these solutions in space and time. In all numerical simulations the parameter values are selected in such a way that they satisfies the constrained conditions for existence of these solutions.

The advantage of Fan sub-equation approach is that its look for more new traveling wave solutions of NLEEs that can be pronounced as a polynomial in an elementary function that satisfies a more general form of sub-equation. Favorably, the Fan sub-equation method can construct exact solutions to the sub-equation that can cover all the solutions of the auxiliary ordinary differential equation, elliptic equation of first kind, and generalized Riccati equations. The exp\((-G(\xi ))\)-function expansion method provides dark soliton, singular soliton and periodic solutions in simple form, which are not obtained by sub-equation and fractional transformation methods. The fractional transformation technique results in new trigonometric function, hyperbolic function and Jacobian elliptic function solutions. It can be seen that some of the results of tanh, F-expansion and auxiliary equation methods are recovered if one can choose the proper values of parameters.

The significance of the utilized approaches of this paper is represented in providing new and generalized solutions, while the shortcomings of them are that they do not produce some other types of analytical solutions of the considered model such as complexiton function solutions where the complexiton function solutions are mixed type solutions of hyperbolic and periodic function solutions.

5 Conclusions

In this paper, the extended Fan sub-equation method, exp\((-G(\xi ))\)-function expansion method and Möbius transformation method have been applied to the (4+1)-dimensional nonlinear integrable Fokas equation and analytically constructed various types of exact traveling wave and localized solutions. These obtained solutions contain the singular and non-singular solitary wave solutions, singular and non-singular periodic solutions, Weierstrass elliptic type solutions, breather solution, Jacobi elliptic kind solutions, exponential function solutions and rational solutions. The projected methods are effective, concise, and may be applied to the study of other higher dimensional NLEEs in near future. Many of the results are novel and more extensive than the results obtained in previous studies. The 2-dimensional figures of some solutions are illustrated to understand the dynamics described by the nonlinear integrable Fokas equation. It is relatively important to know the mechanism of the complex physical phenomena that are modelled by Eq. (1), and the resulting solutions of Eq. (1) may be applied in stability analysis and checking the accuracy of the numerical results. Comparison of our solutions with the previous ones obtained in [5, 6, 23, 41, 42, 43] by using other methods, we deduce that the obtained solutions in this paper are new and not reported elsewhere irrespective of somewhat standard forms.