1 Introduction

Recently, nonlinear sciences have received considerable attention. In general, the nonlinear dynamics and the physical phenomena of waves are major aspects of the natural sciences. These often take place in the integrated system of nonlinear soliton forms, especially in crystals, meta-surfaces, nonlinear optical fibers, liquid crystals, and meta-materials, and so on. Particular physical phenomena in the field of liquid crystals have given rise to common interest among experts with a well-known name: nematicons that first introduced by Assanto in Assanto et al. (2003a, 2003b) and Alberucci and Assanto (2007). In optics, spatial optical solitons in nematic liquid crystals, also defined as nematicons, are now an excellent issue and have been discussed in a collection of publications and published studies. Spatial optical solitons construct a special theme, as the optics in space describe diffraction instead of dispersion, beam size instead of pulse duration, one or two transverse dimensions instead of one in the temporal domain (Raza and Zubair 2018). Researchers have recently addressed a significant number of reports on solitons, and in particular, on space solitons, based on their importance and wide range of applications. For this purpose, variety of schemes have been constructed to solve different types of nonlinear evolution equations analytically and numerically, such as the sine-Gordon expansion method (Ali et al. 2020d, a; Eskitaşçıoğlu et al. 2019), the extended sinh-Gordon expansion method (Dutta et al. 2020; Gao et al. 2019a), the \(\partial \)- dressing method (Dubrovsky and Lisitsyn 2002), the inverse scattering method (Vakhnenko et al. 2003), the generalized exponential rational function method (GERFM) (Osman and Ghanbari 2018; Ali et al. 2020c; Ghanbari 2019), the Bernoulli sub-ODE method (Abdulkareem et al. 2019; Ali et al. 2020b; Ismael and Bulut 2019), the extended Jacobi’s elliptic function approach (Biswas et al. 2018b), the modified Kudryashov method (Hosseini et al. 2019; Aksoy et al. 2016), the multiple exp-function method (Wan et al. 2020), the \(\tan \left( \frac{\phi }{2} \right) \)-expansion method (Aghdaei and Manafian 2016; Manafian et al. 2016; Hammouch et al. 2018), the modified auxiliary expansion method (Gao et al. 2020), the decomposition-Sumudu-like-integral-transform method (Yang et al. 2017), the Riccati–Bernoulli sub-ODE method (Yang et al. 2015; Abdelrahman and Sohaly 2018), the modified \(\exp \left( -\varphi \left( \xi \right) \right) \)-expansion function method (Ilhan et al. 2018; lhan OA, Esen A, Bulut H, Baskonus HM, 2019; Sulaiman et al. 2019), the \(\left( m+{G'}/{G} \right) \)–expansion method (Ismael et al. 2020; Gao et al. 2019b), the Darboux transformation (Guo et al. 2014; Ling et al. 2018; Ye et al. 2019), the modified trial equation method (Bulut et al. 2013; Manafian et al. 2017; Biswas et al. 2018a), the solitary ansatz method (Seadawy and Lu 2017), the shooting method (Ismael 2017; Zeeshan et al. 2018; Ismael and Arifin 2018; Ali et al. 2017), the Adomian decomposition method (Gonzalez-Gaxiola et al. 2019; Ismael and Ali 2017), the finite difference method (Yokus et al. 2018; Pandey and Jaboob 2018; Yokus and Gülbahar 2019), the Adams–Bashforth–Moulton method (Baskonus and Bulut 2015), and the improved Adams Bashforth algorithm (Owolabi and Atangana 2019).

The dimensionless form of the system that represents the dynamics of nematicons in liquid crystals can be expressed as (Ekici et al. 2017):

$$\begin{aligned}&i{{\varLambda }_{t}}+a{{\varLambda }_{xx}}+b\varTheta \varLambda =0, \end{aligned}$$
(1)
$$\begin{aligned}&c{{\varTheta }_{xx}}+\lambda \varTheta +\alpha F{{\left( \left| \varLambda \right| \right) }^{2}}=0. \end{aligned}$$
(2)

The function \(\varLambda \left( x,t \right) \) is the wave profile and \(\varTheta \left( x,t \right) \) is the angle of the tilt of the liquid crystal molecule. In Eq. (1), the first and second terms symbolize the temporal evolution of nematicons, and the group velocity dispersion, respectively. The functional F represents the nonlinearity term of equations, and \(a, b, c, \lambda , \alpha \) all are scalars.

Many researchers investigated the soliton solutions of Eqs. (1) and (2) via different methods. Raza et al. (2019) used the \(\exp \left( -\phi \left( \xi \right) \right) \)-expansion method to study Eqs. (1) and (2) and hyperbolic, periodic as well as rational soliton solutions along with their combo type solutions constructed for both Kerr and parabolic law nonlinearity. Kumar et al. (2019) used the extended sinh-Gordon equation expansion method to reveal dark soliton, bright soliton, mixed dark–bright soliton, singular soliton, mixed singular optical, periodic waves, and dipole optical soliton solutions. Ekici et al. (2017) studied the nematicons in liquid crystals by using the extended trial equation method and some soliton solutions regarding the singular solitons, periodic singular types, shock waves, snoidal waves, plane waves were successfully constructed. Arnous et al. (2017) investigated four types of nonlinearity for Eqs. (1) and (2) via the modified simple equation method and bright soliton, dark soliton, and singular soliton wave solutions to the studied system were derived. Ilhan et al. (2020) used the \(\tan \left( \frac{\phi }{2} \right) \)-expansion method and derived the optical dark soliton, optical bright soliton, mixed optical dark–bright, singular waves, traveling wave, and solitary wave solutions for four types of nonlinearity.

In this research, we use the GERFM to study the optical soliton solutions of nematicons with three laws of nonlinearity namely: Kerr, parabolic, and power law. The GERFM not only has the opportunity to provide a unified formulation to obtain the exact solutions for traveling waves, but it also guides the classification of the types of these solutions. To our knowledge, the W-shaped soliton solutions aren’t constructed beforehand for the suggested equations.

This article has been designed as follows: in Sect. 2, the structures of the GERFM are presented. In Sect. 3, the solutions to the nematic liquid crystals with three laws of nonlinearity are presented, while in Sect. 4, the physical dynamics of the solutions are discussed. In last Sect. 5, the conclusions will be drawn.

2 Method descriptions

Suppose we have nonlinear partial differential equations as the form:

$$\begin{aligned}&{{P}_{1}}\left( u,v,{{u}_{x}},{{u}^{2}}{{u}_{x}},{{u}_{t}},{{u}_{xx}},\text { } \, \ldots \right) =0, \end{aligned}$$
(3)
$$\begin{aligned}&P_{2}\left( v,u,{{v}_{x}},{{v}^{2}}{{v}_{x}},{{v}_{t}},{{v}_{xx}},\text { } \, \ldots \right) =0. \end{aligned}$$
(4)

To investigate the analytical solutions of Eqs. (3–4), we define the wave transformation as:

$$\begin{aligned} u\left( x,t \right) =U\left( \xi \right) ,\, v\left( x,t \right) =V\left( \xi \right) ,\, \xi =\kappa x-\nu t. \end{aligned}$$
(5)

Here, \(\xi \) is the symbol of the wave variable and \(\kappa \), \(\nu \) are nonzero constants. Plugging Eq. (5) on Eqs. (3–4), we get nonlinear ordinary differential equations (NLODE)

$$\begin{aligned}&{{O}_{1}}\left( U,V,\kappa {U}',\kappa {V}',{{\kappa }^{2}}{U}'',{{\kappa }^{2}}{V}'', \text { }\ldots \right) =0 \end{aligned}$$
(6)
$$\begin{aligned}&{{O}_{2}}\left( V,U,\kappa {V}',\kappa {U}',{{\kappa }^{2}}{V}'',{{\kappa }^{2}}{U}'', \text { }\ldots \right) =0. \end{aligned}$$
(7)

Now consider the trial solutions of Eqs. (6–7) have the following forms:

$$\begin{aligned} {{U }}(\xi )= & {} {{a}_{0}}+\sum \limits _{K=1}^{n}{{{a}_{K}}}\psi {{\left( \xi \right) }^{K}}+\sum \limits _{K=1}^{n}{{{b}_{K}}\psi {{\left( \xi \right) }^{-K}}}, \end{aligned}$$
(8)
$$\begin{aligned} {{V }}(\xi )= & {} {{c}_{0}}+\sum \limits _{K=1}^{m}{{{c}_{K}}}\psi {{\left( \xi \right) }^{K}}+\sum \limits _{K=1}^{m}{{{d}_{K}}\psi {{\left( \xi \right) }^{-K}}}, \end{aligned}$$
(9)

where n, m are calculated by the homogeneous balance principle and Eqs. (8) and (9) are used to find the exact solutions to the ordinary differential Eqs. (6) and (7) as an auxiliary solution. The function \(\psi \left( \xi \right) \) is defined as

$$\begin{aligned} \psi \left( \xi \right) =\frac{{{r}_{1}}{{e}^{{{s}_{1}}\xi }}+{{r}_{2}}{{e}^{{{s}_{2}}\xi }}}{{{r}_{3}}{{e}^{{{s}_{3}}\xi }}+{{r}_{4}}{{e}^{{{s}_{4}}\xi }}}, \end{aligned}$$
(10)

where \({{r}_{n}},{{s}_{n}}\,\left( 1\le n\le 4 \right) \) are real/complex constants and \({{a}_{0}}\), \({{a}_{K}}\), \({{b}_{K}}\), \({{c}_{k}}\), \({{d}_{k}}\) are constants to be determined later. Putting Eqs. (8–9) into Eqs. (6–7) with utilizing Eq. (10), as a result, we get the system of polynomial equations. After this, we solve the system via equaling the terms that have the same order and we will determine the values of constants \({{a}_{0}},\,{{a}_{K}},\,{{b}_{K}},\,{{c}_{K}},{{d}_{k}}\). Finally, we can easily obtain the exact solutions of Eqs. (3–4).

3 Mathematical analysis

To derive optical soliton solutions of nematicons in liquid crystals, we define the traveling wave transformation as follows:

$$\begin{aligned} \varLambda \left( x,t \right) =U\left( \xi \right) {{e}^{i\varphi \left( x,t \right) }}, \qquad \varTheta \left( x,t \right) =V\left( \xi \right) , \end{aligned}$$
(11)

where \(\xi \left( x,t \right) =\kappa \left( x-\nu t \right) \) and \(\varphi \left( x,t \right) =-\kappa x+\omega t+{{\theta }_{0}}\). Here \(\nu \) represent the speed of the soliton, and describe the functional form of the wave profile. On the other hand, \(\kappa ,\omega \) and \({{\theta }_{0}}\) are the soliton frequency, the wavenumber of the soliton, and a phase constant, respectively. Substituting Eq. (11) into Eqs. (1–2) and then splitting them into real and imaginary parts leads to a pair of relationships as follows

$$\begin{aligned}&a{{\kappa }^{2}}{U}''-\left( a{{\kappa }^{2}}+\omega \right) U+bUV=0, \end{aligned}$$
(12)
$$\begin{aligned}&c{{\kappa }^{2}}{V}''+\lambda V+\alpha F\left( {{U}^{2}} \right) =0, \end{aligned}$$
(13)
$$\begin{aligned}&-\kappa \nu {U}'-2a{{\kappa }^{2}}{U}'=0. \end{aligned}$$
(14)

From Eq. (14), to find the nearby solution, we can obtain the constraint condition and read

$$\begin{aligned} \nu =-2a\kappa . \end{aligned}$$
(15)

Nematicons can now be examined for the functional F in the presence of three laws of nonlinearly.

3.1 Kerr law

Kerr law is the basic form of nonlinearity observed in the nonlinear optics sense. In this situation, the refractive index of light is dependent on intensity, as formulated by the so-called Kerr law. The nonlinearity of the Kerr rule arises if

$$\begin{aligned} F\left( s \right) =s. \end{aligned}$$
(16)

By using Eqs. (16) and (2) can be rewritten as

$$\begin{aligned} c{{\varTheta }_{xx}}+\lambda \varTheta +\alpha {{\left| \varLambda \right| }^{2}}=0. \end{aligned}$$
(17)

So, Eq. (13) reduces to

$$\begin{aligned} c{{\kappa }^{2}}{V}''+\lambda V+\alpha {{U}^{2}}=0. \end{aligned}$$
(18)

Balancing \({U}''\) with UV in Eq. (9) and \({V}''\) with \({{U}^{2}}\) in Eq. (15), we get \(n=2\) and \(m=2\). Applying these values on Eqs. (8–9), we set up

$$\begin{aligned} {{U }}(\xi )&={{a}_{0}}+{{a}_{1}}\psi \left( \xi \right) +{{b}_{1}}\psi {{\left( \xi \right) }^{-1}}+{{a}_{2}}\psi {{\left( \xi \right) }^{2}}+{{b}_{2}}\psi {{\left( \xi \right) }^{-2}}, \end{aligned}$$
(19)
$$\begin{aligned} {{V }}(\xi )&={{c}_{0}}+{{c}_{1}}\psi \left( \xi \right) +{{d}_{1}}\psi {{\left( \xi \right) }^{-1}}+{{c}_{2}}\psi {{\left( \xi \right) }^{2}}+{{d}_{2}}\psi {{\left( \xi \right) }^{-2}}. \end{aligned}$$
(20)

Putting Eqs. (19) and (20) into Eqs. (12) and (18), we can study the solutions for the following families:

Family 1. When we set \(r=\left\{ -1,-2,1,1 \right\} \), \(s=\left\{ 1,0,1,0 \right\} \), then Eq. (10) becomes:

$$\begin{aligned} \psi \left( \xi \right) =\frac{-{{{\text {e}}}^{\xi }}-2}{{{{\text {e}}}^{\xi }}+1}. \end{aligned}$$
(21)

Inserting Eqs. (19–20) with Eq. (21) into Eqs. (12) and (18), we can investigate the following cases of solutions.

Case 1. When \({{A}_{1}}=\frac{18\sqrt{a}\lambda }{\sqrt{bc\alpha }}\), \({{B}_{1}}=0\), \({{C}_{1}}=-\frac{18a\lambda }{bc}\), \({{D}_{1}}=0\), \({{A}_{2}}=\frac{6\sqrt{a}\lambda }{\sqrt{bc\alpha }}\), \({{B}_{2}}=0\), \({{C}_{2}}=-\frac{6a\lambda }{bc},{{D}_{2}}=0\), \({{A}_{0}}=\frac{13\sqrt{a}\lambda }{\sqrt{bc\alpha }}\), \({{C}_{0}}=-\frac{13a\lambda }{bc}\), \(\kappa =\sqrt{\frac{\lambda }{c}}\), \(\omega =-\frac{2a\lambda }{c}\) then

$$\begin{aligned} \varLambda= & {} \frac{\sqrt{a}\lambda {{\text {e}}^{\frac{\text {i}\left( c{{\theta }_{0}}-\sqrt{c\lambda }x-2a\lambda t \right) }{c}}}\left( \cosh \left( \frac{\sqrt{c\lambda }x+2a\lambda t}{c} \right) -2 \right) }{\sqrt{bc\alpha }\left( 1+\cosh \left( \frac{\sqrt{c\lambda }x+2a\lambda t}{c} \right) \right) }, \end{aligned}$$
(22)
$$\begin{aligned} \varTheta= & {} \frac{a\lambda }{2bc}\left( 3sec{{h}^{2}}\left( \frac{1}{2}\sqrt{\frac{\lambda }{c}}x+\frac{a\lambda }{c}t \right) -2 \right) . \end{aligned}$$
(23)

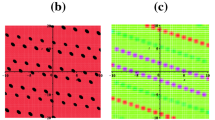
These are W-shaped and bright optical solutions to Eqs. (1) and (2) as shown in Fig. 1.

Fig. 1
figure 1

3D surfaces of Eqs. (22) and (23) are drawn when \(a=1,c=2,\lambda =0.2,\alpha =1,b=0.1,{{\theta }_{0}}=1\) and \(t=2\) for 2D

Full size image
Fig. 2
figure 2

Effect of the parameter a is drawn under Eqs. (22) and (23) when \(c=2,\lambda =0.2,\alpha =1,b=0.1,{{\theta }_{0}}=1\), \(t=2\)

Full size image

Case 2. When \({{A}_{1}}=0\), \({{B}_{1}}=\frac{36\sqrt{a}\lambda }{\sqrt{bc\alpha }}\), \({{C}_{1}}=0\), \({{D}_{1}}=-\frac{36a\lambda }{bc}\), \({{A}_{2}}=0\), \({{B}_{2}}=\frac{24\sqrt{a}\lambda }{\sqrt{bc\alpha }}\), \({{C}_{2}}=0\), \({{D}_{2}}=-\frac{24a\lambda }{bc}\), \({{A}_{0}}=\frac{13\sqrt{a}\lambda }{\sqrt{bc\alpha }}\), \({{C}_{0}}=-\frac{13a\lambda }{bc}\), \(\kappa =\sqrt{\frac{\lambda }{c}}\), \(\omega =-\frac{2a\lambda }{c}\) then

$$\begin{aligned} \varLambda&=\frac{\sqrt{a}\lambda {{\text {e}}^{\frac{\text {i}\left( c{{\theta }_{0}}-\sqrt{c\lambda }x-2a\lambda t \right) }{c}}}\left( 4-8{{\text {e}}^{\sqrt{\frac{\lambda }{c}}x+\frac{2a\lambda }{c}t}}+{{\text {e}}^{\sqrt{\frac{\lambda }{c}}2x+\frac{4a\lambda }{c}t}} \right) }{\sqrt{bc\alpha }{{\left( 2+{{\text {e}}^{^{\sqrt{\frac{\lambda }{c}}x+\frac{2a\lambda }{c}t}}} \right) }^{2}}}, \end{aligned}$$
(24)
$$\begin{aligned} \varTheta&=-\frac{a\lambda \left( 4-8{{\text {e}}^{\sqrt{\frac{\lambda }{c}}x+\frac{2a\lambda }{c}t}}+{{\text {e}}^{\sqrt{\frac{\lambda }{c}}2x+\frac{4a\lambda }{c}t}} \right) }{bc{{\left( 2+{{\text {e}}^{\sqrt{\frac{\lambda }{c}}x+\frac{2a\lambda }{c}t}} \right) }^{2}}}. \end{aligned}$$
(25)

Eqs. (24) and (25) are W-shaped and bright optical soliton solutions to the studied system as seen in Fig. 2, respectively.

Family 2. When we choose \(r=\left\{ -2-i,-2+i,1,1 \right\} \), \(s=\left\{ i,-i,i,-i \right\} \), then Eq. (12) becomes:

$$\begin{aligned} \psi \left( \xi \right) =\frac{\sin \left( \xi \right) -2\cos \left( \xi \right) }{\cos \left( \xi \right) }. \end{aligned}$$
(26)

Inserting Eqs. (19–20) with Eq. (26) into Eqs. (12) and (18), we can investigate the solutions for the following families:

Case 1. When \({{A}_{1}}=-\frac{6\sqrt{a}\lambda }{\sqrt{\alpha bc}}\), \({{A}_{2}}=-\frac{3\sqrt{a}\lambda }{2\sqrt{\alpha bc}}\), \({{C}_{1}}=-\frac{6a\lambda }{bc}\), \({{C}_{2}}=-\frac{3a\lambda }{2bc}\), \({{B}_{2}}=0\), \({{D}_{1}}=0\), \({{D}_{2}}=0\), \({{A}_{0}}=-\frac{15\sqrt{a}\lambda }{2\sqrt{bc\alpha }}\), \({{C}_{0}}=-\frac{15a\lambda }{2bc}\), \(\kappa =-\frac{\sqrt{\lambda }}{2\sqrt{c}}\), \(\omega =-\frac{5a\lambda }{4c}\), \({{B}_{1}}=0\) then

$$\begin{aligned} \varLambda= & {} -\frac{3\lambda \sqrt{a}{{\text {e}}^{\frac{\text {i}\left( 4c\theta _{0} +2\sqrt{c\lambda }x-5a\lambda t \right) }{4c}}}{{\sec }^{2}}\left( \frac{\sqrt{c\lambda }x-a\lambda t}{2c} \right) }{2\sqrt{bc\alpha }}, \end{aligned}$$
(27)
$$\begin{aligned} \varTheta= & {} -\frac{3a\lambda }{2bc}{{\sec }^{2}}\left( \frac{\sqrt{c\lambda }x-a\lambda t}{2c} \right) . \end{aligned}$$
(28)

Eqs. (27) and (28) are dark and bright periodic singular solutions to the studied system, respectively.

Case 2. When \({{B}_{1}}=0\), \({{A}_{1}}=-\frac{12\text {i}\sqrt{\lambda \omega }}{\sqrt{5b\alpha }}\), \({{A}_{2}}=-\frac{3\text {i}\sqrt{\lambda \omega }}{\sqrt{5b\alpha }}\), \({{C}_{1}}=\frac{24\omega }{5b}\), \({{C}_{2}}=\frac{6\omega }{5b}\), \({{B}_{2}}=0\), \({{D}_{1}}=0\), \({{D}_{2}}=0\), \(\kappa =\frac{\sqrt{\lambda }}{2\sqrt{c}}\), \({{A}_{0}}=-\frac{3\sqrt{5\lambda \omega }i}{\sqrt{b\alpha }}\), \({{C}_{0}}=\frac{6\omega }{b}\), \(a=-\frac{4c\omega }{5\lambda }\) then

$$\begin{aligned} \varLambda= & {} -\frac{3\sqrt{\lambda \omega }\text {i}{{\text {e}}^{\frac{1}{2}\text {i}\left( 2{{\theta }_{0}}-\frac{\sqrt{\lambda }}{\sqrt{c}}x+2\omega t \right) }}{{\csc }^{2}}\left( \frac{\sqrt{\lambda }}{2\sqrt{c}}x-\frac{2\omega }{5}t \right) }{\sqrt{5b\alpha }}, \end{aligned}$$
(29)
$$\begin{aligned} \varTheta= & {} \frac{6\omega }{5b}{{\csc }^{2}}\left( \frac{\sqrt{\lambda }}{2\sqrt{c}}x-\frac{2\omega }{5}t \right) . \end{aligned}$$
(30)

Eqs. (29) and (30) are dark periodic singular solutions to the studied system.

Family 3. When \(r=\left\{ 2,0,1,1 \right\} \), \(s=\left\{ -1,0,1,-1 \right\} \), then Eq. (12) becomes:

$$\begin{aligned} \psi \left( \xi \right) ={{\,\mathrm{sech}\,}}\left( \xi \right) (\cosh \left( \xi \right) -\sinh \left( \xi \right) ). \end{aligned}$$
(31)

Inserting Eqs. (19–20) with Eq. (31) into Eqs. (12) and (18), we can study the following cases of solutions.

Case 1. When \({{B}_{^{1}}}=0\), \({{A}_{1}}=-\frac{3\sqrt{a}\lambda }{\sqrt{bc\alpha }} \), \({{A}_{2}}=\frac{3\sqrt{a}\lambda }{2\sqrt{bc\alpha }}\), \({{C}_{1}}=\frac{3a\lambda }{bc}\), \({{C}_{2}}=-\frac{3a\lambda }{2bc}\), \({{B}_{2}}=0\), \({{D}_{1}}=0\), \({{D}_{2}}=0\), \({{A}_{0}}=\frac{\sqrt{a}\lambda }{\sqrt{bc\alpha }}\), \({{C}_{0}}=-\frac{a\lambda }{bc}\), \(\kappa =\frac{\sqrt{\lambda }}{2\sqrt{c}}\), \(\omega =-\frac{5a\lambda }{4c}\), then

$$\begin{aligned} \varLambda= & {} \frac{\sqrt{a}\lambda {{\text {e}}^{\frac{\text {i}\left( 4c\theta _{0} -2\sqrt{c}x\sqrt{\lambda }-5at\lambda \right) }{4c}}}\left( 3 {{\tanh }^{2}}\left( \frac{\sqrt{c\lambda }x+a\lambda t}{2c} \right) -1 \right) }{2\sqrt{bc\alpha }},\nonumber \\ \end{aligned}$$
(32)
$$\begin{aligned} \varTheta= & {} \frac{a\lambda \left( 1-3{{\tanh }^{2}}\left( \frac{\sqrt{c\lambda }x+a\lambda t}{2c} \right) \right) }{2bc}. \end{aligned}$$
(33)

These are W-shaped and dark optical soliton solutions to the nematic liquid crystals.

Case 2. When \({{A}_{0}}=0\), \({{C}_{0}}=0\), \({{A}_{1}}=\frac{3\sqrt{a}\lambda }{\sqrt{bc\alpha }}\), \({{A}_{2}}=-\frac{3\sqrt{a}\lambda }{2\sqrt{b}\sqrt{c}\sqrt{\alpha }}\), \({{C}_{1}}=-\frac{3a\lambda }{bc}\), \({{C}_{2}}=\frac{3a\lambda }{2bc}\), \({{B}_{1}}=0\), \({{B}_{2}}=0\), \({{D}_{1}}=0\), \({{D}_{2}}=0\), \(\kappa =\frac{\sqrt{-\lambda }}{2\sqrt{c}}\), \(\omega =-\frac{3a\lambda }{4c}\) then

$$\begin{aligned} \varLambda= & {} \frac{3\lambda \sqrt{a}{{\text {e}}^{\frac{\text {i}\left( 4c{{\theta }_{0}}-2x\sqrt{-c\lambda }-3at\lambda \right) }{4c}}}{{\,\mathrm{sech}\,}}^{2}\left( \frac{\sqrt{-c\lambda }x-at\lambda }{2c} \right) }{2\sqrt{bc\alpha }}, \end{aligned}$$
(34)
$$\begin{aligned} \varTheta= & {} -\frac{3a\lambda {{\,\mathrm{sech}\,}}^{2}\left( \frac{x\sqrt{-c\lambda }-at\lambda }{2c} \right) }{2bc}, \end{aligned}$$
(35)

providing that \(\lambda <0\). Eqs. (34) and (35) are bright soliton solutions to Eqs. (1) and (2).

3.2 Parabolic law

The nonlinearity of the parabolic rule arises when

$$\begin{aligned} F\left( s \right) ={{C}_{0}}s+{{C}_{1}}{{s}^{2}}. \end{aligned}$$
(36)

By using Eqs. (36 and 2) can be rewritten as

$$\begin{aligned} c{{\varTheta }_{xx}}+\lambda \varTheta +\alpha \left( {{C}_{0}}{{\left| \varLambda \right| }^{2}}+{{C}_{1}}{{\left| \varLambda \right| }^{4}} \right) =0. \end{aligned}$$
(37)

So, Eq. (13) reduces to

$$\begin{aligned} c{{\kappa }^{2}}{V}''+\lambda V+\alpha \left( {{C}_{0}}{{U}^{2}}+{{C}_{1}}{{U}^{4}} \right) =0. \end{aligned}$$
(38)

Balancing \({U}''\) with UV in Eq. (9) and \({V}''\) with \({{U}^{4}}\) in Eq. (38), we get \(n=1\) and \(m=2\). Applying these values on Eqs. (8–9), we get

$$\begin{aligned} {{U}}(\xi )= & {} {{a}_{0}}+{{a}_{1}}\psi \left( \xi \right) +{{b}_{1}}\psi {{\left( \xi \right) }^{-1}}, \end{aligned}$$
(39)
$$\begin{aligned} {V}(\xi )= & {} {{c}_{0}}+{{c}_{1}}\psi \left( \xi \right) +{{d}_{1}}\psi {{\left( \xi \right) }^{-1}}+{{c}_{2}}\psi {{\left( \xi \right) }^{2}}+{{d}_{2}}\psi {{\left( \xi \right) }^{-2}}.\nonumber \\ \end{aligned}$$
(40)

Putting Eqs. (39) and (40) on Eqs. (12) and (38), we can conclude the following families of solutions:

Family 1. If we select \(r=\left\{ -1,-2,1,1 \right\} ,\,\,s=\left\{ 1,0,1,0 \right\} ,\) then Eq. (12) becomes:

$$\begin{aligned} \psi \left( \xi \right) =\frac{-{{{\text {e}}}^{\xi }}-2}{{{{\text {e}}}^{\xi }}+1}. \end{aligned}$$
(41)

Inserting Eqs. (39–40) with Eq. (41) into Eqs. (12) and (38), we can construct the following cases of solutions.

Case 1. When \({{A}_{1}}=0\), \({{C}_{1}}=0\), \({{B}_{1}}=-2\sqrt{\frac{\sqrt{3a}\lambda }{\sqrt{{{a}_{2}}bc\alpha }}-\frac{3{{a}_{1}}}{{{a}_{2}}}}\), \({{D}_{1}}=\frac{1}{bc}\left( \frac{6{{a}_{1}}\sqrt{3abc\alpha }}{\sqrt{{{a}_{2}}}}-6a\lambda \right) \), \({{D}_{2}}=\frac{1}{bc}\left( \frac{4{{a}_{1}}\sqrt{3abc\alpha }}{\sqrt{{{a}_{2}}}}-4a\lambda \right) \), \({{C}_{2}}=0\), \({{A}_{0}}=-\frac{3}{2}\sqrt{\frac{\sqrt{3a}\lambda }{\sqrt{{{a}_{2}}ab\alpha }}-\frac{3{{a}_{1}}}{{{a}_{2}}}}\), \({{C}_{0}}=\frac{1}{16}\left( \frac{34\sqrt{3a\alpha }{{a}_{1}}}{\sqrt{{{a}_{2}}bc}}+\frac{3{{a}_{1}}^{2}\alpha }{{{a}_{2}}\lambda }-\frac{35a\lambda }{bc} \right) \) then

$$\begin{aligned} \varLambda&=\frac{{{\text {e}}^{\text {i}\left( {{\theta }_{0}}-\kappa x+\omega t \right) }}\left( {{\text {e}}^{\kappa \left( x+2a\kappa t \right) }}-2 \right) \sqrt{\frac{\sqrt{3a}\lambda }{\sqrt{{{a}_{2}}bc\alpha \,}}-\frac{3{{a}_{1}}}{{{a}_{2}}}}}{2\left( 2+{{\text {e}}^{\kappa \left( x+2a\kappa t \right) }} \right) }, \end{aligned}$$
(42)
$$\begin{aligned} \varTheta&=\frac{3{{a}_{1}}^{2}\alpha }{16{{a}_{2}}\lambda }-\frac{a\lambda \left( 12-20{{\text {e}}^{\kappa \left( x+2a\kappa t \right) }}+3{{\text {e}}^{2\kappa \left( x+2a\kappa t \right) }} \right) }{16bc{{\left( 2+{{\text {e}}^{\kappa \left( x+2a\kappa t \right) }} \right) }^{2}}} \nonumber \\&+\frac{{{a}_{1}}\sqrt{3\alpha {{a}_{2}}abc}(4-12{{\text {e}}^{\kappa \left( x+2a\kappa t \right) }}+{{\text {e}}^{2\kappa \left( x+2a\kappa t \right) }})}{8{{a}_{2}}bc{{\left( 2+{{\text {e}}^{\kappa \left( x+2a\kappa t \right) }} \right) }^{2}}}. \end{aligned}$$
(43)

These are dark soliton solutions to the suggested system of equations (see Fig. 3).

Fig. 3
figure 3

Effect of the parameter a is drawn under Eqs. (22) and (23) when \(a=1, c=2,\lambda =0.2,\alpha =1,{{\theta }_{0}}=1\), \(t=2\)

Full size image

Case 2. When \({{A}_{1}}=\sqrt{\frac{\sqrt{3a}\lambda }{\sqrt{{{a}_{2}}}\sqrt{bc\alpha }}-\frac{3{{a}_{1}}}{{{a}_{2}}}}\), \({{D}_{1}}=0\), \({{B}_{1}}=0\), \({{C}_{1}}=\frac{1}{bc}\left( \frac{3{{a}_{1}}\sqrt{3abc\alpha }}{\sqrt{{{a}_{2}}}}-3a\lambda \right) \), \({{C}_{2}}=\frac{1}{bc}\left( \frac{{{a}_{1}}\sqrt{3abc\alpha }}{\sqrt{{{a}_{2}}}}-a\lambda \right) \), \({{D}_{2}}=0\), \({{A}_{0}}=\frac{3}{2}\sqrt{\frac{\sqrt{3a}\lambda }{\sqrt{{{a}_{2}}bc\alpha }}-\frac{3{{a}_{1}}}{{{a}_{2}}}}\), \({{C}_{0}}=\frac{1}{16}\left( \frac{34{{a}_{1}}\sqrt{3a\alpha }}{\sqrt{{{a}_{2}}bc}}+\frac{3{{a}_{1}}^{2}\alpha }{{{a}_{2}}\lambda }-\frac{35a\lambda }{bc} \right) \), \(\omega =\frac{1}{16}\left( \frac{10a_{1}\sqrt{3ab\alpha }}{\sqrt{a_{2}c}}+\frac{3{{a}_{1}}^{2}b\alpha }{{{a}_{2}}\lambda }-\frac{11a\lambda }{c} \right) \), \(\kappa =\frac{\sqrt{a{{a}_{2}}{{\lambda }}-{{a}_{1}} \sqrt{3a{{a}_{2}}bc\alpha }}}{\sqrt{2ac{{a}_{2}} }}\), then we have

$$\begin{aligned} \varLambda= & {} \frac{{{\text {e}}^{\text {i}\left( {{\theta }_{0}}-\kappa x+\omega t \right) }}\left( {{\text {e}}^{\kappa \left( x+2a\kappa t \right) }}-1 \right) \sqrt{\frac{\lambda \sqrt{3a}}{\sqrt{{{a}_{2}}bc\alpha }}-\frac{3{{a}_{1}}}{{{a}_{2}}}}}{2\left( 1+{{\text {e}}^{\kappa \left( x+2a\kappa t \right) }} \right) }, \end{aligned}$$
(44)
$$\begin{aligned} \varTheta= & {} \frac{3{{a}_{1}}^{2}\alpha }{16{{a}_{2}}\lambda }-\frac{a\lambda \left( 3-10{{\text {e}}^{\kappa \left( x+2a\kappa t \right) }}+3{{\text {e}}^{2\kappa \left( x+2a\kappa t \right) }} \right) }{16bc{{\left( 1+{{\text {e}}^{\kappa \left( x+2a\kappa t \right) }} \right) }^{2}}} \nonumber \\&+\frac{{{a}_{1}}\sqrt{3a{{a}_{2}}bc\alpha }\left( 1-6{{\text {e}}^{\kappa \left( x+2a\kappa t \right) }}+{{\text {e}}^{2\kappa \left( x+2a\kappa t \right) }} \right) }{8{{a}_{2}}bc{{\left( 1+{{\text {e}}^{\kappa \left( x+2a\kappa t \right) }} \right) }^{2}}}. \end{aligned}$$
(45)

Eqs. (44) and (45) are dark and bright soliton solutions to the nematic liquid crystals as shown in Fig. 3.

Family 2. If we select \(r=\left\{ -2-i,-2+i,1,1 \right\} \), \(s=\left\{ i,-i,i,-i \right\} \), then Eq. (12) becomes:

$$\begin{aligned} \psi \left( \xi \right) =\frac{\sin \left( \xi \right) -2\cos \left( \xi \right) }{\cos \left( \xi \right) }. \end{aligned}$$
(46)

Inserting Eqs. (39–40) with Eq. (46) into Eqs. (12) and (38), we can reveal the following cases of solutions.

Case 1. When \({{A}_{1}}=0\), \({{B}_{1}}=\frac{5{{A}_{0}}}{2}\), \({{D}_{1}}=\frac{5{{A}_{0}}^{2}\left( {{A}_{0}}^{2}{{a}_{2}}-3{{a}_{1}} \right) \alpha }{3\lambda }\), \({{C}_{1}}=0\), \({{D}_{2}}=\frac{25{{A}_{0}}^{2}\left( {{A}_{0}}^{2}{{a}_{2}}-3{{a}_{1}} \right) \alpha }{12\lambda }\), \({{C}_{0}}=\frac{{{A}_{0}}^{2}\left( 17{{A}_{0}}^{2}{{a}_{2}}-48{{a}_{1}} \right) \alpha }{48\lambda }\), \({{C}_{2}}=0\), \(\kappa =\frac{\sqrt{{{A}_{0}}^{2}b\alpha \left( 3{{a}_{1}}-{{A}_{0}}^{2}{{a}_{2}} \right) }}{2\sqrt{6a\lambda }}\), \(\omega =-\frac{{{A}_{0}}^{2}\left( {{A}_{0}}^{2}{{a}_{2}}-6{{a}_{1}} \right) x}{48\lambda }\), \(c=\frac{3a{{a}_{2}}{{\lambda }^{2}}}{b\alpha {{\left( {{A}_{0}}^{2}{{a}_{2}}-3{{a}_{1}} \right) }^{2}}}\) , we get

$$\begin{aligned}&\varLambda ={{\text {e}}^{\text {i}\left( {{\theta }_{0}}-x\kappa +\omega t \right) }} \nonumber \\&\quad \left( {{A}_{0}}+\frac{5{{A}_{0}}\cos \left( \kappa \left( x+2a\kappa t \right) \right) }{2\left( \sin \left( \kappa \left( x+2a\kappa t \right) \right) -2\cos \left( \kappa \left( x+2a\kappa t \right) \right) \right) } \right) , \end{aligned}$$
(47)
$$\begin{aligned}&\varTheta =\frac{{{A}_{0}}^{2}\alpha \left( {{A}_{0}}^{2}{{a}_{2}}-4{{a}_{1}} \right) \left( \begin{array}{l} 12\sin \left( 2\kappa \left( x+2a\kappa t \right) \right) \\ -9\cos \left( 2\kappa \left( x+2a\kappa t \right) \right) \\ \end{array} \right) }{96\lambda {{\left( \sin \left( 2\kappa \left( x+2a\kappa t \right) \right) -2\cos \left( 2\kappa \left( x+2a\kappa t \right) \right) \right) }^{2}}}+ \nonumber \\&\frac{{{A}_{0}}^{2}\alpha \left( 25{{A}_{0}}^{2}{{a}_{2}}-60{{a}_{1}} \right) }{96\lambda {{\left( \sin \left( 2\kappa \left( x+2a\kappa t \right) \right) -2\cos \left( 2\kappa \left( x+2a\kappa t \right) \right) \right) }^{2}}}. \end{aligned}$$
(48)

These are period singular solutions to the studied system of equations.

Case 2. When \({{B}_{1}}=0\), \({{C}_{1}}=\frac{4{{A}_{1}}^{2}\left( 4{{A}_{1}}^{2}{{a}_{2}}-3{{a}_{1}} \right) \alpha }{3\lambda }\), \({{D}_{1}}=0\), \({{C}_{2}}=\frac{{{A}_{1}}^{2}\alpha \left( 4{{A}_{1}}^{2}{{a}_{2}}-3{{a}_{1}} \right) }{3\lambda }\), \({{D}_{2}}=0\), \({{A}_{0}}=2{{A}_{1}}\), \({{C}_{0}}=\frac{{{A}_{1}}^{2}\left( 17{{A}_{1}}^{2}{{a}_{2}}-12{{a}_{1}} \right) \alpha }{3\lambda }\), \(\kappa =\frac{{{A}_{1}}\sqrt{b\alpha \left( 3{{a}_{1}}-4{{A}_{1}}^{2}{{a}_{2}} \right) }}{\sqrt{6a\lambda }}\), \(\omega =\frac{{{A}_{1}}^{2}b\alpha \left( 3{{a}_{1}}-2{{A}_{1}}^{2}{{a}_{2}} \right) }{6\lambda }\),

\(c=\frac{3a{{a}_{2}}{{\lambda }^{2}}}{{{\left( 3{{a}_{1}}-4{{A}_{1}}^{2}a2 \right) }^{2}}b\alpha }\), then

$$\begin{aligned} \varLambda&={{A}_{1}}{{\text {e}}^{\frac{1}{6}\text {i}\left( 6{{\theta }_{0}}+\frac{{{A}_{1}}^{2}\left( 3{{a}_{1}}-2{{A}_{1}}^{2}{{a}_{2}} \right) b\alpha }{\lambda }t-{{\alpha }_{2}}x \right) }}\tan \left( {{\alpha }_{1}}t+{{\alpha }_{2}}x \right) , \end{aligned}$$
(49)
$$\begin{aligned} \varTheta&=\frac{{{A}_{1}}^{2}\alpha }{3\lambda }\left( {{A}_{1}}^{2}{{a}_{2}}+\left( 4{{A}_{1}}^{2}{{a}_{2}}-3{{a}_{1}} \right) {{\tan }^{2}}\left( {{\alpha }_{1}}t+{{\alpha }_{2}}x \right) \right) . \end{aligned}$$
(50)

Where \({{\alpha }_{1}}=\frac{6{{a}_{1}}{{A}_{1}}^{2}b\alpha -8{{A}_{1}}^{4}{{a}_{2}}b\alpha }{6\lambda }\), \({{\alpha }_{2}}=\frac{{{A}_{1}}\sqrt{6b\alpha \lambda \left( 3{{a}_{1}}-4{{A}_{1}}^{2}{{a}_{2}} \right) }}{6\lambda \sqrt{a}}\). Eqs. (49) and (50) are dark and bright periodic solutions to Eqs. (1) and (2), respectively.

Family 3. If we choose \(r=\left\{ -(2+i),2-i,-1,1\right\} \), \(s=\left\{ i,-i,i,-i \right\} \), then Eq. (12) becomes:

$$\begin{aligned} \psi \left( \xi \right) =\frac{\cos \left( \xi \right) +2\sin \left( \xi \right) }{\sin \left( \xi \right) }. \end{aligned}$$
(51)

Inserting Eqs. (39–40) with Eq. (51) into Eqs. (12) and (38), we can study the following cases of solutions.

Case 1. When \({{A}_{1}}=-\frac{{{A}_{0}}}{2}\), \({{B}_{1}}=0\), \({{C}_{1}}=\frac{8a{{\kappa }^{2}}}{b}\), \({{D}_{1}}=0\), \({{C}_{2}}=-\frac{2a{{\kappa }^{2}}}{b}\), \({{C}_{0}}=\frac{4a{{\kappa }^{2}}\left( c{{\kappa }^{2}}-2\lambda \right) }{b\lambda }\), \({{a}_{2}}=\frac{192ac{{\kappa }^{4}}}{{{A}_{0}}^{4}b\alpha }\), \(\omega =\frac{a{{\kappa }^{2}}\left( 4c{{\kappa }^{2}}+\lambda \right) }{\lambda }\), \({{a}_{1}}=\frac{8a{{\kappa }^{2}}\left( 8c{{\kappa }^{2}}+\lambda \right) }{{{A}_{0}}^{2}b\alpha }\), \({{D}_{2}}=0\) then

$$\begin{aligned}&\varLambda ={{\text {e}}^{\text {i}\left( {{\theta }_{0}}-\kappa x+\omega t \right) }} \nonumber \\&\quad \left( {{A}_{0}}-\frac{5{{A}_{0}}\sin \left( \kappa \left( x+2a\kappa t \right) \right) }{2\left( \cos \left( \kappa \left( x+2a\kappa t \right) \right) +2\sin \left( \kappa \left( x+2a\kappa t \right) \right) \right) } \right) , \nonumber \\\end{aligned}$$
(52)
$$\begin{aligned}&\varTheta =\frac{{{A}_{0}}^{2}\alpha \left( {{A}_{0}}^{2}{{a}_{2}}-4{{a}_{1}} \right) \left( \begin{array}{l} 9\cos \left( 2\kappa \left( x+2a\kappa t \right) \right) - \\ 12\sin \left( 2\kappa \left( x+2a\kappa t \right) \right) \\ \end{array} \right) }{96\lambda {{\left( \cos \left( 2\kappa \left( x+2a\kappa t \right) \right) +2\sin \left( 2\kappa \left( x+2a\kappa t \right) \right) \right) }^{2}}} \nonumber \\&\quad +\frac{25{{A}_{0}}^{2}{{a}_{2}}-60{{a}_{1}}}{96\lambda {{\left( \cos \left( 2\kappa \left( x+2a\kappa t \right) \right) +2\sin \left( 2\kappa \left( x+2a\kappa t \right) \right) \right) }^{2}}}. \end{aligned}$$
(53)

These are period singular soliton solutions to Eqs. (1) and (2).

Case 2. When \({{A}_{1}}=0\), \({{B}_{1}}=-\frac{5{{A}_{0}}}{2}\), \({{C}_{1}}=0\), \({{D}_{1}}=\frac{40a{{\kappa }^{2}}}{b}\), \({{C}_{2}}=0\), \({{D}_{2}}=-\frac{50a{{\kappa }^{2}}}{b}\), \(c=\frac{{{A}_{0}}^{4}{{a}_{2}}b\alpha }{192a{{\kappa }^{4}}}\), \(\omega =a{{\kappa }^{2}}+\frac{{{A}_{0}}^{4}{{a}_{2}}b\alpha }{48\lambda }\), \({{a}_{1}}=\frac{{{A}_{0}}^{2}{{a}_{2}}}{3}+\frac{8a{{\kappa }^{2}}\lambda }{{{A}_{0}}^{2}b\alpha }\), \({{C}_{0}}=\frac{{{A}_{0}}^{4}{{a}_{2}}\alpha }{48\lambda }-\frac{8a{{\kappa }^{2}}}{b},\) then

$$\begin{aligned}&\varLambda ={{\text {e}}^{\text {i}\left( {{\theta }_{0}}-\kappa x+\left( a{{\kappa }^{2}}+\frac{{{A}_{0}}^{4}{{a}_{2}}b\alpha }{48\lambda } \right) t \right) }} \nonumber \\&\quad \left( {{A}_{0}}-\frac{5{{A}_{0}}\sin \left( \kappa \left( x+2a\kappa t \right) \right) }{2\left( \cos \left( \kappa \left( x+2a\kappa t \right) \right) +2\sin \left( \kappa \left( x+2a\kappa t \right) \right) \right) } \right) , \nonumber \\\end{aligned}$$
(54)
$$\begin{aligned}&\varTheta =\frac{5\left( {{A}_{0}}^{4}{{a}_{2}}b\alpha -96a{{\kappa }^{2}}\lambda \right) }{96b\lambda {{\left( \cos \left( 2\kappa \left( x+2at\kappa \right) \right) +2\sin \left( 2\kappa \left( x+2at\kappa \right) \right) \right) }^{2}}}+ \nonumber \\&\quad \frac{\left( {{A}_{0}}^{4}{{a}_{2}}b\alpha +96a{{\kappa }^{2}}\lambda \right) \left( \begin{array}{l} 4\sin \left( 2\kappa \left( x+2at\kappa \right) \right) \\ -3\cos \left( 2\kappa \left( x+2at\kappa \right) \right) \\ \end{array} \right) }{96b\lambda {{\left( \cos \left( 2\kappa \left( x+2at\kappa \right) \right) +2\sin \left( 2\kappa \left( x+2at\kappa \right) \right) \right) }^{2}}}. \end{aligned}$$
(55)

These are singular soliton solutions to the system of nematic liquid crystals.

3.3 Power law nonlinearity

The nonlinearity of the power rule arises if

$$\begin{aligned} F\left( s \right) ={{s}^{n}}. \end{aligned}$$
(56)

By using Eqs. (56 and 2) can be rewritten as

$$\begin{aligned} c{{\varTheta }_{xx}}+\lambda \varTheta +\alpha {{\left( {{\left| \varLambda \right| }^{2}} \right) }^{n}}=0. \end{aligned}$$
(57)

So, Eq. (13) reduces to

$$\begin{aligned} c{{\kappa }^{2}}{V}''+\lambda V+\alpha {{U}^{2n}}=0. \end{aligned}$$
(58)

Assume that

$$\begin{aligned} U={{H}^{\frac{1}{n}}}, \end{aligned}$$
(59)

then Eqs. (9) and (58) can be rewritten as

$$\begin{aligned}&a{{\kappa }^{2}}\left( nH{H}''+\left( 1-n \right) {{\left( {{H}'} \right) }^{2}} \right) -{{n}^{2}}\left( a{{\kappa }^{2}}+\omega \right) {{H}^{2}}+\nonumber \\&\quad {{n}^{2}}b{{R}^{2}}V=0, \end{aligned}$$
(60)
$$\begin{aligned}&c{{\kappa }^{2}}{V}''+\lambda V+\alpha {{H}^{2}}=0. \end{aligned}$$
(61)

Balancing \(H{H}''\) with \({{R}^{2}}V\) in Eq. (60) and \({V}''\) with \({{H}^{2}}\) in Eq. (61), we get \(n=2\) and \(m=2\). Applying these values on Eqs. (8–9), we get

$$\begin{aligned} {U}(\xi )&={{a}_{0}}+{{a}_{1}}\psi \left( \xi \right) +{{b}_{1}}\psi {{\left( \xi \right) }^{-1}}+{{a}_{2}}\psi {{\left( \xi \right) }^{2}}+{{b}_{2}}\psi {{\left( \xi \right) }^{-2}}, \end{aligned}$$
(62)
$$\begin{aligned} {V}(\xi )&={{c}_{0}}+{{c}_{1}}\psi \left( \xi \right) +{{d}_{1}}\psi {{\left( \xi \right) }^{-1}}+{{c}_{2}}\psi {{\left( \xi \right) }^{2}}+{{d}_{2}}\psi {{\left( \xi \right) }^{-2}}. \end{aligned}$$
(63)

Inserting Eqs. (62) and (63) into Eqs. (60) and (61), we can study the following families of solutions:

Family 1. If we set \(r=\left\{ -1,-2,1,1 \right\} ,\,\,s=\left\{ 1,0,1,0 \right\} ,\) then Eq. (12) becomes:

$$\begin{aligned} \psi \left( \xi \right) =\frac{-{{{\text {e}}}^{\xi }}-2}{{{{\text {e}}}^{\xi }}+1}. \end{aligned}$$
(64)

Inserting Eqs. (62–63) with Eq. (64) into Eqs. (60) and (61), we can successfully reveal the following cases of solutions.

Case 1. When \({{D}_{2}}=0\), \({{B}_{1}}=0\), \({{C}_{1}}=\frac{{{A}_{1}}^{2}\alpha }{18\lambda }\), \({{D}_{1}}=0\), \({{A}_{2}}=\frac{{{A}_{1}}}{3}\), \({{B}_{2}}=0\), \({{C}_{2}}=\frac{{{A}_{1}}^{2}\alpha }{54\lambda }\), \({{A}_{0}}=\frac{2{{A}_{1}}}{3}\), \({{C}_{0}}=\frac{{{A}_{1}}^{2}\alpha }{27\lambda }\), \(\kappa =\text {i}\sqrt{\frac{\lambda }{c}}\), \(\omega =\frac{{{A}_{1}}^{2}b\alpha \left( {{n}^{2}}-1 \right) }{108\lambda \left( 2+n \right) }\), \(a=\frac{{{A}_{1}}^{2}bc{{n}^{2}}\alpha }{108{{\lambda }^{2}}\left( 2+n \right) }\) then

$$\begin{aligned} \varLambda= & {} {{3}^{-\frac{1}{n}}}{{\text {e}}^{\text {i}{{\theta }_{0}}+\frac{\text {i}{{A}_{1}}^{2}b\left( {{n}^{2}}-1 \right) \alpha }{108\left( 2+n \right) \lambda }t+\frac{\sqrt{\lambda }}{\sqrt{c}}x}} \nonumber \\&\quad {{\left( -{{A}_{1}}{{\text {e}}^{\frac{{{A}_{1}}^{2}b{{n}^{2}}\alpha }{54\left( 2+n \right) \lambda }t+\frac{\text {i}\sqrt{\lambda }}{\sqrt{c}}x}}{{\left( {{\text {e}}^{\frac{{{A}_{1}}^{2}b{{n}^{2}}\alpha }{54\left( 2+n \right) \lambda }t}}+{{\text {e}}^{\frac{\text {i}\sqrt{\lambda }}{\sqrt{c}}x}} \right) }^{-2}} \right) }^{\frac{1}{n}}}, \end{aligned}$$
(65)
$$\begin{aligned} \varTheta= & {} -\frac{\alpha {{A}_{1}}^{2}}{54\lambda }{{\text {e}}^{\frac{{{A}_{1}}^{2}b{{n}^{2}}\alpha }{54\left( 2+n \right) \lambda }t+\frac{\text {i}\sqrt{\lambda }}{\sqrt{c}}x}}{{\left( {{\text {e}}^{\frac{{{A}_{1}}^{2}b{{n}^{2}}\alpha }{54\left( 2+n \right) \lambda }t}}+{{\text {e}}^{\frac{\text {i}\sqrt{\lambda }}{\sqrt{c}}x}} \right) }^{-2}}. \end{aligned}$$
(66)

These are complex solutions to the studied system.

Case 2. When \({{A}_{1}}=0\), \({{A}_{2}}=0\), \({{C}_{1}}=0\), \({{D}_{1}}=-\frac{12a\left( 2+n \right) {{\kappa }^{2}}}{b{{n}^{2}}}\), \({{D}_{2}}=-\frac{8a\left( 2+n \right) {{\kappa }^{2}}}{b{{n}^{2}}}\), \({{B}_{1}}=\frac{12\kappa \text {i}\sqrt{3a\lambda \left( 2+n \right) }}{n\sqrt{b\alpha }}\), \({{B}_{2}}=\frac{8\kappa \text {i}\sqrt{3a\lambda \left( 2+n \right) }}{n\sqrt{\alpha b}}\), \({{A}_{0}}=\frac{4\kappa \text {i}\sqrt{3a\lambda \left( 2+n \right) }}{n\sqrt{b\alpha }}\), \({{C}_{0}}=-\frac{4a{{\kappa }^{2}}\left( 2+n \right) }{b{{n}^{2}}}\), \(\omega =a{{\kappa }^{2}}\left( \frac{1}{{{n}^{2}}}-1 \right) \), \(c=-\frac{\lambda }{{{\kappa }^{2}}}\), \({{C}_{2}}=0\) then

$$\begin{aligned} \varLambda= & {} {{3}^{\frac{0.5}{n}}}{{4}^{\frac{1}{n}}}{{\text {e}}^{\text {i}\left( {{\theta }_{0}}-\kappa x+a{{\kappa }^{2}}\left( \frac{1}{{{n}^{2}}}-1 \right) t \right) }} \nonumber \\&\quad {{\left( -\frac{\text {i}\kappa \sqrt{a\lambda \left( 2+n \right) }{{\text {e}}^{\kappa \left( x+2a\kappa t \right) }}}{n\sqrt{b\alpha }{{\left( 2+{{\text {e}}^{\kappa \left( x+2a\kappa t \right) }} \right) }^{2}}} \right) }^{\frac{1}{n}}}, \end{aligned}$$
(67)
$$\begin{aligned} \varTheta= & {} \frac{4a\left( 2+n \right) {{\kappa }^{2}}{{\text {e}}^{\kappa \left( x+2a\kappa t \right) }}}{b{{\left( 2+{{\text {e}}^{\kappa \left( x+2a\kappa t \right) }} \right) }^{2}}{{n}^{2}}}. \end{aligned}$$
(68)

Eqs. (67) and (68) are bright soliton solutions to Eqs. (1) and (2).

Family 2. If we choose \(r=\left\{ -2-i,-2+i,1,1 \right\} \), \(s=\left\{ i,-i,i,-i \right\} \), then Eq. (12) becomes:

$$\begin{aligned} \psi \left( \xi \right) =\frac{\sin \left( \xi \right) -2\cos \left( \xi \right) }{\cos \left( \xi \right) }. \end{aligned}$$
(69)

Inserting Eqs. (62–63) with Eq. (69) into Eqs. 60) and (61), we can obtain the following cases of solutions.

Case 1. When \({{A}_{2}}=0\), \({{A}_{1}}=0\), \({{C}_{1}}=0\), \({{D}_{1}}=-\frac{40a{{\kappa }^{2}}\left( 2+n \right) }{b{{n}^{2}}}\), \({{D}_{2}}=-\frac{50a{{\kappa }^{2}}\left( 2+n \right) }{b{{n}^{2}}}\), \({{B}_{1}}=\frac{20\kappa \sqrt{3a\lambda \left( 2+n \right) }}{n\sqrt{b\alpha }}\), \({{B}_{2}}=\frac{25\kappa \sqrt{3a\lambda \left( 2+n \right) }}{n\sqrt{b\alpha }}\), \({{A}_{0}}=\frac{5\kappa \sqrt{3a\lambda \left( 2+n \right) }}{n\sqrt{b\alpha }}\), \({{C}_{0}}=-\frac{10a{{\kappa }^{2}}\left( 2+n \right) }{b{{n}^{2}}}\), \(\omega =-\frac{a{{\kappa }^{2}}\left( 4+{{n}^{2}} \right) }{{{n}^{2}}}\), \(c=\frac{\lambda }{4{{\kappa }^{2}}}\), \({{C}_{2}}=0\), then

$$\begin{aligned}&\varLambda ={{3}^{\frac{0.5}{n}}}{{5}^{\frac{1}{n}}}{{\text {e}}^{\text {i}\left( {{\theta }_{0}}-\kappa \left( x+\frac{a\left( 4+{{n}^{2}} \right) \kappa }{{{n}^{2}}}t \right) \right) }} \nonumber \\&\quad {{\left( \frac{\kappa \sqrt{a\lambda \left( 2+n \right) }}{n\sqrt{b\alpha }{{\left( \sin \left( \kappa \left( x+2a\kappa t \right) \right) -2\cos \left( \kappa \left( x+2a\kappa t \right) \right) \right) }^{2}}} \right) }^{\frac{1}{n}}}, \end{aligned}$$
(70)
$$\begin{aligned}&\varTheta =-\frac{10a{{\kappa }^{2}}\left( 2+n \right) }{b{{n}^{2}}{{\left( \sin \left( \kappa \left( x+2a\kappa t \right) \right) -2\cos \left( \kappa \left( x+2a\kappa t \right) \right) \right) }^{2}}}. \end{aligned}$$
(71)

Eqs. (70) and (71) are dark and bright periodic singular solutions to the suggested system of equations as shown in Fig. 4.

Fig. 4
figure 4

Effect of the parameter a is drawn under Eqs. (22) and (23) when \(a=1, b=0.1,\lambda =0.2,\alpha =1,{{\theta }_{0}}=1\), \(t=2\)

Full size image
Fig. 5
figure 5

Effect of the parameter a is drawn under Eqs. (22) and (23) when \(a=1, b=0.1,c=2,\alpha =1,{{\theta }_{0}}=1\), \(t=2\)

Full size image
Fig. 6
figure 6

Effect of the parameter \(\alpha \) is drawn under Eq. (22) when \(a=1,c=2,\lambda =0.2,\lambda =0.2,b=0.1,{{\theta }_{0}}=1\), \(t=2\)

Full size image
Fig. 7
figure 7

3D surfaces of Eqs. (24) and (25) are drawn when \(a=1,c=0.5,\lambda =0.2,\alpha =1,b=0.1,{{\theta }_{0}}=1\) and \(t=1\) for 2D

Full size image
Fig. 8
figure 8

3D figures of Eqs. (42) and (43) drawn when \(a=1\), \(c=0.1\), \(\lambda =0.2\), \(\alpha =1\), \(b=0.1\), \({{\theta }_{0}}=1\), \({{a}_{1}}=-0.1\), \({{a}_{2}}=0.1\), \(\kappa =0.2\), \(\omega =1\) and \(t=2\) for 2D

Full size image
Fig. 9
figure 9

3D figures of Eqs. (70–71) when \(a=1\), \(\lambda =0.2\), \(\alpha =1\), \(b=0.1\), \({{\theta }_{0}}=1\), \(n=3,\kappa =1\) and \(t=2\) for 2D

Full size image

Case 2. When \({{B}_{2}}=0\), \({{A}_{1}}=4{{A}_{2}}\), \({{C}_{1}}=-\frac{2a\left( 2+n \right) \lambda }{bc{{n}^{2}}}\), \({{D}_{1}}=0\), \({{D}_{2}}=0\), \({{B}_{1}}=0\), \({{C}_{2}}=-\frac{a\left( 2+n \right) \lambda }{2bc{{n}^{2}}}\), \({{A}_{0}}=5{{A}_{2}}\), \({{C}_{0}}=-\frac{5a\left( 2+n \right) \lambda }{2bc{{n}^{2}}}\), \(\omega =-\frac{a\left( 4+{{n}^{2}} \right) \lambda }{4c{{n}^{2}}}\), \(\kappa =\frac{\sqrt{\lambda }}{2\sqrt{c}}\), \(\alpha =\frac{3a\left( 2+n \right) {{\lambda }^{2}}}{4{{A}_{2}}^{2}bc{{n}^{2}}}\) then

$$\begin{aligned} \varLambda= & {} {{\text {e}}^{\frac{1}{4}\text {i}\left( 4{{\theta }_{0}}-\frac{2\sqrt{\lambda }}{\sqrt{c}}x-\frac{a\left( 4+{{n}^{2}} \right) \lambda }{c{{n}^{2}}}t \right) }}{{\left( {{A}_{2}}{{\sec }^{2}}\left( \frac{\sqrt{c\lambda }x+a\lambda t}{2c} \right) \right) }^{\frac{1}{n}}}, \end{aligned}$$
(72)
$$\begin{aligned} \varTheta= & {} -\frac{a\left( 2+n \right) \lambda }{2bc{{n}^{2}}}{{\sec }^{2}}\left( \frac{\sqrt{c\lambda }x+a\lambda t}{2c} \right) . \end{aligned}$$
(73)

These are dark and bright periodic singular solutions to the nematic liquid crystals, respectively.

Family 3. If we choose \(r=\left\{ -1,0,1,1 \right\} \), \(s=\left\{ 0,0,1,0 \right\} ,\) then Eq. (12) becomes:

$$\begin{aligned} \psi \left( \xi \right) =-\frac{1}{1+e^{\xi }}. \end{aligned}$$
(74)

Inserting Eqs. (62–63) with Eq. (74) into Eqs. 60) and (61), we can investigate the following cases of solutions.

Case 1. When \({{D}_{2}}=0\), \({{B}_{2}}=0\), \({{C}_{1}}=-\frac{2a\left( 2+n \right) {{\kappa }^{2}}}{b{{n}^{2}}},{{D}_{1}}=0\), \({{B}_{1}}=0\), \({{A}_{2}}={{A}_{1}}\), \({{C}_{2}}=-\frac{2a\left( 2+n \right) {{\kappa }^{2}}}{b{{n}^{2}}},{{A}_{0}}=0\), \({{C}_{0}}=0\), \(\omega =a\left( -1+\frac{1}{{{n}^{2}}} \right) {{\kappa }^{2}}\), \(\alpha =-\frac{12a\left( 2+n \right) {{\kappa }^{2}}\lambda }{{{A}_{1}}^{2}b{{n}^{2}}}\), \(c=-\frac{\lambda }{{{\kappa }^{2}}}\), then we get

$$\begin{aligned} \varLambda= & {} {{\text {e}}^{\text {i}\left( {{\theta }_{0}}-\kappa x+a\left( \frac{1}{{{n}^{2}}}-1 \right) {{\kappa }^{2}}t \right) }}{{\left( -\frac{{{A}_{1}}{{\text {e}}^{\kappa \left( x+2at\kappa \right) }}}{{{\left( 1+{{\text {e}}^{\kappa \left( x+2a\kappa t \right) }} \right) }^{2}}} \right) }^{\frac{1}{n}}}, \end{aligned}$$
(75)
$$\begin{aligned} \varTheta= & {} \frac{2a\left( 2+n \right) {{\kappa }^{2}}{{\text {e}}^{\kappa \left( x+2a\kappa t \right) }}}{b{{n}^{2}}{{\left( 1+{{\text {e}}^{\kappa \left( x+2a\kappa t \right) }} \right) }^{2}}}. \end{aligned}$$
(76)

Eqs. (75) and (76) describe the bright optical soliton solutions to the studied system of equations.

Case 2. When \({{B}_{1}}=0\), \({{B}_{2}}=0\), \({{A}_{1}}=\frac{2\sqrt{3}\sqrt{\left( 2+n \right) \lambda \omega }}{\sqrt{b\left( {{n}^{2}}-1 \right) \alpha }}\), \({{C}_{1}}=\frac{2\left( 2+n \right) \omega }{b\left( -1+{{n}^{2}} \right) }\), \({{D}_{1}}=0\), \({{D}_{2}}=0\), \({{A}_{2}}=\frac{2\sqrt{3}\sqrt{\left( 2+n \right) \lambda \omega }}{\sqrt{b\left( {{n}^{2}}-1 \right) \alpha }}\), \({{C}_{2}}=\frac{2\left( 2+n \right) \omega }{b\left( -1+{{n}^{2}} \right) }\), \({{A}_{0}}=0\), \({{C}_{0}}=0\), \(a=-\frac{{{n}^{2}}\omega }{\left( {{n}^{2}}-1 \right) {{\kappa }^{2}}}\), \(c=-\frac{\lambda }{{{\kappa }^{2}}}\) then

$$\begin{aligned} \varLambda= & {} {{2}^{\frac{1}{n}}}{{3}^{\frac{1}{2n}}}{{\text {e}}^{\text {i}\left( {{\theta }_{0}}-\kappa x+\omega t \right) }}{{\left( \frac{\text {-}\sqrt{\left( 2+n \right) \lambda \omega }{{\text {e}}^{\kappa x+\frac{2{{n}^{2}}\omega }{{{n}^{2}}-1}t}}}{\sqrt{b\left( {{n}^{2}}-1 \right) \alpha }{{\left( {{\text {e}}^{\kappa x}}+{{\text {e}}^{\frac{2{{n}^{2}}\omega }{{{n}^{2}}-1}t}} \right) }^{2}}} \right) }^{\frac{1}{n}}}, \nonumber \\\end{aligned}$$
(77)
$$\begin{aligned} \varTheta= & {} -\frac{2\left( 2+n \right) \omega {{\text {e}}^{\kappa x+\frac{2{{n}^{2}}\omega }{{{n}^{2}}-1}t}}}{b\left( {{n}^{2}}-1 \right) {{\left( {{\text {e}}^{x\kappa }}+{{\text {e}}^{\frac{2{{n}^{2}}\omega }{{{n}^{2}}-1}t}} \right) }^{2}}}. \end{aligned}$$
(78)

The above equations are bright and dark optical solutions to the nematic liquid crystals, respectively.

4 Graphical analysis and discussion

In this section, the graphical representation of some new traveling wave solutions has been illustrated. A family of W-shaped, bright, dark, periodic and singular solitons are displayed for a set of values for various parameters. Matlab software is used to carry out simulations and the 3D plot visualizes the behavior of nematic liquid crystals with three nonlinearity terms constructed from Eqs. (1) and (2).

Figure 1 illustrates \(|\varLambda (x,t)|^{2}\) and \(\varTheta (x,t)\) established in Eqs. (22) and (23) for \(a=1\), \(c=2\), \(\lambda =0.2\), \(\alpha =1\), \(b=0.1\), \({{\theta }_{0}}=1\), respectively; Fig. 2 represents the effect of free parameter a and shows that increase the value of a increases the peak of the solutions on \(|\varLambda (x,t)|^{2}\) and \(\varTheta (x,t)\) found in Eqs. (22) and (23), whereas Fig. 3 determines the effect of a parameter b on \(|\varLambda (x,t)|^{2}\), \(\varTheta (x,t)\) and has the opposite effect of parameter a, while Fig. 4 shows the effect of a parameter c found in Eqs. (22) and (23) and shows that the parameter is look like a decreases coefficient on \(|\varLambda (x,t)|^{2}\) and \(\varTheta (x,t)\); likewise Fig. 5 demonstrates the effect of the parameter \(\lambda \) and look like a increases coefficient; Fig. 6 gives the effect of \(\alpha \) and show that increasing its value will decreases the peak of the optical soliton solutions.

Figure 7 demonstrates \(|\varLambda (x,t)|^{2}\) and \(\varTheta (x,t)\) found in Eqs. (24) and (25) for \(a=1\), \(c=0.5\), \(\lambda =0.2\), \(\alpha =1\), \(b=0.1,{{\theta }_{0}}=1\), whereas Fig. 8 illustrates \(|\varLambda (x,t)|^{2}\) and \(\varTheta (x,t)\) established in Eqs. (42) and (43) for \(a=1\), \(c=0.1\), \(\lambda =0.2\), \(\alpha =1\), \(b=0.1\), \({{\theta }_{0}}=1\), \({{a}_{1}}=-0.1\), \({{a}_{2}}=0.1\), \(\kappa =0.2\), \(\omega =1\), and Fig. 9 determines \(|\varLambda (x,t)|^{2}\) and \(\varTheta (x,t)\) observed in Eqs. (70) and (71) for \(a=1\), \(\lambda =0.2\), \(\alpha =1\), \(b=0.1\), \({{\theta }_{0}}=1\), \(n=3,\kappa =1\).

5 Conclusion

In the present paper, the GERFM utilized to derive some novel optical soliton solutions to the nematic liquid crystals includes Kerr law, parabolic, and power law nonlinearities. Three families of solutions for each nonlinearity are shown. W-shaped surfaces, dark soliton, bright soliton, singular soliton, period singular soliton, periodic waves, and complex solutions are successfully obtained via this method. The outcomes illustrate that the proposed technique is highly accurate and gives different solutions compare with those obtained via other methods, as well as we can construct more different types of solutions. All gained solutions are inserted into the system that represents the dynamics of nematicons in liquid crystals and they satisfy it. Graphically, the effects of free parameters on the peak of soliton solution are also presented. Moreover, we use the constraint conditions to verify their existence. The solutions gained in this research paper may help us to better understand the molecules of soliton in liquid crystals.