1 Introduction

The use of Einstein field equations to model compact relativistic stellar objects such as quark stars, neutron stars, gravastars, dark energy stars and black holes is gaining more exposure in contemporary studies. Diverse views on the features of space-time geometry have been revealed. By considering static and spherically symmetric spacetime, various stellar models have been generated. Sunzu et al. [1,2,3] generated anisotropic quark star models with masses compatible with number of previous findings. Likewise exact models by Maharaj et al. [4] are consistent with Finch and Skea relativistic stars. Thirukkanesh and Maharaj [5] found the realistic compact models with anisotropy present. Models by Mafa Takisa and Maharaj [6] describe the anisotropic quark star with core envelope in the presence of the electric field. Abdalla et al. [7] found a quark star model with anisotropy present. All these models have astrophysical significance in describing the physical properties and geometries of relativistic stellar objects.

Modelling anisotropic relativistic stellar spheres has drastically drawn attention of researchers. Consideration of pressure anisotropy in investigating the behaviour and structure of relativistic compact stellar objects is very significant as clearly pointed out in [8, 9]. The study by Bowers and Liang [10] indicates that due to high gravitational pull and density, no celestial body can have perfectly isotropic fluid distribution. One of the earliest works which conceptualize anisotropy in stellar fluid spheres was performed by Ruderman [11] and Canuto and Chitre [12]. These studies indicate that tangential and radial pressures may not be equal. The state of pressure imbalance influence the existence of pressure anisotropy in a stellar object. Pressure anisotropy is also influenced by some factors including ultra high density in the stellar core [11, 12], pion condensations and phase transitions [13,14,15], gradual fluid rotation [16], stellar sphere having type 3A super fluid [17], etc. Other aspects related to anisotropy in self gravitating systems can be accessed in the performance by Herrrera and Santos [9]. The study by Bowers and Liang [10] paved a way of searching exact models for anisotropic stellar spheres. Various anisotropic neutral stellar models with astrophysical significance have been generated. Recently, Thirukkanesh et al. [18] obtained neutral stellar models which describe the stability and improved physical features of compact, relativistic objects with QEoS. Sunzu [19] generated anisotropic neutral star models with isotropic nature at the vanishing point of anisotropic parameters. Dev and Gleiser [20] shows that the mass and gravitational redshift for relativistic stellar objects are affected by the presence of anisotropic pressure. The study shows that there is relationship between pressure anisotropy and stability of the stellar object. Gleiser and Dev [21] observed the impact of pressure anisotropy to the appearance of the stellar object. The results show that anisotropic pressure may increase the surface redshifts which ultimately cause stellar objects to appear closer than their reality, a phenomena caused by anisotropic distortions. The models by Sunzu et al. [1] show that the mass of anisotropic quark star is less than the mass of isotropic quark star. Other stellar models with anisotropy present include models obtained by Jape et al. [22], Mathias et al. [23], Maurya et al. [24, 25] and Jasim et al. [26].

Star models consider several forms of equations describing the state of gravitating objects. Stellar models generated by Jasim et al. [26, 27], Maurya and Tello-Ortiz [28], Maurya et al. [29], Deb et al. [30], Banerjee [31], Sunzu et al. [3], Sunzu and Danford [32] and Lobo [33] used the linear equation of state (EoS). The performance by Singh et al. [34] applied Color-flavor locked EoS in framework of MIT bag model to model quark stars in energy-momentum squared gravity. Thirukkanesh et al. [18], Sharov [35], Feroze and Siddiqui [36], Maharaj and Mafa Takisa [37], Sunzu and Mashiku [38], Ngubelanga et al. [39] and Lobo [40] applied the QEoS. Malaver [41, 42] and Sunzu and Mahali [43] applied Van der Waal equation of state. Thirukkanesh and Ragel [44], Mafa Takisa and Maharaj [45], Singh et al. [46], Shibata [47] and Lai and Xu [48] applied polytropic equation of state. Recently, Bhar et al. [49], Bhar [50, 51], Rahaman et al. [52] and Benaoum [53] applied Chaplygin EoS.

We are delighted to study the physical behaviour and geometries for neutral stars in general relativity in the presence of pressure anisotropy using QEoS and a choice of one of the gravitational potentials. We formulate a model that regains a potential specified in the work by Pant and Fuloria [54]. We also perform several physical analysis that are rarely performed in other models with similar approach. To achieve this objective we give fundamental and field equations in §2. Our model is then presented in §3. Discussion on graphs for gravitational potentials, matter variables, speed of sound, hydrostatic equilibrium, stability and energy conditions is given in §4. We present tables of radii, stellar masses and surface redshifts in the same section. The conclusion is highlighted in §5.

2 Field equations

We generate a new model for the interior of a stellar object. We consider the spacetime geometry which is static and spherically symmetric with the interior line element

$$\begin{aligned} ds^{2}= & {} -e^{2\nu (r)}dt^{2}+e^{2\lambda (r)}dr^{2}\nonumber \\&\quad +r^{2}(d\theta ^{2} +\sin ^{2}\theta d\phi ^{2}), \end{aligned}$$
(1)

where \(\nu (r)\) and \(\lambda (r)\) are gravitational potentials. We consider the Schwarzschild exterior spacetime with the line element given by

$$\begin{aligned} ds^{2}= & {} -\left( 1-\frac{2M}{r}\right) dt^{2}\nonumber \\&\quad + \left( 1-\frac{2M}{r}\right) ^{-1}dr^{2}+r^{2}(d\theta ^{2}+\sin ^{2}\theta d\phi ^{2}), \end{aligned}$$
(2)

where M is the total mass of the stellar object. The energy momentum tensor for uncharged anisotropic stellar sphere is given by

$$\begin{aligned} T_{ij}=\text{ diag }\left( -\rho ,p_{r},p_{t},p_{t}\right) , \end{aligned}$$
(3)

where \(\rho\), \(p_{r}\) and \(p_{t}\) represent the energy density, radial pressure and the tangential pressure, respectively. These quantities are determined relative to a comoving unit timelike fluid four-velocity, \(u^{a}\). In this model the coupling constant \(\frac{8\pi G}{c^{4}}\) and the speed of light c is assumed to be unity (i.e. \(\frac{8\pi G}{c^{4}}\)=1).

The field equations which describe neutral stellar objects are given by

$$\begin{aligned} \dfrac{1}{r^{2}}\left( 1-e^{-2\lambda }\right) +\dfrac{2\lambda ^\prime }{r}e^{-2\lambda }= & {} \rho , \end{aligned}$$
(4a)
$$\begin{aligned} -\dfrac{1}{r^{2}}\left( 1-e^{-2\lambda }\right) +\dfrac{2\nu ^{\prime }}{r}e^{-2\lambda }= & {} p_{r}, \end{aligned}$$
(4b)
$$\begin{aligned} e^{-2\lambda }\left( \nu ^{\prime \prime }+\nu ^{\prime ^{2}}-\nu ^{\prime }\lambda ^{\prime }+\dfrac{\nu ^{\prime }}{r}- \dfrac{\lambda ^{\prime }}{r}\right)= & {} p_{t}, \end{aligned}$$
(4c)

where primes indicate the derivatives of the gravitational potentials with respect to radial distance r. The function defining the stellar mass with uncharged matter is given by

$$\begin{aligned} M(r)=\frac{1}{2}\int _{0}^{r}\omega ^{2}\rho (\omega )d\omega . \end{aligned}$$
(5)

For a physically realistic stellar star the matter distribution should satisfy a barotropic EoS given by \(p_r = p_r (\rho )\). In this paper, we consider the stellar neutron fluid which admits QEoS defined by

$$\begin{aligned} p_{r}=\alpha \rho ^2+\beta \rho -\gamma , \end{aligned}$$
(6)

where \({\alpha }\), \(\beta\) and \(\gamma\) are real constants.

We adopt the Durgapal and Bannerji [55] transformation for easy simplification of the field equations in the system (4). The transformation takes the form

$$\begin{aligned} x=Cr^{2},\;\;Z(x)=e^{-2\lambda (r)},\;\;A^{2}y^{2}(x)=e^{2\nu (r)}, \end{aligned}$$
(7)

where A and C are arbitrary real constants. With this transformation, the field equations becomes

$$\begin{aligned} \dfrac{1-Z}{x}-2\dot{Z}= & {} \dfrac{\rho }{C}, \end{aligned}$$
(8a)
$$\begin{aligned} 4Z\dfrac{\dot{y}}{y}+\dfrac{Z-1}{x}= & {} \dfrac{p_{r}}{C} \end{aligned}$$
(8b)
$$\begin{aligned} 4xZ \dfrac{\ddot{y}}{y}+\left( 4Z+2x\dot{Z}\right) \dfrac{\dot{y}}{y} +\dot{Z}= & {} \dfrac{p_{t}}{C}, \end{aligned}$$
(8c)

where dot represents differentiation with respect to x. The line element becomes

$$\begin{aligned}&ds^{2}=-A^{2}y^{2}dt^{2}+\frac{1}{4xCZ}dx^{2}\nonumber \\&\quad +\frac{x}{C}(d\theta ^{2}+\sin ^{2}\theta d\phi ^{2}). \end{aligned}$$
(9)

The mass function (5) due to this transformation becomes

$$\begin{aligned} M(x)=\frac{1}{4C^\frac{3}{2}}\int _{0}^{x}\sqrt{\omega }\rho (\omega ) d\omega . \end{aligned}$$
(10)

By incorporating the equation of state (6) in the field equations, the system (4) is presented as

$$\begin{aligned} \rho= & {} \left( \dfrac{1-Z}{x}-2\dot{Z}\right) C, \end{aligned}$$
(11a)
$$\begin{aligned} p_{r}= & {} \alpha \rho ^2+\beta \rho -\gamma , \end{aligned}$$
(11b)
$$\begin{aligned} p_{t}= & {} p_{r}+\Delta , \end{aligned}$$
(11c)
$$\begin{aligned} \Delta= & {} 4xCZ\dfrac{\ddot{y}}{y}\nonumber \\&\quad +2C(2Z+x\dot{Z})\dfrac{\dot{y}}{y}-C^2\alpha \left( \dfrac{1-Z}{x}-2\dot{Z}\right) ^2\nonumber \\&\quad -C\beta \left( \dfrac{1-Z}{x}-2\dot{Z}\right) \nonumber \\&\quad +\dot{Z}C+\gamma \end{aligned}$$
(11d)
$$\begin{aligned} \dfrac{\dot{y}}{y}= & {} \dfrac{\alpha C}{4Z}\left( \dfrac{1-Z}{x}\right) ^2+\dfrac{(1-\beta )(1-Z)}{4Zx}+\dfrac{2\beta C \dot{Z}-\gamma }{4CZ} \end{aligned}$$
(11e)

where \(\Delta = p_{t}-p_{r}\) defines the quantity of pressure anisotropy. The force due to anisotropy is given by \(\frac{2\Delta }{r}\). The study by Gokhroo and Mehra [56] indicates that when \(\Delta <0\) then the anisotropic force has attractive nature and when \(\Delta >0\) the anisotropic force is repulsive in nature.

3 The model

In order to track the system (11), we need to specify one of the unknown variables \(\rho , p_{r},p_t,\Delta , Z\) and y. We choose a rational form of gravitational potential Z in the form

$$\begin{aligned} Z=\dfrac{1+k_1x^2}{(1+k_2x)^3}, \end{aligned}$$
(12)

where \(k_1\) and \(k_2\) are real constants with \(k_1 \ne k_2\ne 0\). This choice ensures regularity and continuity throughout the interior of the stellar sphere. When \(k_1=0\) we regain the potential applied by Pant and Fuloria [54] in their charged stellar model. We are motivated to use a generalized form of potential Z to generate a neutral star model. By applying Z specified in eq. (12) in eq. (11e), we obtain the first-order differential equation

$$\begin{aligned} \dfrac{\dot{y}}{y}= & {} \dfrac{(1+k_2x)^3}{4(1+k_1x^2)}\nonumber \\&\quad \left[ -\dfrac{\gamma }{C}+\dfrac{(1+k_2x)^3+k_1x^2-1}{x(1+k_2x)^3}\right. \nonumber \\&\quad - \dfrac{\beta }{(1+k_2x)^4}(k_1x(-5+k_2x)+k_2(9+6k_2x \nonumber \\&\quad +4k_2^2x^2+k_2^3x^3))^2+\dfrac{\alpha C}{(1+k_2x)^8}(k_1x(-5+k_2x)\nonumber \\&\qquad \left. +k_2(9+6k_2x+4k_2^2x^2+k_2^3x^3))^2\right] , \end{aligned}$$
(13)

defining the metric function y.

By integrating (13) we obtain the general solution as

$$\begin{aligned} y=H(1+k_2x)^{\varphi }(1+k_1x^2)^{\psi } \text {exp}[G(x)] \end{aligned}$$
(14)

where H is a constant of integration. We have set

$$\begin{aligned} G(x)= & {} \dfrac{1}{8}\left[ -\dfrac{k_2^3\gamma x^2}{Ck_1}\right. \nonumber \\&\quad -\dfrac{2k_2^2x(3\gamma + Ck_2(-1+\beta ))}{Ck_1}\nonumber \\&\quad +\dfrac{8C\alpha (k_1-k_2^2)}{k_2(1+k_2x)^3}-\dfrac{18C\alpha (k_1+k_2^2)}{k_2(1+k_2x)^4}\nonumber \\&\quad -\dfrac{4C k_2 \alpha (-9k_1^2+14k_1k_2^2+7k_2^4)}{(1+k_2x)(k_1+k_2^2)^2}\nonumber \\&\quad -\dfrac{2\arctan [x\sqrt{k_1}]}{Ck_1\sqrt{k_1}(k_1+k_2^2)^3}(25C^2k_1^5\alpha \nonumber \\&\quad +2Ck_1^3k_2^3 \nonumber \\&(-4+4\beta +9Ck_2\alpha )+k_2^8(-3\gamma +k_2(C-C\beta ))\nonumber \\&\quad -6k_1^2k_2^4(k_2(C-C\beta )) \nonumber \\&\quad +k_1^4(\gamma +3Ck_2(-1+\beta )-24C^2k_2^2\alpha )\nonumber \\&\quad \left. -k_1(8k_2^6\gamma +3C^2k_2^8\alpha ))\right] , \end{aligned}$$
(15)
$$\begin{aligned} \varphi= & {} \dfrac{2}{(k_1+k_2)^3}\left[ k_1^2k_2^2(18\beta -25Ck_2\alpha )\right. \nonumber \\&\quad \left. -9k_1k_2^4(-2\beta +Ck_2\alpha )-3k_2^6(-2\beta +Ck_2\alpha \right. \nonumber \\&\quad \left. +k_1^3(6\beta +45Ck_2\alpha ))\right] , \end{aligned}$$
(16)
$$\begin{aligned} \psi= & {} \dfrac{1}{Ck_1^2(k_1+k_2^2)^3}\left[ k_2^9\gamma +Ck_1k_2^8(3-3\beta +Ck_2\alpha )\right. \nonumber \\&\quad +Ck_1^5(-1+5\beta +45Ck_2\alpha )\nonumber \\&\quad -2k_1^2k_2^5(3\gamma +2Ck_2(-2+\beta ))\nonumber \\&\quad +2k_1^3k_2^3(-4\gamma +3Ck_2(1+\beta )-3k_1^4k_2(\gamma -4Ck_2\beta \nonumber \\&\left. +8C^2k_2^2\alpha ))\right] . \end{aligned}$$
(17)

Then the gravitational potentials and matter variables for this model becomes

$$\begin{aligned} e^{2\lambda }= & {} \dfrac{(1+k_2x)^3}{1+k_1x^2}, \end{aligned}$$
(18a)
$$\begin{aligned} e^{2\nu }= & {} A^2H^2(1+k_2x)^{2\varphi }(1+k_1x^2)^{2\psi } \text {exp}[2G(x)], \end{aligned}$$
(18b)
$$\begin{aligned} \rho= & {} \dfrac{C}{(1+k_2x)^4}(k_1x(-5+k_2x)+k_2(9+6k_2x+4k_2^2x^2+k_2^3x^3)), \nonumber \\ p_r= & {} \alpha \rho ^2+\beta \rho -\gamma , \end{aligned}$$
(18c)
$$\begin{aligned} p_t= & {} p_r+\Delta ,\end{aligned}$$
(18d)
$$\begin{aligned} \Delta= & {} \dfrac{2C}{(1+k_1x^2)(1+k_2x)^5}\nonumber \\&\left[ (2-k_2x+k_1x^2(4+k_2x))(\dot{G}(x)+k_2(\varphi +x\dot{G}(x)) \right. \nonumber \\&\quad +k_1x(2\psi +x\dot{G}(x)+k_2x(\varphi +2\psi +x\dot{G}(x)))\nonumber \\&+2x((-1+\varphi )(1+k_1x^2)k_2(\dot{G}(x)\nonumber \\&\quad +k_2(\varphi +x\dot{G}(x))+k_1x(2\psi +\dot{G}(x)\nonumber \\&\quad +k_2x(\varphi +2\psi +x\dot{G}(x))))+2x(-1+\psi )k_1 \nonumber \\&(1+k_2x(\dot{G}(x)+k_2(\varphi + x\dot{G}(x))\nonumber \\&\quad + k_1x(2\psi +x\dot{G}(x)+k_2x(\varphi +2\psi +x\dot{G}(x))))\nonumber \\&\quad +(1+k_1x^2)(1+k_2x)\dot{G}(x)(\dot{G}(x)+k_2(\varphi +x \dot{G}(x))\nonumber \\&\quad +k_2x (2\psi + x\dot{G}(x) + k_2x \nonumber \\&(\varphi + 2 \psi + x\dot{G}(x))))+(1+k_1x^2)(1+k_2x)((\ddot{G}(x)\nonumber \\&\quad +k_2(\dot{G}(x)+x\ddot{G}(x))+k_1\nonumber \\&\left. (2\psi +2 x\ddot{G}(x)+x^2(\ddot{G}(x)\right. \nonumber \\&\quad \left. +k_2x(2\varphi +4\psi +3x\dot{G}(x)+x^2\ddot{G}(x)))+F(x)\right] , \end{aligned}$$
(18e)

where,

$$\begin{aligned} F(x)= & {} \dfrac{C\beta }{(1+k_2x)^4} (k_1x(-5+k_2x)+k_2(9+6k_2x+4k_2^2x^2+k_2^3x^3)) \nonumber \\&\quad -\dfrac{C^2\alpha }{(1+k_2x)^8}(k_1x(-5+k_2x)\nonumber \\&\quad + k_2(9+6k_2x+4k_2^2x^2 + k_2^3x^3))^2\nonumber \\&\quad +\dfrac{C(-3k_2+k_1x(2-k_2x))}{(1+k_2x)^4}+ \gamma . \end{aligned}$$
(19)

We note that the exact solution in (18) is presented in terms of elementary functions.

The mass function in eq. (10) becomes

$$\begin{aligned} M(x)= & {} \dfrac{x\sqrt{x}}{6\sqrt{C}(1+k_2x)^4}\nonumber \\&\quad \left[ k_1x(-5+k_2x)+k_2(3 +k_2x)(3+k_2x(1+k_2x))\right] , \end{aligned}$$
(20)

and the line element in eq. (1) becomes

$$\begin{aligned} ds^{2}= & {} -A^2H^2(1+k_2x)^{2\varphi }(1+k_1x^2)^{2\psi } \text {exp}[2G(x)]dt^{2}\nonumber \\&\quad + \dfrac{(1+k_2x)^3}{1+k_1x^2}dr^{2}\nonumber \\&\quad +r^{2}(d\theta ^{2}+\sin ^{2}\theta d\phi ^{2}). \end{aligned}$$
(21)

3.1 Compactness and redshift

The compactness factor \(\mu\) is defined by

$$\begin{aligned} \mu =\frac{M}{R}, \end{aligned}$$
(22)

where M is the total stellar mass and R is the stellar radius at the boundary. By substituting eqn. (20) into (22) we obtain

$$\begin{aligned} \mu (x)= & {} \dfrac{x}{6(1+k_2x)^4}\left[ k_1x(-5+k_2x)+k_2(3 +k_2x)(3+k_2x(1+k_2x))\right] . \end{aligned}$$
(23)

We define the surface redshift \(z_s\) of a stellar sphere by

$$\begin{aligned} z_s=\frac{1}{\sqrt{1-\mu }}-1, \end{aligned}$$
(24)

where \(\mu\) is the compactness factor. By considering the compactness factor \(\mu (x)\) in (23) then eqn. (24) becomes

$$\begin{aligned} z_s(x)= & {} -1+\sqrt{6}(1+k_2 x)^2\left[ 6(1+15k_2 x)+30k_2^2x^2+20k_2^3x^3+5k_2^4x^4\right. \nonumber \\&\quad \left. +k_1x^2(5-k_2x)\right] ^{-\frac{1}{2}} \end{aligned}$$
(25)

3.2 Hydrostatic equilibrium

The state of hydrostatic equilibrium in this model is explored by analysing the Tolman-Oppenheimer-Volkoff (TOV) equation defined by

$$\begin{aligned} p_r' +(\rho +p_r)\nu '-\frac{2\Delta }{r}=0. \end{aligned}$$
(26)

For a neutral stellar object with anisotropic pressure, three forces describing the state of hydrostatic equilibrium include gravitational force \(F_g\), hydrostatic force \(F_h\) and anisotropic force \(F_a\). These forces describe the energy conservation in the stellar object. The forces are defined by

$$\begin{aligned} F_g= & {} -(\rho +p_r)\nu ', \end{aligned}$$
(27a)
$$\begin{aligned} F_h= & {} -p_r', \end{aligned}$$
(27b)
$$\begin{aligned} F_a= & {} \dfrac{2\Delta }{r}. \end{aligned}$$
(27c)

Then since the stellar object is in hydrostatic equilibrium, eq. (26) can be written as

$$\begin{aligned} F_g+F_h+F_a=0. \end{aligned}$$
(28)

The expressions for the forces in (27) are given by

$$\begin{aligned} F_g= & {} \dfrac{\sqrt{x}}{2\sqrt{C}(1+k_1x^2)(1+k_2x)^{13}}\nonumber \\&\quad \left[ -\gamma +(9C(1 + \beta ) - 8 x \gamma )k_2+(81 C^2 \alpha + 42 C x (1 + \beta ) \right. \nonumber \\&\quad - 28 x^2 \gamma ) k_2^2+2 x (54 C^2 \alpha \nonumber \\&\quad + 41 C x (1 + \beta ) - 28 x^2 \gamma ) k_2^3+x^2 (108 C^2 \alpha \nonumber \\&\quad + 89 C x (1 + \beta ) \nonumber \\&\quad - 70 x^2 \gamma ) k_2^4+x^3 (66 C^2 \alpha + 61 C x (1 + \beta ) \nonumber \\&\quad - 56 x^2 \gamma ) k_2^5+28 x^4 (C^2 \alpha + C x (1 + \beta )\nonumber \\&\quad - x^2 \gamma ) k_2^6 +8 x^5 (C^2 \alpha + C x (1 + \beta ) \nonumber \\&\quad - x^2 \gamma ) k_2^7+x^6 (C^2 \alpha + C x (1 + \beta ) - x^2 \gamma ) k_2^8\nonumber \\&\quad +C^2 x^2 \alpha k_1^2 (-5 + x k_2)^2 \nonumber \\&\quad + C x k_1(-5 + x k_2)(1 + \beta + 2 (9 C \alpha + 2 x (1 + \beta )) k_2 \nonumber \\&\quad +6 x (x +2 C \alpha + x \beta ) k_2^2 \nonumber \\&\quad + 4 x^2 (x + 2 C \alpha + x \beta ) k_2^3+ x^3 (x + 2 C \alpha + x \beta ) k_2^4 )) (\dot{G}(x)\nonumber \\&\quad + k_2 (\varphi + x \dot{G}(x))+ x k_1 (2 \psi + x \dot{G}(x) \nonumber \\&\quad \left. + x k_2 (\varphi + 2 \psi + x \dot{G}(x)))\right] \end{aligned}$$
(29)
$$\begin{aligned} F_h= & {} - \dfrac{C}{(1 + x k_2)^9}\left[ (\beta + 2 (9 C \alpha + 2 x \beta ) k_2\right. \nonumber \\&\quad + 6 x (2 C \alpha + x \beta ) k_2^2+ 4 x^2 (2 C \alpha + x \beta ) k_2^3 \nonumber \\&\quad + x^3 (2 C \alpha + x \beta )k_2^4 + 2 C x \alpha k_1 (-5 + x k_2)) (k_1 (5 - 17 x k_2+ 2 x^2 k_2^2) +k_2^2(30 \nonumber \\&\left. + 10 xk_2+ 5x^2k_2^2 + x^3k_2^3)\right] , \end{aligned}$$
(30)

and

$$\begin{aligned} F_a= & {} \dfrac{4C\sqrt{C}}{\sqrt{x}(1+k_1x^2)(1+k_2x)^5}\nonumber \\&\left[ (2-k_2x+k_1x^2(4 +k_2x))(\dot{G}(x)+k_2(\varphi +x\dot{G}(x)) \right. \nonumber \\&\quad +k_1x(2\psi +x\dot{G}(x)+k_2x(\varphi +2\psi +x\dot{G}(x)))\nonumber \\&\quad +2x((-1+\varphi )(1+k_1x^2)k_2(\dot{G}(x)\nonumber \\&\quad +k_2(\varphi +x\dot{G}(x))+k_1x(2\psi +\dot{G}(x)\nonumber \\&\quad +k_2x(\varphi +2\psi +x\dot{G}(x))))+2x(-1+\psi )k_1\nonumber \\&\quad (1+k_2x(\dot{G}(x)+k_2(\varphi + x\dot{G}(x))+ k_1x(2\psi +x\dot{G}(x)\nonumber \\&\quad +k_2x(\varphi +2\psi +x\dot{G}(x))))\nonumber \\&\quad +(1+k_1x^2)(1+k_2x)\dot{G}(x)(\dot{G}(x)\nonumber \\&\quad +k_2(\varphi +x \dot{G}(x)) +k_2x (2\psi + x\dot{G}(x) + k_2x \nonumber \\&(\varphi + 2 \psi + x\dot{G}(x))))\nonumber \\&\quad +(1+k_1x^2)(1+k_2x)((\ddot{G}(x)+k_2(\dot{G}(x) +x\ddot{G}(x))+k_1\nonumber \\&\left. (2\psi +2 x\ddot{G}(x)+x^2(\ddot{G}(x)+k_2x (2\varphi +4\psi +3x\dot{G}(x)+x^2\ddot{G}(x)))+F(x)\right] . \end{aligned}$$
(31)

3.3 Stability conditions

The stability of stellar models is verified under different stability conditions. According to Zeldovich [57] a stellar model is stable if it satisfies the inequality \(\dfrac{p_r}{\rho }<1\). In this model

$$\begin{aligned} \frac{p_r}{\rho }= & {} \left( C (1 + x k_2)^4 (x k_1 (-5 + x k_2) \right. \nonumber \\&\quad \left. + k_2 (9 + 6 x k_2 + 4 x^2 k_2^2 + x^3 k_2^3))\right) ^{-1}(-\gamma + (9 C \beta \nonumber \\&\quad - 8 x \gamma ) k_2 + (81 C^2 \alpha + 42 C x \beta \nonumber \\&\quad - 28 x^2 \gamma ) k_2^2 + 2 x (54 C^2 \alpha + 41 C x \beta - 28 x^2 \gamma ) k_2^3 \nonumber \\&\quad + x^2 (108 C^2 \alpha \nonumber \\&\quad + 89 C x \beta - 70 x^2 \gamma ) k_2^4 + x^3 (66 C^2 \alpha + 61 C x \beta \nonumber \\&\quad - 56 x^2 \gamma )k_2^5 + 28 x^4 (C^2 \alpha + C x \beta - x^2 \gamma ) k_2^6 \nonumber \\&\quad + 8 x^5 (C^2 \alpha + C x \beta - x^2 \gamma )k_2^7+ x^6 (C^2 \alpha \nonumber \\&\quad + C x \beta - x^2 \gamma ) k_2^8+ C^2 x^2 \alpha k_1^2 (-5 + x k_2)^2 + C x k_1 \nonumber \\&(-5 + x k_2) (\beta + 2 (9 C \alpha + 2 x \beta ) k_2\nonumber \\&\quad + 6 x (2 C \alpha + x \beta ) k_2^2 + 4 x^2 (2 C \alpha + x \beta ) k_2^3 \nonumber \\&\quad + x^3 (2 C \alpha + x \beta ) k_2^4)). \end{aligned}$$
(32)

The radial adiabatic index is significant in investigating the stability of stellar configurations. The works performed by Heintzmann and Hillebrandt [58] and Bondi [59] indicate that the collapsing condition for non-relativistic sphere with isotropic matter distribution is given by \(\Gamma < \frac{4}{3}\). On the other hand, Chan et al. [60, 61] indicated that the collapsing condition for relativistic spheres is given by

$$\Gamma <\frac{4}{3}+\left[ \dfrac{1}{3}\kappa \dfrac{\rho _0 p_{r0}}{\vert p_{r0}' \vert }+\dfrac{4}{3}\dfrac{p_{t0}-p_{r0}}{\vert p_{r0}' \vert r}\right] _{\text {max}},$$

where \(\dfrac{1}{3}\kappa \dfrac{\rho _0 p_{r0}}{\vert p_{r0}' \vert }\) is the relativistic correction and \(\dfrac{4}{3}\dfrac{p_{t0}-p_{r0}}{\vert p_{r0}' \vert r}\) is the anisotropic correction. Chandrasekhar [62, 63] assert that the relativistic correction may cause instability within the compact stellar sphere. Moustakidis [64] discussed another strict condition that the critical value \(\Gamma _c\) for radial adiabatic index is given by

$$\begin{aligned} \Gamma _c=\dfrac{4}{3}+\dfrac{19}{21}\mu . \end{aligned}$$
(33)

According to Chandrasekhar [62, 63], adiabatic index \(\Gamma\) of a stable stellar model satisfies the inequality \(\Gamma >\frac{4}{3}\). However, by considering the critical value \(\Gamma _c\), the stability condition is modified to \(\Gamma \ge \Gamma _c\) where \(\Gamma\) is defined by

$$\begin{aligned} \Gamma =\left( \frac{\rho +p_r}{p_r}\right) \frac{dp_r}{d\rho }. \end{aligned}$$
(34)

The expression for \(\Gamma\) in this model is then given by

$$\begin{aligned} \Gamma= & {} \left( (1 + x k_2)^4 (-\gamma + \frac{C \beta }{(1 + x k_2)^4} ( (x k_1 (-5 + x k_2) + k_2 (9 + 6 x k_2+ 4 x^2 k_2^2 \right. \nonumber \\&+ x^3 k_2^3))) + \frac{C^2 \alpha }{(1 + x k_2)^8)}( x k_1 (-5 + x k_2) \nonumber \\&\quad \left. + k_2 (9 + 6 x k_2 + 4 x^2 k_2^2 + x^3 k_2^3))^2)\right) ^{-1} \nonumber \\&(\beta + 2 (9 C \alpha + 2 x \beta ) k_2 + 6 x (2 C \alpha + x \beta ) k_2^2\nonumber \\&\quad + 4 x^2 (2 C \alpha + x \beta )k_2^3 + x^3 (2 C \alpha \nonumber \\&\quad + x \beta )k_2^4+ 2 C x \alpha k_1 (-5 + x k_2)) \nonumber \\&\quad (-\gamma + \frac{C}{(1 + x k_2)^4} (x k_1 (-5 + x k_2) + k_2 (9 + 6 x k_2 \nonumber \\&\quad + 4 x^2 k_2^2 + x^3 k_2^3))\left( \frac{C\beta }{(1 + x k_2)^4}(x k_1 (-5 + x k_2)\right. \nonumber \\&\quad +\left. k_2 (9 + 6 x k_2 + 4 x^2 k_2^2 + x^3 k_2^3))\right) \nonumber \\&\quad +\frac{C^2\alpha }{(1 + x k_2)^8}\nonumber \\&\left( x k_1 (-5 + x k_2) + k_2 (9+ 6 x k_2+ 4 x^2 k_2^2 + x^3 k_2^3)\right) ^2. \end{aligned}$$
(35)

This model indicates that the speed of sound \(v_r^2\) within the stellar sphere is less than the speed of light. This implies that \(0\le v_r^2 \le 1\) where \(v_r^2=\frac{dp_r}{d\rho }\). This behaviour is physically realistic for stable stellar models. In this model

$$\begin{aligned} v_r^2= & {} \frac{1}{(1 + x k_2)^4} (\beta + 2 (9 C \alpha + 2 x \beta ) k_2 \nonumber \\&\quad + 6 x (2 C \alpha + x \beta ) k_2^2 + 4 x^2 (2 C \alpha + x \beta ) k_2^3 \nonumber \\&\quad + x^3 (2 C \alpha + x \beta ) k_2^4 + 2 C x \alpha k_1 (-5 + x k_2)). \end{aligned}$$
(36)

3.4 Energy conditions

This model satisfies the null, dominant and trace energy conditions given as \(\rho \ge 0\), for null energy condition (NEC), \(\rho -p_r\ge 0\) and \(\rho -p_t\ge 0\) for dominant energy condition (\(\text {DEC}_r\) and \(\text {DEC}_t\)) and \(\rho -p_r-2p_t\ge 0\) for trace energy condition (TEC) respectively.

3.5 Matching conditions

It is significant to match the interior solution to exterior Schwarzchild solution at the boundary of the stellar sphere. The conditions for continuity of metric coefficients from the line elements (1) and (2) across the junction (\(r=R\)) are given by

$$\begin{aligned} e^{2\nu (R)}= & {} 1-\dfrac{2M}{R} \end{aligned}$$
(37a)
$$\begin{aligned} e^{2\lambda (R)}= & {} \left( 1-\dfrac{2M}{R}\right) ^{-1} \end{aligned}$$
(37b)

respectively. Likewise, the radial pressure at the boundary of the stellar sphere should vanish which implies \(p_{r(r=R)}=0\). Applying the expressions for metric potentials (18a) and (18b), the mass function in eq. (20) and the transformation in eq. (7), the system (37) and the radial pressure becomes

$$\begin{aligned} 0= & {} 1-(3(1+CR^2k_2)^4)^{-1}\nonumber \\&\quad (CR^2(CR^2k_1(-5+CR^2k_2)+k_2(9+6CR^2k_2 \nonumber \\&+4C^2R^4k_2^2+C^3R^6k_2^3)))\nonumber \\&\quad -A^2H^2(1+C^2R^4k_1)^{2\psi }(1+CR^2k_2)^{2\varphi }\nonumber \\&\text {exp}[2G(R)],\end{aligned}$$
(38a)
$$\begin{aligned} 0= & {} [3(1+CR^2k_2)^4(3(1+CR^2k_2)^4\nonumber \\&\quad -CR^2(CR^2k_1(-5+CR^2k_2), \nonumber \\&+k_2(9+6CR^2k_2+4C^2R^4k_2^2+C^3R^6k_2^3)))^{-1}]-[(1+C^2R^4k_1)^{-1}\nonumber \\&(1+3CR^2k_2+3C^2R^4k_2^2+C^3 R^6k_2^3),\end{aligned}$$
(38b)
$$\begin{aligned} 0= & {} \dfrac{2C^2R^2}{(1+CR^2k_2)^9}(\beta + 2C(9\alpha +2R^2 \beta )k_2\nonumber \\&\quad +6C^2R^2(2\alpha + R^2\beta )k_2^4\alpha k_1\nonumber \\&(-5+CR^2k_2)) + 2C^2R^2(k_1(5-17CR^2k_2+2C^2R^4k_2^2)\nonumber \\&\quad +k_2^2(30+10CR^2k_2+5C^2R^4k_2+C^3R^6k_2^3)), \end{aligned}$$
(38c)

respectively where

$$\begin{aligned} G(R)= & {} \dfrac{1}{8}\left[ -\dfrac{k_2^3\gamma CR^4}{k_1}\right. \\&\quad -\dfrac{2k_2^2R^2(3\gamma + Ck_2(-1+\beta ))}{k_1}\\&\quad +\dfrac{8C\alpha (k_1-k_2^2)}{k_2(1+k_2CR^2)^3}\\&\quad -\dfrac{18C\alpha (k_1+k_2^2)}{k_2(1+k_2CR^2)^4}\\&\quad -\dfrac{4C k_2 \alpha (-9k_1^2+14k_1k_2^2+7k_2^4)}{(1+k_2CR^2)(k_1+k_2^2)^2}\\&\quad -\dfrac{2\arctan [CR^2\sqrt{k_1}]}{Ck_1\sqrt{k_1}(k_1+k_2^2)^3}\\&(25C^2k_1^5\alpha +2Ck_1^3k_2^3 \\&(-4+4\beta +9Ck_2\alpha )+k_2^8(-3\gamma +k_2(C-C\beta ))\\&\quad -6k_1^2k_2^4(k_2(C-C\beta )) \\&\quad +k_1^4(\gamma +3Ck_2(-1+\beta )-24C^2k_2^2\alpha )\\&\quad \left. -k_1(8k_2^6\gamma +3C^2k_2^8\alpha ))\right] . \end{aligned}$$

The system (38) indicates the matching condition for the exact solutions obtained in system (18). The parameters involved are C, R, \(k_1\), \(k_2\), A, H, \(\alpha\), \(\beta\) and \(\gamma\). We note in system (38), that there are sufficient free parameters which satisfy the matching conditions.

4 Results and discussion

Fig. 1
figure 1

The potential \(e^\nu\) against the radial distance r

Full size image
Fig. 2
figure 2

The potential \(e^\lambda\) against the radial distance r

Full size image
Fig. 3
figure 3

Energy density \(\rho\) against the radial distance r

Full size image
Fig. 4
figure 4

Radial pressure \(p_{r}\) against radial distance r

Full size image
Fig. 5
figure 5

Tangential pressure \(p_{t}\) against radial distance r

Full size image
Fig. 6
figure 6

Measure of anisotropy \(\Delta\) against radial distance r

Full size image
Fig. 7
figure 7

Mass M against radial distance r

Full size image
Fig. 8
figure 8

Speed of Sound \(v_r^2\) against radial distance r

Full size image
Fig. 9
figure 9

Compactness \(\mu\) against radial distance r

Full size image
Fig. 10
figure 10

Redshift \(z_s\) against radial distance r

Full size image
Fig. 11
figure 11

Variation of forces in TOV-equation against radial distance r

Full size image
Fig. 12
figure 12

Equation of state \(\frac{p_r}{\rho }\) against radial distance r

Full size image
Fig. 13
figure 13

Adiabatic index \(\Gamma\) against radial distance r

Full size image
Fig. 14
figure 14

Energy conditions against radial distance r

Full size image

In this section we show that the exact model obtained in §3 is well behaved within the interior of the stellar sphere. Mathematical computations have been achieved by using Mathematica software while the graphical plots have been generated using Python programming language. All the graphs are plotted against the radial distance r. We generated graphs by specifying values for the constants as \(\alpha =14.1\), \(\beta =1.0\times 10^{-6}\), \(\gamma =1.9\times 10^{-3}\), \(C=1.25 \times 10^{-3}\) \(k_1=1.0\), \(k_2=2.5\) and \(H=1.0\).

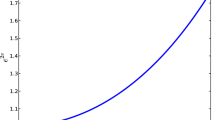
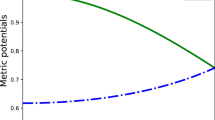
Figs 1 and 2 indicate that the gravitational potentials are regular, continuous and finite throughout the stellar interior. We also note that these profiles are monotonically increasing with positive values at the centre. This feature is physical for well behaved stellar models. Similar profiles can be observed in studies conducted by Maurya et al. [65,66,67,68], Sunzu and Mashiku [38], Jasim et al. [69] and Kileba Matondo et al. [70].

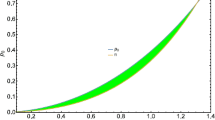
We observe in Figs 3, 4 and 5 that \(\rho\), \(p_r\) and \(p_t\) are monotonically decreasing functions such that \(\rho '<0\), \(p_r'<0\) and \(p_t'<0\). Similar profiles are evident in recent works by Mafa Takisa et al. [71], Das et al. [72], Komathiraj et al. [73], Maurya and Nag [74] and Maurya et al. [75]. The profile for the pressure anisotropy in Fig. 6 shows this ingredient vanishes at the centre of the star then decreases at some interval within the core and then increases as it approaches the surface. It is physically realistic \(\Delta =0\) at the centre of the star. Similar feature is found in recent performance by Thirukkanesh et al. [76]. We find that in Fig. 7 the stellar mass M increases with radial distance. This model also satisfies the causality condition for stability. Fig. 8 indicates that the speed of sound inside the stellar fluid \(v_r^2\le 0.3172\). It implies that \(0 \le v_r^2 \le 1\). This result indicates that the speed of sound inside the stellar sphere is less than the speed of light. In Fig. 9 we observe that the maximum value of compactness \(\mu =0.1538\) which is less than \(\frac{8}{9}\) a maximum value proposed by Buchdahl [77] for neutral compact stars. Fig. 10 shows that the surface redshift \(z_s\le 0.08711\). This value is less than 2 which was determined by Mafa Takisa et al. [78] to be the maximum value for realistic compact stars. In Fig. 11 we observe that the condition for hydrostatic equilibrium is satisfied. All the forces involved sum to zero. This implies that the energy within the stellar sphere is conserved.

This model satisfies different stability conditions. Fig. 12 shows that \(\frac{P_r}{\rho }<1\). This implies that the model is stable as proposed by Zeldovich [57]. The adiabatic stability condition imposed by Moustakidis [64] is also satisfied. Fig. 13 shows that adiabatic index \(\Gamma \ge 3.20378\) and \(0 < \Gamma _c \le 1.4725\). This implies that \(\Gamma >\Gamma _c\) which is the condition for stability of the stellar models. Our model satisfies different energy conditions which include null (\(\rho \ge 0\)), dominant (\(\rho -p_r\ge 0\) and \(\rho -p_t\ge 0\)) and trace (\(\rho -p_r-2p_t\ge 0\)) energy conditions as shown in Fig. 14.

Table 1 Stellar masses consistent with observations
Full size table
Table 2 New stellar masses and surface redshift
Full size table

We have obtained stellar masses and radii compatible with the compact stars PSR J1614-2230 with \(r=9.69\) km and \(M=1.97M_\odot\) and Cen X-3 with \(r=9.178\) km and \(M=1.49M_\odot\), Vela X-1 with \(r=9.56\) km and \(M=1.77M_\odot\) and Exo 1785-248 with \(r=8.849\) km and \(M=1.3M_\odot\) as obtained in Demorest et al. [79], Rawls et al. [80] and Özel et al. [81] respectively. We also generate new stellar masses in the range \((1.298-1.97)M_\odot\) and surface redshifts in the range \(0.0849-0.1607\) which are acceptable ranges for stellar objects. The values used to generate these stellar masses, radii and surface redshifts are presented in Tables 1 and 2.

5 Conclusions

In this paper, we have found an exact model for uncharged stellar object by using QEoS. The model has been obtained by specifying one of the gravitational potentials which generalizes the choice by Pant and Fuloria [54]. The state of hydrostatic equilibrium in our model has been examined by analysing TOV equation. We observe that at some interval from the centre of the stellar star the radial pressure overrides the tangential pressure \((p_r>p_t)\) yielding negative pressure anisotropy. This exhibit attractive anisotropic force within this interval. However, closer to the stellar surface the stellar interior experiences positive pressure anisotropy \((p_t>p_r)\) implying existence of repulsive nature of anisotropic force. Nevertheless, the quantities of hydrostatic and gravitational forces within the stellar sphere are balanced with anisotropic force for hydrostatic equilibrium. The graphs for gravitational potentials, matter variables, compactness, redshifts, hydrostatic equilibrium, stability and energy conditions are well behaved. We have generated stellar masses and radii compatible with the findings in the past including observations by Demorest et al. [79], Rawls et al. [80] and Özel et al. [81]. Our model described stars like PSR J1614-2230, Cen X-3, Vela X-1 and Exo 1785-248. New stellar masses, radii and surface redshifts generated in our model are in acceptable range for realistic stars.