1 Introduction

The structure and properties of relativistic stellar objects can be described by utilizing the nonlinear Einstein–Maxwell field equations. Using these field equations, we can establish the behaviour of relativistic stellar matter in several static spacetime geometries. Relevant stellar objects include compact stars, dark energy stars, quasars, white dwarfs, neutron stars and hybrid strange quark stars. Stellar models with astrophysical significance are generated when using the Einstein–Maxwell field equations. Physical effects include the variation of stellar masses with radii, the study of surface redshifts and many others. Recent exact models with astrophysical significance generated using the Einstein–Maxwell field equations with astrophysical significance are indicated in the works by Dev and Gleiser (2003), Kalam et al. (2013), Rahaman et al. (2012), Sunzu and Danford (2017), Sunzu and Mahali (2018), Sunzu et al. (2014a, b), Matondo et al. (2016) and Mafa Takisa et al. (2016).

It is interesting, on physical grounds, to establish the effect of anisotropy on the properties of gravitating stellar matter. This study can be observed by considering charged or uncharged relativistic spheres. It was indicated by Dev and Gleiser (2002) that pressure anisotropy does affect the stellar mass and redshift. On the other hand, Gleiser and Dev (2004) and Dev and Gleiser (2002) verified that the presence of pressure anisotropy affects the stability of gravitating stellar objects. In the study performed by Sunzu et al. (2014a) it was shown that the anisotropic quark star is less heavy than the isotropic quark star. Anisotropic models in the absence of the electric field include the works performed in Chaisi and Maharaj (2005, 2006a, b), Maharaj and Chaisi (2006a, b), Karmakar et al. (2007), Mak and Harko (2003a, b).

There are some models generated for stellar objects with both electric field and pressure anisotropy present. These include the exact solutions found by Maurya and Gupta (2012), the result by Rahaman et al. (2012), non-singular models generated by Mafa Takisa et al. (2013), isothermal generalized relativistic models in the paper by Maharaj and Thirukkanesh (2009), exact models found by Thirukkanesh and Maharaj (2008), and compact models developed by Esculpi and Aloma (2010). Other recent charged anisotropic models are given by Sunzu and Mahali (2018), Sunzu et al. (2014a, b) and Malaver (2018).

In usual electrostatics for a uniformly charged sphere the electric field increases linearly to the surface. In general relativity the nonlinear effects of the gravitational field allow for more general behaviour. It has been shown that anisotropic stellar objects may have an electric field that decreases with radial distance. Stellar anisotropic models with the electric field intensity that decreases from the centre to the surface include the works of Feroze and Siddiqui (2011), Malaver (2013a) and Sunzu et al. (2014b). It is interesting to observe that there are anisotropic models which indicate that the electric field may initially increase near the centre of the stellar object but then decrease away the centre. This is evident in models generated by Malaver (2013b), Maharaj et al. (2014, 2017), and Sunzu and Mahali (2018).

It is physically reasonable and interesting to have anisotropic models with vanishing pressure anisotropy. Models with this special property can allow us to regain isotropic models as a special case. Most of the models previously generated have nonvanishing pressure anisotropy. This is obvious in models generated by Esculpi and Aloma (2010), Dev and Gleiser (2002), Mak and Harko (2003a) and Paul et al. (2011). Charged exact models generated by Maharaj et al. (2014) assumed a choice of vanishing pressure anisotropy which is a general polynomial function of three degree. On the other hand Sunzu and Mahali (2018) found charged models with a particular anisotropy which is a polynomial of four degree. It is important to generate exact charged models with a new form of pressure anisotropy that is a generalization of anisotropies formulated in the past. This may yield new physical features not contained in earlier investigations.

The objective of this paper is to generate charged relativistic exact models with new choice of measure of anisotropy which generalizes anisotropic models previously found by other researchers. We consider a linear equation of state so that our results are consistent with quark strange stars.

2 Field equations

We model the structure of relativistic quark matter in general relativity. The spacetime geometry is considered to be static and spherically symmetric with the interior line element defined by

$$\begin{aligned} ds^{2}=-e^{2\nu (r)}dt^{2}+e^{2\lambda (r)}dr^{2}+r^{2}(d\theta ^{2}+\sin ^{2}\theta d\phi ^{2}), \end{aligned}$$
(1)

where \(\nu (r)\) and \(\lambda (r)\) are arbitrary gravitational metric functions. We consider the Reissner-Nordstrom line element for the exterior spacetime given by

$$\begin{aligned} ds^{2}= & {} -\left( 1-\frac{2M}{r}+\frac{Q^{2}}{r^{2}}\right) dt^{2} \nonumber \\&+ \left( 1-\frac{2M}{r}+\frac{Q^{2}}{r^{2}}\right) ^{-1}dr^{2}\nonumber \\&+r^{2}(d\theta ^{2}+\sin ^{2}\theta d\phi ^{2}), \end{aligned}$$
(2)

where M and Q is the total mass and charge respectively. These quantities are measured by an observer at infinity. The energy momentum tensor is given by

$$\begin{aligned} T^{i}_{j}= & {} \text{ diag }\left( -\rho -\frac{1}{2}E^{2}, p_{r}-\frac{1}{2}E^{2},\right. \nonumber \\&\left. p_{t}+\frac{1}{2}E^{2}, p_{t}+\frac{1}{2}E^{2}\right) . \end{aligned}$$
(3)

Equation (3) describes gravitating anisotropic matter when an electric field is present. Here the energy density \(\rho \), the radial pressure \(p_{r}\), the tangential pressure \(p_{t}\), and the electric field intensity E are determined relative to a vector u. The vector \(u^{a}\) is comoving, unit and timelike.

The Einstein–Maxwell equations for a charged anisotropic fluid sphere in general relativity is given as

$$\begin{aligned}&\dfrac{1}{r^{2}}\left( 1-e^{-2\lambda }\right) +\dfrac{2\lambda ^\prime }{r}e^{-2\lambda }=\rho + \frac{1}{2}E^{2}, \end{aligned}$$
(4a)
$$\begin{aligned}&-\dfrac{1}{r^{2}}\left( 1-e^{-2\lambda }\right) +\dfrac{2\nu ^{\prime }}{r}e^{-2\lambda }=p_{r} - \frac{1}{2}E^{2}, \end{aligned}$$
(4b)
$$\begin{aligned}&\frac{1}{e^{2\lambda }} \left( \nu ^{\prime \prime }+\nu ^{\prime ^{2}}-\nu ^{\prime }\lambda ^{\prime } +\dfrac{\nu ^{\prime }}{r}-\dfrac{\lambda ^{\prime }}{r}\right) = p_{t}+ \frac{1}{2}E^{2}, \end{aligned}$$
(4c)
$$\begin{aligned}&r^{2}e^{\lambda } \sigma = \left( r^{2}E\right) ^{\prime }, \end{aligned}$$
(4d)

where primes defines derivatives with respect to the radial distance r. The quantity \(\sigma \) stands for the proper charge density. We are considering the units where the coupling constant \(\frac{8\pi G}{c^{4}}=1\) and the speed of light c is unity. The mass for a charged stellar object is given as is defined by

$$\begin{aligned} m(r)=\frac{1}{2}\int _{0}^{r}\omega ^{2}\left( \rho _{*}+E^{2} \right) d\omega , \end{aligned}$$
(5)

where \(\rho _{*}\) is the energy density when the electric field \(E=0\). The equation of state consistent with a quark matter is given by

$$\begin{aligned} p_{r}=\frac{1}{3}\left( \rho -4B\right) , \end{aligned}$$
(6)

where B is the bag constant. We transform the field equations using the Durgapal and Bannerji (1983) transformation which is given by

$$\begin{aligned} x=Cr^{2},\;\;Z(x)=e^{-2\lambda (r)},\;\;A^{2}y^{2}(x)=e^{2\nu (r)}, \end{aligned}$$
(7)

where A and C are arbitrary constants. With this transformation the line element in (1) becomes

$$\begin{aligned} ds^{2}=-A^{2}y^{2}dt^{2}+\frac{1}{4xCZ}dx^{2}+\frac{x}{C}(d\theta ^{2}+\sin ^{2}\theta d\phi ^{2}). \end{aligned}$$
(8)

The mass function (5) is transformed to

$$\begin{aligned} m(x)=\frac{1}{4C^\frac{3}{2}}\int _{0}^{x}\sqrt{\omega }\left( \rho _{*}+E^{2} \right) d\omega , \end{aligned}$$
(9)

where

$$\begin{aligned} \rho _{*}= \left( \frac{1-Z}{x}-2\dot{Z}\right) C, \end{aligned}$$
(10)

and a dot is the derivative with respect to the new variable x.

We can express the Einstein–Maxwell field equations (4), with the quark equation of state (6), in the form

$$\begin{aligned}&\rho = 3p_{r}+4B, \end{aligned}$$
(11a)
$$\begin{aligned}&\frac{p_{r}}{C} = Z\frac{\dot{y}}{y}-\frac{\dot{Z}}{2}-\frac{B}{C}, \end{aligned}$$
(11b)
$$\begin{aligned}&p_{t}= p_{r}+\Delta , \end{aligned}$$
(11c)
$$\begin{aligned}&\Delta = \frac{4xCZ\ddot{y}}{y}+C\left( 2x\dot{Z}+6Z\right) \frac{\dot{y}}{y}\nonumber \\&\quad \,\, + \,C\left( 2\left( \dot{Z}+\frac{B}{C}\right) +\frac{Z-1}{x}\right) , \end{aligned}$$
(11d)
$$\begin{aligned}&\frac{E^{2}}{2C}=\frac{1-Z}{x}-3Z\frac{\dot{y}}{y}-\frac{\dot{Z}}{2}-\frac{B}{C}, \end{aligned}$$
(11e)
$$\begin{aligned}&\sigma = 2\sqrt{\frac{ZC}{x}}\left( x\dot{E}+E\right) . \end{aligned}$$
(11f)

The behaviour for a gravitating anisotropic quark star with electric field present is described by the system (11) above. The variable \(\Delta = p_{t}-p_{r}\) is the measure of anisotropy. The system of equations (11) is in eight variables \((\rho ,\;p_{r},\;p_{t},\;E,\;Z,\;y,\;\sigma ,\;\Delta )\) in six equations. Equation (11d) can be written in a more simplified form as

$$\begin{aligned} \dot{Z}+ \dfrac{\left( 4x^{2}\ddot{y}+6x\dot{y}+y\right) }{2x\left( x\dot{y}+y\right) }Z= \dfrac{\left( \frac{x \Delta }{C}+1-\frac{2xB}{C}\right) y}{2x\left( x\dot{y}+y\right) }. \end{aligned}$$
(12)

This is a nonlinear function in Z and y. However if y and \(\Delta \) are known functions then Equation (12) is linear in the variable Z. In order to find exact solutions to this model we specify the quantities y and \(\Delta \).

We take the metric function y as

$$\begin{aligned} y=\frac{1-ax^{m}}{1+bx^{n}}, \end{aligned}$$
(13)

where a, b, m and n are arbitrary real constants. The metric function y is finite, continuous and well behaved within the stellar interior for a range of values of m and n. It is well behaved at the centre \((x=0)\). We formulate the pressure anisotropy in the form

$$\begin{aligned} \Delta =\sum _{i=1}^{s}A_{i}x^{i}, \end{aligned}$$
(14)

where \(A_{i}\) are arbitrary real constants. The above choice of anisotropy is well behaved. It is continuous throughout the interior of the stellar objects. We observe that \( \Delta =0\) at the centre \((x=0)\) and when \(A_{i}=0\). Then we can regain isotropic models. When \(s=3\), then \(\Delta =\sum _{i}^{3} A_{i}x^{i}\); we obtain the anisotropy used in the models by Maharaj et al. (2014), Sunzu et al. (2014a, b). Therefore we regain anisotropic models generated in the past in this approach. Furthermore, when \(b=0\) and \(a=-1\), we have \(y=1+x^m\). We regain the particular model in the paper by Maharaj et al. (2014), when \(m=\frac{1}{2}\). When \(A_{1}=A_{2}=A_{5}=0\), we have \(\Delta =A_{3}x^{3}+A_{4}x^{4}\) which was introduced in the paper by Sunzu and Mahali (2018).

When Equations (13) and (14) are substituted in (12) we obtain the first order differential equation

$$\begin{aligned}&\dot{Z}+\dfrac{\left[ D(x)-1+ax^{m}\left( 1-D(x)+T(x)\right) \right] }{(1+bx^{n})J(x)}Z\nonumber \\&\quad =-\dfrac{\left( \frac{(\sum _{i}^{s} A_{i}x^{i}) x}{C}+1-\frac{2xB}{C}\right) L(x)}{J(x)}, \end{aligned}$$
(15)

where for simplicity we have set

$$\begin{aligned}&D(x) = 2b(-1+n+2n^{2})x^{n}-b^{2}(1-2n+4n^{2})x^{2n},\\&J(x)=2x\left[ b(n-1)x^{n}-1\right. \\&\qquad \quad \left. +\,ax^{m}(1+m+bmx^{n}-b(n-1)x^{n})\right] ,\\&L(x)=(1-ax^{m})(1+bx^{n}),\\&T(x)= 4(m+bmx^{n})^{2} \\&\qquad \quad -\,2m(1+bx^{n})(b(4n-1)x^{n}-1). \end{aligned}$$

3 Generalized regular model

We can find a desirable regular exact model by choosing values of the parameters

$$\begin{aligned} m=1,\,\, n=\frac{1}{2},\;\;s=5 \,\, \text{ and } \,\, a=b=0. \end{aligned}$$

With these values the potential \(y=1\) and Equation (15) becomes

$$\begin{aligned} \dot{Z}+\frac{1}{2x}Z=\dfrac{C+x( \sum _{i}^{5} A_{i}x^{i}-2Bx)}{2Cx}. \end{aligned}$$
(16)

Solving the differential equation in (16) we obtain

$$\begin{aligned} Z= & {} 1+\frac{x}{C}\left( -\frac{2B}{3}+\frac{A_{1}x}{5}+\frac{A_{2}x^{2}}{7}+\frac{A_{3}x^{3}}{9} \right. \nonumber \\&\left. +\frac{A_{4}x^{4}}{11}+\frac{A_{5}x^{5}}{13}\right) . \end{aligned}$$
(17)

With this we obtain the exact regular model with the following gravitational potentials and matter variables:

$$\begin{aligned}&e^{2\nu }=A^{2}, \end{aligned}$$
(18a)
$$\begin{aligned}&e^{2\lambda }=\dfrac{45045}{45045+\psi (x)}, \end{aligned}$$
(18b)
$$\begin{aligned}&\rho =2B-\frac{3A_{1}x}{5}-\frac{9A_{2}x^{2}}{14}-\frac{2A_{3}x^{3}}{3}\nonumber \\&\qquad -\frac{15}{A}_{4}x^{4}{22}-\frac{9A_{5}x^{5}}{13}, \end{aligned}$$
(18c)
$$\begin{aligned}&p_{r}=-\frac{2B}{3}-\frac{A_{1}x}{5}-\frac{3A_{2}x^{2}}{14}-\frac{2A_{3}x^{3}}{9}\nonumber \\&\qquad -\frac{5A_{4}x^{4}}{22}-\frac{3A_{5}x^{5}}{13}, \end{aligned}$$
(18d)
$$\begin{aligned}&p_{t}= -\frac{2B}{3}+\frac{4A_{1}x}{5}+\frac{11A_{2}x^{2}}{14}+\frac{7A_{3}x^{3}}{9}\nonumber \\&\qquad +\frac{17A_{4}x^{4}}{22}+\frac{10A_{5}x^{5}}{13}, \end{aligned}$$
(18e)
$$\begin{aligned}&\Delta = A_{1}x+A_{2}x^{2}+A_{3}x^{3}+A_{4}x^{4}+A_{5}x^{5}, \end{aligned}$$
(18f)
$$\begin{aligned}&E^{2}= -\frac{4A_{1}x}{5}-\frac{5A_{2}x^{2}}{7}-\frac{2A_{3}x^{3}}{3}\nonumber \\&\qquad -\frac{7A_{4}x^{4}}{11}-\frac{8A_{5}x^{5}}{13}, \end{aligned}$$
(18g)

where we have set

$$\begin{aligned} \psi (x)= & {} \frac{x}{C}\left( -30030B+9009A_{1}x+6435A_{2}x^{2}\right) \\&+\frac{x}{C}\left( 5005A_{3}x^{3}+4095A_{4}x^{4}+5005A_{5}x^{5}\right) . \end{aligned}$$

This model is regular in the gravitational potentials and matter variables. In addition we observe that \(\Delta =0\) and \(E^{2}=0\) at the stellar centre which is physical. From the system (18) the line element (8) becomes

$$\begin{aligned} ds^{2}= & {} -A^{2}dt^{2}+\frac{1}{4xC}\left( \dfrac{45045}{45045+\psi (x)}\right) dx^{2}\nonumber \\ {}&+\frac{x}{C}(d\theta ^{2}+\sin ^{2}\theta d\phi ^{2}). \end{aligned}$$
(19)

Then the mass function (9) becomes

$$\begin{aligned} m(x)= & {} \left( \dfrac{x}{C}\right) ^{\frac{3}{2}}\left( \dfrac{1}{3}B-\frac{3}{10}A_{1}x-\frac{2}{7}A_{2}x^{2}-\frac{5}{18}A_{3}x^{3}\right) \nonumber \\&-\left( {\dfrac{x}{C}}\right) ^{\frac{3}{2}}\left( \frac{3}{11}A_{4}x^{4}+\frac{7}{26}A_{5}x^{5}\right) . \end{aligned}$$
(20)

When \(A_{4}=A_{5}=0\), we obtain models found in Sunzu et al. (2014b). On the other hand, when \(\Delta =0\) and \(E^{2}=0\) the gravitational potentials and matter variables become

$$\begin{aligned}&e^{2\nu }= A^{2},\;e^{2\lambda }=\frac{3003C}{3003C-2002Bx}, \nonumber \\&\rho =2B, \;p_{r}=p_{t}=-\frac{2B}{3}. \end{aligned}$$
(21)

The line element has the form

$$\begin{aligned} ds^{2}= & {} -A^{2}dt^{2}+\left( \frac{3003}{4x(3003C-2002Bx)}\right) dx^{2}\nonumber \\&+\frac{x}{C}(d\theta ^{2}+\sin ^{2}\theta d\phi ^{2}). \end{aligned}$$
(22)

Equation (22) can be written in the form

$$\begin{aligned} ds^{2}= & {} -A^{2}dt^{2}+\left( 1-\dfrac{r^{2}}{{\gamma }^{2}} \right) ^{-1}dr^{2}\nonumber \\&+r^{2}(d\theta ^{2}+\sin ^{2}\theta d\phi ^{2}), \end{aligned}$$
(23)

where \(\gamma ^{2}=\frac{3003}{2002B}\). Equation (23) is the well known neutral Einstein model with isotropic pressure with the equation of state \(p_{r}=p_{t}=-\frac{1}{3}\rho \). This result arises because the energy density is a nonzero constant at the boundary of the quark star. We observe that the exact model in (18) is a generalized Einstein model with charge and anisotropy present.

The model in this section does generate stellar masses consistent with observations. We show this by introducing the transformations \(\tilde{A}_{1}=A_{1}R^{2}\), \(\tilde{A}_{2}=A_{2}R^{2}\), \(\tilde{A}_{3}=A_{3}R^{2}\), \(\tilde{A}_{4}=A_{4}R^{2}\), \(\tilde{A}_{5}=A_{1}R^{5}\), \(\tilde{B}=BR^{2}\), \(\tilde{C}=CR^{2}\). With this transformations we can generate stellar masses and radii in Table 1. For computational acceptability we have set \(R=600\). We compute stellar masses in the range \(0.85M{\odot }-2.86M{\odot }\) consistent with findings in Sunzu et al. (2014a), Mak and Harko (2004), Negreiros et al. (2009), Rawls et al. (2011), Abubekerov et al. (2008), Elebert et al. (2009), Ozel et al. (2009) and Demorest et al. (2010). Therefore the exact solutions in this section do give finite stellar masses consistent with observed masses of physically reasonable astronomical objects.

Table 1 Stellar masses generated using mass function found in a generalized regular model.
Full size table

4 Generalized singular models

We indicate that other exact models for the system (11) are possible. This can be done by choosing different parameters values other than those used in section (3). We choose \(m=1, n=\frac{1}{2}\) and \(a=b^2\). For this choice the metric function \(y=\frac{1-b^2x}{1+b\sqrt{x}}\) which is a nonconstant function. Equation (15) can be written as

$$\begin{aligned} \frac{\left( 1-3b\sqrt{x}\right) \dot{Z}}{x(2-3b\sqrt{x})}= \dfrac{(b\sqrt{x}-1)\left( C+x\left( \Delta -2B\right) \right) }{Cx(3b\sqrt{x}-2 )}. \end{aligned}$$
(24)

Solving (24) we obtain

$$\begin{aligned} Z=\dfrac{2-b\sqrt{x}+\frac{x}{C} \left( B\left( b\sqrt{x}-\frac{4}{3} \right) +f(x)\right) }{{2- 3b\sqrt{x} }}, \end{aligned}$$
(25)

where

$$\begin{aligned} f(x)= & {} A_{1}x\left( \frac{2}{5}-\frac{b\sqrt{x}}{3}\right) + A_{2}x^{2}\left( \frac{2}{7}-\frac{b\sqrt{x}}{4}\right) \\&+A_{3}x^{3}\left( \frac{2}{9}-\frac{b\sqrt{x}}{5}\right) +A_{4}x^{4}\left( \frac{2}{11}-\frac{b\sqrt{x}}{6}\right) \\&+A_{5}x^{5}\left( \frac{2}{13}-\frac{b\sqrt{x}}{7}\right) . \end{aligned}$$

It is important to observe that \(f(x)=0\) for isotropic models. Equation (25) indicates that other exact models in term of elementary functions can be generated.

Using the system (11) we generate the following exact model

$$\begin{aligned}&e^{2\nu } = A^{2}\left( \frac{1-b^{2}x}{1+b\sqrt{x}}\right) ^{2}, \end{aligned}$$
(26a)
$$\begin{aligned}&e^{2\lambda }=\dfrac{2- 3b\sqrt{x}}{2-b\sqrt{x}+\frac{x}{C} \left[ B\left( b\sqrt{x}-\frac{4}{3} \right) +f(x)\right] }, \end{aligned}$$
(26b)
$$\begin{aligned}&\rho =\dfrac{3C\left( \frac{6b}{\sqrt{x}}-10b^{2}+3b^{3}\sqrt{x}\right) }{2(2-3b\sqrt{x})^{2}(b\sqrt{x}-1)}\nonumber \\&\qquad +\dfrac{B\left( -16+47b\sqrt{x}-48b^{2}x+18b^{3}x^{\frac{3}{2}}\right) }{2(2-3b\sqrt{x})^{2}(b\sqrt{x}-1)}\nonumber \\&\qquad +\dfrac{3f_{r}(x)}{2(2-3b\sqrt{x})^{2}(b\sqrt{x}-1)}, \end{aligned}$$
(26c)
$$\begin{aligned}&p_{r}=\dfrac{C\left( \frac{6b}{\sqrt{x}}-10b^{2}+3b^{3}\sqrt{x}\right) }{2(2-3b\sqrt{x})^{2}(b\sqrt{x}-1)}\nonumber \\&\qquad +\dfrac{B\left( \frac{16}{3}-27b\sqrt{x}+40b^{2}x-18b^{3}x^{\frac{3}{2}}\right) }{2(2-3b\sqrt{x})^{2}(b\sqrt{x}-1)}\nonumber \\&\qquad +\dfrac{f_{r}(x)}{2(2-3b\sqrt{x})^{2}(b\sqrt{x}-1)}, \end{aligned}$$
(26d)
$$\begin{aligned}&p_{t}=\dfrac{C\left( \frac{6b}{\sqrt{x}}-10b^{2}+3b^{3}\sqrt{x}\right) }{2(2-3b\sqrt{x})^{2}(b\sqrt{x}-1)}\nonumber \\&\qquad +\dfrac{B\left( \frac{16}{3}-27b\sqrt{x}+40b^{2}x-18b^{3}x^{\frac{3}{2}}\right) }{2(2-3b\sqrt{x})^{2}(b\sqrt{x}-1)}\nonumber \\&\qquad +\dfrac{f_{t}(x)}{2(2-3b\sqrt{x})^{2}(b\sqrt{x}-1)}, \end{aligned}$$
(26e)
$$\begin{aligned}&\Delta =A_{1}x+A_{2}x^{2}+A_{3}x^{3}+A_{4}x^{4}+A_{5}x^{5}, \end{aligned}$$
(26f)
$$\begin{aligned}&E^{2}=\dfrac{C\left( 2b^{2}+3b^{3}\sqrt{x}-\frac{2b}{\sqrt{x}}\right) +B\left( b\sqrt{x}-2b^{2}x\right) }{(2-3b\sqrt{x})^{2}(b\sqrt{x}-1)}\nonumber \\&\qquad \,+\dfrac{f_{e}(x)}{(2-3b\sqrt{x})^{2}(b\sqrt{x}-1)}, \end{aligned}$$
(26g)

where for convenience we have set

$$\begin{aligned}&f_{r}(x) \\&= A_{1}x\left( \frac{8}{5}-\frac{64}{15}b\sqrt{x}+\frac{18}{5}b^{2}x-b^{3}x^{\frac{3}{2}}\right) \\&\quad +A_{2}x^{2}\left( \frac{12}{7}-\frac{141}{28}b\sqrt{x}+\frac{67}{14}b^{2}x-\frac{3}{2}b^{3}x^{\frac{3}{2}}\right) \\&\quad +A_{3}x^{3}\left( \frac{16}{9}-\frac{82}{15}b\sqrt{x}+\frac{82}{15}b^{2}x-\frac{9}{5}b^{3}x^{\frac{3}{2}}\right) \\&\quad +A_{4}x^{4}\left( -\frac{8}{11}+\frac{379}{165}b\sqrt{x}-\frac{26}{11}b^{2}x+4b^{3}x^{\frac{3}{2}}\right) \\&\quad +A_{5}x^{5}\left( -\frac{14}{13}+\frac{9}{13}b\sqrt{x}-\frac{283}{390}b^{2}x+b^{3}x^{\frac{3}{2}}\right) ,\\&f_{t}(x) \\&= A_{1}x\left( -\frac{32}{5}+\frac{416}{15}b\sqrt{x}-\frac{192}{5}b^{2}x+17b^{3}x^{\frac{3}{2}}\right) \\&\quad +A_{2}x^{2}\left( -\frac{44}{7}+\frac{755}{28}b\sqrt{x}-\frac{521}{14}b^{2}x+\frac{33}{2}b^{3}x^{\frac{3}{2}}\right) \\&\quad +A_{3}x^{3}\left( -\frac{56}{9}+\frac{398}{15}b\sqrt{x}-\frac{548}{15}b^{2}x+\frac{81}{5}b^{3}x^{\frac{3}{2}}\right) \\&\quad +A_{4}x^{4}\left( \frac{51}{11}-\frac{1733}{132}b\sqrt{x}+\frac{596}{33}b^{2}x-8b^{3}x^{\frac{3}{2}}\right) \\&\quad +A_{5}x^{5}\left( \frac{35}{13}-\frac{593}{52}b\sqrt{x}+\frac{402}{26}b^{2}x-\frac{111}{16}b^{3}x^{\frac{3}{2}}\right) ,\\&f_{e}(x) \\&= A_{1}x\left( \frac{16}{5}-\frac{64}{5}b\sqrt{x}+\frac{84}{5}b^{2}x-7b^{3}x^{\frac{3}{2}}\right) \\&\quad +A_{2}x^{2}\left( \frac{20}{7}-\frac{313}{28}b\sqrt{x}+\frac{101}{7}b^{2}x-6b^{3}x^{\frac{3}{2}}\right) \\&\quad +A_{3}x^{3}\left( \frac{8}{3}-\frac{154}{15}b\sqrt{x}+\frac{196}{15}b^{2}x-\frac{27}{5}b^{3}x^{\frac{3}{2}}\right) \\&\quad +A_{4}x^{4}\left( \frac{8}{5}-\frac{213}{35}b\sqrt{x}+\frac{268}{35}b^{2}x-\frac{22}{7}b^{3}x^{\frac{3}{2}}\right) \\&\quad +A_{5}x^{5}\left( -\frac{8}{3}+\frac{211}{21}b\sqrt{x}-\frac{5}{4}b^{2}x+\frac{143}{28}b^{3}x^{\frac{3}{2}}\right) . \end{aligned}$$

Then the line element in (8) can be expressed as

$$\begin{aligned}&ds^{2} =-A^{2}\left( \frac{1-b^{2}x}{1+b\sqrt{x}}\right) ^{2}dt^{2} \nonumber \\&+ \dfrac{1}{4xC} \dfrac{2- 3b\sqrt{x}}{2-b\sqrt{x}+\frac{x}{C} \left( B\left( b\sqrt{x}-\frac{4}{3}\right) +f(x)\right) }dx^{2}\nonumber \\&+\dfrac{x}{C}(d\theta ^{2}+\sin ^{2}\theta d\phi ^{2}). \end{aligned}$$
(27)

The mass function becomes

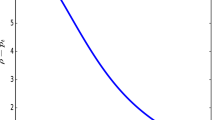
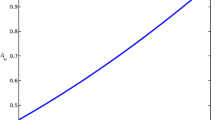
$$\begin{aligned}&m(x) \nonumber \\&=A_1{x^{\frac{5}{2}}}\left( \frac{6}{5}-\frac{64}{15}b\sqrt{x}+\frac{153}{30}b^{2}x+2b^{3}x^{\frac{3}{2}}\right) \nonumber \\&\quad +A_2{x^{\frac{7}{2}}}\left( \frac{8}{7}-\frac{227}{56}b\sqrt{x}+\frac{269}{56}b^{2}x+\frac{15}{4}b^{3}x^{\frac{3}{2}}\right) \nonumber \\&\quad +A_3{x^{\frac{9}{2}}}\left( \frac{5}{3}-\frac{59}{15}b\sqrt{x}+\frac{139}{30}b^{2}x-\frac{9}{5}b^{3}x^{\frac{3}{2}}\right) \nonumber \\&\quad +A_4{x^{\frac{11}{2}}}\left( \frac{9}{2}-\frac{509}{32}b\sqrt{x}+\frac{597}{32}b^{2}x-\frac{231}{32}b^{3}x^{\frac{3}{2}}\right) \nonumber \\&\quad +A_5{x^{\frac{13}{2}}}\left( \frac{98}{495} - \frac{346}{495}b\sqrt{x}+\frac{809}{5449}b^{2}x-\frac{52}{165}b^{3}x^{\frac{3}{2}}\right) \nonumber \\&\quad +CK(1-3b\sqrt{x}+3b^{2}x)\nonumber \\&\quad +\left( 3-4x\right) b^{3}x^{3}+C\left( bx(2-4b\sqrt{x}+3b^{2}x)\right) \nonumber \\&\quad +{x^{\frac{3}{2}}}\left( \frac{4}{3}-\frac{12}{5}x+\frac{16}{15}(-5+8x)b\sqrt{x}\right. \nonumber \\&\quad \left. -\frac{1}{5}(-35+51)b^{2}x\right) . \end{aligned}$$
(28)

It is clear that another exact model to the field equations (11) has been found. Other solutions to Equation (15) can be generated for different choices of parameters m, n, a and b. However it is not clear that other choices are likely to produce solutions in terms of elementary functions. The exact model in the system (26) is singular at the centre. This property is shared with the quark star model generated by Mak and Harko (2004) and Sunzu et al. (2014a, b). Moreover the potentials, stellar mass and anisotropy remain finite and regular. We have plotted the geometrical and matter variables in Figures 1, 2, 3, 4, 5, 6, 7 and 8. It is clear that the model is well behaved.

Fig. 1
figure 1

The potential \(e^{2\nu }\) against radial distance.

Full size image
Fig. 2
figure 2

The potential \(e^{2\lambda }\) against radial distance.

Full size image
Fig. 3
figure 3

Energy density against radial distance.

Full size image
Fig. 4
figure 4

Radial pressure against radial distance.

Full size image
Fig. 5
figure 5

Tangential pressure against radial distance.

Full size image
Fig. 6
figure 6

Electric field against radial distance

Full size image
Fig. 7
figure 7

Pressure anisotropy against radial distance.

Full size image
Fig. 8
figure 8

Mass against radial distance

Full size image

5 Matching conditions

The interior exact solutions found in our models can be matched with the exterior solution at the surface of the stellar object. This is achieved by setting the radius \(r=\mathcal {R}\), and \(x=C\mathcal {R}^{2}\). We illustrate this for the exact solution (18). Using the line elements given in Equations (1) and (2) we can match the interior and exterior exact solutions in the system (18) by setting

$$\begin{aligned}&A^{2}=\left( 1-\frac{2M}{\mathcal {R}}+\frac{Q^{2}}{\mathcal {R}^{2}}\right) ,\end{aligned}$$
(29a)
$$\begin{aligned}&\dfrac{45045}{45045+\psi } =\left( 1-\frac{2M}{\mathcal {R}}+\frac{Q^{2}}{\mathcal {R}^{2}}\right) ^{-1},\end{aligned}$$
(29b)
$$\begin{aligned}&p_{r} =0, \end{aligned}$$
(29c)

at the boundary. Using the expressions for \(p_r, Q\) and M from the system (18) and Equation (20), the matching conditions in system (29) become

$$\begin{aligned}&A^{2}=1-{\mathcal {R}^{2}}\left( \frac{2}{3}B+\frac{1}{5}A_1C{\mathcal {R}^{2}} \right. \nonumber \\&\qquad \left. +\frac{1}{7}A_2C^2{\mathcal {R}^{4}}+\frac{1}{9}A_3C^3{\mathcal {R}^{6}}\right) \nonumber \\&\qquad -{\mathcal {R}^{2}}\left( \frac{1}{11}A_4C^4{\mathcal {R}^{8}}+\frac{1}{13}A_5C^5{\mathcal {R}^{10}}\right) , \end{aligned}$$
(30a)
$$\begin{aligned}&0=18018A_1C{\mathcal {R}^{2}}+12870A_2C^2{\mathcal {R}^{4}} +10010A_3C^3{\mathcal {R}^{6}}\nonumber \\&\qquad +8190A_4C^4{\mathcal {R}^{8}}+8470A_5C^5{\mathcal {R}^{10}}, \end{aligned}$$
(30b)
$$\begin{aligned}&0=\frac{2B}{3}+C{\mathcal {R}^{2}}\left( \frac{1}{5}+\frac{3}{14}A_2C{\mathcal {R}^{2}}+\frac{2}{9}A_3C^2{\mathcal {R}^{4}}\nonumber \right) \nonumber \\&\qquad +C{\mathcal {R}^{2}}\left( \frac{5}{22}A_4C^3{\mathcal {R}^{6}}+\frac{3}{13}A_5C^4{\mathcal {R}^{8}}\right) . \end{aligned}$$
(30c)

The system (30) provides the matching conditions of the exact solution in the system (18). We note that the matching conditions in system (30) is explicitly expressed in terms of constants \(A,\;B, \;C,\;A_{1},\; A_{2},\; A_{3},\; A_{4},\; A_{5}\;, \text {and}\; {\mathcal {R}}\). There are sufficient free parameters to satisfy the conditions that arise.

6 Discussion

We have found several new classes of exact solutions to the Einstein–Maxwell system with charge and anisotropy. The exact models generated in Section 3 and Section 4 are well behaved in the interior of the stellar object. We have generated stellar masses with radii compatible with masses observed by other researchers. This indicates that our models give mass functions that are physically acceptable and have astrophysical significance. The masses generated regains the results obtained in Sunzu et al. (2014a), Mak and Harko (2004), Negreiros et al. (2009), Rawls et al. (2011), Abubekerov et al. (2008), Elebert et al. (2009), Ozel et al. (2009) and Demorest et al. (2010). The masses generated in our model have the same values with several stars observed in the past. The stars regained are Vela X-1 with mass \(1.77M_{\odot }\) and radius 9.56km, Her X-1 with mass \(0.85M_{\odot }\) and radius 8.1km, SAXJI\(808.4-3658\) with mass \(0.9M_{\odot }\) and radius 7.951km, EXO\(1785-248\) with mass \(1.3M_{\odot }\) and radius 8.849km, and PSRJI\(614-2230\) with mass \(1.97M_{\odot }\) and radius 9.69km.

We have also generated graphical plots using the model found in Section 4 The graphs are plotted using the Python programing language. The following values were used for the constants: \(A_1=0.5, A_2=-0.14, A_3=0.25, A_4=-0.2, A_5=-0.2, B=0.2, b=-0.5\). From Figures 1 and 2 it is indicated that the gravitational potentials are regular and continuous throughout the interior of the stellar matter. From Figures 3, 4 and 5 we see that the energy density, radial pressure, and tangential pressure are decreasing functions away from the stellar object. This verifies that \(\rho {'}<0, p_r{'}<0\), and \(p_t{'}<0\). These variables contain a singularity at the centre of the stellar object due to the existence of the term \(\frac{1}{x}\) in their expressions. This behaviour is also shared in the model of Sunzu et al. (2014b). The electric field intensity in Figure 6 is a decreasing function with radial distance in the stellar interior. This behaviour is evident in stellar models found by Feroze and Siddiqui (2011), Malaver (2013a) and Sunzu et al. (2014b). From Figure 7, the measure of anisotropy is a positive increasing function from the centre to the region near the surface of the star. It decreases at the region near the centre. This feature shows that \(p_t>p_r\) throughout the stellar interior. This profile is similar to the model found in Maharaj et al. (2014). From Figure 8 we observe that the mass is an increasing function with radial coordinate r.

Results obtained in this paper are significant for the study of relativistic astrophysical objects. They provide more understanding on the structure and properties of compact stellar objects. Other new results and models can be generated by considering equations of state, a different measure of anisotropy and other metric functions.