1 Introduction

The final stage in the evolution of stars is the formation of compact stellar bodies including neutron stars, white dwarfs and black holes [1, 2]. Evolution of compact objects in astrophysics reveals that mass, matter composition and radius cannot be evaluated by direct observation, because light cannot pass through these objects. This brings the concept of general relativity into practice because it predicts many important aspects of compact objects like mass, red-shift, radius and accelerated expansion of Universe with connection to dark energy [3, 4]. The study of four dimensions contained in Einstein’s theory describes the idea that gravitation is an effect of the curvature of space–time which can be used to study intrinsic and extrinsic geometries of surfaces [5]. In the literature, the demonstration of dimensions of a space in unifying the force of gravitation was extended from the theories of Newton, Einstein’s special and general relativity of space–time [6]. In the 1970s and 1980s, the concept of building a quantum field theory of gravity began to take part in gravity theories with the emergence of supergravity and superstring theories. Both of these ideas are based on the implementation of supersymmetry and reflects a renewal of Kaluza and Klein’s concepts of higher-dimensional spaces [7]. Embedding four dimensions to higher pseudo-Euclidean dimensional space is one among several approaches in general relativity which helps to investigate the internal structure and properties of compact stellar bodies. For detailed description on the embedding approach, see Bhar et al [8, 9], Das et al [10], Maurya and Maharaj [11], Murad [12], and Pandya and Thomas [13].

In generalising the features of relativistic stars, researchers extended Einstein field equations enabling the Einstein–Maxwell systems by including charge. The charge component in relativistic stars has impact on values of mass, luminosities and surface red-shifts. The Einstein–Maxwell equations can also be applied with equations of state, conformal Killing vectors and the Gauss–Bonnet approach in describing the structure and properties of charged compact stellar bodies. A comprehensive analysis of compact stars with electromagnetic field is presented in the works by Komathiraj and Sharma [14, 15], Ivanov [16], Komathiraj and Maharaj [17], Maharaj and Komathiraj [18], Maharaj and Thirukkanesh [19], Feroze and Siddiqui [20] and Sunzu et al [21, 22]. Embedding in five-dimensional flat space–time has been successfully used in various extensive studies in modelling charged stellar objects [23, 24]. The embedding approach gives an additional differential equation called the Karmakar condition [25, 26]. Karmakar [27] established the necessary requirement for a space–time in general relativity to be of class I with a spherically symmetric metric. Since then, several studies have been done to describe the embedding method in generating new exact solutions which are useful in describing compact objects like neutron stars, pulsars and black holes which contain strong gravitational fields. The space–times that allow the embedding of four-dimensional to five-dimensional space are referred to be as class one. Note that the exterior and interior solutions of Schwarzschild [28] are of class two and class one respectively. Investigations by Singh and Pant [29], Singh et al [30], Gedela et al [31], and Maurya and Maharaj [32] developed families of physically acceptable conditions in spherical models that describe the interior regions of the stars.

Anisotropic models with charged fluid distributions describe the behaviour of relativistic stars. Anisotropy implies that the radial pressure is different from the tangential pressure for interiors of stellar bodies with very high densities of about \(10^{15}\) g\(\cdot \)cm\(^{-3}\) [33,34,35,36]. The isotropic pressure decreases with the increase of radial distance and has the highest value at the centre of the relativistic star. Higher-dimensional spaces introduced by the embedding provide models with either isotropic and anisotropic pressures or charge and uncharged models. Randall and Sundrum [37] developed the notion of the brane-world scenario, which established a strong interest in higher-dimensional manifolds and modified gravity theories. Higher-order gravity theories are important in generating models for astrophysical objects and the brane-world scenario provides a natural existence of anisotropic pressure within the stellar fluids [38]. The solutions to the Einstein–Maxwell field equations in general relativity have a number of different applications.

In the earlier studies for class I space–times, the gravitational potentials were chosen in generating exact models. In this model, we consider only the integrability condition that arised from the Karmarkar condition without any limitations on the gravitational potentials. We consider only the existence of the Karmarkar condition. In this study, we transform the Karmarkar condition and the Einstein–Maxwell system using the Durgapal and Bannerji [39] transformation. The technique of transforming Einstein–Maxwell field equations to new forms have been applied in the models of Komathiraj and Sharma [15], Manjonjo et al [40] and Thirukkanesh and Maharaj [41]. With some analytical calculations to the transformed equations, the gravitational potentials y(x) and z(x) are expressed in terms of the electric field and the measure of anisotropy. This enables us to choose suitable forms for the anisotropic factor and electric charge to generate new models that generalise particular solutions from the previous studies.

The outline of this paper is summarised as follows: In §1, we give the introduction on the study of general relativity and embedding. Section 2 describes the Einstein–Maxwell field equations and charged relativistic model. In §3, we present the Einstein–Maxwell field equations via the embedding approach for a spherically symmetric metric. In this section, we also apply the transformation by Durgapal and Bannerji [39] to the field equations. In this section, we present the sufficient and necessary conditions for a class-I space–time. In §4, we present exact solutions. Charge and measure of anisotropy are specified from physical grounds so as to generate the required model. Some particular known solutions are presented in §5 that are regained from the previous section. In §6, we describe physical validity conditions for the solutions. We present the discussion and analysis of the physical results in §7.

2 Einstein–Maxwell field equations

The behaviour of electric and gravitational fields in class-I space–time is considered in four-dimensional space with coordinates \((x^i)=(t, r, \theta , \phi \)). The standard line element described with Schwarzschild coordinates is defined by

$$\begin{aligned} \mathrm {d}s^2 = -\mathrm {e}^{\nu (r)}\mathrm {d}t^2 + \mathrm {e}^{\lambda (r)}\mathrm {d}r^2 + r^2(\mathrm {d}\theta ^2 + \text {sin}^2\theta \,\mathrm {d}\phi ^2), \nonumber \\ \end{aligned}$$
(1)

where \(\nu (r)\) and \(\lambda (r)\) represent gravitational potentials. Reissner and Nordstrom described the exterior line element for a spherical symmetric metric with charge as

$$\begin{aligned} \mathrm {d}s^{2}= & {} -\left( 1-\frac{2M}{r}+\frac{Q^2}{r^2}\right) \mathrm {d}t^{2}\nonumber \\&+ \left( 1-\frac{2M}{r}+\frac{Q^2}{r^2}\right) ^{-1}\mathrm {d}r^{2} \nonumber \\&+\,r^{2}(\mathrm {d}\theta ^{2}+\sin ^{2}\theta \, \mathrm {d}\phi ^{2}), \end{aligned}$$
(2)

where M represents the mass of a relativistic star and Q stands for electric charge. The Einstein–Maxwell field equations for the distribution of anisotropic fluids are given as

$$\begin{aligned} \tau _{j}^{i}+E_{j}^{i} = R_{j}^{i}-\frac{1}{2}Rg_{j}^{i}. \end{aligned}$$
(3)

The energy–momentum tensor and Ricci tensor are represented by \(\tau _{j}^{i}\) and \(R_{j}^{i}\) respectively. R and \(E_{j}^{i}\) stand for the scalar curvature and the electromagnetic field respectively. The energy–momentum tensor and electromagnetic field for anisotropic distribution of matter in (3) are represented by the expressions

$$\begin{aligned}&\tau _{j}^{i} =(\rho +p_t)\upsilon ^{i}\upsilon _{j}-p_t\delta ^{i}_{j}+(p_r-p_t)\chi ^i\chi _j, \end{aligned}$$
(4)
$$\begin{aligned}&E_{j}^{i} =F^{im}F_{jm}-\frac{1}{4}\delta ^{i}_{j}F^{mn}F_{mn}. \end{aligned}$$
(5)

In (4), \(\rho \) stands for energy density, \(p_r\) stands for radial pressure, \(p_t\) stands for tangential pressure, \(\upsilon ^i\) stands for the four-velocity vector and \(\chi ^i\) stands for a unit space-like vector in the radial direction. For uncharged material \(E_{j}^{i}=0\).

The Einstein–Maxwell field equations is determined from eqs (1), (3), (4) and (5) to obtain the following equations:

$$\begin{aligned}&\rho (r)+\frac{1}{2}E^2 = \frac{1-\mathrm {e}^{-\lambda }}{r^2} + \frac{\mathrm {e}^{-\lambda }\lambda ^{\prime }}{r}, \end{aligned}$$
(6a)
$$\begin{aligned}&p_r(r)-\frac{1}{2}E^2 = \frac{\nu ^{\prime }\mathrm {e}^{-\lambda }}{r}-\frac{1-\mathrm {e}^{-\lambda }}{r^2}, \end{aligned}$$
(6b)
$$\begin{aligned}&p_t(r)+\frac{1}{2}E^2 = \frac{\mathrm {e}^{-\lambda }}{4}\bigg (2\nu ^{\prime \prime } + {\nu ^{\prime }}^2-\nu ^{\prime } \lambda ^{\prime } \nonumber \\&\qquad \qquad \qquad \quad \, +\frac{2\nu ^{\prime }}{r}-\frac{2\lambda ^{\prime }}{r}\bigg ), \end{aligned}$$
(6c)
$$\begin{aligned}&\frac{\mathrm {e}^{{\lambda }/{2}}}{r^2}(r^2E)^{\prime } = \sigma , \end{aligned}$$
(6d)
$$\begin{aligned}&\Delta =p_t-p_r \nonumber \\&\quad = {\mathrm {e}^{-\lambda }}\left( \frac{\nu ^{\prime \prime }}{2} -\frac{\nu ^{\prime } \lambda ^{\prime }}{4} +\frac{{\nu ^{\prime }}^2}{4} \right. \nonumber \\&\qquad \left. - \frac{\nu ^{\prime }+\lambda ^{\prime }}{2r} +\frac{\mathrm {e}^{\lambda }-1}{r^{2}}-E^2\right) . \end{aligned}$$
(6e)

In the system of field equations (6), primes represent derivatives with respect to r, \(\Delta \) stands for anisotropy and \(\sigma \) stands for proper charge density. At the centre of the stellar object, \(\Delta =0\). That is, \(p_t=p_r\) with isotropic pressure. In this model, we take into account that the speed of light is unity \((8\pi G=c=1)\).

3 Field equations via embedding

It is well established in general relativity that the line element (1) can be embedded into five-dimensional space giving the Kamarkar condition. Eisenhart [42] proposed the use of the symmetric tensor \(b_{\mu \beta }\) in the Karmarkar condition to describe the structure and properties of stellar bodies. The Riemannian space that utilises the symmetric tensor \(b_{\mu \beta }\) is given by

$$\begin{aligned}&R_{\mu \nu \alpha \beta } = \epsilon (b_{\mu \alpha }b_{\nu \beta }-b_{\mu \beta }b_{\nu \alpha }), \end{aligned}$$
(7)
$$\begin{aligned}&0 = b_{{\mu \nu }; \alpha }-b_{{\mu \alpha }; \nu }, \end{aligned}$$
(8)

with \(\epsilon =+1\) or \(-1\) and semicolons represent covariant derivatives. The non-zero components of the symmetric tensor \(b_{\mu \alpha }\) generate non-zero values of the Riemannian curvature corresponding to (1). These non-zero components of the Riemann curvature are given as

$$\begin{aligned} R_{1414}= & {} -\mathrm {e}^{\nu }\left( \frac{{\nu }^{\prime \prime }}{2}+\frac{{\nu }^{\prime 2}}{4}-\frac{{\lambda }^{\prime }{\nu }^{\prime }}{4}\right) , \end{aligned}$$
(9a)
$$\begin{aligned} R_{2323}= & {} -\mathrm {e}^{\lambda }\,r^{2} \,\text {sin}^{2}\theta \;(\mathrm {e}^{\lambda }-1), \end{aligned}$$
(9b)
$$\begin{aligned} R_{1212}= & {} \frac{1}{2}\,r\,{\lambda }^{\prime }, \end{aligned}$$
(9c)
$$\begin{aligned} R_{3434}= & {} -\frac{1}{2}\,\text {sin}^{2}\theta \; \nu ^{\prime }\mathrm {e}^{\nu -\lambda } . \end{aligned}$$
(9d)

The Karmarkar condition is developed by incorporating the non-zero components \(b_{11}, \, b_{22}, \, b_{33} \) and \(\;b_{14} \; \text {with} \, \; b_{33}=b_{22}\,\text {sin}^{2}\theta \) and the non-zero components of the Riemann curvature tensor (9) to get the equation

$$\begin{aligned} R_{1414}=\frac{R_{1212}R_{3434}+R_{1224}R_{1334}}{R_{2323}}, \end{aligned}$$
(10)

where \(R_{2323}\ne 0\) [30, 43].

Substituting (9) into (10), we obtain a differential equation that is highly non-linear and is given as

$$\begin{aligned} \frac{{\lambda }^{\prime }\mathrm {e}^{\lambda }}{\mathrm {e}^{\lambda }-1}=\frac{{2\nu }^{\prime \prime }}{{\nu }^{\prime }}+{\nu }^{\prime }. \end{aligned}$$
(11)

Solving differential equation (11) gives a useful equation that relates the metric functions \(\nu (r)\) and \(\lambda (r)\) by

$$\begin{aligned} \mathrm {e}^{\frac{{\nu }}{2}}=C+H\int _{}^{}\sqrt{(\mathrm {e}^{\lambda (r)}-1)}\mathrm {d}r\,, \end{aligned}$$
(12)

where C and H are constants of integration. In order to develop a charged exact model in the embedding approach, the gravitational potential \(\lambda (r)\) and electromagnetic field are restricted on physical grounds. In our model, we apply an alternative approach by introducing new variables as described in Durgapal and Bannerji [39]. This provides some useful findings in describing the behaviour of a relativistic star. We have the freedom to choose the anisotropic factor and electromagnetic field in generating the new model.

In implementing new coordinates in (6), an equivalent form of the Einstein–Maxwell field equations is obtained. This is done by utilising the transformation

$$\begin{aligned}&x=r^{2}, \end{aligned}$$
(13a)
$$\begin{aligned}&z(x)= \mathrm {e}^{-\lambda (r)}, \end{aligned}$$
(13b)
$$\begin{aligned}&y(x) = \mathrm {e}^{\nu (r)}. \end{aligned}$$
(13c)

Equations (13) transform system (6) into

$$\begin{aligned}&\rho (x)+\frac{1}{2}E^2= \frac{1-z}{x}-2\,\dot{z}, \end{aligned}$$
(14a)
$$\begin{aligned}&p_r(x)-\frac{1}{2}E^2 = 2\,z\,\frac{\dot{y}}{y}-\frac{{1-z}}{x}, \end{aligned}$$
(14b)
$$\begin{aligned}&p_t(x)+\frac{1}{2}E^2 = 2x\,z\,\frac{\ddot{y}}{y}+\left( 2\,z+x\,\dot{z}\right) \,\frac{\dot{y}}{y}\nonumber \\&\qquad \qquad \qquad \quad \, -x\,z\,\frac{\dot{y}^{2}}{y^{2}} + \dot{z}, \end{aligned}$$
(14c)
$$\begin{aligned}&{\sigma }^2(x) = \frac{z}{4\pi x}(x\dot{E}+E)^{2}, \end{aligned}$$
(14d)
$$\begin{aligned}&\Delta =p_t-p_r \nonumber \\&\quad =z\left( 2x\,\frac{\ddot{y}}{y}-x\frac{\dot{y}^{2}}{y^{2}}\right) -\frac{{1-z}}{x}\nonumber \\&\qquad +\dot{z}\left( 1+ x\frac{\dot{y}}{y}\right) -E^2 , \end{aligned}$$
(14e)

where the dots in (14) represent derivatives with respect to x.

4 Exact solutions

System (14) has eight unknown variables \(z,y,p_r, \Delta ,\) \(p_t, \rho ,E\) and \(\sigma \). To solve these equations, eq. (12) resulted from the Karmarkar condition (11) is expressed in terms of the variables y and z to obtain the gravitational potential

$$\begin{aligned} y(x) =\left( C+\frac{1}{2}H\int _{}^{}\sqrt{\frac{1-z}{xz}}\mathrm {d}x \right) ^{2}. \end{aligned}$$
(15)

We can find a simple case when the integration constant \(H=0\). Then, eq. (15) reduces to

$$\begin{aligned} y(x) =C^2. \end{aligned}$$
(16)

Substituting (16) into (14e), we obtain a simple linear differential equation in z given by

$$\begin{aligned} \Delta =\dot{z}-\frac{z}{x}+\frac{1}{x}-E^2. \end{aligned}$$
(17)

Integrating (17) gives

$$\begin{aligned} z(x)=x\int _{}^{}\frac{ \,\Delta +E^2}{x}\,\mathrm {d}x +mx+1, \end{aligned}$$
(18)

where m is a real constant.

Now, it is possible to write the matter variables in eq. (14) in terms of the electric field \(E^2\) and measure of anisotropy \(\Delta \) as

$$\begin{aligned}&\rho {=}-3\left( \int _{}^{}\frac{ \,\Delta {+}E^2}{x}{+}m\right) -2\Delta -\frac{5}{2}E^2, \end{aligned}$$
(19a)
$$\begin{aligned}&p_r=\left( 2H\,\left( x\int \limits _{}^{}\frac{\Delta +E^2}{x}\,\mathrm {d}x +mx+1 \right) ^{{1}/{2}} \right) \nonumber \\&\qquad \times \left( \frac{\sqrt{1{-}\left( x\int _{}^{}\frac{\Delta {+}E^2}{x}\,\mathrm {d}x {+}mx{+}1 \right) } }{x^{{1}/{2}}\left( C{+}\frac{1}{2}H\int _{}^{}\sqrt{\frac{1{-}\left( x\int _{}^{}\frac{8\,\pi \,\Delta }{x}\,\mathrm {d}x {+}mx{+}1\right) }{x\left( x\int _{}^{}\frac{\Delta {+}E^2}{x}\,\mathrm {d}x {+}mx{+}1\right) }}\mathrm {d}x \right) } \right) \nonumber \\&\qquad +\int \limits _{}^{}\frac{\Delta +E^2}{x}\mathrm {d}x +m+\frac{1}{2}E^2,\end{aligned}$$
(19b)
$$\begin{aligned}&{\sigma }^2 {=} \frac{\left( x\int \limits _{}^{}\frac{\Delta {+}E^2}{x}\,\mathrm {d}x {+}mx{+}1 \right) }{4\pi x}(xE^{'}{+}E)^{2}, \end{aligned}$$
(19c)
$$\begin{aligned}&p_t = p_r+\Delta -E^2 . \end{aligned}$$
(19d)

To fully describe the model’s gravitational behaviour in terms of stability, equilibrium and regularity conditions, one should specify the anisotropic factor and the electric field. In various research works, system (19) has been extensively studied with some particular restrictions in anisotropic factor and electric field. This is seen in models generated by Komathiraj and Sharma [33] and Manjonjo et al [44].

In this study, the following forms of anisotropic factor and electromagnetic field are introduced on physical grounds to generate a realistic model associated with system (19):

$$\begin{aligned}&\Delta =\frac{(a+b^{m}x)x}{(j+cx)^{n+2s}}, \end{aligned}$$
(20)
$$\begin{aligned}&E^2=\frac{k(d+h)x}{(j+cx)^{n+2s}}, \end{aligned}$$
(21)

where \(a,\, b,\, c,\, d,\, h,\, j,\, m,\, n\,\) and s are real constants. We choose these forms to generate realistic astrophysical models that generalise particular solutions derived in previous studies. The choices satisfy the required properties for physical models. We observe that \(\Delta =0\) and \(E=0\) at the centre of the stellar object, that is, at \(x=0\). These behaviours are necessary for physical realistic stellar models.

Some particular choices of charge and anisotropy used by various researchers are derived from our general choices (20) and (21) for some parameter settings. These are obtained in the following cases:

Case I: Plugging \(a=b=0\) and \(n=0, \, c=j=s=k=h=d=1 \) into eqs (20) and (21) respectively, we regain the forms of pressure anisotropy and electromagnetic field that were used by Manjonjo et al [40] in generating Einstein–Maxwell field equations with conformal flat space–time with

$$\begin{aligned}&\Delta =0, \\&E^2=\frac{2x}{(1+x)^2}. \end{aligned}$$

Case II: When \(a=\beta ,\, b=n=0, \, c=a, \,\, j=s=1,\) and \( c=a, \, n=0, \, s=j=k=1, \, h=-\beta , \, \, d=\alpha \) are substituted into eqs (20) and (21) respectively, we regain the forms of anisotropic and electromagnetic fields that were used by Maharaj et al [45] and expressed as

$$\begin{aligned}&\Delta =\frac{(\alpha -\beta )x}{(1+ax)^2}, \\&E^2=\frac{\beta x}{(1+ax)^2}. \end{aligned}$$

Case III: Plugging \(\, d=n=0, \,\,c=j=s=k=1, \, \, h=\alpha \) into eq. (21), we obtain the form of electromagnetic field used by Maharaj and Komathiraj [18] in generating Einstein–Maxwell field equations with

$$\begin{aligned} E^2=\frac{\alpha x}{(1+x)^2}. \end{aligned}$$

Case IV: If \(j=s=1, \, n=0, \, \, k=a\alpha , \, c=d=b,\) \(\,h=-a\) in eq. (21), we regain similar form of electromagnetic field used by Thirukkanesh and Maharaj [46] as

$$\begin{aligned} E^2=\frac{\alpha a(b-a)x}{(1+bx)^2}. \end{aligned}$$

Case V: If \(n=0, \,s=h=j=d=1, \, k=\mathcal {E}, \,c=b, \,\) in eq. (21), we obtain the form of electromagnetic field specified by Mafa Takisa and Maharaj [47] in generating the Einstein–Maxwell field equations model with

$$\begin{aligned} E^2=\frac{2\,\mathcal {E}\,x}{(1+bx)^2}. \end{aligned}$$

Case VI: For \(h=n=0, \,s=j=d=1, \, k=c=b, \,\) in eq. (21) we obtained similar form of electromagnetic field used by Thirukkanesh and Maharaj [41] in generating the well-behaved Einstein–Maxwell field equations model with

$$\begin{aligned} E^2=\frac{\alpha bx}{(1+bx)^2}. \end{aligned}$$

We see from all these cases that \(\Delta =0\) and \(E=0\) at the stellar centre. This shows that our choice of anisotropy and electric field can generate stellar models with physical significance. This is seen from the plots in figures 1–16.

Substituting (20) and (21) into (18) and on integration, the gravitational potential z becomes

$$\begin{aligned}&\!\!z(x)\nonumber \\&\quad = 1-\frac{x\left( j+cx\right) ^{1-n-2s}\left( ac\left( -2+n+2s\right) +B\right) }{c^{2}(-2+n+2s)(-1+n+2s)},\nonumber \\ \end{aligned}$$
(22)

where

$$\begin{aligned} B= & {} b^{m}j+c\left( d(-2+n+2s)+h(-2 \right. \\&\left. +n+2s)b^{m}\left( -1+n+2s\right) x\right) . \end{aligned}$$

We observe from (22) that \(z=1\) at the centre of the sphere \((x=0)\). This shows that our gravitational potentials are regular at the centre. The class-I space–time provides an equation that relates the gravitational potentials. If we have the gravitational potentials z(x), then we can easily obtain the second gravitational y(x) by using eq. (15).

It is now possible to generate the general Einstein–Maxwell field models using system (14) with the following metric functions and matter variables:

$$\begin{aligned}&\mathrm {e}^{\nu }=C^2, \end{aligned}$$
(23a)
$$\begin{aligned}&\mathrm {e}^{\lambda }(x)=\frac{1}{1-\frac{x\left( j+cx\right) ^{1-n-2s}\left( ac\left( -2+n+2s\right) +B\right) }{D}}, \end{aligned}$$
(23b)
$$\begin{aligned}&\rho (x)=\left( \frac{\left( j+cx\right) ^{1-n-2s}}{2D}\right) \left( \left( 6b^mj^2+6cj\right. \right. \nonumber \\&\qquad \quad \quad \times \left. \left. \left( d(-2+n+2s\right) +h(-2+n+2s)\right. \right. \nonumber \\&\qquad \quad \quad \left. \left. +b^m(n+2s)x\right) -2ac(-2+n+2s) \right. \nonumber \\&\qquad \quad \quad \times \left. \left( -3j+c(-5+2n+4s)x\right) -c^2x\left( d\right. \right. \nonumber \\&\qquad \quad \quad \times \left. \left. (-2+n+2s)(-10+4n+8s+k\right. \right. \nonumber \\&\qquad \quad \quad \times \left. \left. (-1+n+2s))+h(-2+n+2s)\right. \right. \nonumber \\&\qquad \quad \quad \times \left. \left. \left( -10+4n+8s+k(-1+n+2s)\right) \right. \right. \nonumber \\&\qquad \quad \quad \left. \left. +2b^m\left( 7+2n^2-18s+8s^2\right. \right. \right. \nonumber \\&\qquad \quad \quad +n\left. \left. \left. \left( -9+8s\right) \right) x\right) \right) , \end{aligned}$$
(23c)
$$\begin{aligned}&p_{r}(x)=\frac{(j+cx)^{-n-2s}}{2}\left( \frac{2\left( j+cx\right) }{D}\right. \nonumber \\&\qquad \quad \quad \times \left. \left( ac(-2+n+2s)+b^mj\right. \right. \nonumber \\&\qquad \quad \quad \left. \left. +c(2d(-2+n+2s)2h+(-2+n \right. \right. \nonumber \\&\qquad \quad \quad \left. \left. +2s)+\left( d+h\right) x+b^m(-1+n\right. \right. \nonumber \\&\qquad \quad \quad \left. +2s)x\right) \bigg ), \end{aligned}$$
(23d)
$$\begin{aligned}&p_{t}(x)=\frac{(j+cx)^{-n-2s}}{2}\left( -\left( d+h\right) x+\frac{2}{D}\right. \nonumber \\&\qquad \quad \quad \times \left. \left( -b^m j^2+ac(-2+n+2s)(-j\right. \right. \nonumber \\&\qquad \quad \quad \left. \left. +c(-2+n+2s)x)-cj(2d(-2\right. \right. \nonumber \\&\qquad \quad \quad \left. \left. +n+2s)+2h(-2+n+2s)\right. \right. \nonumber \\&\qquad \quad \quad \left. \left. +b^m(n+2s)x)+c^2x\left( 2d(-2+n\right. \right. \right. \nonumber \\&\qquad \quad \quad \left. \left. \left. +2s)^2b^m+(3+n^2+4n(-1+s)\right. \right. \right. \nonumber \\&\qquad \quad \quad \left. \left. \left. -8s+4s^2x)\right) \right) \right) , \end{aligned}$$
(23e)
$$\begin{aligned}&{\sigma }^2(x)=\frac{(d+h)^2k^2x^2}{4\pi }(j+cx)^{-2(1+n+2s)}\nonumber \\&\qquad \quad \quad \times (-2j+c(-2+n+2s)x)^2 \nonumber \\&\qquad \quad \quad \times \left( 1-\frac{H\left( ac\left( -2+n+2s\right) +B\right) }{D}\right) , \end{aligned}$$
(23f)

where

$$\begin{aligned} B= & {} b^{m}j+c\left( d(-2+n+2s)+h(-2 \right. \\&\left. +n+2s)b^{m}\left( -1+n+2s\right) x\right) ,\\ D= & {} c^{2}\left( -2+n+2s\right) (-1+n+2s),\\ H= & {} x\left( j+cx\right) ^{1-n-2s}. \end{aligned}$$

The structure and properties at the interior of the stellar bodies from system (23) are found to be free from singularity and well behaved. Other specific models to the Einstein–Maxwell field equations (14) can be deduced for different choices of the gravitational potentials, measure of anisotropy and the electromagnetic field on physical grounds by utilising the Karmarkar condition. This adds value to the research of dimensionality of space–time to higher pseudo-Euclidean dimensional space [2, 12, 23, 25]. Moreover, we have presented the physical analysis and acceptable behaviour of the model through graphical representation.

5 Known physical models

Particular choices for \(\Delta \) and \(E^2\) studied previously are given in the previous section. In addition, we can regain known models, which satisfy the physical requirements, with simple forms for the potential z(x) in (22). From the solution for z(x) represented in (22), we regain some charged or uncharged models found in previous research works. This is done by considering the gravitational potential z(x) in (22) for certain parameter settings. For some particular choices of \(a,\, b, \, c, \, d,\, h,\, j,\) \(\, m,\, n\,\) and s, we obtain the following models:

Model I: When \(s=1, \, a=0, \, b=2\),   \( c=1, \, j=1, \, n=1, \, h=\frac{1}{2}, d=0 \) in eq. (22), we regain the familiar anisotropic models generated by Finch and Skea [48], Hansraj and Maharaj [49] and Manjonjo et al [44] with

$$\begin{aligned} z(x)=\frac{1}{1+x}. \end{aligned}$$

Model II: If \(s=0,\, n=0\),   \( c=0, \, b=1, \, m=1, d=1 \) in eq. (22), we obtain the Schwarzchild metric [28] given by

$$\begin{aligned} z(x)=1+x. \end{aligned}$$

Model III: Plugging \(s=1,\, n=1\),   \( a=0, \, b=2c^3, \, h=\frac{1}{2}, m=1, \, j=1 \) in eq. (22), we obtain the potential used by Feroze and Siddiqui [20] given by

$$\begin{aligned} z(x)=\frac{1}{1+cx}. \end{aligned}$$

6 Physical conditions

In this section, we present a detailed physical analysis of the model generated in this work. In relativistic astrophysics, stellar models need to satisfy physical requirements. For physical acceptability, we need to find out if the exact solution satisfies important conditions including regularity, stability, equilibrium and the energy conditions. These physical conditions are necessary when generating stellar models with astrophysical significance.

6.1 Regularity

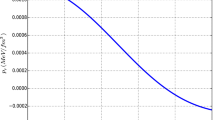
The model is finite, continuous and regular. It is free from physical and geometric singularities with non-zero values of metric functions \(\mathrm {e}^\nu |_{x=0}\) and \(\mathrm {e}^\lambda |_{x=0}=1\). This is shown in figures 1 and 2. The radial pressure, tangential pressure and energy density are also finite and they are decreasing monotonically away from centre. This behaviour is shared in the work by Moopanar and Maharaj [50], Murad [51], and Murad and Fatema [52]. The graphical representation of these matter variables are given in figures 3–5.

Fig. 1
figure 1

Potential e\(^{\nu }\) vs. radial interval r.

Full size image
Fig. 2
figure 2

Potential e\(^{\lambda }\) vs. radial interval r.

Full size image
Fig. 3
figure 3

Energy density \(\rho \) vs. radial interval r.

Full size image
Fig. 4
figure 4

Radial pressure \(p_r\) vs. radial interval r.

Full size image
Fig. 5
figure 5

Tangential pressure \(p_t\) vs. radial interval r.

Full size image
Fig. 6
figure 6

Energy conditions \(\rho -p_r \, \text {and} \,\rho -p_t\) vs. radial interval r.

Full size image
Fig. 7
figure 7

Energy conditions \(\rho -2p_t-p_r\) vs. radial interval r.

Full size image
Fig. 8
figure 8

Energy conditions \(\rho -3p_r \, \text {and} \,\rho -3p_t\) vs. radial interval r.

Full size image
Fig. 9
figure 9

Forces vs. radial interval r.

Full size image
Fig. 10
figure 10

Proper charge density \(\sigma \) vs. radial interval r.

Full size image
Fig. 11
figure 11

Stability index \(\Gamma \) vs. radial interval r.

Full size image
Fig. 12
figure 12

Speed of sound \({\mathrm {d}p_r}/{\mathrm {d}\rho }\) vs. radial interval r.

Full size image

6.2 Energy conditions

Our class of exact solution for anisotropic compact stars satisfies all energy conditions. These conditions include null energy condition (NEC), weak energy condition (WEC), strong energy condition (SEC) and dominant energy condition (DEC) which are described by the following inequalities:

$$\begin{aligned} \mathrm {NEC:}&\rho \ge 0 ,\\ \mathrm {WEC}:&\rho -p_t \ge 0, \, \rho -p_r \ge 0,\\ \mathrm {SEC}:&\rho -2p_t-p_r \ge 0, \\&\rho -3p_r\ge 0, \, \rho -3p_t\ge 0,\\ \mathrm {DEC}:&\rho -|p_t| \ge 0, \, \rho -|p_r| \ge 0. \end{aligned}$$

The plots given in figures 3, 6–8 show that our model satisfies all these inequalities throughout the stellar interior.

6.3 Equilibrium conditions

In order to examine the equilibrium condition for the charged stellar model in (23), the Tolman–Oppenheimer–Volkoff developed by Tolman [53] is used. This is given as

$$\begin{aligned} -\frac{M_G(\rho +p_r)}{r^2}\mathrm {e}^{{(\lambda -\nu )}/{2}}-\frac{\mathrm {d}p_{r}}{\mathrm {d}r}+\sigma E^2\mathrm {e}^{{\lambda }/{2}}=0, \end{aligned}$$
(24)

where \(M_{G}(r)\) is the effective gravitational mass given by

$$\begin{aligned} M_G(r) = \frac{1}{2}r^2\nu ^{\prime }\mathrm {e}^{{(\nu -\lambda )}/{2}}. \end{aligned}$$
(25)

Substituting (25) into (24) gives

$$\begin{aligned} -\frac{\nu ^{\prime }}{2}(\rho +p_r)-\frac{\mathrm {d}p_{r}}{\mathrm {d}r}+\sigma E^2\mathrm {e}^{{\lambda }/{2}} = 0 . \end{aligned}$$
(26)

From (26), we obtain gravitational, hydrostatic and electric forces that are defined by

$$\begin{aligned} F_g= & {} -\frac{{\nu }^{\prime }}{2}(\rho (r) +p_r(r)) , \end{aligned}$$
(27a)
$$\begin{aligned} F_h= & {} -\frac{\mathrm {d}p_r(r)}{\mathrm {d}r}, \end{aligned}$$
(27b)
$$\begin{aligned} F_e= & {} \sigma E^2\mathrm {e}^{{\lambda }/{2}}. \end{aligned}$$
(27c)

The equilibrium condition is satisfied if the sum of the forces in (27) are zero so that

$$\begin{aligned} F_e+F_g+F_h=0. \end{aligned}$$
(28)

On transforming \(M_G(r),\, F_e,\, F_g, \, F_h\), we obtain the following equivalent forms:

$$\begin{aligned}&m_g(x) = x^{{3}/{2}}y^{{1}/{2}}z^{{1}/{2}} \frac{\dot{y}}{y},\\&F_g =m_g(x)\frac{(\rho +p_r(x))}{x}y^{{1}/{2}}z^{{1}/{2}} ,\\&F_h =-\frac{\mathrm {d}p_r(x)}{\mathrm {d}x}, \\&F_e =\sigma E^2\mathrm {e}^{{\lambda }/{2}}\\&\qquad =\frac{z\,E^2(x\dot{E}^{2}+E^2)}{3.544\,x^{{1}/{2}}}. \end{aligned}$$

The explicit forms of these forces for this solution are then given by

$$\begin{aligned} F_g= & {} M_g(x)\frac{(\rho +p_r(x))}{x}y^{{1}/{2}}z^{{1}/{2}}, \nonumber \\ F_h= & {} -\frac{\left( j+cx\right) ^{1-n-2s}}{2}\left( -4hj+d(-4+k)j \right. \nonumber \\&\left. +hkj-4chx+chkx-chknx \right. \nonumber \\&-2ch\left. ksx+cd\left( -4-k\left( -1+n+2s\right) \right) x\right. \nonumber \\&\left. -2b^mcx^2 -2a\left( j+cx\right) \right) , \end{aligned}$$
(29a)
$$\begin{aligned} F_{e}= & {} -\frac{1}{2\sqrt{\pi }}\left( d+h\right) ^2x^{\frac{3}{2}}\left( j+cx\right) ^{-1-2n-4s} \nonumber \\&\quad \times k^2\left( -2j+c\left( -2+n+2s\right) x\right) \left( 1-\frac{H}{D} \right. \nonumber \\&\quad \times \left. (ac(-2+n+2s)+b^mj+c\left( d(-2 \right. \right. \nonumber \\&\quad \left. \left. +n+2s)+h(-2+n+2s)b^m(-1\right. \right. \nonumber \\&\quad \left. +n+2s)x\right) )\bigg ), \end{aligned}$$
(29b)

where

$$\begin{aligned} D= & {} c^{2}\left( -2+n+2s\right) (-1+n+2s),\\ H= & {} x\left( j+cx\right) ^{1-n-2s}. \end{aligned}$$

The behaviour of these forces is illustrated in figure 9.

6.4 Stability through adiabatic index

It is possible to analyse the stability of relativistic stars for the generated solutions. This is done by using the adiabatic index \((\Gamma )\), which is required to be \(\Gamma >\frac{4}{3}\). Singh et al [30] and Matondo et al [54] described that the adiabatic index is given by the condition

$$\begin{aligned} \Gamma =\left( \frac{\rho +p_{r}}{p_{r}}\,\frac{\mathrm {d}p_r}{\mathrm {d}\rho } \right) . \end{aligned}$$
(30)

We note from figure 11 that the adiabatic index is greater than the required lower limit.

6.5 Mass–radius relation

In class-I space–time, the mass to radius relation for a charged compact star is given by

$$\begin{aligned} m(x)= & {} \frac{k}{2}\int _{0}^{x}(\rho (y)+E^2)y^{{1}/{2}}\mathrm {d}y \nonumber \\= & {} \left( \frac{12.56\,x^{{3}/{2}}\left( j+cx\right) ^{-n-2s}\left( 1+\frac{cx}{j}\right) ^{n+2s}}{105c^{2}\left( -2+n+2s\right) (-1+n+2s)}\right) \nonumber \\&\times \left( -35\left( c^2(d+h)k\left( 2+n^2-6s+4s^2 \right. \right. \right. \nonumber \\&+n\left. \left. \left. (-3+4s)\right) +3c(a+2(d+h))(2+n \right. \right. \nonumber \\&\!\left. \left. +2s)j+3b^mj^2(1-10.843x)+3cx\left( 7\left( ac\right. \right. \right. \right. \nonumber \\&\!\left. \left. \left. \left. \left. \times (10-9n+2n+2n^2-18s+8ns+8s^2\right) \right. \right. \right. \right. \nonumber \\&\!\!\left. \left. \left. \left. +bc\left( 2+n^2-6s+4s^2+n+(-3+4s)\right) \right. \right. \right. \right. \nonumber \\&\!\!\left. \left. \left. \left. +c(-2+n+2s)(2d(-5+2n+4s))\right. \right. \right. \right. \nonumber \\&\,+h(\left. \left. \left. \left. \!\!-11+5n+10s)-3b^m(n+2s)\,\right. \right. \right. \right. \nonumber \\&\left. \left. \left. \left. \times \! j(1\!-\!12.9088x\!+\!5b^mc\left( 7\!+\!2n^2\!-\!18s\!+\!8s^2\right. \right. \right. \right. \right. \nonumber \\&\!\!\left. \left. \left. \left. \left. +n(-9+8s)(1-14.0562x)\right) \right) \right) \right) \right) . \end{aligned}$$
(31)

The model shows that the mass function obtained above is acceptable. The nature of variation of the above expression for mass can be easily observed in figure 13.

Fig. 13
figure 13

Mass vs. radial interval r.

Full size image
Fig. 14
figure 14

Compactness \(\mu \) vs. radial interval r.

Full size image

6.6 Matching condition

To develop the anisotropic models for class-I space–time in general relativity, it is important to note that at the boundary \(r=R\) of the relativistic star, the interior and exterior line elements are matched smoothly. Matching also gives the mass–radius relation at the surface of the relativistic star. For matching, we equate eqs (1) and (2) as

$$\begin{aligned} \mathrm {e}^{\lambda }= & {} \left( 1-\frac{2m}{r}+\frac{Q^2}{r^2}\right) ^{-1}, \end{aligned}$$
(32a)
$$\begin{aligned} \mathrm {e}^{\nu }= & {} \left( 1-\frac{2m}{r}+\frac{Q^2}{r^2}\right) . \end{aligned}$$
(32b)

In addition, the radial pressure must vanish at the boundary. This is clearly seen from figure 4. Using eqs (16), (21), (22) and (31) the matching in (32) becomes

$$\begin{aligned} 0= & {} \left( \frac{25.12\,x^{{3}/{2}}\left( j+cx\right) ^{-n-2s}\left( 1+\frac{cx}{j}\right) ^{n+2s}}{105R}\right) \nonumber \\&\times \left( -35\left( c^2(d+h)k\left( 2+n^2-6s+4s^2 \right. \right. \right. \nonumber \\&+n\!\!\left. \left. \left. (-3+4s)\right) +3c(a+2(d+h))(2+n \right. \right. \nonumber \\&\!\left. \left. +2s)j+3b^mj^2(1-10.843x)+3cx\left( 7\left( ac\right. \right. \right. \right. \nonumber \\&\!\!\left. \left. \left. \left. \times \left( 10 -9n+2n+2n^2-18s+8ns+8s^2\right) \right. \right. \right. \right. \nonumber \\&\!\!\left. \left. \left. \left. +bc\left( 2+n^2-6s+4s^2+n+(-3+4s)\right) \right. \right. \right. \right. \nonumber \\&\!\!\left. \left. \left. \left. +c(-2+n+2s)(2d(-5+2n+4s))\right. \right. \right. \right. \nonumber \\&+h\left. \left. \left. \left. (-11+5n+10s)-3b^m(n+2s)\,\right. \right. \right. \right. \nonumber \\&\times j(1 - 12.9088x+5b^mc\left( 7+2n^2-18s+8s^2\right. \nonumber \\&\!\!\!\left. \left. \left. \left. \left. +n(-9+8s)(1-14.0562x)\right) \right) \right) \right) \right) \nonumber \\&\times (ac(-2+n+2s)+B)+x(j+cx)^{(1-n-2s)} \nonumber \\&+R^2\frac{k(d+h)x}{(j+cx)^{n+2s}} \end{aligned}$$
(33a)
$$\begin{aligned} 0= & {} \left( \frac{25.12\,x^{{3}/{2}}\left( j+cx\right) ^{-n-2s}\left( 1+\frac{cx}{j}\right) ^{n+2s}}{105Rc^{2}\left( -2+n+2s\right) (-1+n+2s)}\right) \nonumber \\&\times \left( -35\left( c^2(d+h)k\left( 2+n^2-6s+4s^2 \right. \right. \right. \nonumber \\&\left. \left. \left. +n(-3+4s)\right) +3c(a+2(d+h))(2+n \right. \right. \nonumber \\&\left. \left. +2s)j+3b^mj^2(1-10.843x)+3cx\left( 7\left( ac\right. \right. \right. \right. \nonumber \\&\left. \left. \left. \left. \times \left( 10 -9n+2n+2n^2-18s+8ns+8s^2\right) \right. \right. \right. \right. \nonumber \\&\left. \left. \left. \left. +bc\left( 2+n^2-6s+4s^2+n+(-3+4s)\right) \right. \right. \right. \right. \nonumber \\&\left. \left. \left. \left. +c(-2+n+2s)(2d(-5+2n+4s))\right. \right. \right. \right. \nonumber \\&\left. \left. \left. \left. +h(-11+5n+10s)-3b^m(n+2s) \right. \right. \right. \right. \nonumber \\&\left. \left. \left. \left. \times j(1\!-\!\,12.9088x+5b^mc\left( 7+2n^2-18s+8s^2\right. \right. \right. \right. \right. \nonumber \\&\left. \left. \left. \left. \left. +n(-9+8s)(1-14.0562x)\right) \right) \right) \right) \right) -1\nonumber \\&-\left( C^2+R^2\right) \frac{k(d+h)x}{(j+cx)^{n+2s}}\end{aligned}$$
(33b)
$$\begin{aligned} 0= & {} p_r{(r=R)}. \end{aligned}$$
(33c)
Fig. 15
figure 15

Charge \(E^2\) vs. radial interval r.

Full size image

System (33) represents the matching condition with \(a,\, b,\, c,\, d,\, h,\, j,\, m,\, n\,\) and s being real constants. We also find that the number of free parameters are sufficient to satisfy condition given in system (33).

Fig. 16
figure 16

Measure of anisotropy \(\Delta \) vs. radial interval r.

Full size image

7 Discussion

In the present work, we have used transformations first adopted by Durgapal and Bannerji [39] to transform the Einstein–Maxwell equations. The embedding approach has been used to provide an equation relating the gravitational potentials z(x) and y(x). We have chosen the anisotropic factor and electric field to generate the anisotropic charged solution. The generated solution shows that the gravitational potentials e\(^\nu \) and e\(^\lambda \) are free from geometrical singularities, finite and well behaved. This is clearly seen in figures 1 and 2. The radial pressure, tangential pressure and energy density are monotonically decreasing away from the centre of the relativistic star. This is observed in figures 3–5. In this study, we have generalised the models of interior Schwarzchild metrics [28], Manjonjo et al [40] and Finch and Skea [48]. Moreover, the investigations by Feroze and Siddiqui [20], and Hansraj and Maharaj [49] are also derived from our model. System (23) represents a new class of static spherically symmetric stellar models for charged stars.

We have analysed the model by investigating the behaviour of the matter variables graphically. This was done by using the Python programming language with the particular choices of the real constants: \(s=1, \, m=2, \, h=2.4, \, a=2, \, b=1, \, c=3, \, d=-3, \, \, n=1, \, j=0.166, \, k=2 \). It is clearly seen from figures 3–5 that the matter variables \( \,\rho , \, p_r\, \text {and} \; p_t \) are positive, monotonically decreasing and finite everywhere in the interior of the star. The weak energy condition, strong energy condition, dominant energy condition and null energy condition are simultaneously satisfied by our solution as shown in figures 3, 6–8. We also observe that the sum of the forces (electric force, hydrostatic force and gravitational force) introduced from the TOV equation is zero. This indicates that the model is in an equilibrium state as shown in figure 9. In figure 10, the profile of the proper charge density is non-singular at the origin and it is also monotonically increasing.

We have also analysed the stability of the model by using the variation of the adiabatic index. The behaviour of the adiabatic index is shown in figure 11. This value is greater than the required lower limit, \(\Gamma >\frac{4}{3}\). We observe in figure 12 that the speed of sound is monotonically decreasing and less than the speed of light [55]. From figures 13 and 14, it is observed that the mass and compactness of the model are monotonically increasing from the centre to the surface. The electromagnetic field in eq. (21) guarantees that charged spheres also have the property of physically reasonable uncharged models as addressed in studies by Maharaj and Leach [56], and John and Maharaj [57]. It is important to note that there are anisotropic models in which the charge may initially increase near the centre and decrease away from the centre. In this case, figure 15 displays the magnitude of the charge showing that the charge profile monotonically increases and then decreases. This structure of electric field is acceptable and can be observed in the models by Maharaj et al [45, 58]. The measure of anisotropy as shown in figure 16 obeys the properties of the stellar model which is shared by Maharaj et al [58] and Sunzu et al [59].

Our analysis shows that embedding of class-I space–time can be utilised to generate Einstein–Maxwell exact solutions. This research work gives a broader understanding on the study of compact objects. For further investigations, one can make other choices of gravitational potentials, measure of anisotropy and electromagnetic field to develop new models. Our approach has the advantage of regaining a number of physical models found in the past as illustrated in §5.